Structural and Functional Consequences of Phosphate–Arsenate Substitutions in Selected Nucleotides: DNA, RNA, and ATP

Abstract

A recent finding of a bacterial strain (GFAJ-1) that can rely on arsenic instead of phosphorus raised the questions of if and how arsenate can replace phosphate in biomolecules that are essential to sustain cell life. Apart from questions related to chemical stability, there are those of the structural and functional consequences of phosphate-arsenate substitutions in vital nucleotides in GFAJ1-like cells. In this study we selected three types of molecules (ATP/ADP as energy source and replication regulation; DNA–protein complexes for DNA replication and transcription initiation; and a tRNA–protein complex and ribosome for protein synthesis) to computationally probe if arsenate nucleotides can retain the structural and functional features of phosphate nucleotides. Hydrolysis of adenosine triarsenate provides 2–3 kcal/mol less energy than ATP hydrolysis. Arsenate DNA/RNA interacts with proteins slightly less strongly than phosphate DNA/RNA, mainly due to the weaker electrostatic interactions of arsenate. We observed that the weaker arsenate RNA–protein interactions may hamper rRNA assembly into a functional ribosome. We further compared the experimental EXAFS spectra of the arsenic bacteria with theoretical EXAFS spectra for arsenate DNA and rRNA. Our results demonstrate that while it is possible that dried GFAJ-1 cells contain linear arsenate DNA, the arsenate 70S ribosome does not contribute to the main arsenate depository in the GFAJ-1 cell. Our study indicates that evolution has optimized the inter-relationship between proteins and DNA/RNA, which requires overall changes at the molecular and systems biology levels when replacing phosphate by arsenate.

Introduction

The question of why nature chose phosphate for life on earth has been around for many years.¹ Phosphate diesters are especially adapted to link two nucleotides and still ionize, helping to stabilize the DNA and RNA for carrying and processing genetic information. Arsenic acid, which is the most closely related to phosphoric acid, was thought to be unsuitable because of the fast hydrolysis of arsenic esters.¹ However, arsenate can be incorporated into nucleotides, and adenosine–diphoshate arsenate (ADP–arsenate) can be synthesized by beef heart submitochondrial particles.² Furthermore, a recent finding of a bacterial strain (GFAJ-1) that can rely on arsenic instead of phosphorus raised the questions of if and how arsenate can replace phosphate in biomolecules that are essential to sustain cell life.³ The possibility of arsenate-based cellular life has been questioned, mostly in the form of comments⁴⁻⁷ and a literature review.^8,9 While the GFAJ-1 strain observations await further experimental validation, computational approaches can be effective tools to address scientific questions related to the arsenate–phosphate substitution in bacterial life.¹⁰

Assuming that arsenate can replace phosphate in vital nucleotides, we computationally probe if arsenate nucleotides can retain the structural and functional features of phosphate nucleotides. In order to have a broad representation of the molecular systems in the cell and to ensure biological relevance rather than particular protein/DNA/RNA sequences of the GFAJ-1 cell, the simulated systems are selected based on essential biological functions. We combine quantum mechanical, molecular mechanical and molecular dynamics simulations to investigate arsenate–phosphate replacement in three selected types of molecules (ATP/ADP as energy source and replication regulation; DNA–protein complexes for DNA replication and transcription initiation; a tRNA–protein complex and ribosome for protein synthesis).

The hydrolysis of ATP/ADP as the energy source is coupled to most enzymatic reactions in life, and is involved in processes such as regulation of DNA replication.¹¹ We studied the ATP hydrolysis and ADP–DnaA interactions. We investigated three bacterial DNA–protein complexes which are essential for DNA replication and transcription. The first is the factor for inversion stimulation (Fis)–DNA complex. Fis regulates transcription, replication, and recombination.¹² Fis selects targets mainly through indirect recognition involving DNA bending, using the minor groove shape and the sequence-dependent conformational change over adjacent major groove surfaces.¹³ The Fis–DNA complex provides a test whether the combination of geometry and sequence specificity still allow an arsenate backbone. The second factor is the integration host factor (IHF), which functions in nucleoid structuring, chromosome replication and DNA rearrangements, and transcription regulation¹² in many prokaryotic processes.¹⁴ IHF contacts the DNA exclusively via the phosphodiester backbone in the minor groove, introducing a U-turn into the DNA. Thus, the IHF–DNA complex provides a comparison of phosphodiester versus arsenatediester backbones in DNA recognition. The third complex is the F plasmid Rep protein (RepE) dimer in complex with the repE operator DNA. RepE is essential for stringent regulation of the plasmid copy number in Esherichia coli.¹⁵ In the RepE–DNA complex, the two DNA binding sites are separated by 100 Å). Thus, RepE–DNA provides a test for cumulative structural changes due to As–P replacement in DNA. To investigate a possible phosphate-arsenate substitution in tRNA, we selected the bacterial tRNA lysidine synthetase complex (TilS), which ensures translational fidelity¹⁶. We also compared the conformations and the energy landscape of a “normal” phosphate ribosome with a potential arsenate ribosome. We used the crystal structure of the Thermus thermophilius 70S ribosome bound to RF2¹⁷ as the starting conformation. In this translation termination state, a step just before ribosome recycling, the interactions between 30S and 50S could be sensitive to energy perturbation. Finally, we compared the experimentally observed EXAFS spectra with the theoretical EXAFS spectra for the arsenate DNA and RNA.

In this study, the density functional theory was used to calculate the free energy change of the hydrolysis of adenosine phosphates and adenosine arsenates. Molecular mechanical force fields for the arsenates systems were parametrized using intensive density functional calculations, and then molecular dynamics simulations were employed to investigate the structural and energy changes due to phosphate-arsenate replacement in the selected molecular complexes. Earlier quantum mechanical calculations indicated that arsenate DNA and phosphate DNA may have similar conformational properties.^18,19 Consistently, our work confirms that partial replacement of phosphate by arsenate in DNA can retain certain structural and functional properties; however, this is unlikely to hold for the ribosome. Our study also indicates a perfect match between proteins and phosphate in terms of structure and interaction energy, which are superior to those between proteins and arsenate.

Experimental Methods

1. Quantum Mechanical Calculations

The theoretical free energy changes of hydrolysis of adenosine triarsenate (ATAs) and adenosine diarsenate (ADAs) were based on QM calculations with large basis set (6-311++G**) and include solvation effects. The full geometry optimizations and harmonic vibrational frequency calculations were performed at the B3LYP/6-311++G** level of theory. Vibrational energy corrections and entropies were used to calculate the free energy change of the hydrolysis reactions. Implicit solvent effects with water as the solvent were also considered by the polarizable continuum model (PCM) using the continuous surface charge formalism.²⁰

Gaussian09,²¹ density functional theory at the B3LYP/6-311++G** level was used to calculate the energy change of ATAs hydrolysis. B3LYP/6-31+G* level of theory was used to add arsenate nucleotides into CHARMM27 force field,^22,23 due to the arsenate–phosphate replacement.

2. Force field modification

The parametrization of all-atom empirical force field for arsenate nucleic acids were based on modification of the current CHARMM27 force field for phosphate nucleic acids.²³ All parameters affected by arsenate–phosphate replacement were recalibrated to quantum mechanical calculations of the model compounds listed in Supporting Information, Sup-Figure 1. The corresponding phosphate compounds in the Supporting Information, Sup-Figure 1, were used in the original CHARMM27 force field parametrization. The full geometry optimizations, harmonic vibrational frequency calculations, and potential energy surface for torsion angles were performed at the B3LYP/6-31+G* level of theory using the Gaussian09 program.²¹ Bond lengths and angles related to As atom were fitted to average values obtained from the model compounds. The force constants were fitted to the harmonic vibrational frequency of dimethyl arsenate (Supporting Information, Sup-Figure 1A). Atomic charges were based on NBO calculations at the B3LYP/6-31+G* level, adjusted by fitting the potential energy curve of H₂O---(CH₃)₂AsO₄^– interactions (Supporting Information, Sup-Figure 2). It can be seen that the potential energy curves for the arsenate and phosphate are almost identical, with arsenate shifted to a slightly longer r₀ distance, due to the large vdw radius of the arsenic atom. The partial charges of As, O=As, and O–As were 1.58, −0.59, and −0.8, very closed to that of the related phosphate charges (1.50, −0.57, −0.78). Similarly, the force fields for adenosine triarsenate (ATAs) and adenosine diarsenate (ADAs) were also parametrized. Sup-Figure 3, Supporting Information, compares the vibrational frequencies obtained by density functional theory calculations and our optimized arsenate force field calculations for the ATAs. Supporting Information Table 1 compares selected force field parameters for arsenate and phosphate compounds. Besides the longer As–O bond, the optimized arsenate parameters are very similar to phosphate nucleotides used in the CHARMM force field.²³

3. Molecular Dynamics Simulations

MD simulations were performed using the NAMD package²⁴ and the CHARMM 27 force field,^22,23 with constant pressure ensembles (NPT) at 1 atm and the temperature at 300 K°. The time step was 2 fs with a SHAKE constraint on all bonds with hydrogen atoms.²⁵ Productive MD runs were performed after 5000 steps of minimizations and three 150 ps heating and equilibration runs. Long-range electrostatic interactions were calculated with the particle mesh Ewald method.²⁶

The starting conformations of the pure DNA/RNA and protein–nucleic acid complexes were based on X-ray crystal structures of the phosphate system. The corresponding arsenate complexes were obtained by replacing phosphorus atoms. The ADP–DnaA is the Aquifex aeolicus ADP–DnaA protein complex (PDB code: 1L8Q).²⁷ The PDB codes for Fis–DNA,¹³ IHF–DNA,¹⁴ and RepE–DNA¹⁵ complexes are 3IV5, 1IHF, and 2Z9O, respectively. The tRNA–protein complex is the Bacillus subtilis tRNA in complex with Geobacillus kaustophilus lysidine synthetase¹⁶ (PDB 3A2K). Ribosome crystal structures are taken from the Thermus thermophilus 70S ribosome bound to release factor 2 (PDB codes, 2X9R and 2X9S).¹⁷

The simulated molecules were solvated in a TIP3P water^28,29 box with a margin of at least 15 Å from any edge of the water box. Sodium ions were added to make the overall system neutral. Magnesium, potassium and chloride ions were also added to the simulated system to obtain different ionic conditions. Pure DNA system (7BNA) was neutralized with 22 sodium ions. In the simulation of the tRNA–TilS complex, three ionic concentrations were tested. For low ionic conditions, 33 sodium, 20 magnesium, and 5 chloride ions are added (0.035, 0.021, and 0.005 M, respectively). For the high ionic concentration, the effective ion concentration is around 0.2 M (with 167 sodium, 20 magnesium, 20 potassium, and 160 chloride ions). The system with protonated histidines is similar to the low ionic concentration setup, with 17 sodium, 20 magnesium, and 6 chloride ions. The high ionic concentration (0.25 M) was used for pure tRNA simulations.

For the ribosomal systems, in addition to the existing magnesium ions in the crystal structure, we also added 400 magnesium ions, 2397 sodium ions, and 400 chloride ions to neutralize the overall charges in ribosome. 497327 water molecules are added to solvate the ribosome complex. Before the production run, we have pre-equilibrated the systems with Mg and other ions in the solution. The ribosomes were fixed and only water and ions were allowed to move in the MD simulations for the first 4 ns, which were not included in the productive simulations. The ions were added to the water box randomly for the protein–DNA complex. For the tRNA–protein complex and the ribosome, we used the program Ionize (Theoretical and Computational Biophysics Group, University of Illinois at Urbana–Champaign, http://www.ks.uiuc.edu/Development/MDTools/ionize/license.html) to place magnesium and sodium ions around the negatively charge regions in the RNA.

4. MD Trajectory Analysis

Following the MD simulations, the trajectories were analyzed using the Charmm program.^22,30 The interaction energies were calculated using the Charmm 27 force field.²² Two approximations were used to consider the solvation effect. First, we calculate the buried surface areas for two interacting partners, with a surface tension coefficient of 0.015 kcal/(mol·A²), as recommended by Haberthuer and Caflish.³¹ Second, we include the ions within the first solvation shell (5 Å) of solute in the interaction energy calculation, to consider the ionic shielding effect in the electrostatic interactions. The inclusion of ions in the interaction energy may provide better interaction energies for highly charged nucleotides, especially for the tRNA and ribosome systems.

The normalized correlation matrix was obtained by computing the covariances of the spatial atom displacements of 60 ns MD trajectories for selected pairs of atoms:

1

2

We use P or As atom in the DNA (or RNA) backbone to represent the motions in DNA (or RNA). The Cα carbons were used to represent protein structure. After we obtain the normalized correlation matrix, we compare phosphate and arsenate complexes to obtain the linear correlation between each correlation matrix element.

The rmsd analysis of dynamic trajectories was obtained using starting crystal structures as reference.

5. Theoretical EXAFS Spectra Simulation

Theoretical As K-edge (11867 eV) EXAFS spectra for the arsenate DNA and RNA were simulated with IFEFFIT algorithms in FEFF8, using the graphical utility ARTEMIS.³² All non-hydrogen atoms within an 8 Å distance from As atoms were extracted from the DNA or RNA complexes. The average spectra were obtained by averaging all simulations with As atoms in the DNA system (linear 7bna dodecamer, Fis–DNA, IHF–DNA, and RepE–DNA). The spectra for the ribosome were averaged from 60 arsenic positions in the 30S and 60 arsenic positions in the 50S subunits. Separate averages using only 60 arsenic positions in 30S or only 60 arsenic positions in 50S subunits converged, indicating that the sampling is representative of the ribosome structures.

Results

1. Force Field Modification and Simulation of Arsenate DNA and Arsenate RNA

Our quantum mechanical calculations reveal the As=O bond length is 1.653 Å and As–O is 1.823 Å; thus, the average bond lengths of As=O and As–O is 1.74 Å, which is very close to 1.73 Å, obtained from fitting of EXAHS spectra.³³ As can be seen in Sup-Figure 4, Supporting Information, the vibrational frequencies obtained by density functional theory calculations and our optimized arsenate force field calculations agree very well, indicating a good fit of the force constants. In molecular mechanics calculations, molecular vibrational frequencies are mostly dominated by force constants of bond stretch and bending, and the low frequency vibrational modes are usually mixed with bending and torsional motions of chemical bonds. The fitting of the potential energy surfaces for the torsion angles of compounds A, B, C, and D (see Sup-Figure 1,Supporting Information) are reported in Sup-Figure 5, Supporting Information. In the model compound torsion scans, only the specific torsion angle is fixed, and all other coordinates have no constraints. In the force field parametrization, it is essential to fit the intrinsic molecular mechanics surface to the quantum mechanical surface, and keep the location of the molecular mechanics global minimum for a particular dihedral at the same point as the molecular mechanics global minimum. As can be seen in Sup-Figure 5, Supporting Information, the majority of the molecular mechanics curves overlap the quantum mechanical surface, including the ϵ and ζ which are important for RNA structures. The deviations of two torsional angles, O–C4′–C–O and O–As–O–C3′, are also by less than 0.5 kcal/mol, which is within the range of the accuracy of quantum mechanical calculations. Often, different levels of quantum mechanical calculations and optimized torsion profiles for nucleic acids force field could deviate by more than 0.5 kcal/mol.³⁴ Recently, the CHARMM 27 force field has been improved leading to the CHARMM36 force field^35,36 which has a better treatment of nucleic acids. In this study, we only modified the force field parameters related to phosphate-arsenate substitution; all other parameters are still CHARMM 27.

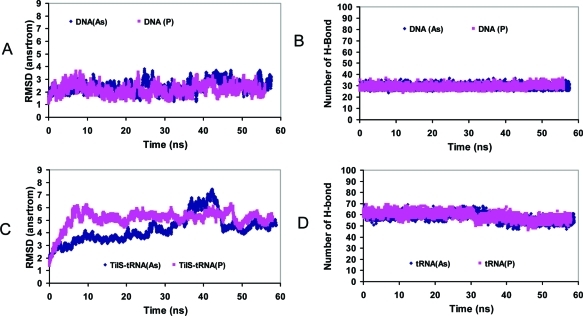
First, we compare pure DNA and RNA with phosphate and arsenate backbones. For DNA, we selected a linear B–DNA dodecamer (the 7bna dodecamer), which Wolfe-Simon et al. used as the representative DNA structure to compare with the observed EXAFS spectra.³ For RNA, we simulated a pure tRNA, which forms the tRNA lysidine synthetase complex (TilS).¹⁶ As can be seen in Figure 1, both phosphate and arsenate DNA are very stable during the 60 ns simulations, with the arsenate DNA being slightly more flexible than the phosphate DNA (Figure 1A). Both phosphate and arsenate DNA are able to keep all Watson–Crick base pairs (Figure 1B). In the tRNA simulations, both phosphate and arsenate tRNAs have larger rmsd fluctuations than DNA (Figure 1C), which is a typical behavior for tRNA molecule in solution.^37,38 Watson–Crick base pairs are also very stable for both phosphate and arsenate tRNA, and only a few opened during simulation (Figure 1D). Overall, our simulations of two DNA and RNA systems indicated that the arsenate DNA and RNA could have similar conformations and the ability to keep the Watson–Crick base pairs, consistent with recent quantum mechanical studies.^18,19

Figure 1.

Pure DNA and RNA with phosphate and arsenate backbones could have similar conformations and the ability to retain the Watson–Crick base pairs. (A) Rmsd of phosphate and arsenate DNA (PBD 7bna). (B) Trajectory of the number of hydrogen bonds between Watson–Crick base pairs in the DNA. (C) Rmsd of phosphate and arsenate tRNAs. (D) Trajectory of the number of hydrogen bonds between Watson–Crick base pairs in the tRNA (PDB 3A2K, chain C).

2. Hydrolysis of Adenosine Triarsenate and Diarsenate in Regulation of DNA Replication

Can ATAs or adenosine diphoshate arsenate (ADP–As)² in the GFAJ1 cell provide energy comparable to that of ATP? To compare the hydrolysis energies of ATP and its arsenate analogues, we calculated the theoretical free energy changes for five reactions (Table 1). Hydrolysis of ATAs releases less energy than ATP. The free energy change obtained for hydrolysis of ADP–As to ADP and As (reaction 2) was calculated to be −3.0 kcal/mol, while hydrolysis of ATAs into adenosine diarsenate (ADAs) gives −2.2 kcal/mol. Hydrolysis of ATAs into adenosine monoarsenate (AMAs) can yield a larger free energy change (−8.1 kcal/mol). The calculated free energy changes for the hydrolysis of ATP are −4.9 kcal/mol (reaction 1) and −11.5 kcal/mol (reaction 4). Thus, GFAJ1 cells may use ATAs to provide energy comparable to ATP.

Table 1. Thermodynamics of Hydrolysis of Adenosine Triphosphate and Adenosine Triarsenate Obtained by Quantum Mechanical Calculation at the B3LYP/6-311++G** Level of Theory^a.

	reaction	ΔH(kcal/mol)	ΔG(kcal/mol)	experiment46(kcal/mol)
1	ATP + H2O → ADP + H2PO4–	–3.32	–4.86	–7.3
2	ADP–As + H2O → ADP + H2AsO4–	–2.06	–3.01
3	ATAs + H2O → ADAs + H2AsO4–	–1.85	–2.23
4	ATP + H2O → AMP + H2P2O72-	–11.44	–11.52	–10.9
5	ATAs + H2O → AMAs + H2As2O72-	–9.7	–8.14

^aATP: adenosine triphosphate. ADP: adenosine diphosphate. ADP–AS: adenosine diphosphate arsenate. ATAs: adenosine triarsenate. ADAs: adenosine diarsenate. AMP: adenosine monophosphate. AMAs, adenosine monoarsenate.

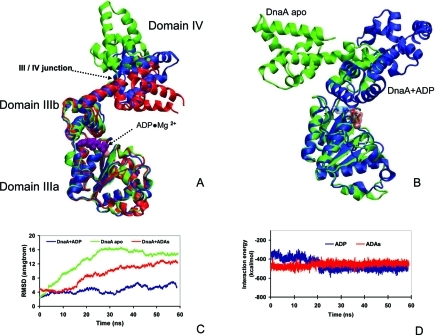
The product of ATP hydrolysis can be used to regulate the initiation of DNA replication, which is a key event in the cell cycle of all organisms. In bacteria, replication initiation occurs at the oriC region which is recognized by the ATP–DnaA and ADP–DnaA complexes. The ATP–DnaA hydrolysis to ADP–DnaA provides energy, and the ADP–DnaA is a large component of the initiation complex at the oriC. Following replication initiation, ATP–DnaA reforms to reinitiate a DNA replication cycle.^11,39 Thus, the ADP–DnaA interaction should be sufficiently strong for DnaA oligomerization; yet, it should also be sufficiently weak to allow ADP replacement by ATP. We used molecular dynamics (MD) simulations to test if ADAs in complex with DnaA can regulate DNA replication similar to ADP. ADP binds DnaA in a pocket between domains IIIa and IIIb (Figure 2A). Without ADP, the domains separate, resulting in misorientation of domains IIIb and IV with respect to IIIa (Figure 2B). When we replaced ADP by ADAs, the interaction between domains IIIa and IIIb in the ADAs–DnaA complex still appeared relatively stable; however, domain IV became more flexible than in the ADP–DnaA complex (Figures 2A and 2C). The interaction between ADAs and DnaA is weaker than in ADP–DnaA (Figure 2D), indicating that it is easier to replace ADAs than ADP during the reinitiation of DNA replication.

Figure 2.

ATP–DnaA hydrolysis to ADP–DnaA provides energy, and ADP–DnaA is a large component of the initiation complex at the oriC region in bacterial replication initiation. ADP binds DnaA in a pocket between domains IIIa and IIIb. MD simulations indicated that adenosine diarsenate (ADAs) may still regulate DnaA conformation change. (A) The crystal structures of the ADP–DnaA complex is represented by red ribbons (PDB code: 1L8Q); the snapshot from simulations of ADP–DnaA is depicted by blue ribbons, and the snapshot from simulations of the ADAs–DnaA complex is in green. (B) Superimposition of the snapshot from the simulations of ADP–DnaA (blue ribbon) and the apo form DnaA (green ribbon). (C) RMSDs along the trajectories with respect to the crystal structure of ADP–DnaA from the three simulations. (D) ADAs interacts with DnaA less strongly than ADP with DnaA.

3. Arsenate DNA–Protein Interactions in Replication and Transcription Initiation

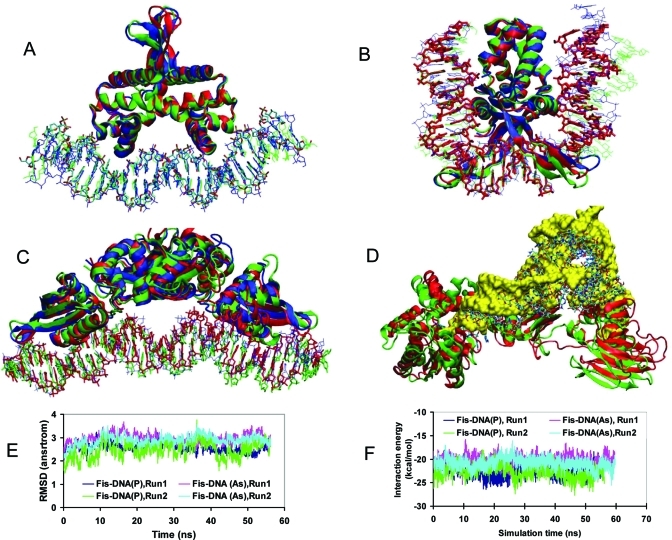
We then investigated selected arsenate DNA–protein complexes using molecular dynamics simulations. Fis–DNA complexes in both phosphate/arsenate forms are stable during the simulations (Figure 3, parts A and E), deviating little from the initial structure. The RMSDs of the MD relaxed snapshots at 50 ns of the arsenate and phosphate DNA-Fis complexes are ∼2.9 Å from the crystal structure (Figures 3A and 3E, Table 2). If we only focus on DNA dynamics, the covariance matrices for phosphate and arsenate DNA are correlated with R² = 0.74 (Sup-Figure 6A, Supporting Information). The IHF–DNA complex presents a large difference between phosphate and arsenate DNA (Figure 3B). While both IHF α and β subunits maintain their interaction with the U-shaped phosphate DNA, the β subunit interacts more weakly with arsenate DNA (green structures, Figure 3B). However, the overall RMSDs for both phosphate and arsenate IHF–DNA complexes are similar (Sup-Figure 7A, Supporting Information, Table 2). The structural deviations of RepE–DNA (Figure 3C) are also larger than those of Fis–DNA, with rmsd of ∼3 Å for phosphate DNA and 4 Å for arsenate DNA (Sup-Figure 7B, Supporting Information, Table 2).

Figure 3.

Arsenic DNA (DNA(As))-protein complexes are more stable than arsenic RNA (RNA(As))–protein complexes. In the figure, the crystal structures of phosphate DNA–protein complexes are represented by red lines (DNA) and ribbons (proteins); snapshots from simulations of phosphate DNA (DNA(P))–protein complexes are correspondingly in blue; snapshots from simulations of the arsenate DNA/RNA–protein complexes are in green. (A) The DNA(As)–Fis protein (green) complex does not deviate significantly from the DNA(P)–protein complexes. (B) Weaker arsenate DNA(As)–IHF protein (green) interaction leads to larger DNA structural fluctuations. (C) The RepE protein is able to accommodate the cumulative DNA structural changes introduced by arsenate–phosphate replacement in a 37 bp DNA fragment, with the two ends separated by 100 Å. (D) The tRNA(As)-TilS complex deviates extensively from the phosphate crystal structure. TilS crystallized with tRNA(P) is represented by red ribbon; green ribbon represents TilS complexed with tRNA(As). tRNA(P) is represented by sticks, while tRNA(As) is shown as yellow surface to highlight the large differences between phosphate and arsenate tRNA–TilS complexes. (E) Two independent simulations for Fis–DNA complex indicate that arsenate DNA protein complex is slightly more flexible than phosphate DNA protein complex. (F) Arsenate DNA interacts less strongly with protein than phosphate DNA protein complex in two simulations of Fis–DNA complex.

Table 2. Interaction Energy and Solvation of DNA and RNA for the Phosphate and Arsenate Systems^a.

	average rmsd (Å)b		interaction energyc (kcal/mol, per nucleotide)		number of water molecules per nucleotide		cations in first solvation shell
	phosphate	arsenate	phosphate	arsenate	phosphate	arsenate	phosphate	arsenate
Fis–DNA, run1	2.59 (2.29)	2.95 (2.75)	–22.3 ± 1.1(−22.1 ± 1.1)	–20.1 ± 1.0(−20.1 ± 1.0)	4.8	5.3	16.5	18.2
Fis–DNA, run2	2.89 (2.48)	2.95 (3.09)	–22.9 ± 1.2(−23.5 ± 1.2)	–21.1 ± 1.1(−21.5 ± 1.1)	4.9	5.3	17.9	18.9
RepE–DNA	3.31 (2.96)	3.87 (3.78)	–25.3 ± 1.7(−24.9 ± 1.1)	–19.7 ± 1.0(−20.3 ± 0.9)	4.9	5.5	22.5	23.5
IHF–DNA	3.32 (3.82)	3.30 (3.76)	–31.2 ± 1.3(−31.0 ± 1.2)	–30.7 ± 1.3(−30.6 ± 1.6)	4.1	4.6	19.8	23.1
TilS–tRNA, Hsp	3.66 (2.78)	4.55 (3.42)	–32.6 ± 0.9(−32.9 ± 0.9)	–28.5 ± 1.7(−27.9 ± 1.4)	4.2	5.3	20.4	22.2
TilS–tRNA, high	5.03 (4.66)	5.55 (3.45)	–32.8 ± 1.2(−33.2 ± 1.2)	–28.3 ± 0.9(−28.3 ± 0.9)	4.1	4.5	32.4	33.1
TilS–tRNA, low	4.90 (3.79)	4.77 (3.86)	–28.1 ± 1.4(−28.1 ± 1.3)	–29.4 ± 1.2(−29.2 ± 1.0)	4.3	4.6	22.7	22.4

^aThree ionic conditions are listed for tRNA–TilS complex: Hsp, protonated histidines in TilS; high, high ionic concentration; low, low ionic concentration.

^bAverage rmsd from crystal structure for whole complex, and rmsd for nucleotides are in parentheses.

^cInteraction energies are averaged over the last 30 ns in the MD simulation trajectories; values in parentheses are the interaction energies averaged over the last 15 ns. The agreement between the interaction energies averaged over different time periods indicates convergence in the simulations.

The interaction energies between the protein and arsenate DNA are slightly smaller than those with phosphate DNA (Table 2). The differences are about 2, 0.5, and 5 kcal/mol, for the Fis–DNA, IHF–DNA, RepE–DNA complexes, respectively. We also performed two independent simulations for Fis–DNA systems. The average interactions from the two simulations are within 0.6 kcal/mol for Fis–DNA (phosphate) and 1.0 kcal/mol for Fis–DNA (Arsenate). The energy differences may depend on DNA geometry. For the IHF–DNA complex, DNA wraps around the IHF proteins (Figure 3B). Therefore, the phosphate-arsenate substitution may not induce geometrical strain in the DNA, leading to almost identical protein–DNA interaction energies for the phosphate and arsenate DNA (Sup-Figure 7B, Supporting Information). The binding distance between two RepE monomers in the RepE–DNA complexes separates to almost 100 Å (Figure 3C); thus, here phosphate-arsenate substitution could have larger effects leading to much weaker protein–DNA interactions in the case of the arsenate DNA (Sup-Figure 7D, Supporting Information).

The smaller protein–DNA interaction energy for arsenate DNA is correlated with its higher exposure to water and cations (Table 2). Overall, even though the arsenate–DNA protein interaction energy is lower than that of the phosphate–DNA counterpart, their dynamics are similar, with correlation coefficients ranging from R² = 0.56 to 0.42 (Sup-Figures 6 and 8, Supporting Information). In summary, we found that the structural and dynamical properties of arsenate DNA and phosphate DNA do not present marked differences. However, the interaction of the arsenate DNA with the protein is weaker than that of phosphate DNA.

3. Protein–RNA Interactions and the Ribosome

We simulated three ionic conditions (low and high salt concentrations, and protonated histidines in the TilS protein). TilS–tRNA interaction energies are similar at high ionic concentration and with protonated TilS histidines (Table 2 and Sup-Figure 7, Supporting Information), and both are stronger than the TilS–tRNA interaction at low ionic concentration. Arsenate substitution weakens the TilS–tRNA interaction, making the gap slightly larger than that observed for protein–DNA interactions (Table 2). The arsenate substitution in the tRNA system leads to larger structural changes and the dynamics of the tRNA and the TilS protein also change (Sup-Figures 7 and 8, Supporting Information). The correlation of the covariance matrices between the phosphate and arsenate tRNA–TilS interaction is only R² = 0.3 (Sup-Figure 6, Supporting Information). Similar to the DNA systems, the arsenate tRNA has higher solvent exposure and contact with cations (Table 2).

The difference in the dynamics of phosphate and arsenate tRNAs raises a pivotal question: can an arsenate ribosome exist and be functional? The interaction energy difference between the small-sized tRNA–protein complexes could be magnified in the largest cellular RNA–protein complex. To address the question of the differences in the energy landscape and dynamics of the assembly between ribosomes made of phosphates and arsenates, we conducted massive MD simulations of phosphate and arsenate ribosomes.

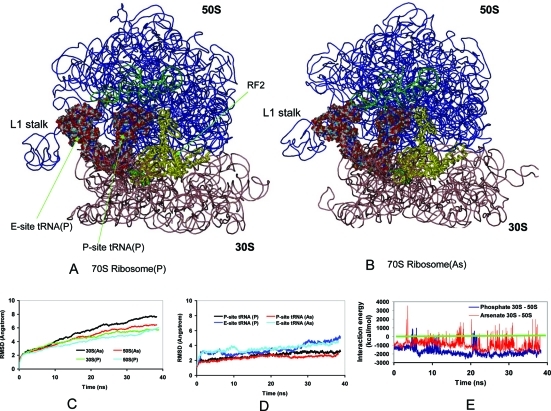
Both phosphate and arsenate ribosomes underwent large conformational changes (Figure 4) after 40 ns simulation at 300 K. During the first 10 ns, the RMSDs of both phosphate and arsenate ribosomes are small, with the structures similar to the crystal structure (Figure 4C). Because arsenate is heavier, one would expect that the arsenate ribosome would have slower conformational dynamics. However, after 10 ns, the structural change of the arsenate ribosome becomes larger than that of the phosphate, mainly because of the change in the arsenate 30S. Both phosphate and arsenate 50S present large RMSDs, mostly because of the portion extruding from the main 50S body, like the L1 stalk where the L1 ribosomal protein binds (Figure 4, parts A and B), which is known to be very flexible.⁴⁰ Apart from this region, the main body of 50S has smaller rmsd than the 30S subunit (Figure 4C). The RMSDs of entire unit are shown in Figure 4C. The RNA backbone follows the same trend as the entire unit, but with a slightly lower magnitude. These conformational changes of both the phosphate and arsenate ribosomes may be mixed with structural relaxation and intrinsic motion since the ribosome is a large molecular machine with large global motions.⁴⁰ As can be seen in Figure 4D, converged motions can be observed at the P-site tRNA already after 20 ns, with arsenate tRNA having smaller rmsd than phosphate tRNA. The E-site tRNA is more flexible, consistent with the anisotropic network model analysis that the E-site tRNA has different dynamics than the P-site tRNA.⁴⁰

Figure 4.

Subunits of arsenate ribosome (ribosome(As)) are more repulsive than those of phosphate ribosome (ribosome(P)), making it more difficult to assemble arsenate rRNA into the functional 70S ribosome than its phosphate counterpart. (A and B) Snapshots from simulations of the ribosome(P) and ribosome(As), respectively. Ribosomal proteins are not included in the figure for clarity. The two tRNAs are shown in surface presentation, with the P-site tRNA sitting between the E-site tRNA and RF2. The green ribbon in the 50S unit is 5S rRNA. The green surface model between 30S and 50S is an mRNA fragment. (C) RMSDs (root mean squared deviations) of ribosome(P) and ribosome(As) from the starting crystal structures during the simulations. (D) E-site tRNA is more flexible than P-site tRNA. (E) Interaction energy between 30S and 50S subunits. The tRNAs, RF2, and mRNA are not included in the calculation. Including these four molecules makes 30S and 50S more repulsive for the arsenate system.

The rmsd differences between the phosphate and arsenate ribosomes coincide with the interaction energy change of the S16 ribosomal protein with its surrounding rRNA, with the S16-arsenate RNA interaction weakening after 10 ns (Sup-Figure 9A, Supporting Information). S16 controls the rRNA conformational switch during the 30S subunit assembly.⁴¹ Several other ribosomal proteins, S4, S17, and S20 are also important for global stabilization of rRNA structure,⁴¹⁻⁴³ and the interaction of arsenate rRNA with all these proteins is weaker than for phosphate rRNA (Sup-Figure 9, Supporting Information). The consistent weaker interaction of arsenate rRNA with ribosomal proteins may hamper the 30S assembly.

If however arsenate rRNA could successfully fold into 30S and 50S subunits, could arsenate 30S and 50S associate as phosphate 30S and 50S do? We compare the interaction energies between 30S and 50S. As can be seen in Figure 4D, while the phosphate 30S and 50S spend most of their time in an attractive energy landscape, the arsenate 30S and 50S could be repulsive to each other.

Assuming that arsenate 30S and 50S can associate into 70S, we examine the energy and dynamics of the P-site and E-site tRNAs, mRNA, and the RF2 protein (Sup-Figure 9, Supporting Information). In the P-site, arsenate tRNA has similar dynamic and interaction energies with RF2 and other molecules; however, in the E-site, the arsenate tRNA is more repulsive to other molecules than its phosphate counterpart. Overall, it appears that it is more difficult to assemble arsenate rRNA into the 30S/50S subunits and into the full 70S ribosome than its phosphate counterpart. This raises the question of whether an arsenate ribosome has been observed in the arsenate cell.

4. Comparison of Experimental and Theoretical Extended X-ray Absorption Fine Structure (EXAFS) Spectra

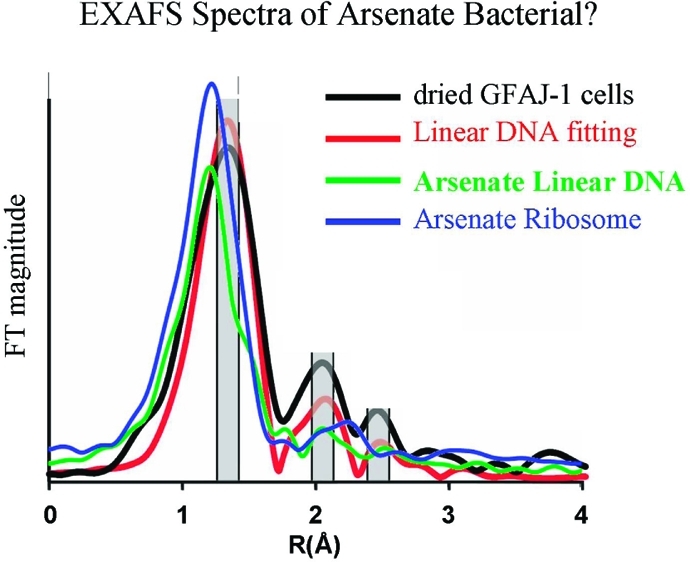
To answer this question, we compare the experimentally observed EXAFS spectra with the theoretical EXAFS spectra for the arsenate DNA and RNA. Wolfe-Simon et al. recorded and fitted As K-edge (11867 eV) EXAFS spectra. There are three characteristic peaks with decreasing magnitude, with the first peak reflecting the As–O bond geometry, and second and third peaks reflecting nonbonded atoms around As (Figure 5A).

Figure 5.

The calculations suggest that linear DNA and rRNA have different EXAFS spectra. Our theoretical spectra of the 70S Ribosome(As) do not match the experimental EXAFS, implying that the arsenate 70S does not contribute to the main arsenate source of experimental EXAFS. (A) Theoretical curves of two As atoms in the 7bna dodecamer DNA(As) (blue and green lines) compared to the observed EXAFS curve (black line) and the Wolfe-Simon’s fitting (red line). (B) The theoretical curves averaged from the 7bna dodecamer DNA (green line) and the 70S (blue line) versus the observed EXAFS curve (black line) and the Wolfe-Simon’s fitting (red line). (C) Two typical theoretical curves from linear 7bna dodecamer DNA (green line) and 70S ribosome (red line). (D) Theoretical curve from bent DNA (red line) is between that of linear DNA (green line) and 70S ribosome (blue line). 7bdna is the PDB code. The experimental EXAFS and Wolfe-Simon’s fitting are taken from ref (3).

On the basis of the structures of arsenate DNA and RNA simulated in this study, we calculated the phase and amplitude of arsenate with the IFEFFIT algorithms in FEFF8, using the program ARTEMIS.³² Wolfe-Simon et al. use a linear B–DNA dodecamer (the 7bna dodecamer) as the representative DNA structure to compare with the observed EXAFS spectra. We also used the same refined 7bna dodecamer structure as a benchmark (with the appropriate As=O and As–O distances). We found that two As atoms may generate theoretical curves that coincide with the observed EXAFS curve and the Wolfe-Simon’s fitting (Figure 5A). The fitting curves averaged from all As atoms in the 7bna dodecamer also have three distinct peaks (Figure 5B).

Bacterial DNA is mostly bent due to packing, binding with proteins, and high salt concentration.⁴⁴ Therefore, the linear 7bna dodecamer may not be a good candidate to represent cellular DNA structures. More importantly, for normal bacterial cells, the ribosome constitutes about 25% of the total mass. Thus, ribosome structures should be included in a comparison between cellular polynucleotide structures and experimental observations. We then tested the nonlinear DNA structures described above and the 70S ribosome. We found that the spectra of bent DNA and RNA around the regions of peaks 2 and 3 are totally different from those of linear DNA. For example, most As atoms in the ribosome have a typical peak around 2.3 Å, whereas there is a valley between peaks 2 and 3 for linear DNA (Figure 5C). The simulated EXAFS spectra for nonlinear DNA progressively change from a linear DNA pattern to that of RNA. For a bent DNA (RepE, Figure 3C), the position and shape of peak 1 overlap with those of rRNA, and the spectra around the 2–3 region lie between those of linear DNA and rRNA (Figure 5D). Overall, the theoretical EXAFS spectra of the As 70S ribosome (blue line, Figure 5B) do not match the experimental EXAFS curve. Thus, our results demonstrate that arsenate 70S ribosome does not contribute to the main arsenate source in Wolfe-Simon’s bacterial cell. Another indication of a negligible concentration of arsenate 70S ribosome comes from comparison of nonbonding As–C distances fitted from experimental EXAFS. The As–C nonbonding distances have been characterized to be 2.35 and 2.92 Å. However, in our simulated arsenate ribosome, the radial distribution for As–C distances is 2.8 Å and there is no density around 2.35 Å (Sup-Figure 10, Supporting Information).

Discussion and Conclusion

The possible existence of arsenate DNA and RNA in the GFAJ-1 cell³ has attracted considerable scientific debate as to whether and how arsenate analogues of phosphate can exist.^4−9,33,45 Because of problems associated with chemical stability, current experimental approaches encounter difficulties in fully assessing the characteristics of arsenate DNA and RNA. Instead, we test computationally possible arsenate–phosphate replacement by examining key molecular systems; however, because of the large size of the molecules our theoretical protocols are also limited. For the ATP and adenosine triarsenate (ATAs) hydrolysis, we used the highest level of quantum mechanical calculations feasible given current computational power (density functional theory at B3LYP/6-311++G** level). The solvation treatment with state of-the-art current quantum mechanical methods also involves approximations. As can be seen in Table 1, while the calculated free energy change for reaction 4 is lower than the experimental value by only −0.6 kcal/mol, the free energy change for reaction 1 deviates significantly from the experimental measurement.⁴⁶ However, we successfully reproduced the trend of the hydrolysis reactions, i.e., hydrolysis to AMP (reaction 4) provides more energy than hydrolysis to ADP (reaction 1). Therefore, we expect that the relative energies of hydrolysis of ATP and ATAs would reflect a trend: hydrolysis of adenosine triarsenate (ATAs) provides 2–3 kcal/mol less energy than ATP.

It is still computationally challenging to calculate the absolute protein interaction energy using molecular mechanics simulations. Nevertheless, our current study revealed that arsenate nucleotides would interact with proteins less strongly than phosphate nucleotides. As can be seen in Table 2, our two independent simulations of the Fis–DNA complex agree quite well: the interaction energies which are estimated from different time periods deviated from each other by less than 1.0 kcal/mol. Overall, the interaction energy differences between phosphate and arsenate DNA are about one to two times the standard deviations, indicating that the differences between the phosphate and arsenate cases are significant. The smaller protein–nucleotide interaction energy for arsenate DNA/RNA could be explained by the larger volume of the arsenate nucleotide, which weakens electrostatic interactions. Our observation of the higher exposure of arsenate DNA/RNA to water and cations also reflects the effects of the larger volume of arsenate. In principle, because the arsenate nucleotides possess larger volumes, the solvation energy changes due to the buried surface area can compensate for the weak arsenate nucleotide-protein interaction; however, our study indicates that the solvation effect can not offset the weaker electrostatic interaction.

Large scale molecular dynamics simulations can provide insights into biological systems;⁴⁷ including DNA flexibility,⁴⁸ DNA–protein interactions,⁴⁹ tRNA³⁷ and tRNA–protein complexes,³⁸ and the mechanism of ribosomal function.⁵⁰⁻⁵³ The computational methods used are sufficiently accurate to reproduce experimental structures⁵⁴ and conformational dynamics⁵⁵ of a variety of molecules. Our evaluation of the structural consequences of phosphate-arsenate substitutions in selected crucial processes in the cell may help in understanding the biological consequences. At the level of small nucleotide hydrolysis as energy source, we found that hydrolysis of adenosine triarsenate (ATAs) provides 2–3 kcal/mol less energy than ATP. Thus, while ATAs hydrolysis may provide the GFAJ-1 cell sufficient energy for some reactions, because ribosome assembly requires many energy-consuming ATP–dependent enzymatic reactions,⁵⁶ the lower free energy obtained in ATAs hydrolysis may lead to an energetic strain that hampers ribosome assembly. On the other hand, at the level of gene replication and transcription, we found that the small adenosine diarsenate molecule may be able to similarly regulate the DnaA protein conformational dynamics. While arsenate DNA interacts with proteins less strongly than phosphate DNA, complexes of proteins with arsenate or phosphate DNA may share similar dynamics.

At the level of translation we found major problems. Arsenate-substituted RNA not only interacts with proteins less strongly than phosphate RNA, but also presents changes in conformational dynamics. The most detrimental arsenate substitution outcome that we observe is that the 30S and 50S may become too repulsive to assemble into a functional 70S ribosome. In principle, mutations in the proteins and in the RNA could make up for some of the structural and energetic changes caused by arsenate replacement. However, while such mutations may be possible in arsenate DNA–protein interactions, this is not the case for the ribosome. To further confirm our doubts regarding the existence of an arsenate ribosome, we examined the experimental EXAFS spectra. Our comparison of the experimental EXAFS spectra of the arsenic bacteria with theoretical EXAFS spectra for arsenate DNA and rRNA only finds evidence for a possible existence of linear arsenate DNA fragments in the dried GFAJ-1 cell, and the characteristic ribosomal structure has not been observed. We hypothesize that the main reason for the slow growth of the GFAJ-1 cell could be the small number of phosphate ribosomes that survived during cellular divisions.

Westheimer asked why Nature chose phosphate.¹ Nature has chosen phosphate not only for its energetic function and its stability; our study points to a perfect match between proteins and phosphate in terms of structure and interaction energy, which are superior to those between proteins and arsenate. Apparently, evolution has optimized the inter-relationship between proteins and DNA/RNA, which requires overall changes at the molecular and systems biology levels when replacing phosphate by arsenate.

Supporting Information Available

Model compounds and related dihedral angles, fitting of the potential energy curve, calculated first 111 frequencies for compound ATAs, comparison of harmonic vibrational frequencies, potential energy surfaces, arsenate–phosphate replacement results, RMSDs and interaction energies, arsenate–phosphate replacement diagrams, interaction energies for selected molecules, radial distributions of As–O and As–C distances, main CHARMM force field parameters of arsenic DNA and RNA, and thermodynamics of hydrolysis of ATAs obtained by quantum mechanical calculation. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States