Acoustic Radiation Force Impulse (ARFI) Imaging: a Review

Abstract

Acoustic radiation force based elasticity imaging methods are under investigation by many groups. These methods differ from traditional ultrasonic elasticity imaging methods in that they do not require compression of the transducer, and are thus expected to be less operator dependent. Methods have been developed that utilize impulsive (i.e. < 1 ms), harmonic (pulsed), and steady state radiation force excitations. The work discussed herein utilizes impulsive methods, for which two imaging approaches have been pursued: 1) monitoring the tissue response within the radiation force region of excitation (ROE) and generating images of relative differences in tissue stiffness (Acoustic Radiation Force Impulse (ARFI) imaging); and 2) monitoring the speed of shear wave propagation away from the ROE to quantify tissue stiffness (Shear Wave Elasticity Imaging (SWEI)). For these methods, a single ultrasound transducer on a commercial ultrasound system can be used to both generate acoustic radiation force in tissue, and to monitor the tissue displacement response. The response of tissue to this transient excitation is complicated and depends upon tissue geometry, radiation force field geometry, and tissue mechanical and acoustic properties. Higher shear wave speeds and smaller displacements are associated with stiffer tissues, and slower shear wave speeds and larger displacements occur with more compliant tissues. ARFI images have spatial resolution comparable to that of B-mode, often with greater contrast, providing matched, adjunctive information. SWEI images provide quantitative information about the tissue stiffness, typically with lower spatial resolution. A review these methods and examples of clinical applications are presented herein.

INTRODUCTION

Clinicians regularly utilize manual palpation to evaluate disease. This method, while invaluable, is limited to structures that are superficial, large in size and in general are considerably stiffer than their surrounding tissue. Methods designed to image the mechanical properties of tissues with improved sensitivity and specificity over clinical palpation have been under investigation for many years. Possible clinical applications for such methods are extensive and include: identifying and characterizing soft tissue lesions, characterizing focal and diffuse atherosclerosis and myocardial ischemia, and providing imaging guidance during minimally invasive surgical procedures, such as prostate biopsy, local anesthetic delivery, and thermal ablation treatments. All elasticity imaging methods involve mechanical excitation of the tissue, and observation of the tissue response. Traditionally, the mechanical excitation has been provided by either external static compression (i.e. elastography, strain-imaging), or external dynamic vibration (i.e. sonoelasticity, transient elastography, magnetic resonance elastography (MRE)), or, by naturally occurring physiologic motion (i.e. cardiac strain-rate imaging). A review of these methods can be found in (1).

Acoustic radiation force based elasticity imaging methods utilize focused acoustic beams to intra-convert acoustic compressional waves to shear waves through the absorption of acoustic energy, and the tissue response to this acoustic radiation force is monitored to derive information about the underlying tissue structure and stiffness. Elasticity imaging methods involving acoustic radiation force have been under investigation for several years, e.g., (2; 3; 4; 5; 6; 7; 8), and many are presented in detail in this special issue (9; 10; 11; 12). These methods offer some advantages over those requiring external excitation: the force is applied directly to the region of interest, thus smaller stresses are used, and challenges associated with coupling the excitation to the desired tissue region are diminished.

ACOUSTIC RADIATION FORCE

In a medium such as soft tissue, in which the primary cause of attenuation is absorption and the contributions to attenuation from scattering can reasonably be neglected (13), the magnitude of radiation force (F) from a focused ultrasound pulse in a specific spatial location is dictated by the absorption (α) and speed of sound (c) of the tissue, and the local temporal average intensity (I) of the acoustic beam (14):

$$F=\frac{2\alpha I}{c}.$$ (1)

This force is in the form of a body force. The geometry of a typical focused radiation force field is directly related to the image shown in Figure 1 (a). This figure portrays the simulated tissue displacement response to a typical impulsive (i.e. < 1 msec) acoustic radiation force excitation; immediately after force application, the displacement response reflects the distribution of the applied force. The volume and geometry of the tissue that is excited (i.e. the region of excitation, or ROE) is spatially distributed throughout the geometric shadow of the active transducer aperture and varies considerably with tissue attenuation. For highly attenuating media, and/or higher acoustic frequencies, appreciable force is generated in the near field, leading to a larger volume of tissue being excited with a more evenly distributed forcing function. In contrast, for moderately attenuating media and/or lower acoustic frequencies, the nearfield losses are negligible, and a smaller volume of tissue within the focal region is excited (15). Because the applied force is dependent upon the acoustic properties of the tissue, its magnitude and geometry are generally unknown in in vivo applications. Typical peak force magnitudes applied during ARFI imaging are on the order of dynes.

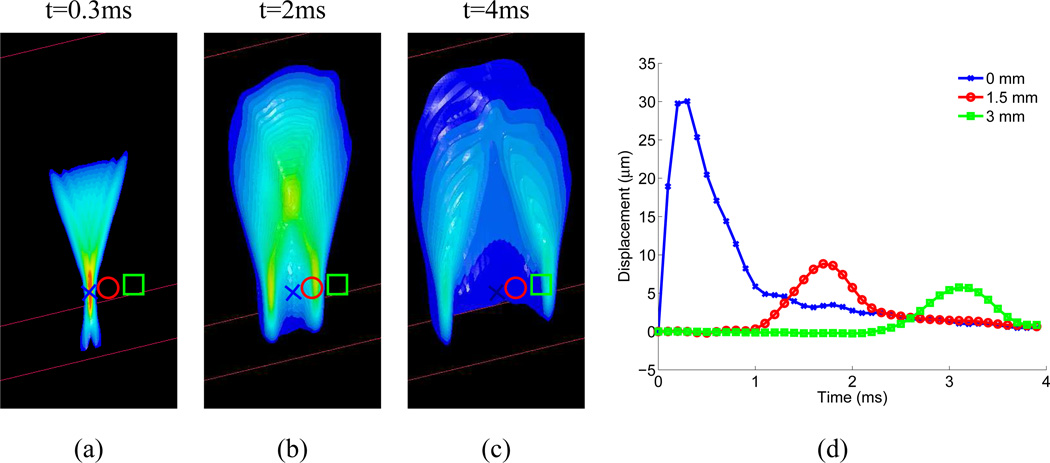
Fig. 1.

Images (a)–(c) portray the simulated axial displacement response in a 3D, homogeneous, isotropic, elastic tissue (E, the elastic Young’s modulus, = 4kPa) to a focused (F/1.3 focal configuration, frequency= 6.7 MHz), impulsive (pulse duration = 50 µs), radiation force excitation, at three snapshots in time after the excitation (0.3ms, 2 ms, and 4ms). The transducer is located at the top of the images, focused in the center of the plane, at 20 mm in depth (marked by the blue X in the images). The red circle is located at 1.5 mm laterally, and the green square at 3 mm laterally in the images. The 3D tissue volume has been bisected so that the central axial/lateral plane is visible. The displacement response at each symbol (x, circle, square) as a function of time after excitation is shown in (d). Positive displacement indicates displacement in the direction of acoustic wave propagation, or down in the images. Initially, (image (a)), the axial displacement response is spatially distributed in the geometry of the applied radiation force, confined within the ROE, with the largest displacement near the focus; the peak focal displacement of 30 µm occurs at 0.4 ms after excitation (blue line in (d)). With increasing time after excitation, a shear wave propagates away from the ROE, decreasing in amplitude with propagation distance due to geometric spreading. In viscoelastic media such as tissue, shear wave attenuation would further decrease the shear wave amplitude with increasing propagation distance. The peak displacement amplitude is inversely proportional to the tissue elastic (shear) modulus, and the speed of the shear wave propagation is quadratically related to the shear modulus.

Some methods of radiation force imaging use steady state or sinusoidal excitation (6; 10; 11; 12), whereas others use short duration, impulse-like excitations, thus evaluating the transient response of tissue to radiation force (2; 4; 7; 9). The impulse-like methods are discussed in detail herein. Figure 1 portrays the simulated, three-dimensional, axial displacement response of a homogeneous isotropic elastic material to an impulsive radiation force excitation at three time-steps after excitation; the transducer is located at the top of the images. The direction of the applied radiation force is in the direction of wave propagation, which is down in this simulation. Initially, the tissue displacement response is localized within the ROE, as shown in Fig 1(a), with the peak displacement occurring near the focal point approximately 0.4 ms after force application. For a given impulsive radiation force in homogeneous media, softer tissues move farther, take longer to reach a peak displacement, and recover more slowly than stiffer tissues. The magnitude of the tissue displacement within the ROE is thus inversely proportional to the tissue elastic (shear) modulus (15). The localized, impulsive radiation force creates shear stresses within the tissue, which generate a shear wave that propagates away from the ROE, as shown in Fig. 1(b)–(d). The propagation speed (c_T) of the shear wave in this elastic, isotropic material is quadratically related to the tissue shear modulus, μ (i.e. $c_T=\sqrt{\frac{\mu }{\rho }}$, where ρ is the tissue density)(16). The shear wavelength for a given excitation is fixed, and is determined by the width of the ROE (under the assumption that ROE width > (c_T * pulse duration)). The temporal frequency content is fairly broadband, and, because the wavespeed varies with the shear modulus of the material, the frequency range varies in different materials.

MONITORING TISSUE DISPLACEMENT RESPONSE

The ability to accurately track displacements induced by acoustic radiation force is essential to generate meaningful images. Correlation based ultrasonic tracking algorithms are commonly used in ultrasound (17; 18; 19; 20). The resolution of a correlation-based tracking algorithm can be derived from the Cramer-Rao lower bound, and depends upon several factors: the signal-to-noise ratio (SNR), the peak correlation and bandwidth of the echoes to be correlated, and the center frequency of the tracking beams. When applied to typical diagnostic ultrasonic data (i.e., SNR=45 dB, ρ=0.99, BW=70%, f_o=7.2 MHz, respectively), the Cramer-Rao lower bound predicts a minimum axial displacement on the order of tenths of a micron (21). While the signal decorrelation due to large axial strain can present a problem for traditional strain imaging methods (22), the axial strains induced during ARFI imaging are so small that this does not pose a problem. However, displacement estimates in ARFI imaging can be compromised by scatterer shearing beneath the point spread function (PSF) of the ultrasonic beams used to track tissue displacement (23; 24). This results in both decorrelation and underestimation of the displacement magnitude (24). The decorrelation is associated with increased jitter, or noise, in the displacement estimates (24). As a result, optimal ARFI beam sequences include a broader, less tightly focused pushing beam (e.g., F/2), and narrower, more tightly focused tracking beams (e.g., F/1.0).

As commercial ultrasonic systems become available with increased parallel processing capabilities, demodulated in-phase and quadrature (IQ) data is typically acquired rather than RF data due to the reduced memory required to store the IQ data vectors (25). While these data can be remodulated back to radio-frequency (RF) data and tracked using cross-correlation as discussed above, autocorrelation based methods are typically used to compute the displacements directly by estimating the phase shift in the IQ data at each depth using algorithms developed by, e.g. Kasai (26) and Loupas (27; 28). The phase shift at each depth represents the localized displacement, though it is restricted to a maximum translation of one-half of the acoustic wavelength, λ, to avoid phase wrapping artifacts. This is generally not a problem for monitoring the micron-scale displacements that are induced with radiation force based imaging methods.

MAKING IMAGES

In elasticity imaging methods, there are two general approaches to image formation: 1) creation of images reflecting relative differences in tissue stiffness (i.e. strain imaging), and 2) performing reconstructions that relate the displacement/strain response to the underlying material properties in order to create quantitative elasticity images. The former approach does not require as much data processing, and generally provides higher resolution images. The latter approach has the advantage of quantification, but typically requires extensive data processing, including smoothing and reconstruction algorithms which generally result in lower spatial resolution. Both types of images can be generated using acoustic radiation force impulsive excitations.

For the generation of images portraying relative differences in tissue stiffness, Acoustic Radiation Force Impulse (ARFI) imaging has been developed (29), in which the tissue displacement response is monitored within the ROE, and image data are generated by sequentially interrogating different lateral positions, as is done in conventional 2D ultrasound imaging. Images are then synthesized of tissue displacement at a given time after radiation force excitation at each interrogation location. Monitoring the displacement response within the ROE has the advantage of higher displacement magnitude and SNR (as compared to outside of the ROE), but quantification of tissue elasticity within this region is challenging due to inertial effects and the excitation source term within the ROE.

To create quantitative elasticity images from impulsive radiation force excitations, the displacement response is typically monitored outside of the ROE. The speed of the shear wave propagation is quantified and used to estimate the tissue shear modulus, as was originally proposed by Sarvazyan et. al. (2). Early implementations of this approach utilized inversion of the homogeneous Helmholtz equation to estimate tissue shear modulus (5; 30). However, most groups have moved to utilization of time-of-flight wavespeed estimation methods, due to challenges associated with differentiation of noisy ultrasonic displacement estimates (31; 32; 33; 34).

ARFI IMAGING

ACOUSTIC RADIATION FORCE IMPULSE (ARFI) IMAGE GENERATION

ARFI images are formed using commercial diagnostic ultrasound scanners to both generate localized, impulsive acoustic radiation forces in tissues, and to monitor the transient, dynamic displacement tissue response within the ROE using correlation based methods. An ARFI pulse sequence consists of tracking beams and pushing beams. The tracking beams are conventional B-mode ultrasound beams (A-lines), and the pushing beams are transmitted along the same A-line and have higher intensity, with typical parameters as specified in Table 1. A typical sequence involves transmitting a series of pre-push reference A-lines, which are used to monitor underlying physiologic motion, followed by a pushing pulse along the same A-line, and then a series of tracking A-lines that are utilized to monitor the tissue displacement response within the ROE of the pushing beam (typically for 3–5 msec at pulse repetition frequencies (PRFs) between 5 and 10 kHz).

Table 1.

Typical parameters used for an ARFI push pulse in different clinical scenarios.

Frequency	2–7 MHz
F-number	F-2
Intensity(Isppa.5)*	1400 W/cm 2
Intensity(Ispta.3)	0.7 W/cm2
Mechanical Index	1.5–3.0
Pulse Duration	0.1–0.5 ms
Temperature Rise	0.02–0.2°C
Displacement (peak)	10–20 µm

^*Acoustic parameters are quantified using a 0.6 mm active spot size PVDF membrane hydrophone (Sonic Technologies) submerged in attenuating fluid (evaporated milk and water) in the appropriate concentration to achieve the desired attenuation (α) in order to accurately quantify the in situ intensity for radiation force and thermal calculations. The peak negative pressure measurement used to determine the Mechanical Index is performed in fluid with α=0.3 dB/cm/MHz as prescribed by its definition. The temporal average intensity is computed using the appropriate duty cycle, which can be modulated to reduce average heating.

In ARFI images, the displacement data from multiple, sequentially interrogated radiation force excitation locations are synthesized into a single dataset representing the temporal displacement response from within each ROE throughout a 2D (or 3D) tissue region of interest (ROI). As shown in Figure 2, these datasets are rich with information about the transient tissue deformation. ARFI images have been generated of tissue displacement at a given time after force application, the maximum tissue displacement, the time the tissue takes to reach its peak displacement, and the time it takes the tissue to recover (4). In the presence of uniform acoustic attenuation, ARFI displacement magnitude images generally reflect tissue structure and relative stiffness. Images of the transient temporal behaviors, such as the time to peak displacement and recovery time can be used to derive quantitative estimates of tissue stiffness (2; 37). The majority of ARFI images generated in clinical applications portray relative displacement at an early time after the force application (i.e. Figure 2b) in order to optimize the accuracy of structural details (35).

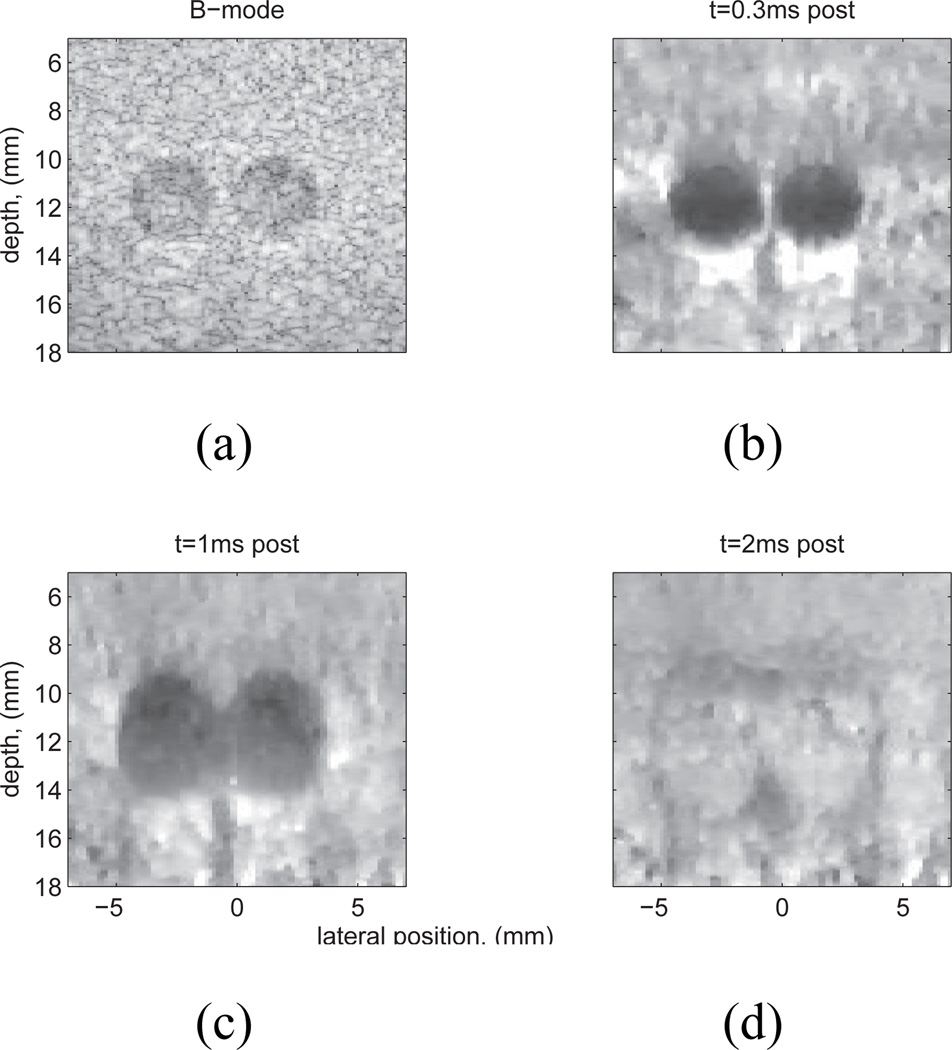
Fig. 2.

Experimental data: matched B-mode (a) and normalized ARFI displacement images, (b)–(d), of a Computerized Imaging Reference Systems, Inc. (CIRS, Norfolk, VA) custom tissue mimicking phantom (E=4 kPa) with two 3 mm spherical lesions (E=58kPa). The lesion contrast in the ARFI images is largest at t=0.3 ms (b), decreases with time after excitation (c), and reverses later in time (d). In addition, the lesion size appears to grow with time post-force, which is caused by shear wave propagation and reflection at lesion boundaries (35). Note also the ’posterior enhancement’, or increase of displacement beneath the lesions (b), (c). This is because the lesions were slightly less attenuating than the surrounding tissue, thus the tissue beneath the lesions experienced larger radiation force than that adjacent to it. Figure reproduced with permission from:(36)

CORRELATION COEFFICIENT THRESHOLDING

In many radiation force based imaging applications, a correlation coefficient threshold algorithm is applied to remove spurious displacement estimates from the data that can arise from hand-held and physiologic motion artifacts, system noise, and poor track beam SNR. When processing RF data with cross correlation to estimate displacement, the correlation coefficient corresponding to each estimate is available for thresholding. When processing IQ raw data from the scanner, the magnitude of the complex correlation coefficient can be computed and utilized for thresholding (38).

MOTION FILTERING

Motion filters are typically applied to radiation force induced displacement data to remove artifacts from underlying physiologic and transducer motion. It is often helpful to acquire multiple reference A-lines before the radiation force excitation to sample baseline motion. Using a priori information as to the maximum expected duration of the tissue response to the ARFI excitation, non-zero displacements at times exceeding this time are assumed to be generated from sources other than acoustic radiation force. The pre-excitation and post-recovery displacement data are then fit to derive an estimate of the underlying motion that is present during the data acquisition, and this motion artifact is subtracted from the raw displacement data (39).

ARFI IMAGE NORMALIZATION

Ideally, an image of a homogeneous region of tissue would appear uniform in an ARFI image. During radiation force application in ARFI imaging, prior to appreciable shear wave propagation, tissue displacement has been shown to be linearly related to applied force (15). However, spatial gradients due to focusing and depth-dependent attenuation losses exist in the applied radiation force field within the ROE, thus an ARFI displacement image in a homogeneous phantom does not appear uniform, unless the displacement response is normalized by the applied force field(36). This is similar to applying Temporal Gain Control (TGC) in B-mode imaging, wherein the loss in signal energy with depth is compensated for through the application of temporally (i.e. depth) dependent gain.

ARFI IMAGE CONTRAST

When imaging structures (i.e. lesions), both high contrast and spatial resolution are desirable. Due to the dynamic nature of ARFI excitation, lesion contrast and apparent size are temporally dependent. Contrast peaks shortly after force cessation (Fig. 2(b)), decreases with time post-force (Fig. 2(c)), and then, in some instances, it can reverse due to shear wave interaction with internal boundaries, differences in shear modulus between lesions and background, and inertial effects (Fig. 2(d)). In images generated shortly after force cessation, lesion contrast: 1) increases with lesion stiffness, 2) increases as the ROE size decreases relative to the size of the structure being imaged, and 3) is independent of the applied radiation force magnitude (36). Due to both the dynamic nature of the lesion contrast in ARFI images, and its dependence on ROE size, the contrast transfer efficiency (i.e. the ratio of the mean displacement inside and outside of a stiff lesion as compared to the ratio of the respective elastic moduli (22; 40)) is not identically 1; and this ratio cannot, in general, be used to quantify the underlying modulus relationship.

LESION SIZE IN ARFI IMAGES

The size of structures portrayed in ARFI images often appears to increase with time after excitation. In Figure 2(b), the 3-mm lesions are portrayed to be approximately 3 mm in diameter. However, in Figures 2(c) and (d), as time after the push increases, although the lesions are still readily visible with clearly delineated edges, they appear larger than at the earlier time steps. This apparent lesion growth with time in ARFI images arises from shear wave reflections at the lesion boundaries that appear within the ROE later in time and impact the tissue recovery dynamics (35).

FRAME-RATE CONSIDERATIONS IN ARFI IMAGING

For maximum contrast in ARFI images, the cross-sectional (lateral/elevation) size of the excitation beam must be smaller than the structure being imaged (36). As a result, where high contrast ARFI images are desired, multiple pushing beam focal zones are utilized, with the information from each combined into a single image after applying normalization. This is similar to what is done for high resolution B-mode imaging. However, the price for such high contrast is slower a frame-rate. In order to improve frame-rates, beam interleaving approaches have been developed, in which multiple independent ROEs can be interrogated and the tracking beams can be interleaved between the different locations (41). In addition, excitation with a larger ROE and the use of parallel receive tracking beams facilitates interrogation of larger regions in a single excitation, thus reducing overall frame acquisition time, but comes at the cost of a reduction in image contrast (25; 36).

REQUIRED ACOUSTIC OUTPUT FOR ARFI IMAGING

ARFI imaging is performed with commercial diagnostic transducers. Typical parameters utilized for ARFI push pulses are shown in Table 1. In general, the pushing frequency is in the lower end of the transducer bandwidth, and the transmit voltage is at the upper end of the system capability. The pushing pulses are similar to those used for Power Doppler imaging, however, they are much longer in duration (i.e. 200 cycles vs. 10 cycles). Radiation force that is sufficient to generate displacements in soft tissue on the order of tens of microns is typically achievable within standard diagnostic limits (MI, TI, Ispta). However, the depths at which these displacements can be generated are shallower than the corresponding maximum B-mode imaging depth for a given transducer. This is due to the attenuation of sound in the intervening tissue, and the fact that more energy is required to push the tissue than to image it. To increase depth penetration while maintaining displacement resolution, the use of separate imaging arrays (higher frequency) and pushing arrays (low frequency) may be beneficial. This approach is under investigation in the application of monitoring High Intensity Focused Ultrasound (HIFU) thermal ablation procedures (7; 8; 10).

Another challenge that can present a limitation for acoustic output during ARFI imaging is transducer face heating, which can be problematic during multi-frame acquisitions. While ARFI imaging has been implemented on several diagnostic transducers for various clinical applications, it is important to be mindful of transducer heating when developing sequences, and to ensure that transducer heating does not exceed acceptable limits (41).

TISSUE THERMAL RESPONSE

In addition to creating acoustic radiation force, the absorption of acoustic energy generates heat within the tissue. Therefore, it is important to accurately quantify the acoustic output utilized for acoustic radiation force based imaging, and to ensure the total tissue heating stays within diagnostic limits (i.e. < 6 °C (42)). It is fortuitous that it takes less energy to displace tissue several microns than to raise its temperature by a fraction of a degree Celsius, due to differences in the thermal and mechanical material properties.

For a single impulsive radiation force excitation, the energy deposition occurs during the pulse duration, which is typically less than 1 msec. In this case, heat loss due to both perfusion and thermal conduction can be neglected, and the temperature rise in the tissue can be estimated using (44; 43):

$$\mathrm{\Delta }T=\frac{q_v}{c_v}t=\frac{2\mathrm{\alpha }I}{c_v}t,$$ (2)

where q_v is the rate of heat production per unit volume generated by the absorption of acoustic energy, c_v is the heat capacity per unit volume of the tissue, α is the absorption coefficient for soft tissue which increases as a function of frequency, I is the in situ pulse average intensity, and t is the duration of the pulse. As shown in Figure 3(a), the heat distribution from a single excitation is largest near the focal point. The typical temperature rise associated with an individual excitation ranges from 0.02–0.2°C, varying primarily as a function of transmit frequency and pulse duration.

Fig. 3.

(a) Simulated temperature increases in the axial-lateral plane (centered in elevation) for a single ARFI interrogation using a relatively high frequency (7 MHz), and tight focal configuration (F/1.3). The transducer is centered along the top of the image, spanning a total of 1.52 cm laterally. The focus is at 2.0 cm. (b) Temperature increases after a single frame of two-dimensional ARFI imaging using the pulse from (a) in a high contrast beam sequence (50 tightly focused, closely spaced (0.35 mm) push pulses, with a time delay of 5 ms between successive locations temporally), assuming a tissue. absorption of 0.5 dB/cm/MHz. Note that the maximum temperature increase has shifted from the focal depth of 2.0 cm (the location of maximum temperature increase for a single ARFI interrogation), to 1.45 cm, which is the region of maximum overlap for the sequence. (c) Real-time, two-dimensional ARFI imaging, using the same sequence as in (b), performed at a frame rate of 3 frames per second for a total duration of 3 seconds. Note that the temperature scale, in degrees Celsius, is different for each figure. Figure reproduced with permission from:(43)

For 2D ARFI images, where multiple pushing locations are sequentially interrogated, tissue thermal conduction is no longer negligible, and must be considered when predicting heating. The location of the peak heating shifts from the focal depth to the region of maximum overlap between excitations, which is generally in the near-field of the focal beam (Figure 3(b)). As with conventional ultrasound imaging, a trade-off exists between the number of interrogations in a single image frame and the overall frame rate that can be implemented while maintaining diagnostic temperature levels (43; 41).

STIFFNESS QUANTIFICATION WITH ACOUSTIC RADIATION FORCE

In order to generate quantitative estimates of the tissue stiffness using acoustic radiation force, methods have been developed that monitor the speed of the shear waves that propagate away from the ROE (2; 30; 5; 9). Early methods performed algebraic inversion of the Helmholtz equation:

$$\mathrm{\rho }\frac{{\partial }^2{\overrightarrow{u}}_i(\overrightarrow{x})}{\partial t^2}=\mu {\overrightarrow{\nabla }}^2{\overrightarrow{u}}_i(\overrightarrow{x})$$ (3)

where u⃗_i(x⃗) is the displacement in the i direction at location x⃗, ρ is density, μ is shear modulus, and t is time. However, these approaches were very susceptible to noise in the tissue displacement estimates, due to the required second order differentiation.

As a result, time-of-flight shear wave speed estimation methods are typically employed to quantify the shear wave speed from the displacement data (32; 45; 33; 31; 34; 9). These methods estimate the time of the arrival of the wave at multiple lateral locations, and use this information to estimate the speed of the wave propagation between the lateral locations. Figure 4 portrays the general approach. In the top row of Figure 4, simulated displacement/time profiles from the focal depth are plotted at different lateral locations relative to the center of the ROE for two materials with different stiffnesses (note the different scales on the plots). In Figure 4 (c), the time of the peak displacement (relative to the time of radiation force excitation) is plotted as a function of lateral position for the two different materials. The inverse slope of the resulting lines provides the shear wave speed. Figure 4 (d) provides shear wave speed estimates obtained using linear regression of the time to peak displacement data at lateral ranges from 2–8 mm over the depth range from 16–20 mm (i.e. the depth of field of the radiation force for this example).

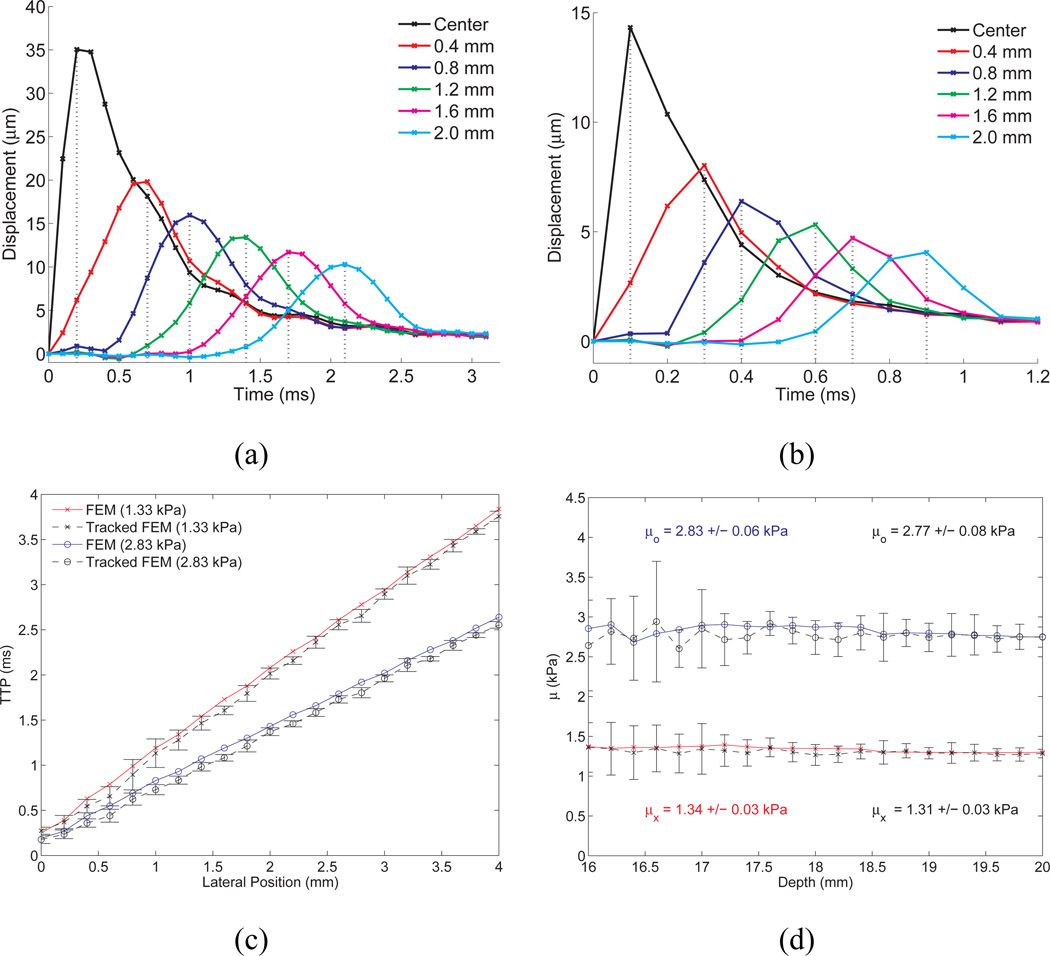
Fig. 4.

TOP ROW: Simulated displacement through time profiles, without ultrasonic tracking, at lateral positions offset from the excitation location for elastic media with shear moduli of (a) 1.33 kPa and (b) 8 kPa. Notice that the curve appears more finely sampled in the more compliant medium (1.33 kPa) because of its slower propagation speed and the fixed 10-kHz temporal sampling (simulating a fixed PRF in the experimental system). The vertical dotted lines indicate the TTP values that would be estimated from this data, although experimentally the data would be upsampled using a low-pass interpolation from the acquired PRF to 50 kHz. Notice that the two plots are on different time scales. BOTTOM ROW: (c) Time of peak displacement at the focal depth (20 mm) as a function of lateral position in simulation data for elastic materials, with shear moduli of 1.33 and 2.83 kPa. The inverse slopes of these lines represent the shear wave speeds in these materials. (d) Reconstructed shear moduli over depths from 16–20 mm using the time to peak displacement data at lateral ranges from 2–8 mm outside of the ROE to estimate the shear wave speed for elastic materials with 1.33 (x) and 2.83 (o) kPa shear moduli. The raw FEM data are represented by the red (x) and blue (o) lines, with the mean ± one standard deviation shear modulus estimates over the range of depths represented in each colored text box. The corresponding ultrasonically-displacement-tracked data, using 20 independent speckle realizations, is shown in the black lines. Figure reproduced with permission from:(33)

A tradeoff exists between the precision of the resulting shear wave speed estimate and its spatial resolution. In a homogeneous medium, in general, the larger the linear regression kernel (i.e. 6 mm in Figure 4(d)), the more precise the estimate. However, time-of-flight methods employ a locally homogeneous assumption, thus, smaller kernels are desirable in the presence of heterogeneous tissue structures (9).

QUANTITATIVE VS. QUALITATIVE IMPULSIVE RADIATION FORCE IMAGES

For clinical applications where visualization of structural information is of importance, such as in lesion identification and monitoring ablation procedures, higher spatial resolution qualitative images can be advantageous. However, in other applications, quantitative information may have more clinical utility. One such area that has shown promise for quantitative analysis is the evaluation of diffuse stiffening associated with advanced liver fibrosis (47; 34; 48). Another area of investigation is the differentiation of malignant and benign lesions based upon their absolute stiffness (31; 9). In addition, longitudinal monitoring of disease progression and response to therapy may benefit from quantitative stiffness characterization.

Although the radiation force push pulses utilized for creating relative stiffness images from within the ROE and for monitoring shear wave propagation outside of the ROE can be identical, the beam sequencing schemes tend to differ. With qualitative ARFI imaging, information is generated within the ROE, thus, adjacent ROEs must be excited to interrogate a large field of view. For shear wave speed quantification, a single interrogation can serve as the source for propagation/quantification over a relatively large region (i.e. 2cm × 2cm). However, because shear waves are quickly attenuated in soft tissues, and the reconstruction algorithms require relatively high displacement data SNR, multiple interrogations are generally utilized to interrogate a large field of view and to employ averaging to increase SNR. Figure 5 portrays ARFI images and overlaid reconstructed shear moduli that were obtained from sequentially acquired quantitative and qualitative datasets in an excised prostate, with matched histology. In general, the darker regions of decreased displacement portrayed in the ARFI images are correlated with increased shear moduli. However, the ARFI image clearly portrays more structural detail than the matched quantitative data provides. With the advent of extensively parallel processing capabilities on newer commercial ultrasound scanners, sequencing methods designed to generate combined ARFI and shear wave speed images are anticipated.

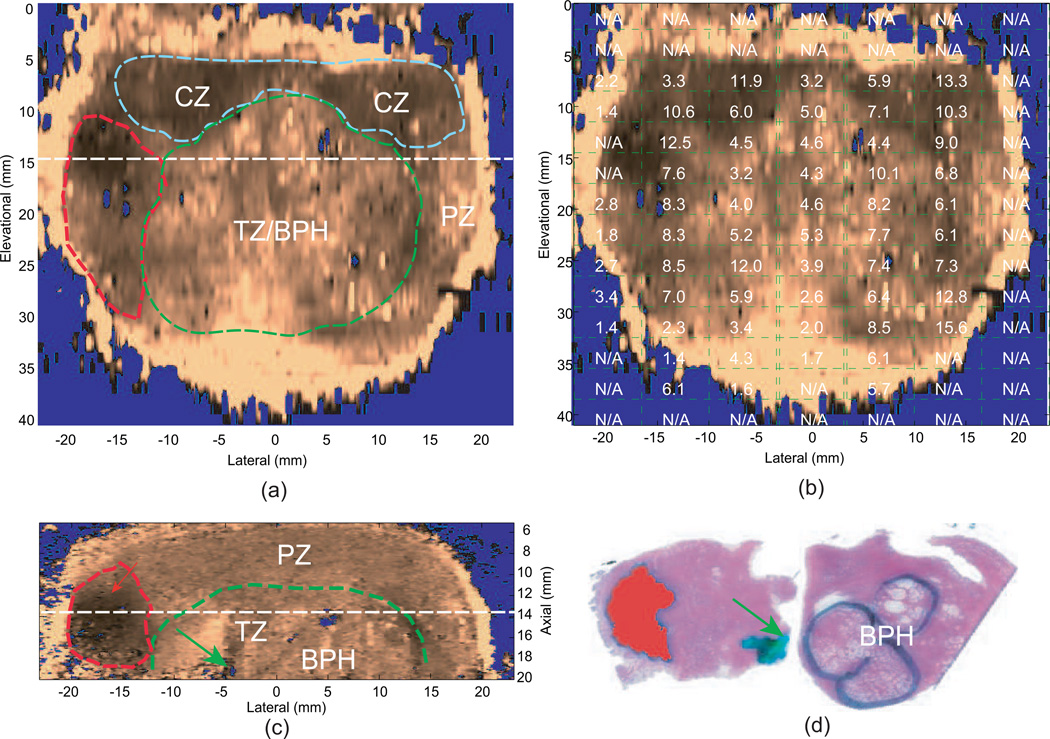
Fig. 5.

Qualitative ARFI images with the co-registered reconstructed shear moduli and matched histological slides from an ex vivo prostate specimen. Images were obtained with a linear array mounted on a translation stage used to interrogate the entire 3D prostate. The central zone (CZ), transition zone with benign prostatic hyperplasia (TZ/BPH) and prostate cancer (PCa) are circled in blue, green and red dashed lines in the ARFI images, respectively. The urethra is indicated by the green arrow. (a) coronal ARFI image with zonal anatomy, PCa and BPH indicated; (b) coronal ARFI image with co-registered reconstructed shear moduli overlaid; (c) axial ARFI image with zonal anatomy, PCa and BPH indicated; (d) co-registered histological slide of the axial ARFI image, in which PCa is masked in red and BPH is circled in black. (a) and (c) are perpendicular to each other and intersect at the dashed lines. These data were obtained with a VF105 linear array mounted to a mechanical translation stage and a Siemens Antares scanner. Figure reproduced with permission from:(46)

CLINICAL APPLICATIONS

Recently, ARFI imaging has been demonstrated in many clinical settings, using various transducers and beam sequences depending upon the application. These include: abdominal imaging (49; 50), cardiac imaging (51), vascular imaging (52), breast imaging (53), nerve imaging (54), prostate imaging (55), and monitoring thermal ablation procedures (56; 57; 58).

For high resolution, high contrast ARFI imaging, single frame, multi-focal zone pushing beams are utilized. An example from an in vivo breast mass is shown in Figure 6. This mass was determined to be a reactive lymph node through biopsy. In this case, the ARFI image portrays considerably more internal structural detail than the B-mode image, which demonstrates one of the advantages of coupling the mechanical excitation directly within the lesion.

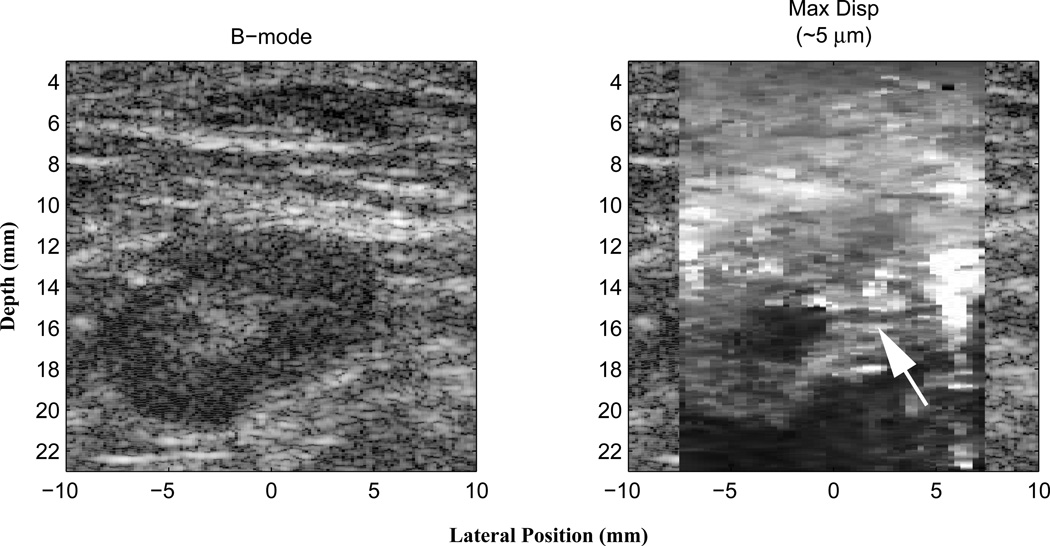
Fig. 6.

B-mode (left) and matched ARFI maximum displacement image (right) of an in vivo, biopsy-proven reactive lymph node in the breast. The lymph node is the darker oval region in the B-mode image appearing from 12–22 mm in depth. The echogenic center of the lymph node is the normal hilum that corresponds to the region of decreased displacement in the ARFI image (darker region). The node itself appears slightly stiffer (darker) than the surrounding tissue, with an efferent ductal, structure clearly visualized (arrow). These data were obtained with an Antares scanner and a VF105 linear array transducer. Figure reproduced with permission from (59)

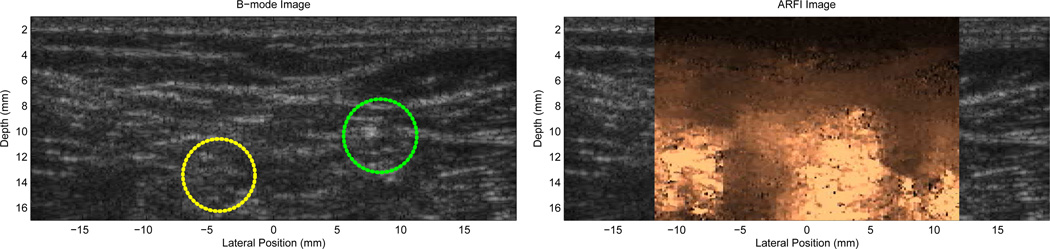
Another example of a single frame, multi-focal zone ARFI image is shown in Figure 7. This is an image of the tibial and common peroneal nerves as imaged from the popliteal fossa. In this example, the ARFI image portrays considerably higher contrast than the matched B-mode image.

Fig. 7.

In vivo B-mode (left) and ARFI (right) images of the tibial and common peroneal nerves in a 29 year old subject, just distal to their bifurcation from the sciatic nerve in the popliteal fossa. The ARFI image was generated using two excitation focal zones at 15 and 20 mm with the VF10-5 linear array. The peak displacement in the ARFI image is 4 µm. ECG data acquisition gating was not used in generating the ARFI image. Notice that the two nerves are clearly delineated as stiffer (darker) circular structures in cross-section; their location is not readily apparent in the B-mode image (they have been outlined in yellow (tibial) and green (popliteal) based on the ARFI image boundaries). The improvement in nerve contrast is over 600% in the ARFI image compared with the B-mode image. Figure reproduced with permission from:(54)

Figure 8 provides matched B-mode and ARFI prostate images obtained in vivo. For 3D prostate ARFI imaging, a mechanical wobbler, curvilinear array has been utilized transrectally (the EV9F4, Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA, USA) to image the entire 3D prostate volume. In this application, only a single focal zone is employed, and a single volume of data is obtained (including 55 lateral interrogation locations per image plane, and 50 individual image planes). In Figure 8, the data is displayed in coronal section (i.e. the elevation/azimuthal plane). This prostate was excised immediately after imaging, and the corresponding histological image portrays a cancerous region corresponding to the location of decreased displacement (i.e. darker region) in the ARFI image, which is portrayed with considerably higher contrast than in the matched B-mode image (55).

Fig. 8.

Co-registered coronal sections of B-mode, ARFI images in vivo and the right half histological slide. The basal area of the prostate is at the top of the images, and the apex is at the bottom. Images were obtained in vivo, immediately prior to radical prostatectomy surgery. In the histological slide, cancerous regions were masked in blue by a pathologist. The obvious stiff structure in the right apex region shown in the ARFI image corresponds to the cancerous lesion. The Gleason’s scores are 4+3. The relatively softer structure to the left side of the lesion is the verumontanum. Another suspicious region (darker, asymmetry) is apparent in the upper left side of the ARFI image, however the corresponding pathology was not available. If utilized for biopsy guidance, both suspicious darker regions would likely have been targeted. These data were obtained with an EV9F4, end-firing, mechanical wobbler, curvilinear array and an Antares scanner. Figure reproduced with permission from:(55)

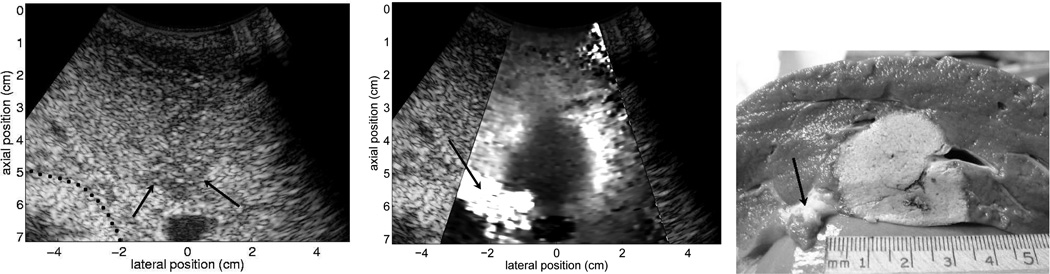
ARFI imaging has also been applied to monitor thermal radiofrequency ablation procedures (56; 57; 58). Figure 9 provides matched B-mode, ARFI and pathology images obtained during an in vivo radiofrequency ablation procedure in an ovine liver. Ablation monitoring appears to be a promising application for ARFI imaging due to the ease of coupling the radiation force excitation to the ablation region, and the generally large mechanical contrast of ablated tissues.

Fig. 9.

B-mode, normalized ARFI displacement, and pathology images from an in vivo ovine ablation monitoring experiment. The matched B-mode and ARFI images were acquired 70 min after ablation with the electrode still in place. The imaging was performed in an open abdomen, with the transducer contacting the diaphragm. The pathology image was obtained in a plane closely matched with the imaging plane shown in the B-mode and ARFI images. The dotted line in the b-mode image indicates the boundary between fatty tissue and the tissue surrounding the bowel wall, and the arrows in the B-mode image show the apparent distal boundary of the thermal lesion. The arrow in the ARFI displacement image points to a region of softer tissue separating liver tissue from bowel, which appears to correspond with fatty tissue in the pathology image. The ablation lesion is well visualized in the ARFI image, as a large region of decreased displacement (dark). These data were acquired with the CH6-2 transducer and the Antares scanner. Reproduced with permission from (57)

The majority of the studies discussed above were performed with diagnostic, commercially available ultrasound transducers, and customized research Antares or S2000 scanners (Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA USA), which have been modified to allow custom beam sequencing and raw data storage, with offline data processing. These studies have demonstrated the underlying physics of ARFI imaging; the clinical feasibility of ARFI imaging in a variety of applications with promising results; and have identified some remaining challenges (e.g. contrast vs. framerate vs. acoustic output). Radiation force based elasticity imaging methods have recently become available commercially, and evaluations of their clinical utility are beginning to appear in the clinical literature, with promising early results (60; 48; 61; 62; 63).