Abstract
Frailty is a physiological state characterized by the deregulation of multiple physiologic systems of an aging organism determining the loss of homeostatic capacity, which exposes the elderly to disability, diseases, and finally death. An operative definition of frailty, useful for the classification of the individual quality of aging, is needed. On the other hand, the documented heterogeneity in the quality of aging among different geographic areas suggests the necessity for a frailty classification approach providing population-specific results. Moreover, the contribution of the individual genetic background on the frailty status is still questioned. We investigated the applicability of a cluster analysis approach based on specific geriatric parameters, previously set up and validated in a southern Italian population, to two large longitudinal Danish samples. In both cohorts, we identified groups of subjects homogeneous for their frailty status and characterized by different survival patterns. A subsequent survival analysis availing of Accelerated Failure Time models allowed us to formulate an operative index able to correlate classification variables with survival probability. From these models, we quantified the differential effect of various parameters on survival, and we estimated the heritability of the frailty phenotype by exploiting the twin pairs in our sample. These data suggest the presence of a genetic influence on the frailty variability and indicate that cluster analysis can define specific frailty phenotypes in each population.
Electronic supplementary material
The online version of this article (doi:10.1007/s11357-011-9257-x) contains supplementary material, which is available to authorized users.
Keywords: Frailty, Aging, Heritability, Twins
Keywords: Life Sciences, Molecular Medicine, Geriatrics/Gerontology, Cell Biology
Introduction
Over the past years, geriatricians and gerontologists have focused their attention on frailty, a common condition of the elderly characterized by a significant increase of the risk of “catastrophic decline” (Fried et al. 2001; Varadhan et al. 2008). Many operational definitions of frailty have been proposed. Some consider frailty as a continuous accumulation of self-reported deficits, reflecting the proportion of potential disabilities in a subject (Mitnitski et al. 2002; Goggins et al. 2005; Rockwood et al. 2005; Woo et al. 2005; Rockwood et al. 2006). Others consider frailty as a distinct clinical syndrome characterized by the deregulation of multiple physiological systems and loss of energy leading to a loss of homeostasis, which finally leads to a high risk of disability, co-morbidity, and death (Fried et al. 2001; Fried et al. 2004). Fried and co-workers reported that muscle strength, physical performance, nutritional, and psychological status are useful parameters to evaluate the frailty status of the oldest subjects (Fried et al. 2001; Walston et al. 2006; Fried et al. 2009). In fact, the impairment of these parameters indicates a deregulation of the physiological homeostasis of the organism.
Recently, in order to obtain an operative population-specific definition of frailty, we demonstrated that a cluster analysis using specific geriatric parameters (measuring cognitive status, physical performances, psychological status, disability) is able to identify frail/nonfrail subjects in a large group of aging people from southern Italy (Montesanto et al. 2010). The diagnostic and predictive soundness of this classification was confirmed by a longitudinal study showing a differential incidence of mortality after 18 and 36 months follow-up of the different groups identified. This approach, which is based on population-specific data under study and does not use any a priori thresholds, may be very promising for determining an objective frailty classification of the elderly within his/her environment and society.
Although there have been some advances in defining a frailty phenotype and in highlighting biomarkers able to characterize the individual frailty status, the core of frailty that is the biological basis of the loss of the homeostatic capacity, is still poorly understood. In particular, it is still debated whether and to what extent the individual genetic background affects the individual frailty status (Frederiksen et al. 2002; Christensen et al. 2006; Cournil et al. 2010).
The aim of the present study was to verify the applicability of the cluster analysis approach (previously set up and validated in a southern Italian population) in a large population of samples collected in northern Europe (Denmark), where different aging conditions have been previously described (Jeune et al. 2006). In addition, by taking advantage of the twins in our sample, we estimated the heritability of the frailty status, in order to shed light on the biological basis of frailty.
Materials and methods
Samples
Two Danish samples were analyzed, totalling 3,719 subjects. All participants provided written informed consent, and the study was approved by the Danish Regional-Scientific Ethical Committee. This approval was valid over all the territory of the survey, and other Institutions involved in the study requested no additional approval.
The first sample (the Danish 1905-Cohort) included 1,380 subjects aged 93 years (390 males and 990 females), recruited in the framework of a nationwide survey of all Danish people born in Denmark in 1905 (Nybo et al. 2001; Nybo et al. 2003; Christensen et al. 2008). Briefly, 2,262 people participated initially in this survey which included a home-based interview aimed at the collection of socio-demographic information, evaluation of physical, cognitive, depressive status, sensory impairments, medications, self-reported health status, and blood sampling. The first recruitment started in 1998, and three follow-ups were performed (2000, 2003, and 2005). Vital status was ascertained for 10 years, from the first visit through January 2009. Information on death or emigration for all the cohort members was retrieved from the Danish Central Population Register, which keeps a record of all those living in Denmark since 1968 and is continuously updated (Pedersen et al. 2006). The participation rate of the survey was 63%, and comparisons of demographical characteristic of participants with non-participants demonstrated that recruited people are a fairly non-selected group of the 1905-Cohort (Nybo et al. 2001).
Of the 2,262 subjects participating in the study, we excluded 882 subjects with missing values for Mini Mental State Examination (MMSE), Hand Grip strength (HG), Activity of Daily Living (ADL), and Self-Reported Health Status (SRHS).
The second sample analyzed included 2,339 subjects (1,016 males and 1,323 females) from the Longitudinal Study of Aging Danish Twins (LSADT) Cohort. The sample was drawn from the older cohorts of the Danish Twin Registry in the framework of a population-based twin study carried out in Denmark from 1995 (Christensen et al. 1999). Briefly, all 3,099 Danish twins aged 75 years and older alive in January 1995 and residing in Denmark were selected for participation. Among all eligible individuals, 2,401 (71%) participated in the baseline assessment. Surviving members of the initial cohort were followed up every 2 years, starting from 1997, and at each survey, additional 70-year-old individuals were recruited (Christensen et al. 2003). Overall, 4,371 subjects completed the baseline assessment consisting of an interview, with socio-demographic information, evaluation of physical and cognitive status, depression, medications, SRHS, and sensory impairments. In the case of the LSADT sample, considering that the variables MMSE, HG, ADL, and SRHS were collected beginning from the 1999 wave of recruitment, we excluded the first two sample cohorts (1995 and 1997) for our analysis because of missing values for those variables, and we thus considered the 1999 sample as baseline and 2001, 2003, and 2005 as three complete follow-ups. Among the 2,339 subjects, 219 were monozygotic (MZ) twin pairs, 266 dizygotic (DZ) twin pairs (264, same sex; two, different sex), and 12 twin pairs with uncertain zygosity. The remaining 1,343 subjects were “single twins,” i.e., the co-twin was either dead or non-participating. In particular, 379 were from MZ twin pairs, 959 were from DZ twin pairs, and seven were from twin pairs with uncertain zygosity. As before, we considered a 10-year follow-up of mortality, from the baseline 1999 Cohort through January 2009. Vital status was again ascertained by the Danish Central Population Register (Pedersen et al. 2006).
Geriatric assessment
Cognitive function
The screening of cognitive impairment was carried out using the MMSE test (Folstein et al. 1975), a 30-point cognitive scale which evaluates several different areas of thinking including memory, judgment, calculation, abstraction, language, and visual-spatial ability. MMSE scores range from 0 (lowest cognitive function) to 30 (highest cognitive function). Since the test is affected by age and educational status, the MMSE scores were normalized for these variables.
Functional activity
The management of activities of daily living (toileting, getting up from bed, rising from a chair, walking around) was assessed using a modification of an international and widely used scale, the Katz’ Index of ADL (Katz et al. 1970). The assessment was based on what the subject was able to do at the time of the visit. Each activity was scored as 0 when the subject was unable to perform the activity analyzed and 1 when able to perform such activity. For survival analysis, ADL scores were dichotomized as 1 if the subject was independent in all items and 0, otherwise.
Physical performance
HG strength was measured by a handheld dynamometer (SMEDLEY’s dynamometer TTM, Tokyo, Japan) while the subject was sitting with the arm close to his/her body. The test was repeated three times with the stronger hand; the maximum of these values was used in the analyses. When a test was not carried out, it was specified if it was due to physical disabilities or because the subject refused to participate.
Self-reported health status
SRHS was assessed by asking the following question: “How is your health in general?” The possible answers were “excellent” (coded as 1), “good” (coded as 2), “acceptable” (coded as 3), “bad” (coded as 4), or “very bad” (coded as 5)”. For survival analysis, SRHS scores were dichotomized as 1 if the subject declared to be in “excellent” or “good” health status and 0, otherwise.
Statistical analyses
The Ward’s method (Ward 1963) was used to obtain two distinct hierarchical Cluster Analyses (CA) on the 1905 and LSADT cohorts, by means of the classification variables proposed by Montesanto et al. (2010). They include MMSE, HG, ADL, and SRHS. In such classifications, in order to choose the optimal number of groups, we plotted the increase in total within-cluster sum of squares against the number of groups. The optimal number of clusters was chosen by observing the largest drop in the total within-cluster sum of squares.
Once CA were performed and in order to obtain an easily understandable model applicable to clinical setting which could rapidly identify frail subjects in the analyzed sample, we availed of a supervised classification approach. In particular, we applied the Classification Tree (CT) algorithm to the baseline data considering the classification provided by the CA analyses of both the 1905 and LSADT cohorts as dependent variable, while the geriatric parameters (MMSE, HG, ADL, and SRHS) as independent variables. Adjusted values (i.e., with normalization) were used for all variables. The performance of the CT model was evaluated in terms of area under the curve (AUC; Bradley 1997) using a tenfold cross-validation strategy.
Kaplan–Meier estimates were used to obtain the survival curves for each group identified by the two classifications in the 1905 and LSADT cohorts. In order to evaluate the predictive value of both classifications with respect to mortality risk, the obtained survival curves were then compared by log-rank test. Subjects alive or immigrated at January 2009 were considered as censored, and this time was used as the censoring date in the survival analyses.
In order to assess individual contributions in predicting the survival time, classification variables of CA were further used as covariates (together with age and sex) for accelerated failure time (AFT) models. AFT models consist in a class of regression methods for survival data that assume a known distribution for the survival time and a direct proportionality between the logarithm of the survival time and the linear combination of model covariates (Eq. 1):
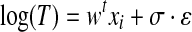 |
1 |
where T is the time to event, w is the vector of model coefficients, xi is the covariates vector of patient i, σ a scaling factor, and ε is the error distribution. Choosing a parametric distribution for ε automatically defines the corresponding parametric distribution for the survival time.
We preferred AFT models over the more commonly used Cox regression (Cox 1972) for several reasons. Firstly, the Schoenfeld residual test (Schoenfeld 1982) indicated that the variable SEX for the 1905 Cohort was not respecting the proportional hazard assumption: when this assumption does not hold, it is improper to use Cox regression as it may entail serious bias and loss of power when estimating or making inference about the effect of a given covariate (Sayehmiri et al. 2008). Secondly, AFT models provide a more comprehensible explanation of covariate effects, by directly linking the estimation of survival time with the values of covariates, while Cox models explain covariates effects in the context of the less intuitive hazard function. Finally, a recent study demonstrated the effectiveness and usefulness of using AFT models in aging research (Swindell 2009).
For both cohorts, we fitted AFT models using the following parametric distributions: Extreme, Logistic, Gaussian, Weibull, Exponential, Rayleigh, Lognormal, Loglogistic, and finally chose the best model on the basis of the Akaike’s Information Criterion (AIC; Akaike 1974).
The obtained AFT regression equation was then used to formulate a synthetic index. This index represents the ratio between the linear combination of covariates and coefficients of such model for a given individual i of the sample and the linear combination obtained in a sex- and age-matched individual with the worst value of covariates (HG, MMSE, ADL, and SRHS). Since this ratio takes higher values for lower frailty status, it seemed more appropriate to refer to it as “Robustness Index Ratio” (RIR).
Biometrical models were then used to estimate the heritability of the RIR in the LSADT sample (Neale et al. 1992). To this purpose, 219 MZ (89 male–male, 130 female–female) and 264 DZ twins (112 male–male, 152 female–female) were analyzed.
Survival and cluster analyses were carried out using R statistical environment (R Development Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria 2011, URL http://www.R-project.org). Decision trees were obtained using WEKA (Hall et al. 2009). Biometrical models were estimated using Stata statistical software (Stata Statistical Software College Station 2005).
A significance level of 0.05 was set for all the tests.
Results
Tables 1 and 2 report general characteristics and post-survey mortality in the Danish 1905 and LSADT cohorts, respectively, including information about some relevant geriatric parameters (MMSE, HG, ADL, SRHS).
Table 1.
General characteristics and post-survey mortality in the Danish 1905-Cohort
| Men | Women | Total | |
|---|---|---|---|
| (n = 390) | (n = 990) | (n = 1380) | |
| Survival | |||
| Deathsa [n (%)] | 382 (97.9) | 963 (97.3) | 1345 (97.5) |
| Person-years | 1244 | 3990 | 5234 |
| Mortality rate per 100 | 30.7 | 24.1 | 25.6 |
| Age (years) | |||
| Mean (SD) | 93.2 (0.3) | 93.1 (0.3) | 93.2 (0.3) |
| Range | 92.7–93.8 | 92.7–93.8 | 92.7–93.8 |
| MMSE | |||
| Mean (SD) | 22.8 (5.6) | 22.0 (5.4) | 22.2 (5.5) |
| Range | 2–30 | 0–30 | 0–30 |
| HG strength | |||
| Mean (SD) | 23.2 (6.5) | 13.6 (4.4) | 16.3 (6.7) |
| Range | 3–46 | 2–29 | 2–46 |
| ADLb [n (%)] | |||
| Not disabled | 180 (46.2) | 318 (32.1) | 498 (36.1) |
| Disabled | 210 (53.8) | 672 (67.9) | 882 (63.9) |
| BMI | |||
| Mean (SD) | 24.1 (3.2) | 22.9 (4.0) | 23.2 (3.8) |
| Range | 15.2–37.6 | 14.0–74.9 | 14.0–74.9 |
| SRHSc [n (%)] | |||
| Good | 227 (58.2) | 584 (59.0) | 811 (58.8) |
| Poor | 163 (41.8) | 406 (41.0) | 569 (41.2) |
aSurvival data are calculated from a 10 year follow-up period
bParticipants were defined as “not disabled” if independent in all items and “disabled” if dependent in at least one item
cParticipants were defined as “Good” if they declared to be in “excellent” or “good” health status and “Poor” otherwise
SRHS Self-reported Health Status, ADL Activity Daily Living, HG Hand Grip, MMSE Mini Mental State Examination
Table 2.
General characteristics and post-survey mortality in the LSADT-Cohort
| Men | Women | Total | |
|---|---|---|---|
| (n = 1016) | (n = 1323) | (n = 2339) | |
| Survival | |||
| Deathsa [n (%)] | 578 (56.9) | 599 (45.3) | 1177 (50.3) |
| Person-years | 7052 | 10256 | 17308 |
| Mortality rate per 100 | 8.2 | 5.8 | 6.8 |
| Age (years) | |||
| Mean (SD) | 77.1 (5.3) | 78.1 (5.8) | 77.7 (5.6) |
| Range | 70.3–95.3 | 70.3–97.8 | 70.3–97.8 |
| MMSE | |||
| Mean (SD) | 26.4 (3.4) | 26.2 (3.3) | 26.3 (3.4) |
| Range | 1–30 | 4–30 | 1–30 |
| HG strength | |||
| Mean (SD) | 34.4 (8.1) | 20.5 (5.4) | 26.5 (9.6) |
| Range | 8–60 | 2–40 | 2–60 |
| ADL [n (%)] | |||
| Not disabled | 897 (88.3) | 1143 (86.4) | 2040 (87.2) |
| Disabled | 119 (11.7) | 180 (13.6) | 299 (12.8) |
| BMI | |||
| Mean (SD) | 25.4 (3.3) | 24.3 (4.2) | 24.8 (3.9) |
| Range | 15.1–25.4 | 14.1–50.7 | 14.1–50.7 |
| SRHS [n (%)] | |||
| Good | 702 (69.1) | 894 (67.6) | 1596 (68.2) |
| Poor | 314 (30.9) | 429 (32.4) | 743 (31.8) |
aSurvival data are calculated from a 10 year follow-up period
SRHS Self-reported Health Status, ADL Activity Daily Living, HG Hand Grip, MMSE Mini Mental State Examination
Classification of frailty in the Danish 1905-Cohort
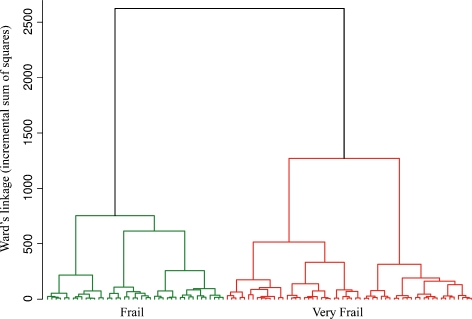
CA was carried out according to the procedure previously described (Montesanto et al. 2010). The values of MMSE and HG were used after adjustment for non-independent variables. In particular, MMSE scores were adjusted for education level (p < 0.001) and sex (p = 0.022); HG values were adjusted for sex (p < 0.001) and Body Mass Index (BMI; p < 0.001). Figure 1 reports the dendrogram plot of the clustering procedure.
Fig. 1.
Dendrogram obtained from the 1905-Cohort by applying a hierarchical cluster analysis which used Mini Mental State Examination (MMSE), Activity Daily Living (ADL), Self-reported Health Status (SRHS), and Hand Grip strength (HG) data as classification variables
In the Danish 1905-Cohort, the analysis of the increase in the total within-cluster sum of squares suggested to stop the clustering process when two clusters were obtained. In Table 3, we report the mean values of the relevant classification variables. On the basis of the mean values of these variables within the different clusters, we defined the two clusters identified by CA as frail (the cluster with subjects showing the best scores for the classification variables) and very frail (the clusters with subjects showing the worst scores for the classification variables) as previously suggested (Passarino et al. 2007; Montesanto et al. 2010).
Table 3.
Mean values (standard error in parenthesis) of Self-reported health status (SRHS), Activity Daily Living (ADL), Hand Grip strength (HG), and Mini Mental State Examination (MMSE) within the categories obtained by cluster analysis (CA) in the 1905-Cohort
| Classification variables (1905-Cohort) | ||||
|---|---|---|---|---|
| SRHS | ADL | HG | MMSE | |
| Frail (N = 876) | 2.24 (0.030) | 3.34 (0.030) | 18.0 (0.152) | 23.7 (0.170) |
| Very frail (N = 504) | 2.46 (0.039) | 1.02 (0.044) | 13.2 (0.200) | 19.6 (0.225) |
For MMSE and HG, adjusted mean values were reported (see Results)
As the table shows, in the very frail cluster, all the mean parameters are lower than those in frail cluster, except for SRHS. This is because of the coding of the SRHS variable, which assumes the highest values correspond to the worst health status (see “Materials and methods”). Figure 1 (Supplementary Material) reports the CT obtained in the Danish 1905-Cohort (AUC, 0.97), which shows how to use the results of CA analysis to set up easy rules to identify frail subjects in this population segment.
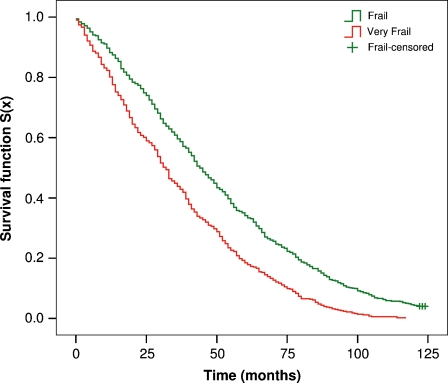
The Kaplan–Meier estimates of the survival functions were obtained according to the CA classification obtained in the 1905-Cohort (Fig. 2).
Fig. 2.
Kaplan–Meier survival functions for the frailty groups defined by cluster analysis (CA) in the 1905-Cohort
We found that the incidence of mortality was highly correlated to the frailty status. In fact, the estimated median survival time for frail subjects was 44 months versus 32 months for very frail subjects (p < 0.001).
In order to evaluate the effect of the different covariates on survival probabilities, an AFT model including as explanatory variables the same classification variables of CA was fitted to the 1905-Cohort. In this model, sex was used as adjunctive covariate (1 male, 0 female), while ADL and SRHS were dichotomized as previously described (see “Materials and methods”).
The AIC criterion indicated the Weibull distribution as the most suitable for the data under analysis. Table 4 reports the estimated coefficients of the fitted model with their standard errors and significance.
Table 4.
Estimated coefficients of the fitted Accelerated Failure Time (AFT) model in 1905-Cohort including Self-reported Health Status (SRHS), Activity Daily Living (ADL), Hand Grip strength (HG), Mini Mental State Examination (MMSE), and SEX as covariates
| Covariate | Coefficient value | Standard Error | p Value* |
|---|---|---|---|
| SEX | −0.260 | 0.042 | <0.001 |
| HG | 0.087 | 0.020 | <0.001 |
| MMSE | 0.140 | 0.020 | <0.001 |
| ADL | 0.198 | 0.042 | <0.001 |
| SRHS | 0.064 | 0.022 | 0.100 |
Standard errors and significance are reported
*p Value refers to Wald test
From Eq. 1, it is clear that positive coefficients lead to an increment of the expected survival time, conversely for negative coefficients. Thus, having high values of HG, MMSE, absence of disabilities, and a better SRHS induces higher probability of surviving while being male tends to decrement expected survival time (however, note that SRHS coefficient is not statistically significant).
The mean value of RIR index obtained from the fitted AFT model (see “Materials and methods”) was equal to 0.17 with a range between 0.04 and 0.27. As expected, with respect to the frailty phenotypes, frail subjects showed a higher RIR than very frail subjects (0.18 versus 0.13, p < 0.001).
Classification of frailty in the LSADT cohort
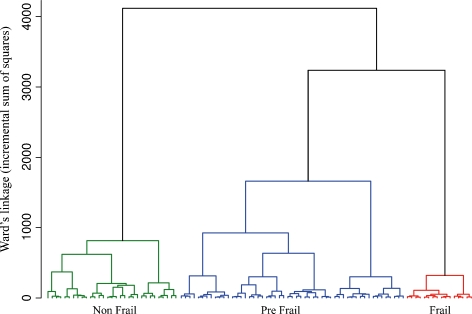
Using the same clustering procedure and classification variables, we performed a second CA on the LSADT dataset. In this sample, MMSE scores were adjusted for education level and age (p < 0.001 in both cases); HG values were adjusted for sex, age, and BMI (p < 0.001 in all cases). The cluster dendrogram plot and the analysis of the increase in the total within-cluster sum of squares suggested stopping the clustering process when three clusters were obtained (Fig. 3).
Fig. 3.
Dendrogram obtained in the LSADT-Cohort by applying a hierarchical cluster analysis (CA) which used Mini Mental State Examination (MMSE), Activity Daily Living (ADL), Self-reported Health Status (SRHS), and Hand Grip strength (HG) data as classification variables
Thus, as in the previous case, on the basis of the average values of the classification variables, we identified the three clusters as nonfrail, prefrail, and frail phenotypes as previously proposed (Passarino et al. 2007; Montesanto et al. 2010). Table 5 reports for each of the groups obtained by CA the mean values of the classification variables.
Table 5.
Mean values (standard error in parenthesis) of Self-reported Health Status (SRHS), Activity Daily Living (ADL), Hand Grip strength (HG), and Mini Mental State Examination (MMSE) within the categories obtained by cluster analysis (CA) in the LSADT-Cohort
| Classification variables (LSADT-Cohort) | ||||
|---|---|---|---|---|
| SRHS | ADL | HG | MMSE | |
| Nonfrail (N = 1315) | 1.560 (0.014) | 3.954 (0.006) | 29.011 (0.143) | 27.023 (0.084) |
| Prefrail (N = 940) | 2.821 (0.025) | 3.781 (0.017) | 23.672 (0.169) | 25.488 (0.099) |
| Frail (N = 84) | 3.131 (0.084) | 0.405 (0.054) | 19.763 (0.573) | 22.916 (0.336) |
For MMSE and HG, adjusted mean values were reported (see Results)
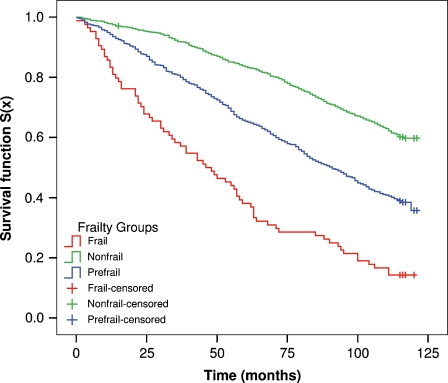
Supplementary Fig. 2 reports the CT obtained in the LSADT-Cohort (AUC, 0.98). Next, to assess the independent predictive validity of these frailty phenotypes, we estimated the Kaplan–Meier survival function according to the CA classification. Figure 4 shows the Kaplan–Meier survival functions according to the CA classification obtained in the LSADT-Cohort (Fig. 4).
Fig. 4.
Kaplan–Meier survival functions for the frailty groups defined by cluster analysis (CA) in the LSADT-Cohort
The mortality was correlated to the frailty status, and the difference among the survival curves of the relevant frailty phenotypes was highly statistically significant (p < 0.001).
Also in this case, an AFT model including the same classification variables of CA was fitted to the LSADT-Cohort. In this model, SEX and AGE were used as adjunctive covariates. ADL and SRHS were dichotomized as previously described. Even in this case, the Weibull distribution was chosen among the others following the AIC criterion. Table 6 reports the estimated coefficients of the fitted model with their standard errors and significance.
Table 6.
Estimated coefficients of the fitted Accelerated Failure Time (AFT) model in the LSADT-Cohort including Self-reported Health Status (SRHS), Activity Daily Living (ADL), Hand Grip strength (HG), Mini Mental State Examination (MMSE), AGE, and SEX as covariates
| Covariate | Coefficient value | Standard Error | p Value* |
|---|---|---|---|
| SEX | −0.360 | 0.039 | <0.001 |
| AGE | −0.068 | 0.004 | <0.001 |
| HG | 0.154 | 0.020 | <0.001 |
| MMSE | 0.047 | 0.017 | <0.001 |
| ADL | 0.231 | 0.054 | <0.001 |
| SRHS | 0.281 | 0.043 | <0.001 |
Standard errors and significance are reported
*p Value refers to Wald test
The main difference with respect to the AFT model referred to the 1905-Cohort, where all participants were of the same age, is that in this case the model introduces the AGE covariate, which negatively influences the expected survival time, i.e., older subjects have a shorter survival expectation. In addition, as the previous model, high values of HG, MMSE, absence of disabilities, and a better SRHS induce higher probability of surviving, while being male tends to decrement expected survival time.
The mean value of RIR index obtained from the fitted AFT model was equal to 0.20 with a range between 0.03 and 0.32. Also in this case, as expected, with respect to the frailty phenotypes, nonfrail subjects showed a higher RIR than prefrail and frail subjects (0.23, 0.18, 0.13, respectively; p < 0.001).
Taking advantage of the twin sample in LSADT-Cohort, once the CA was validated, we analyzed the resemblance in MZ and DZ twin pairs with respect to the classification variables of CA. We found that the mean distance for these geriatric parameters was about 11% lower in MZ than DZ twins (p = 0.038), suggesting that MZ are more similar than DZ twins.
Table 7 reports the polychoric correlations between twins for the RIR values. We see that, for all age groups, the correlation is higher among MZ than DZ. But, we also see for males a higher association between zygosity and the polychoric correlations. In addition, we note also an age difference in the association between zygosity and the polychoric correlations. In fact, the best-fitting model resulting from the biometrical analyses in the LSADT sample showed that 43% (95% CI, 31–53%) of the observed variation in the RIR could be explained by additive genetic effects, with a tendency for higher estimates in males than in females and higher in the oldest subjects.
Table 7.
Twin correlations (95% Confidence Intervals in parenthesis) for the age-adjusted estimated Robustness Index Ratio (RIR) by zygosity, sex, and age group
| Age | MZ alla | MZ male | MZ female | DZ SS alla | DZ male | DZ female | |
|---|---|---|---|---|---|---|---|
| All | Npairs (total) | 598 | 261 | 337 | 1186 | 527 | 659 |
| Npairs (complete) | 219 | 89 | 130 | 264 | 112 | 152 | |
| Correlation | 0.41 (0.27; 0.52) | 0.51 (0.31; 0.65) | 0.29 (0.10; 0.45) | 0.26 (0.13; 0.38) | 0.34 (0.15; 0.49) | 0.14 (−0.06; 0.32) | |
| <77.7 yearsa | Npairs (total) | 333 | 155 | 178 | 657 | 324 | 333 |
| Npairs (complete) | 142 | 60 | 82 | 192 | 87 | 105 | |
| Correlation | 0.36 (0.18; 0.50) | 0.34 (0.04; 0.55) | 0.36 (0.13; 0.53) | 0.14 (−0.01; 0.29) | 0.24 (0.02; 0.42) | −0.02 (−0.23; 0.20) | |
| ≥77.7 yearsa | Npairs (total) | 265 | 106 | 159 | 529 | 203 | 326 |
| Npairs (complete) | 77 | 29 | 48 | 72 | 25 | 47 | |
| Correlation | 0.45 (0.21; 0.60) | 0.71 (0.46; 0.83) | 0.19 (−0.13; 0.45) | 0.42 (0.20; 0.58) | 0.46 (0.11; 0.68) | 0.37 (0.05; 0.58) |
aMean age of analyzed sample
MZ momozygotic, DZ dizygotic, DZ SS dizygotic same sex, Npairs number of pairs (complete is referred to full couples of twins, while total Npairs number comprise also singletons)
Discussion
Frailty refers to a specific physiological state indicating a loss of homeostatic capacity, or resilience, which exposes the elderly to a number of negative outcomes, such as disability, diseases, falls, and death (Ferrucci et al. 2008; Fried et al. 2009). Frailty appears to be multidimensional affecting various systems of an aging organism. This potential deregulation of multiple physiologic systems leads to difficulty in maintaining homeostasis in response to “normal” perturbations which otherwise would not create such problems at younger ages (Yates 2002; Fried and Walston 2003). In this study, we approached two different, although related, aspects of the study of frailty. First, we tested a population-specific approach to define an individual frailty phenotype in a northern European population (the Danes) quite different in terms of quality of aging (see Jeune et al. 2006) from the Calabrian population of southern Italy where the approach was formulated for the first time (Montesanto et al. 2010). Subsequently, we tested the heritability of the individual frailty status in order to estimate the genetic component affecting this phenotype (Table 8).
Table 8.
Model parameters of the best fitted model for Robustness Index Ratio (RIR) heritability
| Gender | Age | A2 (95% CI) heritability | C2 | E2 (95% CI) |
|---|---|---|---|---|
| All | All | 0.43 (0.31; 0.53) | 0 | 0.57 (0.47; 0.69) |
| Males | All | 0.53 (0.37; 0.65) | 0 | 0.47 (0.35; 0.63) |
| <77.7 yearsa | 0.38 (0.14; 0.55) | 0 | 0.62 (0.45; 0.86) | |
| ≥77.7 yearsa | 0.72 (0.51; 0.83) | 0 | 0.28 (0.17; 0.49) | |
| Females | All | 0.29 (0.11; 0.44) | 0 | 0.71 (0.56; 0.89) |
| <77.7 yearsa | 0.28 (0.06; 0.47) | 0 | 0.72 (0.53; 0.95) | |
| ≥77.7 yearsa | 0.27 (0.05; 0.46) | 0 | 0.73 (0.55; 0.95) |
A2 additive genetic parameter, C2 common environment, E2 unique environment
aMean age of the analyzed sample
The successful replication of a cluster analysis approach for the definition of frailty in the Danish population samples suggests that the classification proposed by Montesanto et al. (2010) is applicable to different populations. In fact, cluster analysis based on parameters measuring the psychological and functional status of the subjects (cognitive status, physical performances, psychological status, disability) allowed the identification also in the Danish samples of two groups of subjects among the oldest olds (1905-Cohort) and three groups among old subjects (LSADT-Cohort), which were homogeneous for their frailty status. The mortality data referring to an extended period of follow-up available for our samples allowed testing the predictivities of our classifications in relation to survival. Indeed, we found a highly significant correlation between frailty and survival. It is worth noting that, in the longitudinal analysis of the 1905 sample, we studied a nearly extinct cohort (14 of 1,089 individuals were alive by the 1 January 2010), which increases the statistical power of our analysis. In addition, by availing of AFT models, we could break down the differential effect of distinct parameters on survival. In fact, we found that high values of HG and MMSE induced a higher probability of surviving, while being male, having a low ADL or a poor SRHS tended to reduce expected survival time. In particular, by analyzing the coefficients of the RIR formula obtained in the different aged samples (Tables 4 and 6), we can observe how functional status (HG, ADL) and psychological resource (SRHS) play a major role in frailty, and then on survival chance at youngest ages, while cognitive status is more important at advanced ages, which is in line with Nybo et al. (2003).
In order to compare the status of elderly subjects in Denmark and southern Italy, we applied the CT model inferred from LSADT dataset (Supplemental Fig. 2) to an age-matched sample collected in Calabria (southern Italy; Montesanto et al. 2010). We observed that approximately 70% of the subjects previously classified as nonfrail were reclassified as frail–prefrail (Supplemental Table 1). This result confirms the heterogeneity of the quality of aging and shows that southern European populations are characterized by a worse quality of aging, compared with northern Europeans, in line with Jeune et al. (2006). On the other hand, we found that the frailty groups defined in the Calabrian population using the model of classification inferred from LSADT dataset were not significantly different from each other in terms of survival. These data strongly suggest the necessity of population-specific analyses to define frailty phenotypes based on data gathered in each population and that it is not possible to apply the data universally (either thresholds, decisional trees, or other tools) to a single population.
The features of the LSADT sample, consisting of twin subjects, allowed us to compare the frailty status in MZ and DZ twins and to obtain an estimate of the heritability of this phenotype. For this purpose, we used the estimated RIR. We found that the additive genetic component accounts for 43% of the overall RIR variability. However, the estimate was higher in males than in females and higher in older subjects (above the mean age of 77.7 years of age). These findings are consistent with the presence of a genetic influence on frailty variance and suggest that the frailty status of men is more related to the genetic background while the frailty conditions of females are more dependent on environmental factors. In addition, we found that, as for lifespan (Passarino et al. 2006), the influence of the genetic component is higher at advanced ages. As for frailty indicators, it is worth noting that most heritability measures have been previously determined in samples of Danish twins using the same cohort analyzed in our study. In particular, hand grip strength heritability in Danish twins was estimated to be 52% in both sexes (Frederiksen et al. 2002). A modest degree of heritability for physical functioning was demonstrated by Christensen et al. (2003) in the LSADT-Cohort (approximately 10% for males and 35% for females). As for cognitive abilities, genetic factors accounted for 26–54% of the variance on MMSE and other cognitive measures in twins aged 75 years and older from the LSADT cohort (McGue and Christensen 2001). Finally, genetic factors can account for 25–64% of the variance in the liability of self-rated health (Mosing et al. 2010). As for the Danish population, heritability for SRHS was estimated to be 25% (Christensen et al. 1999).
Estimation of the heritability of a trait is very important for defining the biological basis underlying that given trait, although some cautions are necessary (Visscher et al. 2008; vB Hjelmborg et al. 2006). The data we mentioned may suggest that most of the heritability we observed for the frailty index is related to the heritability of muscular strength. On the other hand, the features observed for the heritability of the frailty index (which is higher in males than in females and is higher among the oldest subjects) are peculiar with respect to the heritability of each of its components, suggesting it may be correlated to the interaction of the different biological and genetic factors affecting frailty. These factors may act either through central pathways (affecting muscular strength or cognitive functions) or indirectly through genes associated with the organism’s homeostatic capacity. It is worth mentioning that heritability is population-specific and therefore it may be found to be different in further studies using the same cluster analysis approach.
The “cluster analysis” approach, based on psychological and functional geriatric parameters, cannot be used as is in each population but requires a preliminary screening of the population under study. However, the reproducibility of this approach in different populations and the consistency of heritability of the estimated RIR suggest that it may be able to classify elderly people according to their frailty level and to predict survival. In addition, the subsequent modeling of classification trees also makes the results of cluster analysis easy to use in clinical practice. The combination of psychological and functional parameters may then be a tool for understanding the physiological decline which is at the basis of frailty (Fried et al. 2001).
Electronic supplementary material
(DOC 30 kb)
(JPEG 1919 kb)
(JPEG 2168 kb)
Acknowledgments
The work was supported by Fondi di Ateneo of the University of Calabria and grants from Danish National Research Foundation and NIH/NIA P01 AG08761. The Danish Aging Research Center is supported by a grant from the VELUX foundation. AM was supported financially by a fellowship (assegno di ricerca) of the University of Calabria. The authors declare that no competing interests exist.
Footnotes
The authors Serena Dato and Alberto Montesanto equally contributed to the study.
References
- Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr. 1974;19:716–723. doi: 10.1109/TAC.1974.1100705. [DOI] [Google Scholar]
- Bradley AP. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997;30:1145–1159. doi: 10.1016/S0031-3203(96)00142-2. [DOI] [Google Scholar]
- Christensen K, Holm NV, McGue M, Corder L, Vaupel JW. A Danish population-based twin study on general health in the elderly. J Aging Health. 1999;11:49–64. doi: 10.1177/089826439901100103. [DOI] [PubMed] [Google Scholar]
- Christensen K, Frederiksen H, Vaupel JW, McGue M. Age trajectories of genetic variance in physical functioning: a longitudinal study of Danish twins aged 70 years and older. Behav Genet. 2003;33:125–136. doi: 10.1023/A:1022501817781. [DOI] [PubMed] [Google Scholar]
- Christensen K, Johnson TE, Vaupel JW. The quest for genetic determinants of human longevity: challenges and insights. Nat Rev Genet. 2006;7:436–448. doi: 10.1038/nrg1871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen K, McGue M, Petersen I, Jeune B, Vaupel JW. Exceptional longevity does not result in excessive levels of disability. Proc Natl Acad Sci USA. 2008;105:13274–13279. doi: 10.1073/pnas.0804931105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cournil A, Jeune B, Skytthe A, Gampe J, Passarino G, Robine JM. Handgrip strength: indications of paternal inheritance in three European regions. J Gerontol A Biol Sci Med Sci. 2010;65:1101–1106. doi: 10.1093/gerona/glq098. [DOI] [PubMed] [Google Scholar]
- Cox DR. Regression Models and Life-Tables. J Roy Stat Soc. 1972;34:187–220. [Google Scholar]
- Ferrucci L, Giallauria F, Schlessinger D. Mapping the road to resilience: novel math for the study of frailty. Mech Ageing Dev. 2008;129:677–679. doi: 10.1016/j.mad.2008.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. Mini-mental state. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12:189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Frederiksen H, Gaist D, Petersen HC, Hjelmborg J, McGue M, Vaupel JW, Christensen K. Hand grip strength: a phenotype suitable for identifying genetic variants affecting mid- and late-life physical functioning. Genet Epidemiol. 2002;23:110–122. doi: 10.1002/gepi.1127. [DOI] [PubMed] [Google Scholar]
- Fried LP, Walston J. Frailty and failure to thrive. In: Hazzard WR, editor. Principles of geriatric medicine and gerontology. 5. New York: McGraw-Hill Professional; 2003. [Google Scholar]
- Fried LP, Tangen CM, Walston J, Newman AB, Hirsch C, Gottdiener J, Seeman T, Tracy R, Kop WJ, Burke G, McBurnie MA, Cardiovascular Health Study Collaborative Research Group Frailty in older adults: evidence for a phenotype. J Gerontol A Biol Sci Med Sci. 2001;56:M146–M156. doi: 10.1093/gerona/56.3.M146. [DOI] [PubMed] [Google Scholar]
- Fried LP, Ferrucci L, Darer J, Williamson JD, Anderson G. Untangling the concepts of disability, frailty, and comorbidity: implications for improved targeting and care. J Gerontol A Biol Sci Med Sci. 2004;59:255–263. doi: 10.1093/gerona/59.3.M255. [DOI] [PubMed] [Google Scholar]
- Fried LP, Xue QL, Cappola AR, Ferrucci L, Chaves P, Varadhan R, Guralnik JM, Leng SX, Semba RD, Walston JD, Blaum CS, Bandeen-Roche K. Nonlinear multisystem physiological dysregulation associated with frailty in older women: implications for etiology and treatment. J Gerontol A Biol Sci Med Sci. 2009;64:1049–1057. doi: 10.1093/gerona/glp076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goggins WB, Woo J, Sham A, Ho SC. Frailty index as a measure of biological age in a Chinese population. J Gerontol A Biol Sci Med Sci. 2005;60:1046–1051. doi: 10.1093/gerona/60.8.1046. [DOI] [PubMed] [Google Scholar]
- Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA Data Mining Software: An Update. SIGKDD Explorations. 2009;11:10–18. doi: 10.1145/1656274.1656278. [DOI] [Google Scholar]
- Jeune B, Skytthe A, Cournil A, Greco V, Gampe J, Berardelli M, Andersen-Ranberg K, Passarino G, Debenedictis G, Robine JM. Handgrip strength among nonagenarians and centenarians in three European regions. J Gerontol A Biol Sci Med Sci. 2006;61:707–712. doi: 10.1093/gerona/61.7.707. [DOI] [PubMed] [Google Scholar]
- Katz S, Downs TD, Cash HR, Grotz RC. Progress in development of the index of ADL. Gerontol Spring. 1970;10:20–30. doi: 10.1093/geront/10.1_part_1.20. [DOI] [PubMed] [Google Scholar]
- McGue M, Christensen K. The heritability of cognitive functioning in very old adults: evidence from Danish twins aged 75 years and older. Psychol Aging. 2001;16:272–280. doi: 10.1037/0882-7974.16.2.272. [DOI] [PubMed] [Google Scholar]
- Mitnitski AB, Mogilner AJ, MacKnight C, Rockwood K. The accumulation of deficits with age and possible invariants of aging. ScientificWorldJournal. 2002;2:1816–1822. doi: 10.1100/tsw.2002.861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montesanto A, Lagani V, Martino C, Dato S, Rango F, Berardelli M, Corsonello A, Mazzei B, Mari V, Lattanzio F, Conforti D, Passarino G. A novel, population-specific approach to define frailty. Age. 2010;32:385–295. doi: 10.1007/s11357-010-9136-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosing MA, Pedersen NL, Martin NG, Wright MJ. Sex differences in the genetic architecture of optimism and health and their interrelation: a study of Australian and Swedish twins. Twin Res Hum Genet. 2010;13:322–329. doi: 10.1375/twin.13.4.322. [DOI] [PubMed] [Google Scholar]
- Neale MC, Cardon LR, North Atlantic Treaty Organization. Scientific Affairs D . Methodology for genetic studies of twins and families. Dordrecht; Boston: Kluwer Academic Publishers; 1992. [Google Scholar]
- Nybo H, Gaist D, Jeune B, Bathum L, McGue M, Vaupel JW, Christensen K. The Danish 1905 cohort: a genetic-epidemiological nationwide survey. J Aging Health. 2001;13:32–46. doi: 10.1177/089826430101300102. [DOI] [PubMed] [Google Scholar]
- Nybo H, Petersen HC, Gaist D, Jeune B, Andersen K, McGue M, Vaupel JW, Christensen K. Predictors of mortality in 2,249 nonagenarians–the Danish 1905-Cohort Survey. J Am Geriatr Soc. 2003;51:1365–1373. doi: 10.1046/j.1532-5415.2003.51453.x. [DOI] [PubMed] [Google Scholar]
- Passarino G, Montesanto A, Dato S, Giordano S, Domma F, Mari V, Feraco E, Benedictis G. Sex and age specificity of susceptibility genes modulating survival at old age. Hum Hered. 2006;62:213–220. doi: 10.1159/000097305. [DOI] [PubMed] [Google Scholar]
- Passarino G, Montesanto A, Rango F, Garasto S, Berardelli M, Domma F, Mari V, Feraco E, Franceschi C, Benedictis G. A cluster analysis to define human aging phenotypes. Biogerontology. 2007;8:283–290. doi: 10.1007/s10522-006-9071-5. [DOI] [PubMed] [Google Scholar]
- Pedersen CB, Gøtzsche H, Møller JO, Mortensen PB. The Danish Civil Registration System. A cohort of eight million persons. Dan Med Bull. 2006;53:441–449. [PubMed] [Google Scholar]
- Rockwood K, Song X, MacKnight C, Bergman H, Hogan DB, McDowell I, Mitnitski A. A global clinical measure of fitness and frailty in elderly people. CMAJ. 2005;173:489–495. doi: 10.1503/cmaj.050051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockwood K, Mitnitski A, Song X, Steen B, Skoog I. Long-term risks of death and institutionalization of elderly people in relation to deficit accumulation at age 70. J Am Geriatr Soc. 2006;54:975–979. doi: 10.1111/j.1532-5415.2006.00738.x. [DOI] [PubMed] [Google Scholar]
- Sayehmiri K, Eshraghian MR, Mohammad K, Alimoghaddam K, Foroushani AR, Zeraati H, Golestan B, Ghavamzadeh A. Prognostic factors of survival time after hematopoietic stem cell transplant in acute lymphoblastic leukemia patients: Cox proportional hazard versus accelerated failure time models. J Exp Clin Cancer Res. 2008;27:74. doi: 10.1186/1756-9966-27-74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schoenfeld D. Partial residuals for the proportional hazards regression model. Biometrika. 1982;69:239–241. doi: 10.1093/biomet/69.1.239. [DOI] [Google Scholar]
- Stata Statistical Software (2005) College Station, TX: StataCorp LP release 9.
- Swindell WR. Accelerated failure time models provide a useful statistical framework for aging research. Exp Gerontol. 2009;44:190–200. doi: 10.1016/j.exger.2008.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varadhan R, Seplaki CL, Xue QL, Bandeen-Roche K, Fried LP. Stimulus-response paradigm for characterizing the loss of resilience in homeostatic regulation associated with frailty. Mech Ageing Dev. 2008;129:666–670. doi: 10.1016/j.mad.2008.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- vB Hjelmborg J, Iachine I, Skytthe A, Vaupel JW, McGue M, Koskenvuo M, Kaprio J, Pedersen NL, Christensen K. Genetic influence on human lifespan and longevity. Hum Genet. 2006;119:312–321. doi: 10.1007/s00439-006-0144-y. [DOI] [PubMed] [Google Scholar]
- Visscher PM, Hill WG, Wray NR. Heritability in the genomics era–concepts and misconceptions. Nat Rev Genet. 2008;9:255–266. doi: 10.1038/nrg2322. [DOI] [PubMed] [Google Scholar]
- Walston J, Hadley EC, Ferrucci L, Guralnik JM, Newman AB, Studenski SA, Ershler WB, Harris T, Fried LP. Research agenda for frailty in older adults: toward a better understanding of physiology and etiology: summary from the American Geriatrics Society/National Institute on Aging Research Conference on Frailty in Older Adults. J Am Geriatr Soc. 2006;54:991–1001. doi: 10.1111/j.1532-5415.2006.00745.x. [DOI] [PubMed] [Google Scholar]
- Ward J. Hierarchical grouping to optimize an objective function. J Am Stat Assoc. 1963;58:236–244. [Google Scholar]
- Woo J, Goggins W, Sham A, Ho SC. Social determinants of frailty. Gerontology. 2005;51:402–408. doi: 10.1159/000088705. [DOI] [PubMed] [Google Scholar]
- Yates FE. Complexity of a human being: changes with age. Neurobiol Aging. 2002;23:17–19. doi: 10.1016/S0197-4580(01)00261-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOC 30 kb)
(JPEG 1919 kb)
(JPEG 2168 kb)