FTEC: a coalescent simulator for modeling faster than exponential growth

Abstract

Summary: Recent genetic studies as well as recorded history point to massive growth in human population sizes during the recent past. To model and understand this growth accurately we introduce FTEC, an easy-to-use coalescent simulation program capable of simulating haplotype samples drawn from a population that has undergone faster than exponential growth. Samples drawn from a population that has undergone faster than exponential growth show an excess of very rare variation and more rapid LD decay when compared with samples drawn from a population that has maintained a constant size over time.

Availability: Source code for FTEC is freely available for download from the University of Michigan Center for Statistical Genetics Wiki at http://genome.sph.umich.edu/wiki/FTEC

Contact: mreppell@umich.edu; szoellne@umich.edu

Supplementary information: Supplementary data are available at Bioinformatics online

1 INTRODUCTION

Recent human sequencing studies have uncovered a pattern of genetic variation characterized by a large proportion of very rare variation. Coventry et al. (2010) sequenced 13 715 individuals across two genes and found on average >1 variant every 24 bases. Singletons and doubletons accounted for 30% of variant sites. Other studies with between 5000 and 14 000 individuals have found that >50% of observed variants are found in at most two individuals (Exome Sequencing Project, unpublished data; M.R.Nelson et al., submitted for publication).

A large fraction of extremely rare variation in a population is evidence of recent dramatic population growth (Tajima, 1989). Growth in the human population has traditionally been modeled as either instantaneous or exponential (Adams and Hudson, 2004; Williamson et al., 2005). Coventry et al. (2010) posited that the pattern of variation observed in their data may have resulted from population growth occurring at an explosive, faster than exponential rate. Incorporating faster than exponential growth into statistical models aimed at estimating population genetic parameters has the potential to improve estimate accuracy. Additionally, refining statistical tools that test for the role of rare variants in disease and trait etiology will require simulated data with an accurate distribution of rare variants. Current time-efficient coalescent software only has the ability to model accelerating exponential growth via piecewise functions, however, it is not clear that this approach is able to easily generate data with the correct distribution of rare variation.

Here, we introduce FTEC, a fast coalescent simulation program capable of modeling haplotype samples drawn from a population which has grown at a faster than exponential rate. FTEC, by accurately modeling a wide range of population growth models, has the potential to simulate data with a frequency spectrum containing variation consistent with high-depth human sequence data. As the first step in understanding the impact of faster than exponential growth, we present linkage disequilibrium and patterns of variation for samples simulated using our software.

2 METHODS

2.1 Faster than exponential growth in the coalescent

The coalescent (Kingman, 1982) is a widely used stochastic process that models the ancestry of a sample backwards in time to its most recent common ancestor. One method for modeling a population which has expanded at a faster than exponential rate is to assume that the rate of change in population size is proportional to a power of the current population size (Tolle, 2003)

Here P is population size, t is time, α and β are constants, with α<0 in a growing population due to the coalescent modeling time backwards from the present. When we use the current population size P₀ as an initial condition, this equation has the general solution

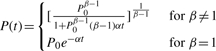(1)

For β > 1, Equation (1) models a population expanding at a faster than exponential rate. Following the notation of Donnelly and Tavaré (1995), P(t) can be transformed as Λ(t)=∫₀^tP₀/P(s)ds to ‘shift’ coalescent times from the standard model into coalescent times for a population with varying size.

2.2 Software

FTEC is implemented in C⁺⁺ and uses a simple command line interface with options for current effective population size; sample size; growth or contraction slower than, equal to or faster than exponential; instantaneous population size changes; uniform recombination; and a two subpopulation island model of population subdivision with migration. As in the Kingman coalescent (Kingman, 1982), FTEC generates times to coalescent, recombination and migration events as independent exponential variables. Mutation events are generated following a Poisson process after the sample's ancestry has been simulated, and are uniformly placed along the sample haplotypes. When simulating continuous growth, times are drawn from the standard model and shifted using the transformation outlined in Section 2.1. FTEC output is a series of haplotypes, designed to be compatible with downstream analysis tools that work with output from the popular ms program (Hudson, 2002).

2.3 Simulation parameters

We used FTEC to simulate 1000 independent samples of 10 000 haplotypes, each 50 kb in length, under 4 population models. Under all 4 models, the ancestral population size is 18 000 haplotypes until 500 generations in the past, and then: (i) the population remains constant in size; (ii) the population instantaneously expands to and then remains at an effective size of 10 000 000 haplotypes; (iii) the population begins growing at an exponential rate; or (iv) the population begins growing at a faster than exponential rate (β = 2) and expands to 10 000 000 haplotypes in size. Our sample sizes were intended to be similar to the recent estimates from M.R.Nelson et al., submitted for publication; we also performed simulations with current effective population sizes of 50 000 and 200 000 000 haplotypes (Supplementary Material). We set the per base mutation rate at 1.2×10⁻⁸ (1000) and set the recombination rate at 1.2 cM/Mb for our region (Kong, 2002). Note that model (i) contradicts the assumption of the coalescent that sample size be much smaller than effective population size, and is only included for comparison. On a 3.0 GHz Intel Core 2 Duo, FTEC required 50, 1125, 409 and 120 min to simulate models (i), (ii), (iii) and (iv), respectively.

3 RESULTS

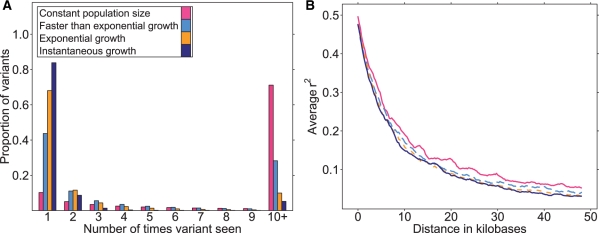
Under a model of faster than exponential growth (β = 2), on average 44% of variants in our samples were singletons and 11% were doubletons (Fig. 1A). These findings contrast with the exponential growth model where on average 68% of variants were singletons and 12% were doubletons, as well as the constant populations size model, where on average 10% of variants were singletons and 5% were doubletons, and the instantaneous growth model where on average 84% of variants were singletons and 9 were doubletons. The rate of pairwise linkage disequilibrium decay is quite similar across the models investigated. Looking closely, linkage disequilibrium decays slowest in constant populations and at an intermediate rate in populations with faster than exponential growth. LD decays fastest in exponentially growing and instantly growing populations (Fig. 1B). Average pairwise r² was >0.25 until a distance of 7.0, 6.9, 6.0 and 5.8 kb for the constant size population, faster than exponential growth, instantaneous growth and exponential growth models, respectively. Results for D^′ decay are qualitatively similar (Supplementary Material).

Fig. 1.

Comparing demographic parameters across population growth models. (A) Site frequency spectrum: average proportion of variants with given allele counts across simulated samples. (B) Average pairwise r² between two variants as a function of distance.

4 CONCLUSION

FTEC provides the opportunity to study easily a broader range of population growth models under the coalescent than has previously been possible. As ever larger sequencing studies bring the rarest portion of the site frequency spectrum into focus, we have provided a tool that can help test theories of how the rarest variation arose and simulate data with a realistic distribution of variants.

Funding: National Institutes of Health [HG000040, HG000376, HG005855].

Conflict of Interest: none declared.