Scaling of growth: Plants and animals are not so different

The relationship of body size to the anatomical, physiological, behavioral, and ecological characteristics of animals has long been a focus of interest in zoology. As one considers animal species of different sizes, regular, predictable changes are seen in the relative proportions of the body's organs and the relative rates of physiological processes such as metabolism and growth. Students of zoology are familiar with these scaling relationships (also called allometries) and many of their ecological and adaptive implications (1–3). For example, the relative scaling of metabolism versus that of the volume of the digestive tract affects the potential diets of herbivorous mammals, which in turn influences their social behavior (4, 5).

Plant biology, on the other hand, does not have a long history of investigation of issues involving the scaling of physiological processes versus body-size, despite a wealth of detailed data on plant morphology and function. This situation is perhaps because plants are seen to exhibit degrees of modular construction, indeterminate growth, and variety of form greater than those shown by animals, so the idea of a plant species even having a “body size” strikes some as problematical. Nevertheless, plant species do have characteristic shapes and sizes and span 20 orders of magnitude in body mass. Niklas's 1994 book on plant allometry (6) has been described fairly as the first attempt to provide a unified treatment of plant form and function from an allometric perspective. However, until even more recently, the scaling of such basic processes as metabolism and growth had remained undocumented for a representative sample of plant species. In this issue of PNAS, Niklas and Enquist (7) present empirical scaling relationships involving the rates of plant growth in species ranging from unicellular algae to large trees. These new analyses reveal that growth scales among plants in the same way that it does among animals, and further underscores the growing realization that the same scaling rules may apply to both animals and plants, and for much the same reasons.

Growth rates, or rates of production of new biomass, are of fundamental importance in linking physiological processes to adaptively important features such as reproductive rates and other life history variables (8). Among animal species, rates of biomass production and growth are proportional to metabolic rate, which scales as the 3/4 power of body mass (M; refs. 1 and 3). This proportionality, where organismal growth rate scales as M^0.75, makes intuitive sense. Cells should divide or otherwise do work at rates roughly proportional to the rates at which they are supplied with energy. Across different species, these rates should be the rates of metabolism, less the energy used for physiological maintenance and ecological demands, and energy lost as heat. Previous work (9) has strongly suggested that plant nutrient flux used for photosynthesis scales as M^0.75. This result implies that plant growth rates should also scale as M^0.75, a value that is confirmed by Niklas and Enquist (7). Further emphasizing this connection between plant metabolic processes and growth rates is the additional demonstration that the anatomical measures of an individual's photosynthetic pigment volume (and thus its presumed ability to obtain energy) also scale as M^0.75.

It is interesting to compare the rates of growth of animals and plants over size ranges that they have in common (Fig. 1). In the Niklas and Enquist study, only the trees represent a sufficient diversity of species to permit comparison with a wide range of animal species, so only a portion of the overall body size range is shown. Although there is insufficient information here to discuss the relative efficiency of plants and animals in the conversion of energy to growth, it is clear that the realized somatic growth rates of both plants and animals of comparable body mass are remarkably similar. This finding suggests that the cells of both plants and animals are similarly limited in the rates by which they can effectuate growth, just as the abilities of different-sized plants and animals to deliver energy to their cells are similarly constrained by scaling relationships.

Figure 1.

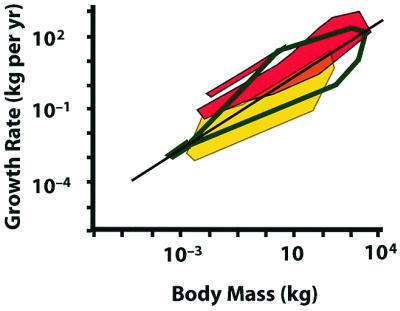
Comparison of growth rates of trees and vertebrates, plotted on a common scale. Polygons represent the regions occupied by the data points. The dark green unfilled polygon encloses tree data from Niklas and Enquist (7). The endothermic vertebrates—mammals (large polygon) and birds (small polygon)—are in red, ectothermic vertebrates in yellow. Ectotherms and endotherms overlap in a narrow region. The regression line is that presented in ref. 7. Vertebrate data recalculated from refs. 18 and 19.

Niklas and Enquist point out that a single linear relationship characterizes the growth allometry of all plants over the 20 orders of magnitude in plant size that they studied. True, among plants, there is no equivalent to the distinction among animal taxonomic groups between “warm-blooded” (endothermic) and “cold-blooded” (ectothermic) metabolic regimes. The tendency toward higher growth rates of endothermic vertebrates is evident in Fig. 1. One should not conclude, however, that variation in growth rates among plants of a similar size is either small or without biological significance. Note that the range of variation in growth rates of trees at some sizes is greater than that found among either ectothermic or endothermic vertebrates taken alone. In fact, there is some reason to believe that the full range of variation in tree growth rates is somewhat underestimated in the Niklas and Enquist dataset (7), so trees may vary almost as much as vertebrates of both kinds together. Thus, although Niklas and Enquist report no differences among the major groups they studied, future research dissecting such datasets may well identify functional correlations between growth rates and physiological or environmental variables.

Students of scaling are also aware of a major unresolved issue that has challenged biologists for more than half a century. 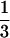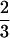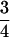Although many anatomical features scale in the way we would expect parts of three-dimensional objects to scale (lengths as M, areas as M, and volumes as M^1.00), rates of physiological processes, structures dependent on those rates, and life history variables usually scale approximately as M, M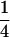, or some similar exponent related to one-fourth. The M^0.75 scaling of metabolic rate is one of the most well established empirical relationships in animal biology, but a fully convincing explanation for it has eluded researchers for decades.

Now, the finding that plants may exhibit exactly the same scaling relationships for metabolism and growth as do animals further constrains the possible mechanisms for generating the 3/4-power scaling rules. Explanations that rely on the properties of animals alone (e.g., ref. 10) are now no longer tenable. A number of researchers have focused attention on the properties of the nutrient transport networks that both plants and animals exhibit.

Niklas and Enquist favor an explanation based on modeling the vascular transport network as a “fractal-like” object (11). Such a model derives the 3/4 scaling exponent of metabolism from a contrast between the scaling of the external dimensions of the body and the scaling of the dimensions of the internal nutrient transport network, which is modeled as having some fractal properties (for a nontechnical explanation, see ref. 12). In this model, it is assumed that natural selection has acted at each size to maximize the internal area for absorbing nutrients and to minimize transport distances. This assumption suggests that maximal rates of metabolic activity are the primary determinants of fitness in most lineages. Consequently, it is not clear why this model would predict that resting rates of metabolism would also scale as M^0.75, unless they are somehow constrained to be a constant fraction of maximal rates.

In further support of this model, Niklas and Enquist (7) present an additional allometric relationship, one not directly related to growth rates. They claim that the fractal model predicts that total body length of plants (L) will scale as M^0.25. This prediction is distinctly different from the expectation of geometric similarity (where L scales as M^0.33), which is supported by extensive previous empirical work on both plants and animals (3, 13). Niklas and Enquist find the 0.25 exponent in their data only within algae and when pooling all of the data for algae and multicellular plants; trees considered by themselves continue to exhibit geometric similarity. Clearly, further empirical work is needed to decide how best to characterize the scaling of L in plants.

Other general models can also be applied to both animals and plants, but with different assumptions (and not involving fractals). Basing their argument on very simple geometric considerations, Banavar et al. (14) show that 3/4 scaling of nutrient delivery (metabolic rate) is the expectation in any efficient three-dimensional transportation network—animate or inanimate. All that needs to be assumed is that tissue composition (e.g., blood to volume ratio) is more or less constant across sizes and that the network supplies nutrients to all sites at a constant rate (both of which are true for animals, at least). Natural selection specifically for maximum capacity is not required; the 3/4 scaling emerges out of the minimal requirements for a functional network.

Another approach might be to generalize the theory of dynamic energy budgets (15) to include plants. Under this modeling scheme, properties such as whole-organism metabolic rates are derived as weighted sums of other rates that are specifically associated either with areas (M^0.67) or volumes (M^1.00). A scaling exponent between 0.67 and 1.00 is thus expected, but considerable variation within different groups is also possible depending on the detailed properties of the organisms.

Whatever the mechanisms are that generate the scaling rules, the fact that plants follow them so well has major practical implications for research in plant ecology and paleobiology. Unlike animal communities, plant communities tend to be dominated by extensive stands of similar-sized individuals. Metabolism and growth rates do not tell us how resources or energy will be partitioned among species of the same or different sizes in the same habitat. However, because plants share the same physiological properties, community level properties such as total energy use and production are expected to be largely independent of species composition. And, suggest Niklas and Enquist, given the fact that the species of dominant stature tend to fill the environment, a tradeoff between numbers and size further suggests that dominant plant stature has little effect on possible rates of community production as well.

Finally, the adherence of plants to regular scaling rules improves our ability to model and reconstruct both plant autecology and ecosystem processes in the fossil record. Paleozoology has benefited greatly from being able to rely on allometries to estimate physiological or ecological variables not directly measurable on fossils (16). Even for dinosaurs, scaling relationships allow us to explore the implications of alternative metabolic physiologies for both the functioning of individuals and their ecology (17). Scaling relationships for plants will, it is hoped, provide a route to even greater understanding of past environments and their biotas.