Abstract
Aedes albopictus, a species known to transmit dengue and chikungunya viruses, is primarily a container-inhabiting mosquito. The potential for pathogen transmission by Ae. albopictus has increased our need to understand its ecology and population dynamics. Two parameters that we know little about are the impact of direct density-dependence and delayed density-dependence in the larval stage. The present study uses a manipulative experimental design, under field conditions, to understand the impact of delayed density dependence in a natural population of Ae. albopictus in Raleigh, North Carolina. Twenty liter buckets, divided in half prior to experimentation, placed in the field accumulated rainwater and detritus, providing oviposition and larval production sites for natural populations of Ae. albopictus. Two treatments, a larvae present and larvae absent treatment, were produced in each bucket. After five weeks all larvae were removed from both treatments and the buckets were covered with fine mesh cloth. Equal numbers of first instars were added to both treatments in every bucket. Pupae were collected daily and adults were frozen as they emerged. We found a significant impact of delayed density-dependence on larval survival, development time and adult body size in containers with high larval densities. Our results indicate that delayed density-dependence will have negative impacts on the mosquito population when larval densities are high enough to deplete accessible nutrients faster than the rate of natural food accumulation.
Introduction
In the field of population ecology, both density independent factors and density dependent factors can influence the dynamics and growth of a population [1]. Density-dependent factors can impact populations by both first order feedback (direct density-dependence) and second order feedback (delayed density-dependence) [2]–[4]. First order factors have direct impacts on the current population or generation of individuals, whereas second order factors have delayed impacts on the current generation or on future generations of the population.
Delayed density-dependence has been shown to cause population fluctuations in plant-herbivore systems [5]–[7] and is associated with predator-prey cycles [8], [9]. However, there has been a long standing debate over the power of various methods for detecting delayed density-dependence [10]–[13].
Most investigators have used time series analysis to determine the role of delayed density-dependence. For example, long-term data have provided evidence for delayed density-dependence in populations of the potato aphid, Macrosiphum euphorbiae, [14], southern pine beetle, Dendroctonus frontalis, [15], forest tent caterpillar, Malacosoma disstria, [16] and in the cohabitating common sardine, Strangomera bentincki, and populations of the anchovy, Engraulis ringens [17].
In the present study, we tested for delayed density-dependence, specifically the impact of a current generation on a future generation of natural populations of Aedes albopictus, the Asian tiger mosquito. Instead of using time series analysis, we conducted a manipulative field experiment. Ae. albopictus is a competent laboratory vector of at least 22 arboviruses [reviewed in 18], including dengue (DENV) and chikungunya viruses (CHIKV) [19], [20]. It is established throughout the United States where its larvae develop in both naturally occurring tree holes and artificial containers such as bird baths, tires, and buckets [21], [22]. Previous studies in the laboratory and semi-field conditions have shown that direct density-dependence can impact larval survival, larval development, and adult body size in container inhabiting mosquitoes [23]–[26].
Aspbury and Juliano studied effects of leaf litter previously exploited by Ae. triseriatus larvae on a subsequent cohort of larvae [27]. In the laboratory, they prepared small containers holding leaf litter to provide two different treatments, one treatment without larvae and one treatment with 25 neonate larvae. All larvae were allowed to reach pupation and both leaf litter treatments were kept in the laboratory for 70 days. After 70 days, all small containers were taken to the field and placed in either a treehole or tire; each contained multiple small caged replicates of both treatments. Twenty-five newly hatched larvae were then placed into each small cage and survival, development time, and adult size were compared between treatments. Aspbury and Juliano found that in treeholes, small cages with leaf litter previously exploited by Ae. triseriatus larvae yielded longer larval development time and smaller adult size in the following cohort of larvae compared to litter that had not been previously exploited by larvae. Although this study is an appropriate starting point to assess the effects of a prior cohort, this study system was an open system in the sense of allowing flow of water between treatments within each treehole, which may reduce the apparent impact of delayed density-dependence. More importantly, number of larvae and amount of food were determined arbitrarily by the investigators.
Delayed density-dependence in container inhabiting mosquitoes is expected when the natural density of larvae are removing accessible nutrients faster than they are replaced by liter accumulation, decomposer growth, and primary production by photosynthetic microorganisms. Notably, we have found no published studies of mosquito species that assesses the impact of naturally-occurring larval densities on delayed density-dependence even in semi-naturally occurring containers.
Because container-inhabiting mosquitoes typically feed on dead and living organic material, including microorganisms such as fungi, protozoans, and bacteria that grow on the container's surfaces, detritus on surfaces or within the water column [28], it is hard to replicate the naturally occurring environment in the laboratory. Ae. albopictus spend more time foraging when leaves are present in a container compared to containers with only water [29], [30]. These leaves provide extra surface for microorganism growth and possibly a superior food source. Other studies have shown that larvae which fed on animal detritus yields higher population growth, larval survival, and adult size when compared to those fed on plant detritus [31], [32]. Our goal was to examine delayed density dependence in environments that closely mimicked those that Ae. albopictus encounter naturally.
Our study took advantage of the fact that in urban environments, Ae. albopictus larvae often develop in artificial containers such as 5-gallon buckets [21]. We used buckets in the field that were experimentally divided in half to provide a method of testing for delayed density-dependence in natural populations. We compared the fates of neonate larvae placed in one side of the bucket that previously had naturally occurring larvae within it to the fates of larvae placed in the other half that had no previous larvae because naturally-laid eggs had been removed. The hypothesis of strong delayed density-dependence predicts that in comparison to the treatment in which eggs were removed, the treatment that had larvae in the previous cohort would yield longer larval development time, lower larval survival, and smaller adult body size for the following cohort of larvae.
Materials and Methods
Study Site
This study took place in Raleigh, Wake County, North Carolina (city population of 356,321), in a suburban area of the city (census.gov). Seven houses within the city were chosen as sites for the study. The mean distance between nearest neighbor houses was 5.6 kilometers and the farthest house was 21 kilometers from the center of the city. The study took place from June through September, 2009 when natural populations of Ae. albopictus are prevalent.
General Experimental Design
Twenty liter paint buckets were used as the experimental containers. Six buckets were placed outside each house for a total of 42 buckets. Prior to initiating the experiment, the buckets were vertically divided in half with styrofoam insulation and all edges between the two sides were sealed with hot glue. This method allowed two treatments within each bucket and ensured that water, nutrients, and larvae could not pass between the two treatments. All buckets were carefully checked to ensure the partition was well sealed before placing the buckets at each experimental site. Buckets were checked throughout the investigation and only one was found to have water passing between the treatments; that bucket was omitted from the analysis.
Our investigation consisted of two sequential experiments. In the first six weeks we manipulated the buckets to produce the two treatments, and in the following weeks we tested the impact of the treatments on survival, development time, and adult body size of a newly introduced cohort of larvae.
Treatment Production
During the first six weeks of the investigation the two treatments were produced within each bucket: a “larvae-present” treatment (hereafter LP) and “larvae-absent” treatment (hereafter LA). The buckets were placed at residences with 1 L of rainwater seeded in each side. All buckets had a hole drilled 1 inch from the top of the bucket on each treatment side to prevent rain water from overflowing the bucket. The buckets were left uncovered for five weeks to allow natural rainwater (no additional water was added by the authors) and detritus to accumulate in the buckets, and for microorganism growth on that detritus. The natural populations of Ae. albopictus laid eggs in the buckets during that time period.
The LA treatment was checked daily for eggs and larvae. Eggs on the sides of the buckets were killed and removed with a paper towel. The water was checked for any larvae, and the small numbers of larvae found during the 5-week period were removed.
In the LP treatment, eggs were allowed to hatch and larvae were left undisturbed through pupation. Pupae were collected daily and placed in individual plastic tubes with water. When adults emerged they were stored frozen in individual 1.5 mL microcentrifuge tubes. Subsequently, adults were identified to species and the right wing was measured as an indicator of adult body size. Wings were measured using QCapture Pro 6.0 software.
On the last day of week 5, all eggs were removed and killed from both sides of the bucket, and all larvae and pupae were removed. All larvae from the LP treatment were counted as they were removed to yield an estimate of the larval density for each bucket. The buckets were covered with a fine mesh cloth to prevent oviposition. All buckets were checked every other day for one week for any new larvae that hatched from missed eggs. Any larvae found were removed.
Effects of treatments
To test for the impact of delayed density-dependence, the same numbers of first instar larvae were placed into both treatments within a given bucket and the bucket was recovered with the fine mesh cloth to prevent further oviposition. If there was delayed density dependence, we expected the new larvae placed in the half of the bucket that previously had larvae would perform more poorly. The buckets contained different numbers of larvae during the first 5 weeks of the experiment. We assumed that the natural density of larvae in the recent past is the best predictor of future natural larval density in a given bucket (see [33] on differential attractiveness of buckets for Aedes oviposition). Therefore, in order to better mimic the expected natural situation, the number of larvae placed in each bucket reflected its past history of infestation.
The number of first instars released in a bucket was determined by a three step calculation: 1) for each bucket, a ratio of the number of pupae on the last day of 5 weeks to the number of larvae counted the same day was calculated, 2) Ratios were averaged across all buckets across all sites to give us an overall estimate of the ratio of pupae to larvae for any given day, 3) the daily number of pupae averaged over the first 5 weeks for each bucket was divided by the average pupae to larvae ratio to provide a rough estimate of the average daily number of larvae for each bucket. This estimate of average daily number of larvae was used to set the number of first instars released into both treatments of a given bucket. First instar larvae were released in two different densities, the natural density, as calculated (referred to as 1×), and ten times the calculated density (referred to as 10×). The numbers of estimated larvae and actual larvae released in each bucket are shown in supplemental material (Table S1). At each house, half of the buckets received larvae at each density, and buckets were randomly assigned to a density. All further references to 1× and 10× densities refer to the post-treatment phase of the experiments.
The first instar larvae (New Orleans, LA strain) for the 2nd part of the experiment were hatched in the laboratory. The colony was maintained at ∼28°C, ∼75% RH, and a photoperiod of 14 h light:10 h dark, including two twilight periods (60 min each). Larvae in both treatments were left undisturbed through pupation. Pupae were removed daily and allowed to develop to adults as described previously. We then compared larval development time, larval survival and adult wing length between the two treatments.
Statistical Analysis
Statistics were computed using SAS Version 9.13 (SAS Institute, Inc., Cary, NC, U.S.A.). To test for treatment effects on development time we used a mixed model analysis of variance (ANOVA) with a main effect of treatment. To test the effects on wing length, we used a mixed model ANOVA with main effects of density (1× and 10×), treatment (LP and LA), and density x treatment interaction. For both analyses, bucket nested within house (for development time), house x density (for wing length), and house were considered to be random effects. Development time and wing length variables were measured as means from the cohorts of each bucket. To test the effects on larval survival, an additional effect of log of estimated larval density was added to the above model. Larval survival and female wing length had different variances for the two levels of density. Therefore, these response variables were modeled with the degrees of freedom divided by density group using the Kenward-Roger method [34], resulting in fractional degrees of freedom. In order to allow comparisons between treatments within each bucket, treatment was modeled as a repeated statement within bucket. For pairwise comparisons, we examined differences in least squares (LS) means of the dependent variables for the LP and LA treatments within each density. Two containers had a Student residual greater than 3.5 and had a large impact on the results; these were considered outliers and removed from the analysis [35].
Development time was measured as the number of days it took for the first instar larvae to pupate. Proportion survival was measured as the total number of larvae that pupated divided by the total number of larvae placed in that container. We found that many buckets had a proportion of larvae surviving higher than 1.0. This could have resulted from unsuccessful killing of all eggs at the end of the first 5 weeks or eggs being laid on the surface of the water [36]. The 1× containers had 20 buckets with survival higher than 1.0 and the 10× containers had 3 buckets with survival higher than 1.0. The extra larvae would be anticipated to have a larger impact on the 1× containers than 10× containers.
Results
Development time
There was not a significant effect of treatment on 1× density containers (F 1, 32 = 0.51, P = 0.482), but there was a significant effect of treatment on 10× containers (F 1, 32 = 9.58, P = 0.004) on development time. On average, larvae in 10× containers developed 8% more slowly in the LP treatment compared to the LA treatment (Figure 1).
Figure 1. Results for development time.
Least squares mean development time (days) for each treatment and density level. Vertical bars represent standard errors. Letters indicate significant differences.
There was no significant relationship between the log of estimated larval density and the difference in development time between the LP and LA treatments in a given container for either level of initial density (Figure S1).
Survival
The mixed model analysis for proportion survival indicated a significant effect of log of estimated larval density (F 1, 19.8 = 13.78, P = 0.001), density (F 1, 19.5 = 10.62, P = 0.004), and a log of estimated larval density x treatment interaction (F 1, 19.2 = 5.22, P = 0.033
Containers that had higher larval densities during the first 5 weeks of the experiment (pre-treatment) had a significantly lower proportion of larvae surviving to pupation and a larger difference in survival between the LP and LA treatments during the post-treatment phase. Using a linear regression, there was a significant relationship between the log of estimated larval density and the difference between the two treatments for proportion survival in 10× containers (r2 = 0.223, df = 19, P = 0.031), but no significant relationship in 1× containers (r2 = 0.019, df = 19, P = 0.567) (Figure 2).
Figure 2. Effect of estimated larval density on proportion survival.
Relationship between the difference in proportion survival between the LA treatment and LP treatment for each container and the log of estimated larval density for both 1× density containers (A) and 10× density containers (B).
Male wing length
Using a mixed model analysis, there was a significant effect of density (F 1, 6 = 18.42, P = 0.005), treatment (F 1, 48 = 5.93, P = 0.019), and a density by treatment interaction (F 1, 48 = 8.23, P = 0.006) on male wing length. Males from containers with a 1× density had significantly longer wing lengths than males from 10× density containers across both treatments (t 6 = 4.29, P = 0.005) (Figure 3).
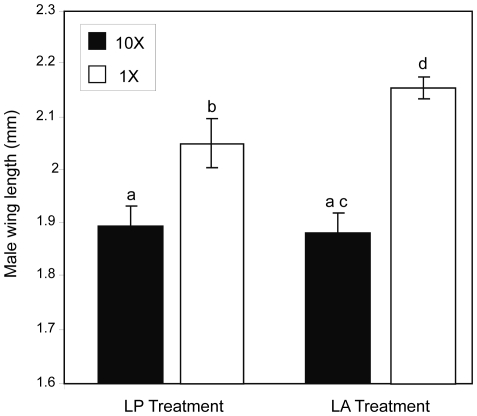
Figure 3. Results for male wing length.
LS mean wing length (mm) for each treatment and density level. Vertical bars represent standard errors. Letters indicate significant differences.
There was a significant difference in male wing length between the LP treatment and the LA treatment for containers with 1× density (t 48 = 3.54, P = 0.033). The average male wing length was larger for the LA treatment (mean = 2.16) than for the LP treatment (mean = 2.04) (Figure 4). There was no significant difference in male wing length between the two treatments for the 10× containers (t 48 = 0.33, P = 0.75).
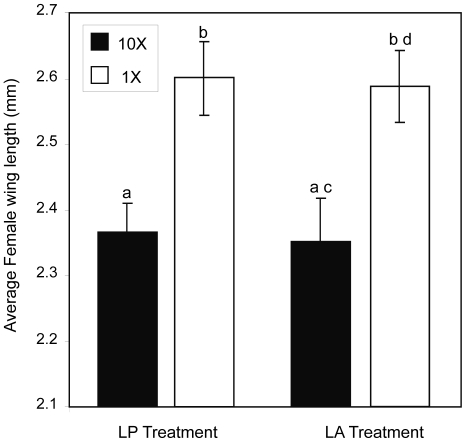
Figure 4. Results for female wing length.
LS mean wing length (mm) for each treatment and density level. Vertical bars represent standard errors. Letters indicate significant differences.
There was not a significant relationship detected between the log of estimated larval density (pre-treatment) and the difference in male wing length (post-treatment) between the two treatments for either the 10× density (r2 = 0.046, df = 17, P = 0.393) or 1× density (r2 = 0.149, df = 14, P = 0.155) (Figure S2).
Female wing length
There was no significant effect of treatment (F 1, 29.3 = 0.09, P = 0.767) or a density by treatment interaction on female wing length (F 1, 29.3 = 0.01, P = 0.941) from the mixed model analysis. However, there was a significant effect of density on female wing length (F 1, 23 = 11.61, P = 0.002) (Figure 4). On average, females that emerged from containers receiving 1× densities (mean = 2.56) had longer wing lengths than those that emerged from containers receiving 10× densities (mean = 2.36).
Similar to the results of male wing length, there was no significant relationship between the log of estimated larval density (pre-treatment) and the difference in female wing length (post-treatment) between the LP and LA treatments for either the 10× density (r2 = 0.182, df = 15, P = 0.09) or 1× density(r2 = 0.108, df = 14, P = 0.232) (Figure S3).
Discussion
Containers with 10× densities had an overall lower proportion of larvae surviving to pupation and smaller wing lengths for both males and females. This suggests that direct density-dependence factors may influence larvae in field populations of Ae. albopictus. Although we cannot definitively conclude this from our data because we specifically added a cohort of neonates as opposed to testing for direct density-dependence on the naturally occurring larvae, our results are in agreement with previous laboratory [23] and semi-field condition studies [26], [37] of Ae. albopictus.
Delayed density-dependent effects were detected on larval survival to pupation when comparing the proportion of larvae surviving to pupation in the LP and LA treatments in containers receiving 10× densities. However, no significant effects of delayed density-dependence on survival were detected in containers receiving 1× densities.
Containers populated by greater numbers of naturally occurring larvae during the first five weeks (pre-treatment) yielded a stronger impact of delayed density-dependence on survival during the post-treatment phase as shown by the larger differences between the LP and LA treatments in containers that initially had high larval densities. These containers not only experienced higher numbers of naturally occurring larvae, but also had higher numbers of larvae released into the containers to test for delayed density-dependence because the numbers of larvae released were based on the naturally occurring larvae found in each container. Our results indicate that delayed density-dependent effects are produced at a larval density, which may be dependent on both previous and current cohorts, that depletes resources faster than the resources accumulate. It is likely that for this reason we did not detect delayed density-dependence in 1× containers. If populations cycle in the field, delayed density-dependence may only have impacts during the higher density points in the cycle when larvae cause a net decline in available nutrients for future cohorts.
Development time was negatively affected by delayed density-dependence, but only in 10× density containers. Consistent with our survival results, this finding further supports the hypothesis of delayed density-dependence acting only when a high larval density is reached. There was no impact of delayed density-dependence on female wing length. As seen with development time, delayed density-dependence negatively affected male wing length, but only in 1× containers. These results for male wing length are inconsistent with development time, in which delayed density-dependence was detected in 10× containers only. We analyzed male and female development time separately but there was no significant effect of treatment on development time for either sex to help explain the discrepancy in results.
One hypothesis for this discrepancy is there is a tradeoff between the rate of larval development and body size. Larvae that develop slower may have an opportunity to grow larger because as more time passes, the container is accumulating more food and because as time passes, more larvae may die, releasing survivors from competition. In the 1× containers, larvae developed faster and this could have impacted the difference between adult body sizes. In the LP treatment, the amount of food may have been sufficient for the larvae to pupate as fast as the LA treatment, but possibly not enough food for the adult sizes to be equivalent.
Gilpin and McClelland showed in laboratory studies that larvae starved for 40 days were able to pupate when liver powder was added to the system [38]. The ability to survive periods of time without food enables larvae to survive until the regeneration of food is able to occur within containers [39]. Both detritus and the microorganisms that feed on it, including bacteria, protozoa, and fungi, have been shown as an important food source for Ae. albopictus larvae and other container inhabiting mosquitoes [40]–[42]. Larval development could therefore also be dependent on the growth rate of microbial populations within the containers. However, we can not definitively test this or other hypothesis with data from our current experiment.
One limitation of this study is the inability to detect the amount of food and types of food present in the buckets. Different species of leaves decompose in water at different rates. Leaves that decompose at a more rapid rate support more larval mosquito growth compared to leaves that decompose slower [43]. It has also been shown that animal detritus decomposes faster than plant detritus and yields higher mosquito population growth [31], [32], [42]. The types and amounts of food likely varied between houses and the buckets within houses; therefore it probably impacted the presence and strength of delayed density-dependence detected in this study. While this is a limitation on our ability to explain the cause of delayed density dependence, this specific design enabled us to more closely estimate the degree of delayed density dependence that occurs in the field.
Our results are similar to those found by Aspbury and Juliano, the only other experiment assessing delayed density-dependence in a container–inhabiting mosquito in a field setting [27]. Both studies found an impact of delayed density-dependence on development time; however our study also detected an impact on larval survival. It is surprising that Aspbury and Juliano detected delayed density-dependence since they used an open flow water system between treatments. The small numbers of larvae used may have been appropriate for the size of the cages tested, but were not necessarily reflective of natural larval population densities. Our study was strengthened by the fact that the larval densities tested in our containers matched the naturally occurring densities assessed during the first part of the experiment. Using these natural larval densities, our study predicts that delayed density-dependence will only have a substantial impact on mosquito populations when the natural larval density is high enough that the available resources are depleted by the larvae faster than it is replenished by detritivores and microbes.
Supporting Information
Effect of estimated larval density on development time (days). Relationship between the difference in development time between the LP treatment and LA treatment for each container and the log of estimated larval density for both 1× density containers (A) and 10× density containers (B).
(TIF)
Effect of estimated larval density on male wing length (mm). Relationship between the difference in male wing length between the LA treatment and LP treatment for each container and the log of estimated larval density for both 1× density containers (A) and 10× density containers (B).
(TIF)
Effect of estimated larval density on female wing length (mm). Relationship between the difference in female wing length between the LA treatment and LP treatment for each container and the log of estimated larval density for both 1× density containers (A) and 10× density containers (B).
(TIF)
Individual container information. Table includes all information for each container including the estimated number of larvae during the pre-treatment phase, the number of larvae added for the post-treatment phase, and results for each parameter measured.
(XLS)
Acknowledgments
We would like to thank Mathieu Legros, Alun Lloyd, Tom Scott, Laura Harrington, Chonggang Xu, and Conseulo Arellano for discussion of experimental design and statistics. We thank the residents of the houses who graciously welcomed and volunteered their homes to us. We would also like to thank Bob Blinn and Dr. Hannah Burrack for the use of their microscopes and computers for wing measurements. Discussions fostered by the FNIH RAPIDD program improved our analysis.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was supported by National Institutes of Health (US) (NIH) grant R01-AI54954-0IA2 and a grant to the Regents of the University of California from the Foundation for the National Institutes of Health through the Grand Challenges in Global Health initiative. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Gotelli NJ. A primer of ecology. 3rd Edition. Massachusetts: Sinauer Associates, Inc; 2001. 265 [Google Scholar]
- 2.May RM, Conway GR, Hassell MP, Southwood TRE. Time delays, density dependence and single-species oscillations. Journal of Animal Ecology. 1974;43:747–770. [Google Scholar]
- 3.Turchin P, Taylor AD. Complex dynamics in ecological time series. Ecology. 1992;73:289–305. [Google Scholar]
- 4.Stenseth NC. Population cycles in voles and lemmings: density dependence and phase dependence in a stochastic world. Oikos. 1999;87:427–461. [Google Scholar]
- 5.Haukioja E. On the role of plant defenses in the fluctuation of herbivore populations. Oikos. 1980;35:202–213. [Google Scholar]
- 6.Harrison S, Karban R. Effects of an early-season folivorous moth on the success of a later-season species, mediated by a change in the quality of the shared host, Lupinus arboreus Sims. Oecologia. 1986;69:354–359. doi: 10.1007/BF00377056. [DOI] [PubMed] [Google Scholar]
- 7.Leather SR, Watt AD, Forrest GI. Insect-induced chemical changes in young lodgepole pine (Pinus contorta): the effect of previous defoliation on oviposition, growth, and survival of the pine beauty moth, Panolis flammea. Ecological Entomology. 1987;12:275–281. [Google Scholar]
- 8.Bowman J, Donovan D, Rosatte RC. Numerical response of fishers to synchronous prey dynamics. Journal of Mammalogy. 2006;87:480–484. [Google Scholar]
- 9.Hanski I, Henttonen H, Korpimaki E, Oksanen L, Turchin P. Small-rodent dynamics and predation. Ecology. 2001;82:1505–1520. [Google Scholar]
- 10.Turchin P. Rarity of density dependence or population regulation with lags. Nature. 1990;344:660–663. [Google Scholar]
- 11.Hunter MD, Price PW. Cycles in insect populations: delayed density dependence or exogenous driving variables? Ecological Entomology. 1998;23:216–222. [Google Scholar]
- 12.Turchin P, Berryman AA. Detecting cycles and delayed density dependence: a comment on Hunter and Price (1998). Ecological Entomology. 2000;25:119–121. [Google Scholar]
- 13.Solow AR. Observation error and the detection of delayed density dependence. Ecology. 2001;82:3263–3264. [Google Scholar]
- 14.Alyokhin A, Drummond FA, Sewell G. Density-dependent regulation in populations of potato-colonizing aphids. Population Ecology. 2005;47:257–266. [Google Scholar]
- 15.Friedenberg NA, Sarkar S, Kouchoukos N, Billings RF, Ayres MP. Temperature extremes, density dependence, and southern pine beetle (Coleoptera: Curculionidae) population dynamics in East Texas. Environmental Entomology. 2008;37:650–659. doi: 10.1603/0046-225x(2008)37[650:teddas]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 16.Cooke BJ, Lorenzetti F. The dynamics of forest tent caterpillar outbreaks in Quebec, Canada. Forest Ecology and Management. 2006;226:110–121. [Google Scholar]
- 17.Pedraza-Garcia M, Cubillos LA. Population dynamics of two small pelagic fish in the central-south area off Chile: delayed density-dependence and biological interaction. Environmental Biology of Fishes. 2008;82:111–122. [Google Scholar]
- 18.Gratz NG. Critical review of the vector status of Aedes albopictus. Medical and Veterinary Entomology. 2004;18:215–227. doi: 10.1111/j.0269-283X.2004.00513.x. [DOI] [PubMed] [Google Scholar]
- 19.Paupy C, Ollomo B, Kamgang B, Moutailler S, Rousset D, et al. Comparative role of Aedes albopictus and Aedes aegypti in the emergence of Dengue and Chikungunya in Central Africa. Vector-borne and Zoonotic Diseases. 2010;10:259–266. doi: 10.1089/vbz.2009.0005. [DOI] [PubMed] [Google Scholar]
- 20.Vazeille M, Mousson L, Martin E, Failloux A. Orally co-infected Aedes albopictus from la Reunion Island, Indian Ocean, can deliver both Dengue and Chikungunya infectious viral particles in their saliva. PLoS Neglected Tropical Diseases. 2010;4 doi: 10.1371/journal.pntd.0000706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Richards SL, Ghosh SK, Zeichner BC, Apperson CS. Impact of source reduction on the spatial distribution of larvae and pupae of Aedes albopictus (Diptera:Culicidae) in suburban neighborhoods of a piedmont community in North Carolina. Journal of Medical Entomology. 2008;45:617–628. doi: 10.1603/0022-2585(2008)45[617:iosrot]2.0.co;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hawley WA. The biology of Aedes albopictus. Journal of American Mosquito Control Association. 1988;(suppl. 4):2–32. [PubMed] [Google Scholar]
- 23.Mori A. Effects of larval density and nutrition on some attributes of immature and adult Aedes albopictus. Tropical Medicine. 1979;21:85–103. [Google Scholar]
- 24.Hawley WA. The effect of larval density on adult longevity of a mosquito, Aedes sierrensis: epidemiological consequences. Journal of Animal Ecology. 1985;54:955–964. [Google Scholar]
- 25.Ho BC, Ewert A, Chew L. Interspecific competition among Aedes aegypti, Ae.albopictus, and Ae. triseriatus (Diptera: Culicidae): larval development in mixed cultures. Journal of Medical Entomology. 1989;26:615–623. doi: 10.1093/jmedent/26.6.615. [DOI] [PubMed] [Google Scholar]
- 26.Lord CC. Density dependence in larval Aedes albopictus (Diptera: Culicidae). Journal of Medical Entomology. 1998;35:825–829. doi: 10.1093/jmedent/35.5.825. [DOI] [PubMed] [Google Scholar]
- 27.Aspbury AS, Juliano SA. Negative effects of habitat drying and prior exploitation on the detritus resource in an ephemeral aquatic habitat. Oecologia. 1998;115:137–148. doi: 10.1007/s004420050500. [DOI] [PubMed] [Google Scholar]
- 28.Merrit RW, Dadd RH, Walker ED. Feeding behavior, natural food, and nutritional relationships of larval mosquitoes. Annual Review Entomology. 1992;37:349–376. doi: 10.1146/annurev.en.37.010192.002025. [DOI] [PubMed] [Google Scholar]
- 29.Yee DA, Kesavaraju B, Juliano SA. Interspecific differences in feeding behavior and survival under food-limited conditions for larval Aedes albopictus and Aedes aegypti (Diptera:Culicidae). Annals of the Entomological Society of America. 2004;97:720–728. doi: 10.1603/0013-8746(2004)097[0720:IDIFBA]2.0.CO;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yee DA, Kesavaraju B, Juliano SA. Larval feeding behavior of three co-occurring species of container mosquitoes. Journal of Vector Ecology. 2004;29:315–322. [PMC free article] [PubMed] [Google Scholar]
- 31.Yee DA, Juliano SA. Consequences of detritus type in an aquatic smicrosystem: effects on water quality, micro-organisms and performance of the dominant consumer. Freshwater Biology. 2006;51:448–459. doi: 10.1111/j.1365-2427.2005.01504.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kesavaraju B, Yee DA, Juliano SA. Interspecific and intraspecific differences in foraging preferences of container-dwelling mosquitoes. Journal of Medical Entomology. 2007;44:215–221. doi: 10.1603/0022-2585(2007)44[215:iaidif]2.0.co;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wong J, Stoddard ST, Astete H, Morrison AC, Scott TW. Oviposition site selection by the dengue vector Aedes aegypti and its implications for dengue control. PLoS Neglected Tropical Diseases. 2011;5 doi: 10.1371/journal.pntd.0001015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Little RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberber O. SAS for Mixed Models. 2nd Edition. SAS Pulbishing 2006 [Google Scholar]
- 35.Ott RL, Longnecker MT. An Introduction to Statistical Methods and Data Analysis. 6th Edition. Duxbury Press; 2008. [Google Scholar]
- 36.O'Gower AK. The influence of the surface on oviposition of Aedes albopictus (Skuse) and Aedes scutellaris katherinensis woodhill (Diptera, Culicidae). Proceeding of the Linnean Society of New South Wales. 1957;82:285–288. [Google Scholar]
- 37.Braks MAH, Honorio NA, Lounibos LP, Lourenco-De-Oliveira R, Juliano SA. Interspecific competition between two invasive species of container mosquitoes, Aedes aegypti and Aedes albopictus (Diptera: Culicidae), in Brazil. Annals of the Entomological Society of America. 2004;97:130–139. [Google Scholar]
- 38.Gilpin ME, McClelland G. Systems analysis of the Yellow Fever Mosquito Ae. aegypti. Fortschritte der Zoologie. 1979;25:355–388. [PubMed] [Google Scholar]
- 39.Arrivillaga J, Barrera R. Food as a limiting factor for Aedes aegypti in water storage containers. Journal of Vector Ecology. 2004;29:11–20. [PubMed] [Google Scholar]
- 40.Walker ED, Lawson DL, Merritt RW, Morgan WT, Klug MJ. Nutrient dynamics, bacterial populations, and mosquito productivity in tree hole ecosystems and microcosms. Ecology. 1991;72:1529–1546. [Google Scholar]
- 41.Merritt RW, Dadd RH, Walker ED. Feeding behavior, natural food, and nutritional relationships of larval mosquitoes. Annual Review of Entomology. 1992;37:349–376. doi: 10.1146/annurev.en.37.010192.002025. [DOI] [PubMed] [Google Scholar]
- 42.Yee DA, Kesavaraju B, Juliano SA. Direct and indirect effects of animal detritus on growth, survival, and mass of invasive container mosquito Aedes albopictus (Diptera: Culicidae). Journal of Medical Entomology. 2007;44:580–588. doi: 10.1603/0022-2585(2007)44[580:daieoa]2.0.co;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fish D, Carpenter SR. Leaf litter and larval mosquito dynamics in tree-hole ecosystems. Ecology. 1982;63:283–288. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Effect of estimated larval density on development time (days). Relationship between the difference in development time between the LP treatment and LA treatment for each container and the log of estimated larval density for both 1× density containers (A) and 10× density containers (B).
(TIF)
Effect of estimated larval density on male wing length (mm). Relationship between the difference in male wing length between the LA treatment and LP treatment for each container and the log of estimated larval density for both 1× density containers (A) and 10× density containers (B).
(TIF)
Effect of estimated larval density on female wing length (mm). Relationship between the difference in female wing length between the LA treatment and LP treatment for each container and the log of estimated larval density for both 1× density containers (A) and 10× density containers (B).
(TIF)
Individual container information. Table includes all information for each container including the estimated number of larvae during the pre-treatment phase, the number of larvae added for the post-treatment phase, and results for each parameter measured.
(XLS)