Modeling of Autonomic Control in Sleep-Disordered Breathing

Abstract

There is ample evidence to support the notion that chronic exposure to repetitive episodes of interrupted breathing during sleep can lead to systemic hypertension, heart failure, myocardial infarction and stroke. Recent studies have suggested that abnormal autonomic control may be the common factor linking sleep-disordered breathing (SDB) to these cardiovascular diseases. We have developed a closed-loop minimal model that enables the delineation of the major physiological mechanisms responsible for changes in autonomic system function in SDB, and also forms the basis for a noninvasive technique that enables the early detection of cardiovascular control abnormalities. The model is “minimal” in the sense that all its parameters can be estimated through analysis of the data measured noninvasively from a single experimental procedure. Parameter estimation is enhanced by broadening the frequency content of the subject’s ventilatory pattern, either through voluntary control of breathing or involuntary control using ventilator assistance. Although the original form of the model is linear and time-invariant, extensions of the model include the incorporation of nonlinear dynamics in the autonomic control of heart rate, and allowing the transfer functions of the model components to assume time-varying characteristics. The various versions of the model have been applied to different populations of subjects with SDB under different conditions (e.g. supine wakefulness, orthostatic stress, sleep). Our cumulative findings suggest that the minimal model approach provides a more sensitive means of detecting abnormalities in autonomic cardiovascular control in SDB, compared to univariate analysis of heart rate variability or blood pressure variability.

Introduction and Background

Recent epidemiological studies, including the multi-center Sleep Heart Health Study, have provided compelling evidence linking sleep-disordered breathing (SDB) to systemic hypertension, coronary artery disease, heart failure and stroke (Roux et al. 2000; Peppard et al. 2000; Shahar et al. 2000). In the Wisconsin Sleep Cohort Study (Peppard et al. 2000), for instance, the adjusted odds ratio for the presence of incident hypertension was found to increase with increasing severity of SDB. Further evidence of an independent causative role of SDB in producing hypertension comes not only from other epidemiological studies but from prospective animal studies as well. Using an elegant canine model of obstructive apnea, Brooks et al. (1997) were able to produce nocturnal and daytime hypertension by exposing the animals to artificially induced periodic airway obstructions for several weeks. There are a number of mechanisms through which SDB can lead to hypertension and other forms of cardiovascular disease, but the cumulative evidence suggests that abnormal autonomic control is a prime factor. For instance, studies utilizing peroneal microneurography or testing of plasma catecholamines have shown that sympathetic tone is substantially elevated in subjects with SDB in both sleep and wakefulness (Carlson et al. 1993; Somers et al. 1995). At the same time, heart rate variability (HRV) is markedly reduced, suggesting impaired parasympathetic control (Narkiewicz et al. 1998; Khoo et al. 1999; Wiklund et al. 2000). Treatment with continuous positive airway pressure (CPAP) partially reverses these effects, as evidenced through reductions in muscle sympathetic nerve activity and plasma norepinephrine levels (Waravdekar et al. 1996; Hedner et al. 1995; Narkiewicz et al. 1999), and increases in HRV (Khoo et al. 1999; Roche et al. 1999). Long-term CPAP therapy also has been found to lower mean daytime and nocturnal arterial blood pressures in patients with SDB, particularly in those subjects who were hypertensive and who were off medication during the treatment period (Fletcher 2000).

The monitoring of heart rate, blood pressure and sympathetic activity can therefore provide highly useful information about autonomic control in subjects suspected of having SDB as well as in diagnosed patients who have been prescribed some form of treatment. However, there are disadvantages associated with the derivation of statistical or spectral measures from these physiological signals on a univariate basis. Measurements of muscle sympathetic nerve activity, for instance, require considerable technical expertise and are highly susceptible to artifactual noise introduced by limb movement. Moreover, microneurography gives only a regionally-confined assessment of sympathetic tone, which can be quantitatively different in the heart and various parts of the vasculature (Mancia et al. 1998). Measurements of plasma or urinary catecholamines are limited in sensitivity (Mancia et al. 1998). The mean values and standard deviations of heart rate and blood pressure are summary statistical measures, conveying information that reflects the net effect of all the factors that contribute to cardiovascular control, thus providing little insight into the underlying physiological mechanisms. Power spectral analyses of HRV and blood pressure variability (BPV) offer promising avenues for investigating the dynamics of cardiovascular autonomic function (Malliani et al. 1991). However, recent studies have challenged the validity of employing spectral measures of HRV to derive conclusions about the relative balance between sympathetic and vagal control (Karemaker 1997; Eckberg 1997).

One way of overcoming the limitations inherent in univariate cardiovascular signal analysis is to consider the relationships between pairs of variables. For instance, the “alpha index”, which represents the gain of the transfer function relating changes in systolic blood pressure (SBP) to changes in R–R interval (RRI), is frequently employed as a measure of baroreflex sensitivity (Parati et al. 2000). However, it is computed by first calculating the power spectra of SBP and RRI, and then taking the square-root of the ratio between RRI power and SBP power in defined frequency bands. A problem with this approach, which relies solely on frequency-domain measures, is that it ignores the fact that RRI and SBP are physiologically coupled to one another in a closed-loop system: changes in SBP produce changes in RRI via the baroreflexes, but changes in RRI can also lead to changes in SBP through variations in cardiac output via the mechanism referred to as the “mechanical feedforward” (Barbieri et al. 1996). The “sequence” method overcomes this limitation by selecting only causally related changes in SBP and RRI (Parati et al. 2000). On the other hand, the sequence method does not directly take into account the powerful and confounding influence of respiration on RRI.

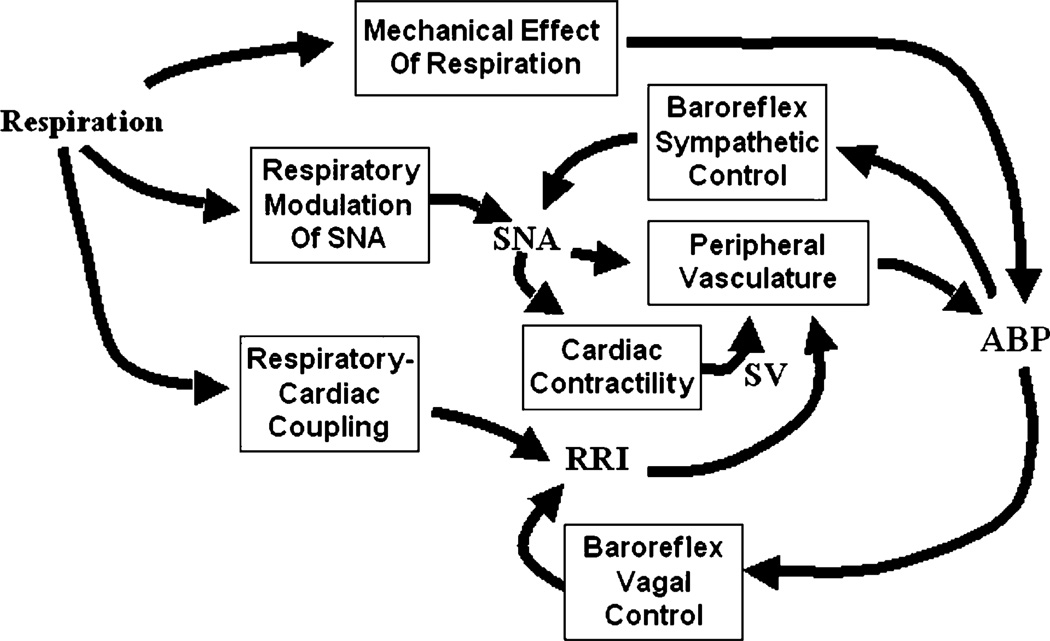
To obtain greater insight into the mechanisms that produce HRV and BPV, it is necessary to ratchet up the level of analysis to a higher level of complexity. Figure 1 shows a schematic representation of the major physiological mechanisms that can contribute to HRV and BPV. Even at this relatively simplified level of organization, there are numerous feedforward and feedback among the key physiological variables. Fluctuations in blood pressure (ABP) can result from the direct mechanical effects of respiration (primarily high-frequency), fluctuations in resistance of the peripheral vasculature (low-frequency), and/or through fluctuations in stroke volume (SV) and RRI (both high- and low-frequency). Fluctuations in RRI stem from direct respiratory-cardiac coupling and/or ABP fluctuations via the baroreflexes. “Respiratory-cardiac coupling” encompasses a variety of mechanisms: direct mechanical stretching, and compression of the sino-atrial node, intrathoracic pressure effects on the cardiopulmonary receptors, vagal feedback from the lung stretch receptors, and respiratory modulation of the cardiovagal neural output. What we normally refer to as “respiratory sinus arrhythmia” is mediated by both respiratory-cardiac coupling and baroreflex responses to respiratory-related fluctuations in ABP. Sympathetic nerve activity (SNA), which influences peripheral resistance, contractility of the heart, as well as heart rate, is itself modulated by baroreceptor output and respiration. One approach would be to develop the mathematical relations among all these variables and construct a large-scale “structured” model using sets of differential equations along the lines of Guyton (1988). While this kind of model might be useful in enabling us to better understand how various mechanisms contribute to particular experimental observations in various subject populations, the large number of parameters prevent us from using such a model to analyze data from individual subjects. An alternative approach is to develop and employ a “minimal model”, i.e. one that is able to account for most of the dynamic features of a set of physiological responses and yet be simple enough that all its characteristic parameters can be estimated from measurements obtained in an individual subject. Thus, although we have also been pursuing in parallel the development of a comprehensive structured model of circulatory control in SDB (Fan and Khoo 2002; Ivanova and Khoo 2004), this article will review only the work that we have carried out in recent years using the “minimal model” approach. In a series of studies, we have employed this approach to better delineate which major physiological mechanisms contributing to HRV and BPV are affected as a consequence of chronic exposure to SDB. The practical significance of this work is that it allows the development of a diagnostic tool that offers the possibility of detecting the cardiovascular effects of SDB in subjects from a relatively short and simple experimental procedure conducted in the clinic during wakefulness.

Fig. 1.

Schematic diagram showing the interrelationships among respiration, sympathetic nerve activity (SNA) and the cardiovascular variables (R–R interval, RRI; ABP, arterial blood pressure; SV, cardiac stroke volume), and how they contribute to heart rate variability and blood pressure variability

Minimal Closed-Loop Model of Autonomic Cardiovascular Control

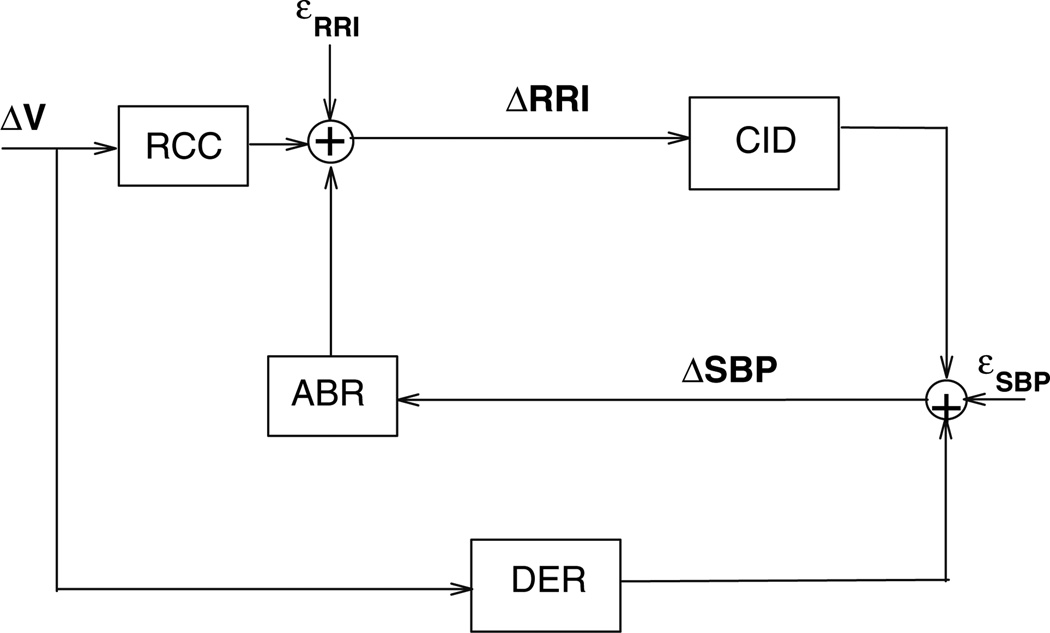
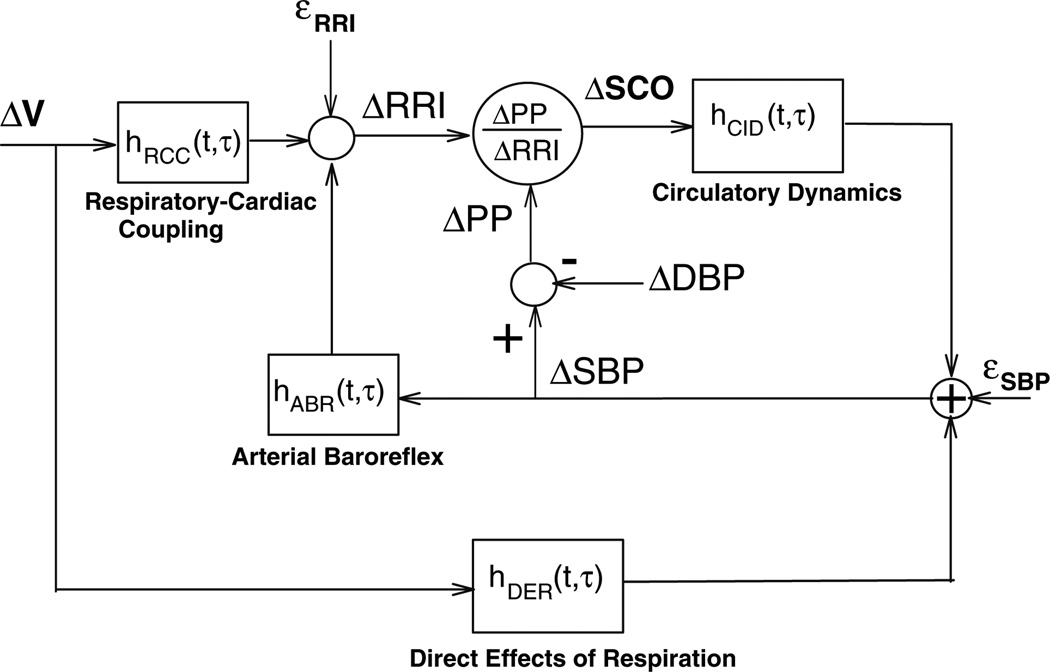
The minimal closed-loop model that we have employed enables the characterization of the dynamic interrelationships between various pairings of the three noninvasively measured variables: respiration, heart rate, and arterial blood pressure (Belozeroff et al. 2000). A schematic block-diagram of the earlier and most basic version of this model (Belozeroff et al. 2002) is shown in Fig. 2. The structure of this model is based on what we know about the major physiological mechanisms that lead to variability in heart rate (or conversely, RRI) and blood pressure, as outlined in the previous section. Fluctuations in RRI (ΔRRI) are assumed to be produced by fluctuations in SBP via the baroreflexes (ABR) and through direct autonomic coupling between respiration (ΔV) and heart rate (RCC). A portion of the changes in SBP, ΔSBP, is assumed to be produced by changes in intrathoracic pressure resulting directly from respiration (DER), which we believe are likely to be primarily mechanical in nature, but may also include respiratory-driven sympathetic modulation of heart contractility (Toska and Eriksen 1993). Another contribution to ΔSBP is derived from the Frank–Starling mechanism and Windkessel “runoff” effects (DeBoer et al. 1987). We refer to the ΔRRI to ΔSBP transfer relation as “circulatory dynamics” (CID). The mathematical equations that characterize the model are as follows:

$$\mathrm{\Delta }\text{RRI}(t)={\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{RCC}}(\tau )\mathrm{\Delta }V(t-\tau -T_{\text{RCC}})+{\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{ABR}}(\tau )\mathrm{\Delta }\text{SBP}(t-\tau -T_{\text{ABR}})+{\epsilon }_{\text{RRI}}(t)$$ (1)

$$\mathrm{\Delta }\text{SBP}(t)={\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{DER}}(\tau )\mathrm{\Delta }V(t-\tau )+{\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{CID}}(\tau )\mathrm{\Delta }\text{RRI}(t-\tau -T_{\text{CID}})+{\epsilon }_{\text{SBP}}(t)$$ (2)

where T_RCC, T_ABR and T_CID are the latencies associated with the RCC, ABR and CID mechanisms, respectively. ε_RRI(t) and ε_SBP(t) represent the stochastic components of ΔRRI(t) and ΔSBP(t), respectively, plus any contributions not accounted for by the postulated mechanisms. Since in Eqs. 1 and 2, the model is assumed to be linear, complete characterizations of dynamics of all four model components are given by their respective (unknown) impulse responses: h_RCC(t), h_ABR(t), h_DER(t) and h_CID(t). In linear systems theory, the impulse response provides a complete characterization of the dynamic properties of the system in question, since the response of this system to any arbitrary input can be predicted by mathematically convolving the input with the impulse response (Khoo 2000). h_ABR(t), for instance, quantifies the time-course of the change in RRI resulting from an abrupt increase in SBP of 1 mmHg, whereas h_RCC(t) quantifies the time-course of the fluctuation in RRI associated with a very rapid inspiration and expiration of 1 l of air. It is important to note that, since respiration, RRI and SBP are measured, it is possible to estimate all four model impulse responses from the data.

Fig. 2.

Block diagram of the minimal closed-loop model of cardiovascular variability. See text for abbreviations

An important feature of this model is that its causal structure allows us to computationally “open the loop” of the closed-loop system, thereby separating the feedforward from the feedback components. As mentioned previously, spectral analysis techniques do not permit this kind of temporal delineation, but this problem is circumvented by solving for the impulse responses in Eqs. 1 and 2 in the time domain (Khoo 2000). One other advantage is that this approach allows us to obtain a comprehensive assessment of the primary mechanisms that contribute to HRV and BPV, using data measured from a single test procedure lasting between 5 and 10 min. Similar approaches, with individual differences in model structure, have been employed by previous workers to investigate the control of heart rate and blood pressure (Baselli et al. 1998; Mukkamala et al. 1999; Lucini et al. 2000); however, none have been used to study autonomic control in SDB.

Parameter Estimation Issues

The minimal model presented here may be considered “kernel-based” (Marmarelis 2004), since the dynamics of its major components are explicitly characterized by their corresponding impulse responses. This contrasts with the more traditional “parametric” approach in which the dynamics are more compactly described using differential equations with unknown coefficients that represent the parameters to be estimated. Although our approach is often referred to as “non-parametric”, the unknown coefficients of the model impulse responses nonetheless may be considered “parameters” that need to be estimated from the data. In order to reduce the level of parametrization and thus increase estimation accuracy, the impulse responses of our model components were constructed using Laguerre basis functions (Marmarelis 1993). Thus, for instance, the ABR impulse response is expanded to be the sum of weighted Laguerre basis functions:

$$h_{\text{ABR}}(\tau )={\displaystyle \sum _{j=0}^{q-1}}{c}_j^{\text{ABR}}{L}_j(\tau )$$ (3)

where the L_j(τ) represents the j-th order discrete-time orthonormal Laguerre function, and $c_j^{\text{ABR}}$ are the corresponding unknown weights that are assigned to L_j(τ) in the ABR impulse response. The important practical advantage of this computational feature is that it can produce a substantial reduction in the number of unknown parameters (from p to q, where p ≫ q) that need to be estimated, thereby allowing greater statistical reliability to be achieved in the parameter estimates (Marmarelis 1993). In practice, p is on the order of 50 while q is generally between 6 and 8. The impulse responses of the other model components (RCC, CID, DER) are similarly expanded as weighted sums of Laguerre functions.

To enhance parameter estimation accuracy, in the experimental protocol, subjects are asked to control their breathing pattern so that it would track a respiratory waveform displayed on a computer monitor. This waveform is generated from an algorithm that assumes a stationary Poisson noise process such that the respiratory duration is varied randomly from breath to breath (Berger et al. 1989). However, the tidal volumes of the target breath pattern are selected so that the average minute ventilation can be maintained at an approximately constant level equal to that deduced from the subject’s previously monitored spontaneous breathing pattern. This helps to maintain chemical drive at relatively constant levels over the course of the procedure.

Quantifying Autonomic Abnormality in SDB During Wakefulness

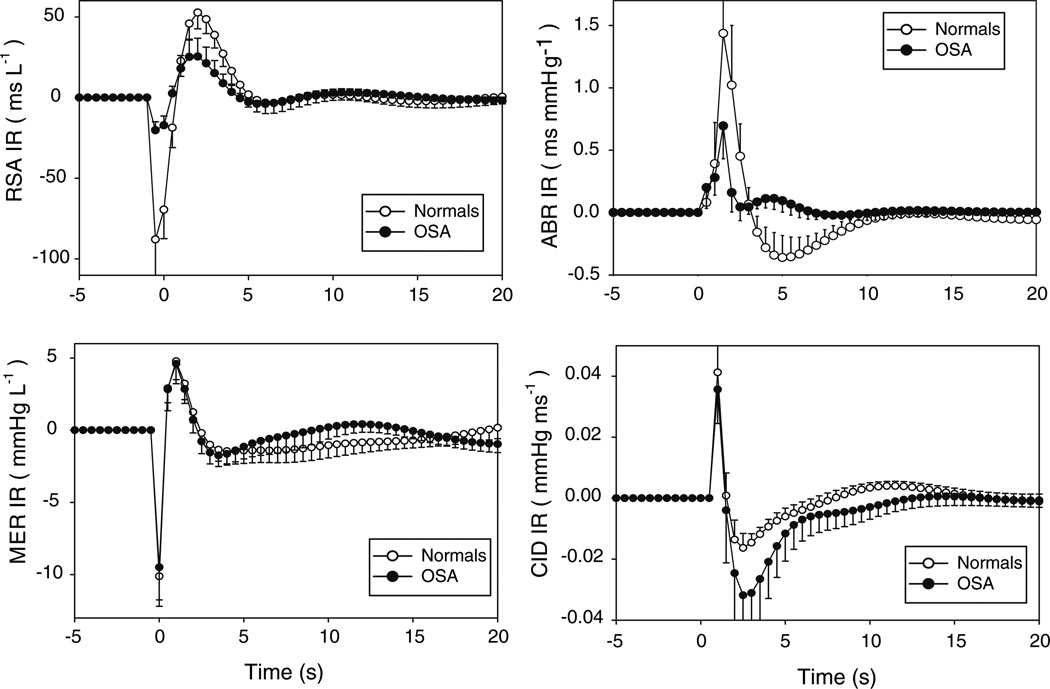
We have completed experimental investigations in which respiration, continuous blood pressure (Finapres) and RRI were recorded during wakefulness in untreated subjects with moderate to severe SDB and normal controls. An example of the results obtained with the minimal model is displayed in Fig. 3; details are reported in Belozeroff et al. (2003). Estimates of h_ABR(t) exhibit a sharp positive peak between 1 and 2 s following an initial latency of ~ 1 s. Peak-to-peak h_ABR(t) magnitude (i.e. the difference between the maximum and minimum values of h_ABR(t)) is significantly lower in SDB versus normals (1.28 ± 0.29 vs. 2.97 ± 0.67 ms mmHg⁻¹, P < 0.05; based on a sample size of 11 in each subject group). In general, h_ABR(t) in normals takes the form of a large positive peak followed rapidly by a substantial negative overshoot, whereas in subjects with SDB there is generally no negative undershoot. We have also consistently found that the initial negative phase of h_RCC(t), representing heart rate acceleration, begins approximately 1 s prior to the start of mechanical inspiration, similar to what was reported in previous studies (Mullen et al. 1997; Chon et al. 1996). The latter portion of h_RCC(t), which coincides largely with expiration, is positive, implying heart rate deceleration. This biphasic time-course is similar to what has been reported previously (Mullen et al. 1997; Chon et al. 1996). h_RCC(t) magnitude is significantly lower in SDB compared to normals (61.8 ± 12.9 vs. 165.0 ± 32.1 ms l⁻¹, P < 0.01). These findings demonstrate that the decreased HRV reported in SDB subjects (Narkiewicz et al. 1998) is due to reductions in both baroreflex (ABR) sensitivity and respiratory-cardiac coupling (RCC) gains.

Fig. 3.

Impulse responses for all four model components, estimated from normal controls (open circles) and subjects with SDB (filled circles) during supine wakefulness. Error bars represent standard errors

The time-course of h_DER(t) shows an abrupt drop in blood pressure immediately following the start of inspiration, as a consequence of the decreased (i.e. more negative) intrathoracic pressure. Subsequently, however, the decreased intrathoracic pressure during inspiration leads to increased diastolic filling, subsequently raising diastolic and systolic pressures. During expiration, intrathoracic pressure becomes less negative, thus negating the earlier increase in SBP. We have found no differences in h_DER(t) between normals and SDB. The time-courses of h_CID(t) in both subject groups show an initial abrupt rise after 1 s (Fig. 3). This may be explained in the following way: an increase in RRI produces an immediate reduction in diastolic blood pressure (termed the “runoff effect” (Baselli et al. 1998)) but, due to the increased time for filling, the subsequent stroke volume and pulse pressure (=SBP − DBP) increases (via the Frank–Starling effect). The net result therefore is an increase in SBP in the next beat. This is followed subsequently by a more sustained decrease, reflecting the effect of a reduction in cardiac output produced by the lowered heart rate. h_CID(t) magnitude was marginally larger in SDB versus normals.

Our findings of significantly lower ABR and RCC gains, along with higher CID gain, in the subjects with SDB indicate that SDB leads to impairment of parasympathetic activity and abnormally high sympathetic activity. As well, we have found that changing from the supine to standing posture led to significant reductions in ABR and RCC gains and corresponding increase in CID gain in both normal controls and subjects with SDB, indicating that these parameters accurately reflect the increased sympathetic dominance and reduction in vagal tone that accompany orthostatic stress.

Quantifying the Autonomic Effects of Long-term CPAP Therapy

The minimal closed-loop model has also been applied to analyze measurements obtained from SDB subjects before and after long-term (~ 6 months) CPAP therapy (Belozeroff et al. 2002). Patient compliance with the prescribed treatment ranged widely from 0 to >8 h per night. For this reason, we divided the subjects into two groups: compliant (“C”) patients, who used CPAP for an average of >3 h per night, and noncompliant patients (“N”) whose average CPAP use was <3 h per night. Long-term CPAP treatment produced very different effects on the estimated model impulse responses in the compliant and noncompliant groups. h_RCC(t) magnitude increased almost threefold in the compliant patients, whereas the noncompliant subjects showed no change. h_ABR(t) magnitude also increased approximately threefold in the compliant patients but did not change in the noncompliant patients. These findings again demonstrate that reduced HRV in SDB is due to both depressed baroreflex sensitivity and respiratory-cardiac coupling, and that treatment with CPAP can partially reverse these changes. However, the beneficial effect of CPAP depends strongly on patient compliance.

What about the model components that influence blood pressure variability? We found a reduction in h_DER(t) magnitude following CPAP therapy in the compliant group, but no change in the noncompliant subjects. The decreased h_DER magnitude in the compliant subjects means that for the same tidal volume and airflow pattern, inspiration led to a smaller reduction in SBP. This suggests that CPAP increased the effective pulmonary compliance in those patients who used it frequently and consistently. An alternative or additional mechanism may have been a reduction in cardiac sympathetic tone following CPAP treatment, which led to a reduction of respiratory-related stroke volume variability (Toska and Eriksen 1993).

h_CID(t) magnitude also decreased following CPAP therapy in the compliant patients, but in the noncompliant patients, there was a tendency for h_CID(t) to increase. Since the “mechanical feedforward” effect of RRI on SBP depends on how RRI changes affect cardiac output which, in turn, affects SBP, a possible explanation for this finding is that CPAP treatment led to decreased systemic vascular resistance in the compliant patients. In the noncompliant patients, lack of treatment may have allowed peripheral resistance to increase with time in some cases.

Thus, analysis of cardiorespiratory data using the minimal closed-loop model indicates that longterm treatment of SDB with CPAP leads to restoration of parasympathetic control of heart rate and a reduction of sympathetic over-activity, consistent with reports by others (Waravdekar et al. 1996; Hedner et al. 1995; Narkiewicz et al. 1999; Roche et al. 1999; Fletcher 2000) that have employed other methods for assessing autonomic control.

Quantifying Autonomic Abnormality in SDB During Sleep

In another study (Jo et al. 2003, 2005), we measured respiration, RRI and continuous blood pressure in relaxed wakefulness, rapid eye movement (REM) sleep, and non-REM (NREM) stage 2 sleep. Since voluntary tracking of the randomized breathing pattern is not possible during sleep, respiration was “controlled” in the following way at various times throughout the night: each subject was connected via nasal mask to a bilevel pressure noninvasive ventilator, which was computer-controlled to deliver inspiratory pressures that varied randomly from breath to breath during the test protocol. The pattern of ventilatory assistance was programmed so that the bandwidth of the breathing pattern was broadened considerably. The SDB subjects were studied with CPAP applied at each individual’s prescribed pressure, thus regularizing their breathing patterns and facilitating comparison with their normal counterparts.

During wakefulness, h_RCC(t) magnitude was substantially lower in SDB versus normals ((39.9 ± 6.6 vs. 59.1 ± 7.9 ms l⁻¹; P < 0.03) and did not change significantly with sleep in both subject groups. h_ABR(t) magnitude was also lower in SDB (1.74 ± 0.43 vs. 2.22 ± 0.22 ms mmHg⁻¹; P < 0.05) during wakefulness. However, h_ABR(t) magnitude increased approximately threefold during sleep in normals, but remained relatively unchanged in the SDB subjects. This finding indicates that the effect of sleep on baroreflex sensitivity in SDB is considerably different from that in normal controls. There were no significant effects of sleep on h^CID(t) and h_DER(t).

Extension of Minimal Model to Incorporate Nonlinear Dynamics

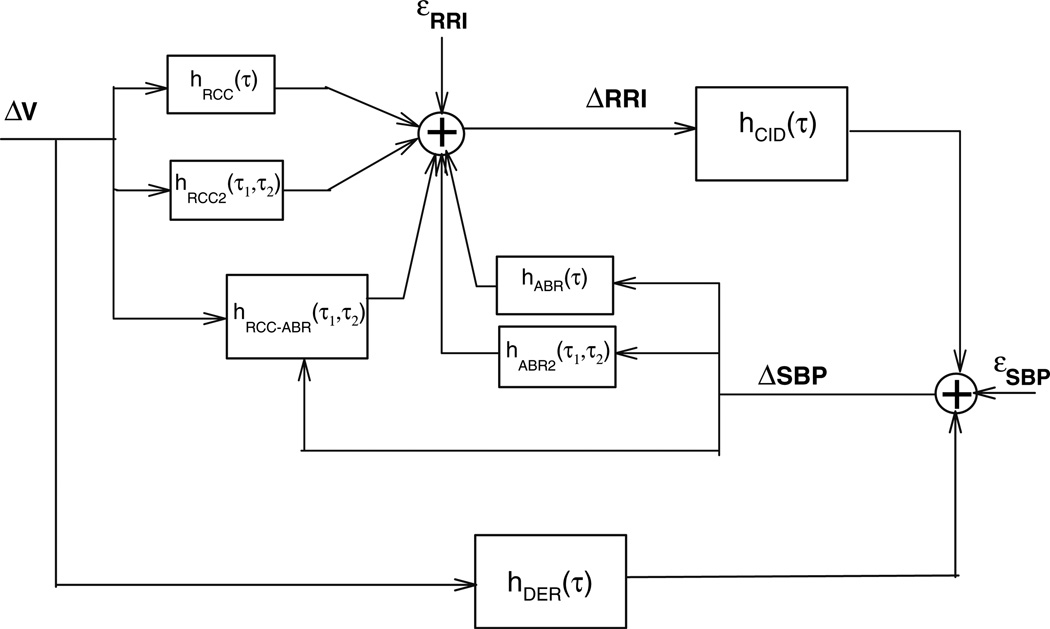
The minimal closed-loop model has been extended to incorporate potential nonlinearities in the dynamics of the autonomic modulation of heart rate (Jo et al. 2007). The structure of this extended model addition is displayed schematically in Fig. 4. The mathematical formulation is as follows:

$$\mathrm{\Delta }\text{RRI}(t)={\displaystyle \sum _{\tau =0}^P}{h}_{\text{RCC}}(\tau )\mathrm{\Delta }V(t-\tau -T_{\text{RCC}})+{\displaystyle \sum _{\tau =0}^P}{h}_{\text{ABR}}(\tau )\mathrm{\Delta }\text{SBP}(t-\tau -T_{\text{ABR}})+{\displaystyle \sum _{{\tau }_1=0}^P}{\displaystyle \sum _{{\tau }_2=0}^P}{h}_{\text{RCC}2}({\tau }_1,{\tau }_2)\mathrm{\Delta }V(t-{\tau }_1-T_{\text{RCC}})\mathrm{\Delta }V(t-{\tau }_2-T_{\text{RCC}})+{\displaystyle \sum _{{\tau }_1=0}^P}{\displaystyle \sum _{{\tau }_2=0}^P}{h}_{\text{ABR}2}({\tau }_1,{\tau }_2)\mathrm{\Delta }\text{SBP}(t-{\tau }_1-T_{\text{ABR}})\mathrm{\Delta }\text{SBP}(t-{\tau }_2-T_{\text{ABR}})+{\displaystyle \sum _{{\tau }_1=0}^P}{\displaystyle \sum _{{\tau }_2=0}^P}{h}_{\text{RCC}-\text{ABR}}({\tau }_1,{\tau }_2)\mathrm{\Delta }V(t-{\tau }_1-T_{\text{RCC}})\mathrm{\Delta }\text{SBP}(t-{\tau }_2-T_{\text{ABR}})+{\epsilon }_{\text{RRI}}(t)$$ (4)

Fig. 4.

Extension of the original minimal closed-loop model, incorporating nonlinear dynamics in the autonomic regulation of heart rate variability

The nonlinear self-kernels h_RCC2 and h_ABR2 represent the quadratic contributions of the RCC and ABR components, respectively. To better understand what these second-order kernels represent, consider, for instance, the effects of two impulsive disturbances in ΔSBP occurring τ₁ and τ₂ from the current time. In a linear system, the response would simply be the superposition of the impulse response at times τ₁ and τ₂ following the occurrences of the impulsive stimuli. In a second-order system, such as that represented by the nonlinear model in Eq. 4, there will be, in addition to the sum of the two impulse responses, another contribution resulting from the interaction between the responses to the two impulses located at times τ₁ and τ₂. This extra contribution is what the second-order kernel, h_ABR2(τ₁, τ₂) represents. The same explanation applies to h_RCC2(τ₁, τ₂). The cross-kernel h_RCC–ABR describes the effect on the output resulting from the second-order nonlinear interaction of the two input signals (ΔV and ΔSBP). These second-order kernels reflect specific characteristics of the RCC and ABR mechanisms, such as dependence of RCC on tidal volume, saturation in the SBP-RRI relation, and respiratory modulation of baroreflex gain (Jo et al. 2007). Each point on an individual kernel represents the additional response to a pair of input impulses that occurred τ₁ and τ₂ seconds away, after accounting for the (linear) responses to each of those impulses (Marmarelis 2004). As such, in Eq. 4, h_RCC2, h_ABR2 and h_RCC–ABR are each functions of two time lags, τ₁ and τ₂.

This extended model has been applied to data obtained from normal controls and subjects with SDB during ventilator-assisted, randomized breathing in wakefulness and sleep. We found a significant improvement (from the linear case) in the goodness of fit between the model-predicted RRI and the corresponding data. For instance, when only linear terms were included, the model accounted for less than 50% of the total variance in the data. After including the nonlinear terms, the proportion of total variance explained by the model increased to approximately 70%. The contribution of the nonlinearities to approximately 20% of total variance was slightly larger but similar in order of magnitude to the findings obtained by Chon et al. (1996) from spontaneous breathing data recorded in a group of healthy young volunteers. Thus, taken together, both our study and Chon’s suggest that nonlinearities account for a significant portion of heart rate variability. The importance of this nonlinear contribution is highest in the very low to low-frequency regions (<0.08 Hz).

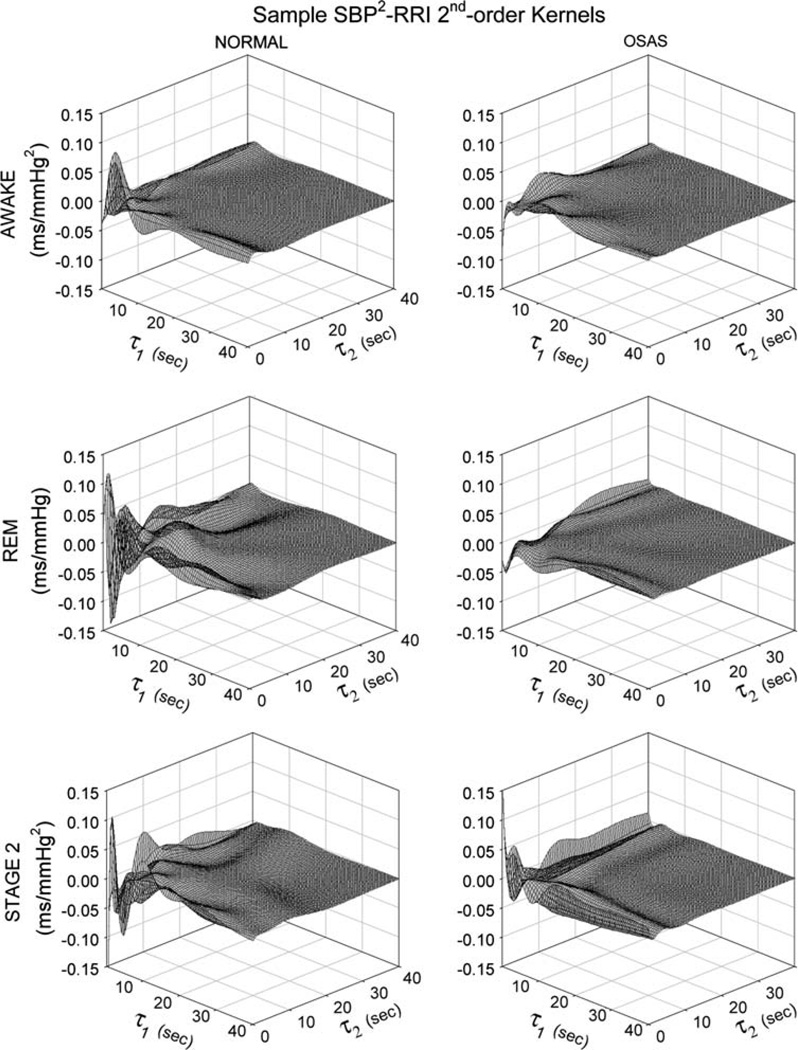
There was a tendency for the magnitude of the nonlinear RCC kernel, h_RCC2(τ₁, τ₂), to be lower in SDB subjects compared to normals (14.8 ± 2.7 vs. 25.9 ± 4.7 ms l⁻², respectively) but this difference was not statistically significant. On the other hand, the magnitude of the nonlinear ABR kernel, h_ABR2(τ₁, τ₂), was significantly lower (P < 0.04) in SDB relative to normals (0.07 ± 0.02 vs. 0.19 ± 0.08 ms mmHg⁻², respectively). The magnitude of the interaction kernel, h_RCC–ABR(τ₁, τ₂) was also significantly reduced in the SDB subjects (1.99 ± 0.35 vs. 4.32 ± 0.91 ms l⁻¹ mm Hg⁻² in normals, P < 0.03). Figure 5 compares the h_ABR2(τ₁, τ₂) kernels estimated from a representative control and a representative SDB subject, during the different states of wakefulness, REM sleep and non-REM sleep. It is quite clear that the magnitude of h_ABR2(τ₁, τ₂) is substantially smaller in the SDB subject relative to the normal control.

Fig. 5.

Comparison of secondorder kernels for SBP → RRI, h_ABR2(τ₁, τ₂), estimated from a representative normal control subject (left column of plots) with corresponding kernels estimated from a representative SDB subject (right column of plots, labeled “OSAS”) during wakefulness, REM sleep and NREM sleep (top, middle and bottom panels, respectively)

Model Extension: Incorporation of Time-Varying Dynamics

We have also extended the closed-loop minimal model to allow for time-varying behavior of the model components responsible for HRV and BPV (Blasi et al. 2006). Thus, in this case, the impulse response of each of the 4 minimal model components is allowed to vary with time:

$$\mathrm{\Delta }\text{RRI}(t)={\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{RCC}}(t,\tau )\mathrm{\Delta }V(t-\tau -T_{\text{RCC}})+{\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{ABR}}(t,\tau )\mathrm{\Delta }\text{SBP}(t-\tau -T_{\text{ABR}})+{\epsilon }_{\text{RRI}}(t)$$ (5)

$$\mathrm{\Delta }\text{SBP}(t)={\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{DER}}(t,\tau )\mathrm{\Delta }V(t-\tau )+{\displaystyle \sum _{\tau =0}^{p-1}}{h}_{\text{CID}}(t,\tau )\mathrm{\Delta }\text{SCO}(t-\tau -T_{\text{CID}})+{\epsilon }_{\text{SBP}}(t)$$ (6)

As in the time-invariant case, the impulse responses of the ABR and RSA components were modeled as linear combinations of Laguerre functions. However, in this case, the unknown Laguerre coefficients were allowed to be time-varying. For instance:

$$h_{\text{ABR}}(t,\tau )={\displaystyle \sum _{j=0}^{q-1}}{c}_j^{\text{ABR}}(t)L_j(\tau )$$ (7)

A recursive least squares algorithm was employed to compute the time-courses of these coefficients following acoustically induced arousals.

Another recent modification of the original minimal closed-loop model is that CID component is now taken to approximate the transfer relation between variations in cardiac output and corresponding fluctuations in SBP (Fig. 6). Since we do not have direct measurements of cardiac output, we define a new input variable for CID: the “surrogate cardiac output” (SCO). SCO is defined in the following way: at beat n, SCO(n) = PP(n)/RRI(n), where PP(n) = SBP(n) − DBP(n), DBP being Diastolic Blood Pressure. Thus, instead of RRI, SCO is now used as the input to the CID transfer function and SBP is considered the “output” of this component. Thus, the estimated CID impulse response in this case is expected to be largely representative of the combined impedance properties of the heart and systemic vasculature. We have found that using SCO instead of RRI as the input to the CID component produces a substantial reduction in the mean squared error between the measured and predicted ΔSBP from ~ 60% to less than 40% of the total variance.

Fig. 6.

Extension of the original minimal closed-loop model, incorporating time-varying dynamics in each of the model component transfer functions. A further modification is that the ratio of pulse pressure and RRI (“surrogate cardiac output”) is used as the input to the CID transfer function

We have applied the time-varying extension of the minimal closed-loop model to cardiorespiratory data measured in subjects with SDB and normal controls during transient arousal from sleep (Blasi et al. 2002, 2006). Transient arousals from sleep in normal subjects are known to produce brief increases in ventilation, heart rate and blood pressure that accompany large surges in sympathetic drive (Blasi et al. 2003). Since subjects with SDB are chronically exposed to repetitive arousals during sleep, a major question that we have sought to explore is whether this long-term exposure leads to impaired autonomic responses to arousals in SDB. To dissociate transient state changes from apnea or hypopneas, the experimental protocol involved the generation of arousals through the application of a brief auditory stimulus while the subjects were in various stages of NREM and REM sleep (Blasi et al. 2003). The minimal model was applied to time-courses of respiration, RRI and SBP, recorded shortly before and several minutes after each arousal, and used to produce estimates of the time-varying impulse responses in Eqs. 5 and 6.

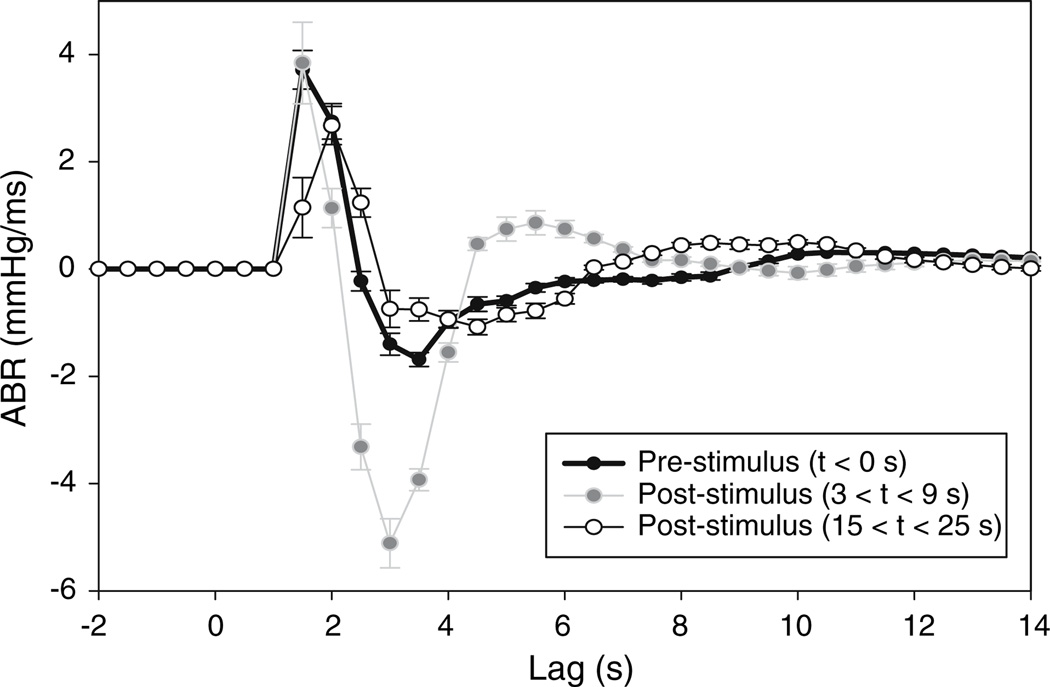
Figure 7 illustrates a representative sample of how the ABR impulse response, estimated from the minimal model, is altered following an acoustically induced arousal in a normal subject. In the immediate several seconds following the application of the arousal stimulus, there is a dramatic increase in magnitude of the ABR impulse response. As well, the ABR impulse response becomes more oscillatory. This is followed subsequently by a more sustained undershoot in the magnitude of h_ABR(t). Similarly, the magnitude of the RCC impulse response increases significantly (P < 0.05) during arousal; however, it remains above baseline up to 30 s following the start of arousal. In contrast, the ABR and RCC impulse responses in SDB subjects remain relatively unchanged during and after arousal.

Fig. 7.

Time-varying changes in the estimated ABR impulse response of a normal control during transient arousal from NREM stage 2 sleep

The large and almost immediate increase in heart rate that accompanies arousal is often interpreted as a dramatic withdrawal of parasympathetic drive. Our model suggests that this transient increase in heart rate can be accounted for as a secondary effect of the concomitant increase in ventilation that accompanies the arousal. However, the increase in heart rate is substantially larger than would be predicted on the basis of pre-arousal levels of RCC gain. Thus, to account for the observed acceleration in heart rate, the model predicts that RCC gain has to increase transiently. Baroreflex gain is also predicted to increase substantially immediately following the start of arousal. It is unclear at this point why this should be the case. However, the increase may be a built-in mechanism for buffering the surge in blood pressure. The lack of these changes in the arousal responses of the SDB subjects suggests that there is an impairment of the sensitivity of the RCC and ABR model components to transient state changes. This impairment may constitute a chronic adaptation of the autonomic cardiovascular system to episodic arousal in SDB.

Autonomic Control in Congenital Central Hypoventilation Syndrome (CCHS)

Another area of application of the minimal closed-loop model has been to young adults and children with CCHS (Lin et al. 2004). Compared to age-matched normal controls, CCHS subjects have substantially lower HRV (coefficient of variation: 4.0 ± 0.6 vs. 7.8 ± 0.9%, P = 0.012). On the other hand, we found no differences in mean heart rate, blood pressure or blood pressure variability between CCHS and controls. Baseline (supine) levels of baroreflex gain were much lower in CCHS relative to normals (2.8 ± 1.3 vs. 19.3 ± 2.7 ms mmHg⁻¹, P = 0.001). Since baroreflex sensitivity is known to be inversely correlated with sympathetic tone, this suggests that the CCHS subjects have abnormally elevated levels of sympathetic tone. Orthostatic stress leads to a further reduction in the already low levels of baroreflex gain in the CCHS subjects.

We have also found CCHS subjects to have lower baseline RCC gains relative to the normal controls (88.8 ± 26.7 vs. 174.7 ± 30.0 ms l⁻¹, P = 0.036), suggesting that the CCHS subjects have blunted parasympathetic control of heart rate. But both groups showed reductions in RCC gain during orthostatic stress.

Autonomic Function in Pediatric SDB

Yet another area that we have explored using the minimal closed-loop model approach has been autonomic control in children with SDB (Lin et al. 2005). Mean heart rate, mean blood pressure, HRV and BPV were found to be not significantly different between the SDB subjects and normal controls studied. Application of the minimal model to baseline data showed that ABR gain is on average almost half as large in SDB subjects as in normals (5.2 ± 2.8 vs. 9.4 ± 3.3 ms mmHg⁻¹). But we found no group differences in the impulse responses of the other model components, including RCC. Orthostatic stress led to significant reductions in baroreflex gains and RCC gains in both subject groups. Thus, the autonomic effects of SDB on children appear to be different from those reported in adults. Unlike the adult form, there appears to be no significant impairment of parasympathetic function in pediatric SDB, as evidenced by the relatively normal RCC impulse response. ABR gain in adults with moderate-to-severe SDB is dramatically attenuated; in pediatric OSAS, baroreflex gain appears to be reduced also but the magnitude of reduction is more subdued.

Conclusions

In a series of several studies, we have demonstrated the utility of employing a closed-loop minimal model of cardiovascular control to determine the chronic effects of SDB on autonomic function, as quantified by HRV and BPV. Table 1 summarizes the major findings obtained with the application of the original version of the model and subsequent extensions to different subject groups. The model-based approach allows us to assess the causal interrelationships among the physiological variables in question, in contrast to univariate signal processing approaches that focus on the time-domain or frequency-domain characteristics of individual time-series, such as RRI or SBP. We believe that this systems-oriented approach has been crucial in increasing the sensitivity with which differences in autonomic control of HRV and BPV can be detected between and within individual subjects. Our current array of measurements, which include only respiration, RRI and continuous blood pressure, imposes limitations on the minimal model in that it does not allow the model to include a mathematical representation of other factors that contribute to cardiovascular variability, such as the sympathetic control of peripheral vascular resistance or sympathetic control of cardiac contractility. However, with the current pace with which medical technology is advancing, it is quite conceivable that these limitations will be circumvented much sooner than expected.

Table 1.

Summary of published studies employing the minimal model

Study (published reference)	Model version/features	Subject pool/study conditions	Summary of findings
Belozeroff et al. (2002)	Original minimal closed-loop Model	SDB subjects studied in wakefulness before and after long-term CPAP therapy; comparison of compliant vs. non-compliant subjects	RCC and ABR gains increased while DER and CID gains decreased in compliant subjects; CID gain showed a tendency to increase in non-compliant subjects
Belozeroff et al. (2003)	Original minimal closed-loop Model	SDB subjects and normal controls studied during wakefulness in supine & standing postures	Reduced ABR and RCC gains, but higher CID gain in SDB subjects; both groups show decreases in ABR and RCC gains and increases in CID gain with change in supine to standing
Jo et al. (2003)	Original minimal closed-loop Model	SDB subjects and normal controls studied during wakefulness and sleep under bilevel pressure ventilation (used to broaden bandwidth of breathing pattern)	RCC and ABR gains lower in SDB subjects vs. normal controls; RCC gain unchanged with sleep in both groups; ABR gain increased with sleep in normals but remained unchanged in SDB subjects
Jo et al. (2007)	Nonlinear dynamics added to RCC and ABR components; assumed interaction between RCC and ABR gains	SDB subjects and normal controls studied during wakefulness and sleep under bilevel pressure ventilation (used to broaden bandwidth of breathing pattern)	Nonlinear ABR gain and magnitude of interaction between ABR and RCC lower in SDB subjects in all sleep-wake states
Blasi et al. (2002, 2006)	Time-varying dynamics incorporated into all components of minimal closed-loop model	Responses to acoustically induced arousals studied in normal and SDB subjects during NREM and REM sleep	RCC gain increased during arousal in NREM but not in REM sleep; ABR gain increased transiently during arousal in both sleep states but subsequently fell below pre-arousal levels. No significant changes in RCC and ABR gains with arousal in SDB subjects
Lin et al. (2004)	Minimal closed-loop model	Subjects with CCHS and age-matched controls studied during wakefulness in supine and standing postures	Substantially lower RCC and ABR gains in CCHS subjects; postural change from supine to standing lowered RCC and ABR gains further
Lin et al. (2005)	Minimal closed-loop model	Pediatric subjects with SDB and age-matched normal controls studied during wakefulness	ABR gain lower in SDB subjects, but no differences with controls in gains of other model components; postural change from supine to standing led to decreases in ABR and RCC gains in both subject groups