Abstract
Protein backbone 15N NMR spin relaxation rates are useful in characterizing the protein dynamics and structures. To observe the protein nuclear-spin resonances a pulse sequence has to include a water suppression scheme. There are two commonly employed methods, saturating or dephasing the water spins with pulse field gradients and keeping them unperturbed with flip-back pulses. Here different water suppression methods were incorporated into pulse sequences to measure 15N longitudinal T1 and transversal rotating-frame T1ρ spin relaxation. Unexpectedly the 15N T1 relaxation time constants varied significantly with the choice of water suppression method. For a 25-kDa Escherichia coli. glutamine binding protein (GlnBP) the T1 values acquired with the pulse sequence containing a water dephasing gradient are on average 20% longer than the ones obtained using a pulse sequence containing the water flip-back pulse. In contrast the two T1ρ data sets are correlated without an apparent offset. The average T1 difference was reduced to 12% when the experimental recycle delay was doubled, while the average T1 values from the flip-back measurements were nearly unchanged. Analysis of spectral signal to noise ratios (s/n) showed the apparent slower 15N relaxation obtained with the water dephasing experiment originated from the differences in 1HN recovery for each relaxation time point. This in turn offset signal reduction from 15N relaxation decay. The artifact becomes noticeable when the measured 15N relaxation time constant is comparable to recycle delay, e.g., the 15N T1 of medium to large proteins. The 15N relaxation rates measured with either water suppression schemes yield reasonable fits to the structure. However, data from the saturated scheme results in significantly lower Model-Free order parameters (〈S2〉 = 0.81) than the non-saturated ones (〈S2〉 = 0.88), indicating such order parameters may be previously underestimated.
Keywords: Spin relaxation, Dephase, Flip-back, Saturation, Recovery time, Order parameter
1. Introduction
Protein backbone 15N spin relaxation rates, the longitudinal (T1) and the transversal (T2) relaxation, are sensitive to the motion of protein N–H bond vectors. Accurately measured T1 and T2 are often used to derive both protein global diffusion parameters and local fast motions of the N–H bonds through numerical fitting, e.g. the Model-Free approach [1,2]. These parameters are useful in describing thermodynamic changes occurring in biomolecules as they function. In addition, since the ratio T1/T2 has been demonstrated to be dependent on the projection of the individual N–H bond to the protein rotational diffusion tensor frame [3], they can be applied as restraints to refine structures [4–6], as well as to relatively position domains within a protein complex [7–10]. The T1/T2 restraints are readily available and could be very helpful in characterizing larger systems. In contrast other NMR restraints are either requiring special treatment of the sample to measure, e.g. residual dipolar couplings (RDC) [11–13] and paramagnetic relaxation enhancement (PRE) [14], or not measurable, i.e. NOEs in deuterated system.
Similar to other solution NMR experiments accurate measurements of 15N T1 and T2 require satisfactory suppression of water 1H signals. One approach is to dephase or saturate water 1H spin coherence with the use of pulse field gradient or composite pulses [15–19]. Alternatively flip-back pulses, which keep water proton spins parallel to the B0 field throughout the pulse sequence, became popular owing to the advantage in minimizing effects of radiation damping on cryogenic probes [20,21]. Here we have incorporated both water suppression schemes into 2D 1H–15N pulse sequences for measuring 15N T1 and T1ρ. Significantly longer T1 values were obtained when water proton spins were saturated by the gradient. Close analysis of relaxation curves and spectral signal to noise (s/n) ratio illustrated that the 15N relaxation difference originated from the varied 1HN recovery caused by water saturation. The conclusion was supported by the fact that doubling the recycle delay reduced the relaxation rate differences. Interestingly such 15N relaxation rate discrepancies did not produce any noticeable differences in their fit to the rotational diffusion tensor, however, the derived order parameters differed significantly. Thus saturating water proton spins causes artifacts in measuring 15N relaxation rates, which also affect the interpretation of fast motion dynamics.
2. Results
2.1. Pulse sequences
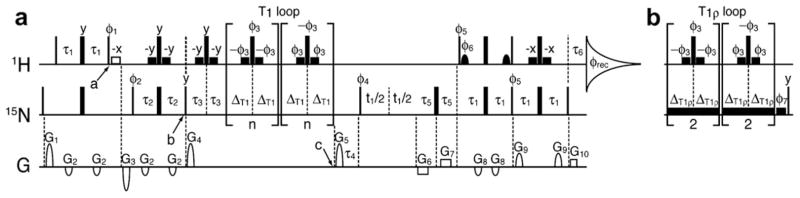
The 2D 1H–15N ST2-PT TROSY pulse sequence [22–24] was modified to include relaxation delays (Fig. 1). Shown in Fig. 1a is the pulse sequence for measuring longitudinal T1 relaxation. Pulses between points b and c in Fig. 1a are replaced with pulses in Fig. 1b to measure the transverse rotating frame relaxation T1ρ. At point a of Fig. 1a the two-spin order HzNz is established and water proton spins are on the transverse plane. For the water flip-back version of the measurement the soft 1.2-ms long 1H pulse, the open rectangle in Fig. 1a, was applied to flip water proton spins to +z. The in-phase Nx component was established at point b for the relaxation delays. Proton water-gate pulses, which flip non-water proton spins 180°, were applied periodically during T1 and T1ρ relaxation delays to cancel cross-correlations [25]. At point c gradient pulse G5 is a z-filter to clean any transverse magnetizations. Shaped and water-gate proton pulses were implemented during the TROSY detection to ensure water spins stay on +z (Fig. 1a).
Fig. 1.
The 2D 1H–15N pulse sequences for measuring 15N spin relaxation time constants T1 (a) and T1ρ (b) under TROSY detection. The pulses in panel 1a between points b and c are replaced with pulses in panel 1b to establish the pulse sequence for T1ρ measurement. The 1H and 15N carrier frequency was set to 4.663 ppm and 118.1 ppm, respectively. Narrow and wide filled rectangles correspond to hard pulses with flip angles of 90° and 180°, respectively. The open rectangle at point a is a 1.2-ms long 90° square pulse, turned on and off for water flip-back and dephase measurements, respectively. Other low-power filled squares on 1H channel are 90° square pulses with a width of 1.0 ms. Filled bells are 90° sinc-shaped water-selective pulses with a duration of 1.9 ms. In panel 1b the spin lock (SL) and the following 2-ms purge pulses on 15N channel had a γB1 field strength of 2000 Hz and were applied with phase φ7. Pulses are x-phase by default. Phase cycles are listed as follows, φ1 = 4(y), 4(−y); φ2 = 8(x), 8(−x); φ3 = 16(y), 16(−y); φ4 = y, −y, x, −x; φ5 = y; φ6 = −y; φ7 = 32(x), 32(−x); φrec = y, −y, x, −x, 2(−y, y, −x, x), y, −y, x, −x. Delay durations are listed as follows, τ1 = 2.3 ms, τ2 = 2.7 ms, τ3 = 2 ms, τ4 = 15 ms, τ5 = 0.4 ms, τ6 = 0.08 ms, ΔT1 = 4.0 ms. All gradient pulses are along z-axis and G6, G7, and G10 are in rectangular shape while the rest are sine-shaped. The duration, sign and strength for gradient pulses are as follows, G1 = 3 ms, 15 G/cm; G2 = 1 ms, −7.5 G/cm; G3 = 2 ms, −25 G/cm; G4 = 1 ms, 25 G/cm; G5 = 2 ms, 25 G/cm; G6 = 200 μs, −15 G/cm; G7 = 200 μs, 15 G/cm; G8 = 0.25 ms, −9 G/cm; G9 = 1 ms, 15 G/cm; G10 = 40.5 μs, 15 G/cm. Quadrature detection on the 15N dimension was achieved via Echo-Antiecho method [49–51] such that the second fid for each increment of t1 was collected with signs of gradient pulses G6 and G7 being switched, and pulse phases of φ4 = y, −y, −x, x, φ5 = −y, and φ6 = y being applied. For T1 measurement the relaxation delay equals ΔT1 × 4 × n where the loop number n was varied to yield different relaxation delays. For T1ρ measurement the relaxation delay equals total SL-duration, ΔT1ρ × 8, and ΔT1ρ was varied. For T1 measurement gradient pulse G4 is a z-filter to clean any magnetization other than Nz. For T1ρ measurement the 15N spin lock pulse was extended for 2 ms after the relaxation blocks to completely remove any component not in the direction of the spin lock (Fig. 1b); the 15N spin was then restored to the z direction by a 90°(y) pulse.
The dephase version of the pulse sequences stay nearly identical to the flip-back ones described above except for replacing the soft 1.2-ms long 1H pulse (the open rectangle in Fig. 1a) with a 1.2-ms delay. Such modification allows water proton spin coherence to be destroyed by the gradient pulse G3. Other than the difference of this soft 1H pulse, the rest of the pulse sequence remains identical between the two water suppression schemes so that any imperfection in canceling 1H–15N cross-correlation would affect the two measurements equally.
2.2. Measured T1 and T1ρ
The protein used to test the pulse sequences is Escherichia coli. Glutamine Binding Protein (GlnBP), which has a total of 226 residues and is highly anisotropic with a moment inertia ratio of 2. Chemical shift assignments of a total of 211 out of 219 non-proline 1H–15N resonances [26] were confirmed using conventional 3D experiments. Amide proton of residues undergoing exchange, A1, D2, G21, D22, D73, N97, N99, and G171, could not be observed. Overlapping residues E74, F136, L146, L196, K199, and K205 were further excluded, and 205 resonances were left for analysis. The NMR sample of 250 μM 2H/15N labeled GlnBP was subject to relaxation measurements under either of the two water suppression schemes (Fig. 1) at 34 °C and a magnetic field of 14.1 T.
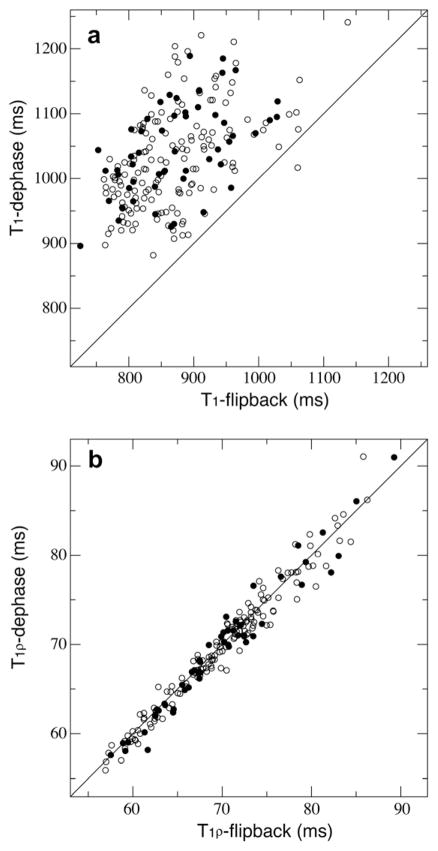
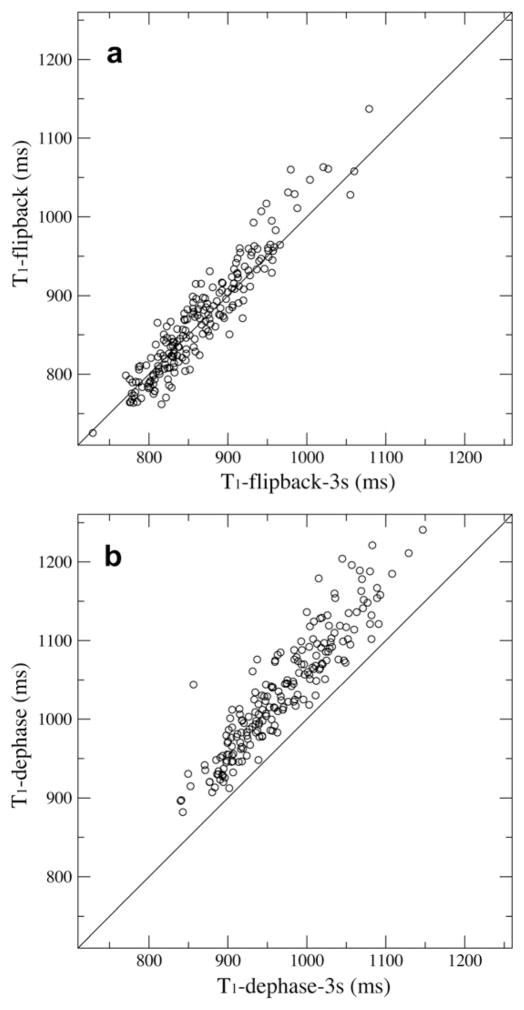
For T1 measurements the average curve fitting errors for the exponential decay function were 1.3% and 1.8% for dephase and flip-back data sets, respectively. Our experimental reproducibility error was 2.4%. The correlation plots of T1 from two different water suppression schemes (Fig. 2a) indicated significant differences between the two data sets with a large r.m.s.d. value of 181 ms between the two, or about 21% of the average T1 of the flip-back data set, which was 869.4 ms. Residues with side-chain being exposed [27] were indicated (Fig. 2a) and there was no correlation between surface exposure and T1 differences. The dephase pulse sequence which saturated water magnetizations resulted in a significantly slower T1 relaxation.
Fig. 2.
The correlation between the two relaxation measurements using the dephase and the flip-back schemes of pulse sequences for T1 (a) and T1ρ (b). Surface exposed residues are shown in filled circles.
For T1ρ the average curve fitting errors were 1.6% and 1.5% for dephase and flip-back data sets, respectively, and the r.m.s.d. between the two was 2.46 ms, about 3.4% of the average T1ρ of the flip-back data set, which was comparable to the reproducibility error of 3.0%. In fact the T1ρ correlation plot in Fig. 2b shows a much better agreement between the two measurements under different water suppression schemes than T1s in Fig. 2a. Similarly surface exposed residues do not differentiate from others.
2.3. 15N relaxation rate differences and spectra s/n
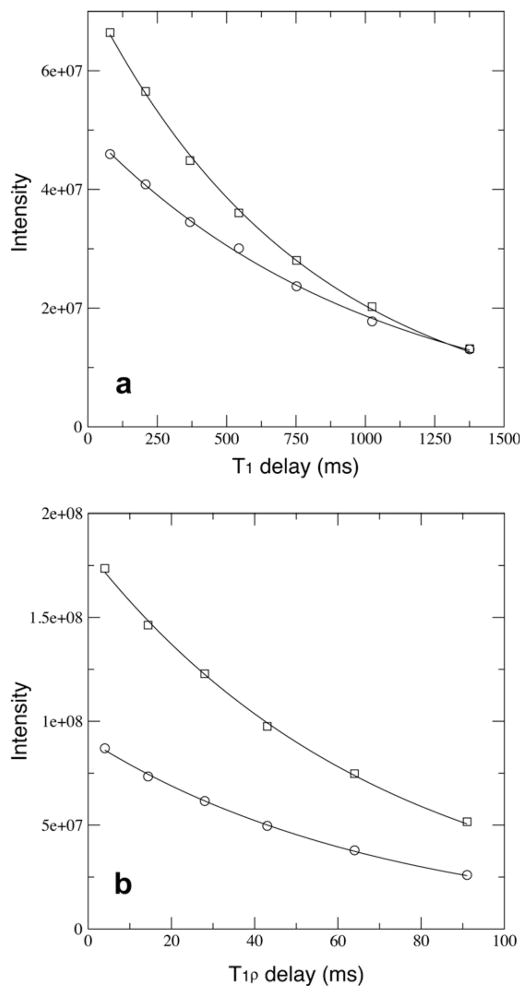
Resonance intensities of 15N T1 and T1ρ relaxation data points for a buried residue A96 were plotted (Fig. 3). Overall the peak intensities for dephase measurements are significantly lower than flip-back ones due to saturation on water 1H and protein 1HN spins. For all relaxation time points in T1ρ experiments there is a relatively constant 50% reduction of peak intensities in the dephase measurement (Fig. 3b). And the fit of T1ρ relaxation time constants from the two measurements are within 1.1%. However, for T1 experiments such peak intensity reduction is not uniform for all time points (Fig. 3a), and the fit T1 relaxation time constants differs by 30%. The varied peak intensity ratio of T1 points indicated the initial 1HN magnetization population was not uniform within the water saturation experiment. The longer the T1 relaxation delay time, the smaller the peak intensity difference between the two measurements (Fig. 3a). Earlier Grzesiek and Bax [28] pointed out a 10–20% increase of s/n of a protein HSQC spectrum was observed when water flip-back pulses were applied for water suppression instead of saturation using a gradient or rf pulses. And such s/n increase was not limited to solvent exposed amide protons because spin diffusion was quite efficient in transferring magnetizations within a protein [28,29]. Therefore it is plausible that saturation of water magnetization will result in variation of the initial 1HN magnetization that in turn will be modulated by the relaxation delay and can affect the measured resonance intensity decay.
Fig. 3.
The T1 (a) and T1ρ (b) relaxations curves for a buried residue A96 with absolute intensities being plotted. Data points from the dephase and the flip-back measurements are shown in squares and circles, respectively. The fit relaxation time constants in (a) are 1019 ms and 783.0 ms for the dephase and the flip-back measurements, respectively. The fit relaxation times constants in (b) are 71.94 ms and 71.15 ms for the dephase and the flip-back measurements, respectively.
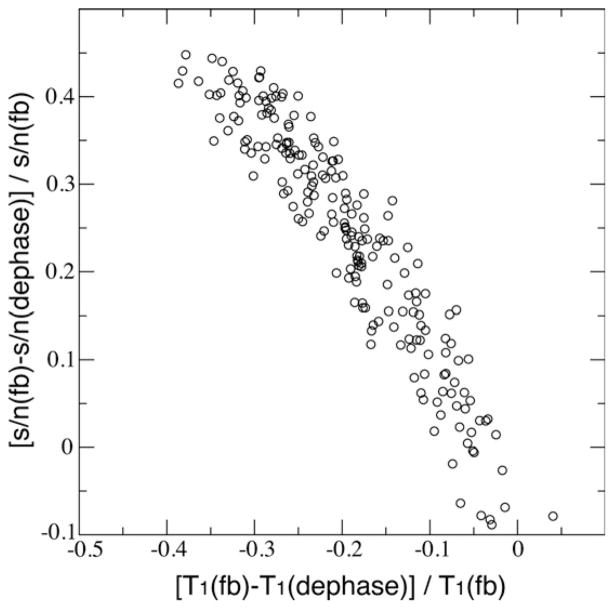
To further confirm the cause-relationship between the initial 1HN intensity and 15N T1 relaxation rate differences, we plotted the s/n differences of the first time-point spectra of dephase and flip-back T1 experiments against the measured 15N T1 differences between the two (Fig. 4). A strong correlation was observed and this confirmed the offset of 15N T1 in the two measurements was an artifact due to the difference in the recovery of 1HN magnetizations that was influenced by water saturation. The longer the relaxation delay, the closer the 1HN magnetizations return to its equilibrium, thus resulting in higher resonance intensity. This will cause an apparent slower decay of the resonance intensity as a function of 15N T1 relaxation delay.
Fig. 4.
The correlation between the normalized differences of s/n and T1 between dephase and flip-back measurements. The spectra s/n were taken from the first time-point in each measurement.
2.4. 15N relaxation rate differences and recycle delay
A simple check to the 1HN recovery problem in 15N T1 relaxation experiments is to increase the recycle delay so that the recovery difference can be reduced. We doubled the recycle delay from 1.5 s to 3.0 s and repeated the same 15N T1 measurements using both dephase and flip-back pulse sequences. Indeed the average difference between the T1 data sets was reduced to 12% from 21%. The two flip-back measurements with different recycle delays are correlated with an r.m.s.d. of 25.1 ms (Fig. 5a), 2.9% of the averaged T1 value. The two dephase measurements have an r.m.s.d. of 72.6 ms, and the T1 values with the 3-s of recycle delay are shorter (Fig. 5b). The dephase measurements do not provide reliable 15NT1 values because they depend on recycle delays. In contrast the flip-back measurement is relatively insensitive to changes in the recycle delay and will yield T1 relaxation times that are closer to the true values.
Fig. 5.
The T1 correlation between the two sets of repeated experiments at varied recycle delay of 1.5 s and 3.0 s. Either the flip-back method (a) or the dephase (b) method was applied for water suppression.
2.5. Dynamics derived from T1 and T2
Since most published relaxation measurements were carried out using the dephase scheme, it would be interesting to test whether dynamics derived from those 15N relaxation rates were reasonable. We used the GlnBP data sets collected with pulse sequences having dephase or flip-back schemes and 1.5-s recycle delay. Both sets of measured relaxation time constants ratios (T1/T2) were fit against the crystal structure of GlnBP [30] to obtain the rotational diffusion tensor [3,31]. After the removal of residues undergoing large amplitude fast motion, K3, K4, A168, T223, E234 and K226, a total of 199 T1/T2 data points were selected for fitting. To avoid over fitting only 20% of data points were randomly chosen to fit the fully anisotropic rotational diffusion tensor. The randomization were repeated 1000 times to yield a distribution of individual tensor parameters, and such distributions were fit to a Gaussian function to yield the means and standard deviations in Table 1. The overall diffusion Dzz from the dephase data set is 8% slower than the value from the flip-back measurement, due to an apparent slower T1 relaxation. The values of anisotropy (2Dzz/(Dxx + Dyy)) and asymmetry (Dyy/Dxx) from the two sets are close to each other, within a standard deviation, so are the Euler angles defining the tensor directions. The accuracy of tensor directions were checked by calculating the projection angle between the principal Z axes of each rotational diffusion tensor out of the T1/T2 fitting and the inertia tensor. The mean values are 8.3° for both data sets (Table 1). Thus both sets of measurements yielded reasonable tensor directions in comparison to a projection angle of 18° that was reported for a smaller anisotropic protein GB3 [32].
Table 1.
The rotational diffusion tensor derived from 15N T1/T2.
| Measurementa | Dzz (107s−1) | 2Dzz/(Dyy + Dxx) | Dyy/Dxx | α (°) | β (°) | γ (°) | χ2 | Projection angle (°)b |
|---|---|---|---|---|---|---|---|---|
| Dephase | 1.74 ± 0.04 | 1.44 ± 0.05 | 1.07 ± 0.04 | 96.4 ± 4.5 | 122 ± 4 | 33.8 ± 29.8 | 11.3 | 8.28 ± 3.26 |
| Flip-back | 1.89 ± 0.06 | 1.41 ± 0.07 | 1.09 ± 0.07 | 98.0 ± 6.9 | 124 ± 5 | 36.9 ± 34.6 | 16.2 | 8.33 ± 4.05 |
The standard deviations in diffusion tensor parameters and projection angles were derived from a Gaussian fitting on a total of 1000 individual T1/T2 fitting results using randomly chosen 20% of the 199 data points.
The angle between the long axes (Z) of the fit diffusion tensor and the inertia tensor.
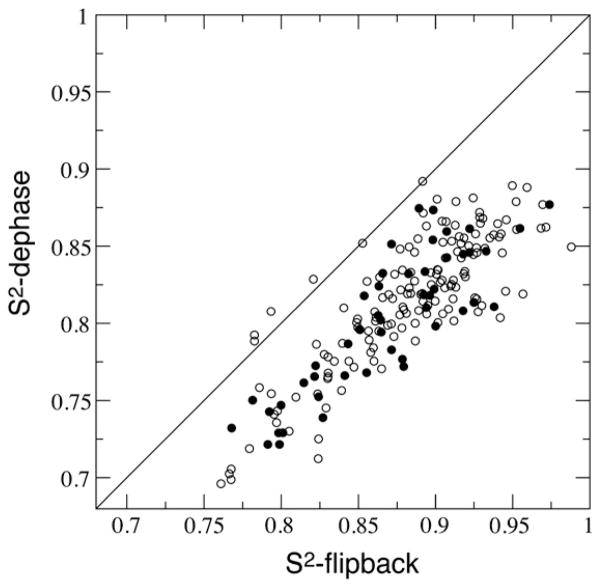
Further minimizations on T1 and T2 with the obtained diffusion tensor parameters resulted in local Model-Free order parameters S2. Shown in Fig. 6 is the correlation between derived S2 from the two measurements with the surface exposed residues indicated. The dephase data set yielded lower order parameter with an average value 〈S2〉 of 0.812, and the 〈S2〉 for the flip-back data set was 0.879. Such order parameter difference is significant.
Fig. 6.
The correlation between the dephase data and the flip-back data derived Model-Free order parameters S2. Surface exposed residues are shown in filled circles.
3. Summary and discussion
We measured 15N spin relaxation time constants T1 and T1ρ with the two different choices of water suppression methods. Measurements using the flip-back scheme keep water proton spins on +z axis while those employing dephasing gradient destroy water spin coherence on the transverse plane. The dephase experiment saturates water proton magnetizations while the flip-back experiment does minimal saturation. Pulse sequences were tested on both a medium sized protein GlnBP and a small protein Ubiquitin (Fig. S1). For both proteins the measured T1 relaxation time constants were significantly longer when the spectra were collected with the dephase pulse sequence. And the longer the T1 values, the larger the difference that was observed between the dephase and the flip-back measurements. Similar T1 differences were also found when HSQC detection scheme was utilized instead of the TROSY method (data not shown). This discrepancy was also observed when the experiments were carried out using a room-temperature probe instead of a cryogenic probe. This phenomenon does not seem to be sensitive to variation in the temperature, or whether the protein was deuterated or protonated. The difference for T1ρ is less prominent.
The apparent slower 15N T1 relaxation obtained from the dephase measurement is due to the difference in 1HN recovery. The variation of T1 relaxation delay results in the different initial 1HN magnetization, which adds to the effect of 15N relaxation in the final signal intensity. The longer the relaxation delay, the closer the 1HN magnetization returns to its equilibrium and the more signal will be observed. This counteracts the signal decay due to 15N relaxation being measured, thus resulting in an apparent longer relaxation time constant. This artifact is only noticeable when the measured 15N relaxation time constant is comparable to or longer than the recycle delay (1–2 s), e.g. 15N T1 of medium to large proteins. The effect is less or unnoticeable if 15N T1 of small proteins (<500 ms) or T2 are measured. Thus the flip-back method for water suppression should be preferable, which cause minimal water saturation [20,21]. The observations that water saturation could reduce the NMR spectrum s/n were made previously [28,29]. Furthermore applications of selective excitation pulses for fast spectrum acquisition were based on the similar principle of minimal water saturation [33,34]. Here we showed that this same effect could also influence measured heteronuclear relaxation times by modulating the initial proton magnetization.
It is also interesting to notice the practical effects of different water treatments on the dynamics analysis. The overall rotational diffusion tensor directions from the two measurements in general agree with the inertia tensor. Therefore structure refinement using T1/T2 ratios should still be valid. The other aspect of dynamics analysis is the Model-Free order parameters S2 describing amplitude of local motions. The data obtained using the flip-back scheme resulted in S2 (〈S2〉 = 0.88) that are globally higher than the values calculated from the dephase data set, which averaged at 0.81. Even though the dephase S2 values are closer to other published values being measured on other proteins at temperatures close to 34 °C [35–37], it is important to note that all of these published order parameters were derived from data acquired using the dephase scheme for water suppression. Thus the true range of Model-Free order parameters could be underestimated. The interpretation of fast-motion dynamics based on 15N spin relaxation depends on water suppression method and the real range of protein backbone N–H bond order parameters need further cross-validation.
4. Materials and methods
4.1. Isotope labeling and protein purification
The E. coli BL21(DE3) cells carrying the cDNA for its periplasmic protein GlnBP [38] constructed in a pET vector were cultured in 500 ml M9 minimal medium prepared in 99% D2O, with 15NH4Cl and glucose as the sole nitrogen and carbon sources, respectively. All isotopes were purchased from Cambridge Isotope Laboratories (Andover, MA). Cells were allowed to grow and express proteins at 37 °C for 2 days. Cell culture was then spun down and supernatant was saved. The cell pellet was further incubated at 25 °C for another 2 days in 100 ml of 20 mM Tris buffer pH 8.0 and 150 mM NaCl. This step allowed the complete secretion of GlnBP proteins from periplasmic space into the buffer. All buffer and the previously collected growth medium were concentrated to 100 ml and dialyzed against the same Tris buffer. The dialyzed sample with added glutamine to 1 mM was then loaded onto a 5-ml gravity column filled with Q-Sepharose resins. The flow-through, containing GlnBP in ligand-bound form, were collected, concentrated to 20 ml, and then dialyzed against 20 mM KPi buffer at pH 6. The dialyzed sample was then loaded onto a 5-ml gravity column filled with SP-Sepharose resins. Flow through was collected and concentrated to 5 ml and mixed with 25 ml of 6 M GuHCl. The mixture was incubated at 37 °C overnight to allow amide deuterons being exchanged to protons. Denatured GlnBP was refolded by a 10-fold dilution into 50 mM potassium phosphate buffer at pH 6.9. Further concentrating and buffer exchange were carried out as needed. The NMR sample for the study is composed of 250 μM 2H/15N labeled GlnBP in glutamine bound form in 50 mM potassium phosphate buffer at pH 6.9 with 0.5 mM EDTA, and 0.02% NaN3.
4.2. T1 and T2 measurements
All experiments were performed on a Bruker Avance 600 MHz spectrometer equipped with cryogenic probe and Z-gradient coil. Temperature was set at 34 °C. Pulse sequences were shown in Fig. 1 with descriptions provided in the caption. The spectral widths were set to 7212 Hz and 2083 Hz for 1H and 15N, respectively. The number of complex data points collected for 1H and 15N dimensions were 1024 and 128, respectively. For T1 measurements a series of seven 2D datasets at varied longitudinal relaxation delays from 80 to 1376 ms were collected in a randomized order. For T1ρ measurements a series of six 2D datasets at varied transverse rotating-frame relaxation delays from 4 to 91 ms were collected in a randomized and interleaved manner. With recycle delay of 1.5 s the total acquisition time for T1 and T1ρ experiments were 37 and 48 h, respectively. NMRPipe [39] was used to process all spectra and relaxation time constants and fitting errors were extracted using minimization routine in Sparky (T.D. Goddard and D.G. Kneller, University of California, San Francisco).
| (1) |
| (2) |
The T2 values were calculated from T1ρ, T1, 15N chemical shift offset ΩN, and spin lock field strength γB1 using Eqs. (1) and (2). ΩN was expressed in Hz and a uniform shift of −45 Hz (≈JHN/2) was applied to remove TROSY frequency offset for 15N spins. The γB1 value was fixed at experimental setup to 2000 Hz.
4.3. T1 and T2 calculations and minimizations
Spin relaxation rates are described by sums of the spectral density functions J(ω) of the N–H bond. The mathematical descriptions of the heteronuclear spin relaxation were described quite sometime ago [40]. The theoretical expressions for amide 15N spin relaxation rates in the absence of conformational exchange contributions are given in Eqs. (3)–(6) [41], where ωH and ωN are Larmor frequencies of 1H and 15N spins in rad/s, respectively, μ0 (4π× 10−7 kg m s−2 A−2) is the vacuum permeability, h (6.6262 × 10−34 kg m2 s−1) is Planck’s constant, γH (2.6752 × 108 rad kg−1 s A) and γN (−2.7126 × 107 rad kg−1 s A) are gyromagnetic ratios of 1H and 15N spins, respectively, rHN (1.02 × 10−10 m) is the inter-nuclei distance between 1H and 15N nuclei, and ΔσN (172 × 10−6) is the chemical shift anisotropy of amide 15N nucleus [42,43], and generally the largest component of 15N chemical shift tensor is assumed to be parallel to the N–H bond [44,45].
| (3) |
| (4) |
| (5) |
| (6) |
The spectral density function J(ω), the only variable in calculating T1 and T2, can be obtained from the Fourier transform of the N–H bond rotational correlation function. The N–H bond motion can be decomposed as the sum of local and global motions within Model-Free approach [1,2]. The global rotational diffusion model can be isotropic, axial symmetric, and fully anisotropic [46,47]. In our analysis we adopted a fully anisotropic diffusion model. The spectral density function can be calculated according to the formula in Lee et al. [41]. The structure coordinates of GlnBP are from the X-ray crystal structure at 1.94 Å resolution (1WDN) [30]. Amide protons were added to the structure using XPLOR-NIH [48].
| (7) |
Numerical minimization on a total number (N) of available relaxation rate ratios T1/T2 was carried out to obtain the global rotational diffusion tensor according to Eq. (7), where the differences between the above calculated ratios and the measured ratios were minimized, and δ(T1/T2) is measurement error. We also carried out a robustness test on the resulting rotational diffusion tensor by repeating the minimization in which the input consists of randomly chosen 20% of the available data points, and yielded estimation for the mean and error range. The Simplex algothrim written in MATLAB 2007b (The Mathworks, MA) was employed for all data minimizations. Residue specific amide bond Model-Free order parameters S2 were obtained by minimizing the χ2 differences between calculated and measured T1 and T2 using the available global diffusion tensor parameters from the previous T1/T2 ratio fitting.
Supplementary Material
Acknowledgments
We thank Dennis Torchia and Stephan Grzesiek for helpful discussions and Motoshi Suzuki for help with the sample preparation. This work was supported by the Intramural Research Program of the NIH, National Heart, Lung, and Blood Institute.
Appendix A. Supplementary material
Supplementary data associated with this article can be found, in the online version, at doi:10.1016/j.jmr.2011.09.042.
References
- 1.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J Am Chem Soc. 1982;104:4546–4559. [Google Scholar]
- 2.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 2. Analysis of experimental results. J Am Chem Soc. 1982;104:4559–4570. [Google Scholar]
- 3.Kay LE, Torchia DA, Bax A. Backbone dynamics of proteins as studied by N-15 inverse detected heteronuclear NMR-spectroscopy – application to staphylococcal nuclease. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- 4.Tjandra N, Garrett DS, Gronenborn AM, Bax A, Clore GM. Defining long range order in NMR structure determination from the dependence of heteronuclear relaxation times on rotational diffusion anisotropy. Nat Struct Biol. 1997;4:443–449. doi: 10.1038/nsb0697-443. [DOI] [PubMed] [Google Scholar]
- 5.Clore GM, Gronenborn AM, Szabo A, Tjandra N. Determining the magnitude of the fully asymmetric diffusion tensor from heteronuclear relaxation data in the absence of structural information. J Am Chem Soc. 1998;120:4889–4890. [Google Scholar]
- 6.Palmer AG. NMR characterization of the dynamics of biomacromolecules. Chem Rev. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- 7.Ryabov Y, Clore GM, Schwieters CD. Direct use of N-15 relaxation rates as experimental restraints on molecular shape and orientation for docking of protein–protein complexes. J Am Chem Soc. 2010;132:5987–5989. doi: 10.1021/ja101842n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ryabov Y, Suh JY, Grishaev A, Clore GM, Schwieters CD. Using the experimentally determined components of the overall rotational diffusion tensor to restrain molecular shape and size in NMR structure determination of globular proteins and protein–protein complexes. J Am Chem Soc. 2009;131:9522–9531. doi: 10.1021/ja902336c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ryabov Y, Fushman D. Structural assembly of multidomain proteins and protein complexes guided by the overall rotational diffusion tensor. J Am Chem Soc. 2007;129:7894–7902. doi: 10.1021/ja071185d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ryabov YE, Fushman D. A model of interdomain mobility in a multidomain protein. J Am Chem Soc. 2007;129:3315–3327. doi: 10.1021/ja067667r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278:1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 12.Bax A, Kontaxis G, Tjandra N. Dipolar couplings in macromolecular structure determination. Methods Enzymol. 2001;339:127–174. doi: 10.1016/s0076-6879(01)39313-8. [DOI] [PubMed] [Google Scholar]
- 13.Prestegard JH, Al-Hashimi HM, Tolman JR. NMR structures of biomolecules using field oriented media and residual dipolar couplings. Q Rev Biophys. 2000;33:371–424. doi: 10.1017/s0033583500003656. [DOI] [PubMed] [Google Scholar]
- 14.Clore GM, Tang C, Iwahara J. Elucidating transient macromolecular interactions using paramagnetic relaxation enhancement. Curr Opin Struct Biol. 2007;17:603–616. doi: 10.1016/j.sbi.2007.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Barbato G, Ikura M, Kay LE, Pastor RW, Bax A. Backbone dynamics of calmodulin studied by N-15 relaxation using inverse detected 2-dimensional NMR-spectroscopy – the central helix is flexible. Biochemistry. 1992;31:5269–5278. doi: 10.1021/bi00138a005. [DOI] [PubMed] [Google Scholar]
- 16.Skelton NJ, Palmer AG, Akke M, Kordel J, Rance M, Chazin WJ. Practical aspects of 2-dimensional proton-detected N-15 spin relaxation measurements. J Magn Reson B. 1993;102:253–264. [Google Scholar]
- 17.Farrow NA, Muhandiram R, Singer AU, Pascal SM, Kay CM, Gish G, Shoelson SE, Pawson T, Forman-Kay JD, Kay LE. Backbone dynamics of a free and a phosphopeptide-complexed Src homology-2 domain studied by N-15 NMR relaxation. Biochemistry. 1994;33:5984–6003. doi: 10.1021/bi00185a040. [DOI] [PubMed] [Google Scholar]
- 18.Korzhnev DM, Skrynnikov NR, Millet O, Torchia DA, Kay LE. An NMR experiment for the accurate measurement of heteronuclear spin-lock relaxation rates. J Am Chem Soc. 2002;124:10743–10753. doi: 10.1021/ja0204776. [DOI] [PubMed] [Google Scholar]
- 19.Massi F, Johnson E, Wang CY, Rance M, Palmer AG. NMR R-1 rho rotating-frame relaxation with weak radio frequency fields. J Am Chem Soc. 2004;126:2247–2256. doi: 10.1021/ja038721w. [DOI] [PubMed] [Google Scholar]
- 20.Zhu G, Xia YL, Nicholson LK, Sze KH. Protein dynamics measurements by TROSY-based NMR experiments. J Magn Reson. 2000;143:423–426. doi: 10.1006/jmre.2000.2022. [DOI] [PubMed] [Google Scholar]
- 21.Chill JH, Louis JM, Baber JL, Bax A. Measurement of N-15 relaxation in the detergent-solubilized tetrameric KcsA potassium channel. J Biomol NMR. 2006;36:123–136. doi: 10.1007/s10858-006-9071-4. [DOI] [PubMed] [Google Scholar]
- 22.Pervushin KV, Wider G, Wuthrich K. Single transition-to-single transition polarization transfer (ST2-PT) in [N-15, H-1]-TROSY. J Biomol NMR. 1998;12:345–348. doi: 10.1023/A:1008268930690. [DOI] [PubMed] [Google Scholar]
- 23.Rance M, Loria JP, Palmer AG. Sensitivity improvement of transverse relaxation-optimized spectroscopy. J Magn Reson. 1999;136:92–101. doi: 10.1006/jmre.1998.1626. [DOI] [PubMed] [Google Scholar]
- 24.Zhu G, Kong XM, Sze KH. Gradient and sensitivity enhancement of 2D TROSY with water flip-back, 3D NOESY-TROSY and TOCSY-TROSY experiments. J Biomol NMR. 1999;13:77–81. doi: 10.1023/A:1008398227519. [DOI] [PubMed] [Google Scholar]
- 25.Boyd J, Hommel U, Campbell ID. Influence of cross-correlation between dipolar and anisotropic chemical-shift relaxation mechanisms upon longitudinal relaxation rates of N-15 in macromolecules. Chem Phys Lett. 1990;175:477–482. [Google Scholar]
- 26.Yu JH, Simplaceanu V, Tjandra NL, Cottam PF, Lukin JA, Ho C. H-1, C-13, and N-15 NMR backbone assignments and chemical-shift-derived secondary structure of glutamine-binding protein of Escherichia coli. J Biomol NMR. 1997;9:167–180. doi: 10.1023/a:1018606304131. [DOI] [PubMed] [Google Scholar]
- 27.Braun W, Fraczkiewicz R. Exact and efficient analytical calculation of the accessible surface areas and their gradients for macromolecules. J Comput Chem. 1998;19:319–333. [Google Scholar]
- 28.Grzesiek S, Bax A. The importance of not saturating H2O in protein NMR – application to sensitivity enhancement and Noe measurements. J Am Chem Soc. 1993;115:12593–12594. [Google Scholar]
- 29.Hiller S, Wider G, Etezady-Esfarjani T, Horst R, Wuthrich K. Managing the solvent water polarization to obtain improved NMR spectra of large molecular structures. J Biomol NMR. 2005;32:61–70. doi: 10.1007/s10858-005-3070-8. [DOI] [PubMed] [Google Scholar]
- 30.Sun YJ, Rose J, Wang BC, Hsiao CD. The structure of glutamine-binding protein complexed with glutamine at 1.94 angstrom resolution: comparisons with other amino acid binding proteins. J Mol Biol. 1998;278:219–229. doi: 10.1006/jmbi.1998.1675. [DOI] [PubMed] [Google Scholar]
- 31.Tjandra N, Feller SE, Pastor RW, Bax A. Rotational diffusion anisotropy of human ubiquitin from N-15 NMR relaxation. J Am Chem Soc. 1995;117:12562–12566. [Google Scholar]
- 32.Hall JB, Fushman D. Characterization of the overall and local dynamics of a protein with intermediate rotational anisotropy: differentiating between conformational exchange and anisotropic diffusion in the B3 domain of protein G. J Biomol NMR. 2003;27:261–275. doi: 10.1023/a:1025467918856. [DOI] [PubMed] [Google Scholar]
- 33.Pervushin K, Vogeli B, Eletsky A. Longitudinal H-1 relaxation optimization in TROSY NMR spectroscopy. J Am Chem Soc. 2002;124:12898–12902. doi: 10.1021/ja027149q. [DOI] [PubMed] [Google Scholar]
- 34.Brutscher B, Lescop E, Schanda P. A set of BEST triple-resonance experiments for time-optimized protein resonance assignment. J Magn Reson. 2007;187:163–169. doi: 10.1016/j.jmr.2007.04.002. [DOI] [PubMed] [Google Scholar]
- 35.Vugmeyster L, Trott O, McKnight CJ, Raleigh DP, Palmer AG. Temperature-dependent dynamics of the villin headpiece helical subdomain, an unusually small thermostable protein. J Mol Biol. 2002;320:841–854. doi: 10.1016/S0022-2836(02)00537-5. [DOI] [PubMed] [Google Scholar]
- 36.Seewald MJ, Pichumani K, Stowell C, Tibbals BV, Regan L, Stone MJ. The role of backbone conformational heat capacity in protein stability: temperature dependent dynamics of the B1 domain of Streptococcal protein G. Protein Sci. 2000;9:1177–1193. doi: 10.1110/ps.9.6.1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chang SL, Tjandra N. Temperature dependence of protein backbone motion from carbonyl C-13 and amide N-15 NMR relaxation. J Magn Reson. 2005;174:43–53. doi: 10.1016/j.jmr.2005.01.008. [DOI] [PubMed] [Google Scholar]
- 38.Tjandra N, Simplaceanu V, Cottam PF, Ho C. Multidimensional H-1 and N-15 NMR Investigation of glutamine-binding protein of Escherichia coli. J Biomol NMR. 1992;2:149–160. doi: 10.1007/BF01875526. [DOI] [PubMed] [Google Scholar]
- 39.Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. Nmrpipe – a multidimensional spectral processing system based on unix pipes. J Biomol NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 40.Abragam A. The Principles of Nuclear Magnetism. Clarendon Press; Oxford: 1961. [Google Scholar]
- 41.Lee LK, Rance M, Chazin WJ, Palmer AG. Rotational diffusion anisotropy of proteins from simultaneous analysis of N-15 and C-13(alpha) nuclear spin relaxation. J Biomol NMR. 1997;9:287–298. doi: 10.1023/a:1018631009583. [DOI] [PubMed] [Google Scholar]
- 42.Kroenke CD, Rance M, Palmer AG. Variability of the N-15 chemical shift anisotropy in Escherichia coli ribonuclease H in solution. J Am Chem Soc. 1999;121:10119–10125. [Google Scholar]
- 43.Boyd J, Redfield C. Characterization of N-15 chemical shift anisotropy from orientation-dependent changes to N-15 chemical shifts in dilute bicelle solutions. J Am Chem Soc. 1999;121:7441–7442. [Google Scholar]
- 44.Fischer MWF, Majumdar A, Zuiderweg ERP. Protein NMR relaxation: theory, applications and outlook. Prog Nucl Magn Reson Spectrosc. 1998;33:207–272. [Google Scholar]
- 45.Palmer AG, Massi F. Characterization of the dynamics of biomacromolecules using rotating-frame spin relaxation NMR spectroscopy. Chem Rev. 2006;106:1700–1719. doi: 10.1021/cr0404287. [DOI] [PubMed] [Google Scholar]
- 46.Woessner DE. Nuclear spin relaxation in ellipsoids undergoing rotational Brownian motion. J Chem Phys. 1962;37:647–654. [Google Scholar]
- 47.Woessner DE. Spin relaxation processes in a 2-proton system undergoing anisotropic reorientation. J Chem Phys. 1962;36:1–10. [Google Scholar]
- 48.Schwieters CD, Kuszewski JJ, Tjandra N, Clore GM. The Xplor-NIH NMR molecular structure determination package. J Magn Reson. 2003;160:65–73. doi: 10.1016/s1090-7807(02)00014-9. [DOI] [PubMed] [Google Scholar]
- 49.Boyd J, Soffe N, John B, Plant D, Hurd R. The generation of phase-sensitive 2d N-15-H-1 spectra using gradient pulses for coherence-transfer-pathway selection. J Magn Reson. 1992;98:660–664. [Google Scholar]
- 50.Davis AL, Keeler J, Laue ED, Moskau D. Experiments for recording pure-absorption heteronuclear correlation spectra using pulsed field gradients. J Magn Reson. 1992;98:207–216. [Google Scholar]
- 51.Tolman JR, Chung J, Prestegard JH. Pure-phase heteronuclear multiple-quantum spectroscopy using field gradient selection. J Magn Reson. 1992;98:462–467. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.