Abstract
Electronic medical record (EMR) systems afford researchers with opportunities to investigate a broad range of scientific questions. In contrast to purposeful study designs, however, EMR data acquisition procedures typically do not align with any specific hypothesis. Subsequent investigations therefore require detailed characterization of clinical procedures and protocols that underlie EMR data, as well as careful consideration of model choice. For example, many intensive care units currently implement insulin infusion protocols to better control patients’ blood glucose levels. The protocols use prior glucose levels to determine, in part, how to adjust the infusion rate. Such feedback loops introduce time-dependent confounding into longitudinal analyses even though they may not always be evident to the analyst. In this paper, we review commonly used longitudinal model specifications and interpretations and show how these are particularly important in the presence of hospital-based clinical protocols. We show that parameter relationships among various models can be used to identify and characterize the impact of time-dependent confounding and therefore help explain seemingly incongruous conclusions. We also review important estimation challenges in the presence of time-dependent confounding and show how certain model specifications may be more or less susceptible to bias. To illustrate these points, we present a detailed analysis of the relationship between blood glucose levels and insulin doses on the basis of data from an intensive care unit.
Keywords: causal inference, glucose, electronic medical records, longitudinal data analysis, medical informatics
1. Introduction
Electronic medical records (EMR) systems conveniently capture vast amounts of clinical data, including laboratory results and medication dosages. Increasingly, clinicians and researchers are looking to EMR for data that can address specific scientific questions. However, a major challenge with associated analyses is that the ascertainment mechanisms and treatment courses for hospitalized patients usually differ in complex ways from those for participants in clinical trials, controlled experiments, or even cohort studies. One example, presented in detail here, regards the attempt to examine the relationship between insulin infusion rates and blood glucose levels in patients in an intensive care unit (ICU).
Modern critical care medicine is based on the principle of restoring aberrant respiratory, cardiovascular, and other functions to normal or even supranormal physiologic levels [1–4]. For patients in an ICU, the biomedical literature suggests that tight blood glucose control may prevent life-threatening adverse events [1,2,4,5]. Towards optimizing ICU patients glucose control, hospitals may employ locally developed computerized decision support (CDS) systems to guide dosing of intravenous insulin infusions [6]. Such systems often use protocol-scheduled blood glucose measurements, together with past ICU data, to determine subsequent adjustments to the patient insulin infusion rates. That insulin infusion rates and blood glucose concentrations are determinants of one another presents important analytical challenges because of time-dependent confounding. A thorough understanding of data acquisition procedures is therefore crucial for subsequent analyses. Unfortunately, the existence of the protocol is typically not evident from the EMR data. Further, in such settings, analysts have a number of longitudinal model choices including cross-sectional, Markov or transition, and distributed lag models. Across these models, parameters measure distinct quantities and, in the absence of a prespecified hypothesis, study conclusions can be impacted dramatically by model choice. When large differences in study conclusions do arise, it is useful to understand potential explanations.
The goal of this paper is to discuss challenges with and to provide insights into analyses of longitudinal clinical laboratory data collected on hospitalized patients. The work here is motivated by an analysis of blood-glucose insulin-dose-rate (BG–IDR) data from Vanderbilt University Hospital. Importantly, we do not seek to evaluate the effectiveness of the CDS protocol for controlling glucose but instead to examine the IDR–BG association in the presence of time-dependent confounding. The CDS protocol that led to the confounding is ‘convenient’ for our research purposes because it allowed us to know the functional form of the confounding mechanism. We can therefore compare and contrast the impact that treatment or propensity model misspecification can have on inferences for the target model parameters. Considerations regarding model choice and time-dependent confounding are central, and the interplay between the two is considered in depth. We find the BG–IDR data to be particularly insightful in that it illustrates the dramatic impact model choice can have on study conclusions. Motivated by this, we discuss approaches to better understand apparent discrepancies. Specifically, we demonstrate how parameters from distinct longitudinal models are closely related and, by appealing to a series of intermediate models, show how they can be calculated from one another. Such calculations provide important insights for analysts attempting to discern biological from data ascertainment mechanisms.
We organize the manuscript as follows. In Section 2, we describe the sample and the blood glucose control protocol utilized during the observation period. In Section 3, we discuss six models that may reasonably be applied to the BG–IDR data and show how parameters in these models can be calculated from one another. We discuss estimation challenges in Section 4, and in Section 5, we present the BG–IDR data analysis. We show the enormous impact that time-dependent confounding can have on inferences from analyses of data collected under a CDS system and further that the parameter relationships described in Section 3 are not approximations but are exact. In Section 6, we provide a summary.
2. Blood-glucose insulin-dose-rate data
2.1. Study sample
The BG–IDR data consist of a subset of patients admitted to the Trauma ICU at Vanderbilt University Hospital from May 31, 2004 through December 31, 2005 [7]. For the sake of this illustrative example, we restricted our examination of the BG–IDR relationship to the first 24 h following admission. Further, we restricted the analyses to patients who were well-controlled during the course of the study period; we excluded patients who experienced severe hyperglycemia, requiring an infusion rate that exceeded 5 U/h. See Section 6 for discussion of the potential selection bias induced by this exclusion.
Table I summarizes demographic characteristics and experiences of the sample. Of the 345 patients, 35% were female, approximately 11% were African American, and approximately 8% were designated an ethnicity other than Caucasian or African American. The median age and body mass index were 52 years and 25 kg/m2, respectively, and the median follow-up time was 22 h with 75% of all patients observed for at least 18 h. We checked blood glucose approximately every 2 h with 50% of time separations between successive glucose checks falling between 1.7 and 2.4 h. We administered dextrose to prevent hypoglycemia following 8% of all glucose checks.
Table I.
Demographics and characteristics of patients in the Vanderbilt Hospital intensive care unit between May 31, 2004 and December 31, 2005. We summarized categorical variables with percents and continuous variables with the 5th, 25th, 50th, 75th, and 95th percentiles.
| Variable | Summary |
|---|---|
| Number of subjects | 345 |
| Female | 35.7 |
| Ethnicity | |
| Caucasian | 80.9 |
| African american | 11.3 |
| Other | 7.8 |
| Admitting Unit | |
| Trauma | 48.3 |
| Surgical intensive care unit | 51.7 |
| Age (years) | 19, 31, 52, 66, 83 |
| Body mass index (kg/m2) | 19, 22, 25, 29, 39 |
| Final observation time (hours since admission) | 9.6, 18.4, 22.4, 23.3, 23.9 |
| Time separation between successive glucose checks (hours) | 1, 1.7, 2, 2.4, 3.7 |
| Insulin rate (U/h) | 0.1, 1, 1.6, 2.4, 3.5 |
| Dextrose given | 8.9 |
| Glucose values (mg/dl) | 74, 91, 102, 115, 139 |
| Difference in successive glucose values (mg/dl) | −38, −14, −1, 12, 38 |
2.2. Notation
The BG–IDR data consist of longitudinal, repeated measures on N = 345 ICU patients. Let ni denote the number of observations for the i th patient and Yij their observed blood glucose concentration at the j th time since admission into the ICU, tj, j ∈ {0, 1, 2, …, ni }. Further, let Xij denote insulin dose rate at the j th time and W ij a vector of one or more potential confounders. For the analyses of Section 5, W ij includes time invariant and baseline covariates, age, gender, race, body mass index, admitting unit (surgical ICU or trauma unit), and baseline glucose level, and time-varying covariates dextrose administered since last glucose check, time since admission into the ICU, tj, and time since the last glucose check (tj −tj−1). Finally, let Zij = Yij − Yij−1 denote the blood glucose change between times tj−1 and tj, with Yi 0 the baseline or admission glucose value for the i th subject. For notational convenience, let Y i = (Yi1, Yi2, … Yini), Z i = (Zi1, Zi2, … Zini) and X i = (Xi1, Xi 2, … Xini) denote the vectors and W i = (W i1, W i 2, … W ini) denote the matrix of subject-specific observed quantities.
The primary scientific goal of the BG–IDR data analysis is to characterize the relationship between insulin dose rates and both blood glucose levels and blood glucose changes. Broadly, using our notation, interest lies in understanding how X i influences the mean of Y i or Z i while adjusting for W i. However, a serious challenge to the analysis arises because the patients under examination are those whose glucose levels were controlled, in part, by a specific computer-based protocol, which we now describe. Recall and as discussed in Section 1, we are not interested in evaluating the CDS but instead interested in estimating the BG–IDR relationships in the presence of time-dependent confounding induced by the CDS.
2.3. Glucose control protocol
At the time a patient is brought into the ICU, hospital staff choose, among other parameters, a target range within which blood glucose concentrations should remain. Lower limits for this range can vary between 65 and 100 mg/dl, in 5 mg/dl increments; upper limits between 105 and 140 mg/dl, in 5 mg/dl increments. Once the patient is initiated into the the glucose control protocol, the protocol-specified insulin dose rate depends on the most recently measured blood glucose level, the patient history, and the target blood glucose range. Specifically, the protocol specifies that the insulin dose rate to be administered to the i th patient during the interval (tj−1, tj] is given by: Xij = Mij−1 · (Yij−1 − 60), where Mij−1 is a multiplicative constant at time tj−1. The multiplier Mij−1 is a function of possibly (i) past M values up to time tj−1; (ii) the lower and the upper limits of the target blood glucose range; and (iii) the baseline blood glucose concentration. Dortch et al. in [7] provided more details including the timing of blood glucose testing and the administration of dextrose to raise low blood glucose concentrations.
A key feature of the protocol is the dependence of Xij on Yij−1; the exposure level at time tj is determined, in part, by the outcome observed at time tj−1. Hence, there is strong potential for time-dependent confounding that must be considered when specifying models of interest as well as estimating their parameters. Note that in the BG–IDR data, the insulin dose rate for the i th patient at time tj is the dose that was determined in response to the prior blood glucose concentration. Consequently, when formulating and interpreting models, it is important to remember that, in our notation, Xij precedes Yij in time.
3. Models specification and relationships between model parameters
Although the BG–IDR data provide an important research opportunity, the data collection procedures were neither developed as part of a specific study design nor was there a prespecified hypothesis or model of interest. As a consequence, analysts may be faced with a rather vague yet typical question of ‘What is the effect of insulin dose rates on blood glucose?’. Without a precise formulation of the study question, the analysis could proceed in a number of directions, although differences in model choice could result in important differences in terms of study conclusions. Here, we present and discuss six reasonable models that might be used to analyze the BG–IDR data.
3.1. Potential model choices
Following the notation of Section 2.2, the six models are the following:
| (Model 1a) |
| (Model 1b) |
| (Model 1c) |
| (Model 2a) |
| (Model 2b) |
| (Model 2c) |
Models 1a–1c (indexed by parameters β) describe the relationship between blood glucose levels and covariate values. Models 2a–2c (indexed by parameters γ) use blood glucose changes as the response. Models 1a and 2a are cross-sectional mean models; hence the superscript C. Models 1b and 2b (superscript T) add the lagged blood glucose value, Yij−1, into the regression model. Model 1b is a transition or a first-order Markov model, though Model 2b is not because it does not include, as an independent variable, its lagged response value (i.e., Zij−1). Models 1c and 2c are second-order distributed lag models (superscript D) in that they include the present and first-order lagged insulin dose rates as predictors. The multivariate distribution of the errors (denoted by ε) and specifically the within-patient covariance structure among responses will differ according to the model specification. Our only assumption is that the error distributions have means equal to 0 and finite variances. Recall from Section 2.2 that in our notation, Xij is the insulin dose rate that the patient was on at the time Yij was measured, and it is the dose that the patient had been on since just after the time Yij−1 was measured. That is, Xij precedes Yij in time. We discussed the covariates included in Wij in Section 2.2.
3.2. Model interpretation
Towards addressing the question ‘What is the effect of insulin dose rates on blood glucose?’, the key parameters of interest are , and . The parameters from models 1a–1c correspond to the differences in covariate adjusted mean glucose levels, and parameters from models 2a–2c correspond to the differences in covariate adjusted mean glucose changes. Other terms in the linear predictor define the adjustment that is made to the mean and therefore are crucial in the interpretation of the parameters. Although each of models 1a–1c and 2a–2c may be a reasonable choice for the BG–IDR analysis, precisely characterizing differences in the interpretations of the key parameters reveals that each captures a different aspect of the ‘effect’ of interest. Because of this, analysts may find themselves in situations where estimates across the various models yield seemingly discrepant study conclusions. By introducing a series of intermediate models, we show that the parameters across the six models are related and can be derived from one another. Understanding these relationships can provide crucial insight into model specification and choice and the impact both can have on study conclusions.
3.3. Intermediate models
Consider the following three ‘intermediate’ models:
| (IM-I) |
| (IM-II) |
| (IM-III) |
IM-I describes the relationship between the lagged blood glucose levels and present the insulin dose; IM-II captures the relationship between successive insulin doses; and IM-III describes the relationship between the lagged blood glucose level and both the present and lagged insulin dose rates. Note that each of these models is ‘backwards’ in that dependent variables precede, in time, independent ones. As such, one cannot reasonably interpret the models in terms of ‘causal associations.’ Mathematically, these relationships exist and their parameters can be estimated using the data. However, we emphasize that the purpose of their development was to act as helpful constructs in explaining the relationships between models 1a–1c and 2a–2c.
Using IM-I, IM-II, and IM-III, and simple conditional expectation arguments, it is straightforward to calculate the relationships among the parameters in the six models of Section 3.1. Figure 1 summarizes these relationships. Two sets of relationships appear; those across parameters within a response class (i.e., focusing either on blood glucose levels, Y, or on blood glucose changes, Z) and those within a model class (e.g., comparing the cross-sectional models for Y and Z).
Figure 1.
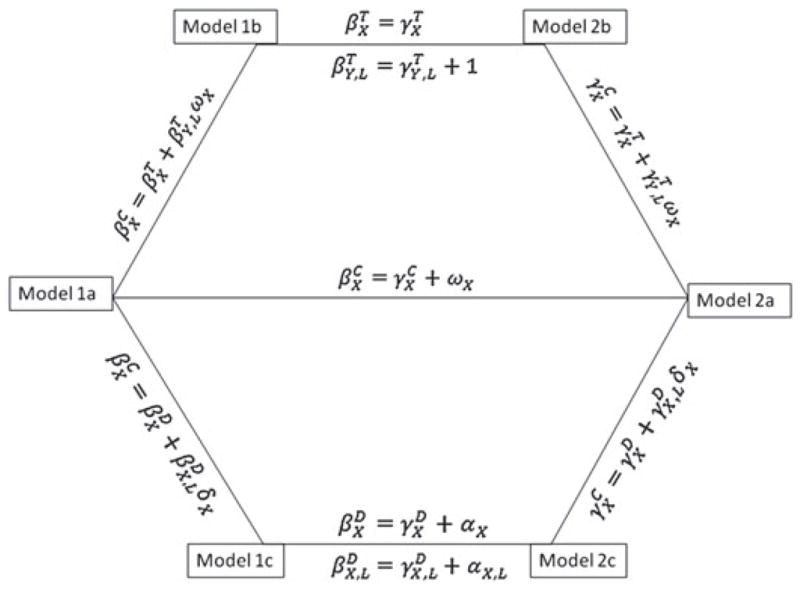
Relationship among key parameters in the models of Section 3.1.
3.4. Relationships within a response class
Within a response class, the parameter corresponding to the insulin effect for a given model is a simple weighted sum of the parameters in each of the other models, with the weights being terms in one of the intermediate models. For example, the parameter in the cross-sectional model for Yij (i.e., in model 1a) is a weighted sum of the parameters in the transition model (i.e., model 1b): . Similarly, the parameters across the blood glucose change models are weighted sums of the terms in the other models. For example, the parameter in the cross-sectional model for Zij (i.e., in model 2a) can be seen to be a weighted sum of the parameters in the distributed lag model (i.e., model 2c): . Note that δX will often fall between 0 and 1 (because it captures the partial correlation between successive insulin doses within a patient). Consequently, the cross-sectional insulin effect can be intuitively interpreted as a combination of the two insulin effects in the distributed lag model with less weight associated with parameter for the lagged insulin dose. We refer the reader to the Introduction of Reference [8] for further discussions. In most settings, particularly if the time period between successive doses is not long, an effect of the lagged dose might reasonably persist (i.e., ). As such, cross-sectional and distributed lag models will likely differ.
3.5. Relationships within a model class
Within a model class, parameters differ by (at most) a single additive, constant term, with the constant given by one of the terms in IM-I, IM-II, or IM-III. For example, the insulin effects in models 1a and 2a differ by . Similarly for each of the other within-model class comparisons. In terms of the insulin effects, models 1b and 2b are equivalent to one another. Specifically, and are equal, and and differ by one. Note that if the protocol succeeds in controlling glucose well, the distribution of the response values does not change drastically with time and will usually fall between 0 and 1. Consequently, the lagged blood glucose value parameter for blood glucose level and blood glucose change models ( and , respectively) are likely to have opposite signs.
3.6. Equivalence conditions
In addition to presenting numerical relationships between the insulin effect parameters, Figure 1 helps highlight conditions under which the target parameters across the models are equivalent. For example, if ωX = 0, then the target parameters in models 1a, 1b, 2a, and 2b all have the same numerical value (i.e., ). In addition, if δX = 0, then the target parameters in all the models have the same numerical value (i.e., ). For the BG–IDR data, the first condition corresponds to lagged response being unrelated to the present insulin dose; the second condition that the lagged insulin dose is unrelated to the present dose. From the description of the protocol in Section 2.3, it is clear that neither of these will be likely to hold in the BG–IDR data.
4. Time-dependent confounding
From the description of the glucose protocol in Section 2.3, there is a feedback loop between insulin dose and blood glucose in the BG–IDR data; the longitudinal insulin dose process is said to be ‘endogenous’ with respect to the blood glucose concentration process [9,10]. Endogeneity presents a particularly important challenge for the analysis of the BG–IDR data. To see this, consider model 1a and note that lagged blood glucose (Yij−1) is both (i) an intermediary variable along the causal pathway between lagged insulin dose (Xij−1) and present blood glucose (Yij) and (ii) a confounder of the relationship between the present insulin dose (Xij) and present blood glucose (Yij) [11]. Estimation is complicated because including the lagged glucose in the regression removes the effect past insulin doses have on present glucose levels and analyses that do not include it ignore the effect of a significant confounder.
4.1. Model susceptibility
Clearly, because the protocol leads to the lagged response being a strong predictor of insulin dose, model 1a is highly susceptible to time-dependent confounding for the BG–IDR analysis. The same argument can be applied to model 1c. By inspecting IM-I and IM-III, time-dependent confounding is likely to lead to relatively large values of ωX and αX, and from Figure 1, this could lead to large differences in parameter estimates from the various models. Model 1b explicitly adjusts for the lagged response Yij−1 in the regression model, thereby removing the confounding. However, such an adjustment blocks the potentially important pathway between insulin history Xij−1 and the present blood glucose concentration Yij. Models 2a–2c are less likely to be susceptible to the impact of time-dependent confounding because the protocol does not directly involve lagged glucose changes Zij−1 in determining insulin dose rates Xij. However, because the lagged glucose concentration is implicit in Zij, the impact of insulin history, Xij−1, on glucose is not captured by parameters from these models. That is, models 2a–2c necessarily focus on short-term exposure effects. In contrast, models 1a and 1c can capture the longer term effects insulin dose history.
4.2. Parameter estimation
In the presence of time-dependent confounding, inverse probability of treatment weighted estimation can yield unbiased estimates of causal effects [9, 11]. The approach works by reweighting contributions to the estimating equation in such a way that removes the relationship between the lagged response (Yij−1 or Zij−1) and present exposure (Xij); intuitively, the weighting corresponds to the construction of a pseudo-population in which lagged responses and present exposures are unrelated. Removal of this relationship means that the lagged response is no longer a confounder. From a scientific perspective, once the confounding is successfully removed, marginal models such as models 1a and 1c may be most appropriate because in addition to capturing the immediate effect of the Xij on Yij, they both also implicitly or explicitly capture the impact of covariate history, Xij, on responses.
The applicability and ultimate success of inverse probability of treatment weighting as a means to overcome time-dependent confounding relies on the adequacy of the model for the exposure process (Xi). For the BG–IDR data, this amounts to appropriate modeling of the insulin dose rates. Although the protocol specified insulin dose rate leads to excellent predictions of actual insulin dose rates, it is not ideal for the inverse probability of treatment modeling approach because it leads to violations of the implicit assumption of positivity [12, 13]. For example, when the protocol dictates that the insulin dose should be, say 5 IU/L, the probability of receiving a dose of 4 IU/L or less is effectively 0. In Section 5, we perhaps counterintuitively do not use the protocol directly for constructing the insulin dose models because not all inputs that determine the protocol specified dose confound the relationships of interest in the BG–IDR analysis. For example, the target glucose range is chosen by hospital staff at the time the patient entered the ICU. Although it is important in the calculation of the recommended insulin dose at all timepoints, it is not independently related to the responses in these models, and therefore it is not a confounder. In cases where the positivity assumption is violated, removal of time-dependent confounding via inverse probability weighting is tenuous [14, 15] and G-computation is a recommended estimation strategy [16,17]. Though most discussions and implementations of inverse probability weighting to correct for time-dependent confounding involve discrete exposures, Reference [18] discussed the approach in generality including for continuous variables and Reference [19, 20] implemented the approach for continuous exposures, which is what we do here.
Although it is well known that covariance weighting can lead to improved estimation efficiency in longitudinal data settings, in the presence of time-dependent confounding, it can lead to bias. Specifically, for the BG–IDR analysis consider the cross-sectional mean model for Yij, model 1a. Pepe and Anderson [21] showed that a sufficient condition to ensure unbiased estimation of a parameter corresponding to a time-varying covariate (i.e., Xij in the BG–IDR analysis) is that the cross-sectional mean model be equal to the full-covariate conditional mean model:
When this condition is violated, unbiased estimates of time-dependent covariate parameters are only guaranteed if independence working covariance weighting is used. Consequently, working covariance weighted generalized estimation equations [22] and likelihood-based mixed models [23] will likely yield biased parameter estimates. Reference [8] provided analytical solutions for the biases incurred from covariance weighting for longitudinal data models with exchangeable and autoregressive correlation structures.
Although Pepe and Anderson specifically discussed this issue in the context of the cross-sectional mean model, their prerequisite condition for sufficiency is violated for all BG–IDR analyses of glucose levels. Specifically, because future insulin doses Xij + 1 are not conditionally independent of present glucose values Yij, it is straightforward to see that E(Yij | Xij, Wij) ≠ E(Yij | Xi, Wi), E(Yij | Xij, Yij−1, Wij) ≠ E(Yij | Xi, Yij−1, Wi), and E(Yij | Xij, Xij−1, Wij) ≠ E(Yij | Xi, Wi). Hence, estimation of parameters in models 1a–1c may be susceptible to the bias described in Pepe and Anderson, and independence covariance weighting may be preferable. In contrast, models 2a–2c may exhibit some robustness to this source of bias because the insulin dose rates are only indirectly affected by glucose changes. That is, Zij may not have a strong, independent relationship with future insulin dose rates (Xij + 1).
5. Data analysis
We now analyze the BG–IDR data and discuss parameter estimates corresponding to the effect of changes in insulin dose rates on outcomes in models 1a–1c and 2a–2c. Following the discussion presented in Section 4.2, we used an independence working covariance matrix for parameter estimation. Further, we obtained standard error estimates that acknowledge additional uncertainty associated with estimating the stabilized inverse-probability weights via a cluster bootstrap approach [24].
5.1. Estimation strategies
The BG–IDR data provide an insightful example for explaining the impact of time-dependent confounding because the glucose control protocol of Section 2.3 was well documented and was closely followed in the ICU. Consequently, for these data, the mechanism underlying the time-dependent confounding is known. This will generally not be the case, and it provides an opportunity to explore estimation in the presence of time-dependent confounding as well as to characterize the impact it has on results and study conclusions. Towards this, we considered three estimation strategies for each of models 1a–1c and 2a–2c. The first, termed the naïve strategy (NS), ignores the potential for time-dependent confounding and estimates model parameters via unweighted working independence generalized estimation equations. The second strategy is to use inverse probability of treatment weighting where the treatment or propensity model is a linear regression of the observed insulin dose rate as a function of the lagged blood glucose concentration and potential confounders at the previous time: Xij ~ Yij−1 + Wij−1. This strategy is termed the lagged glucose value strategy (LVS). The final strategy, termed the lagged glucose change strategy (LCS), is to construct a propensity model as a function of lagged glucose change and potential confounders at the previous time: Xij ~ Zij−1 + Wij−1. Recall that Section 2.2 describes the variables that we included in Wi for the analysis.
It is worth noting that inverse probability of treatment weighted estimation to correct for the impact of time-dependent confounding is almost exclusively applied and rightfully so, in settings where marginal structural models such as models 1a and 1c are of interest because of reasons discussed in Section 4.2. However, we also use them with the conditional models such as model 1b primarily to demonstrate the parameter relationships described in Section 3. As we will show, these relationships hold as long as a single inverse probability weighting scheme for the two models being compared and for the intermediate model is used. Said another way, because weighting schemes can be thought of as a means of applying study results to target populations, the relationships hold as long as the target population for the models being compared is consistent. The use of inverse probability of treatment weighting for conditional models also shows that these models are less susceptible to the impact of time-dependent confounding because they include the confounding variable explicitly as an independent variable (model 1b) or implicitly as part of the response (models 2a–2c).
5.2. Stabilized inverse probability of treatment weighted estimation
Assuming the propensity model is specified appropriately, inverse probability of treatment weighting yields unbiased estimation in the presence of time-dependent confounding. In some settings, particularly when the probability of treatment is low within certain subpopulations, the weights can be extremely large, leading to highly inefficient estimation. One approach to improving efficiency is to ‘stabilize’ the weights via a propensity model that uses Wij−1 only to predict the observed insulin dose rates [9]. The stabilized weights for the LVS and LCS are
respectively. For the BG–IDR analysis, we calculated the numerators and denominators of and using the density of predictive distribution (assuming normality) from the insulin dose rate regression models. Even with the stabilization, weights can take on extremely large values. Though we may have incurred some bias, we followed the recommendations of Cole and Hernan [12] and truncated the weights (at 50) to avoid highly inefficient parameter estimates.
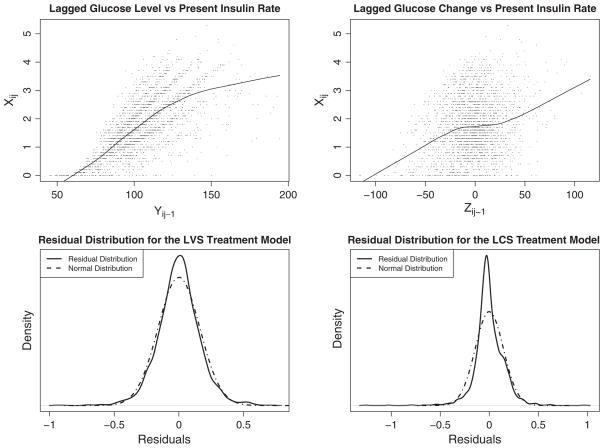
The top two panels of Figure 2 show the marginal relationship between Yij−1 and Xij (left) and between Zij−1 and Xij (right). As expected, Yij−1 is highly related to Xij and although Zij−1 is also related to Xij, the relationship appears much weaker. Thus, the potential impact of time-dependent confounding is much greater in models for glucose level than for glucose change. The bottom two panels of Figure 2 show the kernel densities of the observed residual distribution for the (insulin dose rate) treatment or propensity models. Also included are normal approximations that have the same variance as that observed in the residuals; these normal distributions are used for determining the values of the stabilized weights in LVS and LCS estimation. The normality assumption for the LVS seems quite reasonable. For LCS, the propensity model residual distribution has somewhat heavier tails than the normal distribution; however, truncating stabilized weights at 50 should help to avoid giving extraordinarily high weights to those in the tails of the distribution.
Figure 2.
Scatterplots of lagged response values (Yij−1 and Zij−1) and insulin dose rates (Xij) and kernel density plots of the residual distributions of the insulin dose rate treatment models.
5.3. Results
Table II displays parameter estimates and 95%CI corresponding to 3.0-unit insulin dose changes using the six models (1a–1c and 2a–2c) and the three estimation strategies (NS, LVS, and LCS) described earlier. Within-model comparisons among estimation strategies (across rows) show that time-dependent confounding induced by the glucose control protocol had a substantial impact on all analyses, most noticeably on parameters in models 1a and 1c. Parameter estimates for the insulin dose effects based on the ‘gold standard’ LVS were statistically significant and negative [−24.0, 95%CI: −32.5 to −14.2 for model 1a; −23.3, 95%CI: −32.6 to −14.9 for model 1c], as one would expect physiologically because insulin is used for the purpose of reducing blood glucose levels. In contrast, estimates based on NS were highly statistically significant and positive [6.0, 95%CI: 2.7 to 9.5 for model 1a; 9.5, 95%CI: 5.5 to 13.7 for model 1c]. Hence, conclusions based on models 1a or 1c for which estimation ignored time-dependent confounding would be in the opposite direction from what would be considered physiologically plausible. As should be expected, LCS strategy does not effectively remove the impact of time-dependent confounding on glucose level analyses; parameter estimates for models 1a and 1c indicate no evidence of a relationship between insulin rates and blood glucose levels.
Table II.
Blood-glucose insulin-dose-rate data analysis for patients in the Vanderbilt University Hospital Intensive Care Unit between May 31, 2004 and December 31, 2005. We display adjusteda point estimates and 95%CI corresponding to 3.0 U/h changes in insulin dose rate, 1.0 mg/dl change in the lagged response value, and 3.0 U/h changes in lagged insulin dose rate.
| Outcome/model | Covariate | Estimation strategy
|
||
|---|---|---|---|---|
| NS | LVS | LCS | ||
| Blood glucose, Yij | ||||
| 1a | Insulin rate | 6.0 (2.7, 9.5) | −24.0 (−32.5, −14.2) | −1.1 (−12.1, 11.5) |
| 1b | Insulin rate | −17.9 (−22.3, −13.6) | −23.2 (−30.6, −16.2) | −20.5 (−35.5, −6.6) |
| Glucose lag | 0.6 (0.5, 0.7) | 0.7 (0.5, 0.9) | 0.6 (0.4, 0.8) | |
| 1c | Insulin rate | 9.5 (5.5, 13.7) | −23.3 (−32.6, −14.9) | 1.2 (−11.4, 18.3) |
| Insulin rate lag | −5.4 (−8.7, −2.2) | −1.1 (−10.3, 8.1) | −4.4 (−15.5, 6.0) | |
| Blood glucose change, Zij | ||||
| 2a | Insulin rate | −33.1 (−37.2, −29.3) | −22.8 (−30.8, −15.7) | −31.5 (−45.3, −17.0) |
| 2b | Insulin rate | −17.9 (−22.3, −13.6) | −23.2 (−30.6, −16.2) | −20.5 (−35.5, −6.6) |
| Glucose lag | −0.4 (−0.5, −0.3) | −0.3 (−0.5, −0.1) | −0.4 (−0.6, −0.2) | |
| 2c | Insulin rate | −43.2 (−47.2, −39.1) | −20.4 (−35.6, −7.5) | −32.7 (−53.8, −14.9) |
| Insulin rate lag | 15.8 (12.1, 19.3) | −4.1 (−18.9, 11.2) | 2.8 (−11.8, 20.4) | |
NS, naïve strategy; LVS, lagged glucose value strategy; LCS, lagged glucose change strategy.
Section 2.2 of the text provides a list of adjustment variables included in all regression models.
As noted in Section 4.1, because model 1b includes the lagged response as an independent variable in the regression model, it is expected to be resistant to the impact of time-dependent confounding. The estimates in Table II are consistent with this. In particular, the results across the differing estimation strategies did not have a large impact on parameter estimates or conclusions. Although the estimation strategy for analyses of glucose changes (models 2a–2c) had an impact on the quantitative results, all estimates of insulin dose rate effects were negative and highly statistically significant. This is consistent with previous discussions that glucose change analyses should be less susceptible to confounding than glucose level analyses.
5.4. Parameter relationships
Table III describes the relationships among parameters estimates of the six models, summarized in Figure 1, using the NS and LVS. To capture the relationships, we also fit IM-I, IM-II, and IM-III with the same weighting scheme as was used to fit the six models. For example, when comparing models using the LVS, we fit the intermediate models with the same stabilized LVS weighting scheme. As discussed earlier, the intermediate model estimates are useful for understanding relationships and explaining apparent discrepancies among parameters in the various models. Consider the relationship between the insulin-dose-rate effect estimates in models 1a and 1b. Using the NS, ; using the LVS, it was . In contrast, was −17.88 and −23.22 for the NS and LVS, respectively. The reason for the apparent discrepancy both between in the two estimation strategies and between and using the NS involves estimates of ωX. Recall that ωX describes the relationships between Yij−1 and Xij and so it can be used to identify the potential for time-dependent confounding. With the NS, the value was ω̂X = 39.06 indicating a very strong relationship between Yij−1 and Xij; however, by reweighting the observations so as to remove this relationship using the LVS, ω̂X = −1.21. This points towards the successful removal of the confounding effect of Yij−1. Likewise, comparing model 1c and 2c estimates (last line of the table), under the NS, the estimated value of αX was 52.65, thus leading to large differences between estimates of and . After reweighting the observations using the LVS, the estimate of αX was only −2.90 and estimates of and agreed closely.
Table III.
Numerical relationships among parameters estimatesa shown in Figure 1 using the naïve and lagged glucose value strategies based on the blood-glucose insulin-dose-rate analysis.
| Model | Relationship | NS | LVS | |
|---|---|---|---|---|
| 1a and 1b | 6.02 = −17.88 + 0.61 · 39.06 | −24.02 = −23.22 + 0.72 · −1.21 | ||
| 1a and 1c | 6.02 = 9.48 + −5.40 · 0.64 | −24.02 = −23.34 + −1.05 · 0.64 | ||
| 2a and 2b | −33.05 = −17.88 + −0.39 · 39.06 | −22.81 = −23.22 + −0.282 · −1.21 | ||
| 2a and 2c | −33.05 = −43.17 + 15.83 · 0.64 | −22.81 = −20.44 + −4.05 · 0.64 | ||
| 1a and 2a | 6.02 = −33.05 + 39.06 | −24.02 = −22.81 + −1.21 | ||
| 1b and 2b | −17.88 = −17.88 | −23.22 = −23.22 | ||
| 1c and 2c | 9.48 = −43.17 + 52.65 | −23.34 = −20.44 + −2.90 |
NS, naïve strategy; LVS, lagged glucose value strategy.
Estimates are presented to two decimal places, although calculations are exact.
6. Discussion
We have discussed modeling considerations and approaches to longitudinal data arising from EMR systems. Although careful consideration and prespecification of models is crucial, when analyzing data from EMR systems, one has to keep in mind that the data collection procedures are not tied to any specific hypothesis. Because treatment in hospital-based settings often require adjustment in response to patient outcomes over time, a key challenge for longitudinal data analysis in this setting is the potential for time-dependent confounding. This has important implications for both model specification and estimation. Via a series of intermediate models, we showed how parameters in several longitudinal models can be calculated from one another. Understanding these relationships can provide important insight into underlying data acquisition mechanisms that may induce time-dependent confounding. Because these mechanisms are well documented and understood for the BG–IDR example, we were also able to explore the impact that time-dependent confounding can have on study results and conclusions in a real-worked analysis. As with the BG–IDR analysis, if the data acquisition mechanism is reasonably well known, model choice can actually be a means of protecting oneself from the impact of time-dependent confounding. For example, with some understanding of the confounding mechanism, and if interest is in short-term exposure effects, one might chose to model response change rather than response level.
The focus of this paper has been on understanding relationships between commonly used longitudinal models and the use of such relationships in gaining insight into potential time-dependent confounding, with application to a subset of patients from the Vanderbilt University Trauma ICU. More broadly, modeling an unstable patient sample, such as those who are in an ICU, is very challenging and the BG–IDR dataset is extremely rich in interesting statistical problems. Several key simplifications of our analyses deserve further work. Firstly, as mentioned in Section 2.1, we removed those subjects whose glucose was not well controlled during the 24 h observation period. From a validity perspective, it is easy to justify the removal of patients with uncontrolled glucose at baseline. However, removing those who became hyperglycemic at some later point likely introduced a selection bias. That is, the population to whom results generalize may no longer correspond to the population of patients who enter the ICU (at Vanderbilt University). Secondly, we did not address the potential for bias because of differential intensity of follow-up or dropout. Many care protocols direct that ICU patients with abnormal laboratory values be tested more frequently than patients who have achieved normal values, whereas discharge from an ICU usually occurs only after patients are clinically stabilized. Given these mechanisms, if the target population is represented by the admission sample, the observed data would likely contain a disproportionate number of subjects whose laboratory values are abnormal. In the BG–IDR data, we observed the vast majority of the subjects for at least 18 of the 24 h of follow-up, and more than 50% of all time separations between successive glucose checks were between 1.7 and 2.4 h. Given the regular glucose checks and relatively consistent discharge times, we felt these challenges were less pressing than those addressed in the manuscript. If, however, the follow-up period had been longer than 24 h, then closer scrutiny would likely be unavoidable. There is an extensive literature on longitudinal data analysis in the presence of irregular follow-up and dropout and on how one should adjust for the nonrepresentativeness of the observed data [25–30]. Finally, an additional variable in the glucose control protocol was the intensity with which participants were examined. Hospital staff chose the intensity of follow-up at the time the patient entered the ICU. Although our goal was to examine the impact of insulin rates on glucose levels and changes, staff choices of both the target blood glucose range and the intensity with which patients were observed could be evaluated with dynamic treatment regime methods such as those that have been described in References [31–34].
The question ‘What is the effect of the insulin dose rate on glucose?’ or more broadly ‘What is the effect of an exposure on a response?’ that was mentioned earlier is extremely vague. We have discussed six models that could theoretically be used to evaluate this question, and in the scenario we studied, results describing the ‘effect’ of Xij on Yij were shown to range from highly statistically significant and negative to highly statistically significant and positive. This points to the importance of precisely defined scientific questions and considerations of data acquisition processes. In the BG–IDR data, time-dependent confounding is a crucial consideration; however, in many other EMR data scenarios, intensity of follow-up, dropout, nonmonotone missingness, and many other challenges will be central. Other authors have discussed the importance of precise-defined scientific questions, including [35] that specifically addressed challenges related to addressing another vague scientific question ‘What is the effect of obesity on mortality?’
To summarize, we note that it is generally very difficult to envision how study conclusions might change had different model choices been made unless alternative analyses are conducted. We believe it is instructive for analysts to consider examining how broad study conclusions could possibly shift based on seemingly minor changes to regression models. We believe the framework presented here to be complementary to common data description and analysis methods, providing researchers with a means of reconciling what could otherwise appear to be conflicting study results.
Acknowledgments
The NIH grants R01 LM007995 from the National Library of Medicine and R01 HL094786 from the National Heart Lung and Blood Institute funded this project.
References
- 1.Finney SJ, Zekveld C, Elia A, Evans TW. Glucose control and mortality in critically ill patients. Journal of the American Medical Association. 2003;290:2041–2047. doi: 10.1001/jama.290.15.2041. [DOI] [PubMed] [Google Scholar]
- 2.van den Berghe G, Wouters P, Weekers F, Verwaest C, Bruyninckx F, Schetz M, Vlasselaers D, Ferdinande P, Lauwers P, Bouillon R. Intensive insulin therapy in the critically ill patients. New England Journal of Medicine. 2001;345:1359–1367. doi: 10.1056/NEJMoa011300. [DOI] [PubMed] [Google Scholar]
- 3.Rivers E, Nguyen B, Havstad S, Ressler J, Muzzin A, Knoblich B, Peterson E, Tomlanovich M. Early goal-directed therapy in the treatment of severe sepsis and septic shock. New England Journal of Medicine. 2001;345:1368–1377. doi: 10.1056/NEJMoa010307. [DOI] [PubMed] [Google Scholar]
- 4.Evans TW. Hemodynamic and metabolic therapy in critically ill patients. New England Journal of Medicine. 2001;345:1417–1418. doi: 10.1056/NEJM200111083451910. [DOI] [PubMed] [Google Scholar]
- 5.Wiener RS, Wiener DC, Larson RJ. Benefits and risks of tight glucose control in critically ill adults: a meta-analysis. Journal of the American Medical Association. 2008;300:933–944. doi: 10.1001/jama.300.8.933. [DOI] [PubMed] [Google Scholar]
- 6.Boord JB, Sharifi M, Greevy RA, Griffin MR, Lee VK, Webb TA, May ME, Waitman LR, May AK, Miller RA. Computer-based insulin infusion protocol improves glycemia control over manual protocol. Journal of the American Medical Informatics Association. 2007;14:278–287. doi: 10.1197/jamia.M2292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dortch MJ, Mowery NT, Ozdas A, Dossett L, Cao H, Collier B, Holder G, Miller RA, May AK. A computerized insulin infusion titration protocol improves glucose control with less hypoglycemia compared to a manual titration protocol in a trauma intensive care unit. Journal of Parenteral and Enteral Nutrition. 2008;32:18–27. doi: 10.1177/014860710803200118. [DOI] [PubMed] [Google Scholar]
- 8.Schildcrout JS, Heagerty PJ. Regression analysis of longitudinal binary data with time-dependent environmental covariates: bias and efficiency. Biostatistics. 2005;6(4):633–652. doi: 10.1093/biostatistics/kxi033. [DOI] [PubMed] [Google Scholar]
- 9.Hernán MA, Brumback B, Robins JM. Marginal structural models to estimate the joint causal effect of nonrandomized treatments. Journal of the American Statistical Association. 2001;96(454):440–448. [Google Scholar]
- 10.Diggle P, Heagerty PJ, Liang K-Y, Zeger SL. Analysis of Longitudinal Data. Oxford University Press; 2002. [Google Scholar]
- 11.Hernán MA, Brumback BA, Robins JM. Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Statistics in Medicine. 2002;21:1689–1709. doi: 10.1002/sim.1144. [DOI] [PubMed] [Google Scholar]
- 12.Cole SR, Hernán MA. Constructing inverse probability weights for marginal structural models. American Journal of Epidemiology. 2008;168:656–664. doi: 10.1093/aje/kwn164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hernán MA, Robins JM. Estimating causal effects from epidemiological data. Journal of Epidemiology and Community Health. 2006;60:578–586. doi: 10.1136/jech.2004.029496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Robins JM. Marginal structural models versus structural nested models as tools for causal inference. In: Halloran ME, Berry DA, editors. Statistical Models in Epidemiology, the Environment and Clinical Trials. Springer-Verlag Inc; Berlin, NY: 2000. pp. 99–134. [Google Scholar]
- 15.Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- 16.Robins J. A new approach to causal inference in mortality studies with a sustained exposure period—application to control of the healthy worker survivor effect. Mathematical Modeling. 1986;7(9–12):1393–1512. [Google Scholar]
- 17.Robins JM, Greenland S, Hu F-C. Estimation of the causal effect of a time-varying exposure on the marginal mean of a repeated binary outcome. Journal of the American Statistical Association. 1999;94(447):687–712. [Google Scholar]
- 18.Robins JM. ASA proceedings of the section on bayesian statistical science. American Statistical Association; 1997. Marginal structural models; pp. 1–10. [Google Scholar]
- 19.Tager I, Haight T, Sternfeld B, Yu Z, van der Laan M. Effects of physical activity and body composition on functional limitation in the elderly: application of the marginal structural model. Epidemiology. 2004;15:479–493. doi: 10.1097/01.ede.0000128401.55545.c6. [DOI] [PubMed] [Google Scholar]
- 20.Haight T, Tager I, Sternfeld B, Satariano W, van der Laan M. Effects of body composition and leisure-time physical activity on transitions in physical functioning in the elderly. American Journal of Epidemiology. 2005;162:607–617. doi: 10.1093/aje/kwi254. [DOI] [PubMed] [Google Scholar]
- 21.Pepe MS, Anderson GL. A cautionary note on inference for marginal regression models with longitudinal data and general correlated response data. Communications in Statistics: Simulation and Computation. 1994;23:939–951. [Google Scholar]
- 22.Liang K-Y, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 23.Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- 24.Efron B, Tibshirani R. An Introduction to the Bootstrap. Chapman & Hall Ltd; 1993. [Google Scholar]
- 25.Lin DY, Ying Z. Semiparametric and nonparametric regression analysis of longitudinal data. Journal of the American Statistical Association. 2001;96(453):103–113. [Google Scholar]
- 26.Lipsitz SR, Fitzmaurice GM, Ibrahim JG, Gelber R, Lipshultz S. Parameter estimation in longitudinal studies with outcome-dependent follow-up. Biometrics. 2002;58:621–630. doi: 10.1111/j.0006-341x.2002.00621.x. [DOI] [PubMed] [Google Scholar]
- 27.Little RJA, Rubin DB. Statistical Analysis with Missing Data. John Wiley & Sons; 2002. [Google Scholar]
- 28.Sun Y, Wu H. Semiparametric time-varying coefficients regression model for longitudinal data. Scandinavian Journal of Statistics. 2005;32(1):21–47. [Google Scholar]
- 29.Schafer J. Analysis of Incomplete Multivariate Data by Simulation. Chapman & Hall Ltd; 1995. [Google Scholar]
- 30.Daniels MJ, Hogan JW. Missing Data in Longitudinal Studies: Strategies for Bayesian Modeling and Sensitivity Analysis. Chapman & Hall Ltd; 2008. [Google Scholar]
- 31.Murphy SA. Optimal dynamic treatment regimes. Journal of the Royal Statistical Society, Series B: Statistical Methodology. 2003;65(2):331–366. [Google Scholar]
- 32.Robins JM. Proceedings of the second seattle symposium in biostatistics – analysis of correlated data. Springer-Verlag Inc; 2004. Optimal structural nested models for optimal sequential decisions; pp. 189–326. [Google Scholar]
- 33.Moodie EEM, Richardson TS, Stephens DA. Demystifying optimal dynamic treatment regimes. Biometrics. 2007;63(2):447–455. doi: 10.1111/j.1541-0420.2006.00686.x. [DOI] [PubMed] [Google Scholar]
- 34.Moodie EEM, Platt RW, Kramer MS. Estimating response-maximized decision rules with applications to breastfeeding. Journal of the American Statistical Association. 2009;104(485):155–165. [Google Scholar]
- 35.Hernán MA, Taubman SL. Does obesity shorten life? The importance of well-defined interventions to answer causal questions International Journal of Obesity (London) 2008;32 (Suppl 3):8–14. doi: 10.1038/ijo.2008.82. [DOI] [PubMed] [Google Scholar]