Abstract
A cross-validation (CV) method based on state-space framework is introduced for comparing the fidelity of different cortical interaction models to the measured scalp electroencephalogram (EEG) or magnetoencephalography (MEG) data being modeled. A state equation models the cortical interaction dynamics and an observation equation represents the scalp measurement of cortical activity and noise. The measured data are partitioned into training and test sets. The training set is used to estimate model parameters and the model quality is evaluated by computing test data innovations for the estimated model. Two CV metrics normalized mean square error and log-likelihood are estimated by averaging over different training/test partitions of the data. The effectiveness of this method of model selection is illustrated by comparing two linear modeling methods and two nonlinear modeling methods on simulated EEG data derived using both known dynamic systems and measured electrocorticography data from an epilepsy patient.
Index Terms: Cross-validation (CV), effective connectivity, Granger causality, model selection, state-space model
I. Introduction
Effective and functional connectivity are of great interest for study of functional integration in the brain [1]. Determining effective connectivity requires identification of a model describing cortical signals in the brain. A wide variety of models have been proposed, including linear multivariate autoregressive (MVAR) models [2]–[4] and nonlinear models such as local autoregressive (AR) models [5], nonlinear AR models based on polynomial or Gaussian kernels [6], and differential equation models [7]–[9]. Furthermore, different methods for estimating cortical model parameters from scalp EEG or MEG (E/MEG) have been proposed, e.g., the authors in [10]–[12] describe different approaches for estimating MVAR model parameters in order to measure cortical interactions from scalp recordings of electric or magnetic fields. The true functional or effective connectivity in human data is unknown, so it is very difficult to establish whether one model or estimation method is better than others. Typically simulated data are used to establish model efficacy, while the knowledge of brain anatomy and function is employed to support cortical connectivity conclusions derived from human data (see, e.g., [13] and [14]).
In this paper, we introduce a cross-validation (CV) methodology for quantitative comparison of state-space cortical interaction models using measured scalp E/MEG data. Our approach employs a state-space framework consisting of an observation equation representing the scalp measurement of cortical signals and a state equation describing the cortical interaction model of interest. The innovations sequence is defined as the difference between the measured data and that predicted by the state-space cortical interaction model. To apply CV, the dataset is partitioned into training and test sets and model parameters are estimated using the training data. Next, a model quality metric, such as the normalized mean-squared error (NMSE) or log-likelihood (LL), is computed for the test data using the innovations.
Existing model selection methods include the asymptotic methods such as Akaike information criterion [15] and Bayesian information criterion (BIC) [16], bootstrapping [17], and Bayes factors [18]. Asymptotic methods employ the maximized likelihood of a candidate model with a penalty proportional to the number of model parameters as the selection criterion. However, the optimality properties of asymptotic methods apply only when the data are generated from the same class of models as those being evaluated, an assumption that is certainly violated with E/MEG data. Given the complexity of the brain and physics of E/MEG, it is extremely unlikely that any mathematical model exactly represents the true nature of cortical interactions. Bootstrapping may be used to perform model selection, but is very computationally expensive. The Bayes factor approach selects the candidate model with the highest integrated likelihood, but requires prior probability density assumptions for the unknown parameters to compute integrated likelihood. Our CV method involves no priors and does not rely on the true model being included within the set being compared. Instead, the CV approach chooses the model that best predicts the data. CV techniques have been widely applied in statistics [19]–[21] and are known to have asymptotically optimal risk performance and convergence [22], [23].
The value for mathematical models of cortical interactions lies in their ability to predict behavioral, disease related, or other attributes of brain function. CV directly evaluates the predictive power of a model and thus is well matched philosophically to the end goal of cortical interaction modeling. Estimated cortical signals do not provide a common baseline for evaluating predictive ability—different estimation methods give different signal estimates due to the ill-posed nature of the inverse problem and typically low signal-to-noise ratio (SNR) of measured scalp E/MEG data. Our innovations approach employs the observed data as a common baseline.
Our CV approach to model comparison is demonstrated by comparing two different model estimation methods: 1) a two-stage estimation method wherein cortical signals are first estimated from scalp EEG using a nulling beamformer [11] and then an interaction model is fit to the estimated signals; and 2) a maximum likelihood approach that estimates the models directly from EEG data using an expectation-maximization (EM) algorithm [12]. Both linear MVAR and nonlinear radial basis function (RBF) interaction models are employed with each model estimation approach. We show that our CV approach correctly identifies the correct cortical interaction model in four simulated data scenarios. We also show that the integrated EM-based maximum likelihood estimation method consistently outperforms the two-stage approach.
This paper is organized as follows. Section II introduces our CV method for selecting state-space cortical interaction models from scalp E/MEG. Section III reviews the MVAR and RBF interaction models, as well as the two-stage and integrated EM parameter estimation methodologies used to illustrate the CV method. We apply CV to these models and estimation methods using simulated cortical signals in Section IV and measured electrocorticography (ECoG) data in Section V. This paper concludes with a discussion in Section VI. Boldface lower and upper case symbols represent vectors and matrices, respectively, while superscript T denotes matrix transpose. Subscripts n, j denote time sample n from trial j, while integer superscripts index matrix or vector elements.
II. Cross Validation of State-Space Models
Any parametric model of cortical interactions for E/MEG data can be expressed in state-space form. A state-space model consists of a state equation representing the time evolution of cortical signals originating from predefined cortical regions of interest (ROIs) and a linear observation equation describing the transformation of cortical signals to observed scalp E/MEG signals. The physics relating cortical activity to E/MEG data are very well approximated as linear and normally described in terms of the leadfield matrix [24]. On the other hand, the cortical interactions modeled by the state equation may be approximated as a linear or nonlinear dynamical system.
Let , n = 1, …, N, j = 1, …, J be the jth trial of an M by 1 state vector representing samples of cortical signals from M ROIs at time n. Define as a P by 1 vector containing the past P samples of the cortical signal from the mth ROI and let be a P by M matrix of P past samples from all M regions being modeled. Let the model of cortical dynamics be f(Xn−,j; Γ), where Γ represents the parameters describing the cortical dynamics. Examples for f() include MVAR, local AR, and RBF models. The L by 1 E/MEG measurement data yn,j are then represented by the following dynamical state-space model:
| (1) |
| (2) |
Here, the vectors wn,j and vn,j are M by 1 and L by 1 state and observation noise vectors, respectively, C = [C1, …, CM] is an L by MF matrix with the F columns of Cm containing basis functions describing how a signal from the mth cortical ROI appears in the scalp E/MEG, and Λ is an MF by M block diagonal matrix with F by 1 vectors λm on the diagonal representing any unknown parameters describing the spatial distribution of activity in the mth ROI. In the case of a dipolar source model with unknown moment, Cm has F = 3 columns, each representing the leadfield due to a dipole oriented in the x-, y-, and z-directions, and λm is the unknown dipole moment. Patch and multipole source models are obtained by choosing Cm as patch or multipole bases [25], [26] and λm represents the corresponding patch or multipole coefficients describing the spatial distribution of activity in the mth ROI. This observation model implies that the measured signal due to the mth ROI is , so the spatial attribute of the source, e.g., dipole moment or spatial activity distribution, is assumed constant over time. Time-varying spatial models are easy to incorporate in this framework by assigning multiple source time series to each ROI, but are not considered here for notational and practical reasons. Both the state and observation noise vectors are assumed in this paper to be independent and identically distributed Gaussian noise processes with zero mean and covariance matrices Q (M by M) and R (L by L), respectively. We further assume that the PM by 1 initial state vec{X1−,j} is a Gaussian distributed random vector with mean μ0 and covariance Σ0. Let Θ = {Γ, Λ, Q, R, μ0, Σ0} be the set of state-space model parameters. Other parameterizations may also be used with our CV framework.
Our goal is to develop a CV procedure that uses the measured data yn,j to quantify the predictive quality of a given state-space model parameterized by Θ and, thus, provides a basis for objective, data-driven comparison of different models. The proposed approach is inspired by Stoffer and Wall's [27] method for using innovations to bootstrap the mean and standard deviation of parameter estimates in state-space models. Here, we perform CV using innovations. Given a state-space model parameterized by Θ and observed data yn,j, the innovations sequence en,j (Θ) is the difference between the observed data and the data predicted by Θ using data prior to time n of the jth trial [28]. That is
| (3) |
where is a one-step prediction estimate of the state xn,j. The innovations sequence is computed using a Kalman filter [29] for linear state-space models, while nonlinear state-space models may approximate innovations using an extended Kalman filter [29] or other nonlinear estimation methods such as particle filtering [30].
In general, some or all of the model parameters are unknown, so CV is performed by partitioning the available data into training and test sets. Any unknown model parameters are estimated using the training data. Then, the estimated model is used to compute the innovations for the test data, and a CV score is computed from the test data innovations. Formally, we perform K-fold CV by partitioning the J trials of measured data yn,j, j = 1, …, J into K sets Dk, k = 1, …, K of Jk trials each, where the Jk are approximately equal. Define as the training data—all data except Dk, and let be the parameter values of a state-space model estimated using the training data. We define two CV metrics that can be obtained from the innovations sequence. The CV NMSE is defined by
| (4) |
while in light of [31], the CV LL is written as
| (5) |
where is the innovations covariance matrix
| (6) |
Here, Σn∣n − 1,j (Γ,Q) is the state prediction error covariance matrix at time n of the jth trial given data up to time n − 1.
Confidence intervals or other measures of precision may be calculated using the innovations to assess the significance of differences in the CV scores. We report the standard error of the mean based on the CV values for each training/test data partition. If the CV values for each partition are Gaussian distributed, then the 90% confidence interval is obtained from 1.64 times the standard error. More sophisticated procedures could be used to obtain confidence intervals or distributions if desired.
III. Example Cortical Interaction Models AND Estimation Methods
The CV approach is illustrated in this paper using linear MVAR state-space models and nonlinear RBF network state-space models. We also consider two different previously proposed model parameter estimation methods: a two-stage approach in which cortical signals are estimated by solving the observation equation (2), and then, estimated cortical signals are used to estimate the state model parameters Γ and Q [11]; and an integrated maximum likelihood approach based on joint solution of state (1) and observation (2) equations using an EM algorithm [12], [32]. In both cases, the ROIs are assumed known and thus C is known. This section introduces these cortical signal models and estimation methods.
A. State Model for Cortical Signals
Two types of state models are considered to describe the dynamics of cortical signals. The first one is the linear MVAR model. This type of model has been widely applied to the recorded local field potential data (see [33] and references therein). A Pth-order MVAR model for representing the cortical signals xn,j is described as
| (7) |
where Ap, p = 1, … , P is a set of M by M MVAR model coefficient matrices describing the influence of the past P samples of cortical signals (xn−1,j,xn−2,j, …, xn−P,j) from all ROIs on the present sample xn,j.
The second type of cortical signal model considered here is the RBF network. We choose the RBF network because it satisfies the invariance property required to evaluate Granger causality [34]. Also, the universal approximation theorem for RBF networks [35] states that an RBF network is capable of approximating any smooth function to an arbitrary degree of accuracy. Thus, it is capable of modeling nonlinear dynamics of cortical signals with different nonlinear characteristics. An application of RBF networks to measure nonlinear Granger causality for intracranial EEG signal analysis is reported in [36]. The state equation for estimating cortical connectivity between M cortical ROIs using the RBF network is written as
| (8) |
where ψ is an M by MI matrix of RBF weights, and is an MI by 1 vector of nonlinear real functions of P variables, where is an I by 1 vector of RBF kernels, each with center and covariance matrix Si = σ2I
| (9) |
The elements of ψ reflect the coupling between ROIs.
B. Model Parameter Estimation Methods
The two-stage approach first estimates the cortical signals of interest from the measured E/MEG data using methods such as weighted minimum norm [10] or linear constrained minimum variance (LCMV) beamforming [37]. Next, a state model, e.g., MVAR or RBF, is fit to the estimated cortical signals to obtain model parameter estimates for connectivity analysis. Recently, Hui et al. [11] have proposed a nulling formulation of the LCMV beamformer for handling coherent E/MEG sources when studying cortical interactions. This method has significant advantages over other two-stage methods [11] and is employed to obtain the two-stage results presented in later sections. Given estimated cortical signals, the MVAR model coefficients are obtained by solving the Yule-Walker equations [38]. Assuming the RBF kernel centers are known or identified separately, the RBF coupling weights ψ are estimated from the cortical signals by solving a system of linear equations [39]. The values of observation equation parameters Λ and R are estimated for the two-stage method similarly to those for the integrated EM approach as described in [12]. That is, the cortical signal statistics—mean and covariances—are obtained from the nulling beamformer.
The integrated approach seeks ML estimates of the state-space model parameters using the relationships implied by both the state (1) and observation (2) equations. Closed-form estimates are not available, so EM algorithms that are guaranteed to find local maxima of the likelihood surface have been proposed. In particular, Cheung et al. [12] extended the EM algorithm developed by Shumway and Stoffer [40] for linear state-space models to structured observation equations of the form (2). Similarly, Cheung and Van Veen [32] extended the EM algorithm of Roweis and Ghahramani [41] for estimating RBF state models to the structured observation equation (2). These algorithms are employed to obtain the results in later sections and are now briefly summarized here.
Let {Y,X} denote the so-called complete data, where Y = {y1,1,…, yN,1,…, y1,J,…, yN,J} and X = {x0,1,…, xN,1,…, xN,j} are the observed and hidden data, respectively. The EM algorithm computes the ML estimates of Θ = {Γ,Λ,Q,R,μ0,Σ0}, where Γ = Ap, p = 1,…P for the MVAR (linear) state-space model and Γ = ψ for the RBF (nonlinear) state-space model. We assume for simplicity that and σ of the RBF network parameters are known or identified separately. The EM algorithm [42] iteratively maximizes the conditional expectation of the LL of the complete data using two steps in each iteration. The conditional densities needed in the EM algorithm for the MVAR state-space model can be computed using the fixed interval smoother [43]. However, for the RBF state-space model, these conditional densities cannot be evaluated analytically. Numerical integration methods based on sequential Monte Carlo simulation can be used to approximate them [30], but are computationally intensive so we approximate the nonlinear dynamics with the extended Kalman smoother [29]. Updates for Θ are found in [12] for MVAR state-space models and [41] for RBF state-space models.
IV. Simulation Results
A. Simulated Data
Three examples of simulated state-space time-series are presented to illustrate the effectiveness of our CV approach for state-space model selection when the true state model is known. All of them involve two cortical signals, and , with unidirectional cortical interaction from to
Scenario 1 (Coupled Bivariate AR System): The following linear first-order (P = 1) system is used to generate cortical signals and
| (10) |
Here, the variances of and are 0.2.
Scenario 2 (Coupled Logistic System [36]):
| (11) |
Here, a = 3.8 and both the variances of and are 1 × 10−4.
Scenario 3 (Coupled Henon System [44]):
| (12) |
Here, a = 1.4 and both the variances of and are 1 × 10−4.
For each example, we use N = 150 samples, J = 10 trials, and L = 56 EEG channels. Each cortical signal is assumed to be associated with a patch of cortex of radius 5 mm and has a raised cosine spatial pattern. The leadfields are computed using a four-shell spherical head model. The patch for is located in the temporal lobe and in the parietal lobe. Hence, the observed data are generated as
| (13) |
where β1 = H1α1 and β2 = H2α2. Here, H1 and H2 are the collection of leadfields associated with each source patch and α1 and α2 are the corresponding weights for the raised cosine spatial pattern. The observation noise vn,j is spatially white. We define
| (14) |
as the ratio of observed power due to cortical activity to that due to noise. Each scenario is evaluated at SNR of 10 and 0 dB.
B. Cortical State-Space Models
CV is used to compare the predictive ability of MVAR and RBF state-space models (sMVAR and sRBF, respectively) estimated using both the two-stage nulling beamforming and EM methods described in Section III-B for all three scenarios. The memory P, number of RBF kernels I, and kernel centers are kept the same for both two-stage and EM estimation methods and are chosen as follows. The memory P for the MVAR models is chosen using the BIC criterion [12] applied to the sMVAR model estimated with the EM approach and all of the data. That is, we choose the value P that minimizes
| (15) |
where T = NJ, ϕ(P) is the number of free variables of the sMVAR model, and
| (16) |
The constant C does not affect the P that minimizes the BIC.
The RBF kernel center locations are chosen using cortical signals estimated by the EM-based sMVAR model that has the minimum BIC. For each RBF network, we varied P from 1 to 4 and I from 2 to 12 for Scenarios 1 and 2, and 10 to 80 for Scenario 3. The ranges of P and I are chosen such that the minimum BIC is covered within these ranges for each scenario. At each P and I, we use the estimated cortical signals and the fuzzy c-means clustering algorithm [39] to locate the kernel centers assuming a kernel radius of σ = 0.5. Next, we use the EM algorithm to estimate an sRBF model from all of the measured scalp data for each set of P, I, and kernel centers and compute the BIC value using (15) with ϕ(P) replaced by ϕ(I), the number of free variables of the sRBF model. Finally, the values of P and I that minimize the BIC are selected.
The values of P for the sMVAR model and P, I for the sRBF model selected using these procedures are shown in Table I. Unless we note otherwise, F = 3 spatial basis vectors are associated with each source and the basis vectors are chosen as described in [26] assuming knowledge of the patch locations and spatial extent. Note that the true observation model—a raised cosine distribution within each patch—is not described exactly by the cortical patch basis vectors, even with F = 4, so the assumed observation equation is only an approximation to the actual source forward model.
TABLE I.
State-Space Model Parameters for The Three Simulation Scenarios
| sMVAR | sRBF | |||||
|---|---|---|---|---|---|---|
| 10 dB | 0 dB | 10 dB | 0 dB | |||
| Scenario | P | P | P | I | P | I |
| Bivariate AR | 1 | 1 | 1 | 8 | 1 | 8 |
| Logistic | 6 | 5 | 1 | 4 | 2 | 8 |
| Henon | 10 | 8 | 2 | 30 | 3 | 30 |
C. Cross-Validation Results
EM and two-stage methods for estimating sMVAR and sRBF models are compared using tenfold CV on the simulated measured data for each scenario and SNR. In each scenario, we also compute reference CV scores for an sMVAR (Scenario 1) or sRBF (Scenario 2 and 3) model by fitting either an MVAR or RBF model to the true cortical signals and computing the innovations (3) and innovations covariance (6) using the true observation vectors β1 and β2 and observation noise covariance matrix R. We call this the “omniscient sMVAR” or “ominiscient sRBF”model as it represents an interaction model derived from the true cortical signals and exact observation equation parameters. All CV scores are reported as the score ± standard error.
Scenario 1 (Coupled Bivariate AR System): The CV scores for the four state-space models with the first-order AR system of (10) are provided in Table II. The best model for each SNRs and CV metric is depicted in boldface type. Independent of SNR and CV metrics, the models are ranked by CV from best to worst as 1) EM sMVAR, 2) EM sRBF, 3) two-stage sMVAR, and 4) two-stage sRBF. The underlying cortical dynamics are linear, so the sMVAR model is expected to fit the data better than the sRBF model. Note that the nonlinear EM sRBF model is a better fit than the linear two-stage sMVAR model. As expected, CV-NMSE increases and CV-LL decreases as the SNR decreases.
TABLE II.
Tenfold Cross-Validation Scores With Standard Errors for Bivariate AR System
| Model Type | SNR = 10 dB | SNR = 0 dB | ||
|---|---|---|---|---|
| CV-NMSE | CV-LL | CV-NMSE | CV-LL | |
| EM sMVAR | 0.500 ± 0.020 | 167.27 ± 1.45 | 0.735 ± 0.031 | 104.93 ± 1.45 |
| Two-stage sMVAR | 0.531 ± 0.024 | 167.11 ± 1.46 | 0.754 ± 0.033 | 104.66 ± 1.47 |
| EM sRBF | 0.514 ± 0.023 | 167.22 ± 1.46 | 0.741 ± 0.033 | 104.89 ± 1.46 |
| Two-stage sRBF | 0.544 ± 0.027 | 167.09 ± 1.46 | 0.767 ± 0.036 | 104.63 ± 1.47 |
| Omniscient sMVAR | 0.494 ± 0.019 | 168.54 ± 1.34 | 0.731 ± 0.031 | 106.19 ± 1.53 |
Scenario 2 (Coupled Logistic System): The CV scores for EM and two-stage sMVAR and sRBF models are depicted in Table III. Both metrics and SNRs rank the models from best to worst as 1) EM sRBF, 2) EM sMVAR, 3) two-stage sRBF, and 4) two-stage sMVAR. The standard errors imply that the differences between models are significant. The underlying cortical system is nonlinear, so the sRBF model is expected to better fit the data than the sMVAR model. Interestingly, the linear (sMVAR) model estimated with EM is a better fit to the data than the nonlinear (sRBF) model estimated with the two-stage approach. Also, the EM sRBF model slightly outperforms the omniscient sRBF model in the CV-NMSE score at low SNR.
TABLE III.
Tenfold Cross-Validation Scores With Standard Errors for Logistic System
| Model Type | SNR = 10 dB | SNR = 0 dB | ||
|---|---|---|---|---|
| CV-NMSE | CV-LL | CV-NMSE | CV-LL | |
| EM sMVAR | 0.152 ± 0.002 | 158.34 ± 0.09 | 0.540 ± 0.001 | 95.18 ± 0.08 |
| Two-stage sMVAR | 0.190 ± 0.005 | 157.54 ± 0.09 | 0.572 ± 0.003 | 94.24 ± 0.09 |
| EM sRBF | 0.098 ± 5e-4 | 159.65 ± 0.11 | 0.522 ± 0.002 | 95.47 ± 0.10 |
| Two-stage sRBF | 0.159 ± 0.003 | 157.66 ± 0.10 | 0.563 ± 0.003 | 94.28 ± 0.10 |
| Omniscient sRBF | 0.097 ± 7e-4 | 160.99 ± 0.08 | 0.530 ± 0.003 | 96.25 ± 0.12 |
Note that the cortical signals for Scenario 2 are much more predictable than those for Scenario 1 due to the reduced variance of and and the more persistent dynamics of the logistic system. Hence, the CV-NMSE values at high SNR are also much smaller. In fact, at SNR = 10 dB, the simulated EEG contains ten parts (power) due to cortical activity and one part due to observation noise. Thus, perfect prediction of the cortical signal would lead to an CV-NMSE of 1/11 = 0.091, which is slightly less than the omniscient sRBF score.
Scenario 3 (Coupled Henon System): Table IV depicts the CV scores for EM and two-stage sMVAR and sRBF models for this scenario. At SNR = 10 dB, both metrics rank the models from best to worst as 1) EM sRBF, 2) two-stage sRBF, 3) EM sMVAR, and 4) two-stage sMVAR. There is a significant difference in the CV scores of these models for the SNR = 10 dB case. At SNR = 0 dB, CV-NMSE ranks the models in the same order, but CV-LL ranks the EM sMVAR model ahead of the two-stage sRBF model. In this case, the difference between EM sMVAR and two-stage RBF models may not be significant. Overall preference of the EM sRBF model is consistent with the nonlinear nature of the underlying cortical signals generated by the Henon system.
TABLE IV.
Tenfold Cross-Validation Scores With Standard Errors for Henon System
| Model Type | SNR = 10 dB | SNR = 0 dB | ||
|---|---|---|---|---|
| CV-NMSE | CV-LL | CV-NMSE | CV-LL | |
| EM sMVAR | 0.505 ± 0.033 | 135.25 ± 0.26 | 0.740 ± 0.021 | 72.90 ± 0.27 |
| Two-stage sMVAR | 0.537 ± 0.032 | 135.05 ± 0.26 | 0.767 ± 0.021 | 72.63 ± 0.77 |
| EM sRBF | 0.153 ± 0.005 | 137.31 ± 0.26 | 0.614 ± 0.009 | 73.46 ± 0.25 |
| Two-stage sRBF | 0.282 ± 0.010 | 135.93 ± 0.26 | 0.707 ± 0.014 | 72.81 ± 0.26 |
| Omniscient sRBF | 0.145 ± 0.005 | 137.73 ± 0.46 | 0.579 ± 0.006 | 74.72 ± 0.20 |
V. Application to EEG Data Simulated From ECoG Recordings
In this section, we apply CV to simulated EEG data derived from ECoG signals recorded in an epilepsy patient and compare model fitting and connectivity analysis of the ECoG data to that on the corresponding simulated EEG signals.
A. ECoG Data
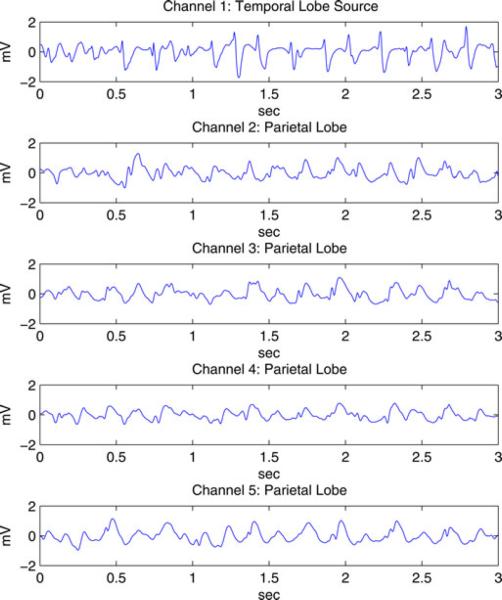
Data from a surgery candidate with typical mesial temporal lobe epilepsy were collected at the Comer Children's Hospital at the University of Chicago. The clinical neurophysiologist determined seizure onset times and leading channels using visual analysis of the EEG/ECoG and the audiovisual recording. The EEG and ECoG time series were recorded with a bandwidth of 0.5–100 Hz, and digitized at 400 samples/s with a 12-bit analog-to-digital converter using a BMSI 6000 unit (Cardinal Health, Dublin, OH). All channels used a common scalp reference. As part of the preoperative evaluation, the activity of 128 channels was recorded as a combination of intracranial (Radionics Medical Products, Inc., Burlington, MA) and scalp electrodes. Intracranial electrodes were placed on the cortical surface in locations dependent on expected seizure onset location. We selected 60 s of ECoG data from each of three seizures beginning well after seizure onset from five intracranial electrodes. A channel located in the temporal lobe is identified as the source channel by the clinician. The other four channels we selected are located in the parietal lobe and are identified by the clinician as channels to which the seizure activity propagates. The signals are filtered with passband 1–20 Hz (−40 dB net stopband attenuation at 25 Hz) and downsampled to a 50-Hz sampling rate. The 60 s of data from each seizure are segmented into twenty 3-s epochs. Following [45], a single-channel Kolmogorov-Smirnov test with P > 0.05 is applied to exclude epochs that contain obvious nonstationary activity. The first ten 3-s epochs that pass the test are selected to represent each of the three seizures. Fig. 1 shows an example 3-s epoch of ECoG signals from these five channels. The cortical interaction analysis assumes the activity is stationary across the ten epochs representing each seizure.
Fig. 1.
Example 3-s epoch of seizure ECoG signals from five channels.
B. Modeling of ECoG Signals
Distinct MVAR and RBF models are fit to each of the three ECoG seizure datasets to obtain a performance baseline for our analysis of the corresponding simulated EEG signals. The BIC is applied to all ten epochs for each seizure to identify MVAR model order P, RBF memory P, and the number of kernels I. We varied P for the RBF model from 1 to 4 and I from 2 to 20. The kernel centers are chosen using the fuzzy c-means clustering algorithm assuming a kernel radius of 0.5. The MVAR memory was selected as P = 24 for seizures 1 and 2, and P = 22 for seizure 3. The RBF parameters were selected as P = 2, I = 10 for seizures 1 and 2, and P = 2, I = 8 for seizure 3 following the procedure described in Section IV-B.
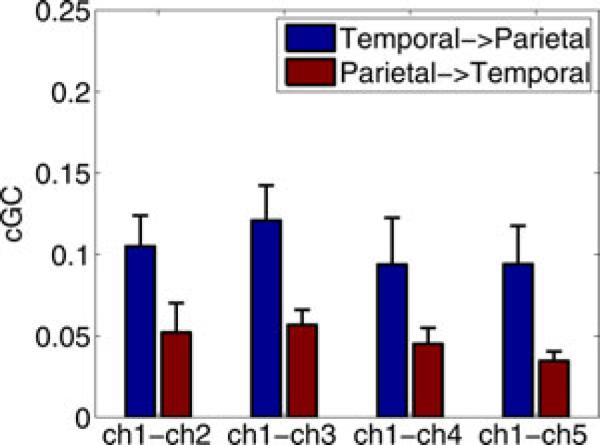
The results of tenfold CV on the ECoG data are given in Table V. We only calculate CV-NMSE since, in the absence of an observation equation, LL is proportional to NMSE [46]. The results indicate that the MVAR model has much greater predictive power than the RBF model for all three seizures and that the difference between models is significant. Fig. 2 depicts the mean conditional Granger causality (cGC) between the temporal source channel and each parietal channel, averaged over the three seizures. The cGC is calculated by integrating the spectral representation over frequency using the partitioned matrix technique of [47]. The cGC suggests a dominant flow from the temporal lobe source to the sources in the parietal lobe, consistent with the clinical information.
TABLE V.
Tenfold Cross-Validation NMSE Scores With Standard Errors for Seizure ECoG Data
| Model Type | Seizure 1 | Seizure 2 | Seizure 3 |
|---|---|---|---|
| MVAR | 0.118 ± 0.009 | 0.152 ± 0.022 | 0.146 ± 0.022 |
| RBF | 0.324 ± 0.025 | 0.439 ± 0.075 | 0.387 ± 0.057 |
Fig. 2.
Mean cGC over three seizures calculated from the MVAR models of the ECoG data computed over 0 to 25 Hz. Error bars denote the standard error of the mean.
C. Simulated EEG
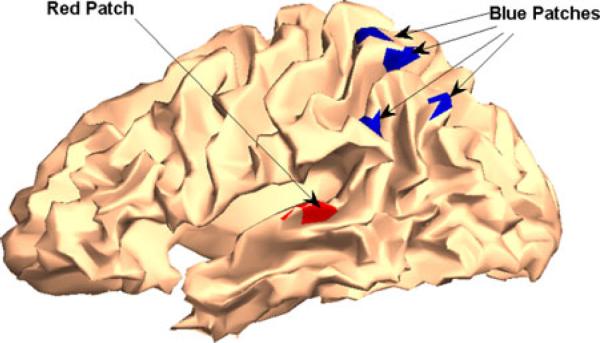
EEG data are simulated by associating each ECoG signal with a source represented by a 5-mm radius cortical patch as shown in Fig. 3. The goal is to obtain a physiologically realistic scalp EEG, not mimic the EEG signals of this patient. The following observation equation is used to simulate 56-channel EEG signals:
| (17) |
where Hm is the collection of leadfields in the mth ROI, αm is the corresponding spatial activity distribution, is the mth ECoG signal, and vn,j is white Gaussian noise. The spatial distribution αm is chosen as a raised cosine for each source. The SNR is set to 10 dB.
Fig. 3.
Five cortical sources for simulated EEG signals representing seizures of temporal origin. The red patch in the temporal lobe represents the leading source. The activity propagates to the four blue patches in the parietal lobe.
D. Cross-Validation Analysis of Simulated EEG
MVAR and RBF state-space models are fit to the simulated EEG signals from each seizure using both EM and two-stage estimation methods. The procedure described in Section IV-B is employed to determine the MVAR model order P, the RBF memory P, and the number of RBF kernels I. MVAR order P = 6 was selected for all seizures. The RBF parameters were P = 2, I = 8 for seizures 1 and 2, and P = 2, I = 10 for seizure 3. The presence of observation noise leads to a significant reduction in MVAR model order, while the RBF parameters remain comparable to the ECoG case.
The results of tenfold CV for both metrics and all three seizures are shown in Table VI. These results assume that F = 3 spatial basis vectors are used to represent each cortical source. As previously, the omniscient sMVAR results provide reference CV scores and are obtained by fitting an MVAR model to the ECoG signals and computing the innovations (3) and innovations covariance (6) using the true observation equation source distributions αm, m = 1, …, 5 and noise covariance matrix. Both CV-NMSE and CV-LL indicate that the best to worst model performance is: 1) EM sMVAR, 2) EM sRBF, 3) two-stage sMVAR, and 4) two-stage sRBF.
TABLE VI.
Tenfold Cross-Validation Scores With Standard Errors for Simulated EEG Seizure Data
| Model Type | Seizure 1 | Seizure 2 | Seizure 3 | |||
|---|---|---|---|---|---|---|
| CV-NMSE | CV-LL | CV-NMSE | CV-LL | CV-NMSE | CV-LL | |
| EM sMVAR | 0.350 ± 0.024 | 156.04 ± 2.26 | 0.327 ± 0.036 | 167.80 ± 3.14 | 0.275 ± 0.023 | 166.06 ± 2.71 |
| Two-stage sMVAR | 0.613 ± 0.059 | 152.59 ± 2.35 | 0.549 ± 0.049 | 164.52 ± 3.15 | 0.474 ± 0.035 | 162.10 ± 2.73 |
| EM sRBF | 0.424 ± 0.027 | 155.63 ± 2.26 | 0.379 ± 0.041 | 167.41 ± 3.17 | 0.327 ± 0.030 | 165.62 ± 2.72 |
| Two-stage sRBF | 0.770 ± 0.061 | 152.26 ± 2.32 | 0.723 ± 0.074 | 164.22 ± 3.18 | 0.680 ± 0.075 | 161.74 ± 2.77 |
| Omniscient sMVAR | 0.258 ± 0.015 | 158.43 ± 2.16 | 0.235 ± 0.025 | 170.67 ± 2.68 | 0.207 ± 0.021 | 168.74 ± 2.54 |
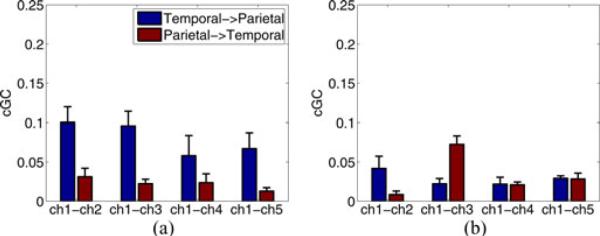
The differences in CV scores between models are generally significant, especially for CV-NMSE. Identification of the sMVAR model as the best model is consistent with the analysis of the ECoG data given in Section V-B. Note that the EM approach produces results that are significantly better than the two-stage approach in each seizure and the sRBF estimated using EM performs much better than the sMVAR model estimated with the two-stage approach. The mean cGC estimated with the EM and two-stage sMVAR models is depicted in Fig. 4. The EM-based results are consistent with the ECoG analysis depicted in Fig. 2 and show dominant flow from the temporal source to the parietal ROIs. In contrast, the two-stage results do not show such dominant flow and are not consistent with the ECoG analysis.
Fig. 4.
Mean cGC over three seizure datasets computed over 0 to 25 Hz. (a) EM sMVAR model applied to simulated EEG. (b) Two-stage sMVAR model applied to simulated EEG. Error bars denote the standard error of the mean.
Next, we use CV on the simulated EEG to evaluate the number of basis vectors employed in the observation equation. The EM sMVAR method is compared for F = 1, 2, 3, and 4. The best CV scores result for F = 3, with F = 2 and 4 having comparable scores. The score for F = 1 is significantly worse than those for F = 2, 3, and 4, suggesting more than one spatial basis vector is needed to represent the cortical signal contribution to the measured data. Fig. 5 depicts cGC for F = 1, 2, 3, and 4. The need for more than one spatial basis vector in the observation equation is apparent. The mean cGC values for F = 2, 3, and 4 are nearly identical, consistent with the similarity in CV scores and are similar to the cortical cGC values depicted in Fig. 2. However, the cGC for F = 1 is much different than the others and the ECoG-based cGC and has much greater variability across the three seizures.
Fig. 5.
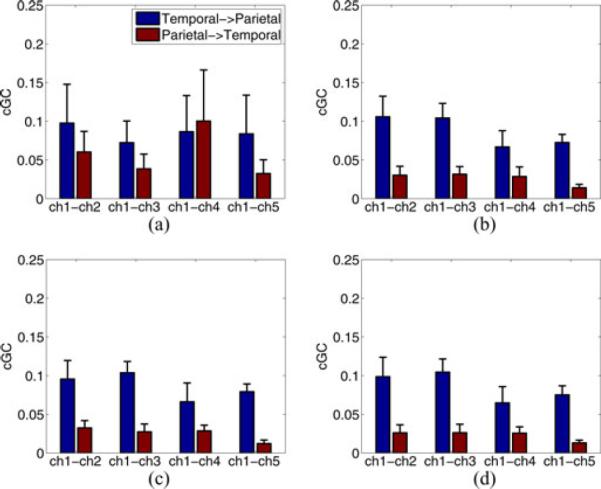
Mean cGC over three seizure datasets calculated over 0 to 25 Hz using EM sMVAR model with different spatial basis dimension (F) in the observation equation (a) F = 1, (b) F = 2, (c) F = 3, and (d) F = 4. Error bars denote the standard error of the mean.
VI. Discussion
We have introduced a CV methodology for evaluating the predictive ability of state-space cortical interaction models using measured scalp E/MEG data. It is applicable to any cortical time series model—linear or nonlinear—coupled with an observation equation describing the relationship between cortical and measured scalp signals. An observation equation is always present, either explicitly or implicity, when cortical signals or interaction models are estimated from scalp E/MEG measurements. Our CV method is based on the innovations sequence that is the prediction error between the measured data and the data predicted by the state-space cortical interaction model. The predicted scalp signal sample is based on the one-step, minimum mean-squared error prediction of the current cortical signal sample given the past cortical and measured scalp signal samples. CV cannot be correctly performed at the cortical level using estimated cortical signals since then the conclusions depend on the method used to estimate the unknown cortical signals. The state-space model selection problem must be formulated using measured data and the use of innovations computed by the Kalman filter satisfies this constraint. We have demonstrated two innovations-based CV metrics—NMSE and the observed data likelihood. Both of these have sound motivation for model selection.
In our examples, CV-NMSE leads to greater distinctions between models than does CV-LL with respect to the standard errors. CV-NMSE also has the potential to indicate how well the cortical activity is predicted. Assuming independent noise samples, a value of 1/(SNR+1) is the best possible NMSE, while a value of unity is the practical maximum1 and results from setting the cortical interaction model to zero. The CV-NMSE scores for the logistic and Henon systems at SNR = 10 dB are much closer to the theoretical lower bound than the bivariate AR system due to the large contributions of and in the AR system, which are not predictable. On the other hand, CV-LL identifies the most likely model. Note that other metrics could be used with the CV approach to emphasize other aspects of model selection.
Predictive ability is a natural criterion for model selection, since the fundamental purpose of modeling is to predict or describe a phenomenon. CV thus offers significant advantages over other model selection methods. In particular, AIC and BIC assume the data are generated by a model within the class of models under comparison, an assumption that is certainly violated in EEG and MEG. In contrast, CV has been proposed as a surrogate for maximizing expected utility in model selection when the data are not believed to be generated by a model in the class of models being compared [48]. The primary limitation of CV approaches is computational complexity, as they require evaluation over multiple partitions of the data.
The results provide clear evidence for the effectiveness of our proposed CV approach. In particular, the results in Section IV-C demonstrate that our CV approach correctly distinguishes between linear and nonlinear cortical interactions at both high and low SNRs (see Tables II–IV). We show that CV can be used to select the best number of basis vectors in the observation equation (see Table VII). The ECoG-derived EEG simulations in Section V show that the CV score predicts the quality of estimated effective connectivity measures, such as cGC. If the number of basis vectors is such that the CV metrics are near optimum, the cGC (see Fig. 5) agrees with the “true” cGC calculated using the ECoG signals (see Fig. 2). In contrast, the relatively poor CV scores for the F = 1 case result in poor cGC estimates. Similarly, the relative poor CV scores for the two-stage sMVAR model result in poor cGC estimates (see Fig. 4).
TABLE VII.
Tenfold Cross-Validation Scores With Standard Errors for EM sMVAR Models With Different Numbers of Spatial Basis Vectors in the Observation Equation
| Model Type | Seizure 1 | Seizure 2 | Seizure 3 | |||
|---|---|---|---|---|---|---|
| CV-NMSE | CV-LL | CV-NMSE | CV-LL | CV-NMSE | CV-LL | |
| F = 1 | 0.474 ± 0.040 | 154.46 ± 2.37 | 0.477 ± 0.057 | 164.76 ± 2.94 | 0.371 ± 0.042 | 164.05 ± 2.64 |
| F = 2 | 0.352 ± 0.023 | 155.96 ± 2.30 | 0.335 ± 0.036 | 167.75 ± 3.15 | 0.277 ± 0.023 | 166.03 ± 2.70 |
| F = 3 | 0.350 ± 0.023 | 156.00 ± 2.29 | 0.332 ± 0.037 | 167.77 ± 3.14 | 0.275 ± 0.023 | 166.06 ± 2.71 |
| F = 4 | 0.350 ± 0.023 | 156.00 ± 2.29 | 0.335 ± 0.037 | 167.76 ± 3.14 | 0.276 ± 0.023 | 166.05 ± 2.71 |
| Omniscient sMVAR | 0.253 ± 0.013 | 158.42 ± 2.17 | 0.224 ± 0.024 | 170.81 ± 2.68 | 0.207 ± 0.022 | 168.74 ± 2.54 |
The CV scores clearly indicate that the integrated approach to estimating cortical interaction models using the EM algorithm results in higher quality models than two-stage estimation approaches. The EM approach results in consistently better CV scores when the underlying system is linear or nonlinear, and when human ECoG seizure data are used to simulate EEG. In both the bivariate AR system (see Table II) and simulated seizure EEG data examples (see Table VI), the EM sRBF model has better CV scores than the two-stage sMVAR model, even though the cortical data are better described by an MVAR model. That is, the “wrong”model estimated with EM has better predictive ability than the “correct” model estimated with the two-stage method in these examples.
The proposed CV approach can also be used to select model complexity, as illustrated in Fig. 5 and Table VII, because it naturally discriminates against under- or overfitting of models by using predictive quality as the selection metric.
The examples employed tenfold CV. We choose K = 10 to balance computational complexity and estimation precision of the CV metrics. Given a fixed amount of data, increasing K reduces the number of data values in the test set, but increases the number of test sets. If the number of data values in the test set is too small, then the startup transient of the state-estimation filter (e.g., Kalman or extended Kalman) may dominate the CV metric. Startup transients result because the initial state is unknown. The state-estimation filter needs to evolve from a given initial state to the state sequence in the data. In our examples, we used the mean initial state estimated from the training data as the state-estimation filter initial state and found that it converged visually to a steady-state tracking condition within five samples. Five out of 150 samples are a small fraction in our test data partitions, so we used the entire innovations sequence to compute our CV metrics. If the number of samples required for the state-estimation filter to converge to a steady-state tracking is a significant fraction of the test partition, then these initial samples should be excluded from the CV metric computation to avoid biasing the results by the assumed initial state.
The CV approach quantifies the performance of a model using the data. Hence, it is imperative that the data describe the phenomenon of interest. If, for example, the data are dominated by artifacts, the CV approach will prefer the model that best describes artifacts.
The CV method proposed here is sensitive to both the cortical interaction model and any unknown parameters in the observation equation. This endows it with the ability to identify the best observation equation parameters, such as the number of spatial basis vectors. In principle, our CV methodology can be used to compare models that assume different source locations. However, the computational cost of doing so escalates rapidly as the number of sources with uncertain location increases. Note that it is also theoretically possible that a lower quality cortical interaction model could have the best CV score given a fortuitous set of observation equation parameter estimates. This possibility is somewhat lessened by the fact that the dynamics of interaction are represented only in the cortical interaction model while observation noise samples are assumed temporally independent. Errors in assumed cortical source locations or models are potentially more problematic. If the observation equation assumes incorrect source locations or forward model physics, then incorrect conclusions may result. This issue is endemic to cortical analysis of E/MEG data and not limited to the proposed CV approach.
In human data, the true cortical interactions are never quantitatively known a priori. Consequently, performance comparison of different models or estimation methods is typically performed using simulations that cannot replicate the complexity of the human brain. Although the CV methodology presented here cannot establish that a given model captures the true cortical interactions in a quantitative sense, it does offer a principled and quantitative means for comparing the predictive ability of different models using only measured data.
Acknowledgments
This work was supported in part by the Wisconsin Alumni Research Foundation, the National Institutes of Health under Award R21EB009749, and the Dr. Ralph and Marian Falk Medical Research Trust. This research was performed using resources and the computing assistance of the UW-Madison Center For High Throughput Computing.
Biographies

Bing Leung Patrick Cheung (M'11) received the B.A.Sc. degree (Hons.) in computer engineering from the University of British Columbia, Vancouver, BC, Canada, in 2000, and the M.S. degree from Virginia Tech, Blacksburg, in 2002, and the Ph.D. degree from the University of Wisconsin-Madison, Madison, in 2011, both in electrical engineering.
From 2002 to 2006, he was a Wireless System Engineer specialized in radio algorithm development and digital signal processing at Nortel Networks, Mississauga, ON, Canada. His research interests in clude statistical signal processing, time series analysis and system modeling, and identification for communications and biomedical applications.
Dr. Cheung received the International Union of Radio Science Best Student Paper Award in 2002, Nortel Invention Award in 2006, and Natural Sciences and Engineering Research Council of Canada Postgraduate Scholarship for 2008–2010.

Robert Nowak (F'10) received the B.S., M.S., and Ph.D. degrees in electrical engineering from the University of Wisconsin-Madison, Madison, in 1990, 1992, and 1995, respectively.
He was a Postdoctoral Fellow at Rice University in 1995–1996, an Assistant Professor at Michigan State University from 1996 to 1999, held Assistant and Associate Professor positions at Rice University from 1999 to 2003. He is currently the McFarland-Bascom Professor of engineering at the University of Wisconsin-Madison. He has held visiting positions at INRIA, Sophia-Antipolis, France, 2001, and Trinity College, Cambridge, 2010. His research interests include signal processing, machine learning, imaging and network science, and applications in communications, bioimaging, and systems biology.
Dr. Nowak has served as an Associate Editor for the IEEE Transactions on Image Processing and the ACM Transactions on Sensor Networks, and as the Secretary of the SIAM Activity Group on Imaging Science. He was a General Chair for the 2007 IEEE Statistical Signal Processing workshop and Technical Program Chair for the 2003 IEEE Statistical Signal Processing Workshop, and the 2004 IEEE/ACM International Symposium on Information Processing in Sensor Networks. He received the General Electric Genius of Invention Award in 1993, the National Science Foundation CAREER Award in 1997, the Army Research Office Young Investigator Program Award in 1999, the Office of Naval Research Young Investigator Program Award in 2000, and IEEE Signal Processing Society Young Author Best Paper Award in 2000.

Hyong Chol Lee received the B.S. degree in physics from California Institute of Technology, Pasadena, in 1994, and the Ph.D. degree in astronomy from Northwestern University, Chicago, IL, in 2001.
He is currently a Software Engineer in the Department of Pediatrics, University of Chicago, Chicago, IL.

Wim van Drongelen was born in Vlissingen, The Netherlands. He studied biophysics at the Leiden University, Leiden, The Netherlands. After a period in the Laboratoire d'Electrophysiologie, Université Claude Bernard, Lyon, France, he received the Doctoral degree (cum laude). In 1980, he received the Ph.D. degree from the University of Wageningen, The Netherlands.
He was with the Netherlands Organization for the Advancement of Pure Research (ZWO) in the Department of Animal Physiology, Wageningen, The Netherlands. He lectured and founded the Medical Technology Department, HBO Institute Twente, The Netherlands. In 1986, he joined the Benelux office of Nicolet Biomedical as an Application Specialist and in 1993, he relocated to Madison, WI, where he was a Lead Scientist and Systems Designer involved in the research and development of equipment for clinical neurophysiology and neuromonitoring. In 2001, he joined the Epilepsy Center at The University of Chicago, Chicago, IL. He is currently a Professor in the Department of Pediatrics, Department of Neurology, Committee on Computational Neuroscience, Technical and Research Director of the Pediatric Epilepsy Center, and Senior Fellow with the Computation Institute, and he teaches the applied mathematics courses for the Committee on Computational Neuroscience. His current research interests include the application of signal processing and modeling techniques to help resolve problems in neurophysiology and neuropathology.

Barry D. Van Veen (S'81–M'86–SM'97–F'02) was born in Green Bay, WI. He received the B.S. degree from Michigan Technological University, Houghton, in 1983, and the Ph.D. degree from the University of Colorado, Boulder, in 1986, both in electrical engineering.
In the spring of 1987, he was with the Department of Electrical and Computer Engineering, University of Colorado-Boulder. Since August 1987, he has been with the Department of Electrical and Computer Engineering, University of Wisconsin-Madison, Madison, where is currently the Lynn H. Matthias Professor of electrical engineering. He coauthored Signals and Systems (1st and 2nd ed. New York: Wiley, 1999 and 2003) with S. Haykin. During his Ph.D. studies, he was an ONR Fellow. His research interests include signal processing for sensor arrays and biomedical applications of signal processing.
Dr. Van Veen received the 1989 Presidential Young Investigator Award from the National Science Foundation and the 1990 IEEE Signal Processing Society Paper Award. He served as an Associate Editor of the IEEE Transactions on Signal Processing. He has also served on the IEEE Signal Processing Society's Statistical Signal and Array Processing and Sensor Array and Multi-channel Technical Committees. He received the Holdridge Teaching Excellence Award from the ECE Department, University of Wisconsin in 1997.
Footnotes
Values greater than one are possible if the estimated state is the negative of the true state, but this is extremely unlikely because the Kalman filter could then obtain better prediction by changing the sign of the estimated state in (3).
References
- [1].Friston K. Functional and effective connectivity: A review. Brain Connect. 2011;1(1):13–36. doi: 10.1089/brain.2011.0008. [DOI] [PubMed] [Google Scholar]
- [2].Bressler S, Ding M, Yang W. Investigation of cooperative cortical dynamics by multivariate autoregressive modeling of event-related local field potentials. Neurocomputing. 1999;26-27:625–631. [Google Scholar]
- [3].Bernasconi C, Konig P. On the directionality of cortical interactions studied by structural analysis of electrophysiological recordings. Biol. Cybern. 1999;81:199–210. doi: 10.1007/s004220050556. [DOI] [PubMed] [Google Scholar]
- [4].Brovelli A, Ding M, Ledberg A, Chen Y, Nakamura R, Bressler S. Beta osciallations in a large-scale sensorimotor cortical network: Directional influences revealed by granger causality. Proc. Nat. Acad. Sci. 2004;101(26):9849–9854. doi: 10.1073/pnas.0308538101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Freiwald W, Valdes P, Bosch J, Biscay R, Jimenez J, Rodriguez L, Rodriguez V, Kreiter A, Singer W. Testing non-linearity and directedness of interactions between neural groups in the macaque infer-otemporal cortex. J. Neurosci. Methods. 1999;94:105–119. doi: 10.1016/s0165-0270(99)00129-6. [DOI] [PubMed] [Google Scholar]
- [6].Marinazzo D, Liao W, Chen H, Stramaglia S. Nonlinear connectivity by Granger causality. NeuroImage. 2010;58:330–338. doi: 10.1016/j.neuroimage.2010.01.099. [DOI] [PubMed] [Google Scholar]
- [7].Nykamp D, Tranchina D. A population density approach that facilitates large-scale modeling of neural networks: Analysis and an application to orientation tuning. J. Comput. Neurosci. 2000;8:19–50. doi: 10.1023/a:1008912914816. [DOI] [PubMed] [Google Scholar]
- [8].Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19:1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- [9].David O, Friston KJ. A neural mass model for MEG/EEG: Coupling and neuronal dynamics. NeuroImage. 2003;20:1743–1755. doi: 10.1016/j.neuroimage.2003.07.015. [DOI] [PubMed] [Google Scholar]
- [10].Astolfi L, Cincotti F, Mattia D, Marciani M, Baccala L, de Vico Fallani F, Salinari S, Ursino M, Zavaglia M, Ding L, Edgar J, Miller G, He B, Babiloni F. Comparison of different cortical connectivity estimators for high-resolution EEG recordings. Human Brain Mapping. 2007 Feb.28:143–157. doi: 10.1002/hbm.20263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hui H, Pantazis D, Bressler S, Leahy R. Identifying true cortical interactions in MEG using the nulling beamformer. NeuroImage. 2010 Feb.49:3161–3174. doi: 10.1016/j.neuroimage.2009.10.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Cheung BL, Riedner B, Tononi G, Van Veen B. Estimation of cortical connectivity from EEG using state-space models. IEEE Trans. Biomed. Eng. 2010 Sep.57(9):2122–2134. doi: 10.1109/TBME.2010.2050319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Astolfi L, Cincotti F, Mattia D, Marciani M, Baccala L, de Vico Fallani F, Salinari S, Ursino M, Zavaglia M, Babiloni F. Assessing cortical functional connectivity by partial directed coherence: Simulations and application to real data. IEEE Trans. Biomed. Eng. 2006 Sep.53(9):1802–1812. doi: 10.1109/TBME.2006.873692. [DOI] [PubMed] [Google Scholar]
- [14].Marreiros AC, Kiebel SJ, Friston KJ. A dynamic causal model study of neuronal population dynamics. NeuroImage. 2010;51:91–101. doi: 10.1016/j.neuroimage.2010.01.098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Akaike H. A new look at the statistical model identification. IEEE Trans. Automat. Control. 1974 Dec.AC-19(6):716–723. [Google Scholar]
- [16].Schwarz G. Estimating the dimension of a model. Ann. Stat. 1978;6:461–464. [Google Scholar]
- [17].Efron B. Estimating the error rate of a prediction rule: improvement on cross-validation. J. Amer. Stat. Assoc. 1983;78:316–331. [Google Scholar]
- [18].Wasserman L. Bayesian model selection and model averaging. J. Math. Psychol. 2000;44:92–107. doi: 10.1006/jmps.1999.1278. [DOI] [PubMed] [Google Scholar]
- [19].Stone M. Cross-validatory choice and assessment of statistical predictions. (Series B).J. Royal Stat. Soc. 1974;36(2):111–147. [Google Scholar]
- [20].Geisser S. The predictive sample reuse method with applications. J. Amer. Stat. Assoc. 1975;(350):320–328. [Google Scholar]
- [21].Shao J. Linear model selection by cross-validation. J. Amer. Stat. Assoc. 1993;88(422):486–494. [Google Scholar]
- [22].van der Vaart AW, Dudoit S, van der Laan MJ. Oracle inequalities for multi-fold cross validation. Stat. Decis. 2006;24(3):351–371. [Google Scholar]
- [23].van der Laan MJ, Polley E, Hubbard AE. Super learner. Stat. Appl. Genetics Molecular Biol. 2007;6(1) doi: 10.2202/1544-6115.1309. Art. 25. Available: http://www.bepress.com/sagmb/vol6/iss1/art25/ [DOI] [PubMed] [Google Scholar]
- [24].Baillet S, Mosher J, Leahy R. Electromagnetic brain mapping. IEEE Signal Process. Mag. 2001 Nov.18(6):14–30. [Google Scholar]
- [25].Nolte G, Curio G. Current multipole expansion to estimate lateral extent of neuronal activity: A theoretical analysis. IEEE Trans. Biomed. Eng. 2000 Oct.47(10):1347–1355. doi: 10.1109/10.871408. [DOI] [PubMed] [Google Scholar]
- [26].Limpiti T, Van Veen B, Wakai R. Cortical patch basis model for spatially extended neural activity. IEEE Trans. Biomed. Eng. 2006 Sep.53(9):1740–1754. doi: 10.1109/TBME.2006.873743. [DOI] [PubMed] [Google Scholar]
- [27].Stoffer D, Wall K. Bootstrapping state-space models: Gaussian maximum likelihood estimation and the Kalman filter. J. Amer. Stat. Assoc. 1991;86(416):1024–1033. [Google Scholar]
- [28].Haykin S. Kalman filters. In: Haykin S, editor. Kalman Filtering and Neural Networks. ch. 1. Wiley; New York: 2001. pp. 1–21. [Google Scholar]
- [29].Anderson B, Moore J. Optimal Filtering. Prentice-Hall; Englewood Cliffs, NJ: 1979. [Google Scholar]
- [30].Doucet A, Godsill SJ, Andrieu C. On sequential monte carlo sampling methods for bayesian filtering. Stat. Comput. 2000;10(3):197–208. [Google Scholar]
- [31].Shumway R. Applied Statistical Time Series Analysis. Prentice-Hall; Englewood Cliffs, NJ: 1988. [Google Scholar]
- [32].Cheung BL, Van Veen B. Estimation of cortical connectivity from E/MEG using nonlinear state-space models. Proc. 36th Int. Conf. Acoust., Speech Signal Process; Prague, Czech Republic. May, 2011. pp. 769–772. [Google Scholar]
- [33].Bressler S, Richter C, Chen Y, Ding M. Cortical functional network organization from autoregressive modeling of local field potential oscillations. Stat. Med. 2007;26:3875–3885. doi: 10.1002/sim.2935. [DOI] [PubMed] [Google Scholar]
- [34].Ancona N, Stramaglia S. An invariance property of predictors in kernel-induced hypothesis spaces. Neural Comput. 2006;18(4):749–759. doi: 10.1162/089976606775774660. [DOI] [PubMed] [Google Scholar]
- [35].Park J, Sandberg IW. Universal approximation using radial-basis function networks. Neural Comput. 1991;3:246–257. doi: 10.1162/neco.1991.3.2.246. [DOI] [PubMed] [Google Scholar]
- [36].Ancona N, Marinazzo D, Stramaglia S. Radial basis function approach to nonlinear Granger causality of time series. Phys. Rev. E. 2004;70:56 221–56 227. doi: 10.1103/PhysRevE.70.056221. [DOI] [PubMed] [Google Scholar]
- [37].Van Veen B, van Drongelen W, Yuchtman M, Suzuki A. Localization of brain electrical activity via linearly constrained minimum variance spatial filtering. IEEE Trans. Biomed. Eng. 1997 Sep.44(9):867–880. doi: 10.1109/10.623056. [DOI] [PubMed] [Google Scholar]
- [38].Ding M, Chen Y, Bressler L. Granger causality: Basic theory and application to neuroscience. In: Schelter B, Winterhalder M, Timmer J, editors. Handbook of Time Series Analysis. ch. 17. Wiley; Weinheim, Germany: 2006. pp. 437–459. [Google Scholar]
- [39].Nelles O. Nonlinear System Identification. Springer-Verlag; Berlin, Germany: 2001. [Google Scholar]
- [40].Shumway R, Stoffer D. An approach to time series smoothing and forecasting using the EM algorithm. J. Time Series Anal. 1982;3(4):253–264. [Google Scholar]
- [41].Roweis S, Ghahramani Z. Learning nonlinear dynamical system using the expectation-maximization algorithm. In: Haykin S, editor. Kalman Filtering and Neural Networks. ch. 6. Wiley; New York: 2001. pp. 175–220. [Google Scholar]
- [42].Dempster A, Laird N, Rubin D. Maximum likelihood from incomplete data via the EM algorithm. (Series B).J. Royal Stat. Soc. 1977;39(1):1–38. [Google Scholar]
- [43].Rauch H, Tung F, Stiebel C. Maximum likelihood estimates of linear dynamic systems. AIAA J. 1965;3:1445–1450. [Google Scholar]
- [44].Schiff S, So P, Chang T, Burke R, Sauer T. Detecting dynamical interdependence and generalized synchrony through mutual prediction in a neural ensemble. Phys. Rev. E. 1996;54(6):6708–6724. doi: 10.1103/physreve.54.6708. [DOI] [PubMed] [Google Scholar]
- [45].Salazar R, Konig P, Kayser C. Directed interactions between visual areas and their role in processing image structure and expectancy. Eur. J. Neurosci. 2004;20:1391–1401. doi: 10.1111/j.1460-9568.2004.03579.x. [DOI] [PubMed] [Google Scholar]
- [46].Stoica P, Selen Y. Model-order selection. IEEE Signal Process. Mag. 2004 Jul.21(4):36–47. [Google Scholar]
- [47].Chen Y, Bressler S, Ding M. Frequency decomposition of conditional granger causality and application to multivariate neural field potential data. J. Neurosci. Methods. 2006;150:228–237. doi: 10.1016/j.jneumeth.2005.06.011. [DOI] [PubMed] [Google Scholar]
- [48].Bernardo JM, Smith AFM. Bayesian Theory. Wiley; New York: 2000. [Google Scholar]