Abstract
Understanding how a simple chemical system can accurately replicate combinatorial information, such as a sequence, is an important question for both the study of life in the universe and for the development of evolutionary molecular design techniques. During biological sequence replication, a nucleic acid polymer serves as a template for the enzyme-catalyzed assembly of a complementary sequence. Enzymes then separate the template and complement before the next round of replication. Attempts to understand how replication could occur more simply, such as without enzymes, have largely focused on developing minimal versions of this replication process. Here we describe how a different mechanism, crystal growth and scission, can accurately replicate chemical sequences without enzymes. Crystal growth propagates a sequence of bits while mechanically-induced scission creates new growth fronts. Together, these processes exponentially increase the number of crystal sequences. In the system we describe, sequences are arrangements of DNA tile monomers within ribbon-shaped crystals. 99.98% of bits are copied correctly and 78% of 4-bit sequences are correct after two generations; roughly 40 sequence copies are made per growth front per generation. In principle, this process is accurate enough for 1,000-fold replication of 4-bit sequences with 50% yield, replication of longer sequences, and Darwinian evolution. We thus demonstrate that neither enzymes nor covalent bond formation are required for robust chemical sequence replication. The form of the replicated information is also compatible with the replication and evolution of a wide class of materials with precise nanoscale geometry such as plasmonic nanostructures or heterogeneous protein assemblies.
Keywords: algorithmic self-assembly, DNA nanotechnology, self-assembly
In cells, long genomes are accurately replicated via a complex replication process involving tens or sometimes hundreds of enzymes. Nearer to life’s origins, a much simpler system must have been responsible for genome replication; evolution of this information then produced more and more complex forms. How a chemical system could be capable of sustained replication and evolution and yet be simple enough to arise spontaneously is an open question.
Enzyme-free autocatalytic systems, which are generally simpler than those with enzymes, are known to exponentially replicate one or a small set of species (1–5), but none of these systems replicate an arrangement of subunits defining a combinatorial sequence of information. Without the capacity for combinatorial information replication, open-ended evolution, in which complexity increases without bound (6), cannot occur.
Some RNA sequences have been shown to act as RNA polymerases that can assemble a general RNA sequence given a template (7). If such an RNA sequence polymerized a copy of itself, the required enzyme would be produced by the replication process, making it self-sustaining. However, fidelity sufficient for RNA-mediated RNA self-replication has not yet been observed (8, 9). Similarly, extension of nucleic acid primers can occur accurately without enzymes (10, 11), but it is not yet known whether arbitrary sequences could be assembled this way; further difficulties are introduced by the need for the template and its newly assembled complement to separate before another round of replication can commence.
Homogeneous 2- and 3-dimensional crystal growth occurs spontaneously in nonliving systems and defect rates during crystal growth can be as low as error rates during genome replication (12). Like prion growth (13), crystal growth can be autocatalytic if mechanical forces fragment crystals, increasing the number of crystal growth fronts (14). If a crystal stored information in its arrangement of monomers, growth could propagate that information and scission could, by creating new growth fronts for propagation, replicate it. A crystal’s information would then be subject to Darwinian evolution, as postulated by Cairns-Smith almost 50 years ago (15) (Fig. 1A). While replication of chemical sequences through crystal growth has continued to be of interest (16) because of its simplicity and potential compatibility with a wide variety of chemistries, such replication has never been demonstrated. The replication of information in the form of crystal defects has been observed, but fidelity was very low (17).
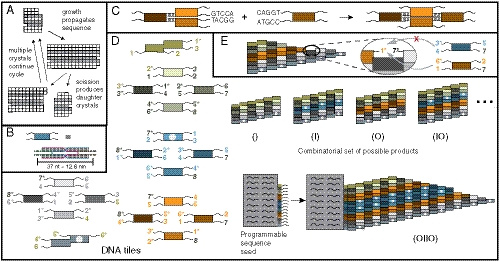
Fig. 1.
Crystal replication. (A) An information sequence (here a column of white or black squares within a 2D crystal) is replicated in two stages. (B–E) DNA tile crystals. (B) DNA tiles are self-assembled, multihelical complexes with 5-nucleotide, single-stranded sticky ends. (C) Tiles attach to crystals via cooperative sticky end hybridization. (D) A tile set that can form ribbon crystals containing any sequence of indigo (I) or orange (O) tile blocks (or the null sequence). Using these tile types, an n-bit wide ribbon could carry any of 2n possible sequences. The two “double” tiles are edge tiles, while the four green tiles below the top edge tile and the four gray tiles above the bottom edge tile, the nucleation barrier tiles, create a thermodynamic barrier to the nucleation of new crystals (25, 24). The four indigo (blue) tiles are the I block tiles and the four orange tiles are the O block tiles. White dots are biotin; colored digits denote sticky end types. Sticky end complements have a *. A crystal seed programmed with sticky ends for a sequence templates growth of that sequence. (E) To be favorable, tiles must attach by at least two sticky ends simultaneously, so growth copies the crystal sequence.
Here we show that DNA tile crystals (18, 19) can robustly replicate combinatorial information, as theoretically proposed earlier (20). DNA tiles are crystal monomers consisting of four to six synthetic strands of DNA folded into a double crossover structure (Fig. 1B). Tiles crystallize via sticky end hybridization (Fig. 1C), and under appropriate growth conditions, complementary sticky ends hybridize, while noncomplementary sticky ends are unlikely to interact.
We recently demonstrated that tiles can assemble ribbon-shaped crystals that propagate a sequence of information during growth (19). In that study, individual bits were copied highly accurately, but errors in propagation such as sequence truncation (i.e., the reduction of crystal width), or the spurious nucleation of crystals carrying new random sequences were more common. To decrease the rates of sequence truncation and spurious nucleation, we designed an improved tile set. The tiles in Fig. 1D form ribbons containing an arbitrary sequence of 2-tile-thick indigo (I) or orange (O) layers. During growth, only a tile matching the previous layer’s color can attach favorably (i.e., sticky ends) (21, 22) (Fig. 1 C and E), so ribbon growth propagates the sequence, one layer at a time (SI Appendix, Fig. S1). To improve fidelity, sequence copying is proofread: information is incorrectly propagated only if two tiles in a row misattach (23, 19). The gray nucleation barrier blocks likewise make sequence truncation difficult by requiring that multiple tiles mismatch for truncation to occur. These tiles also increase the energetic barrier to new nucleation, making spurious nucleation of crystals not propagating the templated sequence rare (24, 25) (SI Appendix, Supplemental Methods sections 1–3 and 12).
Results
Crystal Growth.
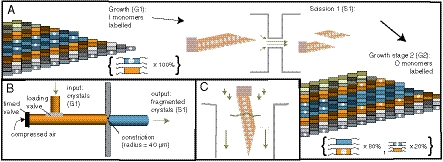
To study whether DNA crystal sequences could be replicated via growth and scission, we characterized the increases in the numbers of crystal layers and growth fronts as we grew crystals (stage G1), created new growth fronts via scission (S1) and then continued growth (G2) (Fig. 2A). Without crystal seeds, tiles produce an ensemble of crystal sequences dominated by those easiest to nucleate, crystals containing neither orange nor indigo layers (25, 24). To study the replication of a specific crystal sequence, we therefore programmed a DNA origami crystal seed (26, 19) to template crystals with the sequence OIIO (Fig. 1D and SI Appendix, Fig. S2). Previously, DNA crystals have been grown via annealing, which gradually increases tile interaction strength as temperature and concentration decrease. To permit cycles of growth and scission, we developed a method for constant temperature growth (SI Appendix, Supplemental Methods sections 4 and 5). To ensure consistently low supersaturation, tiles were not depleted during growth, and G1, S1, and G2 and transfers occurred in a temperature-controlled chamber. For G1, we mixed approximately 25 nM tile monomers with 25 pM crystal seeds and let them grow for 8 h at 31 °C, just below the crystal melting temperature (25). To characterize the ribbon crystal population, we collected images of crystals at random locations on a mica surface via atomic force microscopy (AFM) at room temperature in fluid (SI Appendix, Supplemental Methods sections 6 and 7). To prevent crystal growth from occurring at room temperature during imaging, we added DNA “guard” strands to the sample to be imaged while it was still at 31 °C. Guard strands reduce or prevent the rate of further crystal growth by binding to free tiles and growth fronts and removing the sticky end strands at these edges. Without sticky ends, the tiles and crystals cannot interact (SI Appendix, Supplemental Methods section 8 and Figs. S7–S10). To distinguish O from I tile blocks in the crystals and thus read their sequences, I block and edge tiles were biotin-labeled during G1 (Fig. 2A and SI Appendix, Fig. S3). Just before imaging we added streptavidin (SI Appendix, Figs. S4–S6) which binds to biotin and is large enough to see in our images (Fig. 3). To minimize sampling error, we pooled data from several experiments.
Fig. 2.
Replication stages. (A) After growth (G1), crystals undergo scission (S1) and further growth (G2). (B–C) Scission mechanism. Compressed air propels solution containing crystals through a constriction (B), where high elongational flows fragment crystals [zoom, (C)]. Arrow lengths indicate rough fluid velocity.
Fig. 3.
Predicted and observed crystals. Predicted (cartoons) and example crystals (AFM images) for G1 (blue), S1 (yellow), and G2 (red). Gray-framed images (Top right) show errors in G1: spuriously nucleated crystals and a bit flip at the arrow. Beige and brown lines (G2, Bottom) denote G1 and G2 growth, respectively. OIIO labels show seeds’ templated sequences. Scale bars 100 nm.
During G1, 0.017% ± 0.013 of bits propagated (3 of 18,029) were flipped, and for 0.084% ± 0.026 of bits (16 of 18,029), an error shortened or lengthened the propagated sequence (SI Appendix, Supplemental Methods section 10), rates 5–7 times lower than previously reported (19). As a result, by the end of G1 76% ± 6 of templated growth fronts still propagated OIIO (Fig. 4). Almost half of these mutations occurred when the first crystal layer was copied from the seed. Such mutations happened at 10% ± 3 of seeds. The mean length of templated sequences was 620 ± 40 nm, or 39 ± 3 layers; i.e. during growth an average crystal copied its sequence 39 times (SI Appendix, Supplemental Note 2). Errors also occurred because of spurious nucleation of new crystals that did not carry the OIIO sequence. Because the nucleation barrier grows with crystal width (24, 25), the 9% ± 3 of crystals that were spuriously nucleated were easily identified as crystals with zero or, occasionally, one sequence bit (Fig. 3). Because each sequence is copied many times per generation and mutations are amplified, the high fidelity we observed during sequence propagation and the low rate of spurious nucleation are essential for sustained sequence replication (27).
Fig. 4.
Changes in the number and fraction of correct growth fronts and crystal length with replication stage. Top: Solid lines show measured number of growth fronts (purple) and crystal length (green) per seed. Dashed lines show the same values predicted by Eqs. 1–2 for the reported Ls[0], Fs[0] and the resulting best fits for f and g. Bottom: Fraction of correct growth fronts and fraction of crystal length that is correct, out of the total number of templated growth fronts and total templated crystal length, respectively. Errors here and elsewhere are 95% confidence intervals determined by bootstrapping.
Crystal Scission.
We next sought to determine whether crystal scission could create new OIIO growth fronts. Elongational flow in a constricted channel induces DNA tile crystal scission because of differing amounts of drag force experienced along a crystal’s span (Fig. 2C) (28). However, previous studies did not characterize the structure of the crystal facets produced by elongational-flow-induced scission: facet damage could prevent sequence propagation after scission or cause a mutated sequence to be propagated. But because elongational flow can cause the alignment of rod or polymer-shaped molecules along a flow gradient (29), it induces tension primarily along the long axis. We therefore hypothesized that fragmenting ribbon crystals via elongational flow could create new growth fronts without significant layer loss or damage, and that elongational flows could also fragment ribbon crystals. To test these hypotheses, we designed a channel with a constriction and pressure drop predicted to fragment OIIO crystals into approximately 200 nm fragments (SI Appendix, Supplemental Note 4). To accommodate an 800 psi pressure drop, we used a compressed air tank, high-pressure tubing and a metal disk with a laser-cut orifice as a constriction (Fig. 2 B and SI Appendix, Fig. S11 and Supplemental Methods section 11).
After scission, the percentage of templated growth fronts that were correct (80% ± 3) was the same to within error as the percentage before scission. The number of seeds remained constant throughout our experiments (SI Appendix, Supplemental Note 5) and more correct growth fronts per seed were observed after scission (2.6 ± 0.3) than before (0.81 ± 0.07), implying that scission produced many correct new correct growth fronts. However, holes (Fig. 3) and frayed edges (SI Appendix, Fig. S12) were sometimes observed, and scission of a few crystals cut through the sequence rather than between layers (SI Appendix, Fig. S13).
Continued Sequence Propagation.
To determine how well the new growth fronts could propagate their sequences, we diluted one part S1 mixture into four parts fresh monomers and let growth continue in the fresh mixture for 6–8 h (G2). In order to distinguish G2 growth from G1 growth, the fresh solution contained biotin-labeled O and unlabelled I tiles (Figs. 2A and 3).
After G2, there were 1,750 ± 400 nm of correct layers per seed vs. 620 ± 40 nm per seed after G1 (Fig. 4), suggesting that the new growth fronts increased the population’s rate of sequence propagation; i.e., replication occurred. This increased rate of sequence propagation was observed despite the fact that around 20% of growth fronts appeared to be inactive; no layers were added to them during G2.
To determine the implied replication rate, we modified models of autocatalysis by simultaneous growth and stochastic scission (30, 31) to separate growth and scission into stages. For simplicity, the model does not consider mutation. For sequence s, the number Fs of growth fronts and the total length Ls of crystal layers after n + 1 generations is
| [1] |
| [2] |
where g is the growth rate in nm per growth front per generation and f is the per nm probability of layer scission. Asymptotically,
and
 |
with
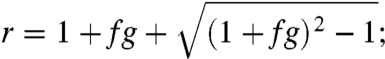 |
i.e., growth is exponential with replication rate r. The best fit of our data to the model is f = 0.0016 ± 0.0003 and g = 570 ± 90, for which r, the replication rate, is 3.5 ± 0.4 (SI Appendix, Supplemental Notes 6–8 and Fig. S14). A replication rate of 3.5 implies that over many generations we would expect that the number of growth fronts and crystal layers bearing the OIIO sequence to increase by a factor of 3.5 per generation.
Sustained self-replication of a chemical sequence requires not only that the abundance of the sequence grow with each generation; mutants also must not replicate faster than the original sequence (27). In our experiments, mutants observably replicated (SI Appendix, Fig. S15), and in a few cases, crystals were twisted where G1 growth ended and G2 growth began incorrectly, suggesting crystal lattice defects (SI Appendix, Fig. S16). “Monster” crystals propagating > 6 bits, which may have arisen via facet growth or side-to-side joining (SI Appendix, Fig. S17), and crystals joined end-to-end (SI Appendix, Fig. S18 and Supplemental Note 9) were also observed during G2.
Surprisingly, however, almost the same proportion of templated growth fronts (78% ± 6) and layers (79% ± 5) were correct after G2 as after G1 (Fig. 4). The mutants also did not propagate faster than correct crystals: Between G1 and G2, the total number of incorrect growth fronts increased at the same rate as the number of correct growth fronts (3.2 ± 0.5 vs. 3.1 ± 1.0). Similarly, incorrect and correct growth fronts added the same amount of length on average (530 ± 290 nm vs. 460 ± 140 nm). To estimate whether the observed mutation rate and replication rate of mutants could allow sustained self-replication of the original OIIO sequence, we simulated further generations using growth, scission and error rates sampled from the measured means and standard deviations. A simulated 1,000-fold replication of correct growth fronts took on average 7 generations, after which on average 47% ± 35 of templated crystals were correct (SI Appendix, Supplemental Note 10).
Like errors that change the sequence propagated during crystal growth or scission, spurious nucleation of crystals produces new mutants that can grow and replicate. Therefore, for sustained self-replication it is also necessary that spurious nucleation occur only rarely, so that spurious nuclei arise and replicate more slowly than crystals with the desired sequence. Spuriously nucleated crystals arose at 1.7 ± 0.6 × 10-7 nM/s during G2 and 0.9 ± 0.3 × 10-7 nM/s during G1 (SI Appendix, Supplemental Notes 11 and 12). After S1, 14 ± 7 times more spurious growth fronts and 19 ± 9 times more spurious layers were observed as after G1. However, almost all of these were observed after scission experiments where, unintentionally, the scission device audibly released cold air onto the crystals (SI Appendix, Figs. S22 and S23). Cool air increases supersaturation and could have temporarily increased spurious nucleation rates. When the 3 (of 6) experiments where cooling may have occurred are omitted (SI Appendix, Fig. S22), only 0.6 ± 0.4 times as many spuriously nucleated layers and 1.3 ± 0.7 times as many spuriously nucleated growth fronts were observed, respectively. Interestingly, the number of spuriously nucleated layers may have decreased because the forces applied to the crystals during scission could in some cases be enough to melt the spuriously nucleated crystals (SI Appendix, Supplemental Note 13). Therefore, these thinner crystals may have been selected against.
To determine how spurious nucleation would affect the replication process, we repeated the simulations of replication of the OIIO sequence, this time taking both mutation rates and spurious nucleation into account (an omitting the experiments where cooling may have occurred). We found that spuriously nucleated crystals would comprise only 7% ± 14 of crystals after 1,000-fold replication (SI Appendix, Supplemental Note 10). Thus this and the previous simulation support self-sustained, high-yield 1,000-fold replication of the templated sequence (SI Appendix, Fig. S24, Supplemental Note 14, and Tables S1–S2).
Discussion
Here we have demonstrated that information can be propagated by DNA crystals that we designed with error rates that are lower than 1 in 4,000 bits copied. In a fluid flow environment, these crystals fragment into on average 3.5 pieces containing the same sequence information; and after additional crystal growth, the rate at which new errors arise is almost unmeasurable. Together, these results imply that it is possible to robustly store and replicate combinatorial information within crystals. Simulations of growth that use measured growth rates, scission rates, and error rates during each generation suggest that over many generations, replication would produce at least 1,000 times more crystal growth fronts with an initial “seed” sequence with a high yield of correct copies.
The methods for replicating a chemical sequence that we describe are not specific to the OIIO sequence: other sequences were replicated (SI Appendix, Fig. S15) and a combinatorial set of sequences could be templated (19) and undergo scission using the same protocols. Replicating longer sequences will require that more sequence copies are made before fragmentation and that the forces that induce fragmentation are of the right scale, just as a long sequence template and its copy require sufficient energy to separate in other types of replication.
An important contributor to the robustness of crystal replication is that no coordination is needed between crystal growth and crystal scission processes for replication to occur. In contrast, in replication processes where a single sequence copy is made from a polymer template in each generation, template copying and the separation of the sequence copy and its template must occur one after the other in a tightly orchestrated process. One result of this difference is that end-product inhibition, the failure of the template and copy to separate, plagues other in vitro replication schemes (which are based on the template copy model) but does not affect crystal growth and scission-based replication. As a consequence, attempts at de novo design of self-replication using DNA nanotechnology (32) to implement the template copy mechanism have yielded cumbersome theoretical proposals (33, 34) while in a recent experimental demonstration (35) each 7-bit sequence could be copied only two times each, producing a population of “granddaughters” of which only 31% had the correct sequence (8.0% error rate per bit copied), amid an excess of spurious side products. This contrasts to our 4-bit sequences that were copied roughly 110 times each by the end of G2, after which 78% remain correct (0.02% error rate per bit copied), a fidelity rate 400 times higher. Spurious nucleated crystals also remain a minor side product.
DNA tile crystal growth and fragmentation is also not conceptually limited to the replication (and evolution) of crystals that passively store information. DNA tile crystals can be programmed to process information during growth and thereby create complex algorithmic patterns (19, 22, 36, 37). In the context of self-replication, such algorithmic growth processes could result in the selection of tile sequence patterns that have adapted in complex ways to their environment (30, 37). In theory, crystals can exhibit other lifelike behavior such as the programmed growth of complex 2- or 3-dimensional structures (38), self-healing after damage (39), or the regrowth of complex shapes after fragmentation (40). These examples point to a rich evolutionary landscape that can be explored to elucidate evolutionary principles in nonbiological chemical systems.
In a nonbiological context, previous work has recognized the technological value of exponential amplification of a specific material (such as carbon nanotubes with a specific width and chirality) by means of repeated growth and fragmentation from seeds (41). Similarly, the method for crystal replication we have demonstrated could also be applied to the discovery of functional materials: DNA crystals can serve as templates for proteins, small molecules, and nanoparticles (42), allowing the use of this system for the exploration via directed evolution of photonic or plasmonic nanostructures (43, 44) or of how the specific nanoscale arrangements of proteins gives rise to specific biological function (45). And while DNA crystals are more complex than most natural crystals, crystal growth processes and strong mechanical forces are varied and ubiquitous, suggesting the plausibility of a natural crystal growth process and environment that together support crystal information replication.
Materials and Methods
Tile Design and Assembly.
Tile sequences and adapter strands—i.e. the strands which attached to a DNA origami structure to form seeds—were designed as previously (19) by using a computer program that produced sequences with the required complementarity to form desired structures but with minimal complementary when forming alternative structures. All crystal growth reactions were performed in Tris-Acetate EDTA buffer containing 12.5 mM hydrous Mg(CH3COO)2. The seeds consisted of 25 pM of DNA origami scaffold, 50 nM of each of the accompanying staples strands that fold the scaffold into a rectangle (26), and 50 nM of each of the adapter strands. The assembly mixture included 25 nM of the nucleation barrier tiles and edge tiles and 100 nM of the orange and indigo tiles (in which the biotin label was on an orange tile strand). For G1, solutions of tiles and seeds were heated to 90 °C, then cooled to 31 °C in an Eppendorf Mastercycler PCR machine. The temperature was held at 31 °C during the growth period. The tiles for G2 included 25 nM of the edge and nucleation block tiles and 100 nM of the orange and indigo block tiles (in which the biotin label was on an indigo tile strand). For G2 growth, 12.5 μL of S1 crystals were added to 50 μL of G2 tiles that had been freshly cooled to 31 °C from above the melting temperature of the ribbons.
Scission.
G1 growth took place inside a PCR machine housed within a glove box held at 31 °C. Procedures for S1 all took place within this glove box, to maintain the solution at a temperature where crystal growth occurs at a low error rate and spurious nucleation rates are minimal. After G1, crystals were loaded into biocompatible HPLC tubing (inner diameter 500 μm) containing a constriction formed by a metal gasket with a r = 40 μm diameter, l = 125 μm long orifice. Eight hundred psi pressure air was used to propel the crystal solution through the construction. The maximum elongational flow experienced by the crystals is approximately  , where ΔP is the pressure drop across the channel and μ is the sample viscosity. The tension T experienced within a crystal as a result of this elongational flow is approximately
, where ΔP is the pressure drop across the channel and μ is the sample viscosity. The tension T experienced within a crystal as a result of this elongational flow is approximately 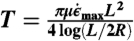 (28). If this tension exceeds the amount of force needed to force melt a single helix (approximately 65 pN at room temperature (46)) times the number of helices in a crystal (for 4-bit sequences, n = 28), scission should occur.
(28). If this tension exceeds the amount of force needed to force melt a single helix (approximately 65 pN at room temperature (46)) times the number of helices in a crystal (for 4-bit sequences, n = 28), scission should occur.
Imaging.
AFM imaging was performed on a Veeco Multimode AFM scanner with Nanoscope IIIa controller at room temperature in buffer on a mica substrate. To ensure that the crystals did not grow at room temperature, samples were prepared for imaging in a temperature-controlled glove box. “Guard strands,” which removed unbound sticky end strands from tiles, were added to the samples to prevent crystal growth during imaging. The samples were then cooled to room temperature and imaged over several hours. Controls in which guard strands were not added before imaging suggest that these strands did not significantly affect the shape of seeded crystals during the imaging process.
Detailed descriptions of experiment design, protocols and analysis as well as a list of all DNA sequences are included in SI Appendix, Supplemental Methods.
Supplementary Material
ACKNOWLEDGMENTS.
The authors thank Graham Cairns-Smith, Rizal Hariadi, Andrew Ellington, Andrew Turberfield, Damien Woods, and Paul Rothemund for discussion and suggestions. The authors acknowledge grants from the Miller Institute of Basic Science to R.S. and National Aeronautics and Space Administration Astrobiology Grant NNG06GA50 and National Science Foundation CCF: “The Molecular Programming Project,” Grant 0832824 to E.W.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1117813109/-/DCSupplemental.
References
- 1.Paul N, Joyce GF. Minimal self-replicating systems. Curr Opin Chem Biol. 2004;8:634–639. doi: 10.1016/j.cbpa.2004.09.005. [DOI] [PubMed] [Google Scholar]
- 2.Vidonne A, Philp D. Making molecules make themselves: The chemistry of artificial replicators. Eur J Org Chem. 2009;2009:593–610. [Google Scholar]
- 3.Rubinov B, Wagner N, Rapaport H, Ashkenasy G. Self-replicating amphiphilic β-sheet peptides. Angew Chem Int Ed. 2009;48:6683–6686. doi: 10.1002/anie.200902790. [DOI] [PubMed] [Google Scholar]
- 4.Lincoln TA, Joyce GF. Self-sustained replication of an RNA enzyme. Science. 2009;323:1229–1232. doi: 10.1126/science.1167856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Carnall JMA, et al. Mechanosensitive self-replication driven by self-organization. Science. 2010;327:1502–1506. doi: 10.1126/science.1182767. [DOI] [PubMed] [Google Scholar]
- 6.Rasmussen S, et al. Transitions from nonliving to living matter. Science. 2004;303:963–965. doi: 10.1126/science.1093669. [DOI] [PubMed] [Google Scholar]
- 7.Johnston WK, Unrau PJ, Lawrence MS, Glasner ME, Bartel DP. RNA-catalyzed RNA polymerization: Accurate and general RNA-templated primer extension. Science. 2001;292:1319–1325. doi: 10.1126/science.1060786. [DOI] [PubMed] [Google Scholar]
- 8.Wochner A, Attwater J, Coulson A, Holliger P. Ribozyme-catalyzed transcription of an active ribozyme. Science. 2011;332:209–212. doi: 10.1126/science.1200752. [DOI] [PubMed] [Google Scholar]
- 9.Deck C, Jauker M, Richert C. Efficient enzyme-free copying of all four nucleobases templated by immobilized RNA. Nat Chem. 2011;3:603–608. doi: 10.1038/nchem.1086. [DOI] [PubMed] [Google Scholar]
- 10.Schrum JP, Ricardo A, Krishnamurthy M, Blain JC, Szostak JW. Efficient and rapid template-directed nucleic acid copying using 2′-amino-2′,3′-dideoxyribonucleoside-5′-phosphorimidazolide monomers. J Am Chem Soc. 2009;131:14560–14570. doi: 10.1021/ja906557v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kervio E, Hochges A, Steiner UE, Richert C. Templating efficiency of naked DNA. Proc Natl Acad Sci USA. 2010;107:12074–12079. doi: 10.1073/pnas.0914872107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Scheel HJ, Fukuda T. Crystal Growth Technology. John Wiley and Sons; 2003. [Google Scholar]
- 13.Collins SR, Douglass A, Vale RD, Weissman JS. Mechanism of prion propagation: Amyloid growth occurs by monomer addition. PLoS Biol. 2004;2:e321. doi: 10.1371/journal.pbio.0020321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Viedma C. Chiral symmetry breaking during crystallization: Complete chiral purity induced by nonlinear autocatalysis and recycling. Phys Rev Lett. 2005;94:065504. doi: 10.1103/PhysRevLett.94.065504. [DOI] [PubMed] [Google Scholar]
- 15.Cairns-Smith AG. The origin of life and the nature of the primitive gene. J Theor Biol. 1966;10:53–88. doi: 10.1016/0022-5193(66)90178-0. [DOI] [PubMed] [Google Scholar]
- 16.Orgel LE, Crick FHC. Anticipating an RNA world. Some past speculations on the origin of life: Where are they today? FASEB J. 1993;7:238–239. doi: 10.1096/fasebj.7.1.7678564. [DOI] [PubMed] [Google Scholar]
- 17.Bullard T, Freudenthal J, Avagyan S, Kahr B. Test of Cairns-Smith’s crystals-as-genes hypothesis. Faraday Discuss. 2007;136:231–245. doi: 10.1039/b616612c. [DOI] [PubMed] [Google Scholar]
- 18.Winfree E, Liu F, Wenzler LA, Seeman NC. Design and self-assembly of two-dimensional DNA crystals. Nature. 1998;394:539–544. doi: 10.1038/28998. [DOI] [PubMed] [Google Scholar]
- 19.Barish RD, Schulman R, Rothemund PWK, Winfree E. An information-bearing seed for nucleating algorithmic self-assembly. Proc Natl Acad Sci USA. 2009;106:6054–6059. doi: 10.1073/pnas.0808736106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schulman R, Winfree E. Advances in Artificial Life, 8th European Conference. Vol. 3630. Berlin Heidelberg: Springer-Verlag; 2005. Self-replication and evolution of DNA crystals. [Google Scholar]
- 21.Mao C, LaBean TH, Reif JH, Seeman NC. Logical computation using algorithmic self-assembly of DNA triple-crossover molecules. Nature. 2000;407:493–496. doi: 10.1038/35035038. [DOI] [PubMed] [Google Scholar]
- 22.Rothemund PWK, Papadakis N, Winfree E. Algorithmic self-assembly of DNA Sierpinski triangles. PLoS Biology. 2004;2:e424–436. doi: 10.1371/journal.pbio.0020424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Winfree E, Bekbolatov R. Proofreading tile sets: Error-correction for algorithmic self-assembly. In: Chen J, Reif J, editors. DNA Computing 9. Vol. LNCS 2943. Berlin Heidelberg: Springer-Verlag; 2004. pp. 126–144. [Google Scholar]
- 24.Schulman R, Winfree E. Programmable control of nucleation for algorithmic self-assembly. SIAM J Comput. 2009;39:1581–1616. [Google Scholar]
- 25.Schulman R, Winfree E. Synthesis of crystals with a programmable kinetic barrier to nucleation. Proc Natl Acad Sci USA. 2007;104:15236–15241. doi: 10.1073/pnas.0701467104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rothemund PWK. Folding DNA to create nanoscale shapes and patterns. Nature. 2006;440:297–302. doi: 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
- 27.Eigen M, McCaskill J, Schuster P. Molecular quasi-species. J Phys Chem. 1988;92:6881–6891. [Google Scholar]
- 28.Hariadi R, Yurke B. Elongational-flow-induced scission of DNA nanotubes in laminar flow. Phys Rev E. 2010;82:046307. doi: 10.1103/PhysRevE.82.046307. [DOI] [PubMed] [Google Scholar]
- 29.Cloitre M, Mongruel A. Dynamics of non-Brownian rodlike particles in a nonuniform elongational flow. Phys Fluids. 1999;11:773–777. [Google Scholar]
- 30.Schulman R, Winfree E. How crystals that sense and respond to their environments could evolve. Nat Comp. 2008;7:219–237. [Google Scholar]
- 31.Knowles TPJ, et al. An analytical solution to the kinetics of breakable filament assembly. Science. 2009;326:1533–1537. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- 32.Seeman NC. Nanomaterials based on DNA. Ann Rev Biochem. 2010;79:65–87. doi: 10.1146/annurev-biochem-060308-102244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang DY, Yurke B. A DNA superstructure-based replicator without product inhibition. Natur Comp. 2006;5:183–202. [Google Scholar]
- 34.Chandran H, Gopalkrishnan N, Yurke B, Reif J. Meta-DNA: Synthetic biology via DNA nanostructures and hybridization reactions. J R Soc Interface. 2012 doi: 10.1098/rsif.2011.0819. rsif.2011.0819v1-rsif20110819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang T, et al. Self-replication of information-bearing nanoscale patterns. Nature. 2011;478:225–228. doi: 10.1038/nature10500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fujibayashi K, Hariadi R, Park SH, Winfree E, Murata S. Toward reliable algorithmic self-assembly of DNA tiles: a fixed-width cellular automaton pattern. Nano Lett. 2008;8:3554–3560. doi: 10.1021/nl0722830. [DOI] [PubMed] [Google Scholar]
- 37.Schulman R, Winfree E. Simple evolution of complex crystal species. In: Sakakibara Y, Yongli M, editors. DNA Computing 16. Vol. 6518. Berlin Heidelberg: Springer-Verlag; 2010. [Google Scholar]
- 38.Soloveichik D, Winfree E. Complexity of self-assembled shapes. SIAM J Comput. 2007;36:1544–1569. [Google Scholar]
- 39.Winfree E. Self-Healing Tile Sets. In: Chen J, Jonoska N, Rozenberg G, editors. Nanotechnology: Science and Computation. Berlin Heidelberg: Springer-Verlag; 2006. pp. 55–78. [Google Scholar]
- 40.Chen HL, Goel A, Winfree E, Luhrs C. Self-assembling tile systems that heal from small fragments. In: Garzon M, Yan H, editors. Preliminary Proceedings of DNA Computing 13. Vol. LNCS 4848. Berlin Heidelberg: Springer-Verlag; 2007. pp. 30–46. [Google Scholar]
- 41.Smalley RE, et al. Single wall carbon nanotube amplification: En route to a type-specific growth mechanism. J Am Chem Soc. 2006;128:15824–15829. doi: 10.1021/ja065767r. [DOI] [PubMed] [Google Scholar]
- 42.Li H, Carter JD, LaBean TH. Nanofabrication by DNA self-assembly. Mater Today. 2009;12:24–32. [Google Scholar]
- 43.Wang H, Brandl DW, Nordlander P, Halas NJ. Plasmonic nanostructures: Artificial molecules. Acc Chem Res. 2007;40:53–62. doi: 10.1021/ar0401045. [DOI] [PubMed] [Google Scholar]
- 44.Dutta PK, et al. DNA-directed artificial light-harvesting antenna. J Am Chem Soc. 2011;133:11985–11993. doi: 10.1021/ja1115138. [DOI] [PubMed] [Google Scholar]
- 45.Huppa JB, Davis MM. T-cell-antigen recognition and the immunological synapse. Nat Rev Immunol. 2003;3:973–983. doi: 10.1038/nri1245. [DOI] [PubMed] [Google Scholar]
- 46.Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.