Improving biodiversity conservation through modern portfolio theory

Conservationists must make hard choices about where to invest limited resources for the protection of biological diversity. Numerous prioritization schemes have identified places where biodiversity is especially rich or risks are especially urgent (1). Application of return on investment (ROI) thinking promises to make conservation investments much more efficient by explicitly incorporating economic costs alongside considerations of biodiversity (2–5). ROI approaches can also account for uncertainty but do not consider correlations that could increase exposure to risk (6). In PNAS, the work by Ando and Mallory (7) shows how modern portfolio theory (MPT), a standard financial tool, can be applied to prioritize conservation investments in a way that explicitly accounts for correlated uncertainty and risk–reward tradeoffs associated with the potential impacts of climate change.

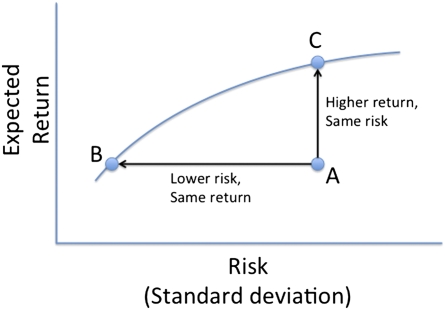
MPT (8, 9) is commonly used by financial managers to diversify investments and spread the risk within an investment portfolio. In addition to considering expected returns and standard deviations (risk) of individual investment options, MPT analyzes the covariance structure to limit aggregate risk to a portfolio of investments. A portfolio of investments that covary positively would be riskier than one comprised of investments that covary negatively, much as a metapopulation is more likely to go extinct if subpopulations vary synchronously (10). MPT enables an investor to quantify an efficient frontier along which returns are maximized for a given level of risk and risk is minimized for a given level of return. This frontier informs the allocation of investments that will yield a portfolio with the best possible balance between reward and risk. As economic conditions change, investments can be bought or sold to maintain a desired reward–risk balance (Fig. 1).

Fig. 1.

An efficient frontier for allocation of resources to optimize balance between reward and risk in an investment portfolio. The arc of the efficient frontier defines the maximum return that can be achieved for a given level of risk and the minimum level of risk that can accompany a given return for an optimized investment portfolio. The efficient frontier is determined by the expected returns, standard deviations, and covariance of available investment options. Asset allocation within an investment portfolio determines where the portfolio sits in relation to the efficient frontier. Investment portfolio A is inefficient, because portfolio B achieves the same return with lower risk, and portfolio C achieves higher return with the same risk. Future investments in portfolio A can be selected to move it closer to the efficient frontier and achieve an optimal balance between reward and risk. In PNAS, the work by Ando and Mallory (7) shows how this financial management tool can be applied to guide investments for conservation of biological diversity.

The work by Ando and Mallory (7) adapts MPT to evaluate priorities for conservation investment in the Northern Prairie Potholes region of North America, a vital breeding habitat for waterfowl. In their example, conservation investments can be made in three subregions that vary in terms of habitat quality (their measure of conservation return) and cost. Future habitat quality could change under different climate change scenarios, and therefore, there is also some risk to those investments determined by the assumed likelihood of climate change and the correlated variability that it introduces into expected future habitat quality. Along the efficient frontier, the optimal allocation of investment in each of the three subregions shifts depending on whether the desired return–risk tradeoffs favor higher returns or lower risk (7).

Even with this simple formulation, using MPT to explicitly balance tradeoffs between reward and risk can substantially improve the performance of conservation investments. Comparing the current allocation of conservation investments with the efficient frontier reveals that returns could be increased by 6% for the same level of risk or risks could be decreased by 21% for the same level of expected returns across the Northern Prairie Potholes region (7). Subsequent conservation investments can be allocated to subregions that move the portfolio closer to the efficient frontier. Deliberate resource allocation informed by MPT also performs dramatically better than simplistic bet hedging that spreads investments evenly among the subregions (7).

Conservationists, and those individuals who support them, should be eager to adapt MPT to inform more strategic investments. Biodiversity conservation has many parallels to investment portfolio management. Both aim to achieve high returns with low risk. There are many investment options from which to choose, each with a different reward–risk profile. Changing climate and other uncertainties create investment risks that may be correlated and so affect aggregate risk exposure of the investment portfolio.

MPT offers a quantitative way to choose conservation investments so that the portfolio makes the preferred tradeoff of reward versus risk (7). The efficient frontier explicitly defines the relationship between potential reward and risk, and it provides a benchmark against which the performance of a conservation portfolio can be measured. MPT can also help to rebalance the reward–risk tradeoffs in a portfolio as new investments are made. What is optimal today may not be optimal in the future as conditions change. As uncertainties about future conditions are resolved or as expectations about future risks such as climate change are revised, priorities for conservation investment can be updated to keep the overall portfolio close to the efficient frontier. This adaptability contrasts with conventional conservation planning that uses optimization algorithms to define a fixed set of conservation priorities based on a static view of where biodiversity is distributed in relation to threats (11–13).

MPT can help conservationists make smarter investments of limited resources. MPT has been applied to fisheries management (14) and reforestation (15), and it should be suitable for a wide array of conservation investment decisions for which expected returns and risks vary. However, a caution is warranted; underestimating risks can have significant and severe consequences should unexpected events come to pass (16). Thus, adapting MPT will depend on our ability to assess conservation risks as accurately as possible.