Assessing the contribution of cell body and intracellular organelles to the backward light scattering

Abstract

We report a method of assessing the contribution of whole cell body and its nucleus to the clinically most relevant backward light scattering. We first construct an experimental system that can measure forward scattering and use the system to precisely extract the optical properties of a specimen such as the refractive index contrast, size distribution, and their density. A system that can simultaneously detect the backscattered light is installed to collect the backscattering for the same specimen. By comparing the measured backscattering spectrum with that estimated from the parameters determined by the forward scattering experiment, the contribution of cell body and nucleus to the backward light scattering is quantitatively assessed. For the HeLa cells in suspension, we found that the cell body contributes less than 10% and cell nucleus on the order of 0.1% to the total backscattering signal. Quantitative determination of the origin of backscattered light may help design a system that aims for detecting particular structure of biological tissues.

1. Introduction

Light scattering spectroscopy has emerged as a valuable tool for cancer diagnosis over the past ten years. Morphological information, critical to disease diagnoses, has been extracted from both angle and wavelength-dependent light scattering distributions based on simplified cell models. Light scattered from the cellular structures provides information about the morphological changes accompanying early stage malignancy. The virtue of this technique lies in the ability to extract key morphological information such as size distributions of nucleus and submicron-sized particles with minimal data acquisition, mainly due to model-based data analysis [1–11]. These studies have dealt with the basic morphology and biochemistry of normal and cancerous cells [1–3,6,7,9,10,12], animal models of cancer development [5,8] and human tissue studies in laboratory and clinical settings [1,4,11]. The validity of the extracted information, however, tends to be highly dependent on the accuracy of the cell/tissue scattering models, which typically poses constraints on the specimen under study. Hence, the sensitivity of the method for different models can hamper its usefulness for basic cell research and its clinical applications.

In our previous works, we assessed clinical usability of the model-based light scattering in the monolayers of cells, tissue models and fully intact tissues samples [5,11,13]. In these studies, scattered light from tissue sample is collected in the reflection geometry. Whether the outcome is clinically relevant or not depended heavily on the assumption of the sub-cellular origin of scatterers being either nuclei [11,13], or small particles [13] or continuous refractive index variations [5]. In the most recent study, we identified sub-cellular origins of light scattering from a single cell [14]. Unlike the previous studies, forward scattered light is collected in this experiment using previously developed tomographic phase microscopy [15]. The single cell study allowed for accurate identification of the contributions of various sub-cellular structures (such as whole cell body, nucleus and nucleolus) due to simplicity of the sample and dominant contributions of larger-than-wavelength structures to the forward scattering [14].

In the present work, we take advantage of the forward scattering experiment to guide the multi-cellular study in the backscattering. Specifically, forward scattering measurement capability is added to the light scattering instrument previously developed for the tissue studies [5]. According to Mie theory and the single cell study [14], whole cell body dominantly contributes to the forward light scattering and can be well modeled as a spherical particle. Based on this, the measured forward scattering distribution from a population of cells in suspension is analyzed using Mie theory [16], and size distribution and refractive index contrast of cell body to the medium are extracted. The extracted parameters are validated by an additional control experiment in which the refractive index-matching protein solution is used to reduce refractive index contrast of the specimen by known amount. Once parameters for the population of the cells are determined, they are used to estimate the scattering contribution of cellular body to the backscattering. For the same specimen, we experimentally measure the backscattering distribution and found that the measured signal is ten times higher than the estimation from the parameters measured by forward scattering experiment. This strongly suggests that backscattering by cell body contributes to only 10% of the total scattering. For the cell nucleus, we use the refractive index and size measured from single cell study to assess its contribution to the backscattering. It turns out that the scattering from nucleus accounts for only 0.1% of the total scattering. Our method of simultaneous detection of forward and backward light scattering provides a means of quantitatively assessing the contribution of large particles to the backward light scattering.

2. Optimize light scattering instrument based on Mie theory

Conventional light scattering systems [1,2,10,17,18] measure intensity of the scattered light either as a function of wavelength at a fixed scattering angle or as a function of angle for a fixed wavelength. Mie theory for spherical particles can be used for optimizing detection and interpretation of the scattering from the various structures [13,16] to the extent that objects of interest behave like homogeneous spheres. In our previous publication, we have shown that variations in angular intensity of the forwardly scattered light from the cell body and intracellular organelles, such as nucleus and nucleolus, can be modeled by Mie theory [14]. Previous version of our conventional light scattering instrument was designed to collect wavelength spectra at the clinically most suitable exact backscattering direction (reverse of the illumination direction) [5].

In the current study, we optimized the collection angle of our system to be suitable for the detection of the particles larger than wavelength (whole cells and cell nuclei) based on Mie theory. For that purpose, we calculated differential scattering cross-sections,σ, of the 5 um diameter sphere and 50 nm diameter spheres (Fig. 1 ). Differential scattering cross-section indicates the probability of the photon scattering into the unit solid angle into specified direction and is directly proportional to the ratio of incident and scattered light intensities measured in the conventional scattering experiments [16]. The calculated results are presented on the Fourier plane on which light scattered at the same angle from various points of the sample converges to the same point [19]. Three pairs of Fourier plane angular maps σ(0<θ<10 or 170<θ<180, 0<φ<360, λ = 550nm, n_o = 1.337 (media refractive index), n = 1.4 (particle refractive index)) covers most of our detection range of interest in scattering angle. The forward (0°) and the backward (180°) scattering angles θ are defined with the respect to the propagation direction of incident light. The variation of the differential scattering cross-section as a function of scattering angle θ is plotted for the total angular range of ten degrees from exact forward or exact backward scattering directions. The wavelength of the incident light is fixed, and azimuthal scattering angle φ is varied between 0° and 360°. Backscattering parallel (σ_II) and perpendicular (σ_⊥) differential cross-sections are defined with respect to linear polarizer orientation on the scattered beam parallel and perpendicular to the incident beam polarization, respectively. Calculated forward scattering is presented on a log scale, while the calculated backscattering is shown on a linear scale. Brighter areas have a higher differential scattering cross-section than the darker areas relative to a specific image color bar.

Fig. 1.

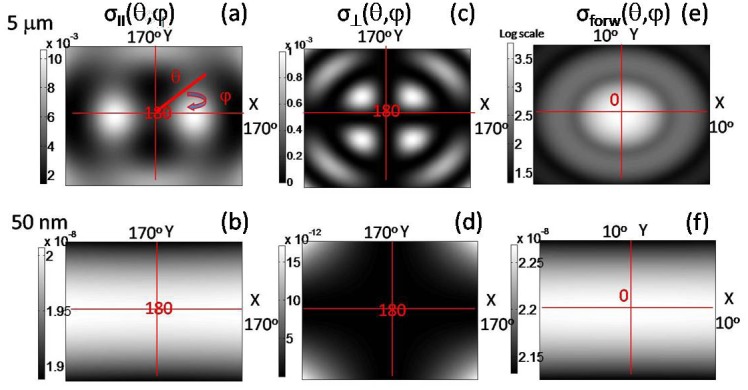
Polar plots of differential scattering cross-section σ as a function of scattering angles θ and φ (Mie simulation). Color bar is the magnitude of the differential cross-section in μm²/sr. Origin of the maps is either 0° (forward scattering) or 180° (backscattering). Top row for 5 μm-size particle. Bottom row for 50 nm-size particle. (a,b) Backscattering parallel cross-section. (c,d) Backscattering perpendicular cross-section. (e,f) Forward scattering cross-section.

Absolute and relative amplitude of differential scattering cross-sections can be compared for different particle size and polarization. In and near forward scattering direction (Fig. 1(e)), the absolute maximum of the large particle scattering cross-section (σ_forw,5um≅10³ µm²/sr) along with the greatest contrast between larger and smaller signals (~10⁻¹¹:1, σ_forw,50nm/σ_forw,5um) is achieved (compare Figs. 1(e) and 1(f)). Backscattering parallel has the strongest overall contribution of small particles relative to the large ones according to the amplitude scale (~10⁻⁶:1, σ_⊥,50nm/σ_⊥,5um). Backscattering perpendicular has the smallest absolute amplitude for a large particle cross-section (10⁻³, σ_⊥ vs. 10⁻², σ_II vs. 10³, σ_forw), but smaller relative contribution of small particle, than backscattering parallel (~10⁻⁸:1, σ_⊥,50nm/σ_⊥,5um). Thus, at least within the boundaries of the spherical particle model the forward scattering is most suited for the detection of large sub-cellular structures.

We designed our light scattering instrument with two-fold goal in mind (Fig. 2 ). It is optimized for the detection of large subcellular organelles as well as it can collect the clinically relevant backscattering light. We optimized our previous system [5] by setting proper beam diameter and divergence so as to maximize light energy delivery to the sample and maintain sufficient angular resolution at the same time. The beam diameter was set to 5 mm and divergence was set to 0.45 degrees half-angle. The incident beam travels on the two different paths to deliver incident light from above the sample (for backscattering measurements) and below the sample (for forward scattering measurements). The angular distribution of the scattered light is created on the focal plane of Fourier lens while sample is positioned in the other focal plane of the Fourier lens [19]. The angular distribution is imaged onto the surface of the coherent fiber bundle. The rotation of the output of the fiber bundle causes rotation of the Fourier plane image on a spectrograph entrance slit.

Fig. 2.

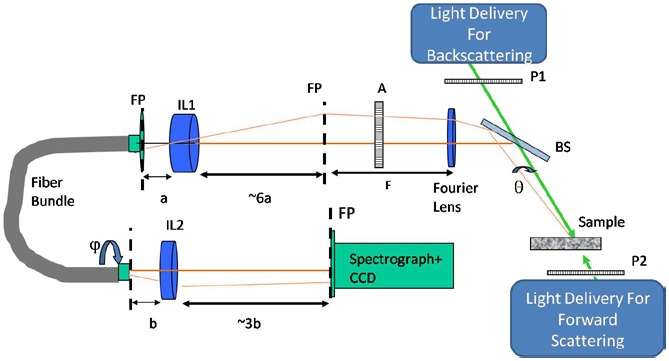
Light scattering instrument. System components: P1, P2 incident beam polarizers, BS-beam splitter, A – analyzer, FP – Fourier plane, F-focal distance of Fourier Lens, IL1 and IL2 – imaging lenses with focal distances of a and b. Traces of the incident light are shown in green. Brown and light brown traces belong to scattered light at 0°, 180° and at θ degrees away from them.

The Fourier plane is aligned in such a way that a range of radial scattering angles θ simultaneously imaged on the spectrograph slit corresponds to the same value of the azimuthal angle φ. Light passing through the spectrograph slit is dispersed into its spectral components. Two-dimensional CCD detector (512 × 512 pixels, 25 μm² area per pixel, Princeton Instruments) is placed on the output of the spectrograph (10 mm slit height, 10 μm - 3 mm adjustable slit width, Acton Pro SP150, Princeton Instruments) registering scattering intensity as a function of scattering wavelength λ and scattering angle θ for the fixed value of azimuthal scattering angle φ. The range of collected wavelengths is 430-710 nm. The range of the scattering angle θ is between 180°-169.8° for backscattering and 1.2°-10.4° in forward scattering, while φ = 90° degrees. The collected range in forward scattering is reduced due to a small beam stop placed in the first Fourier plane to prevent incident light from reaching the detector. The beam stop is removed for the backscattering measurements.

Given the Mie scattering predictions, large cellular structures will dominate scattering in the forward direction. Therefore, we measure forward scattering of a suspension of single cells and use Mie theory to extract their whole cell size distribution and average refractive index contrast. Thereafter, we use this information to predict the contribution of the cell body and large intracellular particles to backscattering.

3. Forward scattering from ensemble of HeLa cells

3.1 Cell sample selection and preparation

Single cell suspensions are used in the number of conventional light scattering studies [1–3,6,9,10,12]. The Mie theory will stay valid for an ensemble of scatterers only if these scatterers are independent. In our study, we used human cell line – HeLa cervical cancer cell line [20]. This cell line was also previously used in light scattering studies [12,21]. HeLa cell suspension had shown significantly smaller degree of cell aggregation compare to other cell types we have tried in our experiment, and linear change of scattering intensity was observed with the concentration of cells.

HeLa cells were grown in the high-glucose Dulbecco's modified Eagle medium supplemented with 10% fetal calf serum, 5% penicillin and streptomycin mixture (all products from Gibco, Invitrogen Corp.). Cells were incubated in 75 cm² and 25 cm² culture flask (Falcon) at 37° C in a humidified atmosphere of 5% CO₂ in the air. Cells were passaged upon reaching confluency (fully grown single layer of cells), which happened every 3 days. Trypsin at 0.25% mixed with EDTA (Gibco, Invitrogen Corp.) was used to remove cells from substrate and break inter-cellular junctions.

For light scattering measurements, trypsinized cell medium was replaced through 3-cycle centrifugation and rinsing with optically clear Hanks Balanced Salt Solution (HBSS) or Phosphate Buffer Solution (PBS from Gibco, Invitrogen Corp.). A small volume of cell suspension (~90μl) was placed between two #1 glass coverslips (Electron Microscopy Sciences) separated by double-sided adhesive insert (0.5 mm thick, GraceBio-Labs Inc.). Two centimeter diameter opening of an insert allowed for clear transmission of light (5 × 7 mm² excitation area), and the coverslips were optically transparent in the visible range of wavelengths. Due to the double adhesive layers, there was no de-hydration of the sample during the experiment. The sample was immediately transferred to the experimental system for the scattering measurements. Adhesive insert geometry allowed microscopic evaluation of the sample before and/or after the light scattering experiment.

3.2 Experimental measurements of forward scattering

The phase contrast image and normalized forward scattering measurement from a suspension of HeLa cells are presented in Fig. 3 . The experimental data were collected in 200 ms. Background measurement was taken only for the cell media. Systematic variations in the instrument response and the source spectral profile were taken into account by measuring the 99% reflectance standard (R99, Labsphere Inc.), which has a flat response in wavelength and almost Lambertian uniform behavior in angle. The difference between collected sample and background signal is normalized to the reflectance standard measurement. The normalized signal is presented with respect to the reflectance standard intensity measured for the same amount of time in 1/R99 units. The color of the image corresponds to variation of the scattering cross-section.

Fig. 3.

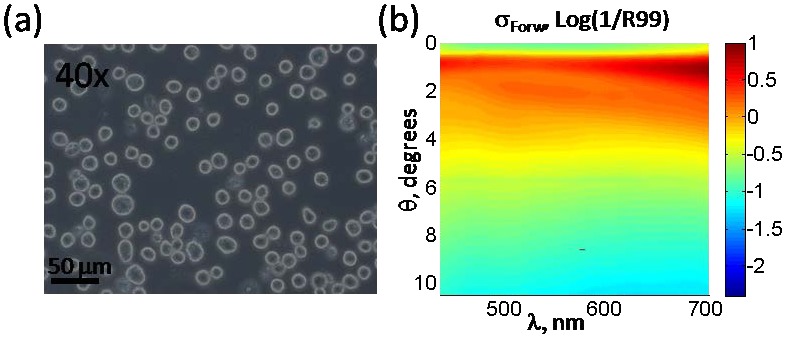
(a) Phase contrast image of HeLa cells at 40x magnification. (b) Light scattering measurements normalized in wavelength λ and angle θ. Color bar is in 1/R99 units.

In our single sell study, several oscillatory periods were observed [14] in the forward scattering of the single cell. The forward scattering spectrum of a large population of cells in suspension is rather smooth due to overlap of the scattering from cells of various sizes. Therefore we focused on the prominent oscillatory feature near two degrees from the exact forward scattering. Three wavelength spectra at fixed angles of 1.34°, 2.14° and 2.95° and three angular spectra at fixed wavelengths of 450, 550 and 633 nm were analyzed using look-up-table approach. In detail, the 4-D look-up-table of differential scattering cross-section values was created using Mie theory. The scattering cross-section σ was calculated as a function of the sphere diameter d, from 5 to 30 μm in 0.01 μm steps, for the wavelengths λ from 375 to 750 nm in 15 nm steps, and the scattering angles ranging from 0° to 15° in 0.5° steps. The range of the relative refractive index m (m = n/n_o, where n_o = 1.36) was from 1.01 to 1.05 in 0.001 steps. The steps in angle and wavelength were chosen so as not to affect the resultant spectra after convolution with the angular and spectral response of the system (0.45° and 20 nm). Three parameters were varied in least-square minimization of the Mie theory prediction to the experimental data: size d (5:0.1:30 μm), relative refractive index m (1.01:0.001:1.05) and width of the size distribution std (0.1:0.1:3.5 μm), assuming a single Gaussian shape. For the fitting, the wavelength experimental data were mean-centered, and the shapes at three angles were analyzed for best simultaneous match to Mie theory. The values of the parameters, that minimized the difference between experimental data and Mie theory for the three wavelength spectra were d = 16, std = 1.6 μm and m = 1.027 (Fig. 4(a) ). Thereafter, the same parameters were used to generate angular scattering distribution by Mie theory (Fig. 4(b)). The excellent agreement between the experimental data and Mie theory for both angular and wavelength spectra validates the accuracy of our experimental system and the accuracy of relative refractive index determination.

Fig. 4.

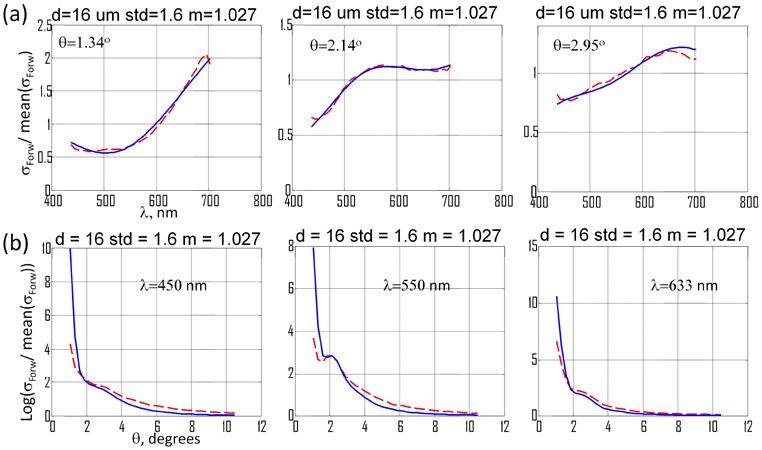
Results of fitting experimental data to Mie theory. Scattering measurements and Mie theory are mean-centered. (a) Wavelength spectrum measurements (blue) at fixed scattering angles with fits to Mie theory (red). (b) Angular spectrum measurements (blue) at fixed wavelengths with fits to Mie theory (red).

The relative refractive index contrast of 1.027 was comparable to 1.02 value extracted in the single cell study of HT29 cell [14]. The difference in relative refractive index values can be attributed to the difference in the cell types. According to the Mie theory, light scattering is a function of a size parameter, which is proportional to the ratio of particle diameter to the wavelength of the scattered light [16]. The refractive index of the culture medium in the experimental data is 1.337 while the look-up-table calculated by Mie theory was generated assuming that refractive index of the medium is 1.36. In order to account for this difference, the mean diameter of 16 μm determined from Mie theory analysis of the experimental data was calibrated to the value of 16.3 μm. This was done by preserving the size parameter for the different indices of media. Size distribution of the cells in the sample was estimated from morphometrical analysis of phase contrast images. The sizes for the 109 cells, which is about 5% of the total number of cells, were measured and, the mean diameter and the standard deviation were determined to be d = 15.7 µm and std = 2.4 µm, respectively. The next largest structure in the cell is cell nucleus, which is only about 70% of the whole cell diameter as can be determined from our single cell studies [14,15]. The morphological measurement confirms that structure responsible for forward cell scattering is on the order of the size of the whole cell. Therefore, according to the model-based analysis of the forward scattering data, a major feature of the signal is related to cell-media interface and can be fitted to Mie theory with a single Gaussian distribution of the whole cell sizes and an average relative index contrast value for the whole cell.

3.3 Experimental validation of the cell border contribution to the scattering signal

Although the forward scattering Mie analysis for the cells in suspension is in good agreement with the results of our single cell study, we intended to confirm that extracted scattering information is related to the whole-cell scattering. In the single cell study [14], we were able to directly manipulate refractive index space of the sample and media to obtain contributions of the cellular components. The same experimental approach was used to determine whether the scattering signals are indeed coming from the cell border. Cell media was mixed with a higher refractive index substance, bovine serum albumin (BSA), which is a purified protein fraction and has been previously used to match the refractive index of cell cytoplasm [22,23]. BSA was added to the cell suspension until the cell border contrast is visibly diminished in phase microscopy images (Fig. 5(a) vs. 5(b)). As a consequence, this also highlighted the internal structures of the cells.

Fig. 5.

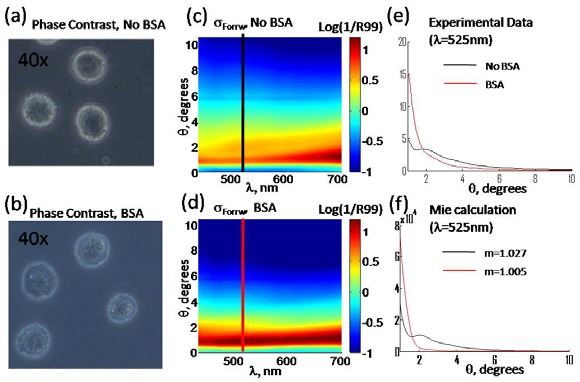
Phase contrast image of HeLa cells in regular culture media (a) and in the media containing BSA (b). Measured forward light scattering distribution in culture media (c) and in BSA solution (d). Angular light scattering distribution for BSA and no-BSA samples from the measurement (e) and Mie theory (f).

The refractive index change could be precisely estimated from the amount of BSA being added [22]. The relative refractive index between cell border and media dropped from 1.027 to 1.005. In the light scattering measurements, drop of the refractive index caused elimination of the oscillatory feature around 2° (Fig. 5(c) vs. 5(d)). The observed disappearance of the oscillatory feature in the experimental data was accurately described by the Mie theory using the new value of the refractive index of the media (Fig. 5(e) vs. 5(f)). The reduced refractive index contrast between the cell border and the media causes the reduction in oscillation amplitude of the angular spectrum for individual cells. This results in a disappearance of the oscillation. Agreement between experimental data and Mie theory confirms that the parameters measured at Section 3.2 correspond to those of the whole cell body. It can be noticed that experimental data have a slower drop-off in the scattering spectrum than Mie theory (compare red spectra on Fig. 5(e) vs. 5(f)). As the cell border contribution is attenuated due to the refractive index matching, the contribution of the other sub-cellular scatterers becomes more pronounced.

4. The contribution of large cellular components on the backscattering

We used the results of the forward scattering analysis to predict contribution of the whole cell to the scattering signal in the clinically relevant backscattering direction [24,25]. We also combine results of the single cell studies [14,15] and forward scattering to predict cell nuclei portion of the backscattering signal. According to Mie theory predictions in section 2, small structures will have the larger contribution to the scattering signal in the backscattering, especially in the co-polarized geometry. Their contribution can only be estimated based on empirical assumptions about the origin of the signals, thus will be sensitive to the specific model used [2,5]. In this experiment we chose not to analyze small cellular structures’ contribution to backscattering but to simply compare the amplitudes of the observed backscattering signal with the expected scattering from the whole cell derived from the forward scattering experiments and from the nucleus derived from our previous single cell studies [14,15].

In order to do the comparison accurately, the conversion factor was needed between measured differential scattering cross-section in detector counts (or normalized units) and Mie scattering cross-section values. Measured differential scattering cross-section from the suspension of 10 μm polystyrene beads (Polysciences Inc.) was compared to Mie theory prediction. A conversion factor was calculated between Mie theory and the experimental data through the following equation: ρ_conversion × σ_Data(d = 10μm)/R99_units = N_beads × SizeDistrib_Mie(d = 10 μm) × σ_Mie(d = 10 μm). Area under the size distribution for Mie theory was normalized to one, and it was scaled up by the bead number density N_beads in a beam area. The bead’s density was determined from the direct observation of the small sub-volumes under microscope. Same stock of 10 μm beads was used for calibration of backscattering and forward scattering amplitude. The conversion factor was 4 × 10⁷ for forward scattering measurements and 4 × 10⁶ for backscattering, respectively. The correction factor was checked with the suspension of the 50 nm beads (Polysciences Inc.), in which good agreement was achieved between experimental data and Mie theory prediction in shape and amplitude. The determined number of particles was 1.05 × 10¹⁰ from the experimental data and 1.25 × 10¹⁰ from the manufacturer specifications.

In the HeLa cell experiment, backscattering data were collected immediately following the forward scattering measurements (Fig. 6(a) ). Backscattering experimental data were collected in 30 seconds. The overall signal was featureless in angle with the monotonous decay towards longer wavelengths. That type of behavior is characteristic of the small structure scattering [2,5,13]. Whole cell size distribution with d = 16 and std = 1.6 μm, and refractive index contrast of m = 1.027 were used for the Mie theory prediction of the whole cell signal in backscattering (Fig. 6(b)). The maximum predicted signal is at 180° backscattering, but the normalization and background correction at this angle are the most complicated and prone to error. The experimental data at exact backscattering have a dip, while the prediction signal peaks. Therefore, predicted and measured backscattering wavelength spectra were compared at 178°, which are dashed and solid lines, respectively, in Fig. 6(c). At this angle, predicted signal had shown much lower absolute amplitude than measured backscattering signal. To quantify comparison, the signals were averaged over the observed range of wavelengths. In addition to co-polarized geometry, cross-polarized geometry was also measured. The comparisons of the mean amplitudes of measured and predicted scattering signals are summarized in Table 1 .

Fig. 6.

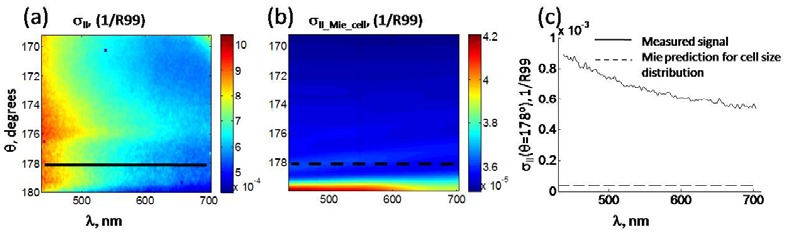
(a) Measured backscattering cross-section of the HeLa cells in suspension. (b) Calculated backscattering cross-section for the whole cell body. Both intensities are in 1/R99 units. (c) Comparison of the cross-sections at θ = 178°.

Table 1. Comparing Observed Backscattering Intensity and Predicted Whole Cell and Nucleus Signal^a .

Backscattering mode	Backscattering experimental data, 1/R99 units	Cell scattering, Mie prediction 1/R99 units	Nuclear scattering, Mie prediction, 1/R99 units
σII(θ = 178°)	6.7 × 10−4	3.8 × 10−5	3.6 × 10−7
σ⊥(θ = 178°)	6.8 × 10−5	3.8 × 10−5	9.4 × 10−11

^aThe signals are averaged over wavelength.

The observed mean backscattering intensity was more than an order of magnitude higher than the predicted signal for the whole cell. Although, explicitly the nuclear scattering signal was not obtained in the measurements, its amplitude could be estimated based on correlative measurements. In the single cell studies, we measured 3D refractive index map of the single live cells such as HeLa cell and HT29 cell using tomographic phase microscopy [14,15]. Since the average index of cell cytoplasm and nucleus are different, cell nucleus is clearly resolved in the refractive index tomogram. Therefore, the size and average refractive index of cell nucleus were deterministically calculated from the measured tomogram. Based on the results of the single cell work, nuclear size distribution can be estimated from whole cell size distribution using the relative size of nucleus to the whole cell. Assuming the same nucleus to whole cell ratio of 0.70 as in the single cell studies [14,15], the mean nuclear size for HeLa cell suspension becomes d_nuclei = 11 μm. The width of the nuclear size distribution will be similar to cell width distribution, i.e. 10% of the mean diameter, with std = 1.1 μm. Also, we assumed similar refractive index correlation between whole cell in HeLa and HeLa cell nucleus, as it was for HT29 and HeLa cell in the single cell experiments [14,15], m = 1.01. Based on these assumptions, the nuclear boundary scattering signal was predicted for our system (Table 1). As can be seen from the table, the nuclear boundary signal was at least three orders of magnitude lower than observed backscattering signal (see Table 1).

From this experiment, we found that light scattering from cell body contributes below 10% to the observed backscattering signal, and furthermore light scattering from cell nucleus contributes only 0.1%. The rest of the signal represents other, smaller cellular structure scattering. There are two limitations to extracting nuclear scattering signatures on such a large background: system sensitivity and modeling of a background signal. The shot noise will represent a fundamental limit of system sensitivity to target signal. Even in the case, when system is theoretically sensitive enough, small variations of the background signal can significantly affect the correct extraction of the nuclear signal.

5. Summary and conclusion

In summary, we develop a comprehensive method that connects forward light scattering and backscattering experiments to evaluate the contribution of cell body and cell nucleus to the backscattering. Since the forward light scattering experiment is sensitive to the light scattering from large particles, it was used to determine the scattering parameters of the cell body. The validity of the extracted parameters was confirmed by the additional experiment in which refractive index of culture medium was matched to the index of the cytoplasm. For the cell nucleus, scattering parameters were extracted from the 3D map of refractive index imaged by the tomographic phase microscopy. By introducing a calibration measurement that connects the light scattering signal between forward and backward scattering experiments, we could use the scattering parameters of the cell body and cell nucleus to estimate their contribution to the backscattering. Our study suggests the required level of signal-to-noise ratio for the detection of backscattering from the cell body and cell nucleus, and may serve as a guide for designing experimental system for the clinical studies.