Quantification of the hydrophobic interaction by simulations of the aggregation of small hydrophobic solutes in water

Abstract

The hydrophobic interaction, the tendency for nonpolar molecules to aggregate in solution, is a major driving force in biology. In a direct approach to the physical basis of the hydrophobic effect, nanosecond molecular dynamics simulations were performed on increasing numbers of hydrocarbon solute molecules in water-filled boxes of different sizes. The intermittent formation of solute clusters gives a free energy that is proportional to the loss in exposed molecular surface area with a constant of proportionality of 45 ± 6 cal/mol⋅Ų. The molecular surface area is the envelope of the solute cluster that is impenetrable by solvent and is somewhat smaller than the more traditional solvent-accessible surface area, which is the area transcribed by the radius of a solvent molecule rolled over the surface of the cluster. When we apply a factor relating molecular surface area to solvent-accessible surface area, we obtain 24 cal/mol⋅Ų. Ours is the first direct calculation, to our knowledge, of the hydrophobic interaction from molecular dynamics simulations; the excellent qualitative and quantitative agreement with experiment proves that simple van der Waals interactions and atomic point-charge electrostatics account for the most important driving force in biology.

The hydrophobic effect is the most important force in stabilizing biological structures ranging from native conformations of proteins to cellular membranes. The origin of this effect has been the topic of much investigation, both experimental and theoretical. Solvent transfer experiments show that for a wide range of different hydrocarbon molecules, the hydrophobic interaction energy depends linearly on the burial of solvent accessible surface area with a constant of proportionality around 25 cal/mol⋅Ų (1–4). Data from calorimetric studies indicate that around room temperature, the hydrophobic effect is primarily entropy driven (5). Both of these results indicate that the interaction must be short-range and must depend on a shell of water molecules. The entropy effect is attributed to the solute imparting additional structure to the surrounding shell waters and reducing their entropy relative to the bulk solvent (6). Unfortunately, these macroscopic studies do little to shed light on our understanding of the detailed microscopic solute–solvent interactions that drive the hydrophobic effect.

Although the microscopic details cannot be distinguished by experiment, theoretical studies are ideal for modeling atomic-level interactions, and a great deal of our understanding of the hydrophobic effect has come from theoretical studies. Classically, there are two aspects to the hydrophobic effect. The first is termed hydrophobic hydration and concerns the effects of the solute on the surrounding water molecules. The second aspect is often referred to as the hydrophobic interaction, the tendency for nonpolar molecules to associate in water. This second aspect is the focus of the present study.

A common theoretical treatment of the hydrophobic interaction has been to study the association of simple hydrophobic solutes (typically Lennard–Jones spheres or methane) in infinitely dilute water solution. Most of these simulation studies show no tendency for the aggregation of the solute molecules, favoring instead the solvent-separated pair (7–12). These results are in contrast to the “bulk” hydrophobic interaction measured experimentally by solvent transfer, which clearly favors association (1–4). Other simulations, however, do show a more favorable contact pair (13). These conflicting theoretical results have been attributed to differences in the structure (14) and polarizability (15) of the water model used. Simulations at increased temperature typically show an increased tendency to aggregate (12, 16), mirroring experimental evidence that the hydrophobic effect increases with temperature (17).

One limitation of the above studies is that they contain relatively few solute molecules (typically two or four). Indeed, it has been argued that the formation of stable clusters may be cooperative and thus would require more solute molecules (9). In simulations of 18 methane-like molecules, Wallqvist observed not only aggregation but also phase separation (18, 19). There must, however, be a regime where the formation of hydrophobic clusters of intermediate size is accessible for study. Previously, our group used molecular dynamics (MD) simulations to study hydrophobic clusters on the order of the size of the cores of small proteins (20). In the present study, we have expanded this method to quantify the energetics of cluster formation.

Materials and Methods

MD Simulations.

MD simulations were performed by using the program encad (M. Levitt, Stanford, CA), by using an NVE ensemble (constant number of molecules in the box, volume, and energy). The solute types used were methane, butane, isobutylene, and benzene. MD simulations were run for 1 ns at 298 K in explicit solvent under periodic boundary conditions and by using a 2-fs time step. A fully flexible three-centered water model and all-atom representations of the solute molecules were used. The number of solute molecules in the box ranged from 1 to 112, depending on the solute type. Four box sizes were used: the canonical box containing 216 water molecules and boxes two, four, or eight times larger (volumes from 6,500 to 52,000 ų containing 204–1,726 water molecules, with solute concentrations from 0.03 to 3.5 M). The solute molecules were initially spaced on a regular grid and placed in a periodic water box. Overlapping water molecules were removed, and the box volume was adjusted to the proper density. The solvent density was 0.997 g ml⁻¹, and the densities of the solutes were the densities of the pure liquids at room temperature (21). The exception was methane, and its density was set to the density of liquid methane at its boiling point. The entire system was equilibrated by energy minimization and dynamics, and then dynamics were run for 1 ns, with coordinates output every 0.5 ps. Three simulations that differed only in the random number seed used to assign the initial velocities were run for each number of solutes in the smallest box size. A single simulation was performed for each number of solutes in the larger box sizes.

Determination of Clustering and Molecular Surface Areas.

Solute clusters were determined explicitly by using a method based on calculating a Voronoi polyhedron around each atom. This method, which has been described previously (22), divides the volume of the simulation box into volumes surrounding each atom center. The atomic volumes are determined by planes that bisect the vectors between two neighboring atoms. Contacts between molecules are determined exactly; atoms that share a face of a polyhedron are in contact. Furthermore, the areas of the faces of these polyhedra can be used to determine the total molecular surface area of each atom, as well as the amounts buried in a cluster or exposed to solvent. The Voronoi method also allows exact determination of hydration shell waters and is more accurate than those that use simple distance cutoffs to determine contacts. Solute clusters were determined for each output time step of each simulation, and total, solvent-exposed, and buried molecular surface areas were averaged for clusters of each size over the entire trajectory.

Results

Nonpolar Solutes Aggregate in Solution.

MD simulations were run on increasing numbers of small, nonpolar, solute molecules (methane, butane, isobutylene, and benzene) in water-filled boxes under periodic boundary conditions. Simulations were also run in water boxes with two, four, and eight times greater volume. This allowed us to compare the results of runs with a constant number of solute molecules in progressively larger volumes and runs at the same solute concentration with different numbers of solutes in the box. This overlap of conditions is important, as the maximum cluster size in each simulation is always limited to the total number of solute molecules in the box.

The canonical ensemble used in the MD simulations was NVE, that is, constant number of molecules in the box, volume, and energy. This ensemble does differ from experimental conditions, which typically involve NPT ensembles, with constant number of molecules, pressure and temperature. encad has been highly optimized to run at constant energy, and the rescaling of velocities was a relatively rare occurrence during the simulations. For example, in the 173 methane simulations, over 86,000,000 time steps of dynamics were calculated, and the velocities were rescaled only 128 times after the initial temperature equilibration. The temperature of each simulation was monitored and remained relatively constant at about 300 ± 4 K.

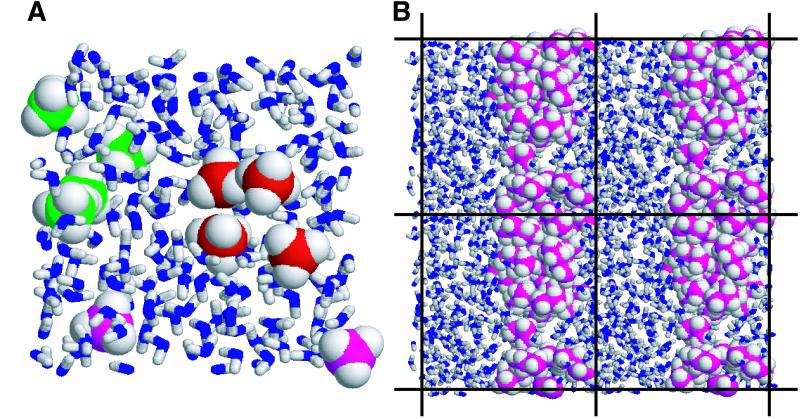
In these simulations, we see the dynamic formation and disruption of solute aggregates (Fig. 1A). These clusters vary in size from single, isolated, and fully hydrated solute molecules to clusters comprised of all of the solutes in the box. Each cluster observed has a unique shape and solvent-packing geometry. The shapes of the clusters vary from compact globular structures to elongated irregular shapes. Because of the periodic boundary conditions, clusters that span the box boundary are observed. Over the course of a 1-ns trajectory, we see many transitions from small to large cluster sizes (Fig. 2 A–C). These transitions predominantly occur through repeated addition or subtraction of a single solute from a cluster. Larger clusters are more stable and persist for longer periods of time.

Figure 1.

Snapshots from the simulations. (A) Ten methane and 204 water molecules in a 6,700-ų box. Methane molecules are space-filled, and water molecules are represented as sticks. Two clusters of size 4 are shown with carbon atoms colored red and green, respectively. The two magenta molecules are fully solvated. Note that the crescent shape of the green cluster permits a solvent-filled cavity. (B) A projection of four adjacent 13,500-ų periodic boxes, each containing 20 butane and 338 water molecules. The butane molecules form an aggregate that is continuous across the boundaries of the periodic box (indicated by lines). This arrangement reflects phase separation and is very stable because of the additional buried surface area at the box boundary interfaces.

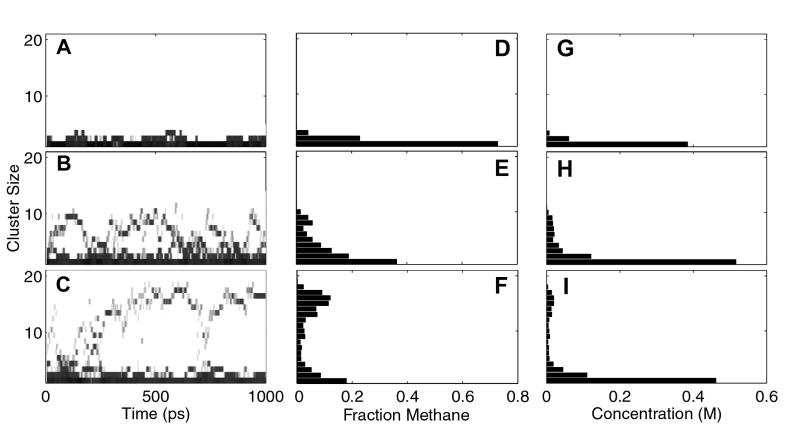
Figure 2.

Kinetic and equilibrium representations of methane trajectories with increasing numbers of solute molecules in a ≈12,700-ų box. (A, D, G) Four methane and 412 water molecules. (B, E, H) Twelve methane and 401 water molecules. (C, F, I) Twenty methane and 391 water molecules. (A–C) The occurrence of clusters of each size throughout the trajectory, smoothed over a 20-timestep window for clarity. Multiple transitions from small to large clusters can clearly be seen in each trajectory. (D–F) The distribution of methane molecules into clusters of each size, averaged over the entire trajectory. (G–I) Histograms of the average molar concentrations of clusters of each size for each simulation. These concentration values were used in the free energy calculations.

The formation of clusters depends on the concentration of solute molecules in the box, with the likelihood of aggregation increasing with increased number of solutes in the simulation, or with a reduction of box size. Fig. 2 D–F show the distribution of the methane molecules into clusters of each size, averaged over the entire trajectory. At low concentrations, solute molecules are unclustered or grouped in small clusters (Fig. 2D). At intermediate concentrations, clusters of a wide range of sizes are populated to a similar extent (Fig. 2E). When a critical cluster size is achieved, however, we see a bimodal distribution, where single or small clusters along with large cluster sizes are preferred, with sizes in between less favored (Fig. 2F).

At very high solute concentrations, the solutes form large cylindrical clusters (Fig. 1B). These clusters span the simulation box, resulting in phase separation between the solute cluster and a solute-saturated water phase. This arrangement is very stable, in that it maximizes solute burial by forming an aggregate that is continuous across the periodic box boundary. This phenomenon has been observed previously in simulations of methane-like particles and is a direct result of the periodic boundary conditions (18, 19). In this study, we want to investigate the energetics of forming solvated clusters, not phase separation. Therefore, simulations in which these continuous clusters were observed in greater than 1% of the output time steps were omitted from the analysis. Despite this limitation, we were able to observe large solvated clusters by increasing the simulation box dimensions.

The Free Energy of Cluster Formation Is Computed Directly from the Distribution of Clusters.

Because of the wealth of data we acquired (a total of 360 simulations each consisting of 2,000 observations of the positions of 652 to 5,181 atoms), we decided to take a novel approach in determining the free energy of hydrophobic cluster formation: compute it directly from the distribution of cluster sizes observed in the trajectories. We first assumed that the simulations were under equilibrium conditions. Several lines of evidence indicate this assumption is valid. First, many transitions are observed throughout the course of each simulation. Second, the energies we calculate agree over a wide range of solute types, concentrations, and simulation box volumes (see below). We chose to compute the series of equilibrium constants corresponding to the addition of one solute molecule (S₁) to a cluster (S_n), because the majority of the transitions observed in the trajectories are additions or subtractions of a single solute from a cluster:

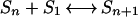1

The average concentration of each cluster size over the course of each simulation was determined (Fig. 2 G–I). Equilibrium constants for the above series of reactions, 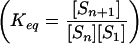, and their corresponding free energies, ΔG = −RT ln K_eq, where R is the gas constant and T is the simulation temperature, were computed for each simulation, up to the total number of solutes in the box. The free energies for each reaction were then averaged over all simulations with the same solute and at the same box volume, as the equilibrium constants for any particular reaction should not depend on competing reactions. These energies reflect an ensemble average over a large distribution of cluster shapes and realistic solvent packing interactions. This is in contrast to previous studies where only one or a few solute packing geometries are sampled (7, 8, 13).

Cluster Formation Is Cooperative.

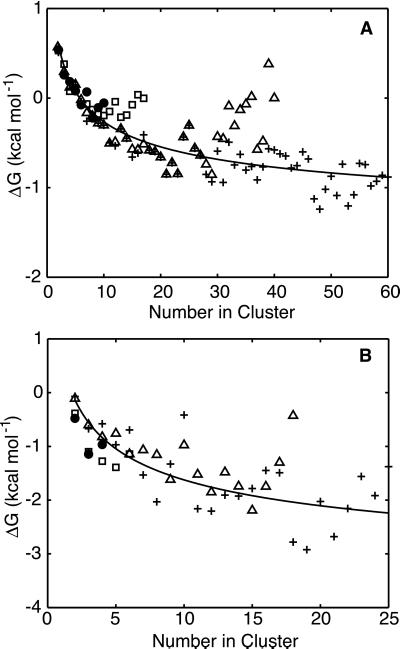
The free energy of adding a solute to a cluster of given size becomes more favorable as the final cluster size increases, showing clear cooperativity in cluster formation (Fig. 3). This result explains why studies of methane dimers are too limited to reveal this important aspect of the hydrophobic effect. The shape of these graphs is complex. Although a purely additive effect would show a simple linear dependence, the slope of these graphs is steep at small cluster sizes but tapers off at large cluster sizes.

Figure 3.

Change in free energy on adding a single solute to a cluster vs. final cluster size. (A) Methane data for all box sizes. Symbols identify the different volume boxes: (●) original box (≈6,570 ų), (□), 2× larger box (≈12,700 ų), (Δ) 4× larger box (≈26,000 ų), (+) 8× larger box (≈52,400 ų). (B) Benzene data for all box sizes. Symbols are the same as in A. The lines are the least square fits of the data to Eq. 2. For methane, β = 4.6 ± 0.3 kcal and C = −0.362 ± 0.008 kcal/mol⋅Ų. For benzene, β = 7.9 ± 1.4 and C = −0.51 ± 0.04 kcal/mol⋅Ų. As β = λα and 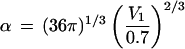, we can calculate λ, the constant of proportionality between free energy and surface area from β, if we know V₁, the volume of a single solute molecule. We computed this value based on the molecular surface area of each unclustered solute from our simulations, assuming the solute to be a perfect sphere. The resulting values for V₁ in ų were 71, 176, 173, and 188 for methane, butane, isobutylene, and benzene, respectively. This gives λ values in cal/mol⋅Ų of 44, 66, 20, and 40 for methane, butane, isobutylene, and benzene, respectively. These values are all fairly close to the experimental value that we estimate to be 45 cal/mol⋅Ų of molecular contact area.

Is such curved dependence of free energy on cluster size expected? In fact, it can be predicted from simple geometric considerations. If we approximate a cluster of n solute molecules as a sphere, then its surface area A_n is related to its volume V_n by 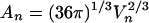. In addition, V_n can be related to the volume of a single solute molecule, V₁, through the packing density, ρ, which for close-packed spheres is about 0.7. [The packing density for close-packed spheres varies from 0.64 for a random arrangement (23) to 0.74 for regular face-centered cubic lattice (24)]. This gives V_n = nV₁/ρ≈nV₁/0.7. Therefore, the surface area of a cluster depends on the number of solute molecules that comprise it, .

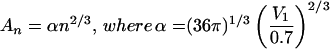Our final assumption, taken from experimental observations, is that the hydrophobic interaction energy of a cluster of size n, G_n, is related to its surface area, A_n, with a constant of proportionality, λ, so that G_n = λA_n. Substituting for A_n gives 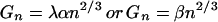, where β = λα. The change in free energy of adding a single solute molecule to an existing cluster is ΔG = G_n+1 − G_n or:

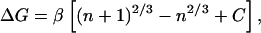2

where C is simply an offset term to allow for rotational and translational entropy that makes the association of a dimer unfavorable at a concentration of 1 M. Fig. 3 A and B show graphs of the free energy of adding a solute to a cluster vs. final cluster size for methane and benzene and their fits to Eq. 2. Although this model is crude, it does indeed correctly capture the attenuated cooperativity of cluster formation observed for these solutes. It also indicates that in our simulation, the free energy may indeed depend on the surface area.

The free energies of formation of large clusters show a tendency to increase at high solute concentrations for each box size (see, for example, the squares and triangles in Fig. 3A). This tailing upwards reflects errors because of the relatively poorer sampling of the large clusters in the simulations. For instance, the smallest cluster sizes (n = 1 or 2) will be observed in virtually all of the simulations, but the largest cluster sizes are observed in only a few simulations. Our assumption of equilibrium conditions might also begin to break down at these high solute concentrations.

Dependence of the Free Energy on Solvent-Exposed Molecular Surface Area.

A hallmark of the hydrophobic effect is the empirical observation that the interaction free energy is proportional to the solvent-exposed surface area. Traditionally, the solvent-accessible surface area, or the area transcribed by the center of a spherical “solvent” molecule (typically with a radius of 1.4 Å) rolled over the surface of the solute, is used for this comparison. However, it has been argued that the molecular surface area, or the envelope of the volume of the solute molecule that solvent cannot penetrate, is more appropriate (25). Conveniently, the Voronoi procedure we used to determine clustering also computes the surface area of each molecule. This surface area is a molecular surface area that is determined explicitly by contacts with the surrounding solvent and solute atoms. Furthermore, the surface area of a particular solute can be separated into solvent-exposed and buried areas based on the molecules it contacts. We computed the change in exposed surface area (ΔESA) for each equilibrium reaction [ΔESA = ESA(S₁) + ESA(S_n−1) − ESA(S_n)] from the average ESA for each cluster size and solute type from all of the trajectories.

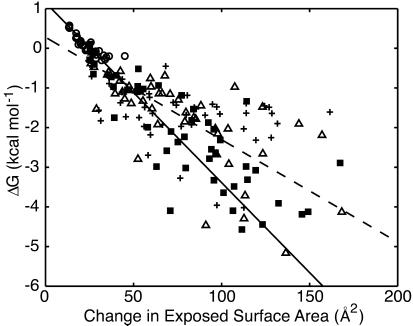
In Fig. 4, we plot the free energy of adding a solute molecule to a cluster for each of the solute types vs. ΔESA. The results from all of the solutes agree well with each other and show a definite linear trend. A robust fit of these data gives a slope of 45 cal/mol⋅Ų (Fig. 4, solid line). We created 20 bootstrap data sets from our original data to look at the distribution of the fit parameters we obtained. Each bootstrapped set was fit by using the robust method. The average slope of the fits from the bootstrapped sets was 44.9 cal/mol⋅Ų, with a standard deviation of 6.4 cal/mol⋅Ų, indicating that our slope is well determined despite the scatter in our data set. These results can be compared with the results of a simple least squares fit of the data, which gives a slope of 24 cal/mol⋅Ų (Fig. 4, dashed line). Fitting in this manner, however, poorly models the most reliable data points, those that are located in the upper right corner of the plot. These two fits represent the range of slopes that are consistent with our data.

Figure 4.

Change in free energy on adding a single solute to a cluster vs. the change in exposed molecular surface area for all of the solutes. (○) methane, (■) butane, (+) isobutylene, (Δ) benzene. Data shown for each solute type include results from each of the different box sizes. A robust fit to all of the data (solid line) has a slope of −45 ± 6 cal/mol⋅Ų and an intercept of 1.1 ± 0.2 kcal/mol. The errors are the standard deviation of the distribution of the fit parameters from a bootstrapping analysis. Fitting the data by using a simple least squares method (dashed line) gave a slope of −25 ± 2 cal/mol⋅Ų and an intercept of 0.3 ± 0.1 kcal/mol.

Discussion

Experimental measurements of the hydrophobic effect are often made with respect to the solvent-accessible surface area (SASA), the area transcribed by the center of a solvent atom in contact with the solute (26). The SASA is therefore larger than the molecular surface area. For example, the SASA of methane is 154 Ų (4), whereas the average ESA for single unclustered methane molecules obtained by our method is 83 Ų. Adjusting the slope obtained from the robust fit to account for this difference gives a slope of 24 cal/mol⋅Ų, in complete agreement with experimental solute transfer experiments, which vary from 16 to 33 cal/mol⋅Ų (1–4).

This result shows that our MD simulations provide an accurate model of the hydrophobic effect. Our simulations used the exact energy functions, parameters, and protocol that we have used on proteins and nucleic acids for a decade (27–30). They consist of terms for bond stretching, bond angle bending, torsion angle twisting, van der Waals nonbonded interactions, and atomic point-charge electrostatics. The hydrophobic effect, which is reproduced so well here, is simply a consequence of the geometries of the molecules and the detailed balance of the different energy terms.

A particularly interesting feature of Fig. 4 is that the formation of small clusters of methane molecules (n < 5) is thermodynamically unfavorable (ΔG > 0). This result corroborates previous potential of mean force calculations on methane and Lennard–Jones spheres that show that the solvent-separated pair is favored over the contact pair (7–12). It appears from our data that more than 25 Ų in surface area needs to be buried from solvent to form a stable hydrophobic interaction. The favorable interactions for an interface of this size most likely compensate for the loss of solvent entropy in forming the contact pair. The small size of methane probably allows it to be accommodated within the hydrogen-bonding network of the water without much entropic cost. The larger solutes, however, cannot be easily accommodated within the hydrogen-bonding network of the water and thus form energetically stable pairs.

Abbreviations

MD

molecular dynamics

ESA

exposed surface area