Interplay of the Glass Transition and the Liquid-Liquid Phase Transition in Water

Abstract

Water has multiple glassy states, often called amorphous ices. Low-density (LDA) and high-density (HDA) amorphous ice are separated by a dramatic, first-order like phase transition. It has been argued that the LDA-HDA transformation connects to a first-order liquid-liquid phase transition (LLPT) above the glass transition temperature T_g. Direct experimental evidence of the LLPT is challenging to obtain, since the LLPT occurs at conditions where water rapidly crystallizes. In this work, we explore the implications of a LLPT on the pressure dependence of T_g(P) for LDA and HDA by performing computer simulations of two water models – one with a LLPT, and one without. In the absence of a LLPT, T_g(P) for all glasses nearly coincide. When there is a LLPT, different glasses exhibit dramatically different T_g(P) which are directly linked with the LLPT. Available experimental data for T_g(P) are only consistent with the scenario including a LLPT.

The ubiquity and biological importance of water, as well as its numerous puzzling anomalous properties, have sparked a long history of water research. Over the last 40 years, there have been several frameworks proposed to explain the unusual behavior of liquid water¹,²,³, most notably the liquid-liquid critical point (LLCP) hypothesis⁴,⁵, the stability limit conjecture⁶, and the singularity-free scenario⁷. Most relevant to this work is the LLCP hypothesis, which proposes that the unusual behavior of liquid water can be explained by the existence of two thermodynamically distinct phases – a low-density liquid (LDL) and high-density liquid (HDL) – below a critical temperature T_c. In this scenario, LDL and HDL are separated by a liquid-liquid phase transition (LLPT) ending at a LLCP. While there are many simulations of atomistic water models⁴,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷ and other tetrahedrally coordinated liquids¹⁸,¹⁹,²⁰,²¹ that support this possibility, direct experimental confirmation of this proposal has been prevented by the nucleation of crystalline ice. Recent experiments of water confined at the nanoscale (e.g., Ref.22), where crystallization can be suppressed, support the view that two liquids, LDL and HDL, exist at low temperatures. Although encouraging, it is not clear at present what role the confining surfaces play on water phase behavior (see, e.g., Ref.23).

Some of the strongest experimental evidence suggesting a liquid-liquid transition in water are obtained from glassy water. Specifically, experiments show the presence of two distinct glassy states, low-density (LDA) and high-density amorphous (HDA) ice, which can be reversibly interconverted by the application (or removal) of pressure²⁴,²⁵,²⁶,²⁷,²⁸. Very recently, Winkel et al. observed the transformation from high- to low-density water by removal of pressure at 140 K, and suggested it to be of first-order in the ultraviscous liquid domain just above T_g²⁹. In the context of the LLCP hypothesis, LDA and HDA are envisioned as the glass counterparts of LDL and HDL, respectively. Unambiguous evidence that LDA and HDA are thermodynamically distinct and that they are thermodynamically continuously connected with LDL and HDL, respectively, would imply the existence of polymorphism in liquid water and strongly support the existence of a LLCP. Unfortunately, the rapid crystallization and non-equilibrium nature of glassy water complicates elucidating the relationship between the equilibrium liquid and LDA/HDA, and hence complicates determining whether two liquid phases exist in water.

A possible way to overcome this challenge is to take advantage of the fact that, at the glass transition temperature T_g, the ergodic liquid is restored (if only briefly before crystallization occurs³⁰,³¹,³²). Consequently, the pressure dependence of T_g(P) provides valuable information on the thermodynamics of the liquid state. This is conceptually similar to using the metastable melting loci to extract information about the liquid state, an approach developed by Mishima and Stanley⁵. If there are thermodynamically distinct liquid states (which have a discontinuous change in dynamics at the LLPT) there should be a discontinuous change in the locus T_g(P) obtained from quenching the liquid under pressure. Additionally, pressure treated glassy states are expected to have dramatically different T_g(P)³³. Hence, T_g(P) may offer a direct indicator of a LLPT. The primary obstacle to examining this approach experimentally is maintaining specific large pressure and avoiding crystallization during thermal studies of various glasses, although some researchers²⁹,³⁴,³⁵,³⁶ have begun to overcome these problems.

Motivated by these considerations, here we examine the behavior of the locus of T_g(P) for the amorphous ices using computer simulations of two models of water – one that has a highly accessible LLPT (the ST2 model)⁴,⁸,¹¹,¹²,¹⁷, and one that does not (the SPC/E model)³⁷,³⁸,³⁹. We select these models to provide clearly contrasting behavior, rather than for their accuracy (or lack thereof) in reproducing quantitative experimental behavior of water. Our simulations show that, in the absence of a LLPT (the SPC/E model), the glass transition loci T_g(P) of HDA and LDA are nearly indistinguishable, and that T_g(P) varies smoothly with pressure. In marked contrast, when there is a LLPT (the ST2 model), the T_g(P) loci of LDA and HDA have opposite pressure dependences. By also evaluating T_g(P) from glasses obtained by hyperquenching the equilibrium liquid under pressure, we show that this T_g(P) (which is directly related to liquid states) roughly coincides with that of LDA at low pressure, and with that of HDA at high pressure; this T_g(P) exhibits a sharp change from LDA- to HDA-like behavior at the intersection with the known LLPT line. The qualitative differences between the results obtained with the SPC/E and ST2 models provide a template to interpret experiments measuring T_g(P) from amorphous ices, and hence to distinguish whether or not the behavior of water is indicative of an LLPT. We also discuss the available experimental data, which are qualitatively consistent with the LLPT scenario shown by the ST2 model, and inconsistent with the SPC/E model; further experiments are needed for confirmation.

Results

Glassy States under Consideration

The many glassy states of water can be broadly categorized into low- and high-density forms. The properties of the glassy states of the SPC/E and ST2 models have been previously examined, and it has been shown that both models qualitatively reproduce the LDA and HDA states⁴⁰,⁴¹,⁴²,⁴³,⁴⁴,⁴⁵. In the following sections, we will examine hyperquenched glassy water (HGW) under compression, and HDA under both compression and decompression; we also examine LDA, obtained by heating HDA at low pressure. We follow procedures similar to those used in experiments²⁴,³¹,⁴⁶ to prepare these states, although the cooling/heating and compression/decompression rates accessible in simulations are significantly faster than those used in experiments. See the Methods section for a complete description of the preparation of these glasses.

For the ST2 model case, we also examine glasses formed by direct hyperquenches of the liquid at different pressures. Since these hyperquenched glasses (HQG) are obtained by quenching the liquid under pressure, they are directly related to the liquid state at the same pressure. Note that for the particular case of P = 0.1 MPa (and only for this pressure) HQG is the same as HGW. Rapid quenching of bulk samples under pressure is experimentally very challenging; this approach has been pursued experimentally only for μm size droplets of emulsified water where crystallization is suppressed³⁴.

For each glass we form, we evaluate the glass transition temperature locus, T_g(P). For a given glass at pressure P, we determine T_g(P) following a procedure analogous to that employed in differential scanning calorimetry (DSC) experiments (see Methods section). The data presented are an average over twenty independent simulations for each glass.

Glass Transition in the Absence of a Liquid-Liquid Phase Transition

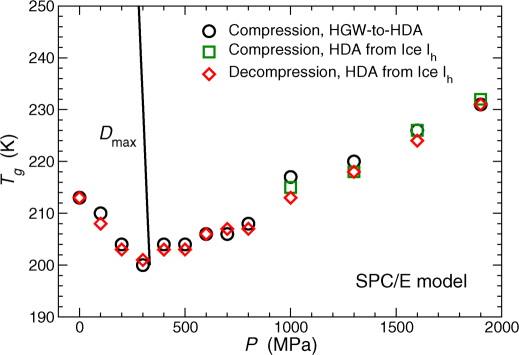
We first consider the behavior of the various glasses in the SPC/E model, where there is no interference of an LLPT to complicate the behavior of T_g(P). Figure 1 shows the T_g(P) loci for (i) compressed HGW, 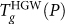, (ii) HDA obtained during compression of ice I_h, and (iii) decompressed HDA, (again, averaged over twenty independent simulations). All glasses are heated from an initial temperature of T = 80 K.

Figure 1. Pressure-dependence of the glass transition temperature T_g(P) for the SPC/E model.

The behavior of T_g(P) is nearly independent of the glass preparation procedure. At pressures , compression of HGW yields HDA (see methods section on preparation of glasses). The maximum diffusivity line (D_max-line) is taken from Ref.38.

Remarkably, Fig. 1 shows that in the absence of an LLPT, the T_g loci are almost completely independent of the starting glassy state, i.e., 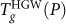and (under compression or decompression) all roughly collapse onto a single T_g(P) locus. This is particularly surprising given that the initial density of these glasses can differ by more than 20%, such as in the case of compressed HGW and decompressed HDA at (see Methods section to compare the initial densities). However, it should be noted that, while T_g(P) of the various glasses are nearly the same, the behavior of c_P(T) (from which T_g(P) is determined) and ρ(T) upon heating differs significantly for T < T_g (Fig. 2).

Figure 2. Isobaric specific heat and density for glasses of the SPC/E model on heating.

(a) Isobaric specific heat, c_P(T), and (b) density, ρ(T), upon heating compressed HGW (solid lines) and decompressed HDA (dashed lines) at various pressures. T_g(P) (defined by the inflection of c_P(T) below its maximum temperature) occurs at nearly the same temperature for compressed HGW and decompressed HDA. However, the behavior of the c_P(T) and ρ(T) differ significantly in the glassy state (e.g., at T < 200 K for all pressures). For clarity, curves in (a) have been successively shifted by 30 kJ/(K·mol) for increasing pressure.

Interestingly, Fig. 1 shows that T_g(P) has a minimum at P ≈ 300 MPa. Such a minimum occurs at the intersection of the T_g(P) locus and the maximum diffusivity line (D_max-line). The D_max-line is defined as the set of pressures at which the diffusion coefficient D exhibits a maximum upon isothermal compression; its presence is a consequence of the well-known anomalous pressure-dependence of water diffusivity. The coincidence of the T_g(P) minimum and the D_max-line is a reassuring consistency of the definition of T_g employed in this work, since we define T_g by a thermodynamic (rather than dynamic) criterion.

We can quantitatively explain the observed relation between the minimum of T_g(P) and the D_max locus by considering the diffusive relaxation time τ ∝ (D/T)^{−1 47} as an explicit function of T and P. Consider the total differential

Experimentally, T_g(P) is often defined as the temperature at which τ(T, P) reaches a fixed value (typically 100 s) for a given cooling/heating rate⁴⁸. Since all glasses in our simulations are formed using the same cooling/heating rate at all pressures, it follows that τ should be constant along the T_g(P) locus, and thus dτ = 0 along T_g(P). Therefore, rearranging eq. (1),

along the T_g(P) locus. The denominator (∂τ/∂T)_P < 0 and finite, since τ is a monotonically decreasing function of T. Hence, dT_g(P)/dP = 0 (where T_g(P) is minimum) only if the numerator (∂τ/∂P)_T = 0 at T_g, and hence τ (and correspondingly D) must be an extremum as a function of P. Moreover, it can be shown from eq. (2) that a maximum in D corresponds to a minimum in T_g(P), and vice versa. Accordingly, the D_max-line must intersect the T_g(P) locus at the pressure at which T_g(P) has a minimum. Additionally, at very low pressure approaching the liquid spinodal, it is known that the SPC/E model exhibits a minimum of D, due to “tearing apart” hydrogen bonds at very low density³⁸,⁴⁹. Equation 2 requires that the associated D_min-line must intersect with a maximum on T_g(P). We do not observe this feature, since D_min occurs at negative pressures that are not explored in this work.

Glass Transition in the Presence of a Liquid-Liquid Phase Transition

We now turn our attention to the ST2 model where the LLPT is accessible in equilibrium simulations and can significantly impact the behavior of glassy states. Due to vast differences in the behavior of T_g(P) for various glasses, we examine the T_g(P) locus for each glass separately.

T_g from Hyperquenching under Pressure

To unambiguously associate a glass with a liquid for a given pressure, the glass should be formed by isobaric quench from the liquid state at that pressure. So far, cooling under pressure is only experimentally feasible for emulsion samples³⁴. Fortunately, the experimental complications pose no problem in computational studies. Therefore, we first examine T_g(P) obtained by hyperquenching the equilibrium liquid under pressure and reheating at the same P using our standard cooling/heating rate; we refer to the glass transition temperature of the resulting hyperquenched glasses (i.e. HQG) as . The behavior of the T_g(P) formed in this straight-forward approach provides a useful baseline to interpret the T_g(P) behavior we will see for compressed HGW and decompressed HDA.

The 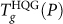locus is shown in Fig. 3a. Qualitatively similar to the T_g(P) locus of SPC/E water, we see that 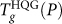for the ST2 model is also negatively sloped at low pressure (due to the diffusion anomaly), and positively sloped at high pressures. The data for the ST2 model does not extend to very high pressures due to crystallization on heating that complicates determination of T_g. Interestingly, unlike the SPC/E model case, there is a sharp change in T_g(P) at P = 250 MPa.

Figure 3. Pressure-dependence of the glass transition temperature T_g(P) for glasses of the ST2 model.

(a) determined by hyper-quenching the equilibrium liquid at the desired pressure P, and reheating the resulting glass at that same P. As discussed in the text, the dramatic change of T_g^HQG(P) around 250 MPa can be understood from the location of the equilibrium LLPT line (taken from Ref.13). The D_max locus is taken from Ref.50. The color gradient represents the density ρ of HQG on heating. (b) Comparison of the glass transition temperature of compressed HGW, , with 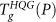. At low P, 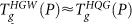while at high P, compressed HGW converts to a high density glass (HDA′) before a glass transition to HDL occurs (violet solid line). The dotted portion of the locus indicates the temperature at which compressed HGW transforms to HDA′. Included is the HDL-to-LDL spinodal line from Ref.12. Here the color gradient represents ρ of compressed HGW on heating. (c) Comparison of the glass transition temperature of decompressed HDA, 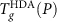, with . At high P, while at low P, decompressed HDA converts to LDA (dashed line) before a glass transition to the liquid occurs at T_g^LDA(P) (green solid line). Here the color gradient is ρ of decompressed HDA on heating, which helps to identify the transformation to LDA.

The sharp change of at P = 250 MPa can be understood by superimposing the known location of the LL coexistence line for ST2 (taken from ref.13). Figure 3a shows that, for P < 250 MPa, the 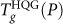locus is at higher T than the liquid-liquid coexistence line. Accordingly, on hyperquenching, the liquid falls out of equilibrium (into a low-density glass) before the LLPT occurs, and so is smooth at all P < 250 MPa. At P = 250 MPa, the locus intersects the LL coexistence line, and consequently the system is now sensitive to the equilibrium LLPT, and so there should be a LLPT before vitrification (into a high-density glass). Accordingly, the large difference in the dynamical properties of LDL (for 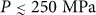) and HDL (for ) is reflected by a large change in at P = 250 MPa. A similar discontinuity in T_g(P) has been observed in computer simulations of a polyamorphic monatomic liquid³³.

This dramatic change in the liquid properties is indicated by the presence of two distinctive features in c_P(T) upon heating HQG at P = 250 MPa (Fig. 4) (similar characteristics are observed in ρ(T), see Fig. 5). Specifically, in addition to the typical c_P peak, characteristic of the glass-to-liquid transition observed at P < 250 MPa, a shoulder in c_P(T) develops at slightly lower temperature, T ≈ 220 K (Fig. 4a). As we discuss below, this lower-T feature of c_P(T) can be associated to the transformation of the high-density glass (HDA) to the low-density glass (LDA); the upper-T feature of c_P(T) can be related to a glass-to-liquid transition, from the low-density glass to the liquid. At P = 250 MPa, this last transformation occurs at the intersection of the 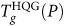and liquid-liquid coexistence T_LL(P) loci. At higher pressure, a simpler behavior reemerges. Specifically, for P > 250 MPa, hyperquenching the liquid yields a high-density glassy state that connects smoothly with the behavior of the liquid at high pressure (Fig. 3a)⁴³.

Figure 4. Isobaric specific heat for glasses of the ST2 model on heating.

Comparison of the isobaric specific heat c_P(T) for (a) HQG (solid lines) and compressed HGW (dashed lines) and (b) HQG (solid lines) and decompressed HDA (dashed lines) at various pressures. For clarity of the figure, curves for increasing pressure have been successively shifted vertically by 100 kJ/(K·mol) and horizontally by-10 K. For the case of compressed HGW [panel (a)], there are two features at high pressures. For example, at P = 500 MPa, compressed HGW converts to a high density glass similar to HDA at T ≈ 190 K, which on further heating converts to an equilibrium liquid at T ≈ 240 K. Similarly, for decompressed HDA at low pressure [panel (b)], there are two features at low pressures. For example, at P = 0.1 MPa, HDA converts to LDA (similar to HGW) at T ≈ 150 K, which on further heating converts to an equilibrium liquid at T = 275 K.

Figure 5. Density for glasses of the ST2 model on heating.

Comparison of the density ρ(T) for (a) HQG (solid lines) and compressed HGW (dashed lines), and for (b) HQG (solid lines) and decompressed HDA (dashed lines) at various pressures.

A minimum in apparently develops at approximately 250 ≤ P ≤ 300 MPa, close to the P where it exhibits a discontinuity – at the intersection with the T_LL line. This discontinuity is consistent with the fact that, across the T_LL locus, τ will show a discontinuity with the change in phase. Like the SPC/E model, Fig. 3a also shows that the D_max-line approaches the minimum in .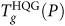

T_g of Compressed HGW

We next compare the behavior of with that of . Since HGW is formed by hyperquenching the liquid at atmospheric pressure, it is natural to expect that, at low pressure, the T_g resulting from heating compressed HGW should be very similar to that of the glass formed by hyperquenching the pressurized equilibrium liquid (i.e., HQG). For P ≤ 200 MPa, Fig. 3b confirms that indeed . Moreover, the behavior of c_P(T) of the two glasses, even at T < T_g, is nearly identical in this pressure range (Fig. 4a). For P > 250 MPa, the and 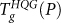loci differ significantly. Specifically, while is affected by the proximity to the LLPT, is nearly insensitive to the presence of the liquid-liquid transition.

We can understand the difference between the 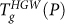and loci at high pressure based on the preparation of compressed HGW. Since we compress HGW at very low T, compressed HGW cannot relax during compression; thus, compressed HGW retains the characteristics of the low-density glass state, even at pressures where the high-density state may have lower free energy. This is analogous to the fact that HDA can be decompressed to atmospheric pressure and retain its high density, provided the temperature is kept sufficiently low. Since the equilibrium LLPT occurs at temperatures below (for the present heating/cooling rate), the locus continues as a smooth extension of its low pressure behavior to P much larger than 250 MPa (where the T_g(P) of HQG has an apparent discontinuity).

Since compressed HGW remains mechanically stable for P > P_c (P_c = 190 MPa), it is natural to ask to what liquid compressed HGW transforms on heating at high pressures. We separately consider the cases P_c < P < 400 MPa and P > 400 MPa, since at P ≈ 400 MPa the 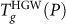and loci intersect one another.

In the range P_c < P < 400 MPa, compressed HGW transforms to HDL without intermediate phases. That the final liquid is HDL can be understood by noting the location of the LDL-to-HDL spinodal (see Fig. 3b). It can be seen that is greater than the spinodal temperature. Therefore, on heating, the glass transition must be from HGW to HDL, since HDL is the only (meta)stable liquid at these (P,T). This is confirmed by the dramatic increase in density at 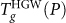shown in Fig. 5a for P_c < P ≤ 400 MPa.

At P > 400 MPa, the final liquid resulting from heating compressed HGW is also HDL. However, the progression to the HDL state is more complex at these pressures. At P > 400 MPa, and, as a result, when compressed HGW reaches T_g, no metastable liquid state is accessible. Thus, HGW makes a glass-glass transition to an HDA-like glass – the glassy extension of HDL. We refer to this form as HDA′ since it has similar (but not identical) properties to HDA on decompression. The HGW→HDA′ transformation is dominated by an orientational reordering of the molecules, and does not require significant translational displacements. For 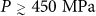– the glass-glass and glass-liquid transitions are well separated, and we can detect two distinct transformations in c_P(T) (Fig. 4a) – the first being HGW→HDA′, followed on heating by HDA→liquid, defining 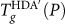which roughly coincides with . It is important to notice that the glass-glass HGW→HDA′ transition is a natural continuation of the from lower P, showing that the shape of the 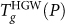depends only on the form of the glass, and not the liquid (or glass) to which HGW transforms. Hence, the HGW-to-HDA′ transition is a result of HGW reaching its kinetic (not thermodynamic) limit of stability, and becoming caught in another out-of-equilibrium state, HDA′, before the liquid becomes available upon further heating. Considering that LDA and HGW are largely the same, it follows that the LDA-to-HDA′ transition upon heating at high pressures is not related to the LDL-to-HDL spinodal, but instead to the LDA T_g. A similar scenario holds for the case of decompressed HDA, as discussed in the next section.

T_g of Decompressed HDA

We finally examine the T_g(P) locus of decompressed HDA. This form of HDA is most closely related to that of experimentally prepared uHDA⁵¹. The behavior of is easiest to understand at high pressure since HDA is formed under high pressure conditions. Specifically, we expect that the high pressure behavior of should approximately follow that of the glass from the hyper-quenched liquid at the same pressure. Indeed, Fig. 3c shows that, for 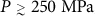, 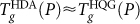. We note that at P ≈ 260 MPa, the locus intersects the HDL-to-LDL spinodal on decompression. Therefore, the liquid to which HDA transforms at is HDL.

We next consider the behavior of 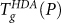at P < 250 MPa, where the equilibrium liquid forms a low-density glass on isobaric quenching. Just as in experiments, HDA in our simulations is mechanically stable at liquid N₂ temperatures down to atmospheric pressure. Furthermore, as known experimentally, but not observed for the SPC/E model, decompressed HDA shows a clear conversion to a low density amorphous glass upon heating, normally referred to as LDA. The conversion to LDA, as well as the conversion of LDA to a liquid upon further heating, appear as two distinct features in the specific heat (Fig. 4b). This is particularly clear at P = 0.1 and 200 MPa where c_P(T) exhibits minima at T ≈ 190 and 230 K (respectively) below the temperature at which the c_P maximum, that is characteristic of the glass transition, occurs.

As observed in experiments, the HDA-to-LDA (glass-glass) transformation, readily seen by a similar exothermic feature (Fig. 4b), is accompanied by a dramatic decrease of density (Fig. 5b). Like the conversion of compressed HGW to HDA′ at high pressure discussed in the previous subsection, the HDA-to-LDA transformation is primarily associated with a reorientation of the molecules without significant translational motion. Figure 3c shows that the locus of the HDA-to-LDA (dashed violet line) connects smoothly with the locus (solid violet line) at high pressure. This demonstrates that the HDA-to-LDA transition is a result of HDA reaching its T_g; rather than transforming to the liquid at T_g, the system becomes caught in another out-of-equilibrium state, LDA, before the liquid becomes available upon further heating. It follows that the HDA-to-LDA transition is not related to the thermodynamic HDL-to-LDL spinodal. However, the HDL-to-LDL spinodal on decompression does signal the terminal pressure of the HDA-to-LDA conversion locus. At large pressures, , HDA converts directly to HDL.

Experimentally, LDA is known to have similar T_g to HGW at atmospheric pressure⁵². Therefore, we expect that the T_g(P) locus from heating LDA should be similar to both T_g(P) for compressed HGW and HQG. Indeed, Figs. 3b and 3c show that for P < 100 MPa, . Nearing the region of the LLPT, the behavior of the T_g loci for the different low-density glasses have similar pressure dependence but no longer coincide – not surprising since the density of LDA is noticeably different from compressed HGW at P ≈ 200 MPa and T < 260 K (Fig. 5b).

Relationship to Experiments

The results obtained for the SPC/E (without a LLPT) and the ST2 (with a LLPT) models present clearly distinguishable scenarios for the behavior of the T_g(P) loci of the different glasses. In this section, we compare available experimental data for real water with these scenarios. In short, we find that the available experimental data for (i) the T_g(P) loci of LDA and HDA, (ii) the pressure-dependence of the LDA-to-HDA and HDA-to-LDA transition temperatures, and (iii) the location of the D_max-line for liquid water are consistent with the LLPT scenario of the ST2 model, and inconsistent with the simulations using the SPC/E model that lack an accessible LLPT. We explain the comparisons in the following. To simplify the discussion, we use T_g(P) to refer to both the locus of glass-glass and glass-liquid transitions.

We first consider the ST2 model scenario, where HDA and LDA (or HGW) exhibit distinct T_g(P) loci. Experimental data for the transitions of the amorphous solids are shown in Fig. 6, which can be compared with Fig. 3. We observe several key qualitative similarities. Specifically, we see that (i) the experimental T_g(P) locus of HDA on heating³⁵ and the decompression induced HDA-to-LDA transition line²⁶ are both positively sloped and can be identified with the qualitative behavior of the 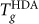locus of the ST2 model; (ii) conversely, the compression induced LDA-to-HDA transition line²⁶ is negatively sloped, and, if we associate this line with a pressure induced glass-glass transition, the behavior is consistent with the ST2 model; (iii) the location of the D_max line is consistent with a change of the T_g(P) locus from one like LDA at low pressure (negative slope), to one like HDA (positive slope) at high pressure; (iv) the calorimetric T_g of LDA is higher than the calorimetric T_g of HDA at ambient pressure³⁵. Based on the similarity between the ST2 results and experiments, we can make a crude prediction for the experimental T_g(P) locus of LDA (or HGW) on heating (Fig. 6). The negative slope of the predicted T_g(P) locus is supported by the fact that D has anomalous pressure dependence in this region. Confirmation of such qualitative behavior would strongly support the possibility of a LLPT.

Figure 6. The experimental behavior of T_g(P) for LDA and HDA.

Data for T_g are primarily from ref.35. We also compare with data for the isothermal, pressure driven LDA/HDA transition²⁶. The difference in path and rate between these experiments precludes a quantitative comparison. However, the data show the same qualitative features as the ST2 model that exhibits a LLPT (Fig. 3). Given these facts, the dashed green line offers a prediction for the approximate behavior of T_g(P) for LDA. The prediction is determined by scaling and shifting from the ST2 model to match the experimental 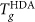(the resulting locus is indicated by the dashed violet line); this scaling factor is then applied to from the ST2 model, and shifted so that it matches experiments at atmospheric pressure.

While the similarities are favorable for the scenario of the ST2 model, there are complicating factors based on differences with the experimental details that we should consider. The first complication regards possible differences between the behavior of eHDA and uHDA. The experimental T_g(P) locus³⁵ for HDA (Fig. 6) is derived from eHDA (annealed at low pressure), while our simulations examine uHDA. T_g for these two forms is very similar. However, they apparently differ in the nature of the transformation: careful annealing just above T_g for eHDA results in an apparently high-density liquid state for P ≤ 300 MPa³⁵, while uHDA transforms immediately to LDA on heating at low pressure⁵³ (as found here for the ST2 model). Fig. 6 includes the compression-induced LDA-to-HDA and decompression-induced HDA-to-LDA transition line from ref.26. These experiments were performed using uHDA. The slope of the experimental locus³⁵ is very similar to the slope of the experimental HDA-to-LDA transition line²⁶ (see Fig. 6). This is consistent with the conclusion that the HDA-to-LDA transition is a result of HDA reaching its T_g, rather than being associated with the HDL-to-LDL spinodal. The experimental difference between eHDA and uHDA seems to be that the HDA-to-LDA transition is shifted to higher temperature in the former²⁹. This difference opens a window where HDL is accessible in isobaric heating experiments done with eHDA³⁵, whereas uHDA transforms to LDA without access to HDL. Another complication is that (above atmospheric pressure) the experimental ³⁵ has been obtained volumetrically. However, simulations indicate that T_g measured from calorimetry and volume experiments are very close to each other⁵⁴; we made a similar analysis using our volume data, and find consistent results with the calorimetric method (see supplementary information).

We next consider a comparison of experimental data with the SPC/E scenario. In addition to the glass transition temperatures of LDA and HDA, Fig. 6 also shows the location of the experimental D_max line¹,⁵⁵. To show that the experimental data is inconsistent with the SPC/E scenario, we note that in the SPC/E scenario: (i) there is a single T_g(P) locus for all amorphous ices, and (ii) the T_g(P) locus exhibits a single minimum that intersects the D_max-line. Figure 6 indicates that points (i) and (ii) cannot be simultaneously satisfied. Specifically, if there were a single T_g(P) locus, then its minimum must occur at approximately P ≤ 115 MPa in order to intersect the LDA and HDA T_g loci in Fig. 6. However, the pressure of the D_max-line, which should coincide with a minimum of T_g(P) locus, clearly extrapolates to much larger pressure, P ≥ 190 MPa. Hence, conditions (i) and (ii) cannot both be satisfied, and so the SPC/E picture is not supported by the experiments. In other words, observation of two distinct values of T_g(LDA) and T_g(HDA) at approximately 200 MPa, where the Dmax line intersects, can be used as a criterion to positvely identify a liquid-liquid phase transition scenario and to rule out a scenario without such a transition. The predictions made here combined with the experimental scenario strongly suggest this to be the case, but definite experimental confirmation remains an open issue.

Discussion

We have evaluated the pressure dependence of T_g for various forms of amorphous water in two simulation models, one with an accessible liquid-liquid transition, and one without. Our findings indicate a much richer behavior for T_g(P) in the presence of a LLPT, and that this behavior appears to be consistent with the available experimental data. The behavior of T_g from simulations in the absence of an LLPT is inconsistent with the available experimental data. Hence our findings support the possibility of multiple liquid states and a critical point in supercooled water. Based on these results, we have made a rough prediction for T_g(P) of LDA. Further experimental work to evaluate the T_g(P) loci of HGW or LDA, will be valuable to confirm or refute these hypotheses.

Methods

Simulation models and methods

Our findings are based on extensive molecular dynamics (MD) simulations of water using two different models: (i) the extended simple point charge (SPC/E) model⁵⁶, and (ii) the Stillinger “ST2” potential⁵⁷. These models have been extensively applied to the study of thermodynamic and dynamic properties of supercooled water and, to a lesser degree, to the study of glassy water²⁸. Both models reproduce qualitatively the most common anomalies characteristic of liquid water. The primary difference between the models, and the reason we select them, is that the ST2 model exhibits a LLPT that is readily accessible by computer simulation⁴,¹¹,¹²,¹⁷, while the SPC/E model does not. If it exhibits a LLPT, it occurs at a temperature well below the lowest temperatures accessible in equilibrium simulations³⁷,³⁸,³⁹.

The basic potential parameters and simulation protocols, such as simulation time step and cutoff distance used for the truncation of the interactions, etc. are described in previous studies: we follow precisely the parameterization described in refs.³⁸ and¹² for the SPC/E and ST2 models, respectively. The temperature and pressure are controlled using the Berendsen technique⁵⁸. All data are averaged over 20 independent samples to improve statistics. For glasses obtained from an initially liquid state, we use a 1000-molecule cubic system with periodic boundary conditions. For glasses obtained from the amorphization of ice I_h, we use a system of 1024 molecules in a rectangular unit cell (with periodic boundary conditions) that matches the unit cell geometry of ice I_h. Proton disorder in the initial ice configuration is generated by identifying closed hydrogen bond loops, and exchanging hydrogens between molecules, as described in Ref.59. For the ST2 model, some samples crystallize on heating the glass for . We have excluded these samples from our analysis.

Preparation of Glassy States

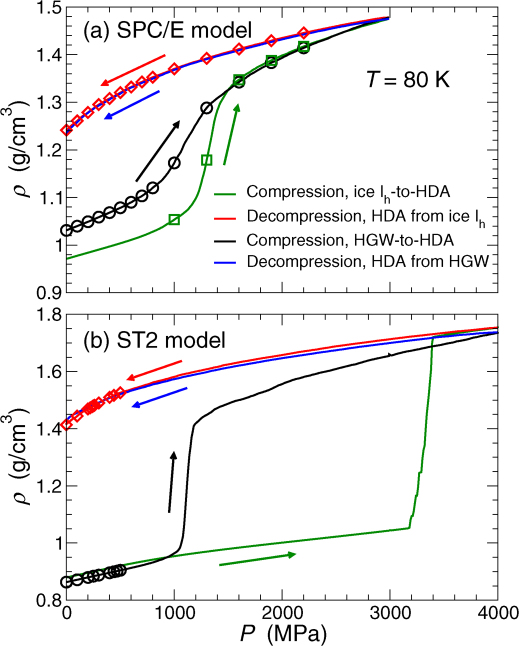
The glass obtained by rapidly quenching bulk water at ambient pressure is referred to as hyperquenched glassy water (HGW)³¹. To obtain HGW in simulation, we first equilibrate liquid water at relatively high temperature (T = 300 K for SPC/E, and T = 350 K for ST2) and P = 0.1 MPa. We isobarically cool the liquid to T = 80 K at a rate q_T = 30 K/ns. To study the pressure dependence of T_g for the case of HGW, we first isothermally compress HGW at a rate q_P = 300 MPa/ns from P = 0.1 MPa to the desired P at T = 80 K; we then isobarically heat the sample at the same P and recover a pressurized liquid state. We note that HGW can be compressed at T = 80 K to P ≈ 700 MPa, for the SPC/E model case, and to P ≈ 1000 MPa, for the ST2 model case; further compression causes HGW to collapse to an HDA-type glass for both models (Fig. 7). A similar collapse from an LDA-type glass to an HDA-type glass is observed experimentally²⁶,⁶⁰.

Figure 7. Compression/Decompression behavior of LDA, HDA, and ice I_h.

Evolution of density at T = 80 K upon compressing ice I_h (green line) and HGW (black line) to form HDA, followed by decompression of HDA (red and blue lines correspond to decompression of HDA obtained from ice I_h and HGW, respectively). Results are for (a) the SPC/E and (b) the ST2 model. In both models, the sudden changes in density correspond to the ice I_h-to-HDA (green line) or HGW-to-HDA (black line) transition, respectively. Symbols indicate the starting densities for glass configurations that are heated at fixed P to determine T_g, shown in subsequent figures.

We also obtain HDA by following the corresponding experimental procedure⁴⁶, i.e., we isothermally compress proton-disordered ice I_h (at the rate q_P) at T = 80 K to high pressure. Since we do not anneal HDA, the closest experimental counterpart to our procedure is “unrelaxed” HDA (uHDA), as opposed to relaxed (rHDA) or expanded (eHDA) treatments⁵¹. Figure 7 shows the density as function of pressure during compression of ice I_h; the results differ significantly between the two models. For the SPC/E model, the collapse to HDA happens over a narrow, but gradual and continuous range of pressure, , while for the ST2 model, the collapse happens over a very narrow window around P = 3200 MPa. Given that these results are an average over independent compressions, examining individual runs shows that the collapse of ice I_h is indeed discontinuous in the case of the ST2 model; the width in the average density change in Fig. 7a is a result of the fact that different realizations collapse at slightly different P. An examination of individual runs for SPC/E water shows that the behavior of each realization has the same gradual behavior as the average. The difference in the sharpness in the two models is presumably a consequence of the fact that ST2 water has a clear LLPT and LLCP, accessible to equilibrium simulations, while SPC/E water does not (at least for our rapid cooling and compression rates). We note that the experimental amorphization of ice I_h⁴⁶ more closely resembles the behavior of ST2 water, albeit at significantly smaller P. The ST2 model shows a larger transition pressure, both due to the rapid pressurization in the simulation and because ST2 so strongly emphasizes tetrahedral (ice-like) structure. We note that for both water models and also in experiments²⁸, the conversion of ice I_h to HDA occurs at higher pressures than the pressures at which HGW converts to HDA. However, the structure of HDA obtained by compression of HGW or ice I_h is indistinguishable. As a result, decompression (at rate q_P) of HDA formed from ice or HGW shows the same P(ρ) dependence (Fig. 7).

To obtain LDA we follow the typical experimental procedure²⁴, i.e., we first decompress HDA to low pressures (at rate q_P) at T = 80 K and then, heat decompressed HDA at constant pressure (at rate q_T). As in the experimental case, HDA does not convert to LDA at P = 0.1 MPa at low T. Conversion to LDA only occurs on heating decompressed-HDA. The starting HDA configurations are obtained by isothermal compression of ice I_h at T = 80 K, as previously explained. The main text shows that the HDA-to-LDA transformation can be clearly identified for the ST2 case; for SPC/E, the HDA-to-LDA transformation is more gradual, and not easily delineated⁴⁴. We note that for both the ST2 and SPC/E potentials, the decompressed HDA prepared from an initial compression of ice or HGW for each model is nearly indistinguishable in terms of density (see Fig. 7) and structure (as measured by pair correlations).

Determination of T_g

Experimentally, T_g is typically determined from differential scanning calorimetry experiments where the sample is heated at a fixed rate at ambient pressure³⁰,³². The glass transition is apparent from a peak in the specific heat c_P(T), the height and width of which depend on fragility⁴⁸. The specific value of T_g can be assigned by a variety of methods; we assign T_g as the temperature corresponding to the inflection point of c_P(T) on heating. More specifically, we evaluate the (non-equilibrium) isobaric specific heat, c_P(T) = (∂H/∂T)_P, by heating glasses at the same rate q_T = 30 K/ns used to cool initial samples. To calculate c_P(T), we calculate the energy U(T) and volume V(T) of the system as function of T, the enthalpy being H(T) = U(T) + P V(T). We associate T_g(P) with the inflection point of c_P(T) prior to the glass transition maximum. Thus, T_g(P) can be obtained from the location of the maximum in dc_P(T)/dT that occurs at temperature below the c_P(T) glass transition maximum.

We have tested several common definitions for T_g, for example by the intersection of a linear extrapolation of the low T glass behavior of c_P(T) with its linear rising part at higher T, before the c_P(T) maximum occurs. This is usually referred as the “onset” glass transition temperature, T_g,onset. While our T_g values are slightly higher than the corresponding T_g,onset values, the qualitative pressure dependence of T_g we report is robust for any reasonable definition of T_g. Note that DSC methods typically do not operate at low T and high P at the same time; consequently, there is no experimental standard method to measure T_g at large pressure. In these cases, T_g can be measured from dilatometry experiments (see SI).

Author Contributions

NG, TL, FS designed research and wrote manuscript. All authors performed research and reviewed the manuscript.

Supplementary Material

Supplementary Information

Suplementary Information