Relative luminance and binocular disparity preferences are correlated in macaque primary visual cortex, matching natural scene statistics

Abstract

Humans excel at inferring information about 3D scenes from their 2D images projected on the retinas, using a wide range of depth cues. One example of such inference is the tendency for observers to perceive lighter image regions as closer. This psychophysical behavior could have an ecological basis because nearer regions tend to be lighter in natural 3D scenes. Here, we show that an analogous association exists between the relative luminance and binocular disparity preferences of neurons in macaque primary visual cortex. The joint coding of relative luminance and binocular disparity at the neuronal population level may be an integral part of the neural mechanisms for perceptual inference of depth from images.

The properties of the natural environment are essential to understanding behavior (1). The study of the statistics of natural images has been instrumental in advancing our understanding of the visual system. Examples are numerous: Center–surround receptive fields of retinal ganglion cells can be understood in terms of their whitening effects on highly self-correlated natural image signals (2). In primary visual cortex (V1), the need to further separate visual signals into their underlying causes provides a potential sparse code explanation for the wavelet-like receptive fields of V1 simple cells (3, 4).

Thus far, knowledge of the statistics of natural images has been most useful for understanding how images are represented and transmitted in the early visual pathway (5). However, efficient image representation is only one of many goals of the visual system. To effectively study perceptual inference in the visual system, we must have an understanding of the joint statistics of images together with their perceptual goals. In particular, to understand how depth and 3D shape are inferred in the brain, we need to first understand the statistical trends that exist between natural images and their underlying 3D structure.

Statistical trends in natural scenes often manifest as a perceptual bias in psychophysical studies (6–12). One perceptual bias that has been observed is that, all other things being equal, humans perceive lighter image regions as being closer. This perceptual effect was first discovered by Leonardo da Vinci who said, “Among bodies equal in size and distance, that which shines the more brightly seems to the eye nearer,” (ref. 13, p. 332). Over the last century, a number of psychophysical studies have characterized this relationship between relative luminance and depth (14–21). We have previously shown that a corresponding negative correlation (r = −0.14) between image intensity and depth (r = −0.24 for log intensity vs. log depth) was found in the statistics of natural scenes (22). This result suggests that the perceptual bias in the psychophysical tests has an ecological basis and is revealing a statistical trend stored within our visual system. Such a trend could be used by the visual system to infer depth in a scene when binocular and other visual cues are either ambiguous or absent.

In this article, we demonstrate that the relationship between relative luminance and binocular disparity tuning of neurons in the primary visual cortex of awake, behaving macaques is consistent with these statistical trends found in natural scenes. We then discuss how the brain could exploit this correlation to estimate depth when the binocular disparity information presented to the receptive fields of these neurons is uncertain or ambiguous.

Results

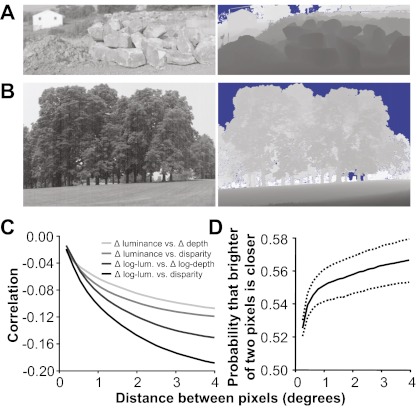
There is a negative correlation between image intensity and depth in the statistics of natural scenes (22). However, intensity and depth information is represented in relative rather than absolute values—e.g., darker than the mean intensity and farther than the fixation depth—even in the earliest stages of the visual system, such as V1, due to gain control, binocular fixation, pupillary dilation, and other factors. Evidence suggests, however, that the negative correlation between image intensity and depth is a consequence of shadows in natural scenes (22–24). The correlation is most apparent on surfaces found in natural scenes that often contain concavities and crevices (22). Concave surfaces are exposed less to the environment and, therefore, are often shielded from ambient and direct light and thus tend to be darker, and the interior points lie farther from the observer. Convex surfaces are exposed more to the environment and, therefore, are often exposed to more light, especially when the light is ambient, and the exterior points lie closer to the observer. Strong examples of this phenomenon can be found in the spaces between piles of large objects (Fig. 1A) and in the depths of leafy foliage (Fig. 1B); pixels deeper into a tree or wooded area tend to be darker, on average. This phenomenon describes a relationship between relative intensity (a point inside a shadow vs. a point outside) and relative depth (a point within a crevice vs. a point outside). Here, we performed further analysis to confirm this relationship exists between relative values of intensity and depth (Fig. 1 C and D). For example, we observe similar negative correlation between comparative metrics applied to the image and range data, respectively (Fig. 1C). Additionally, we can illustrate the relationship between relative intensity and relative depth probabilistically: Given two nearby pixels, the one that is lighter is more likely to be the nearer of the two (Fig. 1D).

Fig. 1.

Examples of the correlation between intensity and depth in natural scenes. (A) Shadows (Left) are produced in the crevasses (range data, Right) of piles of objects. Lighter means farther for the range data images (blue regions were not recorded because they were beyond the range of the scanner). (B) There are also shadows seen in the more distant sections of foliage. (C) Correlation between relative luminance and relative depth using four different metrics (Materials and Methods). (D) Given two pixels, the one that is lighter is more likely to be nearer. Statistical significance of these measurements is described in Materials and Methods.

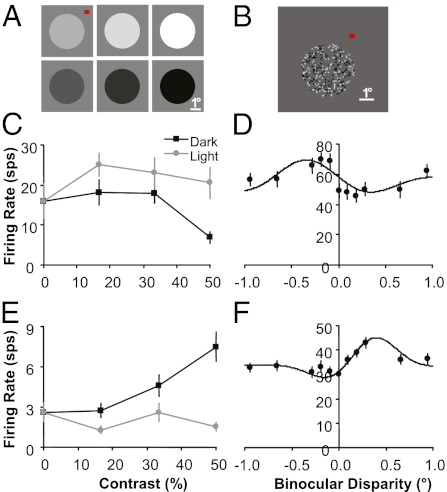
Because the statistics in 3D natural scenes predicted a negative correlation between relative intensity and relative depth, we hypothesized there was an analogous correlation among the neuronal responses in V1 of macaques. Neurons in V1 respond selectively to both the relative luminance (whether an edge, a figure, or a surface is lighter or darker with respect to the background) (25–28) and, via stereo disparity, the depth of a stimulus relative to the fixation plane (29–32) so examining the joint tuning distribution provides a straightforward test of our hypothesis. Using two to eight glass- or epoxy-insulated electrodes simultaneously inserted into V1 of two monkeys and a chronically implanted 100-electrode Utah array into V1 of a third monkey (Materials and Methods), we recorded from a total of 818 single- and multiunits over multiple recording sessions (n = 128, 190, and 500 neurons for monkeys D, F, and I, respectively). We tested the preferences of neurons for relative luminance and depth (rendered by introducing binocular disparity) independently. To determine relative luminance preference, we presented 1-s static 3.5° diameter disks with luminance ranging from progressively darker (black) to progressively lighter (white) on a mean gray background (Fig. 2A). The disk was large enough so that no edge, and therefore no binocular disparity information, was available to each V1 classical receptive field (typically having a diameter of <1°). To determine binocular disparity preference, we presented a 1-s dynamic random dot stereogram (DRDS) in a 3.5°-diameter aperture with disparities ranging from −1° to 1° (Fig. 2B). A DRDS allowed us to measure binocular disparity preference for each neuron without introducing any systematic monocular pattern or structure to each V1 receptive field (30–32).

Fig. 2.

Single-neuron examples of relative luminance and binocular disparity tuning. (A) Disk stimuli used to measure luminance tuning. (B) DRDS stimuli used to measure binocular disparity tuning (image for one eye shown). (C and D) A neuron that responds better to light surfaces and near disparities. (E and F) A neuron that responds better to dark surfaces and far disparities. All error bars are trial-to-trial SE.

Two example neurons whose joint tuning properties are consistent with our statistical prediction are (i) a neuron that responds more strongly to white disks compared with black disks (Fig. 2C) and near binocular disparities (negative) compared with far disparities (Fig. 2D) and (ii) a neuron that responds more strongly to black disks compared with white disks (Fig. 2E) and far binocular disparities (positive) compared with near disparities (Fig. 2F). To confirm whether a general trend of negative correlation exists between relative luminance and binocular disparity preference in V1, we assigned a single value for each characteristic for each recorded neuron. The relative luminance preference for each neuron was assigned a luminance index, which is the ratio of the mean firing rate to the white disk (W) compared with the black disk (B): (W − B)/(W + B). The binocular disparity preference for each neuron was assigned the disparity that produced the maximum mean firing rate in a Gabor function fit (31–35) to the responses of the 11 disparities presented.

To be included in our analysis, first, neurons had to have significant binocular disparity tuning (n = 10–60 trials, one-way ANOVA based on 11 disparities, P < 0.05). Slightly more than half of V1 neurons have significant binocular disparity tuning when measured from the responses to the DRDS (30, 32). We recorded from 357 neurons (44%) with significant disparity tuning (n = 62, 98, and 199 neurons). A higher percentage of neurons were excluded from monkey I (61%) because many electrodes on the array were not close enough to neurons and cannot be moved independently, to provide enough isolation to record from reliable single units with significant disparity tuning. Binocular disparity tuning of single units and multiunits is not correlated in V1 (31) so single-unit isolation is important for observing significant disparity tuning and determining preferred disparity. Second, we discarded a small percentage of disparity-tuned neurons (14%, n = 48 neurons) that had two distinct disparity peaks with firing rates that were not significantly different (t-test, P < 0.05; i.e., “tuned-inhibitory” neurons) (29), because we could not assign these neurons a preferred disparity. And finally, the remaining neurons had to respond significantly to the luminance disk (n = 10–20 trials, one-way ANOVA based on six disks and the mean gray background, P < 0.05). Although disk stimuli with contrast outside of the V1 classic receptive fields have been documented to generate significant V1 responses, the response rates are much lower than those of more traditional stimuli with contrast within the receptive field (26, 36) (Fig. S1). The relatively conservative ANOVA test based on seven disks, therefore, was used to make sure that we included only neurons (64%) with robust responses and reliable luminance index estimates. These criteria provided us with 199 neurons that were suitable candidates for our hypothesis and that we were able to test for a correlation between luminance index and preferred binocular disparity (n = 45, 59, and 95 neurons for monkeys D, F, and I, respectively).

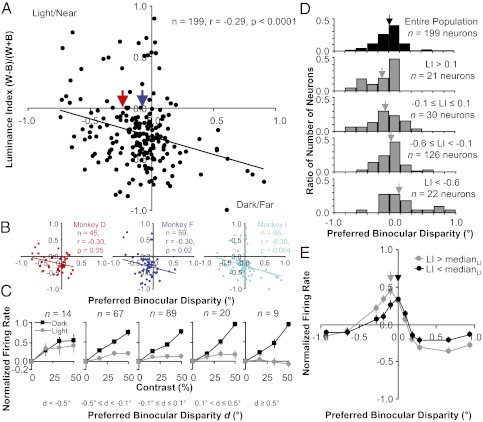
On the basis of these 199 neurons, there was a significant negative correlation that supported the natural scene prediction (Fig. 3A; Pearson's r = −0.29, P < 0.0001) and this trend was very consistent across all three monkeys (Fig. 3B; all negative and overlapping trend lines with r = −0.30, P < 0.05). Because of the uncertainty with the distribution characteristics of our data, we carried out a more rigorous examination of the correlation between the two variables. First, we found that Spearman's rank correlation was similar in magnitude and still highly significant (ρ = −0.24, P < 0.001). Second, we preformed robust regression analysis to test whether potential outliers were strongly influencing the correlation estimate. Using a wide range of weighting functions (provided in the Matlab Statistics Toolbox) and tuning constants, we always observed only very modest changes in the slope of the regression fit, which was always negative and significant (P < 0.005; Fig. S2).

Fig. 3.

Negative correlation between luminance index and preferred binocular disparity. (A) Aggregate scatter plot of measurements made from neurons recorded from all three monkeys. (B) Scatter plot of measurements made from neurons recorded from each monkey individually. (C) Population average of contrast response curves for light and dark disks. Each plot uses a different group of neurons on the basis of their preferred disparity d. The response to a blank gray screen (0%) was subtracted from the contrast response curve for each neuron and then the curve was normalized by the peak firing rate before averaging. Error bars are population SE. (D) Histograms of preferred binocular disparity. Each histogram uses a different group of neurons on the basis of their luminance index LI, ranging from preferring white to preferring black (top to bottom). Arrows are mean preferred binocular disparity. (E) Population average of disparity tuning curves. Each plot uses a different group of neurons on the basis of their luminance index LI. The mean response to all disparities was subtracted from the disparity tuning curve for each neuron and then the curve was normalized by the peak firing rate before averaging. Error bars are population SE.

Because the luminance index uses only the responses to the lightest white and darkest black disk, we also examined the responses to all disks presented to see how they varied with respect to preferred binocular disparity (Fig. 3C). With increasing light or dark contrast, most neurons responded with increasing mean firing rates. Sometimes there was a decrease, saturation, or acceleration in mean firing rate with increasing contrast (e.g., Fig. 2 C and E). Additionally, neurons in V1 responded much more strongly to black disks vs. white disks on average (μ_LI = −0.25 ± 0.02, P = 1 × 10⁻²⁰). This dark bias is consistent with a recent study that examined this particular phenomenon more directly with stimuli that had contrast within the classical receptive field (28) and could also have an ecological basis (37). Overall, you can see that the population average of the contrast response curves for light disks more strongly saturates and even decreases as you move from near to far binocular disparities (Fig. 3C, gray curves, left to right) whereas the population average of the contrast response curves for dark disks increases and accelerates (Fig. 3C, black curves, left to right).

The majority of the neurons in V1 are tuned for disparities near zero (31, 32), which is another trend in the data that matches what is observed in natural scene statistics (38). A histogram of the preferred disparities for our data is consistent with these observations with a large number of neurons with a preferred disparity at or near zero (Fig. 3D, black histogram). The negative correlation between luminance index and preferred binocular disparity results in the strongest white-preferring neurons (luminance index >0.1) being composed of a higher percentage of near-tuned neurons and very few far-tuned neurons (Fig. 3D, top gray histogram, n = 20 neurons). Also, the negative correlation results in the strongest black-preferring neurons (luminance index <−0.6) being composed of a higher percentage of far-tuned neurons and very few near-tuned neurons (Fig. 3D, bottom gray histogram, n = 22 neurons). These shifts in the distribution of preferred disparity for a small subset of the population of neurons lead to subtle, but significant shifts in preferred disparity for the entire population based on white or black preference. The mean preferred disparity for all white-preferring neurons (μ = −0.23 ± 0.06°, luminance index >0, n = 29 neurons; Fig. 3A, red arrow) is significantly nearer (P < 0.005) than the preferred disparity for all black-preferring neurons (μ = −0.07 ± 0.02°, luminance index <0, n = 165 neurons; Fig. 3A, blue arrow).

Because the preferred binocular disparity is based on the response to only one disparity, we also examined the responses to all disparities presented to see how they varied with respect to the luminance index (Fig. 3E). Because the tuning for disparity is narrower than that for the contrast response curves averaged in Fig. 3C, especially near zero disparity (32, 38), population averages of disparity tuning for small groups of neurons (Fig. 3D, second and fourth rows) spread across a relatively wide range of disparities are not very informative and do not resemble single-neuron tuning curves. Therefore, we divided the data into two groups with respect to the luminance index with a large and equal number of samples: neurons with a luminance index above and below the median. Overall, one can see that the population average of the disparity tuning curves for relatively lighter-preferring neurons (Fig. 3E, gray curve; LI > median_LI, n = 97 neurons) responds to relatively nearer disparities than the population average of the disparity tuning curves for relatively darker-preferring neurons (Fig. 3E, black curve; LI < median_LI, n = 97 neurons).

Discussion

In this article, we described the perceptual phenomenon of lighter surfaces appearing to be nearer than darker surfaces. We then described the correlations between image and 3D natural scene statistics, which might provide an ecological basis for this phenomenon. This correspondence suggests that the behavior is evidence of a statistical trend that humans make use of when inferring 3D shape in images. Most previous studies that sought to understand the visual system by analyzing the statistics of natural scenes have explained neurophysiological properties that were already well known, such as the center–surround antagonistic and wavelet-like receptive field structures (2–4), as well as contextual modulation of receptive field responses to contour segments outside the classical receptive field (6, 7, 39). Our study is one of a few studies (5) that instead confirm a prediction made by theoretical studies of natural scenes, using neurophysiological experiments.

Within a given image region, darker surfaces are more likely to be part of a shadow and are thus more likely to be farther away than nearby lighter surfaces. The comparative statistics (Fig. 1) illustrate the tendency for shadowed regions to lie farther from the observer. In addition, these comparative statistics are related to response properties of neurons in V1. Neural responses to luminance in V1 are relative to both the absolute intensity of light striking the retina and also the local relative intensity of the region, due to the center–surround receptive field structure found throughout the early visual system. Likewise, neurons are selective to absolute binocular disparity, which is not a measure of absolute depth from the observer. It is instead a measure of relative depth from the fixation plane, which is commonly focused to minimize stereo disparity for the object fixated at the fovea.

With the neurophysiology experiments, we demonstrated that there is a significant negative correlation between relative luminance preference and preferred binocular disparity among a population of V1 neurons (Fig. 3A). Neurons that respond to near binocular disparities also respond relatively better to lighter disks compared with darker disks than neurons that respond to far disparities. The negative correlation observed is invariant to changes in several disk and aperture sizes that we tested (Figs. S3 and S4). The trend is also clear in the population averages of light and dark contrast response curves as the composition of neurons in each population varied in tuning from near to far preferred binocular disparities (Fig. 3C). Regardless of how we defined the relative luminance preference or ratio between the responses to light disks vs. far disks, we always observed a significant negative correlation so the trend did not depend on any specific choice of a luminance index (SI Text). Overall, the neurophysiological results were robust and consistent with the prediction derived from the analysis of natural scene statistics.

The subtle shifts in disparity estimated from our population response in V1 due to relative luminance preference (Fig. 3 A, D, and E) are comparable to those measured in perception. For example, in psychophysical experiments, a white disk on a gray background at a distance of 125 cm is perceived as 5 cm nearer than a black disk on a gray background (18). Similarly the shift in preferred disparity that we measured between disparity-tuned neurons preferring white and black disks (Fig. 3A, red and blue arrows) would correspond to a difference in depth of 10 cm at distance of 125 cm. The association we measured does not imply that the actual depth-decoding process, including the neural correlate of the perceptual bias, would be located in V1. Because discs were presented binocularly and the disparity of the disk was not ambiguous, the bias would not play a role in the subject's perception (18). More sophisticated experiments would be necessary to uncover the neural correlate of the perceptual bias. Our results reveal that the association in V1 is a possible component of the mechanism of depth inference rather than a by-product of the perception.

Looking at how the modest trend between intensity and depth in natural scene statistics impacts computer vision solutions to estimating depth on the basis of image information can provide insight into how the subtle shift in the neurophysiological response might contribute to the strong perceptual effect. For example, when a regression-based algorithm is trained to infer depth from natural scenes, it learns both shading cues and shadow cues from scene statistics. The shadow cues, which consist of a learned correlation between relative brightness and relative nearness, account for 72% of the algorithm's total performance (24).

Correlations between tuning for populations of neurons and the integration of information by individual neurons for several of the potential depth and 3D shape cues are observed throughout the visual system. In area V1, there is a correlation observed between preferred binocular disparity and temporal frequency of the responses to drifting gratings, which can provide information about the depth cue of motion parallax (40). Motion and disparity information are also integrated in the middle temporal visual area (MT) (41). In V2, orientation tuning measured from responses to binocular disparity-defined edges is correlated with orientation tuning measured from responses to luminance-defined edges (42, 43). Additionally, neurons in several extrastriate areas that respond selectively to more complex depth gradients and 3D shapes appear to generalize their tuning across multiple depth cues including binocular disparity, perspective, and texture (44–47).

Determining depth and identifying 3D shape from images is a difficult problem that our visual system handles very efficiently. Features, structures, and patterns in an image can have numerous potential 3D interpretations, which necessitates that depth perception is solved by inference using a multitude of visual cues to gather as much evidence as possible. Using inference as our foundation, we have approached the issue of full-cue depth perception by first understanding the statistical relationships between images and depth to formulate hypotheses for neurophysiological experiments. We have now identified the neurophysiological basis for one form of cue coupling as early as the primary visual cortex. However, understanding the full scope of depth–cue integration requires studies extending throughout the visual hierarchy. In this work, we have focused on the link between relative intensity and relative depth, a powerful form of cue coupling, and elucidated how this statistical trend in natural scenes might be encoded in a neuronal population in V1 to support the perceptual inference of depth.

Materials and Methods

Range Data.

Scans were collected using the Riegl LMS-Z360 laser range scanner, which measures depth at each pixel by measuring the time before echo of an infrared laser pulse. Simultaneously, a single integrated color photosensor measures the color of visible light within that pixel location. Thus, corresponding pixels of the two images correspond to the same point in space. All images were taken outdoors, under sunny conditions throughout the day (see SI Text for the implications of atmospheric conditions). The camera was kept level with the horizon and positioned either on the ground or on a tripod, ∼1 m off the ground. The resulting dataset includes >30 million pixels.

Depth accuracy of the LMS-Z360 is within 12 mm for objects between 2 and 200 m away. Multiple scans were averaged together for increased accuracy. The range scanner cannot receive echo pulses from surfaces that are out of range (such as sky) or surfaces that are highly reflective (such as water). These regions were excluded from our study (blue regions in Fig. 1; see SI Text and Fig. S5 for the implications of this exclusion). Images in the database had a variety of spatial resolutions; for this study we used 50 images with resolutions of 22.5 ± 2.5 pixels per degree. Each color and depth measurement is acquired independently of its neighbors; no global image postprocessing was applied to any of the images. Each image required minutes to scan; hence, only stable and stationary scenes were taken. All scanning is performed in spherical coordinates. For the purposes of this study, red, green, and blue color values were combined into one grayscale light intensity value according to the International Commission on Illumination (CIE) 1931 definition of luminance. More details on the range image database can be found in our previous article (22).

Binocular disparity was estimated from the range data by assuming a hypothetical subject was fixated at the first pixel and then computing what the binocular disparity of the second pixel would be, assuming that the subject's eye separation was 3.8 cm (typical for rhesus monkeys). Relative luminance and relative depth, such as shown in Fig. 1C, was computed from the range data using the following four metrics: Δ luminance vs. Δ depth, Δ luminance vs. binocular disparity, Δ log luminance vs. Δ log depth, and Δ log luminance vs. binocular disparity.

The statistical correlation between intensity and depth (22) and the range data results are all statistically significant. With >30 million pixels, any standard test for statistical significance results in an extremely high confidence level. However, because nearby pixels within an image are not independent, direct application of a t test would be invalid and overly weak. One strategy for accurately assessing significance is to perform a variation of bootstrapping where the permutation is chosen to preserve the autocorrelation of the data (48). Here, we apply random toroidal shifts to the range data and compute correlation with the (unperturbed) intensity images: Of 5,000 trials, correlation never exceeded the observed values. Another strategy for assessing the significance of correlation is to reduce the number of degrees of freedom of a t test in accordance with the autocorrelation found in natural range and intensity images. The method of Dutilleul (49) suggests that the effective sample size is only 652 or only 13 independent samples per image. Despite this substantial reduction, P < 0.0005 for all correlation values. Ninety-five percent confidence intervals were computed using standard bootstrapping techniques. We used a conservative approach by assuming there was only a single effective sample per image (50 samples in total). We randomly selected 50 images (with replacement), computed the probability that the brighter of two pixels was nearer, and repeated this procedure 1,000 times. Each point on the dotted curve shows the 2.5th percentile or 97.5th percentile value of the bootstrapped samples (sorted independently for each point).

Neurophysiological Recordings.

We used two different procedures for collecting data from three awake, behaving rhesus monkeys (Macaca mulatta) performing a fixation task that were approved by the Institutional Animal Care and Use Committee of Carnegie Mellon University and are in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

For monkeys D and F (female and male, respectively), their data were collected simultaneously with data reported in our previous article where the recording procedures and physiological preparation are described in detail (33). Transdural recordings using two to eight tungsten-in-epoxy and tungsten-in-glass microelectrodes were made in a chamber overlying the operculum of V1. Recordings were digitally sampled at 24.4 kHz and filtered between 300 Hz and 7 kHz, using a Tucker-Davis RX5 Pentusa base station and OpenExplorer software. Disk and DRDS stimuli were presented over the center of each neuron's receptive field while the monkeys performed a fixation task. Receptive fields were at eccentricities ranging from 2° to 5° and were on average <1° in size. Details about measuring disparity tuning, the DRDS stimulus, monitoring eye movements, and receptive field mapping are described elsewhere (33). For testing relative luminance preference, 1-s static 3.5°-diameter disks were presented with seven luminances ranging from progressively darker (black) to progressively lighter (white) on a mean gray background with Michelson contrasts of 0%, 16.7%, 33.3%, and 50% (Fig. 2A). One-second DRDSs were presented in a 3.5° aperture with 0.094° black-and-white dots on a mean gray background, with 25% density, and patterns were updated at a rate of 12 Hz (Fig. 2B). Eleven disparities between corresponding dots for the left- and right-eye images were tested: ±0.94°, ±0.658°, ±0.282°, ±0.188°, ±0.094°, and 0°. Mean firing rates for both stimuli were computed over their entire duration (SI Text and Fig. S6). A window of ±0.5° around a small red dot was used to determine when to reward the monkey for fixation. On the basis of digitally sampled (976-Hz) data from implanted scleral eye coils, the monkeys fixated with a precision of < ±0.1°. Minimum response fields were determined with drifting black or white bars.

For monkey I (male), all procedures were identical to those referenced and described above except for two differences. First, we recorded from neurons using a 10 × 10 Utah Intracortical Array (400-μm spacing), using methods described previously (50, 51). Recordings were digitally sampled at 30 kHz and filtered between 250 Hz and 7.5 kHz, using a Cerebus data acquisition system and software. For this experiment, the array was chronically implanted to a depth of 1 mm in V1 and both sides of the sutured dura were protected by a small piece of artificial pericardial membrane before reattaching the bone flap with a titanium strap. All wires were protected by a silicone elastomer. Data were collected over seven recording sessions that were several days and up to several months apart. On the basis of the distinction in response properties, we determined that we recorded from a different population of neurons during each session. Even on the basis of a single session that yielded enough neurons that responded significantly to both types of stimuli, the primary result of this study was robust for this third monkey because we observed the negative correlation between luminance index and preferred binocular disparity (n = 22 neurons, r = −0.41, P < 0.06). The second difference for monkey I was that stimuli were not centered on the receptive field for each individual neuron, but were rather centered on the mean position of the receptive fields for the population of neurons determined by both minimum response fields on the basis of bar stimuli (33) and spike-triggered receptive fields on the basis of reverse correlation with white noise stimuli (51). Because of the small size of the receptive fields (at an eccentricity of 2° with sizes always <l°) and their tight clustering (highly overlapping), all receptive fields were well within the 3.5° DRDS and disk stimuli.