Hierarchical processing of complex motion along the primate dorsal visual pathway

Abstract

Neurons in the medial superior temporal (MST) area of the primate visual cortex respond selectively to complex motion patterns defined by expansion, rotation, and deformation. Consequently they are often hypothesized to be involved in important behavioral functions, such as encoding the velocities of moving objects and surfaces relative to the observer. However, the computations underlying such selectivity are unknown. In this work we have developed a unique, naturalistic motion stimulus and used it to probe the complex selectivity of MST neurons. The resulting data were then used to estimate the properties of the feed-forward inputs to each neuron. This analysis yielded models that successfully accounted for much of the observed stimulus selectivity, provided that the inputs were combined via a nonlinear integration mechanism that approximates a multiplicative interaction among MST inputs. In simulations we found that this type of integration has the functional role of improving estimates of the 3D velocity of moving objects. As this computation is of general utility for detecting complex stimulus features, we suggest that it may represent a fundamental aspect of hierarchical sensory processing.

In the early stages of the primate visual system the receptive fields of neurons can be readily estimated from the responses to simple stimuli such as spots, bars, and gratings or even by hand mapping (1–3). However, for neurons farther along the visual pathways, the relationship between stimulus input and neuronal output is often far from obvious, particularly in areas that respond to complex stimuli such as faces, objects, or optic flow patterns (4–7). Uncovering this relationship is crucial for understanding the computations that underlie important behavioral functions such as object recognition and navigation.

One well-known example of complex cortical processing is the range of selectivities found in the medial superior temporal (MST) area of the primate visual cortex. Previous work has shown that MST neurons are highly selective for visual stimuli composed of combinations of motion patterns such as expansion, deformation, translation, and rotation (8–12). Although this selectivity has been documented many times over the last 25 y, very little is known about the computations by which it is derived. One prevalent hypothesis is that the selectivity of MST neurons is determined by specific strategies used by the brain to calculate one's direction of motion, or heading, through the world (13–15). In these models, heading is computed by combining the output of detectors tuned to specific motion patterns, and these patterns are reflected in the internal structure of an MST neuron's receptive field.

Although this hierarchical account of MST selectivity is appealingly simple, it has been difficult to confirm experimentally. Indeed previous studies have concluded that MST responses to complex stimuli often cannot be predicted, even qualitatively, from their responses to simple ones (7–9, 16). For example, a recent paper by Yu et al. (7) found that MST receptive field substructure failed to account for the response patterns of MST neurons to combinations of motions. This result led the authors to speculate that highly complex interactions must occur among MST inputs, perhaps involving specific wiring of dendritic compartments. Such findings call into question the simple hierarchical scheme that has been at the heart of most previous models.

In this work we have examined the hierarchical nature of MST processing, using a unique experimental stimulus and a rigorous computational framework. Specifically, we have developed a visual stimulus that efficiently and thoroughly explores the space of complex motion stimuli and used the resulting data to test MST models with different structures. We find that the most successful models take into account the specific properties of MST's most proximal source of afferent input, the middle temporal (MT) area (17–19). Furthermore, we find that such hierarchical models are capable of capturing all of the main features of MST stimulus selectivity, provided that a particular style of nonlinear integration is used to transform MT inputs into MST outputs. We show that this mechanism is consistent with the known properties of cortical neurons and that it can be expressed in a simple mathematical form. Finally, we demonstrate in simulations that this type of integration is useful for extracting the 3D velocity of objects relative to the observer, as it provides strong tuning for velocity with little dependence on other stimulus features. This work therefore provides quantitative validation of a number of existing notions about MST function, while supplying a crucial element (nonlinear integration) that has been previously missing.

Results

MST Neurons Are Tuned to Complex Optic Flow.

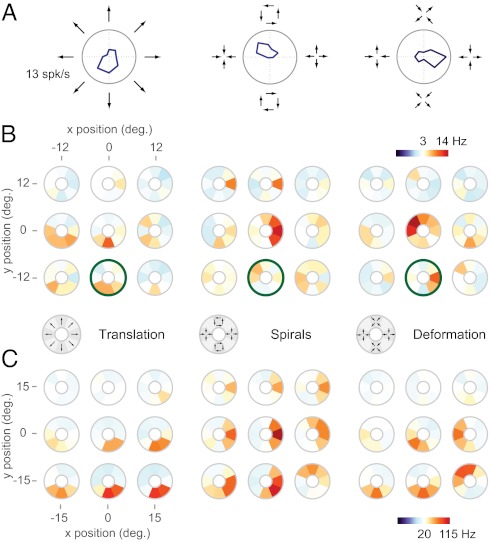
We recorded from 61 neurons in area MST of two awake, fixating macaque monkeys. In most cases we first obtained an estimate of the neuron's selectivity for optic flow by measuring responses to the tuning curve stimuli depicted in Fig. 1A. For a given position in space, 24 tuning curve stimuli were presented, with 8 stimuli corresponding to translation (motion in a single direction), 8 corresponding to spirals (including expansion, contraction, rotation, and their intermediates), and 8 corresponding to deformation (expansion along one axis and contraction along the other). These tuning curve stimuli span the space of first-order optic flow patterns and have proved useful in characterizing optic flow selectivity in the dorsal visual stream (11, 20). These 24 tuning curve stimuli were presented at nine positions lying on a 3 × 3 rectangular grid that spanned most of the central 50° of the visual field, allowing us to examine the positional invariance of the selectivity (21).

Fig. 1.

Tuning of MST neurons for complex optic flow. (A) Tuning curves for a single MST neuron to visual motion composed of translation (Left), spirals (Center), and deformation (Right). Stimuli were presented at one position on a 3 × 3 grid centered on the fovea. (B) Tuning mosaics, in which large responses are represented by red colors, small responses by blue, and median responses by white. Each mosaic captures the tuning for one of the stimulus types shown in A at nine positions in the visual field. The mosaics highlighted in green correspond to the tuning curves shown in A. This cell consistently preferred downward translation (Left) and tuning for spirals (Center) and deformation (Right) varied across positions. (C) Tuning mosaics for a second example cell. This cell consistently preferred downward translation (Left) and expansion (Center) at most spatial positions.

Fig. 1A shows the responses of an example MST cell to the 24 optic flow stimuli when they were displayed in the lower-middle part of the 3 × 3 grid. Here the cell preferred downward-translational motion (Fig. 1A, Left), contracting counterclockwise spirals (Fig. 1A, Center), and deformation with a horizontal divergent axis (Fig. 1A, Right). These responses are replotted in Fig. 1B as tuning mosaics, which are color-coded versions of the standard direction tuning curves. Each mosaic shows the response of a cell to 8 stimuli of a type at a given position in the receptive field, with red representing responses above baseline firing rate and blue responses below baseline. The most saturated red corresponds to maximal firing rate across all stimuli, whereas white corresponds to the median firing rate; tuning mosaics are not otherwise normalized. The mosaics outlined in green correspond to the tuning curves shown in Fig. 1A.

The translation mosaics (Fig. 1B, Left) indicate that this cell shows a preference for downward motion in the bottom and center portions of the screen. The spiral mosaics (Fig. 1B, Center) show that the cell's spiral tuning shifts from position to position, with the strongest preference being for expansion motion at the top and center of the visual field. A weaker response to contraction can be seen near the bottom of the visual field. The deformation mosaics (Fig. 1B, Right) show that tuning for deformation motion also varies from position to position. This cell therefore shows selectivity for a range of stimuli and a strong dependence of stimulus preference on spatial position.

In contrast, Fig. 1C shows a cell with tuning for expansion (Fig. 1C, Center) that is nearly invariant with spatial position. This second cell's translation tuning (Fig. 1C, Left) is similar to that of the cell in Fig. 1B, indicating that there is no obvious relationship between the tuning for translation and that for spirals. Thus, our results, in agreement with previous reports (8, 9), suggest that MST neurons exhibit complex tuning in a high-dimensional stimulus space. To explore this tuning in quantitative detail, we developed a stimulus that sampled the space of optic flow far more thoroughly than the tuning curve stimulus described above. Specifically, we used a continuous optic flow stimulus that consisted of continuously evolving, random combinations of translation, spirals, and deformation stimuli, each of which elicited robust responses from most MST neurons (Movie S1). This approach typically allowed us to measure responses to several thousand optic flow stimuli.

On the basis of the responses to this rich repertoire of stimuli, we sought to develop a quantitative account of the neuronal computations that lead to the variety and complexity of neuronal responses exemplified in Fig. 1. Our approach was to describe each neuron's responses using several mathematical models, all of which shared the same basic structure. In the first stage, the input stimulus is processed by a number of subunits, each of which is selective for motion in a part of the visual field. The output of these subunits is fed to the simulated MST neuron, which sums its inputs and translates the result into a predicted firing rate through an expansive static nonlinearity. Such linear–nonlinear cascade models have strong theoretical foundations that have been described elsewhere (22, 23).

For each MST neuron we optimized the choice of subunits to maximize the quality of the fit to the continuous optic flow data (Methods). We controlled the complexity of the model by cross-validation and evaluated its performance by predicting a neuron's response to the tuning curve stimuli, on which the model was not trained. As a check on the validity of our approach and its implementation, we verified that our methods converge to correct estimates of receptive fields in simulated data (SI Appendix, SI Methods and Fig. S1). As described in detail below, our approach allowed us to examine particular hypotheses about neuronal computation in MST.

Hierarchical Processing Partially Accounts for MST Responses.

The simplest model that could in principle account for the data shown in Fig. 1 involves a computation in which MST neurons linearly compare the visual stimulus to an internal template, with the output reflecting the degree of match. This linear model is directly analogous to the linear spatiotemporal receptive field models that have been used in the luminance domain to study early visual areas (2, 24). Furthermore, it is mathematically tractable, and previous modeling work has shown promise in capturing the complex tuning properties seen in MST (25, 26). We found, however, that whereas such a model can capture some preference to translation, it is unable to capture the more complex selectivities of MST neurons (SI Appendix, SI Methods and Fig. S2).

This result may be expected, as MST neurons have no direct access to the visual stimulus, instead receiving the bulk of their input from MT neurons, which are tuned for both direction and speed (17, 27). Thus, a more promising model involves a computation in which MST neurons linearly sum the output of appropriately tuned MT subunits. Indeed this idea is implicit in many existing MST models (9, 13, 14, 16, 28). We thus developed a hierarchical model in which the input stimulus is first transformed into the outputs of a population of MT-like subunits tuned for stimulus direction and speed (Fig. 2A). The mathematical form of these subunits was chosen to provide an accurate and parsimonious account of the responses of real MT cells. Specifically, MT subunits had receptive fields that were smaller than those found in MST and responses that were tuned for direction and speed, with bandwidths matching those found in real MT cells (SI Appendix, SI Methods).

Fig. 2.

Performance of the linear hierarchical model. (A) The stimulus was processed by groups of MT-like filters (only two groups shown for clarity), which could vary in preferred direction, spatial position, and speed. The outputs of these filters were weighted, summed, and nonlinearly transduced to a firing rate. (B) Predicted tuning mosaics for the same cell as in Fig. 1B under the hierarchical model. The hierarchical model correctly captures the optic flow tuning of this cell, including the preferences for spiral motion (Center). (C) Same as in B but for the example cell shown in Fig. 1C. The hierarchical model fails to capture this cell's tuning to complex optic flow (spirals and deformations).

Fig. 2B shows the predicted tuning curves under this hierarchical model for the example cell shown in Fig. 1B. In this case the model captures the tuning, including the general preference for downward translation (Fig. 2B, Left) and the variety of selectivities for spiral and deformation motion (Fig. 2B, Center and Right). The quality of the prediction can be assessed using , the proportion of explainable variance accounted for (29) (Methods). For this example cell, , which compares favorably with results reported previously in other areas (30–33). Across the MST population, however, the model fared considerably worse, with median . Indeed we found some cells with tuning characteristics that could not be explained even qualitatively with this model structure, and the neuron originally shown in Fig. 1C is an example of this category. Fig. 2C shows that, whereas the hierarchical model successfully captures this cell's tuning for translation (Fig. 2C, Left), it consistently underestimates the responses to spiral stimuli (Fig. 2C, Center). This pattern of errors in the hierarchical model was common across our population of cells, being present in 58% of the cells (21/36, stimulus class comparisons, P < 0.001) (Methods). Thus, we conclude that, although a hierarchical model can account for some MST tuning properties, there is strong evidence that such a model responds too strongly to translation and too weakly to complex optic flow.

Nonlinear Integration Is Necessary to Explain MST Stimulus Selectivity.

Stated in more general terms, the stimulus selectivity of the hierarchical MST model is too similar to that of its inputs, and there appears to be no spatial arrangement of inputs that can bring this model into closer agreement with the data. This result suggests that MST selectivity requires a nonlinear operation that transforms the output of one area before summation by the next (2, 18, 34); indeed such a mechanism has been proposed in other contexts throughout the primate visual system (3, 5, 30, 35). We therefore examined the consequences of adding a nonlinearity (Fig. 3A) that shaped the output of each MT subunit. In particular, we added a flexible, static nonlinearity, represented by a single free parameter β, that could be either compressive (β < 1) or expansive (β > 1) (Methods). For each MST cell the nonlinearity was constrained to be identical across subunits.

Fig. 3.

Performance of the hierarchical model with nonlinear integration. (A) The stimulus was processed by groups of MT-like filters. The output of these filters was passed through a nonlinearity and then weighted, summed, and transduced to a firing rate. For each MST cell, the nonlinearity could vary from compressive to expansive and was identical across all subunits. (B) Predicted tuning mosaics for the same cell as in Fig. 1C under the nonlinear integration model. This model accurately captures the tuning and relative response levels of this cell to translation and spirals. (C) Quality of tuning curve predictions for the hierarchical model with and without nonlinear integration. The nonlinear integration model improves performance in 75% of the tested cells.

Remarkably, this minimal change to the hierarchical model structure yielded far better fits to the data (Fig. 3B) for the expansion-selective cell originally presented in Fig. 1C. In particular, the nonlinear integration model showed enhanced responses to optic flow stimuli such as expansion and rotation, while maintaining strong tuning for translation, with an overall increase in the goodness-of-fit from an = 0.41–0.70. This improved fit to the data was not a trivial consequence of the additional free parameter, as the model was evaluated with a validation procedure (defined in Methods) that was robust to the overall model complexity. Fig. 3C shows that predictions improved for the majority (75%) of MST cells from which we recorded, with the median goodness-of-fit improving from 0.31 to 0.50. These improvements are also reflected in the cross-validated goodness-of-fit measured with the continuous optic flow stimulus, shown in SI Appendix, Fig. S3B. Similar results were obtained if we allowed each subunit to have its own nonlinearity (Table 1, unrestricted nonlinear model) (SI Appendix, SI Methods), suggesting that the shared nonlinearity is sufficient.

Table 1.

Summary of quality of fits of all models considered

Model	Median LL/s, continuous stimulus (median % difference relative to nonlinear MT model)	Median R2, tuning curve stimuli (median % difference relative to nonlinear MT model)
Linear	0.38 (−54)	0.19 (−48)
MT	1.11 (−9)	0.31 (−21)
Nonlinear MT	1.23	0.50
Nonlinear MT (unrestricted)	1.23 (2)	0.45 (−6)
Divisive surround	1.20 (4)	0.48 (−1)
Asymmetric surround	1.12 (−2)	0.34 (−15)
Nonlinear asymmetric surround	1.22 (5)	0.45 (0)
Subtractive surround	1.09 (−3)	0.36 (−15)
Nonlinear subtractive surround	1.22 (4)	0.47 (−1)

Goodness-of-fit for continuous stimulus is defined as cross-validated log-likelihood accounted for per second of data. Quoted percentage values are the median ratio of goodness-of-fit for target model divided by goodness-of-fit for nonlinear MT model. Note that the ratio of medians is not necessarily equal to the median of individual ratios. LL, log-likelihood.

In principle there are two ways in which the introduction of nonlinear integration could improve the fit of the model to the data. The first would be to increase the overall level of responses to spiral and deformation stimuli relative to translation stimuli, while preserving the shape of tuning curves within stimulus categories. This modulation would compensate for the above-mentioned tendency of the hierarchical model to underestimate firing rates for spiral and deformation stimuli. The second would be to improve the ability of the model to match the shapes of the tuning curves, apart from overall response levels for individual stimulus classes. To untangle these two factors, we performed an additional analysis after first normalizing the responses within each stimulus class (translation, spirals, and deformation). SI Appendix, Fig. S3C shows that the nonlinear integration model still improves the quality of predictions in 78% (28/36) of the cells (stimulus class comparisons; Methods). This result indicates that the nonlinear integration model captures aspects of the MST responses that cannot be related simply to stimulus-specific level modulation. Rather the nonlinear integration mechanism is necessary for producing the stimulus selectivity seen in MST responses to optic flow.

We also verified that the success of the model was not influenced by errors in the centering of the stimuli, as stimulus position profoundly affects MST stimulus selectivity (20). We estimated receptive field centers from the tuning curve stimuli and compared the quality of model fits for recordings in which the stimuli were well centered (within 7° of the centers) and those in which the centering was worse (12.4° on average). The addition of the nonlinearity improved the model fits for both groups of neurons (15/19 in the first group, 12/17 for the second group), indicating that our conclusions about nonlinear integration are robust to stimulus centering. Indeed the results were noticeably better when the stimulus was well centered (median = 0.56 for well-centered cases and 0.36 when the centering was worse), which indicates that the model captures the bulk of the selectivity in the center of the receptive field.

Substructure of MST Receptive Fields.

The success of the nonlinear modeling approach allowed us to examine the types of subunit arrangements that were recovered for each neuron. Fig. 4A shows the subunits that contribute most critically to the highly nonlinear neuron shown in Fig. 3B (SI Appendix, SI Methods). Each circle in Fig. 4A corresponds to the position and size of a single MT subunit's receptive field; the direction of each arrow indicates the preferred direction of the subunit; the opacity of the color indicates the weighting; and the color denotes the sign of the contribution, with red being excitatory and blue being inhibitory. The results of this analysis show that this MST neuron's response is largely explained by the selectivity of subunits tuned to downward-left motion in the bottom left portion of the visual field and downward-right motion in the bottom right. This result is consistent with this cell's tuning for both expansion and downward motion.

Fig. 4.

Diversity of receptive field substructures in MST. (A) Receptive field substructure for the example cell shown in Fig. 1C. This visualization was produced by constructing a compact representation of the subunits in the nonlinear integration model. Red represents excitatory input, blue inhibitory input, opacity the magnitude of the weight of the subunit, and the direction of the arrow the preferred direction of the subunit. This cell's tuning for downward motion and expansion is explained by downward-left–tuned subunits in the lower left portion of the visual field and downward-right–tuned subunits in the lower right. (B) Substructure of example cell shown in Fig. 1B. This cell's receptive field was composed of a single, downward-left–tuned subunit. (C–E) The most critical subunits for three expansion-tuned cells. Whereas these cells and the one presented in Fig. 5A can all be described as expansion tuned, they show a diversity of receptive field arrangements. (F) Histogram of number of subunits found by the visualization procedure.

For some MST cells the subunit nonlinearity was less critical, and an example of this type of receptive field is illustrated in Fig. 4B (same cell as in Fig. 1B). Here the cell's receptive field is summarized by a single downward-tuned, centrally located subunit. This cell's nonlinearity had an exponent of 0.6, closer to unity than most neurons in the MST sample (see below for details); the quality of the prediction went from 0.55 to 0.62 with the additional nonlinearity, a comparatively small change. Thus, this MST cell's response properties were similar to those found in MT.

The receptive fields of three more MST neurons are shown in Fig. 4 C–E. Like the cell originally shown in Fig. 1C, these three cells are selective for expansion at multiple positions in the visual field. However, despite the similarity in the tuning, the most critical subunits of these neurons revealed a variety of receptive field substructures. In particular, the position and relative motion directions of the subunits varied substantially from cell to cell, suggesting that these MST cells are not detectors of expansion per se. Rather, the selectivity of these cells appears to be captured by nonlinear combinations of a small number of excitatory and inhibitory inputs,. Estimated time filters and additional examples of receptive fields are shown in SI Appendix, Fig. S6, and the tuning mosaics and predictions for more MST cells are shown in SI Appendix, Fig. S7.

As can be seen in Fig. 4, another prominent feature of MST receptive fields is the spatial overlap of the subunits. Although differences in direction and speed preference tended to increase with spatial distance between subunits (SI Appendix, Fig. S8 D and E), there was also substantial variation on spatial scales smaller than a single subunit (e.g., Fig. 4C). This variation may be important for estimating optic flow quantities such as motion parallax, in which multiple motion vectors occur at nearby spatial locations. More generally, the complex selectivity observed here is likely to be useful in natural contexts, in which motion patterns are determined in part by the structure of the surrounding environment and hence are not constrained to resemble the canonical flow fields typically used experimentally. Overall these results parallel the finding that selectivity for analogous stimuli (e.g., non-Cartesian gratings) in the ventral stream of the visual cortex is related to selectivity for combinations of orientations or other features (4, 30, 36).

As suggested by Fig. 4, the number of subunits recovered by the model differed from cell to cell. This variability is summarized in Fig. 4F, which shows that the number of subunits contributing significantly to individual MST neurons ranged from 2 to 45, with a median value of 9 (SI Appendix, SI Methods). Most of these subunits were excitatory, with a median proportion of excitatory subunits of 81% across our population of cells. The remaining inhibitory subunits can be interpreted either as removal of excitation from tonically active MT cells or as indirect MT influences via MST interneurons, as interareal projections are almost exclusively excitatory. These conclusions are of course contingent upon the assumptions underlying our modeling approach. However, for the most part these assumptions are quite conservative, and, as we show in the next section, relaxing them does not change the main results.

Importance of Compressive Nonlinearities Across the MST Population.

Although Fig. 4 shows that the receptive field substructure varied substantially from cell to cell, we found that the shape of the nonlinearity recovered by the model was highly consistent across neurons. This result is illustrated in Fig. 5A, which plots the distribution of the parameter β for all of the cells in our MST population. The distribution is heavily skewed toward values <1, as shown earlier in individual examples, suggesting that a compressive input nonlinearity is an important property of MST neurons.

Fig. 5.

Analysis of optimal subunit nonlinearity across the MST population. (A) In the nonlinear integration model, subunit outputs were processed by a nonlinearity of the form f(x) = max(0, x)^β. β values <1 correspond to a compressive nonlinearity, whereas values >1 indicate an expansive nonlinearity. Most MST cells required a compressive nonlinearity at the level of each subunit. (B) In the divisive surround model, the output of the center of subunits is divided by the output of a pool of subunits differing in tuning bandwidth and spatial extent. A strongly tuned divisive surround with small spatial extent is equivalent to a static compressive nonlinearity.

Influence of Surround Suppression.

Given the importance of the compressive nonlinearity in accounting for the MST data, we next sought to relate it to potential physiological mechanisms. One important candidate mechanism is surround suppression at the level of MT (37–40). Surround suppression attenuates the responses of MT neurons to pure translation, and so it might account for the above-mentioned observation that the compressive nonlinearity decreases the relative influence of translation on MST responses (Fig. 3B). We therefore extended the model output for each MT subunit to include divisive modulation (41) by a suppressive field that could vary in terms of its spatial extent, its tuning to motion, and its strength. We defined these quantities as free parameters and allowed the model to specify which characteristics best fit the data (Fig. 5B) (SI Appendix, SI Methods).

The results of these simulations indicate that in most cases the optimal surround was well tuned for motion direction and, surprisingly, that it covered a spatial extent similar to that of each subunit's excitatory receptive field (SI Appendix, Fig. S4A). In other words the suppressive influence recovered by the model was typically identical to the excitatory influence, so that stimuli that activated a subunit also limited its output. This type of suppressive mechanism is mathematically indistinguishable from a pure compressive nonlinearity. Indeed the full center-surround model yielded little or no improvement in the quality of the fits relative to the simple nonlinear integration model (SI Appendix, Fig. S4B, and Table 1). Similar results were obtained if we used spatially asymmetric surrounds (40), symmetric surrounds that interacted with the centers via subtraction (34, 38) rather than division, and surrounds that had their own output nonlinearities (SI Appendix, SI Methods). Although these models generally performed better than the linear integration model, none consistently outperformed the one-parameter nonlinear integration model. These results are summarized in Table 1.

Of course these results do not contradict the important role for MT surrounds in motion processing (38, 42), but they do suggest that the contribution of these surrounds to MST optic flow selectivity might be fairly subtle; we return to this issue in the Discussion.

Computational Properties of Nonlinear Motion Integration.

Intuitively the compressive nonlinearity has a straightforward interpretation: As the input to an individual subunit increases, the output saturates quickly, and as a consequence the MST cell responds best to stimuli that drive many different subunits, even if each subunit is activated weakly. This mechanism thus favors stimuli, such as complex motion, that activate many subunits.

This operation is similar to multiplicative subunit interactions described in other contexts (43–46). That is, the compressive nonlinearity is similar to a logarithm (SI Appendix, Fig. S3A), and thus the combination of compressive input nonlinearities and expansive output nonlinearity approximates multiplication through the identity a⋅b = exp(log a + log b). Indeed, we verified in additional simulations that explicit multiplicative interactions between subunits outperformed models of similar complexity in 79% of the MST cells (SI Appendix, SI Methods and Fig. S5).

To quantitatively examine the functional utility of this mechanism we used optimal linear decoding to measure the ability of area MST to represent stimulus information, with and without the nonlinear integration mechanism in place. Specifically, we used our model MST cells to estimate the responses to various stimuli and then trained a simple decoding algorithm to extract various quantities from the population response (Fig. 6A). This method provides insight into the type of information that would be available to a brain region that had access to the output of the MST population (47, 48).

Fig. 6.

Role of nonlinear integration revealed by population decoding. (A) In a decoding simulation, stimuli were processed by a population of MST model cells estimated from the recorded data. The goal of the linear decoder (Top) was to deduce physical parameters of the stimulus on the basis of the output of the MST population. (B) Example stimuli used in the object-decoding simulation corresponding to motion of an object in three dimensions. (C) Performance of the decoder based on input from the hierarchical model population with (black bars) and without (gray bars) nonlinear integration. Results are quantified as the mean error relative to the range tested; smaller values indicate better performance. Error bars indicate 1 SD from the mean, determined through a resampling procedure (Methods). The sensitivity of the nonlinear integration mechanisms to combinations of inputs facilitates the decoding of object velocity on the basis of the output of the MST population.

In our simulations the model MST population responded to a series of discrete objects moving in various directions and speeds, in various positions in the visual field (Fig. 6B). The goal of the decoder was to recover the different components of each object's velocity, independently of its position in visual space. Although we have not explored more complex situations involving different visual environments and observer motion, the position-invariant readout of 3D object velocity is necessary for common behavioral situations, such as vergence eye movement control (49, 50) and estimation of time to contact (51).

The results of this simulation (Fig. 6C) show that the model with nonlinear integration of MT inputs (Fig. 6C, black bars) outperforms the linear hierarchical model (Fig. 6C, gray bars) in reconstructing velocity in all three dimensions. The difference is especially large (a 60% drop in reconstruction error) in the case of the z-component of the velocity, which is defined by expansion optic flow. As mentioned above, the nonlinear integration approximates a multiplicative operation that renders the model less sensitive to the individual components of expansion stimuli, which are ambiguous with respect to the speed of motion in depth. This result suggests that the nonlinear aspects of MST motion encoding are useful for functions that rely heavily on measurement of motion in depth and for which retinal position is relatively unimportant (Discussion).

Discussion

Hierarchical Encoding of Visual Stimuli.

In this work we have found that neurons in area MST can be effectively characterized by a hierarchical model that takes into account the properties of neurons in MT. An important result from this work is that cells with similar stimulus selectivity, as assessed by relatively low-dimensional tuning curve stimuli, can have subunit structures that differ significantly (Fig. 4). Although we cannot say that the subunits recovered by our model correspond exactly to the anatomical inputs received by each MST neuron, they do represent an optimal estimate under a conservative set of assumptions about MT responses. The formidable challenges associated with a direct characterization of the feed-forward inputs to the extrastriate cortex (52) suggest that a model-based approach is particularly valuable.

In addition to a plausible subunit representation, the model requires a nonlinear integration mechanism, which for most neurons is compressive (Fig. 5). Functionally, the compressive nonlinearity appears to be useful primarily for implementing a multiplicative operation similar to that seen in other visual cortical areas (5) and in sensory processing in other species (43–45). A similar approach has recently been proposed to account for the pattern and speed selectivity of MT neurons (53) and for shape selectivity in V4 (30). Indeed a similar idea was suggested as a qualitative account of optic flow tuning in MST (9). To the extent that the tuning properties found in different brain regions share the same nonlinear integration mechanism, one might expect to find that they share similar temporal dynamics (54, 55) and contrast dependencies (56); these predictions will be tested in future work.

In a complementary analysis, we tested the hypothesis that the compressive effect could be a result of center-surround interactions (37–40). We tested a wide variety of interaction types (Table 1), with the result that no mechanism consistently outperformed the simple nonlinear model. Moreover, the surrounds recovered by the model were typically the same size as the centers, suggesting that a spatially extended surround is not necessary to account for MST optic flow selectivity. A likely functional rationale for these surrounds is in performing motion segmentation and shape from motion (42).

Regardless of its precise functional interpretation, the compressive nonlinear operation could plausibly be implemented through inhibitory interactions among MT neurons with similar receptive field positions and stimulus selectivities; a similar “self-normalization” operation at the level of V1 has been posited to be of primary importance in explaining selectivity in MT cells (18, 34, 57). An alternate explanation is synaptic depression at the level of the MT–MST synapse (58). Both mechanisms are equivalent to a compressive static nonlinearity for slowly varying inputs (59). However, self-normalization would have visible effects on the tuning of MT cells, including bandwidth broadening. Given the current knowledge of MT, synaptic depression appears somewhat more plausible and would reconcile our use of a compressive nonlinearity with previous work showing that expansive output nonlinearities are sufficient for modeling the MT output (18). On the other hand, our results are unlikely to arise from contrast normalization or untuned surround suppression at the level of MT (SI Appendix, Fig. S4A).

An alternative explanation for the compressive effect is a form of normalization among MST neurons. A number of different nonlinear tuning operations can be performed through the interplay of feed-forward excitation and divisive normalization (60), including multiplicative input interactions. Although it is reasonable to assume that normalization shapes MST responses given its important role in areas V1 and MT (18, 34, 41, 61), the nature of the normalization pool in MST is unexplored, and as a result it would be difficult to incorporate into our model.

Previous MST models include those that are linear in the velocity domain (25, 26) and those that derive their selectivity primarily from the spatial arrangement of MT-like inputs (11, 13, 14, 28), as well as other more informal proposals (7, 9, 16). Each of these models is capable of reproducing certain qualitative aspects of the MST data, but to date there has been no statistical comparison of different model classes. Most recently, Yu et al. (7) attempted to estimate MST receptive field substructure by stimulating each cell with a small set of 52 canonical optic flow patterns. These authors concluded that the failure of the resulting receptive field models to account for tuning to complex optic flow stimuli implied that MST stimulus selectivity might result from an unknown mechanism that is sensitive to specific pairwise interactions within MST receptive fields.

Although this idea is of course possible, there are two main methodological shortcomings in the Yu et al. (7) work. First, the use of a small stimulus set permitted very limited inference power; our results suggest that thousands of different stimuli are necessary to estimate MST receptive field substructure. Second, the model-fitting approach implemented by the authors involved a comparable number of data points and free parameters and hence would be unlikely to generalize to novel stimuli even with a sufficiently rich training dataset. We therefore suggest that the previously reported lack of correspondence between receptive substructure and stimulus selectivity is not due to any intrinsic feature of MST, but rather to the stimulus and modeling methods used in that study.

Decoding of MST Population Activity.

Functionally, MST neurons are likely to be involved in navigation (14, 62, 63). Indeed, many previous MST models have assumed that MST receptive fields are arranged to compute heading angle during self-motion (13, 14). However, our nonlinear integration model suggests that the properties of MST neurons reflect a more general mechanism that allows MST to participate both in heading and in 3D velocity estimation. Indeed, in naturalistic scenes, heading and object velocity often cannot be estimated separately (64).

In addition to heading, MST is likely involved in controlling tracking eye movements that maintain fixation on moving objects (50). Such eye movements require accurate estimates of motion direction, and our simulation results (Fig. 6C) suggest that the estimation of 3D object velocity relies critically on the computational properties we have identified in MST. Specifically, whereas frontoparallel motion can be recovered with reasonable accuracy by the MT population, accurate calculation of the velocity of motion in depth requires the nonlinear integration mechanism of the kind used by MST neurons. Consistent with this idea, previous work has shown that MST is important for estimating object velocity (49) and lesions of MST impair vergence movements (50).

Our simulations (Fig. 6C) show that a position-independent estimate of 3D velocity can be readily extracted from the output of the MST population and that nonlinear integration improves such estimates substantially. Thus, our findings indicate that nonlinear integration allows MST to form a distributed representation of 3D objects that supports a wide range of behaviors through a simple decoding mechanism (47, 48).

Methods

Electrophysiological Recordings.

Two rhesus macaque monkeys took part in the experiments. Both underwent a sterile surgical procedure to implant a titanium headpost and a plastic recording cylinder. Following recovery the monkeys were seated in a custom primate chair (Crist Instruments) and trained to fixate on a small red spot on a computer monitor in return for a liquid reward. Eye position was monitored at 200 Hz with an infrared camera (SR Research) and required to be within 2° of the fixation point for the reward to be dispensed. All aspects of the experiments were approved by the Animal Care Committee of the Montreal Neurological Institute and were conducted in compliance with regulations established by the Canadian Council on Animal Care.

We recorded from well-isolated single neurons in the MST area. Single waveforms were sorted on-line and then resorted off-line, using spike-sorting software (Plexon). MST was identified on the basis of anatomical magnetic resonance imaging (MRI) scans and its position relative to MT (just past MT during a posterior approach to the superior temporal sulcus). Most of the neurons from which we recorded had large receptive fields that extended into the ipsilateral visual field and that responded to expansion and rotation stimuli in addition to translation. These tuning properties suggest that most of our recordings were from the dorsal, rather than the ventral, portion of MST, but this has not been verified histologically.

Procedure and Visual Stimuli.

Upon encountering a well-isolated MST neuron, we performed a preliminary receptive field mapping with flashed bars and dot fields. For any neuron that was visually responsive, we characterized its responses in terms of tuning curves for three optic flow types: translation, expansion/rotation (spirals), and deformation (eight measurements per optic flow type; see SI Appendix, SI Methods for equations). Random-dot stimuli were presented in a 24° or a 30° aperture at nine different spatial positions on a 3 × 3 grid with adjacent center positions 12° or 15° apart. The grid was placed over the approximate center of the receptive field as determined by preliminary hand mapping.

To explore the space of optic flow stimuli more thoroughly, we also developed a novel continuous optic flow stimulus consisting of dots moving according to a continuously evolving velocity field generated by random combinations of six optic flow dimensions (see SI Appendix, SI Methods for equations). Dots moving according to this velocity field were presented in a circular aperture 24° or 30° wide, which moved slowly around the screen (Movie S1). The stimulus was presented for 6–10 min.

In all cases, dots were 0.1° in diameter at a contrast of 100% against a dark background. The screen subtended 104° × 65° of visual angle at a distance of 32 cm. The stimuli were presented at a resolution of 1,920 × 1,200 and refreshed at frame rates of 60 or 75 Hz. During continuous stimulus presentation, the animal was rewarded after maintaining fixation for 1 s.

Models.

To understand the computations underlying MST optic flow selectivity, we fitted the continuous optic flow data from each cell to models with various types of subunits. In all cases we first binned the spike trains at 50 ms resolution and excluded time periods during which more than half of the stimulus was off the screen or the animal's gaze deviated >1.5° from the fixation point, as well as from 100 ms before loss of fixation to 250 ms following recovery of fixation. This method yielded a series of firing rates, which we describe as a response vector y. For the model, we assumed that this response was generated by a Poisson process with rate r, computed deterministically from the stimulus. The log-likelihood of the model L(y, r) is then given up to an additive constant (22) by

We assumed that the firing rate was given by the rectified output of the receptive field acting on the stimulus, r_t = g(η_t). g must be nonnegative for r to be meaningful; additional constraints on the derivatives of g are required to yield a model that is straightforward to optimize (22, 65). We thus chose g ≡ exp.

The spatiotemporal receptive field acted on the stimulus to yield a response η_t:

Here, F(ρ, θ) is a nonlinear spatial filter that acts on the optic flow stimulus, which is described by the local motion speed ρ(t, x, y) and direction θ(t, x, y). c is a constant offset. We sampled the stimulus at a spatial resolution of 24 × 24 samples, generally covering from 48° to 60° of visual angle. The temporal filter w(τ) was assumed to last five time steps, spanning from −50 ms to −250 ms. This formulation embodies an assumption of separable, linear temporal processing, which is supported by earlier studies of the temporal behavior of MST neurons (66).*

The nonlinear spatial filter F(ρ, θ) was assumed to be given by the sum of M nonlinear subunits f(ρ, θ, p^m), where p^m denotes the parameters of the mth subunit:

We examined the compatibility of the data with several different models, each of which was defined by the structure of its subunits.

Hierarchical model.

This model embodies the assumption that MST responses are approximately linear in terms of their feed-forward input from area MT, which provides one of the strongest projections to MST (27). The tuning of the modeled subunits is determined by three components. Subunits were assumed to have log-Gaussian speed tuning with preferred speed p_ρ:

Note that a second log-Gaussian is subtracted from the first to constrain the response to be zero when there is no motion. Although MT cells tuned to low speeds have robust responses to static stimuli (67), we did not model such responses, as our stimulus poorly sampled slow speeds. We set the speed tuning width to σ_ρ = 1, similar to the mode of the distribution of speed tuning widths reported in MT (68).

The direction tuning of the subunits was given by a Von Mises function with preferred direction p_θ:

The value 1 is subtracted from the result so that by convention a stimulus moving in a direction orthogonal to the preferred direction elicits no response, and a stimulus moving in the nonpreferred direction elicits a negative response; a similar convention was used in previous models of MST (14, 15). The bandwidth parameter was chosen to be σ_θ = 2.5, corresponding to a full-width at half-maximum bandwidth of 86°, similar to the mean value of 83° measured with moving random dots reported in ref. 19. Finally, subunits had a Gaussian spatial profile

The direction, speed, and spatial response of the subunits were combined to form the response of the subunit:

Here p_g denotes the gain of the subunit, and the function h(x) = max(x, 0) returns the positive part of the response (half-wave rectification).

Hierarchical model with nonlinear integration.

This model provides each subunit with a nonlinearity that exhibits either compressive or expansive behavior depending on a free parameter (expansive when β > 1, compressive when β < 1). Subunits take the same form as Eq. 7, but with the nonlinearity replaced by h(x) = max(x, 0)^β. This model reduces to the previous model when β = 1. Importantly, β is shared across all subunits for a given model fit. In practice, we fitted the model for seven different values of β ranging from 0.2 to 1.4 and selected the optimal β for a cell on the basis of the cross-validated likelihood.

Model Fitting.

Estimating the models described above is challenging, as they contain many free parameters and must be fitted with rather noisy data. To constrain the parameters and to obtain fits that extrapolate well to novel data, the fitting procedure must limit the dimensionality of the model. This dimensionality reduction is typically done by including explicit assumptions about the parameters (23). A particularly powerful assumption is that a model is sparse, meaning that most of its parameters are zero (69). In a neurophysiological context, this corresponds to the assumption that only a modest number of subunits are driving a given cell, which is consistent with anatomical and correlation studies of early sensory areas (70, 71). Models fitted with assumptions of sparseness have proved increasingly useful in estimating the receptive field properties of high-level neurons (22, 31, 33). We thus used gradient boosting, a stepwise fitting procedure that introduces an assumption of sparseness (69). The number of free parameters was limited through fivefold cross-validation (23).

Validation and Accuracy Metrics.

For those cells for which the continuous optic flow stimulus spanned the spatial range of the tuning curve stimulus (36/61), we predicted the responses to the tuning curve stimuli on the basis of the continuous optic flow fit. Note that the continuous optic flow stimulus samples a large, six-dimensional space of optic flow, of which the tuning curve stimuli comprised a small number of points. Thus, this approach is a rigorous test of the model's ability to extrapolate to novel stimuli.

For these simulations we ignored the temporal component of the responses, instead predicting the total spike count in response to a stimulus. We allowed the gain and baseline firing rate to be estimated from the data using standard techniques (65) rather than predicted from the continuous optic flow stimulus. Given a predicted response r and an observed response y, the quality of the prediction may be assessed using the standard R² metric of variance accounted for:

In practice the value R² = 1 cannot be attained, as Var(y − r) for a perfect prediction is the variance of the noise, which is nonnegligible in physiological measurements. To recover a natural scale we thus used a corrected R² metric, also known as predictive power (29):

Here is the variance of the unobserved noiseless signal . The explainable signal variance is estimated from the pattern of disagreement between responses in different presentations of the same stimulus (equation 1 in ref. 29).

To determine whether the relative level of responses to different classes of optic flow (translation, spirals, deformation) was correctly accounted for by the different models, we also computed a stimulus class that introduced a free gain per optic flow type. In the case of the hierarchical model, we found that the relative level of responses across stimulus types was misestimated for 70% of cells (25/36, P < 0.001, likelihood-ratio test), and in a majority of these cases (84%, 21/25) predicted responses were too weak for spiral stimuli relative to translation stimuli. We emphasize that the stimulus class metric is not an accurate reflection of the quality of the model predictions, but rather is an artifice that allowed us to isolate one mechanism underlying quality of fit.

Decoding Simulations.

We compared the capacity of an optimal linear estimator to extract information relevant to behavior. From the 61 fits (1 per cell) under the hierarchical models, we generated 61 × 4 = 244 virtual cells through reflections across the x and y axes to compensate for inhomogeneous sampling of visual space. Because the cells were tested at different resolutions and at different screen positions, we scaled and repositioned the receptive fields to span the central 120° × 120° of the visual field. Stimuli were cropped to the central 90° × 90° of the visual field to avoid artifacts around receptive field edges.

An object 1/16th the size of the visual field was simulated as undergoing 3D motion in 1 of 17 directions (left, up, down, right, toward the observer, and intermediate directions; Fig. 6B). The object could be located in 1 of 25 positions lying inside the receptive field. The speed of the object was chosen on a log scale from 2 to 16 Hz; the physical speed of the object may be reconstructed in meters per second or degrees per second if the distance to the object is known.

We reconstructed the physical parameters of the stimulus, using an optimal linear estimator given the outputs of a population of MST cells (47). We picked 122 cells at random from the pool of 244 to yield a decoding population of a size comparable to that previously used in the literature (47). The variables to reconstruct were the signed log velocities in each direction, for example sign(ν_x)log(| ν_x | + 1) for the velocity in the x direction. To do so we computed the weights w that minimized the squared error between the reconstruction Xw and the variable to decode y. Here X is a matrix with one row for each stimulus and 123 columns (1 for each cell and an offset). The quality of the reconstruction was determined by the root mean square (RMS) error and was expressed as a percentage of the range of log velocity in the x direction (5.67 log Hz). Each decoding simulation was repeated for 50 different random choices of decoding population to yield a mean value and SD.