A Bayesian Approach to Joint Modeling of Protein-DNA Binding, Gene Expression and Sequence Data

Abstract

The genome-wide DNA-protein binding data, DNA sequence data and gene expression data represent complementary means to deciphering global and local transcriptional regulatory circuits. Combining these different types of data can not only improve the statistical power, but also provide a more comprehensive picture of gene regulation. In this paper, we propose a novel statistical model to augment proteinDNA binding data with gene expression and DNA sequence data when available. We specify a hierarchical Bayes model and use Markov chain Monte Carlo simulations to draw inferences. Both simulation studies and an analysis of an experimental dataset show that the proposed joint modeling method can significantly improve the specificity and sensitivity of identifying target genes as compared to conventional approaches relying on a single data source.

1 Introduction

Accurate identification of target genes regulated by specific transcription factors (TF) is a crucial step toward understanding organization and function of genetic regulatory networks. Recently, the studies of genome-wide transcription regulation have benefited from the availability of different types of genomic data. Chromatin immunoprecipitation on arrays (ChIP-chip data or genome-wide DNA-protein binding data) [1, 2] provide evidence of direct interaction in vivo between a TF and its targets. At the same time, microarray gene expression data identifies genes that are differentially transcribed in a transcription factor-dependent manner, without discriminating between direct and indirect effects of a regulator [3]. Lastly, DNA sequence data [4] contains information about potential binding affinities for transcription regulators and corresponding regulatory sequences. These data provide valuable information about different aspects of gene regulation, but each type of data individually does not suffice to explain observed patterns of gene regulation. More importantly, because of the noisy nature of high-throughput data, there is limited statistical power to identify true TF binding targets using only one source of data. Thus, integrating these heterogenous and independently obtained data is motivated to improve the detection power as a key step to understanding the mechanism of transcriptional regulation on a genome-wide level [5, 1, 2, 6].

However, how to integrate genomic data efficiently still remains a very challenging problem in current bioinformatics research [7]. Most existing approaches take the sequential steps to combine different data sources [8, 9, 10, 11, 12, 13, 14, 15, 16]. Bie et al [17] proposed a method to use ChIP-chip data, gene expression data and motif data simultaneously to infer the transcriptional modules, but this method did not account for the measurement errors. Beyer et al [18] proposed a probabilistic model which assigns transcription factors to target genes using integration of different sources of evidence. They showed that the new model has a greater accuracy rate than some previous methods. The method requires a training set, including positive and negative controls, which may be unreliable or even unavailable for some TFs. Several other studies used statistical models to combine ChIP-chip data with gene expression data in a coherent framework: Sun et al [19] proposed a Bayesian error analysis model; Xie et al [20] used a shrinkage method; and Pan et al [21, 22] proposed a nonparametric and parametric empirical Bayes approaches respectively to joint modeling. These approaches have demonstrated the feasibility and the advantages of using rigorous statistical methods to integrate two types of data. In this paper, we propose a fully Bayesian parametric approach to joint modeling of DNA-protein binding data (ChIP-chip data), gene expression data and DNA sequence data to identify gene targets of a transcription factor. The proposed method could be extended to incorporate more types of data and provide a general statistical framework for integrated analysis in genomic studies.

Although each source of binding data, gene expression data and DNA sequence data contains information on transcriptional modules, only binding data provide direct evidence of interaction between a TF and its binding targets. So we will use binding data as the primary data while gene expression data and DNA sequence data as secondary in our model. The proposed hierarchical model will automatically account for heterogeneity of different data sources. The information from the secondary data will be incorporated into the inference automatically when the secondary data is correlated with the primary data; otherwise, the inference will mainly rely on the primary data. This is a unique feature of our model.

In the study, we apply the new model to describe the regulon of leucine responsive protein (Lrp) in Escherichia coli(E. coli). Lrp is one of the main regulators of metabolism in E.coli; it regulates transcription of genes involved in transport, biosynthesis and degradation of amino acids, energy and one carbon metabolism [23]. Because of its role in carbon and amino acid metabolism, Lrp has been suggested to be important when bacterial cells make transitions between rich and poor nutritional conditions. Such transitions are essential for microbial adaptation and survival in different environments. Lrp was shown to control expression of over 400 genes in E. coli, consistent with its role as a global regulator [3]. In addition, Lrp is widely distributed and highly conserved in archaea and bacteria [24], underscoring the importance of its regulatory function.

2 Data

2.1 Genome-wide DNA-protein binding data

We mapped Lrp binding sites in the E.coli genome using a standard protocol for two-channel ChiP-chip experiments [1, 2]. Briefly, DNA fragments bound by Lrp were obtained by immuno-precipitating DNA with Lrp-specific antibodies from formaldehyde cross-linked wild type cells, followed by crosslinking reversal and amplification using specific adaptor sequences. The control samples were obtained either from DNA precipitated with Lrp-specific antibodies from lrp knock-out cells or from DNA precipitated in the absence of Lrp antibodies, using the same procedure as with experimental samples. Following DNA amplification, experimental and control samples were labeled with different fluorescence dyes (Cy3 and Cy5) and hybridized against each other using whole-genome E. coli DNA microarrays. The ratio of fluorescence intensities obtained for each spot on the microarray provided a measure of the extent of Lrp binding to the corresponding genomic locus. Although the transcription factor was expected to interact primarily with promoters, most of which reside in intergenic intervals, our microarrays contained only predicted coding sequences in E. coli. We argue that because intergenic regions in the genome of E. coli are short, with only about 20 sequences longer than 1 kbp, DNA sequences enriched in the immunoprecipitation reactions are long enough, 1 kbp on average, to span both regulatory and coding regions. This experiment design does not fit for Eukaryotic organisms due to the size of their regulatory regions, and promoter arrays are more commonly used for those organisms. However, the statistical model proposed in this paper can be adopted to the other experimental platforms. In this experiment, we used five independent replicates.

2.2 Gene expression data

Another microarray experiment was carried out to comprehensively define a family of genes whose transcription depends on the activity of Lrp. Specifically, we identified genes differentially expressed between lrp⁺ (wild type)and lrp⁻ (lrp mutant type)E. coli strains. RNA samples from two strains were compared directly using two-color hybridization on whole-genome DNA microarrays [3]. In this experiment, we obtained data from six independent replicates.

2.3 DNA sequence data

RegulonDB [25] is a database that contains information and tools to study the transcriptional regulation for E. Coli K12. In RegulonDB, 54 input sites (the sites that have evidence to be the binding targets) of Lrp were used to generate the sequence alignment matrix (consensus). Table 1 is the alignment matrix for Lrp downloaded from the RegulonDB database. Using this alignment matrix, we can predict the binding affinity of any given sequence. We use Hertz and Stormo’s method [26] to obtain the score for a given sequence:

$$E=\sum _{l=1}^M\log \left[\frac{n_{lB}+p_{lB}}{p_{lB}\times (N+1)}\right]$$ (1)

where M is the length of the binding site motif, B is the base at position l within the motif, n_lB is the number of occurrences of base B at position l according to alignment matrix, p_lB is the a priori probability of base B at position l (we use 0.25 for any base at any position), and N is the total number of input sites for the alignment matrix. For this particular Lrp alignment matrix, the length of binding site motif M = 13 and the number of input sites N = 54. The idea of this method is to compare the given sequence with the consensus sequence: the more similar to the consensus sequence, the higher score it will have. Therefore, we used mean sequence scores for Lrp DNA sequence data.

Table 1.

Alignment matrix for Lrp downloaded from RegulonDB.

Base	1	2	3	4	5	6	7	8	9	10	11	12	13
A	25	4	15	27	14	27	24	13	26	4	10	13	2
T	23	7	15	19	30	19	29	33	11	30	15	6	38
C	1	7	19	2	7	0	1	0	9	20	21	26	4
G	5	36	5	6	3	8	0	8	8	0	8	9	10

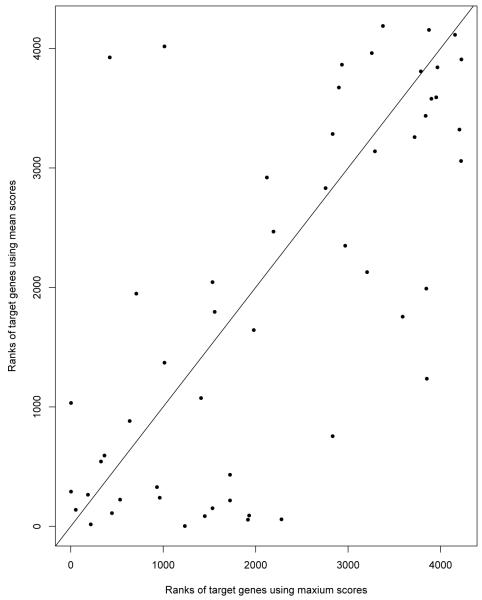
Based on this method, we scanned 500 bp regions upstream of each gene in the E. coli genome and obtained a score for each moving window of size 13 (the width of Lrp position-weight matrix). The averages of 488 scores obtained for each gene were used to represent binding affinity of Lrp to its cognate target sequence. In our choice of a summary statistic, we compared the maximal and mean scores in their ability to identify known Lrp targets (as they are annotated in RegulonDB). Figure 1 presents the scatter plot of the ranks of the known Lrp target genes using the mean and the maximum scores. The lower the rank, the more informative the score is. Figure 1 shows that the mean scores have lower ranks compared to the maximal scores. Supplementary Figure 1 shows that using mean sequence scores can identify more known target genes.

Figure 1.

The scatter plot of ranks of the known Lrp target genes when using maximum sequence scores vs mean sequence scores to summarize the sequence data for Lrp data.

2.4 Data preprocessing and data structure

In order to identify genes whose transcription is controlled directly by Lrp, we combined the DNA-protein binding data, gene expression data and sequence data described above through a joint modeling procedure. There are 3924 genes in each array used for the analysis. Based on our empirical experience for the in-house two-channel microarray experiments, we preprocessed microarray data without background correction, and applied the global and Lowess normalization [27] to binding and expression data sets, respectively. The data structure of the binding data is a 3924 × 5 matrix, with 3924 rows representing genes and 5 columns representing arrays, each element is the log ratio of intensities, which measures relative abundance of sequences bound by Lrp. Similarly, a 3924 × 6 matrix is the data structure for expression data and the sequence data is an array of 3924 × 1.

3 Statistical Models

3.1 Analyzing binding data alone

We used a Bayesian mixture model to analyze binding data. Specifically, suppose X_ij is the log ratio of the intensities of test and control samples in ChIP-chip experiment for gene i (i = 1, …, G) and replicate j (j = 1, …, n). We specify the model as following:

$$\begin{array}{cc}\hfill X_{ij}\mid {\mu }_{ix}& \stackrel{iid}{\sim }N({\mu }_{ix},{\sigma }_{ix}^2),\hfill \\ \hfill {\mu }_{ix}\mid I_{ix}=0& \stackrel{iid}{\sim }N(0,{\tau }_{0x}^2),\hfill \\ \hfill {\mu }_{ix}\mid I_{ix}=1& \stackrel{iid}{\sim }N({\lambda }_x,{\tau }_{1x}^2),\hfill \\ \hfill I_{ix}\mid p_x& \stackrel{iid}{\sim }\mathit{Ber}\left(p_x\right).\hfill \end{array}$$

where μ_ix is the mean of log ratio for gene i; I_ix is an indicator variable taking the value 0 for non-binding target genes and 1 for binding target genes. We assume that the mean log-ratios of non-target genes concentrate around 0 with small variance (${\tau }_{0x}^2$), while the expected mean log-ratios of target genes follow a normal distribution with a positive mean. The prior distribution for indicator I_ix is a Bernoulli distribution with probability p_x. The advantage of this hierarchical mixture model is that we can borrow information across genes to estimate the expected mean intensity, and we can use the posterior probability of being a binding target gene to do inference.

3.2 Joint modeling

Similar to binding data, we used mixture models to fit expression data Y_ij and sequence data z_i. For expression data:

$$\begin{array}{cc}\hfill Y_{ij}\mid {\mu }_{iy}& \stackrel{iid}{\sim }N({\mu }_{iy},{\sigma }_{iy}^2),\hfill \\ \hfill {\mu }_{iy}\mid I_{iy}=0& \stackrel{iid}{\sim }N(0,{\tau }_{0y}^2),\hfill \\ \hfill {\mu }_{iy}\mid I_{iy}=1& \stackrel{iid}{\sim }N({\lambda }_y,{\tau }_{1y}^2),\hfill \\ \hfill {\mu }_{iy}\mid I_{iy}=2& \stackrel{iid}{\sim }N(-{\lambda }_y,{\tau }_{1y}^2),\hfill \\ \hfill I_{iy}\mid I_{ix}=0& \stackrel{iid}{\sim }\mathit{Multilinomial}(p_{y00},p_{y10},p_{y20}),\hfill \\ \hfill I_{iy}\mid I_{ix}=1& \stackrel{iid}{\sim }\mathit{Multilinomial}(p_{y01},p_{y11},p_{y21}).\hfill \end{array}$$

where Y_ij is the observed expression intensity for gene i, array j; I_iy is a three-level categorical variable: I_iy = 0 indicates an equally expressed gene, I_iy = 1 represents an up-regulated gene, and I_iy = 2 means a down-regulated gene; p_y00, p_y10 and p_y20 represent conditional probabilities of being equally expressed genes, up-regulated genes and down-regulated genes for non-binding target genes respectively; p_y01, p_y11 and p_y21 represent conditional probabilities of being equally expressed genes, up-regulated genes and down-regulated genes for binding target genes respectively. Here we used conditional probabilities to connect the binding data and the expression data. Intuitively, the probability of being equally expressed for a non-binding target gene, p_y00, should be higher than the probability of being equally expressed for a binding-target gene, p_y01. The difference between the conditional probabilities measures the correlation between the binding data and the expression data. If the two data sets are independent, the two sets of conditional probabilities will be the same. Therefore, this model is flexible to accommodate the correlations between data.

Similarly, we model the sequence data as:

$$\begin{array}{cc}\hfill z_i\mid I_{iz}=0& \stackrel{iid}{\sim }N({\lambda }_{z1},{\tau }_{1z}^2),\hfill \\ \hfill z_i\mid I_{iz}=1& \stackrel{iid}{\sim }N({\lambda }_{z2},{\tau }_{2z}^2),\hfill \\ \hfill I_{iz}\mid I_{ix}=0& \stackrel{iid}{\sim }\mathit{Ber}\left(p_{z0}\right),\hfill \\ \hfill I_{iz}\mid I_{ix}=1& \stackrel{iid}{\sim }\mathit{Ber}\left(p_{z1}\right),\hfill \end{array}$$

where z_i is the sequence score derived from alignment matrix for gene i; I_iz = 1 indicates that gene i is a potential target gene based on sequence data and I_iz = 0 means gene i is a non-potential gene.

In summary, the model combines expression data and sequence data with binding data through the indicator variables. This model can automatically account for heterogeneity and different specificities of multiple sources of data. The posterior distribution of being a binding target can be used to explain how this model integrates different data together. For example, if we combine binding data with expression and sequence data, the posterior distribution of being a binding target gene I_ix is:

$$\begin{array}{cc}\hfill I_{ix}\mid \cdot & \sim \mathit{Ber}\left(p_{ix}\right)\hfill \\ \hfill p_{ix}=& \frac{A}{A+B}\hfill \\ \hfill A=& p_x{\left({\tau }_{1x}^2\right)}^{-\frac{1}{2}}\mathit{exp}(-\frac{{({\mu }_{ix}-{\lambda }_x)}^2}{2{\tau }_{1x}^2})p_{y01}^{I_{iY}=0}{p}_{y11}^{I_{iY}=1}{p}_{y21}^{I_{iY}=2}{p}_{z1}^{I_{iz}=1}{(1-p_{z1})}^{I_{iz}=0}\hfill \\ \hfill B=& (1-p_x){\left({\tau }_{0x}^2\right)}^{-\frac{1}{2}}\mathit{exp}(-\frac{{\mu }_{ix}^2}{2{\tau }_{0x}^2})p_{y00}^{I_{iY}=0}{p}_{y10}^{I_{iY}=1}{p}_{y20}^{I_{iY}=2}{p}_{z0}^{I_{iz}=1}{(1-p_{z0})}^{I_{iz}=0}\hfill \end{array}$$

where I_ix|· represents the posterior distribution of I_ix condition on all other parameters in the model and the data. We define $\overrightarrow{p_{y0}}=(p_{y00},p_{y10},p_{y20})$ and $\overrightarrow{p_{y1}}=(p_{y01},p_{y11},p_{y21})$. If the expression data does not contain information about binding, then $\overrightarrow{p_{y0}}=\overrightarrow{p_{y1}}$ and all the terms containing Y in the formula cancel. In this case, information contained in expression data is not used to do inference. On the other hand, when expression data contains information about binding, the difference between $\overrightarrow{p_{y0}}$ and $\overrightarrow{p_{y1}}$ will be big and the information in expression data I_iY will be used for the inference. For example, if binding data and expression data are positively correlated, p_y11 is expected to be bigger than p_y10; for an up-regulated gene i, I_iY = 1, p_y11 will be the only parameter for expression data in term A and p_y10 will be the only parameter for expression data in term B. In this case, p_ix derived from this joint model is bigger than that using binding data alone. On the other hand, if binding data and expression data are negatively correlated, p_y11 is expected to be smaller than p_y10 . In this case, for an up-regulated gene i, the probability of being binding target genes, derived from this joint model is smaller than that using binding data alone.

3.3 Prior distributions

The prior distributions of all hyperparameters can be seen in the Supplementary Materials. We specified non-informative priors for ${\tau }_{0x}^2$, ${\tau }_{1x}^2$, λ_x, $\overrightarrow{p_{y0}}$, $\overrightarrow{p_{y1}}$, λ_y, ${\tau }_{0y}^2$, ${\tau }_{1y}^2$, λ_z, p_z0 and p_z1; and because of the identifiability issue [28], we used an informative prior for p_x as p_x ~ Beta(100, 900). We investigated the robustness of using the informative priors in both simulated and real data example. For the individual variance ${\alpha }_{ix}^2$, we plugged in the regularized variance from the data, which greatly reduced the number of parameter estimates in the MCMC computation.

3.4 Statistical inference

Assuming that the binding, expression and sequence data are conditionally independent (condition on the indicator I_ix), we can get the joint likelihood for the model. Based on the joint likelihood, we can obtain the closed form of full conditional posterior distribution for most of the parameters (except λ_x, λ_y and d_z, see Supplementary Materials). Gibbs sampler was used to do Markov chain Monte Carlo (MCMC) simulations for the parameters having closed forms. For λ_x, λ_y and d_z, Metropolis-Hastings algorithm [29] was applied to draw the simulation samples. We ran 2000 iterations, the first 1000 iterations were used as burn-in samples, and the iterations 1000-2000 were used as posterior simulation samples. The posterior samples were used for statistical inferences. The choice of the number of iterations as 2000 is based on the extensive computation load due to thousands of parameters included in the model. We also used 20, 000 iterations for simulation studies and the results are similar to using 2, 000 iterations; we also investigated the parameter convergence issue in Lrp data example.

The goal of the analysis is to identify the true binding target genes, which equals to identifying the genes with I_ix = 1. We used the rank of the posterior probability of being a binding target gene p_ix = P r(I_ix = 1|·) to prioritize candidate target genes. In Lrp data example, we selected the genes with p_ix > 0.5 as the predicted binding target genes, but the number of identified target genes is sensitive to the choice of prior distribution; more comments on this issue is provided in the Discussion section.

4 Simulations

4.1 Simulation set-up

We used simulation studies to evaluate the feasibility and the performance of the proposed method. In each simulation study, we simulated data 10 times and used means and standard errors of sensitivities to evaluate the performance of joint modeling. We simulated 1000 genes, 200 of which were true binding target genes and the other 800 genes were non-target genes. We simulated 5 arrays for binding data and 6 arrays for expression data. For binding data, the observed log-ratios of non-target genes follow a Normal distribution: X_ij~N(0, 1) for j = 1, …, 5; while for target genes, we simulated μ_ix~N(1, 0.5²) and X_ij~N(μ_ix, 1) for j = 1, …, 5.

We used 4 different simulation set-ups. Simulation 1 was a relatively ideal scenario: we assumed that expression and sequence data are highly informative. We assumed that 160 out of 200 true binding target genes are also true differentially expressed genes in the expression data set, and the remaining 40 binding target genes were not differentially expressed. All the true binding targets are also true potential binding genes in the sequence data. Specifically, we simulated 6 arrays of expression data, the expression level of equally expressed genes followed a Normal distribution: Y_ij~N(0, 0.25²) for j = 1, …, 6; while differentially expressed genes followed a Normal distribution Y_ij~N(μ_iy, 0.25²) ,and μ_iy followed a Normal distribution μ_iy~N(1, 0.3²) for 100 up-regulated genes and μ_iy~N(−1, 0.3²) for 100 down-regulated genes. In sequence data, we simulated the calculated mean sequence score Z_i for each gene to follow normal distributions with variance 1, where the mean of target genes was −5, and the mean of non-target genes was −8. The simulation setting for sequence data was based on the distribution of the calculated mean sequence scores from Lrp data.

In simulation 2, we assumed that expression data was informative and used the same simulation set-up as in simulation 1. But we assumed that the sequence data contained no information about true binding target. We randomly selected 200 genes as potential target genes. Simulation 3 assumed that sequence data was informative and we used the same set-up as in simulation 1. But we assume expression data does not contain information, we randomly selected 200 genes as differentially expressed genes and other 800 genes as equally expressed genes. Simulation 4 represented a more practical scenario, we assumed that expression and sequence data contained partial information. We simulated 200 differentially expressed genes, and 140 of them were true binding target genes and the others were non-target genes. For sequence data, we assumed 180 genes were true target genes among 200 total potential genes. Our expectations were: the joint modeling can detect more target genes when the expression or sequence data were informative; and even when the expression and sequence data were non-informative, the joint modeling would not give poorer results. Table 2 summarizes the simulation parameters.

Table 2.

The summary of true parameters used for simulation set-up 1-4.

Simulations	Pr(Iix=1)	Pr(DE|Iix=0)	Pr(DE|Iix=1)	Pr(Iiz=1|Iix=0)	Pr(Iiz=1|Iix=1)
Set-up 1	0.2	0.05	0.8	0.0	1.0
Set-up 2	0.2	0.05	0.8	0.2	0.2
Set-up 3	0.2	0.2	0.2	0.0	1.0
Set-up 4	0.2	0.075	0.7	0.025	0.9

We used simulations 5 and 6 to check the robustness of the model to the assumptions. Simulations 5 and 6 were similar to simulation 1, but in simulation 5, X_ij came from a t distribution with degree of freedom 5; in simulation 6, X_ij were not independent, we assumed the correlation between X_ij and X_ik is 0.5 for j ≠ k.

We used another simulation study (Simulation set-up 7) to further explore the performance of joint model in a practical scenario, where expression and sequence data contained partial information about binding. Among 200 differentially expressed genes,100 were true binding target genes and the others were non-target genes. For sequence data, 140 genes were true target genes among 200 total potential genes.

4.2 Results

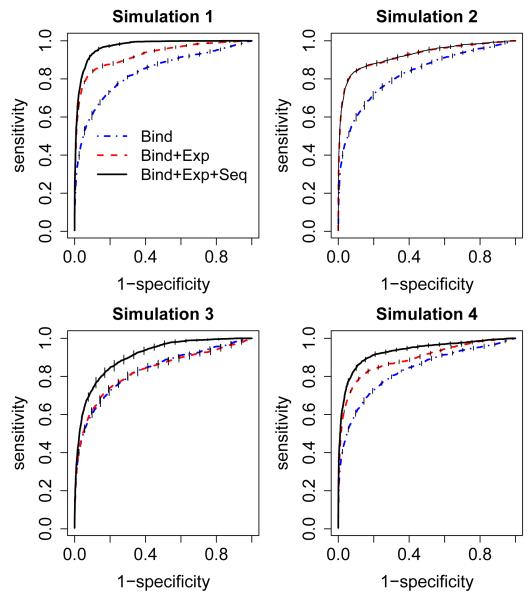
Table 3 shows the conditional probability estimates from MCMC for simulation set-up 1-4. We specified the prior distribution for p_x as Beta(200, 800). In simulation 1, both expression and sequence data were very informative, i.e most of the true binding target genes were also differentially expressed (DE) genes and potential genes. Under this scenario, the estimated probability of being DE genes for binding target genes was 0.865 with standard error 0.021, while the estimated probability of being DE for non-binding target genes was 0.004 with standard error 0.001. The big difference between the two conditional probabilities implies high correlation between the binding data and the expression data. So the parameter estimation and the conclusion were consistent with the truth. Receiver operating characteristic (ROC) curves were used to compare the joint modeling with using binding data alone. Figure 2 shows that in simulation 1, combining expression data with binding data can detect more true binding target genes, and the performance can be further improved after adding sequence data.

Table 3.

The means and standard errors of the posterior probabilities of being binding target genes ($\widehat{\mathit{Pr}}(I_{ix}=1)$), probabilities of being differentially expressed genes for non-binding target genes ($\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=0)$), probabilities of being differentially expressed genes for binding target genes ($\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=1)$), probabilities of being potential genes for non-binding target genes ($\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=0)$), probabilities of being potential genes for binding target genes ($\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=1)$) from 10 simulated data sets for each set-up. The prior distribution for p_x is Beta(200, 800).

Simulations	$\widehat{\mathit{Pr}}(I_{ix}=1)$	$\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=0)$	$\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=1)$	$\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=0)$	$\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=1)$
Setup 1	0.214±0.003	0.004±0.001	0.865±0.021	0.152±0.031	0.966±0.006
Setup 2	0.198±0.005	0.032±0.007	0.878±0.035	0.639±0.051	0.640±0.061
Setup 3	0.204±0.006	0.201±0.012	0.173±0.050	0.365±0.085	0.929±0.032
Setup 4	0.218±0.003	0.005±.001	0.833±0.031	0.169±0.023	0.955±0.007

Figure 2.

ROC curves for simulation studies 1-4. Each simulation study was performed 10 times, the mean and standard errors of sensitivities (the vertical tick marks on the line) were used to evaluate the performance of each model.Bind: using binding data alone; Bind+Exp: using binding data and expression data; Bind+Exp+Seq: using binding data, expression data and sequence data.

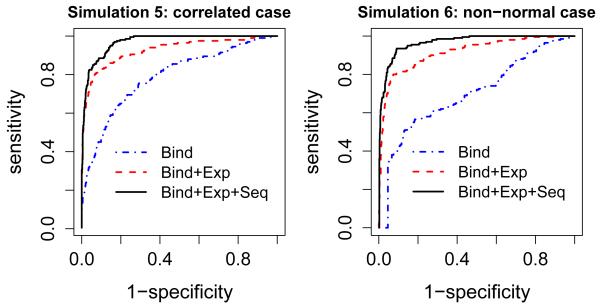
When the sequence data was random and expression data was informative as in Simulation set-up 2, the probabilities of being DE genes were also different for binding and non-binding target genes (0.03 v.s 0.88). But the probabilities of being potential genes were similar for binding and non-binding target genes (0.639 v.s 0.640). ROC curves show that adding expression data can detect more target genes, but adding the sequence data does not improve the performance, which is consistent with our expectation. An advantageous feature of this model is that the performance will not get worse even if the sequence data is random, which is a desirable property for joint modeling because we do not know the quality of different data sources. Similarly, when the expression data was random in simulation 3 , the estimated conditional probabilities of being DE genes were similar (0.20 v.s 0.17) for binding and non-binding genes. A joint model that includes expression data did not detect more true direct target genes. In Simulation set-up 4, the probabilities of being DE genes for binding and non-binding target genes were 0.83 and 0.005, and the probabilities of being potential genes for binding and non-binding genes were 0.955 and 0.169. Figure 2 shows that the joint modeling can improve the detection of true binding target genes. Similar results can be seen for Simulation set-up 7 (Supplementary Figure 2). For Simulation set-up 7, we also calculated the area under curve (AUC) for each method (the simulation was repeated 50 times), and the results were summarized by boxplots (Supplementary Figure 3). It shows the significant improvement (p-value < 0.0001) of the proposed joint modeling approach. Figure 3 illustrates that even when the normal distribution and independence assumptions are violated, the joint modeling still has better performance than using binding data alone.

Figure 3.

ROC curves for simulation studies 5 and 6.

In order to demonstrate the advantage of considering the correlations among different data in the model, we compared the proposed joint modeling approach with combining p-value approach [30, 31], which is commonly used in Genomics data meta-analysis. Supplementary Figure 4 compares ROC curves by using joint modeling and combining p-value approaches in Simulation set-up 2, where the expression data is informative but the sequence data is random. It shows that joint modeling outperforms combining p-value approach when one data set does not contain any information about binding. Similar results can be seen for Simulation set-up 3. When both expression and sequence data contain binding information ( Simulation set-ups 1, 4 and 7), the performance of joint modeling and combing p-values are similar.

We also investigated the effects of using different priors on the parameter estimations and identifying binding target genes. In Simulation set-up 1, we specified different priors for p_x as p_x ~ Beta(200, 800) (prior 1) and p_x ~ Beta(100, 900) (prior 2). Supplementary Table 1 compares the parameter estimations using the two priors and the true parameters in Simulation set-up 1. It shows that the parameter estimations are sensitive to the prior specifications. However, Supplementary Figure 5 shows that ROCs are almost identical when using different priors and the performance of identifying target genes is very good. Therefore, the ability to identifying binding target genes is robust to the prior specification.

5 Application to the Lrp regulator in E. coli

5.1 Results

Table 4 gives the posterior means and quantiles of some important parameters based on 2000 simulation draws from the Bayesian hierarchical joint model applied to Lrp data. The estimated mean of probability of being target genes (P_x) was 0.1. The probability of being DE genes for binding target genes was 0.61 with 95% credible interval (0.40 - 0.77), which was significantly higher than that for non-binding genes (0.1 with 95% credible interval 0.07-0.13). The probabilities of being potential genes for binding and non-binding genes were also different (0.55 v.s 0.43), but this difference was not statistically significant. So the correlation between binding data and expression data was higher than the correlation between binding data and sequence data.

Table 4.

The posterior mean and quantiles of probabilities for lrp data example when using prior p_x ~ Beta(100, 900).

Parameters	Posterior quantiles
	mean	2.5%	25%	median	75%	97.5%
$\widehat{\mathit{Pr}}(I_{ix}=1)$	0.10	0.09	0.09	0.10	0.11	0.12
$\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=0)$	0.10	0.07	0.09	0.10	0.11	0.13
$\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=1)$	0.61	0.40	0.54	0.63	0.69	0.77
$\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=0)$	0.43	0.37	0.41	0.43	0.45	0.49
$\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=1)$	0.55	0.42	0.50	0.54	0.60	0.68

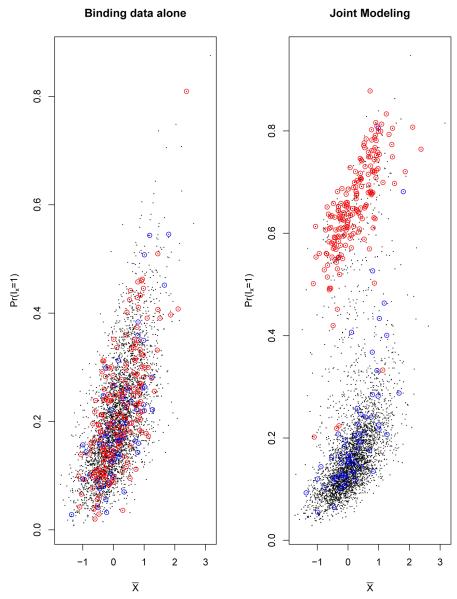
We used the scatter plots to illustrate the posterior probabilities of being target genes. Figure 4 shows that when using the binding data alone, the estimated posterior probabilities were positively associated with the mean binding intensities from binding data. The relationship between the posterior probability and the mean intensities (fold changes) was not strictly monotone because the posterior probability also accounts for the measurement error for each gene [28]. In this model, the posterior probabilities of being binding target genes do not depend on the expression data or sequence data. On the other hand, following joint modeling, the posterior probabilities of being binding target genes for the genes with high expression values are increased compared to using binding data alone, but the sequence scores have less effects on the estimation of posterior probabilities for this data.

Figure 4.

The scatter plots of posterior probability of being binding target genes(P r(I_x = 1))vs mean binding intensities ($\stackrel{‒}{X}$) for using binding data alone model and joint modeling for Lrp data. Each black dot represents one gene in E. Coli chromosome, X-axis represents the observed binding intensities from binding data, Y-axis represents the estimated posterior probability of being binding target genes from either binding data alone model (left panel) or from joint modeling (right panel). The dots with red circles represent the genes with high expression values ($\mid \stackrel{‒}{Y}\mid >2$). The dots with blue circles represent the genes with high sequence scores (z > −4). In binding data alone model, the estimated posterior probabilities are positively associated with the mean binding intensities, and the posterior probabilities do not depend on the expression data or sequence data. In joint modeling, the posterior probabilities of the genes with high expression values (with red circles) increase compared to using binding data alone; the sequence scores have less effects.

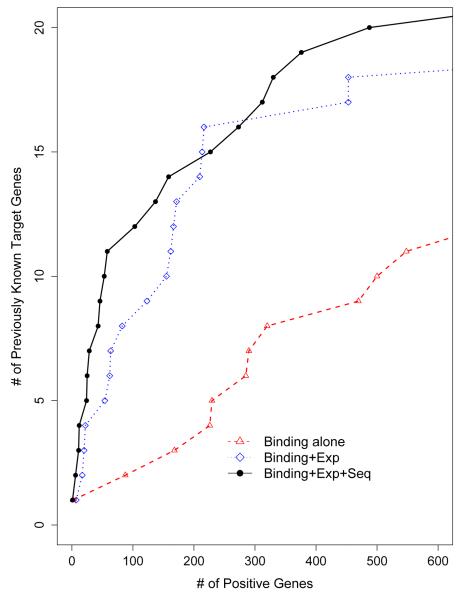
We evaluated the performance of joint modeling by 24 previously known Lrp binding target genes. Figure 5 demonstrates that the joint modeling can identify more previously known target genes as compared to using binding data alone. For example, there were 16 known target genes among top 300 gene list identified by joint modeling, and the corresponding number was 7 with the binding data alone. Table 5 lists the names of 24 known Lrp target genes and their ranks generated by joint modeling and the binding data alone.

Figure 5.

Number of the genes previously known to be bound by Lrp based on the literatures among the top ranked genes for Lrp data.

Table 5.

The ranks of known Lrp target genes generated by joint modeling method and binding data alone. The lower is the rank, the better is the performance of a model.

Gene	Rank (Binding)	Rank (joint)
livJ	2	1
serA	168	6
gltB	2218	11
fimA	226	12
sdaA	285	24
lrp	1150	25
ilvL	470	28
osmY	1382	43
stpA	1382	46
kbl	1435	53
ilvI	290	58
ompF	2323	103
gcvT	1750	137
lysU	680	158
serC	548	227
ompC	3460	273
osmC	2770	312
leuL	88	330
aidB	2400	376
fimE	320	488
malT	230	792
livK	500	802
dadA	1944	1036
yeiL	2596	2513

The genes without previous knowledge about the Lrp binding were also investigated. hdeA was identified as the binding target genes by joint modeling, but was not identified by using binding data alone. HdeA (hns-dependent expression protein A) is a single domain alpha-helical protein localized in the periplasmic space and is involved in acid resistance that is essential for infectivity of enteric bacterial pathogens. The intensity level for hdeA was very high in expression data, which increased the posterior probability of being target gene by using the joint modeling. Another interesting gene identified by joint modeling was BrnQ (ranked 19th). All binding data, expression data and sequence data provided moderate evidence of BrnQ as the target gene, but only analyzing three data sets together could provide significant evidence that BrnQ as the target gene. BrnQ is a branched chain amino acid transporter and is related to Lrp binding.

We also used the functional enrichment analysis to illustrate the biological significance of top 100 genes identified by joint modeling or the binding data alone. The results can be seen in Table 6 and Table 7.We used MultiFun cell function assignment schema [32] from the databases GenProtEC (http://genprotec.mbl.edu) to assign the gene function. The function codes indicate which function group the genes belong to. For example, function code 1.1.3 represents function “amino acids metabolism”; its parent node is function 1.1, “Carbon compound utilization ”; the function codes 1.1.3.2 and 1.1.3.7 are its child nodes, which are “L-serine degradation” and “Threonine catabolism” respectively. Therefore, the function codes represents the relationship among function groups in the tree structure. Table 6 shows that joint modeling can identify 21 functional groups with gene enrichment (p < 0.01) . Among these enriched functional groups, 4 groups were related to amino acids biosynthesis (Function code 1.5.1) including Leucine biosynthesis; and 5 groups were related to carbon compound utilization (Function code 1.1) . These findings were consistent with the knowledge that Lrp plays an important role in carbon and amino acid metabolism. On the other hand, among 100 genes identified by using binding data alone (Table 7), 13 functional groups were enriched ; 4 of these groups were related to amino acid biosynthesis and 1 was related to carbon compound utilization. Compared to using binding data alone, joint modeling allowed identification of a more complete set of functional groups.

Table 6.

The functional groups whose genes were over-represented among top 100 genes, as identified by the joint model applied to the Lrp data set. The function code indicates which function group the genes belong to and the relationship among function groups in the tree structure. For example, function code 1.1.3 represents function “amino acids metabolism”; its parent node is function 1.1, “Carbon compound utilization ”; the function codes 1.1.3.2 and 1.1.3.7 are its child nodes, which are “L-serine degradation” and “Threonine catabolism” respectively.

Function names	Function code	P-values
Trehalose degradation	1.1.1.18	0.001897
Ribose degradation	1.1.1.22	0.006116
Amino acids metabolism	1.1.3	0.002218
L-serine degradation	1.1.3.2	0.000643
Threonine catabolism	1.1.3.7	0.000114
ATP proton motive force interconversion	1.3.8	0.002989
Serine biosynthesis	1.5.1.11	0.009022
Alanine biosynthesis	1.5.1.17	0.001897
Isoleucine biosynthesis	1.5.1.18	2.22E-07
Leucine biosynthesis	1.5.1.19	3.40E-05
Glycoprotein biosynthesis	1.6.11	0.001692
rRNA Information transfer	2.2.6	−2.09E-17
Nucleoproteins transfer	2.3.7	0.005848
periplasmic binding component transport	4.3.A.1.p	0.008304
F-ATPase Superfamily transport	4.3.A.2	0.001207
The PTS Galactitol (Gat) Family transport	4.4.A.5	0.006116
L-leucine transport	4.S.108	0.009022
H+ transport	4.S.82	0.000437
Adaptation to stress ( Osmotic Pressure)	5.5.1	0.000976
Adaptation to stress ( pH response)	5.5.4	1.06E-05
Transposon related	8.3	2.57E-09

Table 7.

Among top 100 genes identified by using the binding data alone, the enriched function groups and the corresponding P-values for Lrp example.

Function names	Function code	P-vlues
Ribose degradation	1.1.1.22	0.00015
Serine biosynthesis	1.5.1.11	0.008847
Alanine biosynthesis	1.5.1.17	0.00186
Leucine biosynthesis	1.5.1.19	0.00055
Ribonucleoside biosynthesis	1.5.2.4	0.00186
Pentose phosphate shunt	1.7.3	0.001172
rRNA Information transfer	2.2.6	7.04E-17
Methylation	3.1.1.2	0.008847
Sigma factors	3.1.2.1	0.009653
Stimulon regulation	3.3.3	0.000796
L-leucine transport	4.S.108	0.000295
tyrosine transport	4.S.154	0.000507
Transposon related	8.3	2.58E-08

5.2 Model diagnostics and sensitivity analysis

In Lrp data analysis, we specified an informative prior to the proportion of binding target genes p_x as Beta(100, 900) distribution to address the identifiability problem [28]. We investigated whether the prior distribution of p_x influenced the main analysis results by using a different prior p_x ~ Beta(200, 800). Table 8 shows that the overlap between the lists of top genes for two priors was high, indicating that the candidate lists are robust to the choice of priors. Table 9 gives the posterior means and quantiles of the same parameters as in Table 4 but using prior p_x ~ Beta(200, 800). It leads to the similar conclusion as using prior p_x ~ Beta(100, 900): the correlation between binding data and expression data is higher than the correlation between binding data and sequence data. Thus the gene ranks are relatively robust to the informative prior. On the other hand, the posterior probability of being binding target gene depends on the prior distribution of p_x, so the cut-off for claiming the binding target genes is sensitive to the priors. Section 6 gives more discussion on this issue.

Table 8.

The overlap between two different priors in Lrp data analysis.

Number of Genes	Overlaps
100	68
200	152
300	258
400	356
500	444
600	529
700	599

Table 9.

The posterior mean and quantiles of probabilities for lrp data example when using prior p_x ~ Beta(200, 800).

Parameters	Posterior quantiles
	mean	2.5%	25%	median	75%	97.5%
${\widehat{P}}_x$	0.21	0.18	0.20	0.21	0.22	0.24
$\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=0)$	0.07	0.01	0.05	0.07	0.09	0.12
$\widehat{\mathit{Pr}}(\mathrm{DE}\mid I_{ix}=1)$	0.48	0.30	0.40	0.48	0.54	0.70
$\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=0)$	0.43	0.35	0.41	0.43	0.45	0.50
$\widehat{\mathit{Pr}}(I_{iz}=1\mid I_{ix}=1)$	0.51	0.42	0.47	0.50	0.54	0.62

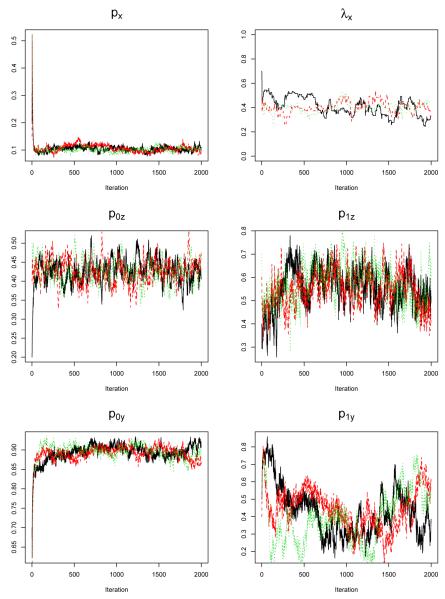
In MCMC simulations, we ran 2000 iterations and used 1000 – 2000 iterations as our simulation samples. We also used different initial values to look at the convergence of the MCMC simulations. Figure 6 shows the trace plots of some parameters, the MCMC converged well for the parameters. Gelman and Rubin statistics [33] for p_x, λ_x, p_0z, p_1z, p_0y, p_1y have been calculated, and all of them were around 1 (less than 1.1), indicating the good convergence of chains.

Figure 6.

Convergence check.

6 Discussion

With the rapid accumulation of data from high-throughput experiments such as gene expression, protein-protein interactions, genome sequences and genome-wide DNA-protein binding maps, there is an urgent need to develop reliable and robust methods for integrating these heterogeneous data to generate systematic biological insights into states of cells, mechanisms of diseases and treatments. The proposed joint modeling approach specifically addresses such a need. Through both simulations and a real data example, we illustrated that our method can improve specificity and sensitivity of the analysis as compared to the conventional approaches relying on a single data source. In this study we jointly modeled DNA-protein binding data, expression data and DNA sequence data, and the approach could be extended to combine more sources of data within the presented general statistical framework. Similar to other high throughput data analysis methods, exploratory data analysis will facilitate selecting appropriate integrated analysis methods for a specific data set.

We want to emphasize that the purpose of the proposed model is to combine the primary data, which contains direct information to answer the specific biology question, with some secondary data, which might contain relevant information to answer the specific biology question indirectly. In the Lrp example, the specific biology question is: which genes are the direct binding targets of Lrp? Binding data can be used alone to directly answer this question and is regarded as the primary data. Expression data comparing lrp⁺ and lrp⁻ strains could identify genes which express differentially between the wild type and the Lrp knockout stains. If binding data and expression data are correlated, information from expression data will be used to identify binding targets as illustrated in the real data application. However, if binding data and expression data are not correlated, it may indicate that most of differentially expressed genes are in the downstream of the Lrp regulation pathway; i.e. these genes are not the direct binding targets of Lrp. In this context, expression data should not be used to infer the binding targets and our model could automatically detect it and largely ignore the secondary data. Therefore, in this aspect, the application of our model is different from the traditional integrative analysis or meta-analysis, where different data sources are all forced to contribute to final results.

For both simulated and real data, we have shown that the posterior probability of being a binding target and the parameter estimates are not robust to the prior specification for p_x. This is mainly due to the identifiability problem of the parameter p_x [28]. These results illustrate the challenges and difficulties in estimating the proportion of true target genes in high dimensional and complex datasets. In particular, we do not recommend any direct use of the estimated p_x from this model, such as in choosing a cut-off for identifying binding target genes in practice. However, the ranks of genes for being binding targets are robust to the specified priors in both simulated and real data. In practice, the ranking of the genes is important because it provides a critical guidance to selecting a subset of the genes for the following more expensive and time-consuming functional verification experiment. For this purpose, the proposed joint modeling method clearly outperforms using binding data alone, and the results are robust to the prior specification. If we need to choose a cut-off for identifying binding target genes, some use of the false discovery rate (FDR) may be helpful, though further studies are needed.

Recently, genome-wide gene networks, represented by directed/undirected graphs with genes as nodes and gene-gene interactions as edges, have been constructed using high-throughput data [34, 35]. It is reasonable to assume that the neighboring genes in a network are more likely to share biological functions and thus to participate in the same biological processes, therefore, their expression levels are more likely to be similar to each other. Some work has attempted to incorporate genome-wide gene network information into statistical analysis of microarray data to increase the analysis power [36, 37, 38]. It will be interesting to incorporate the existing gene regulatory networks in the proposed joint modeling in the future.

In the Lrp example, the available sequence data contain little information about binding (because the conditional probabilities are not much different). There are several possible reasons: First, the sequence specificity of Lrp regulation may not be strong. Lrp is a global gene regulator, the mechanism of its regulation remains unknown. Robison [4] and our preliminary results show that the sequence specificity of Lrp regulation is much lower than other TFs, such as lexA. To verify this assumption, we can do similar experiments and analysis for lexA in the future. Second, the input sequences in regulonDB for the sequence data of Lrp may be incomplete, and there may be other unknown informative motifs for Lrp. To partially address this problem, we can use the results of our joint modeling as an input to obtain new sequence data and run joint modeling iteratively, which may improve our ability to detect the binding targets of Lrp.

We implemented our method in R, and our R code is available upon request.