Abstract
Understanding the effect of cold storage on arterial tissues is essential in various clinical and experimental practices. Cold storage techniques could significantly affect the post-cryosurgical or post-cryopreservation mechanical behavior of arteries. Previously, arteries were considered homogenous and elastic and the changes in material properties due to cold storage were inconclusive. In this study, using a custom-made nanoindentation device, changes to the local viscoelastic properties of porcine thoracic aorta wall due to three common storage temperatures (+4°C, –20°C and –80°C) within 24 hours, 48 hours, 1 week and 3 weeks were characterized. The changes to both elastic and relaxation behaviors were investigated considering the multilayer, heterogeneous nature of the aortic wall. The results showed that the average instantaneous Young's modulus (E) of +4°C storage samples decreased while their permanent average relaxation amplitude (G∞) increased and after 48 hours these changes became significant (10%, 13% for E, G∞ respectively). Generally, in freezer storage, E increased and G∞ showed no significant change. In prolonged preservation (> 1 week), the results of –20°C showed significant increase in E (20% after 3 weeks) while this increase for –80°C was not significant, making it a better choice for tissue cold storage applications.
Keywords: Cold storage, Cryopreservation, Nanoindentation, Viscoelasticity, Multilayer Mechanical properties, Arteries
Introduction
Preservation and storage of biological tissues for different periods of time are challenging tasks for subsequent use in experimental and clinical practices. For example, arterial homografts, which are used to repair or replace diseased arteries, are often preserved using cold storage or freezing protocols for various time periods before being used. 10,16,25,26 Moreover, implementation of novel techniques for developing mechanical characteristics of arteries, such as nanoindentation or atomic force microscopy (AFM), requires smooth surfaces that can be achieved easier using a cryomicrotome.2,9 Cold storage can damage the material and substructure of arteries, e.g. collagen network or smooth muscle cells, due to water redistribution and formation of ice crystals.1,14,18,20,29 These changes imply that the storage techniques may alter the tissue mechanical characteristics which could affect the post-cryosurgical or post-cryopreservation performance of arteries. Although many studies are performed to investigate the biological aspects of such treatments, little is known about the changes to the mechanical properties due to cold storage as the studies in this area are limited and inconclusive.
Many of previous studies are limited to uniaxial tensile and ring stretching tests in order to determine the Young's modulus (modulus of elasticity) of arteries.1,21,26,28 Adham et al.1 evaluated mechanical characteristics of human descending thoracic aorta after preservation at +4°C in EuroCollins solution for 4, 7, 21 and 31 days or cryopreserved at –135°C for 2 and 4 months. Their results indicated that no differences were found between cryopreserved aorta and fresh specimens. They found a reduction in the Young's modulus at large strains for samples preserved at +4°C; however, the difference was not statistically significant. Pukacki et al.21 assessed the effect of cryopreservation at –80°C for 22 days on the elasticity and compliance of arterial allografts undergoing uniaxial tensile tests. They used unpaired Student's t-test and found that the Young's modulus of the control group was not significantly different from the cryopreserved group. Graham et al.8 in a study on the effect of aging on the mechanical properties of aorta reported no observable difference in the quasi-static engineering stress-strain curves between fresh and thawed (after snap freezing in liquid nitrogen) sheep aortas at strains up to 80%. Venkatasubramanian et al.28 tested frozen-thawed pig femoral arteries in a controlled rate freezer and found that the modulus of elasticity was higher compared to fresh samples in the physiological regime (stress below 50 kPa). Uniaxial results of Stemper et al.26 on porcine aorta showed that Young's modulus significantly decreased in 24 and 48-hour-refrigerated specimens compared to fresh specimens, but fresh and frozen (–20°C and –80°C for 3 month) results were not significantly different. Chow et al.4 used biaxial tensile testing to measure the changes in the mechanical properties of bovine thoracic aortas that had been stored at three common storage temperatures (+4°C up to 48 hours; –20°C and –80°C up to 3 weeks). Their refrigerated samples showed a significant decrease in the initial slope of the stress-strain curve. For the frozen samples, they concluded no significant change in the initial slope. However, their statistical results showed that for –20°C the initial slope generally decreased.
The muscular artery is a dynamic tissue composed of three layers.12 The innermost layer is the intima that is composed of a single layer of endothelial cells. The middle layer or media consists of elastic lamellae, interlamellar elastin fibers, and collagen fibers between them. The interlammellar elastin fibers include radial elastin struts that branch from one elastic lamella and extend to an adjacent lamella, providing a direct radial interlamellar connection. The lamellar and interlammellar units form a cage-like structure and surround the smooth muscle cells (SMC).19 The outermost layer or adventitia is composed of mostly longitudinally running collagen fibers, thin elastic fibers, fibroblasts, and capillaries. Despite this heterogeneous anatomy, in previous studies related to cold storage, the arterial wall was considered as a homogeneous single layer vessel. The mechanical characteristics of physically separated arterial layers have been studied by a few investigators11,27 but the effect of cold storage on arterial layers has not been reported. Moreover the focus of previous investigations on the effects of cold storage was the elastic properties and the viscoelasticity of arteries was ignored.7
Nanoindentation has recently emerged in tissue engineering applications as a viable technique for assessment of the local mechanical properties of soft tissues including vascular tissues.2,5,15 Matsumoto et al.17 developed a scanning micro indentation setup, a scaled-up version of AFM (with 0.5 μm resolution), and determined the distribution of the longitudinal and transverse Young's modulus of the lamellar unit (separated media) of porcine aorta in the range of 50 to 180 kPa. They proposed that the lower and higher values corresponded to SMC and elastic lamina respectively.
In this study, using a nanoindentation technique, changes to the viscoelastic properties (both elastic and relaxation behaviors) of porcine thoracic aorta wall due to cold storage at several time points were characterized with a resolution that addresses the multilayer nature of arteries. The results could be used as a reference for the effects of cold storage on arteries in experimental and clinical applications.
Materials and Methods
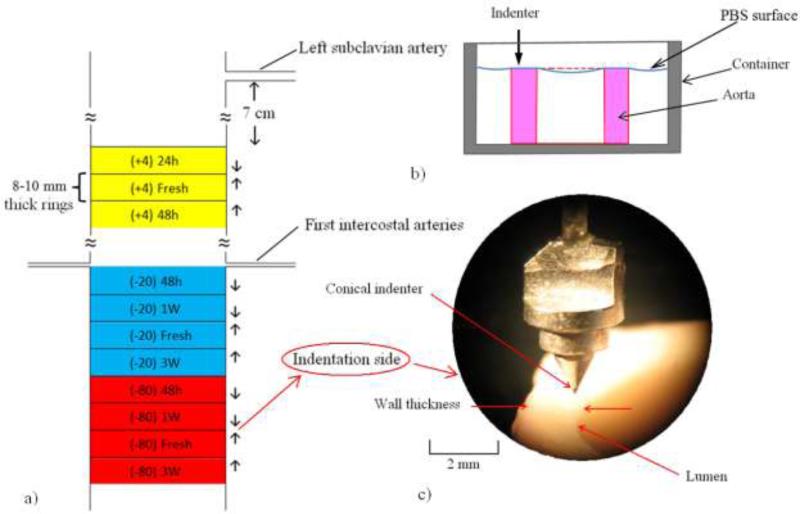
Fourteen porcine aortas were excised from sacrificed pigs at a local slaughterhouse (Hatfield Quality Meats, Hatfield, PA) immediately post-mortem and submerged in Phosphate Buffered Solution (PBS) and stored in an ice-filled cooler while transported to the laboratory. After removing the surrounding tissues, aortas were cut in the transverse direction in 8-10 mm-long cylindrical samples using a razor blade. A cylinder of polyethylene foam (McMaster-carr Catalog No. 93295K35, 15.87 mm diameter) that cut easier than aorta, was inserted in the aortas to prevent excessive folding and allow cutting straight edges. In total, 74 samples were extracted and divided into 3 categories of storage temperatures based on their location: The refrigerator, i.e., +4°C storage group (n=21) from approximately 7 cm inferior to the left subclavian artery; the –20°C storage group (n=27) at the first intercostal arteries and the –80°C storage group (n=26) from 4 cm inferior to –20°C group (Fig. 1-a). The time duration for refrigerator storage was 24 and 48 hours and for the freezer storage was 48 hours, 1 week and 3 weeks (each time subgroup consisted of 6 or 7 samples). These storage times are also used in several previous studies.4,21,26 For each storage group, adjacent fresh samples were extracted as controls. To minimize the variability due to the longitudinal location, the axial distance between indentation locations in each storage group and the corresponding fresh controls was less than 10 mm.
Fig. 1.
a) Schematic of locations of 3 different storage groups of +4°C, –20°C and –80°C and their indentation test directions. 1-b) Schematic of sample cross section submerged in PBS. 1-c) Photograph of conical indenter and aorta wall (100×).
A custom-made test setup was designed to perform the nanoindentation tests (Fig. 2) consisting of a Z-axis nano-positioner with 0.2 nm resolution and 100 μm range of motion (Nano-Z100, MCL,WI) combined with a horizontal piezo micro-positioner (M-663.4 PX, PI, MA). The test setup was mounted on an active vibration isolation table (TMC 63-533, Peabody, MA). A conical indenter (XPT, Agilent Technologies, CA, 55° tip angle, 10 μm tip rounding radius) was attached to a force transducer (Model 406A, Aurora Scientific, Ontario, Canada) with resolution of 0.1 μN. The setup is equipped with a 300x stereo microscope (Olympus SZX7) for contact visualization.
Fig. 2.
Experimental setup for nanoindentation.
Soft tissues material properties are sensitive to hydration.25 Preliminary results showed that the elastic modulus of aorta increased when the tissue dried. Therefore, to avoid dehydration, samples were placed in a 15 mm height aluminum container and were submerged to their top surface in PBS (Fig. 1-b). Since the density of aorta is more than PBS, samples stayed stationary and no adhesive was used. As the indenter tip was lowered to make contact with the sample top surface, it first became in contact with a thin layer of PBS and resulted in a small tensile load due to the liquid surface tension. The tip was lowered further to the point when the tensile load started to decrease, which was considered to be the initial point of contact with the tissue.
The indentation tests were performed in the longitudinal direction at various points along the thickness of the aorta wall (Fig. 1-c). For each sample, the indenter tip was aligned to the outermost layer of aorta and the first point of indentation was 100 μm inward from this point. Successive indentation tests were performed toward the innermost layer with distances of 100 μm or 200 μm between the points. The average wall thickness was 1.76±0.05 mm. In total, 611 points were reported that were tested at 90° counter-clockwise with respect to intercostal arteries to minimize the variability due to the circumferential location. Samples were moved upward toward the indenter with a ramp and hold displacement with 40 μm indentation depth, 10 ms ramp time and 30 s hold time. The force and displacement data were collected at 5 kHz.
Freezer storage samples were embedded in Optimal Cutting Temperature compound (Tissue-Tek O.C.T. Compound, Sakura Finetek, Torrance, CA) and covered with a cylindrical aluminum foil (with an outer diameter about 5 mm larger than the aorta diameter) and were fast frozen (1 min) by submerging in liquid nitrogen. Keeping this period short helps preventing water movement in the tissue and minimizing structural changes to the tissue.28 Prior to experiments, frozen samples were thawed for one hour at the ambient temperature and all indentation tests were conducted at the room temperature (25°C).
Theory
The mechanical behavior of the vessel was characterized assuming the material to be locally homogeneous, isotropic and linearly viscoelastic. The force history of the indenter P(t) was written in terms of the indentation depth h(t) using a quasi-linear viscoelastic (QLV) model:7
| (1) |
in which Pe(h) is the instantaneous elastic force that can generally be a nonlinear function of h. G(t) is the reduced relaxation function that was assumed to be a Prony series:
| (2) |
in which Gi and βi represent the relaxation amplitudes and decay rates respectively. According to the ramp and relaxation times, four decay rates were chosen to capture the decays that occurred on the orders of magnitude of 0.01, 0.1, 1.0 and 10.0 s. The total elastic load necessary to cause a penetration h for a conical indenter can be written as:24
| (3) |
where β is the cone angle with respect to the horizontal axis (β=62.5°), E is the Young's modulus, and v is the Poisson's ratio which was assumed to be 0.5 (incompressible) for aorta due to its high water content. The short and long term viscoelastic behaviors are manifested in E and G∞ indicating the instantaneous stiffness and the steady state decay of the material response respectively. Comparisons of samples mechanical characteristics were mainly made based on the distribution of these two parameters over the thickness of aorta. The long-term (steady state) Young's modulus E∞ can be calculated from EG∞.
Test Setup Validation
To calibrate the test setup and check the repeatability of the results, indentation tests were conducted on a cylindrical homogeneous extra soft polyurethane specimen with Durometer grade 7A (McMaster-Carr Catalog No. 20125K61, 12.7 mm diameter) using a flat indenter (tungsten carbide with 200 μm diameter) and the conical indenter. The calibration specimen was placed vertically and indentation was conducted in the axial direction and repeated at three different locations.
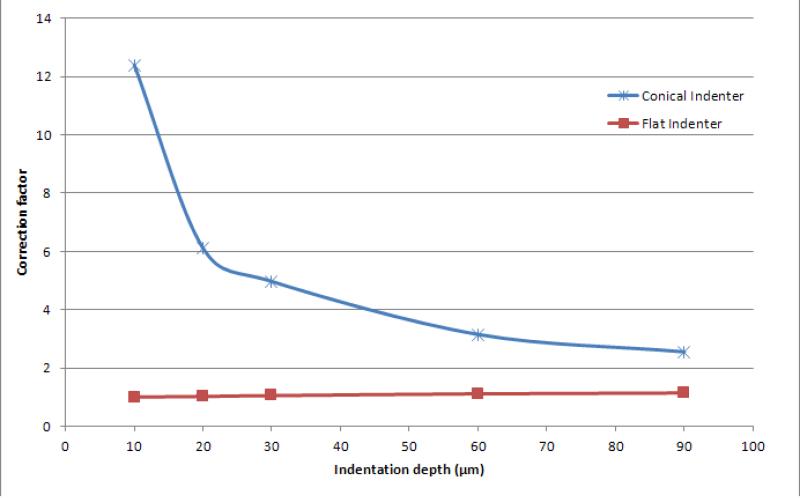
The correspondence principle that is assumed in writing Eq. (1) requires the contact area to be constant during the indentation test (as in a flat indenter), whereas in the case of conical indenter the contact area increases with penetration depth. From the calibration tests conducted on the polyurethane sample with the flat indenter, the instantaneous Young's modulus was determined to be approximately 500 kPa which is in agreement with the reported data for Duromoeter 7A rubber.22 Furthermore, the ratios of experimental to theoretical instantaneous Young's moduli were determined for various penetration depths (Fig. 3). For a flat indenter, where the correspondence principle applies, a ratio of approximately 1 was obtained with some deviation that can be explained by the material nonlinearity. Using the conical indenter, the material instantaneous Young's modulus was overestimated. A correction factor, as a function of indentation depth, was defined for the conical indenter which was about 4 for the depth of 40 μm used in this study. This correction factor is expected to be merely a geometric factor for a specific loading rate that depends on the indenter shape and not the material properties. The relaxation behavior for both indenters was determined to be the same and independent of the penetration depth which implied that the given correction factor is independent of the material properties.
Fig. 3.
The correction factor of the conical indenter.
Results
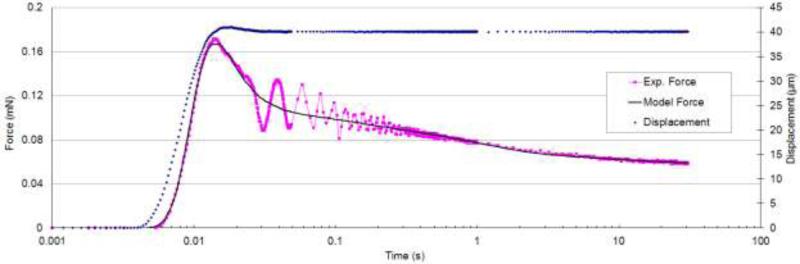
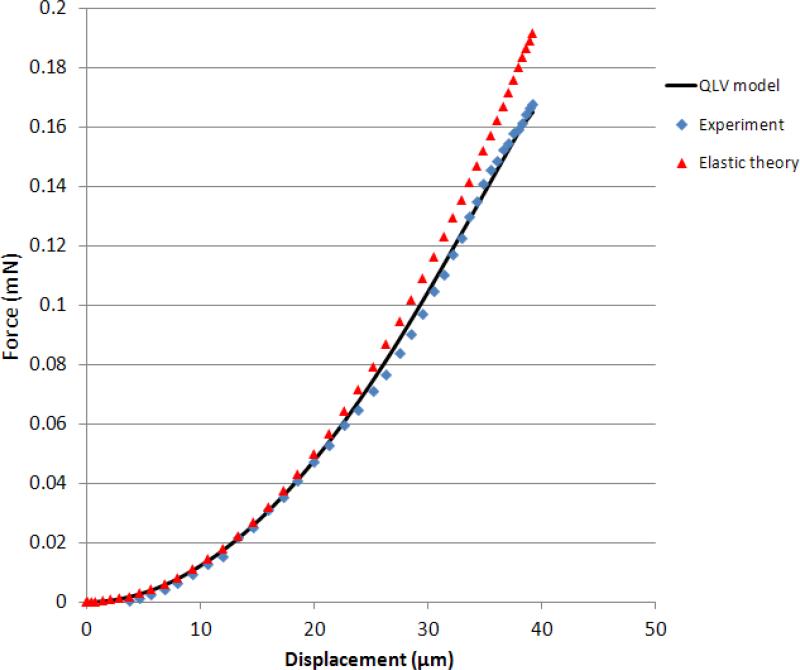
The viscoelastic model coefficients (Eqs. 2 and 3) were obtained by fitting the model to the whole experimental force history curves using a direct integration technique for a viscoelastic response23 and the method of least squares. The relaxation data was resampled (0-0.05 s at 5 kHz, 0.05-1 s at 250 Hz, 1-30 s at 5 Hz) to give approximately equal weights to different time scales. As shown in a representative curve fit in Fig. 4, the experimental forces were matched adequately by the model and overall R2 values of 0.9 or greater were achieved. The transient vibration observed in the response after the peak force was due to samples’ natural frequency which was neglected by the viscoelastic model. The force displacement curves in the ramp region (Fig. 5) showed that the QLV model closely followed the experimental data and they both showed a second order behavior that is in agreement with Equation 3. The deviation of the experimental and QLV results with respect to the elastic model at higher indentation depths is due to viscoelastic relaxation which is small due to the small ramp time.
Fig. 4.
Force and displacement history curves from a typical test.
Fig. 5.
Representative indentation force-displacement curves for the elastic theory, experimental data and QLV model.
The results of E and G∞ for refrigerated and frozen samples are summarized in Tables 1 and 2 along with the p values of paired two-tail t-tests for comparing different storage times with respect to the corresponding fresh control samples (p<0.05 was considered to be significant). The results demonstrate that the instantaneous Young's modulus of refrigerate storage samples decreased (Fig. 6) and their G∞ increased. After 48 hours, these changes became significant (10% and 13% for E and G∞ respectively) while there was no significant difference between the 24-hour and 48-hour results.
Table 1.
Average values of E and G∞ for fresh and refrigerator storage samples and their standard error and p values of paired two-tail t-tests for comparing the storage samples with respect to the corresponding fresh control samples.
| Storage Temperature (°C) | E(kPa) | G ∞ | ||||
|---|---|---|---|---|---|---|
| Fresh | 24 hours | 48 hours | Fresh | 24 hours | 48 hours | |
| +4 | 63.4±4.1 | 59.0±4.3 (0.16) | 56.9±4.4 (0.014)* | 0.30±0.02 | 0.33±0.01 (0.23) | 0.34±0.02 (0.019)* |
Table 2.
Average values of E and G∞ for fresh and different frozen samples and their standard error and p values of paired two-tail t-tests for comparing the frozen samples with respect to the corresponding fresh control samples.
| Storage Temperature (°C) | E(kPa) | G ∞ | ||||||
|---|---|---|---|---|---|---|---|---|
| Fresh | 48 hours | 1 Week | 3 Weeks | Fresh | 48 hours | 1 Week | 3 Weeks | |
| –20 | 64.6±4.8 | 66.2±3.6 (0.23) | 66.5±6.3 (0.74) | 77.11±7.1 (0.01)* | 0.347±0.017 | 0.359±0.014 (0.52) | 0.354±0.010 (0.70) | 0.380±0.010 (0.16) |
| –80 | 69.32±3.4 | 69.12±5.1 (0.97) | 74.3±9.2 (0.72) | 75.7±5.0 (0.11) | 0.358±0.012 | 0.343±0.012 (0.28) | 0.385±0.010 (0.06) | 0.370±0.011 (0.78) |
Fig. 6.
Changes of the instantaneous Young's modulus in refrigerator storage samples (+4°C).
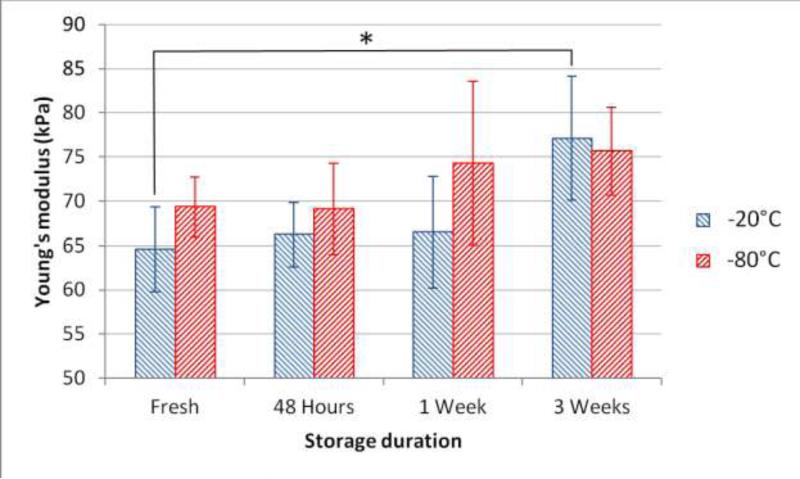
The results in Table 2 imply that the instantaneous Young's modulus generally increased with time in freezer storage samples (Fig. 7). The changes were small for short time storage (≤ 1 week) in both temperatures and no significant difference was observed. However, for long term storage, the change in –20°C was larger than –80°C and resulted in a significant increase (20%) in E after 3 weeks. The statistical results of G∞ showed there was no significant difference in the relaxation behavior in freezer storage samples.
Fig. 7.
Changes of the instantaneous Young's modulus in freezer storage samples (–20°C and –80°C).
Separated comparison of media and adventitia (inner and outer halves) revealed that when the changes of Young's modulus due to storage were significant, i.e., fresh vs. +4°C after 48 hours and fresh vs. –20°C after 3 weeks, the change in media was more pronounced than adventitia since it showed a smaller p-value (Table 3).
Table 3.
p values of paired two-tail t-tests for fresh samples vs. two significant cases of changes in E for the whole thickness and separated media and adventitia layers.
| Comparison of fresh vs. | p-value | ||
|---|---|---|---|
| Whole Thickness | Media | Adventitia | |
| +4°C after 48 hours | 0.014 | 0.002 | 0.329 |
| –20°C after 3 weeks | 0.009 | 0.031 | 0.042 |
Comparison of the results of –20°C and –80°C fresh specimens showed that their instantaneous Young's moduli are significantly different (p=0.03 for paired t-test) and there was 7.3% increase for 4 cm distal distance. However, comparisons of the coefficients of reduced relaxation functions of the two groups revealed that they were not significantly different. In other words, the aortas were homogeneous with respect to the relaxation properties but inhomogeneous with respect to the elastic properties.
Discussion
An indentation technique was developed to study the changes in the elastic and relaxation behavior of porcine thoracic arterial wall due to cold storage. This technique enabled calculating local material properties with approximately 40 μm resolution in the wall thickness without physically separating the layers. The cylindrical shape of the samples caused tissues to remain intact in the circumferential direction and keep the circumferential residual stress. However, the longitudinal residual stress was clearly lost in the samples. The obtained instantaneous Young's moduli of samples are consistent with the range of 50-180 kPa reported in the literature for porcine aorta in physiological strains (below 30%).17,28
The refrigerator storage results showed that there was a decreasing trend in the instantaneous Young's modulus which became significantly different after 48 hours. This trend is consistent with other studies.1,4,26 Freezer storage results revealed that there was a general trend of increase in the instantaneous Young's modulus with respect to the storage time. A significant increase (20%) was observed in the –20°C group after 3 weeks. This trend is in agreement with results of Pukacki et al.21 and Stemper et al.26. The changes in the –80°C group, which is the standard storage temperature in most biological labs, showed similar trends but was consistently not significant, making it a better choice for tissue storage applications.
In several studies1,14,21 changes in the material properties due to freezer storage did not result in statistically significant trends while this study clearly showed that storage at –80°C was advantageous to –20°C with respect to the preservation of material properties. The reason that the methodology used in this study is more sensitive than previous studies is two-fold. First, the sample preparation and nanoindentation methods allowed minimization of material heterogeneity in the axial and circumferential directions and determination of the radial (through thickness) distribution of material properties with sub-millimeter resolution. Second, the applied experimental design allowed proximity of indentation test locations (less than 10 mm apart) and as result the paired t-test comparison could be employed which is more sensitive than the unpaired t-test used in other studies. In other words, application of the paired test eliminated the sample to sample variability that could be comparable to the changes in each aorta due to cold storage.
A few studies have investigated the biochemical effects of freezer storage on arteries. Venkatasubramanian et al.28 showed that cell injury could happen in frozen pig arteries. Chow and Zhang3 investigated the biochemical changes in the collagen network. Their results showed there was a significant decrease in the amounts of acid soluble, pepsin soluble, and insoluble collagen in frozen samples after 1 week and 3 weeks storage time but the percent of cross-linked collagen did not change significantly. Therefore, the observed changes in mechanical properties may be attributed to reduced contributions from SMC and collagen to the overall mechanical properties. It is generally accepted that when frozen at –20°C, lysogenic enzymes are not completely denatured, but at –80°C they are. Therefore, when the aortas are frozen at –20°C, a small percentage of cells would lyse and release their enzymes into the tissue. If the enzymes had been inactivated (at –80°C), then there would be less degradation of SMC than an aorta that had been exposed to autolytic enzyme.
The separated comparison of media and adventitia revealed that when significant changes were observed in the instantaneous Young's modulus, these changes were more pronounced in media, concluding that media could be more vulnerable than adventitia to cold storage. The cellular composition of media is different from that of adventitia, particularly with respect to SMC and elastic lamina composition. The effect of freezing on SMC, as discussed above, can explain why the changes in media due to freezing were more significant than adventitia. Moreover, it can be concluded that in medium size arteries (muscular), that the proportion of SMC is higher than in large (elastic) arteries, the effect of freezing would be more pronounced.
The long-term viscoelastic behavior of aortic tissue was characterized by G∞ which showed that the steady-state Young's modulus for fresh samples was about 34% of the instantaneous Young's modulus, confirming the viscoelastic assumption for aorta material behavior. Comparing the G∞ results of different storage types revealed that freezer storage kept G∞ unchanged while refrigerator storage increased G∞ more than 13% after 48 hours, i.e., the tissue became more elastic.
Surface detection is a challenge in nanoindentation of soft materials and the changes in the adhesion force curve are generally used to determine the point of contact.3,6,13 In this study, the adhesion force between the PBS layer and indenter tip was maximum 6 μN tension and the initial decrease in this force (after about 1-2 μm displacement) was considered as the point of contact which is agreement with Cao and Yang.3 This force was much smaller than the maximum indentation force (about 170 μN).
A limitation of this study is that Equation (3) used for the elastic solution of conical indenters is derived for infinitesimal deformations. However, since the deviation of the model result from experimental data in the ramp phase was negligible (Fig. 5), it was concluded that using this equation in this study was valid. The QLV model it is the most widely used viscoelastic model for soft tissues including arteries.7 The independence of the reduced relaxation function from strain (a fundamental assumption in the QLV theory) was not verified in this study. However, the good matches between the experimental and model results in both ramp and relaxation regions justified the application of this model. The transient vibration observed in the relaxation responses was due to samples’ natural frequency that is related to their geometry and material properties. Also, the ramp rate was relatively high (10 ms), which caused the transient vibration to be more pronounced. The high ramp rate used enabled obtaining a better estimate of the instantaneous elastic response for applications involving injuries and rupture. It was assumed that the effect of this transient vibration was negligible in the conclusions of this study as the viscoelastic model goes approximately through the local average forces. The amplitude of vibration can be reduced by reducing the sample thickness. Sectioning of the tissue involves local plastic deformation and failure and may result in changes in the material properties of the separated surfaces. In this study, the same sectioning method, i.e., cutting fresh aortas with a razor blade was used for all the samples to the make comparison of different storage methods with fresh tissues meaningful.
The results of this study could be used as a reference for arteries cold storage in experimental and clinical applications. Particularly since the results of instant freezing showed no difference for less than one week storage, arteries could be cryosectioned to get improved surface qualities for studies requiring nanoindentation or AFM methods.
Acknowledgement
The support for this study was provided partially by the NHLBI under Grant Number K25-HL086512 and Grant Number R21-HL088159.
Footnotes
Conflict of interest statement
There are no conflicts of interest of any kind in the work presented in the manuscript.
References
- 1.Adham M, Gournier JP, Favre JP, Roche EDL, Ducerf C, Baulieux J, Barral X, Pouyet M. Mechanical characteristics of fresh and frozen human descending thoracic aorta. J. Surg. Res. 1996;64:32–34. doi: 10.1006/jsre.1996.0302. [DOI] [PubMed] [Google Scholar]
- 2.Akhtar R, Schwarzer N, Sherratt MJ, Watson REB, Graham HK, Trafford AW, Mummery PM, Derby B. Nanoindentation of histological specimens: Mapping the elastic properties of soft tissues. J. Mater. Res. 2009;24:638–646. doi: 10.1557/JMR.2009.0130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cao Y, Yang D, Soboyejoy W. Nanoindentation method for determining the initial contact and adhesion characteristics of soft polydimethylsiloxane. J. Mater. Res. 2005;20:2004–2011. [Google Scholar]
- 4.Chow MJ, Zhang Y. Changes in the Mechanical and Biochemical Properties of Aortic Tissue due to Cold Storage. J. Surg. Res. 2010 doi: 10.1016/j.jss.2010.04.007. In press. [DOI] [PubMed] [Google Scholar]
- 5.Ebenstein DM, Pruitt LA. Nanoindentation of soft hydrated materials for application to vascular tissues. J. Biomed. Mater. Res. 2004;69A:222–232. doi: 10.1002/jbm.a.20096. [DOI] [PubMed] [Google Scholar]
- 6.Ebenstein DM. Nano-JKR force curve method overcomes challenges of surface detection and adhesion for nanoindentation of a compliant polymer in air and water. J. Mater. Res. 2011;26:1026–1035. [Google Scholar]
- 7.Fung YC. Biomechanics mechanical properties of living tissues. Springer; New York: 1996. p. 568. [Google Scholar]
- 8.Graham HK, Akhtar R, Kridiotis C, Derby B, Kundu T, Trafford AW, Sherratt MJ. Localised micro-mechanical stiffening in the ageing aorta. Mech ageing. Dev. 2011;132:459–467. doi: 10.1016/j.mad.2011.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gupta S, Carrillo F, Balooch M, Pruitt L, Puttlitz C. Simulated soft tissue nanoindentation: A finite element study. J. Mater. Res. 2005;20:1979–1994. [Google Scholar]
- 10.Hawkins JA, Hillman ND, Lambert LM, Jones J, Di Russo GB, Profaizer T, Fuller TC, Minich L, Williams RV, Shaddy RE. Immunogenicity of decellularized cryopreserved allografts in pediatric cardiac surgery: Comparison with standard cryopreserved allografts. J. Thorac. Cardiovasc. Surg. 2003;126:247–252. doi: 10.1016/s0022-5223(03)00116-8. [DOI] [PubMed] [Google Scholar]
- 11.Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. AM. J. Physiol-Heart. C. 2005;289:H2048–H2058. doi: 10.1152/ajpheart.00934.2004. [DOI] [PubMed] [Google Scholar]
- 12.Holzapfel GA, Gasser CT. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000;61:1–48. [Google Scholar]
- 13.Kaufman JD. Surface detection errors cause overestimation of the modulus in nanoindentation on soft materials. J Mech Behav Biomed Mater. 2009;2:312–317. doi: 10.1016/j.jmbbm.2008.08.004. [DOI] [PubMed] [Google Scholar]
- 14.Lally C, Reid AJ, Prendergast PJ. Elastic behavior of porcine coronary artery tissue under uniaxial and equibiaxial tension. Ann. Biomed. Eng. 2004;32:1355–1364. doi: 10.1114/b:abme.0000042224.23927.ce. [DOI] [PubMed] [Google Scholar]
- 15.Levental I, Levental KR, Klein EA, Assoian R, Miller RT, Wells RG, Janmey PA. A simple indentation device for measuring micrometer-scale tissue stiffness. J. Phys.: Condens. Matter. 2010;22:194120–194129. doi: 10.1088/0953-8984/22/19/194120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leseche G, Castier Y, Petit M, Bertrand P, Kitzis M, Mussot S, Besnard M, Cerceau O. Long-term results of cryopreserved arterial allograft reconstruction in infected prosthetic grafts and mycotic aneurysm of the abdominal aorta. J. Vasc. Surg. 2001;34:616–622. doi: 10.1067/mva.2001.116107. [DOI] [PubMed] [Google Scholar]
- 17.Matsumoto T, Goto T, Furukawa T, Sato M. Residual stress and strain in the lamellar unit of the porcine aorta: Experiment and analysis. J. Biomech. 2004;37:807–815. doi: 10.1016/j.jbiomech.2003.08.014. [DOI] [PubMed] [Google Scholar]
- 18.Muller-Schweinitzer E, Grapow M, Konerding MA, Zerkowski HR. Freezing without surrounding cryomedium preserves the endothelium and its function in human internal mammary arteries. Cryobiology. 2005;51:54–65. doi: 10.1016/j.cryobiol.2005.04.005. [DOI] [PubMed] [Google Scholar]
- 19.O'Connell MK, Murthy S, Phan S, Xu C, Buchanan J, Spilker R, Dalman RL, Zarins CK, Denk W, Taylor CA. The three-dimensional micro- and nanostructure of the aortic medial lamellar unit measured using 3D confocal and electron microscopy imaging. Matrix Biol. 2008;27:171–181. doi: 10.1016/j.matbio.2007.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pascual G, Escudero C, Rodriguez M, Corrales C, Serrano N, Bellon JM, Bujan J. Restoring the endothelium of cryopreserved arterial grafts: Co-culture of venous and arterial endothelial cells. Cryobiology. 2004;49:272–285. doi: 10.1016/j.cryobiol.2004.09.006. [DOI] [PubMed] [Google Scholar]
- 21.Pukacki F, Jankowski T, Gabriel M, Oszkinis G, Krasinski Z, Zapalski S. The mechanical properties of fresh and cryopreserved arterial homografts. Eur. J. Vasc. Endovasc. Surg. 2000;20:21–24. doi: 10.1053/ejvs.2000.1120. [DOI] [PubMed] [Google Scholar]
- 22.Qi HJ, Joyce K, Boyce MC. Durometer hardness and the stress-strain behavior of elastomeric materials. Rubber Chem. Technol. 2003;72:419–435. [Google Scholar]
- 23.Simo JC, Hughes TJR. Computational inelasticity. Springer; 1998. p. 392. [Google Scholar]
- 24.Sneddon IN. The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965;3:47–57. [Google Scholar]
- 25.Solanes N, Rigol M, Castella M, Khabiri E, Ramirez J, Segales J, Roque M, Agusti E, Perez-Villa F, Roig E, Pomar JL, Sanz G, Heras M. Cryopreservation alters antigenicity of allografts in a porcine model of transplant vasculopathy. Transplant. Proc. 2004;36:3288–3294. doi: 10.1016/j.transproceed.2004.10.053. [DOI] [PubMed] [Google Scholar]
- 26.Stemper BD, Yoganandan N, Stineman MR, Gennarelli TA, Baisden JL, Pintar FA. Mechanics of fresh, refrigerated, and frozen arterial tissue. J. Surg. Res. 2007;139:236–242. doi: 10.1016/j.jss.2006.09.001. [DOI] [PubMed] [Google Scholar]
- 27.Teng Z, Tang D, Zheng J, Woodard PK, Hoffman AH. An experimental study on the ultimate strength of the adventitia and media of human atherosclerotic carotid arteries in circumferential and axial directions. J. Biomech. 2009;42:2535–2539. doi: 10.1016/j.jbiomech.2009.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Venkatasubramanian RT, Grassl ED, Barocas VH, Lafontaine D, Bischo JC. Effects of freezing and cryopreservation on the mechanical properties of arteries. Ann. Biomed. Eng. 2006;34:823–832. doi: 10.1007/s10439-005-9044-x. [DOI] [PubMed] [Google Scholar]
- 29.Xu Y, Hua TC, Sun DW, Zhou GY. Experimental study and analysis of mechanical properties of frozen rabbit aorta by fracture mechanics approach. J. Biomech. 2008;41:649–655. doi: 10.1016/j.jbiomech.2007.09.023. [DOI] [PubMed] [Google Scholar]