Probing Tubulin-Blocked State of VDAC by Varying Membrane Surface Charge

Abstract

Reversible blockage of the voltage-dependent anion channel (VDAC) of the mitochondrial outer membrane by dimeric tubulin is being recognized as a potent regulator of mitochondrial respiration. The tubulin-blocked state of VDAC is impermeant for ATP but only partially closed for small ions. This residual conductance allows studying the nature of the tubulin-blocked state in single-channel reconstitution experiments. Here we probe this state by changing lipid bilayer charge from positive to neutral to negative. We find that voltage sensitivity of the tubulin-VDAC blockage practically does not depend on the lipid charge and salt concentration with the effective gating charge staying within the range of 10–14 elementary charges. At physiologically relevant low salt concentrations, the conductance of the tubulin-blocked state is decreased by positive and increased by negative charge of the lipids, whereas the conductance of the open channel is much less sensitive to this parameter. Such a behavior supports the model in which tubulin's negatively charged tail enters the VDAC pore, inverting its anionic selectivity to cationic and increasing proximity of ion pathways to the nearest lipid charges as compared with the open state of the channel.

Introduction

Interaction between the voltage-dependent anion channel (VDAC) of the mitochondrial outer membrane and the abundant cytosolic protein tubulin is manifested as a reversible blockage of the channel to a well-defined partially conductive state (1–3). The conductance of the tubulin-blocked state is ∼40% of the open channel conductance, but what is physiologically important, is virtually impermeable for ATP (4). Because VDAC constitutes a major pathway for ATP, ADP, and other metabolites across the mitochondrial outer membrane, it is not surprising that the evidence emerging from different laboratories suggests that VDAC-tubulin interaction is a potent mechanism of regulation of the outer membrane permeability and hence, mitochondrial respiration in health and pathology (5–8). At the same time, the nature of the tubulin-blocked state remains unclear.

Dimeric tubulin, the elementary subunit of a microtubule, is α- and β-tubulin heterodimer of 100 kDa total molecular mass and approximate dimensions of 8 × 4.5 × 6.5 nm (9,10). It is far too large to permeate through VDAC pore of 2.4 × 2.7 nm in inner cross-sectional dimensions (11). Therefore, we proposed earlier that the plausible candidates for VDAC block are long and flexible anionic C-terminal tails (CTT) of tubulin. We suggested a simple straightforward tail-in-the-pore model of VDAC blockage by tubulin (1–3). According to this model, the blocked state is realized when one of the negatively charged CTTs of tubulin enters the predominantly positively charged pore of VDAC (11–13) and stays there, restricted from translocating through the pore to the opposite side of the membrane by the bulky tubulin body. The lengths of α- and β-CTTs are ∼3.7 and 6.3 nm, respectively (2,14), so both tails could reach binding site(s) inside the pore of the length ∼3.5 nm (11) from either side of the membrane. The cross section of the unstructured CTT is smaller than that of VDAC's open pore and, according to molecular dynamics simulations (T. Luchko, University of Alberta, personal communication, 2009), allows comfortable fit of CTT inside the VDAC pore (see Fig. 5 B, later). The tail-in-the-pore model is based on a number of experimental observations including strong voltage dependence of the blockage (2), inversed ionic selectivity, and reduced aperture of the tubulin-blocked state in comparison with the open state (4), and the absence of the time-resolved blockage events for both CTT synthetic peptides and tailless tubulin with truncated CTTs (2). However, certain similarities between the effects of tubulin and of several negatively charged synthetic polymers, shown to enhance VDAC gating sensitivity to voltage (12,15,16), stipulate further investigations into the nature of this highly physiologically relevant (3) VDAC-tubulin interaction.

Figure 5.

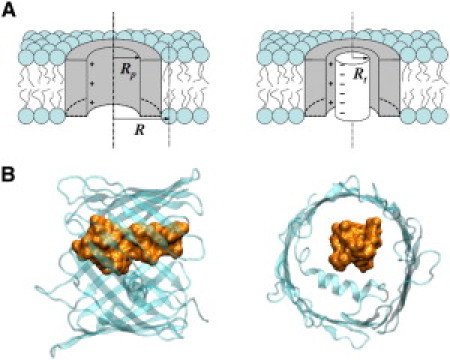
(A) Cartoon illustrating the model and the parameters used in the nonlinear Poisson-Boltzmann approximation described by Eqs. 3–7. R_t is the effective radius of the tubulin tail and R_p is the radius of the VDAC water-filled pore. The difference in the effect of lipid charge on channel ionic conductance in the open (left panel) and tubulin-blocked (right panel) states is due to the combination of the following factors: (i) the average distance between the charges on the nearest lipid heads and the ionic current pathways is reduced when the tubulin tail blocks the channel; (ii) the channel selectivity turns from anionic to cationic when the tubulin tail enters into the pore, thus changing the distribution of positive and negative ions inside the channel; and (iii) the lipid charge determines the sign of the majority of ions available at the mouth of the channel. (B) Tubulin C-terminal tail fits comfortably inside the VDAC pore. A schematic representation of the β-barrel of human VDAC1 viewed perpendicular (left figure) and parallel (right figure) to the membrane plane is adapted from (41). Molecular dynamics simulation of the β-CTT of tubulin is courtesy of T. Luchko.

In this study, we report the results of channel reconstitution experiments in which we vary the surface charge of the membrane incorporating a single channel. We study its conductance in the open and tubulin-blocked states as well as the voltage-dependent equilibrium between these two states at different salt concentrations in the bulk. We use the positively charged dioleoyl trimethylammonium propane (DOTAP), neutral diphytanoyl phosphatidylcholine (DPhPC), and negatively charged diphytanoyl phosphatidylserine (DPhPS) to form bilayer membranes that host reconstituted VDAC. Studying the voltage sensitivity of the blockage, we find that the effective gating charge of the blockage is virtually independent of lipid charge and only slightly decreases from 14 to 10 elementary charges when the bulk solution concentration is increased from 0.1 M to 1.5 M KCl.

We find that although the effect of the lipid charge on conductance of the channel open state is negligible in the concentration range of 0.05–1 M KCl, the conductance of the blocked state displays clear dependence on the surface charge. At physiologically relevant low salt concentrations, the positive charge of DOTAP hinders ion current through the tubulin-blocked state of VDAC in comparison with neutral DPhPC; the negative charge of DPhPS facilitates the current. We demonstrate that these observations can be quantitatively explained by the moderate cationic selectivity of the blocked state and the geometric constriction of the channel by the tubulin tail that makes ion pathways to be positioned closer to the charges of the surrounding lipids. Our findings agree with the initially proposed blockage model (1–3) in which tubulin's negatively charged tail enters the VDAC pore and overcompensates its net-positive charge, thus confirming the newly discovered physiological role for tubulin CTTs.

Materials and Methods

VDAC reconstitution experiments were performed as described previously (2) in a two-compartment (cis and trans) Teflon chamber, divided by a thin Teflon film with a hole of ∼70 μM. Planar lipid membranes were formed using a lipid-monolayer apposition technique (modified Montal-Mueller method). Membranes were prepared from neutral diphytanoyl phosphatidylcholine (DPhPC), singly negatively charged diphytanoyl phosphatidylserine (DPhPS⁻¹), singly positively charged dioleoyl trimethylammonium propane (DOTAP⁺¹), and the mixture of the polar lipid extract (PLE) from soybeans with cholesterol (10:1). All lipids were purchased from Avanti Polar Lipids (Alabaster, AL). Membrane-bathing solutions contained 0.05–1.5 M KCl with 5 mM HEPES, buffered at pH 7.4. In some experiments, the channel was reconstituted in 0.1 M KCl and then aliquots of 4 M KCl were injected in both compartments to increase the salt concentration. All measurements were performed at room temperature (21 ± 1.5°C). Frozen mitochondrial membrane fractions of mouse liver was a kind gift of Marco Colombini (University of Maryland, College Park, MD). Voltage-dependent anion channel (VDAC) was isolated from mitochondrial membrane fraction by the standard method (17) and then purified following the regular procedure (18). After the VDAC channel was reconstituted into the bilayer, aliquots of the bovine brain tubulin (Cytoskeleton, Denver, CO) were added to both sides of the membrane under constant stirring for 2 min.

Conductance measurements were performed using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA) in a voltage-clamp mode. Transmembrane potential was defined as positive when it is greater at the side of VDAC addition (cis-side). The amplifier output signal was filtered by an in-line low-pass eight-pole Butterworth filter (Model 9002; Frequency Devices, Haverhill, MA) at 15 kHz and saved with a sampling frequency of 50 kHz using Digidata 1322A and Clampex 8.2 software (Axon Instruments). Amplitude and lifetime analysis were performed using a Clampfit 10.2 (Molecular Devices, Eugene, OR) and Origin 8.5 (OriginLab, Northampton, MA) software. For data analysis by Clampfit, a digital 8-pole Bessel low-pass filter was set at 700 Hz and applied to all records. The individual events of tubulin blockages were discriminated manually using Clampfit single-channel search protocol. VDAC open probability was calculated as the relative time spent by the channel in the open state over the entire time of the interval of analysis; the lifetimes were calculated by fitting logarithmic single exponentials to logarithmically binned histograms (19) of at least 150 blockage events.

Results

Representative tracks of ion currents through the single VDAC channels in the presence of tubulin are given in Fig. 1. The channels were reconstituted into planar lipid membranes made of a 4:1 mixture of the negatively charged DPhPS and neutral DPhPC (traces on the left), neutral DPhPC (traces in the center), and a 2:1 mixture of the positively charged DOTAP and neutral DPhPC (traces on the right). It is seen that in 1.5 M KCl (the lower traces) the depth of the blockage and, therefore, the residual current in the tubulin-blocked states are virtually the same, whereas in 0.1 M KCl (the upper traces) they are functions of lipid composition. In the negatively charged DPhPS-containing membranes, the residual current is significantly larger than in neutral membranes. On the contrary, in the positively charged DOTAP-containing membranes the residual current is reduced compared with neutral ones.

Figure 1.

Currents through single VDAC channels reconstituted into lipid bilayers of varying surface charge are transiently blocked by tubulin. Concentration of tubulin was adjusted to obtain the open channel probability close to 0.5 at 20 mV of applied voltage, and, depending on particular experimental conditions, was varied within the range of 10–100 nM. When bathed by 0.1 M KCl (upper row), the residual currents through the tubulin-blocked states in the negatively charged DPhPS/DPhPC (4:1) bilayers are higher than through these states in neutral DPhPC bilayers. On the contrary, in the positively charged DOTAP/DPhPC (2:1) bilayers, the residual currents are smaller. The current traces measured in 1.5 M KCl (lower row) demonstrate that the lipid charge effect is salted-out by high salt. The depth of the blockage is no longer sensitive to the lipid. The applied voltage was 20 mV.

The effects of lipid charge on conductance of VDAC and its tubulin-blocked state as a function of bulk solution salt concentration are summarized in Fig. 2. Fig. 2 A shows that current through the open state (open symbols) approximately scales with the bulk salt concentration. At the reduced concentrations, 0.1 and 0.2 M KCl, the experimental points for the open channel current in the positively charged membrane tend to be slightly higher than in the negatively charged membrane, but the effect is close to the measurement error bars. The main origin of the error is a small but finite spread in conductances of individual channels. At the same time, the residual current through the tubulin-blocked state (solid symbols) shows systematic deviations from the simple scaling with salt concentration. Fig. 2 B presents the normalized residual conductance defined as a ratio of the current through the blocked state to the current through the open state of VDAC. This kind of normalization permitted us to minimize errors due to the finite spread in conductances of individual channels mentioned above. The effect of lipid charge on the residual conductance is now clearly visible. At reduced salt concentrations, the presence of DOTAP decreases the residual conductance relatively to pure DPhPC membranes, whereas the presence of DPhPS increases it.

Figure 2.

(A) Currents through single channels in their open and tubulin-blocked states monotonically increase with the salt concentration in the bulk, but, at small concentrations, show lipid charge dependence in the blocked state. Negative charge of the membrane surface increases the current in this state (DPhPS/DPhPC (4:1); PLE/cholesterol (9:1)), whereas positive charge decreases it (DOTAP/DPhPC (2:1)). (B) The relative current, plotted as a ratio of the current in the tubulin-blocked state to the current through the open state, shows the effect of the lipid charge more clearly. The solid lines are calculated applying the nonlinear Poisson-Boltzmann approximation to the tail-in-the-pore model as described in Discussion in the main text. Experimental conditions are the same as for Fig. 1. Each data point is an average of 3–4 independent experiments ± SE.

Considering that neither of the charged synthetic lipids used in our study is present in the mitochondrial outer membrane, we performed experiments using a polar lipid extract (PLE) from soybeans with 10% cholesterol admixing. This lipid mixture of PC/PE/PI/PA (4.6:2.2:1.8:0.7) mimics a natural content of mammalian mitochondrial outer membranes (20,21) where the main source of the negative charge is phosphatidylinositol (PI). There is ∼25% total of the negatively charged PI and phosphatidic acid in PLE. It is seen that conductance of the tubulin-blocked state in these membranes increased in low salt (Fig. 2 A), similarly to that in the PS-containing membranes.

Fig. 3 shows that the probability to find the channel in the open state, P_O, in the presence of tubulin is a strong function of the applied voltage V. Fig. 3 A shows single-channel current traces for five rising voltages, from 10 to 30 mV, demonstrating that the blockage probability increases with voltage. Fig. 3 B presents the results of statistical analysis of the open probability for 0.1 M and 1.5 M KCl bulk salt concentrations fitted by the expression

$$P_O=\frac{1}{1+\exp \left(\frac{ne\left(V-V_0\right)}{k_{\text{B}}T}\right)},$$ (1)

where k_B and T have their usual meaning of the Boltzmann constant and absolute temperature, and e is the elementary charge. V₀ is a fitting parameter that depends on experimental conditions, most importantly on tubulin bulk concentration and VDAC phosphorylation state (22), and n is another fitting parameter that gives the dimensionless effective gating charge characterizing sensitivity of the blockage reaction to voltage.

Figure 3.

(A) Tubulin blockage demonstrates high voltage sensitivity. The blocking events, virtually nonexistent at 10 mV (uppermost current trace), dominate the current at 30 mV of applied voltage (lowermost trace). (B) The probability to find a channel in the open state quickly decreases with the increasing voltage. The data were obtained on the same single channel initially reconstituted in 0.1 M KCl with 10 nM tubulin followed by increase of KCl concentration to 1.5 M. The lines through the data are drawn according to Eq. 1 with the effective gating charges n = 13 for 0.1 M KCl and n = 10 for 1.5 KCl, respectively. The bilayers were formed from DPhPC. Each point is an average of 6–7 measurements ± SE recorded on one representative single channel.

Table 1 summarizes results of our analysis of the voltage dependence of VDAC blockage by tubulin for different lipids and salt concentrations. It is seen that the effect of both lipid charge and bulk solution salt concentration is rather small. Whereas smaller salt concentrations show higher gating charge in all lipid composition studied, the value of gating charge stays within 10–14 elementary charges.

Table 1.

Effective dimensionless gating charge, n, of VDAC blockage by tubulin measured in the membranes of different lipid compositions and at different salt concentrations

Membrane composition	Effective dimensionless gating charge, n
	0.1 M KCl	1.5 M KCl
DPhPS/DPhPC, 4:1	11.6 ± 1.7	11.2 ± 1.8
DPhPC	14 ± 1	10.2 ± 1.0
DOTAP/DPhPC, 2:1	13.5 ± 1.5	11.8 ± 2.5

Gating charges were calculated from fitting the open probability data, example of which is given in Fig. 3B, using Eq. 1. Each n value is an average of 3–4 independent experiments ± SE.

To study the kinetics underlying the voltage dependence of VDAC blockage by tubulin, we first analyzed the distributions of times in the open state of the channel between blockage events. In agreement with the earlier published results (2), the distributions are satisfactory described by a single exponential fitting. The examples of open time histograms at two different salt concentrations are shown in Fig. 4. Solid lines represent logarithmic exponential fittings with the average values τ_O = 18.8 ms and τ_O = 46.2 ms in 0.1 M and 1 M KCl, respectively.

Figure 4.

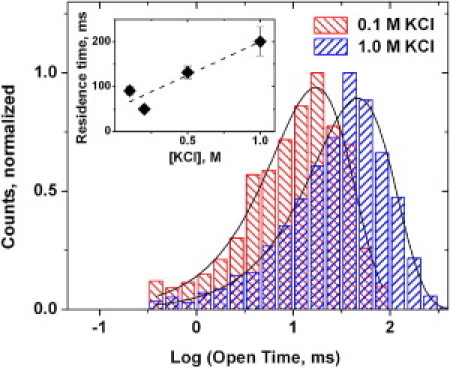
Representative histograms of the times spent by the channel in the open state between successive blockages by tubulin are adequately described by single exponential fitting. This allows for a reliable measurement of the averages in the whole range of salt concentrations used in this study. (Inset) The average residence time of VDAC blockage by tubulin increases at increasing salt concentration. Due to its complex, non-single-exponential distribution, the average time was calculated using Eq. 2 from the channel open probability, example of which is given in Fig. 3B, and the average open time. The dashed line through the data points is a linear regression. Each point is an average of 6–7 measurements ± SE obtained for the same single channel. The bilayers were formed from DPhPC, the applied voltage was 20 mV, and tubulin concentration was 10 nM.

The distribution of the residence times of the blockage, i.e., the times spent by the channel in the tubulin-blocked state, is more complex. Earlier it was found that fitting of the residence time histograms requires a sum of at least two exponents (2). Because of this complication, to obtain the residence time averages, τ_B, we used a relation for the probability to find the channel in the open, unblocked state,

$$P_O=\frac{{\tau }_O}{{\tau }_O+{\tau }_B},$$ (2)

which allows calculation of τ_B from P_O, obtained from the graphs presented in Fig. 3 B, and time τ_O. The average residence time of the blockage as a function of salt concentration is given in the inset of Fig. 4.

Discussion

Results of this study combined with those of the earlier work are consistent with the originally proposed tail-in-the-pore model for VDAC blockage by tubulin (1–3). The previously reported reduction of the channel aperture measured with the polymer partitioning (4) and the inversion of the weakly anionic selectivity of the open channel to weakly cationic of the blocked state (2,4) are in accord with the notion of the negatively charged tail of tubulin residing inside the VDAC pore. The model also provides a rationale for explaining the sensitivity of the current through the blocked state to the charge of membrane lipids. It is based on the tubulin tail-induced change in proximity of ion translocation pathways to the charges of surrounding lipid molecules. A similar idea of the changing proximity was used to explain the changing sensitivity of different alamethicin-conducting states to lipid charge (23). Experimentally, it was shown that when salt concentration in the membrane-bathing solution was decreased, the lipid charge manifested itself as an increase in the current through the lowest conductance levels that corresponded to the smallest alamethicin aggregates. Theoretically, it was demonstrated that the effect of surface charge could be rationalized within the nonlinear Poisson-Boltzmann approach. Larger alamethicin aggregates showed weaker effects, sometimes below the accuracy of the measurements, as the distance from the nearest lipid charge to the center of the channel mouth increased.

Fig. 5 A is a cartoon illustrating the possible origin of the difference in conductance sensitivity to lipid charge in the open and tubulin-blocked states. In the tubulin-blocked state, the effective distance to the nearest lipid charge from the channel aperture available for ion translocation is approximately two times smaller, thus making the Debye screening of the lipid charge less effective. This results in a higher effect of the charge as compared with that for the open state. The parameters in the figure and equations below are as follows: R_t is the effective radius of the tubulin tail, R_p is the radius of the VDAC water-filled pore, and R is the distance between the channel center and the nearest lipid charge.

Guided by one of the approaches described earlier (23,24) we define the potential over the channel mouth as

$$\phi \left(r\right)=\frac{4k_{\text{B}}T}{e}{\tanh }^{-1}\left[\tanh \left(\frac{e{\phi }_0}{4k_{\text{B}}T}\right)\exp \left(\frac{r-R}{{\lambda }_D}\right)\right],$$ (3)

where φ₀ is potential at the charged membrane surface

$${\phi }_0=\frac{2k_{\text{B}}T}{e}{\sinh }^{-1}\left(\frac{\sigma }{\sqrt{8k_{\text{B}}T\epsilon {\epsilon }_0\left[n\right]}}\right),$$ (4)

and λ_D is the Debye screening length

$${\lambda }_D=\sqrt{\frac{\epsilon {\epsilon }_0{k}_{\text{B}}T}{2\left[n\right]e^2}}.$$ (5)

Here σ is the surface charge density, εε₀ is the dielectric constant of water, and [n] is the number KCl concentration in the membrane-bathing solution related to the molar concentration [C] through Avogadro's number N_A as [n] = 10³ N_A[C]. Taking into account the cationic and anionic transport numbers for the open (t⁺_open and t⁻_open) and blocked (t⁺_block and t⁻_block) states, for the conductances of these states we can write

$$G_{open}=const\underset{0}{\overset{R_p}{\int }}\left[t_{open}^{+}\exp \left(\frac{-e\phi \left(R-r\right)}{k_{\text{B}}T}\right)+t_{open}^{-}\exp \left(\frac{e\phi \left(R-r\right)}{k_{\text{B}}T}\right)\right]rdr,$$ (6)

$$G_{blocked}=const\underset{R_t}{\overset{R_p}{\int }}\left[t_{block}^{+}\exp \left(\frac{-e\phi \left(R-r\right)}{k_{\text{B}}T}\right)+t_{block}^{-}\exp \left(\frac{e\phi \left(R-r\right)}{k_{\text{B}}T}\right)\right]rdr.$$ (7)

Numerical integration of these equations gives the ratios shown in Fig. 2 B as solid lines through the experimental data. The following geometric parameters of the model in Fig. 5 were used in calculations: R_p = 1.2 nm (11,12), R_t = 0.9 nm (estimated from the conductance reduction to 0.4 of that of the open channel upon its blockage by tubulin in 1 M KCl), and the only free parameter of the model—the distance between the channel center and the nearest lipid charge, R—was chosen to be 3 nm (25). The surface charge density was calculated from the actual lipid mixtures to be 0.2 C/m² for DPhPS/DPhPC (4:1) membranes and 0.165 C/m² for DOTAP/DPhPC (2:1) membranes. The transport numbers for the open, t⁺_open = 0.2 and t⁻_open = 0.8, and blocked, t⁺_block = 0.7 and t⁻_block = 0.3, states were taken from recent publications (2,4). It is seen that for both lipid compositions the agreement between this simple theoretical approach and experiment is surprisingly good. A similar calculation using the same parameters was performed for the open state conductance. It gave a significantly smaller (and inversed) effects of –15% for the negatively, and +28% for the positively, charged membranes versus neutral membranes at 0.1 M KCl, which are compatible with the data in Fig. 2 A.

It should be noted that though our approach does not explicitly deal with the charges on the tubulin tail, these charges are indeed important and are taken into account via the changed cationic and anionic transport numbers in the tubulin-blocked state. The correspondence between the crude quantitative analysis given by Eqs. 3–7 and experimental data in Fig. 2 B strongly favors the tail-in-the-pore model of VDAC blockage by tubulin (1–3). However, it should be noted here that the perfectly symmetric structure shown in Fig. 5 A, which allows analytical treatment of the problem, is only an approximation. The actual structure of the tubulin tail-pore assembly is indeed much more complex and less symmetric, as Fig. 5 B attempts to illustrate.

One of the surprising findings of this study is that the residence time of the blockage is a weak increasing function of salt concentration. This is in a stark contrast with a recent study of another β-barrel channel blockage by multicharge blockers (26). Interaction of anthrax's protective antigen channel with the chemically modified β-cyclodextrins carrying seven positive charges was characterized by a strong dependence of the blocker residence time on salt concentration of the bathing solution. Within a similar salt concentration range as that used in Fig. 4, the cyclodextrin residence time was reported to change by two orders of magnitude, decreasing with the increasing salt concentration. This was interpreted as an indication of strong involvement of long-range electrostatics in the balance of forces responsible for the high blockage efficiency (26,27).

The VDAC-tubulin blockage equilibrium is impressively voltage-dependent. For example, the recently reported voltage dependence of the equilibrium binding constant between Tom40, another β-barrel channel of the mitochondrial outer membrane, and precursor peptides, was found to be much weaker (28). The effective gating charge given in Table 1 that characterizes blockage sensitivity to voltage compares well with that reported for voltage-gated channels of electrophysiology (29). However, the underlying interaction is that between the tubulin charges and the applied transmembrane field. As for the Coulomb interactions between the charges on the VDAC molecule and the tubulin charges, those do not seem to be dominant. Instead of decreasing with salt concentration, the residence time even slightly increases (Fig. 4, inset), implying that at zero applied voltages some kind of hydrophobic interactions between CTT and VDAC pore prevails.

Conclusions

The role of the surface charge of the pore interior is among important topics of the modern nanopore research (30–32). However, not only the charge on the pore wall, but also the charge on the membrane in which the pore resides, is able to modulate ion transport. The effect of lipid charge was mostly studied with benchmark channel-forming short peptides such as gramicidin (24) and alamethicin (23) or highly selective channels of neurophysiology (33–37). Membrane surface charge affects the properties of these channels either because the channel pore is narrow enough to be influenced by the charge of the surrounding lipids, or, sometimes, because lipids directly constitute a part of the ion pathway (38). For the large transport β-barrel channels as VDAC, the average distance between ion pathway and the nearest lipid headgroups usually exceeds the Debye length, so the effect of lipid charge is minimized. Here we have shown that this situation could change substantially when protein-protein interactions come into play.

We find that, at reduced salt concentrations, the relative residual conductance of the tubulin-blocked state of VDAC is sensitive to the surface charge of the membrane (Figs. 1 and 2). Such a behavior agrees well with the tail-in-the-pore model of the tubulin-blocked VDAC state suggested earlier (1,2), in which the conductance reduction and ionic selectivity reversal are attributed to the tubulin's negatively charged tail entering the VDAC water-filled pore. A moderate cationic selectivity of the blocked state explains the DPhPS-induced increase in this state conductance. Negatively charged DPhPS attracts cations that are predominant in the ionic current through the tubulin-blocked state. Conversely, positively charged DOTAP depletes cations at the channel entrance, thus reducing conductance. Analytical considerations, Eqs. 3–7, fully support this interpretation. The opposite behavior is expected for the open state because of its moderate anionic selectivity. However, because the average distance to the nearest lipid charge in the open state is approximately two times larger (Fig. 5 A), the effect on its conductance is small (Fig. 2 A) and hard to measure due to the natural spread of conductances from channel to channel (39,40).

The effective gating charge of the blockage is only weakly dependent on both electrolyte concentration and the charge of the membrane-forming lipids (Table 1). Within the framework of the model, this suggests that ion condensation on the tubulin tail in the pore is negligible, so that its charge is not salted-out even by KCl concentrations as high as 1.5 M. It is important to note that the absolute value of the gating charge, 10–14 elementary charges, is too high to be accounted for by the charges on the tubulin tail only. This indicates the existence of some additional voltage-dependent step(s) in the blockage process such as tubulin-membrane interactions (T. K. Rostovtseva, P. A. Gurnev, M.-Y. Chen, and S. M. Bezrukov, unpublished).

The findings reported in this study give additional insights on the nature of the ATP-impermeant tubulin-blocked state of VDAC. More generally, we believe that they are important for understanding of common mechanisms of functional protein-protein interactions by providing both kinetic and thermodynamic features of such interactions at a single-molecule level.