On Resistance to Virus Entry into Host Cells

Abstract

In this article, we adopt a continuum model from Sun and Wirtz (2006. Biophys. J. 90:L10–L12) to show that, for the enveloped virus entry into host cells, the binding energy of the receptor-ligand complex can drive the engulfment of the viral particle to overcome the resistance alternatively dominated by the membrane deformation and cytoskeleton deformation at a different engulfing stage. This is contrary to the conclusions by Sun and Wirtz that the cytoskeleton deformation is always dominant. This discrepancy occurs because the energy of membrane deformation in their article is incorrect. Such an unfortunate small error has led to a severe underestimation of the contribution from membrane deformation to the total energy of the system, which then led them to improperly conclude that the cytoskeleton deformation plays the dominant role in the virus entry into host cell. By using the correct energy expression, our conclusion is justified by energy comparisons under a large range of virus sizes and Young's moduli of cytoskeleton. We even find that a critical radius of virus exists, beyond which the resistance to the virus engulfment becomes dominated by the membrane deformation during the whole stage, contrary to the point of view of Sun and Wirtz.

We read with interest the study by Sun and Wirtz (1). In their study, they developed an equilibrium analysis of virus-cell interaction by considering the elastic deformations of both cell membrane and cytoskeleton, and the interaction between the virus and the host cell through ligand-receptor complexes. By defining h as the engulfment depth, the total system energy E has been expressed in terms of h as (1)

$$E\left(h\right)=E_1\left(h\right)+E_2\left(h\right)+E_3\left(h\right),$$

where E₁(h) = −Aa, E₂(h) = ∫ (2κH² + γ)dA, and E₃(h) = 2$\sqrt{R}{h}^{5/2}/5u$ are the energy of ligand-receptor complex formation, deformation energy of the plasma membrane, and the deformation energy of the cell body (1), respectively, and A = 2πRh is the area of contact between the cell and virus, a the binding energy density, R the radius of virus, H, κ, and γ are the mean-curvature, bending modulus, and surface tension of the membrane, respectively, and u = 3[(1 – σ²₁)/ε₁ + (1 – σ²₂)/ ε₂]/4 is the combined elastic modulus, ε_1,2 and σ_1,2 being Young's moduli and Poisson's ratios of the cell and the virus.

We need to emphasize that the mean-curvature H of the deformed membrane in the contact zone, which is assumed by Sun and Wirtz (1) as a spherical surface with radius R, should be expressed as 1/R (2,3). Unfortunately, Sun and Wirtz (1) have incorrectly expressed it as H = 1/2R. By using the correct expression of the mean curvature, one can show that

$$\frac{E_2\left(h\right)}{4\pi R^2}\approx \frac{\kappa h}{R^3}+\gamma \left(\frac{h}{2R}-\frac{2Rh-h^2}{4R^2}\right).$$

Comparing the correct total energy expression

$$\frac{E\left(h\right)}{4\pi R^2}\approx -\frac{ah}{2R}+\frac{\kappa h}{R^3}+\gamma \left(\frac{h}{2R}-\frac{2Rh-h^2}{4R^2}\right)+\frac{h^{5/2}}{10\pi u{R}^{3/2}}$$

to the original expression in Sun and Wirtz (1),

$$\frac{E\left(h\right)}{4\pi R^2}\approx -\frac{ah}{2R}+\frac{\kappa h}{4R^3}+\gamma \left(\frac{h}{2R}-\frac{2Rh-h^2}{4R^2}\right)+\frac{h^{5/2}}{10u{R}^{3/2}},$$

it can be seen that the membrane-bending energy term in the total energy expression given by Sun and Wirtz (1) is only one-quarter of the correct value. (Note that, in the last term of the energy expression, Sun and Wirtz have missed a prefactor 1/π. However, they may have taken into account this missing factor in their calculations, and we therefore think it is just a typo.)

The above error in the system energy expression then permeated throughout all the quantitative results plotted in Fig. 2 of the Sun and Wirtz article. For comparison, we replot these results in Figs. 1–4 based on the correct energy expression together with those in Sun and Wirtz (1) based on the incorrect energy expression. Figs. 1–4 clearly show large discrepancies between our calculations and those in Sun and Wirtz (1).

Figure 2.

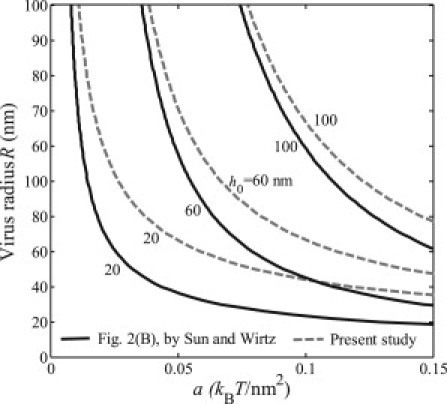
Relations between the virus radius R and the binding energy density a for various values of the virus equilibrium depth h₀, based on the incorrect energy expression a = 2R(κ/R³ + h₀γ/2R² + h₀^3/2/4πuR^3/2) provided by Sun and Wirtz (1) and the corrected energy expression.

Figure 1.

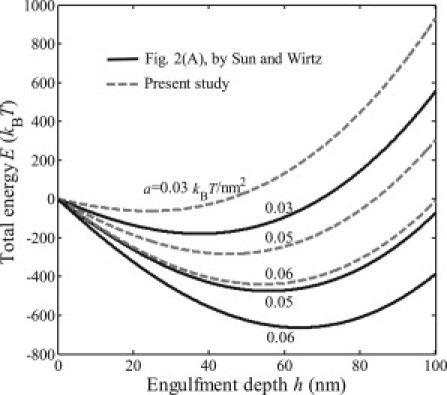
Relations between the total energy E of cell-virus interaction and the virus engulfment depth h with various values of binding energy density a, based on the incorrect energy expression provided by Sun and Wirtz (1) and the corrected energy expression.

Figure 3.

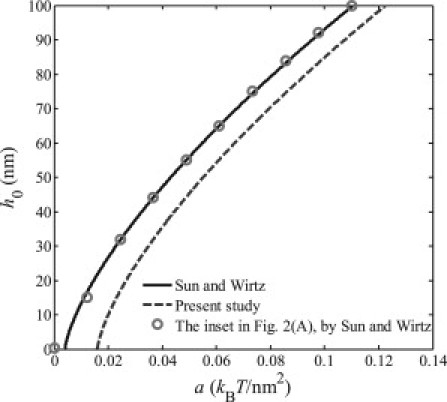
Relations between the virus equilibrium depth h₀ and the binding energy density a based on the incorrect energy expression and the inset in Fig. 2A provided by Sun and Wirtz (1) and the corrected energy expression.

Figure 4.

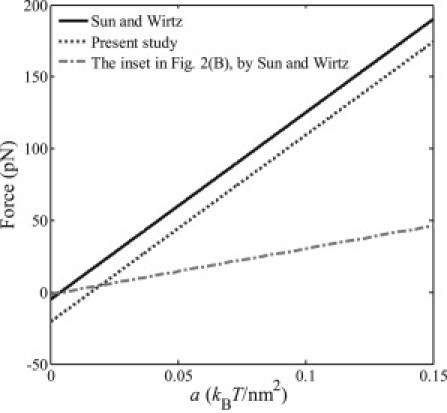
Relations between the force F driving the engulfment and the binding energy density a based on the incorrect energy expression and the inset in Fig. 2B provided by Sun and Wirtz (1) and the corrected energy expression.

In addition to the incorrect energy expression and the subsequent analysis results, we found that some of the plots by Sun and Wirtz (1) are not even consistent with their own energy expression. For example:

• 1.
  Sun and Wirtz (1) derived an equilibrium engulfment depth h₀ as the root of equation ∂E/∂h = 0, or the root of

  $$a=2R\left(\frac{k}{4R^3}+\frac{h_0\gamma }{2R^2}+\frac{h_0^{3/2}}{4\pi u{R}^{3/2}}\right)$$

  associated with their own incorrect energy expression. (The prefactor 1/π has been added to the third term of the equation, according to the special note above.) Following these equations, one can easily deduce that h₀ = 0 should correspond to a = κ/2R² (note that the correct energy expression would give that a = 2κ/R² when h₀ = 0), according to the incorrect energy expression in Sun and Wirtz (1). Sun and Wirtz (1) have plotted the equilibrium engulfment depth h₀ as a function of the ligand-receptor binding energy density in the inset of Fig. 2 A in their article. However, from their plot, we can see that h₀ = 0 corresponds to a = 0, which is inconsistent with the result derived from their own energy expression and the correct energy expression, as shown in Fig. 3.

• 2.
  Sun and Wirtz (1) have also derived the initial force driving the engulfment as

  $$F=-{\frac{\partial E}{\partial h}|}_{h=0}.$$

  Based on their own energy expression (1), this force should read F = 2πRa – πκ/R, and was plotted as a function of the binding energy density a in the inset of Fig. 2 B in their article (1). However, from Fig. 4, one can see that the plot by Sun and Wirtz (1) is inconsistent with both their own force expression and the force expression based on the correct energy expression, F = 2πRa – 4πκ/R.

Based on the incorrect energy expression, Sun and Wirtz (1) concluded that the cytoskeleton deformation should play the dominant role in the determination of the engulfment depth h, i.e., E₃(h) >> E₂(h). If the correct energy expression is used, we find that there exists a critical engulfment depth of

$$h_{\text{cr}}\approx \frac{1}{R}\left[{\left(10\pi \kappa u\right)}^{2/3}+\frac{5}{3}\gamma {\left(10\kappa {\pi }^4{u}^4\right)}^{1/3}\right],$$

below which the energy associated with cytoskeleton deformation is smaller than that of the membrane deformation, i.e., E₃(h) < E₂(h). Fig. 5 illustrates the comparison between the deformation energy of the plasma membrane and that of the cell body with a wide range of Young's moduli, 10 kPa, 20 kPa, 30 kPa, 50 kPa, or 100 kPa, where other parameters have been adopted the same as in Sun and Wirtz (1): R = 50 nm, κ ≈ 20 k_BT, γ ≈ 0.005 k_BT/nm², u = 5.625 × 10⁻⁵ Pa⁻¹, and T = 300 K. It is seen that there always exists a critical engulfment depth h_cr when h < h_cr, the deformation energy of the membrane, is larger than that of the cell body. Fig. 6 plots such critical engulfment depth h_cr as a function of Young's modulus of cell for different radii of virus particle, where h_cr/R = 0 or h_cr/R = 2, respectively, corresponding to the cases that resistance is fully dominated by the deformation of cytoskeleton or membrane. We can see from Fig. 6 that for virus with different radii h_cr/R = 0 is never reached but h_cr/R = 2 is always reached as long as the Young's modulus of cell is small enough, indicating that under certain conditions the deformation energy of cytoskeleton can always be smaller than that of the cell membrane during the entire engulfment process. Therefore, the conclusion given by Sun and Wirtz (1) as the main conclusion of their article that the resistance to the engulfment of virus is dominated by the deformation energy of cytoskeleton, is not justified by their model.

Figure 5.

Comparisons between the deformation energy of the plasma membrane (E₂) and that of the cell body (E₃) when the virus radius R is taken to be 50 nm and Young's modulus of the cell is 10 kPa, 20 kPa, 30 kPa, 50 kPa, or 100 kPa.

Figure 6.

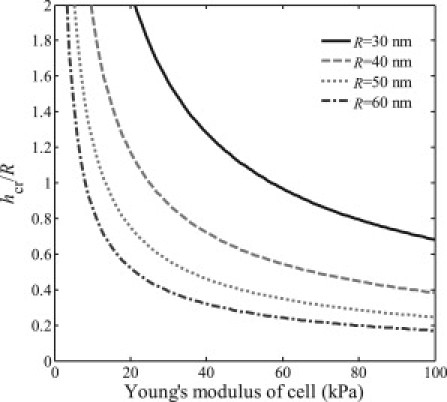
Critical engulfment depth h_cr, corresponding to E₂(h_cr) = E₃(h_cr), E₂(h > h_cr) < E₃(h > h_cr), E₂(h < h_cr) > E₃(h < h_cr), as a function of Young's modulus of host cell for different radii of viral particle.

In summary, we have found that the deformation energy of cell membrane has been incorrectly expressed by Sun and Wirtz (1), which has led to a severe underestimate of the contribution of membrane deformation to the total system energy and the questionable conclusion that the cytoskeleton deformation plays the dominating role in the virus entry into host cell. Based on the correct energy expression, one cannot conclude the deformation energy of cytoskeleton must dominate that of membrane. The question whether the resistance to engulfment is dominated by the membrane deformation or the cytoskeleton deformation depends on the virus size, the engulfing stage, and the Young's modulus of cell.

We further note that, by considering the cell body as a linear elastic half-space, the model adopted by Sun and Wirtz (1) likely overestimates the deformation energy of the cytoskeleton. This model has a number of highly debatable assumptions:

• 1.The model treats cytoskeleton as a linear elastic half-space over a timescale on the order of tens of minutes or hours, thereby neglecting entirely the time-dependent viscous deformation of cytoskeleton that can relax the cytoskeleton as the viral particle enters cell.
• 2.It neglects the discrete nature of cytoskeleton at the scale of a viral particle.
• 3.Even within an elastic model, the process of virus entry into a host cell should clearly invoke very large nonlinear deformation and geometric nonlinearity.

Before these assumptions can be fully justified, an alternative approach to modeling cell entry into host cell is to neglect the cytoskeleton deformation (4,5), which could be substantially relaxed on the viral entry timescale.