Role of Elongation and Secondary Pathways in S6 Amyloid Fibril Growth

Abstract

The concerted action of a large number of individual molecular level events in the formation and growth of fibrillar protein structures creates a significant challenge for differentiating between the relative contributions of different self-assembly steps to the overall kinetics of this process. The characterization of the individual steps is, however, an important requirement for achieving a quantitative understanding of this general phenomenon which underlies many crucial functional and pathological pathways in living systems. In this study, we have applied a kinetic modeling approach to interpret experimental data obtained for the aggregation of a selection of site-directed mutants of the protein S6 from Thermus thermophilus. By studying a range of concentrations of both the seed structures, used to initiate the reaction, and of the soluble monomer, which is consumed during the growth reaction, we are able to separate unambiguously secondary pathways from primary nucleation and fibril elongation. In particular, our results show that the characteristic autocatalytic nature of the growth process originates from secondary processes rather than primary nucleation events, and enables us to derive a scaling law which relates the initial seed concentration to the onset of the growth phase.

Introduction

The level of interest focused on understanding the assembly and structure of nanoscale protein fibrils has increased significantly in the last decade due to the realization that the formation of amyloid fibrils is intricately associated with a range of neurodegenerative disorders, including Parkinson's (1) and Alzheimer's diseases (2–5), and other medical conditions including type II diabetes. The underlying similarities in the structures and behavior of protein fibrils found in connection with apparently disparate disorders, together with the finding that many proteins, both with and without connection to disease, are able to undergo fibrillar assembly in vitro, has led to the idea that the amyloid state represents a generally accessible alternative form of organized protein structure (6,7).

Despite the apparent simplicity associated with the description of amyloid growth as a homomolecular assembly phenomenon, it has become apparent that this process is characterized by a remarkable degree of complexity on the molecular level, and that many different molecular events contribute to the overall assembly pathway. It is widely agreed that fibril formation is initiated by a primary nucleation step (8) wherein soluble proteins come together to form aggregates capable of subsequent growth through incorporation of further species and leading to elongation of the structures when they acquire fibrillar character (9–14). In many cases, it has been shown that this subsequent growth is resulting from the incorporation of monomers rather than oligomers, a conclusion in agreement with the finding that fibril growth can be observed under conditions where no significant oligomer populations can be detected (10,14) and the fact that the elongation of fibrils has been found to be directly proportional to the concentration of soluble protein (10,11).

A crucial characteristic of such fibrillar assembly phenomena is the sigmoidal nature of the reaction profile: the rate of assembly accelerates during the first part of the process, and then slows down to reach an equilibrium end-point that results from the depletion of available protein in solution. The origin of the acceleration in the reaction rate for early times is, however, still a topic of investigation and discussion. It is important to note that, if the number of fibril ends present in solution remains constant, the rate of the overall conversion of soluble protein into the fibrils will be linear in the monomer concentration because the growth occurs primarily at the ends of the fibrils. A higher than linear concentration dependence requires, therefore, the multiplication of such fibrils in number in order to increase the number of ends where the growth occurs (15–17). This type of proliferation in the number of fibrils in some studies has been attributed to further primary nucleation, where new fibrils emerge from soluble protein in parallel to the growth of existing fibrils, but in others to secondary pathways, where additional growth centers are formed from growing fibrils, e.g., by fibril breakage, surface-catalyzed nucleation, or branching (see (15,18,19) for a more detailed description of secondary pathways).

In the literature, the term “fibril growth” is commonly used to indicate both fibril elongation and multiplication, and combinations of such processes; relatively little work has focused on the challenge of identifying the true contribution of the elongation process relative to the contributions of primary and secondary nucleation. Indeed, parameters in empirical sigmoidal functions, such as the logistic function (14), combine both microscopic rates into phenomenological parameters such as the lag-time or the apparent maximal growth rate. A further complication results from the fact that the relative populations of different types of fibrils and their structures can be shifted dramatically upon changes in the environment (20,21). This changing picture of fibril polymorphism can, however, be avoided by seeding with preformed fibrils, thereby templating the subsequent growth of one fibril type without the requirement for primary nucleation.

Materials and Methods

General notes

All S6 mutants were expressed recombinantly, purified, and dialyzed against deionized water as described previously in Otzen et al. (22). Protein concentrations were determined by absorption at 280 nm using an ND-1000 spectrophotometer (NanoDrop, ThermoScientific, Wilmington, DE). A theoretical extinction coefficient at 12.700 cm⁻¹, M⁻¹ was used. Fibril formation was carried out in 10 mM HCl (pH 2), 0.4 M NaCl at 42°C with agitation (900 rpm during seed formation and 180 rpm in plate reader experiments). All Thioflavin T (ThT) fluorescence measurements were performed in triplicate.

Asymmetric flow field-flow fractionation

Here, we used asymmetric flow field-flow fractionation (AF4). Samples of 100 μM S6 VA88 were harvested from the kinetic plate reader experiments over a period of five days and centrifuged at 13,400 rpm for 15 min in a MiniSpin centrifuge (Eppendorf, Hamburg, Germany). A 100-μL sample was injected onto an AF2000 asymmetrical flow field-flow fractionation system (Postnova, Landsberg, Germany) equipped with an S3240 UV/Vis detector monitoring absorbance at 205 and 280 nm, PN3140 refractive index, and a PN3070 7-angle light scattering detector. The system was equipped with a 5-kDa MWCO ultrafiltration membrane and a 350-μm spacer, and was equilibrated in 10 mM HCl (pH 2), 0.4 M NaCl at room temperature. The sample was separated, injected, and focused for 5 min at 0.2 mL/min with a focus flow of 2.3 mL/min and cross-flow of 2 mL/min. The detector flow was kept constant at 0.5 mL/min throughout the injection, focusing, and separation. After focusing, a cross-flow gradient from 2 to 0.15 mL/min over 20 min followed by a 10-min gradient to 0 mL/min was applied to separate potential S6 species. The system was then washed at 0 mL/min cross-flow for 15 min.

Seed formation

Mature fibrils were prepared in 1.5 mL test tubes containing 100–250 μM of S6 under fibril forming conditions and incubated in a Vortemp 56 evc. Eppendorf shaker (Tehtnica, Zĕlezniki, Slovenia). Fibril formation was followed using ThT fluorescence: samples were diluted 12 times with a ThT solution (40 μM ThT final, 10 mM HCl, pH 2, 10 mM NaCl) and incubated for 10 min in an Eppendorf shaker under conditions identical to those used for fibril growth. Fluorescence measurements were carried out on a LS55 Luminescence spectrometer (Perkin-Elmer, Norwalk, CT) using emission and excitation slit widths of 10 nm, excitation at 450 nm, and emission at 465–555 nm. Seeds were obtained by sonication on ice of mature fibrils using a HD 2070 Bandelin Sonuplus Sonicator (Buch & Holm, Copenhagen, Denmark) for three times,1 min, at 60% power. Seeds were kept at 4°C.

Fibril formation kinetics with platereader

Seeded fibril growth from different mutant variants was monitored using ThT-fluorescence (using excitation at 450 nm and emission at 485 nm) performed every 20 min on a GENios Pro Plate Reader (TECAN, Männedorf, Germany) in 96-well plates. All samples contained 40 μM ThT, 10mM HCl (pH 2), 0.4 M NaCl. The temperature was kept at 42°C, shaking was linear at 180 rpm, and shaking duration was 3 min in every 20-min cycle.

Atomic force microscopy

For analysis by atomic force microscopy (AFM), mature fibrils and seed samples were prepared as described above from a 100 μM S6 monomer solution. 5 μL sample aliquots were deposited on freshly cleaved mica (SPI supplies, West Chester, PA). Samples were imaged by AFM, under ambient conditions at room temperature, using a NanoWizard II (JPK Instruments, Cambridge, UK) and Ultrasharp NSC36 cantilevers (MikroMasch, Tallinn, Estonia) in contact mode at a line rate of 1.5 Hz and a resolution of 512 × 512 pixels. Images were analyzed with the open source software Gwyddion (http://gwyddion.net/).

Fourier transform infrared spectroscopy

Fourier transform infrared spectroscopy (FTIR) spectra of fibrils and monomeric solutions were obtained with a Tensor 27 FT-IR (Bruker Optics, Billerica, MA). Spectra were accumulations of 68 scans, measured with a resolution at 2 cm⁻¹ in the range from 1000 to 3998 cm⁻¹. Data processing, consisting of atmospheric compensation, baseline subtraction, and fitting with Lorentzian curves, was performed with the software OPUS ver. 5.5 (http://www.stsci.edu/software/OPUS/kona2.html). For the comparison of seed and second-generation fibrils, spectra were normalized.

Transmission electron microscopy

Transmission electron microscopy (TEM) was carried out as described previously in Pedersen et al. (20). Briefly, a 5-mL aliquot (50–100 mM S6, incubated as above) was placed on a 400-mesh, carbon-coated, glow-discharged grid for 30 s. Grids were washed in two drops of double-distilled water and stained with 1% (w/v) phosphotungstic acid at pH 6.8 and blotted dry on filter paper. Samples were viewed with a model No. 1010 transmission electron microscope (JEOL, Peabody, MA) at 25,000 magnification.

Results and Discussion

In order to identify the effects of fibril elongation and secondary pathways relative to other processes contributing to the overall fibril growth process, we can analyze systematic variations in the growth kinetics that result from changes in the quantities of preformed aggregates that are added and of monomer. We illustrate this approach in this article by studying members of a library of single and double mutants of the ribosomal protein S6 from Thermus thermophilus. The protein S6 has emerged as an outstanding system for probing protein folding (22–24) and aggregation (20). Under acid-denaturing conditions which promote fibril formation (0.4 M NaCl, 10mM HCl (pH 2), 42°C), the native state of S6 (N) is destabilized and the protein can undergo amyloid assembly. The choice of S6 as the system of study in this work also gives rise to a key advantage, in that the primary nucleation of amyloid structures from S6 monomers is slow under these conditions (Fig. 1), providing a window within which it is possible to study elongation and multiplication of fibrillar species in the knowledge that primary nucleation is not contributing significantly to the evolution of observed fibrillar structures.

Figure 1.

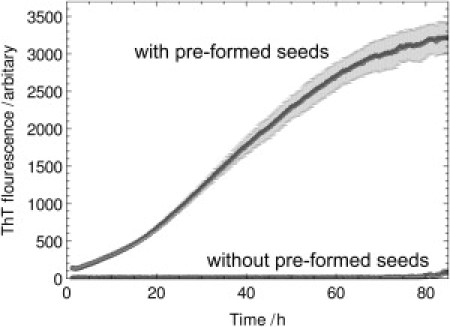
Kinetic traces for the fibril formation of S6 protein (LA30) with and without the initial addition of seeds of preformed fibrils. In the absence of such seed material (lower trace), no fibrillar material is detected over the time course of 80 h. With the addition of preformed seeds (upper trace), however, all monomer is incorporated into aggregates within this time window. Hence, the sigmoidal rate profile that is observed in this case unambiguously reflects the role of secondary pathways. In addition, the preseeded trace demonstrates the different scaling of the ThT fluorescence signal with initial seed material and the new material formed during the reaction, as given by Eq. 1. The system had initial seed concentration 8.3 μM and initial monomer concentration 100 μM. The ratio of the total monomer concentration in the system, 108.3 μM, to the initial seed concentration, 8.3 μM, is ∼13, yet the ratio of the final/initial signal reported by ThT is ∼24.

By the use of preseeding, hence avoiding the effects of polymorphism, within this window where primary nucleation does not contribute significantly to the fibril population, we reduce the number of variables that need to be defined in the self-assembly reaction. We confirmed directly that no oligomers were present in our preseeded experiments using AF4, AFM, and TEM measurements (see the Supporting Material). We can then use an array of different S6 mutants to span a broad range of fibril formation kinetics to test the validity of our model over an extended parameter range. The fibril kinetics are followed using in situ ThT fluorescence measurements; we have previously shown by electron microscopy that S6 fibrils formed under these conditions lead to high ThT signals (25).

Initial examination of the data describing fibril kinetics reveals that there is a difference between the ThT signal given from pregrown seeds and fibril material that forms in the reaction through addition to the seeds, although the structures of seeds and fibrils grown from seeds are very similar when compared using FTIR and AFM measurements (see the Supporting Material). In other words, the observed ThT signal obeys a dependency of the form

$$\begin{array}{c}\text{Signal}=\rho M_{\text{initial}\text{seeds}}+\sigma M_{\text{new}\text{material}}\\ =\rho M\left(0\right)+\sigma \left[M\left(t\right)-M\left(0\right)\right]\end{array},$$ (1)

where M denotes the concentration of monomer in aggregates, ρ is fixed so that the seed concentration is reported correctly at the beginning of the reaction, and σ is fixed so that the total monomer concentration is defined correctly at the end of the reaction. This effect can be seen in Fig. 1 where the initial seed concentration is 8.3 μM and the initial monomer concentration is 100 μM. The ratio of the final/initial ThT signal is ∼24, whereas the ratio of total monomer to monomer initially in seeds is ∼13, implying σ ≈ 2ρ.

Elongation

The time evolution of a population of fibrillar species proliferating through primary nucleation, elongation, and secondary pathways has been studied extensively over the past 40 years (16–18,26–28). Much work has focused on integrated rate laws valid for the early stages of the reaction (10,15,18,29–31), first derived in the pioneering work of Ferrone et al. (18,32) in their studies of sickle hemoglobin gelation; more recently these solutions have been extended, using a self-consistent approach, to give integrated rate laws valid for the entire reaction time course (16,17,33). Solutions valid over the entire reaction will be vital in studying secondary nucleation later in this article, whereas the early time behavior is related to elongation in this section.

The early stages of aggregation in the S6 system can be used to study unambiguously the elongation of fibrillar species. We focused first on the effect of seed concentration on the addition of monomeric protein to fibrillar species in the initial stages of the reaction. For a system where primary nucleation does not contribute significantly to the fibril population, and for which preformed seeds are instead used to initiate the reaction, the fibrillar mass-concentration, M(t), evolves in the initial stages of the reaction according to (17),

$$M\left(t\right)=m\left(0\right)C_{+}{e}^{\kappa t}-m\left(0\right)C_{-}{e}^{-\kappa t},$$ (2)

$$\stackrel{t\to 0}{=}M\left(0\right)+2{\tilde{k}}_{+}m\left(0\right)P\left(0\right)t+\mathcal{O}\left(t^2\right),$$ (3)

where P(t) denotes the number-concentration of fibrils and m(t) denotes the free monomer concentration. The constants in Eq. 3 are given as

$$\begin{array}{c}\kappa =\sqrt{2{\tilde{k}}_{+}{k}_{2}m{\left(0\right)}^{n_2}}\\ C_{\pm }=\frac{{\tilde{k}}_{+}P\left(0\right)}{\kappa }\pm \frac{M\left(0\right)}{2m\left(0\right)}.\end{array}$$ (4)

The kinetic rate constant for elongation from each end is given as ${\tilde{k}}_{+}$ and that for the secondary pathway by k₂. The elongation rate constant in this formulation, ${\tilde{k}}_{+}$, may not be independent of the monomer concentration; we discuss this later in this section. The parameter n₂ describes the monomer-dependence of the secondary pathway such that n₂ = 0 corresponds to the monomer-independent case of fragmenting filaments (15,16,18,27,34,35); a nonzero value of n₂ represents a monomer-dependent secondary pathway, for example, where the surface of existing filaments is active in catalyzing the formation of new growth nuclei (15,18,33,36). Equation 3 shows that, for early times, the secondary pathway is less important in defining the overall consumption of free monomer m(t) than the direct elongation of fibrils proportional to $2{\tilde{k}}_{+}m\left(0\right)$.

Equation 3 shows that for kinetic data describing seeded growth, the intercept is the initial seed concentration M(0) and the initial reaction rate r₀ is given as

$$r_0={\frac{dM}{dt}|}_{t\to 0}=2{\tilde{k}}_{+}m\left(0\right)P\left(0\right).$$ (5)

For systems of fixed initial monomer concentration and varying initial seed concentration, Eq. 5 shows that the initial gradients are expected to be proportional to the initial seed number-concentration, P(0), and the intercept to be proportional to the initial seed mass-concentration, M(0). The mass concentration of seeds added to the system is known for all of our data, and for a given seed preparation used to preseed a series of experiments, the seed number concentration is linked to the seed mass concentration through the average seed length in the preparation, 〈L(0)〉, so that P(0) = M(0)/ 〈L(0)〉. Therefore, the intercept and initial gradient are both expected to vary linearly with the seed mass-concentration. These predictions are validated in the scaling behavior seen in the data for a range of mutants in Fig. 2.

Figure 2.

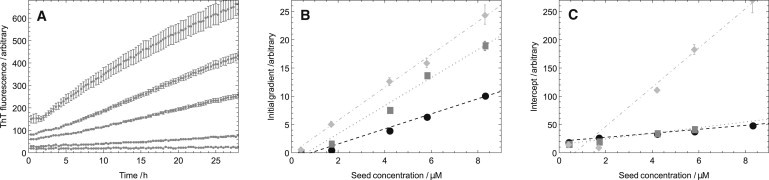
Scaling of the intercept and initial gradient with a varying initial seed concentration at a fixed initial monomer concentration as predicted by Eqs. 3 and 5. (A) Example of raw data (using VA37) for the early-time evolution of the polymer mass at increasing seed concentration (bottom to top). (B) The slope of the initial linear growth phase shows a linear dependency with the seed concentration. (C) The intercepts obtained from linear regression of the initial linear phases also reveal a linear dependency on the seed concentration. The fixed monomer concentration was 100 μM and the data (both seed and monomer) for the variants AG35 (circle), IA8 (square), and VA37 (diamond).

The separation of fibril elongation from primary nucleation and secondary pathways, as described above, provides an opportunity to investigate the sensitivity of fibril elongation toward single and double mutations. The final (plateau) fluorescence intensities in the experiments, at a given monomer concentration, vary by significantly less than one order of magnitude, showing that the changes in the initial fluorescence intensity reflect principally changes in the intrinsic elongation rates rather than variation in ThT binding affinity or degree of fluorescence enhancement. Under this assumption, the elongation rates for a range of mutant/seed combinations have been evaluated and are shown in Table 1. This assumption is further confirmed by noting that the relative elongation rates when WT and LA30/VA65 seeds are grown with monomeric IA8 (2.8 and 4.5, respectively) and monomeric LA61 (0.2 and 0.4, respectively) result in very similar ratios of the elongation rates of 0.6 (2.8/4.5) and 0.5 (0.2/0.4) (Table 1).

Table 1.

Data for the linear variation of the initial gradient of fibril growth with seed concentration at a fixed monomer concentration

Seed species	Monomer species	∂r0/∂M(0)	Correlation coefficient	Nominal relative elongation rate
WT	YA63	70.7	0.98	1.0
WT	LA75/MA67	154.9	0.97	2.2
WT	LA30	246.9	0.99	3.5
WT	AG35	103.5	0.99	1.5
WT	IA8	194.6	0.98	2.8
WT	VA37	267.6	0.99	3.8
WT	LA61	14.1	0.99	0.2
WT	IA8/LA26	25.1	0.98	0.4
LA30/VA65	IA8	319.8	0.99	4.5
LA30/VA650	LA61	29.7	0.99	0.4

Gradients determined from linear regression analysis, ∂r₀/∂M(0), equivalent to those of the fitted lines shown in Fig. 2, are tabulated. Data are shown for a range of seed/monomer mutant combinations at fixed monomer concentration (100 μM). The correlation coefficient from the linear fits, R, is given in the table. The final column gives the relative elongation rates that can be extracted as the ratios of the gradients of the linear regressions as discussed in the text.

This finding reflects the dominant role of the protein that is converted into its aggregated form rather than the nature of the seed in defining the elongation rate of amyloid fibrils (37,38). In an earlier study, we have reported that single and double mutants of S6 strongly affect the primary nucleation rate (20). Our study clearly demonstrates that the elongation rate is highly affected by single and double mutations, even in the case of conservative mutations. A search performed for correlations between the elongation rates found with WT seed (Table 1) and the corresponding physico-chemical properties of the mutants did not reveal significant trends between the elongation rate and the folding parameters (unfolding rate constant k_u, refolding rate constant k_f, and melting temperature T_m; (20) and data not shown). This finding indicates that factors other than the thermodynamic stability of the folded state relative to unfolding control the changes in the elongation rates of the S6 mutant variants. Indeed, mutations can affect parts of the energy landscape that relate to the formation of inter- rather than intramolecular contacts which are involved in amyloid fibril growth but not the unfolding of a single chain.

Considering now the complementary case of systems with a fixed initial seed concentration and varying initial monomer concentration, Eq. 5 shows that, if ${\tilde{k}}_{+}$ is independent of the monomer concentration, the theory predicts that the initial gradient will be proportional to the total monomer concentration; indeed, the fibril elongation rate is given as

$${\partial }_t^{\text{elongation}}M\left(t\right)=2{\tilde{k}}_{+}m\left(t\right)P\left(t\right).$$

At high monomer concentrations, however, diffusion of monomers to the fibril ends is no longer rate-limiting; instead, the structural reorganization of the polypeptide chain subsequent to its initial attachment to a fibril end takes over this role. For the overall elongation step, therefore, the rate exhibits a concentration dependence (10,39,40), which is analogous to that of the Michaelis-Menten scheme (41) for enzymatic reactions,

$$r_0=2{\tilde{k}}_{+}m\left(0\right)P\left(0\right)=\frac{2k_{+}m\left(0\right)}{1+K_m^{-1}m\left(0\right)}P\left(0\right),$$ (6)

where k₊ is a true elongation rate constant that is independent of the monomer concentration, and K_m is the crossover concentration above which elongation is rearrangement-limited. This form emerges naturally from the landscape model of protein folding (39), without the requirement to assume two discrete steps in the overall conversion process. It is interesting to note that the elongation rate constant k₊, which is partially determined by the probability of success of a given encounter between a monomer and a fibril end, is expected to be highly dependent on changes in reaction conditions, point mutations, etc.; the crossover concentration, K_m, may be less effected by such changes (39). Differences in r₀ between S6 mutants could be expected to reflect, therefore, primarily changes in the elongation rate constant k₊. For lower monomer concentrations such that K_m⁻¹m(0) ≪ 1, Eq. 6 reduces ${\tilde{k}}_{+}=k_{+}$ and the reaction rate increases linearly with the total monomer concentration. However, for very high monomer concentrations such that K_m⁻¹m(0) ≫ 1, Eq. 6 shows that the initial rate of incorporation of monomers into fibrils saturates and no longer possesses a concentration dependence. The data shown in Fig. 3 show that the elongation rate increases with the concentration of monomer for lower concentrations before becoming saturated at higher monomer concentrations, as predicted by the theory.

Figure 3.

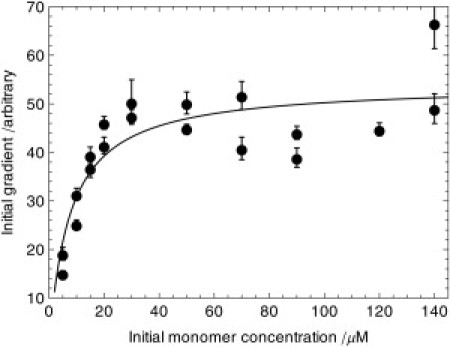
Saturation of the initial gradient of fibril growth at high monomer concentration as prediction by Eq. 6. By varying the initial monomer concentration at a fixed initial seed concentration, we identify clearly the predicted saturation in the initial gradient corresponding to the transition from diffusion to conformational-rearrangement limited fibril elongation discussed in the text, in Eq. 6; the line is a fit to this predicted form. The seed concentration is 8.3 μM. The data shown are for IA8 seed and monomer.

Secondary pathways

We now turn to the analysis of the lag-phase in order to identify the role of secondary pathways in the fibrillation reaction. The existence of a lag-phase in a system where primary nucleation does not make a significant contribution to the increase in the number of fibrils or their mass over the time course of the experiment is direct evidence for the presence of a fibril-dependent secondary pathway responsible for the proliferation of fibrils, and has previously provided support for the role of filament fragmentation in prion propagation (42) and lateral growth in the aggregation of glucagon (43). Indeed, for seeded growth in the absence of a secondary pathway, it is not possible to observe a lag-phase (17,44). In systems which exhibit a significant contribution from primary nucleation, the identification of secondary pathways is more complicated. Indeed, it is in general difficult to establish under such conditions what fraction of the bulk kinetic behavior can be attributed to secondary pathways, and what fraction may originate instead from potentially very complex, and possibly incompletely understood, primary nucleation pathways. This problem does not exist with the system studied in this work and the results represent a striking example of a system where secondary pathways alone lead to a very clear sigmoidal rate profile.

We see in Fig. 1 that in the S6 system, primary nucleation does not generate a significant fibril population over the timecourse shown. However, upon addition of initial seed material, we are able to observe fibril formation within this window, and moreover the reaction follows a sigmoidal rate profile. The measurement of this rate profile, where without the influence of primary nucleation the reaction rate nevertheless initially accelerates even as the monomer is depleted, provides an unambiguous and striking identification of the role of secondary pathways in S6 aggregation.

We can analyze our data further within the standard framework of filamentous growth through elongation and secondary pathways (16–18,26,27,34). In a previous analysis (16), closed-form analytical solutions to the rate equations for filament assembly that are valid for the entire reaction time course were derived using a self-consistent approach to extend the validity of the well-known linearized solution (15,18,29); see Eq. 2. Interestingly, within this theoretical framework it has been shown (16) that for a constant initial monomer concentration and varying initial seed concentration, the time for the reaction to reach half-completion, τ_50%, varies logarithmically with the initial seed concentration, M(0):

$${\tau }_{50\text{\%}}\propto \text{const}-\text{log}\left(M\left(0\right)\right).$$ (7)

This result was derived (16) in the regime where the elongation rate is proportional to the monomer concentration, ${\tilde{k}}_{+}=k_{+}$; the self-consistent solution (16,17) is required to derive Eq. 7 in this case because the previously known linearized form, Eq. 2, is no longer valid at the half-time (Fig. 4 A). It is interesting to note that in the opposite regime, where the elongation rate is saturated and no longer depends on the monomer concentration, m(0) ≪ K_m, the nonlinearity of the rate laws (17,18,29) is reduced significantly, resulting in the linearized solution (Eq. 2), having extended validity. For the low values of n₂ ≤ 4 typically observed for amyloid formation (10,16,36), the linearized solution has validity, in the case where the elongation rate is saturated, that extends to the time to half-completion (Fig. 4 B). In this case, inversion of the linearized rate law (Eq. 2) predicts also a scaling relationship (15,18,42) for the half-time identical to Eq. 7. Therefore, the scaling law Eq. 7 has general validity independent of whether the elongation rate is saturated or not, as verified in Fig. 4 C.

Figure 4.

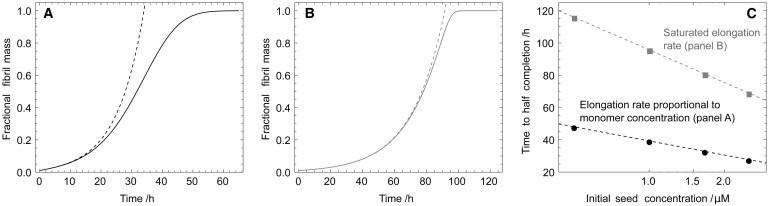
Effect of the saturation of the elongation rate on the time course of the reaction, and comparison with the well-known linearized solution to the rate equations (29,18,15). (A) Time course computed numerically (17) (solid line) for the aggregation reaction for the case where the elongation rate depends linearly on the monomer concentration (16). In this case, the linearized solution (dotted line), from Eq. 2, is only accurate for the early part of the reaction time course. A self-consistent solution has been derived previously that is accurate for the full time-course in this case (16). (B) Time-course computed numerically (17) (solid line) for the case where the elongation rate is saturated (39) and does not depend on the monomer concentration. In this case, the nonlinearity in the rate equations (17) is reduced, increasing the range of validity of the linearized solution (dotted line), from Eq. 2. (C) Scaling of the half-time with the seed concentration calculated numerically for the cases shown in panels A (solid) and B (shaded). In both cases a logarithmic scaling, from Eq. 7, is found. In panel A, ${\tilde{k}}_{+}=k_{+}$ with k₊ = 5 · 10³k₊ = 1 M⁻¹ s⁻¹; in panel B, ${\tilde{k}}_{+}=k_{+}/\left[1+m\left(0\right)/K_m\right]$ with K_m = m(0)/10 and k₊ = 1 · 10⁴k₊ = 1 M⁻¹ s⁻¹. For panels A and B, the other parameters are: m(0) = 50 μM, k₋ = 2 · 10⁻⁹ s⁻¹, k_n = 0, n₂ = 0, M(0) = m(0)/100, and P(0) = M(0)/5000. Panel C has parameters from panel A (shaded) and panel B (solid), respectively, except for the varying seed (mass) concentrations shown.

This scaling from Eq. 7 is observed clearly in our data in Fig. 5. The decrease in lag-time with increasing initial seed concentration can be explained by noting that with a higher seed concentration the incorporation of monomers through elongation is accelerated, and also that concordantly the number of bonds and the surface area of fibrillar species in the system increases faster, resulting in secondary pathways being active at an earlier time.

Figure 5.

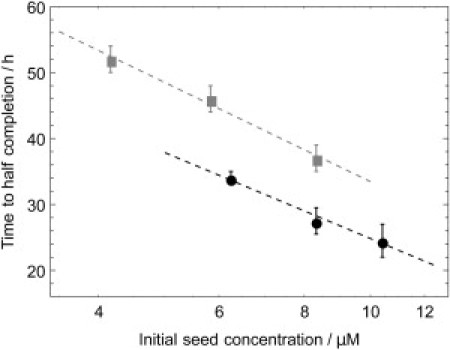
Logarithmic scaling of the time to half-completion of the fibril formation reaction with the initial seed concentration as predicted by Eq. 7; the data are extracted from the traces shown in Fig. 4. (Solid circles) Monomer LA75/MA67 in solution and added seed from LA30/VA65, with a fixed initial monomer concentration 80 μM. (Shaded squares) Monomeric LA30 and WT seed, with a fixed initial monomer concentration of 100 μM.

An additional feature characteristic of the aggregation of S6 is the pronounced transition from the early phase linear growth into the late stage sigmoidal growth at a finite time after the beginning of the reaction. In order to gain insight into this behavior, we first consider the case where the elongation rate is linear in the concentration of monomeric peptide, ${\tilde{k}}_{+}=k_{+}$. It is possible to derive the expected dependency of this characteristic time to onset on the initial seed concentration, because the initial gradient and the maximum gradient are known (17). By solving for the intercept of these two straight lines M_early(t) and M_growth(t) (Fig. 6 a), we find the time to onset, τ_on, given from the condition M_early(τ_on) = M_growth(τ_on), where

$$M_{\text{early}}\left(t\right)=M\left(0\right)+2k_{+}m\left(0\right)P\left(0\right)t,$$ (8)

$$M_{\text{growth}}\left(t\right)=\frac{m\left(0\right)\kappa }{e}t-\frac{\text{log}\left(C_{+}^{-1}\right)+1}{e}+1,$$ (9)

yielding

$${\tau }_{\text{on}}=\frac{eM\left(0\right)+m\left(0\right)\left[1-e+\text{log}\left(C_{+}^{-1}\right)\right]}{\left[\kappa -2eP\left(0\right)k_{+}\right]m\left(0\right)}.$$ (10)

The condition for the existence of a lag-phase is κ ≫ 2eP(0)k₊m(0) (17), and so for low seed concentrations, M(0) ≪ m(0), the result reduces in this limit to an equivalent logarithmic relation to that found for the time to half-completion:

$${\tau }_{\text{on}}\propto \text{const}-\text{log}\left(M\left(0\right)\right).$$ (11)

This result has been derived for the case where the elongation rate depends linearly on the monomer concentration (16,17); an identical result emerges in the case where the elongation rate is saturated, through the use of the linearized solution (Eq. 2), as discussed for Fig. 4. The scaling result, Eq. 11, is applied to our measurements in Fig. 6 where the predicted scaling is observed. It is interesting to note that in the other limiting situation where no lag-phase exists, κ ≪ 2eP(0)k₊m(0), the full relationship Eq. 10 returns the scaling law t ∼ 1/P(0), a finding consistent with the solution M(t) ∼ $e^{-2k_{+}P\left(0\right)t}$ in this limit.

Figure 6.

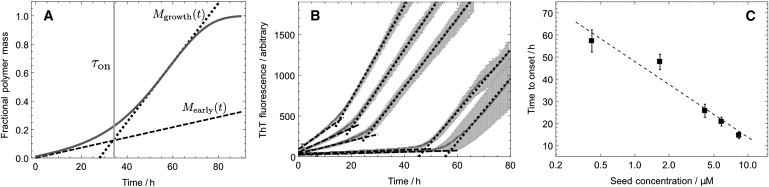
Logarithmic scaling of the time to onset of the growth phase with the initial seed concentration as predicted by Eq. 11. (A) The time to onset of the growth phase is defined as the time at the intercept of the straight lines M_early(t) and M_growth(t) shown. (B) Extraction of the characteristic time defined in this way. The data are for monomer LA30 with WT seed with a fixed monomer concentration 100 μM. (C) The predicted logarithmic scaling with a line of best fit to the predicted form, from Eq. 11.

Interestingly, the effects of mutations in the sequence of S6 on the fibril elongation rate also imply changes in the time to the onset of the growth phase. Indeed, Eq. 10 shows that this time is, to first-order, inversely proportional to the parameter κ which contains a dependency on the elongation rate κ ∼ k₊^1/2. In agreement with this deduction, WT seed with monomeric mutant YA63, which has a low relative elongation rate (1.0; Table 1), was found not to reach the growth phase during the time course of 100 h, whereas substituting mutant LA75/MA67 as monomer (relative elongation rate 2.2; Table 1) resulted in a shorter time to the growth phase, and substituting mutant LA30 as monomer (relative elongation rate 3.5; Table 1) resulted in a still further decrease in the observed time to onset.

Conclusions

In conclusion, the analysis of the aggregation behavior of a selection of site-directed mutants of the model protein S6 from Thermus thermophilus has enabled us to separate unambiguously the action of secondary pathways from that of primary nucleation and that of fibril elongation. Because multiple processes contribute to the rate of the overall growth reaction, we employed an approach whereby a given system parameter, here the seed concentration, was varied systematically while keeping the others constant. Furthermore, our results show that the generation of new fibrils in this system originates from secondary pathways rather than primary nucleation events, and that a lag phase can originate even in the absence of primary nucleation.