Effect of Calcium and Magnesium on Phosphatidylserine Membranes: Experiments and All-Atomic Simulations

Abstract

It is known that phosphatidylserine (PS⁻) lipids have a very similar affinity for Ca²⁺ and Mg²⁺ cations, as revealed by electrokinetic and stability experiments. However, despite this similar affinity, experimental evidence shows that the presence of Ca²⁺ or Mg²⁺ induces very different aggregation behavior for PS⁻ liposomes as characterized by their fractal dimensions. Also, turbidity measurements confirm substantial differences in aggregation behavior depending on the presence of Ca²⁺ or Mg²⁺ cations. These puzzling results suggest that although these two cations have a similar affinity for PS⁻ lipids, they induce substantial structural differences in lipid bilayers containing each of these cations. In other words, these cations have strong ion-specific effects on the structure of PS⁻ membranes. This interpretation is supported by all-atomic molecular-dynamics simulations showing that Ca²⁺ and Mg²⁺ cations have different binding sites and induce different membrane hydration. We show that although both ions are incorporated deep into the hydrophilic region of the membrane, they have different positions and configurations at the membrane. Absorbed Ca²⁺ cations present a peak at a distance ∼2 nm from the center of the lipid bilayer, and their most probable binding configuration involves two oxygen atoms from each of the charged moieties of the PS molecule (phosphate and carboxyl groups). In contrast, the distribution of absorbed Mg²⁺ cations has two different peaks, located a few angstroms before and after the Ca²⁺ peak. The most probable configurations (corresponding to these two peaks) involve binding to two oxygen atoms from carboxyl groups (the most superficial binding peak) or two oxygen atoms from phosphate groups (the most internal peak). Moreover, simulations also show differences in the hydration structure of the membrane: we obtained a hydration of 7.5 and 9 water molecules per lipid in simulations with Ca²⁺ and Mg²⁺, respectively.

Introduction

The interaction between metal cations (particularly Ca²⁺) and lipids plays an essential role in the structure and function of biological membranes. In studies of this interaction, phospholipid liposomes (or vesicles) have been widely used as models of biological membranes (1–8). For instance, it has been shown that multivalent cations can mediate membrane fusion by interacting with negatively charged phospholipids (9–12). Because phosphatidylserine (PS) is the most abundant negatively charged lipid in cell membranes, cation-induced fusion of phospholipid liposomes composed of pure bovine brain PS (PS⁻) has been extensively studied. In particular, many studies have paid special attention to the ability of Ca²⁺ or Mg²⁺ to induce aggregation and fusion of liposomes made of only PS⁻ or mixtures of PS⁻ with other phospholipids (1,3,6,7,13–21). In most of these works (and studies cited therein), aggregation of PS⁻ vesicles induced by Ca²⁺ and Mg²⁺ appears to be a prerequisite for fusion of PS⁻ membranes. Moreover, such aggregation and fusion processes seem to be intimately related to the ability of these cations to bind to phospholipid headgroups and form dehydrated intermembrane complexes. In this sense, the effectiveness of Ca²⁺ and Mg²⁺ in inducing membrane aggregation and fusion has been correlated to their respective binding constants. To that end, procedures based on a modified version of the classical Derjaguin-Landau-Verwey-Overbeek (DLVO) colloidal stability theory have been used to interpret stability results (1,3,6,7,13–21), whereas analyses using mass action models have been applied to the description of fusion (7,22). In the case of divalent cations (such as Ca²⁺), more sophisticated approaches beyond the Poisson-Boltzmann electrostatics embedded in classical DLVO theory have been proposed to take into account electrostatic and binding effects in membrane fusion (23).

In any case, recent studies (24–26) showed that the different effect of Ca²⁺ and Mg²⁺ in membranes is more profound than a simple numerical difference in binding constants (which nevertheless are of the same order of magnitude). In these studies, the aggregation processes of PS⁻ vesicles induced by Ca²⁺ and Mg²⁺ were examined with the use of both static and dynamic light-scattering techniques. In this way, the investigators studied not only the kinetics of aggregation of PS⁻ liposomes induced by Ca²⁺ and Mg²⁺ but also the structure of the resulting clusters. Accordingly, the ability of these cations to bind to PS⁻ membranes, as well as other factors involved in the destabilization of these liposomes, was studied. In particular, the kinetic exponents of the aggregating curves as well as the fractal dimensions of the resulting clusters were reported. Surprisingly, the morphology of the aggregates depended strongly on the divalent cation used to induce aggregation: PS⁻ aggregates formed by Ca²⁺ were branched structures, whereas dense structures were observed for PS⁻ clusters induced by Mg²⁺. Also, Fourier-transform infrared (FTIR) spectroscopy measurements clearly showed that PS⁻ membranes have different hydration in the presence of Ca²⁺ or Mg²⁺. In fact, the different structures of the aggregates were rationalized in terms of an ion-specific, short-range interaction depending on the different degrees of hydration of PS⁻ liposomes in the presence of these divalent cations. At this point, it is interesting to recall that the difference in hydration of PS⁻ lipids in the presence of Ca²⁺ or Mg²⁺ could be related to the binding thermodynamics of these ions. Calorimetric measurements (27,28) show that the binding of Ca²⁺, Mg²⁺, and La³⁺ cations to PS⁻ is endothermic and entropy driven. The dominant entropic contribution likely comes from the liberation of solvating water molecules from lipid headgroups. Hence, their different binding constants may be related to their different dehydration abilities.

These reported differences also suggest the possibility of different binding modes or binding sites for Ca²⁺ and Mg²⁺ with PS⁻ lipids. A first insight was provided by NMR studies, which allow a comparison of the relative distribution of membrane bound cations within the three-dimensional space associated with the lipid-solution interface. Roux and Bloom (29) showed that both Ca²⁺ and Mg²⁺ are deeply buried in the membrane (more buried than monovalent cations), and their results also suggest different binding locations for these ions. In addition, Portis (13) suggested that Ca²⁺ binds to the carboxyl group of PS⁻ lipids, inducing a trans lipid complex, whereas Mg²⁺ favors a cis geometry. These different conformational effects on the lipid bilayers induced by Ca²⁺ and Mg²⁺ may be responsible for the dissimilar aggregation and fusion of PS⁻ bilayers in the presence of these cations. However, other experimental studies (12), based on infrared spectroscopy in phosphatidylcholine (PC)/PS mixtures, indicated that Mg²⁺ binds to PS in a fashion similar to that of Ca²⁺.

In the case of Ca²⁺, it seems clear that the most probable stoichiometry is two PS⁻ lipids per bound Ca²⁺ (30). In addition, NMR studies showed the existence of at least two different binding sites (29). Early infrared spectroscopic studies showed the formation of a strong Ca²⁺-PO⁻₄ complex (31), although a combination of MD simulations with magic angle spinning (MAS) and solid-state NMR measurements favored a binding of Ca²⁺ to carboxyl in the PS headgroup (32). In addition, Boettcher et al. (32) showed that Ca²⁺ induced the formation of microdomains of PS in mixtures containing PC and PS lipids. In fact, Ca²⁺ induces rapid demixing in PS/PC mixtures (19,33). In the case of Mg²⁺, Schultz et al. (12) showed experimentally the formation of cation-PS microclusters in membranes made of mixtures of PC and PS⁻ lipids, but, of interest, Mg²⁺ did not induce phase separation.

Summing up all this accumulated evidence, it seems clear that Ca²⁺ and Mg²⁺ have slightly different affinities for PS⁻ lipids and induce different phenomena. As we mentioned above, Ca²⁺ and Mg²⁺ induce different structures of PS⁻ aggregates and different clustering and mixing behaviors of PS⁻ with PC. These observed effects suggest the possibility of substantial differences in the atomistic details of the binding of Ca²⁺ and Mg²⁺ cations in membranes. Our objective in this work was to understand in more depth the interaction of Ca²⁺ and Mg²⁺ with PS⁻ lipids. We conducted experiments and all-atomic molecular-dynamics (MD) simulations to examine the interaction between PS⁻ lipids with Ca²⁺ and Mg²⁺. In our experiments we aimed to emphasize the similarities and differences between Ca²⁺ and Mg²⁺ in their interactions with PS⁻ lipids, and in the simulations we focused on elucidating the atomistic details of the cation–lipid interaction (such as the location of binding sites for the ions, and the identity of the chemical groups involved in the binding and hydration effects in both lipids and cations).

Materials and Methods

PS liposomes

We prepared PS⁻ liposomes as follows: Lipids (3-sn-phosphatidyl-L-serine from bovine brain) with purities > 99% mass were obtained from Avanti Polar Lipids (Alabaster, AL). This type of lipid was chosen in agreement with previous experimental works in which similar lipids were used to prepare the corresponding liposomes of PS⁻ (24–26). Accordingly, our experimental results are directly comparable with those found in the cited references. Phospholipids at the proportions indicated below were dissolved in a mixture (2:1, volume ratio) of chloroform and methanol in a round-bottom flask and dried in a rotary evaporator at low pressure at 40°C to form a thin film on the flask. The film was hydrated with deionized water (conductivity < 18 μS cm⁻¹; MilliQ-Millipore, Billerica, MA) to give a lipid concentration of 30 mM. A polydisperse population of multilamellar vesicles was formed by constant vortexing for 4 min on a vortex mixer and sonication in a Transonic Digitals bath sonifier (Elma, Germany) for 10 min. Multilamellar vesicles were transformed to large unilamellar vesicles (with a reduction on the polydispersity) by means of a sequential extrusion procedure (extruder device from Lipex Biomembranes, Vancouver, British Columbia, Canada). The suspension was then filtered by polycarbonate membrane filters of variable pore size under nitrogen pressures of up to 55 × 10⁵ N.m⁻² (34) in three steps: first, three consecutive extrusions through a 0.8 μm pore diameter filter, and then three other consecutive extrusions through two stacked 0.4 μm membranes. The resulting lipid suspension was finally extruded 15 consecutive times through two stacked 0.2 μm filters. After preparation was completed, a nitrogen stream was passed to displace the air, and the liposomes were stored at 4–7°C.

Electrophoretic mobility

We used a ZetaPALS instrument (Brookhaven, Upton, NY), based on the principles of phase analysis light scattering (PALS), to measure electrophoretic mobilities (μ_e). The setup is especially useful for high ionic strengths and nonpolar media, where mobilities are usually low. Under this situation, a phase analysis is employed instead of the traditional spectral analysis based on the shifted frequency spectrum. Both techniques analyze a mixture of scattered light from a suspension of colloidal particles moving in an electric field and light direct from the source (reference beam light). The scattered light is frequency-shifted by the Doppler effect, and its superposition on the unshifted reference light leads to a beating at a frequency that depends on the speed of the particles. When the particle velocity is low, the spectral analysis is not able to generate a complete cycle of the detected signal. However, phase analysis takes place over many cycles of the respective waveforms because the optical phase of the scattered light is characterized by means of the so-called amplitude-weighted phase difference (AWPD) function instead of a simple correlation treatment. This function improves the statistical behavior because the detected signal fluctuates in amplitude due to the relative movements of particles and concentration fluctuations. For a complete discussion of the PALS method and AWPD treatment, we refer the reader to Tscharnuter (35).

Our electrophoretic mobility measurements were performed at 25°C and pH = 5.5. The particle concentration (ρ_p) was 1.4 × 10⁹ particle · mL⁻¹. We chose this value after plotting the corresponding μ_e versus ρ_p curves. The electrolytes used to perform the experiments were Ca(NO₃)₂ and Mg(NO₃)₂.

Stability ratio

To study the stability of the liposome suspensions, we carried out stability measurements at pH 5.5 and adjusted the ionic strength between 0.1 mM and 300 mM by adding Ca(NO₃)₂ and Mg(NO₃)₂. We determined the Fuchs stability ratio W (or stability factor) by spectrophotometric monitoring. This magnitude is a criterion for the stability of the colloidal system: W = k_r/k_s, where the rate constant k_r describes rapid coagulation and k_s is the rate constant for the slow coagulation regime. Thus, the inverse of the stability ratio provides a measure of the effectiveness of collisions leading to coagulation. Here, we obtained the stability ratio experimentally from the rate constant of coagulation of the liposomes by measuring the dispersed light with a commercial spectrophotometer (microplate reader model 680; Bio-Rad). Information on the kinetics-aggregation constants of dimer formation can be directly derived from the initial slopes of the absorbance versus time curves (dAbs/dt) (36). Accordingly, plotting W as a function of the electrolyte concentration in a double-logarithmic scale becomes useful to estimate the critical coagulation concentration (CCC), which is defined as the minimum concentration of electrolyte required to induce coagulation (W = 1). The CCC value is therefore related to destabilization processes (i.e., low CCC means low stability).

Turbidity measurements

We studied the turbidity of the vesicle suspensions as a function of Ca²⁺ and Mg²⁺ concentrations at 400 nm of wavelength by using a commercial spectrophotometer (Thermo/Milton Roy Spectronic Genesys 5, Champaign, IL). The volume fraction of vesicles samples was 0.1%, and we increased the ion concentration step by step by adding small amounts of its concentrated salt solution. We measured the change of absorbance at 400 nm (ΔA₄₀₀) 2 min after changing the ion concentration. The procedure was repeated until the absorbance no longer changed. All experiments were performed at room temperature, and each reported data point is the average of six measurements.

Kinetic aggregation and structural properties of aggregates

Kinetic aggregation experiments with PS liposomes induced by divalent cations and subsequent structural analyses of the resulting aggregates were carried out in previous works (24,25). In those studies, the calcium- and magnesium-induced aggregation of the liposomes was examined by means of static and dynamic light-scattering techniques, and the kinetic exponents of the aggregating curves and fractal dimensions of the resulting clusters were reported. The experimental procedure is described in detail in the above-cited references.

MD simulations

To obtain a molecular picture of the cation–PS⁻ interaction, we performed all-atomic MD simulations in the NPT ensemble of a fully hydrated PS⁻ bilayer in contact with neutralizing divalent counterions (Ca²⁺ or Mg²⁺). Our simulation box contains 14,720 atoms from a membrane with 128 PS⁻ molecules distributed in two leaflets (as in previous simulations (37,38)), 2624 water molecules, and 64 divalent counterions to ensure charge neutrality (Ca²⁺ or Mg²⁺ depending on the simulation). The model and force field employed to describe the PS⁻ molecules were those developed by Pandit and Berkowitz (37). The force field is based on a united atom description modified to include explicitly the hydrogen atoms of the NH₃⁺ group. Partial atomic charges and bond, angle, and dihedral parameters were derived from ab initio calculations, and are given in Fig. 2 and Table 1 of Pandit and Berkowitz (37). Water was modeled using the standard TIP3P model. In modeling the ions, we employed the Lennard-Jones parameters developed for several ions in (39), which were compatible with the TIP3P model of water. All Lennard-Jones interactions between atoms were cut off at a distance of 1.5 nm. This large cutoff was used to avoid any possible spurious effects due to truncation of the Lennard-Jones interactions, as recently reported in the literature (40). In our simulations, the use of this large cutoff results in substantial computational costs. Long-range electrostatic interactions were computed using the Ewald summation method with a precision of 10⁻⁴ with periodic conditions along all three directions. All simulations correspond to a temperature of 350 K as in previous simulation studies (37,41), which is well above the main transition temperature (330 K), so we can be sure that our simulated bilayer is in the liquid crystalline state. In real experiments at ambient temperature, PS⁻ lipids are assumed to be in the liquid crystalline state because the mixture of PS⁻ lipids with different hydrocarbon tails prevents crystallization. Also, the use of the same temperature (350 K) employed in previous simulations of PS lipids with other cations (37,41) facilitates comparison with previous results. The temperature was maintained constant by means of a Nosé-Hoover thermostat with a relaxation constant of 0.5 ps. Our simulations were also performed under a pressure of 1 atm maintained by a Nosé-Hoover isotropic barostat with a relaxation constant of 0.5 ps. All simulations were performed with the use of the DLPOLY2.19 package (42). The equations of motion were solved using the Verlet leapfrog algorithm with a time step of 2 fs. On average, the cost of a simulation time step is ∼0.23 s with the code running in parallel on 64 PowerPC processors. The protocols employed to generate the initial configurations, equilibration, and production runs were identical to those employed in our previous study of the same lipid bilayer in the presence of La³⁺ (38). The values of quantities of interest, such as the area per lipid and the number of adsorbed cations, were typically stabilized after 1–2 ns of simulation as in previous works (37,38). Hence, we decided to perform production runs of 10 ns preceded by equilibration runs of 4 ns. Visualization and representation of the resulting trajectories were performed with VMD software (43).

Figure 2.

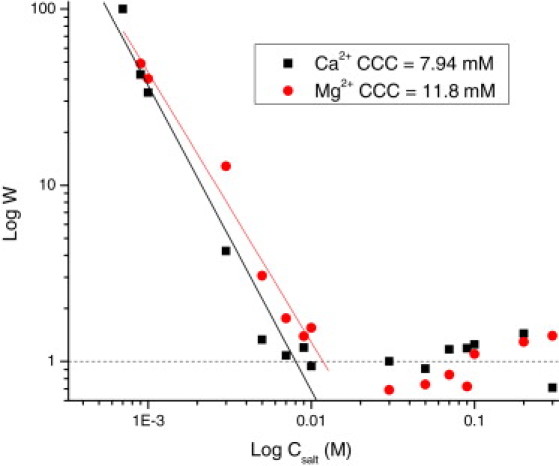
Stability ratio of PS⁻ liposomes as a function of Ca(NO₃)₂ and Mg(NO₃)₂. Determination of the experimental critical coagulation concentration (CCC). Squares and circles stand for Ca(NO₃)₂ and Mg(NO₃)₂, respectively.

Table 1.

Experimental kinetic exponents and fractal dimensions for PS⁻ liposomes

Electrolyte (5 mM)	α	df
Ca(NO3)2	−0.54 ± 0.02	1.75 ± 0.06
Mg(NO3)2	−0.35 ± 0.02	3.46 ± 0.08

The data correspond to 5 mM of Ca(NO₃)₂ or Mg(NO₃)₂ and were obtained from Roldán-Vargas et al. (24,25).

Results and Discussion

Electrokinetic and stability characterization

We first performed electrokinetic measurements to characterize the affinity of our PS⁻ liposomes for Mg²⁺ and Ca²⁺. In previous works (13,17,18), it was found that the affinity of PS⁻ liposomes for Ca²⁺ is only slightly greater than their affinity for Mg²⁺. This concept is confirmed by our electrokinetic results shown in Fig. 1. In this figure, we show the electrophoretic mobility of PS⁻ liposomes as a function of the salt concentration for Mg(NO₃)₂ and Ca(NO₃)₂. As can be seen, very similar electrokinetic behaviors are obtained for the two salts. In both cases, the magnitude of the electrokinetic mobility decreases with increasing electrolyte concentrations, and a feeble inversion in the mobility appears at very high salt concentrations (∼60 mM for Ca²⁺ and 100 mM for Mg²⁺). We note that the value of the concentration of charge inversion is a valuable quantitative measure of the affinity of ions for interfaces that can be obtained directly from experiments without any theoretical assumption (in contrast to quantities such as binding constants, which require an a priori formulation of a theoretical model (44)). Our results give a slightly larger affinity of PS⁻ for Ca²⁺ than for Mg²⁺, in agreement with previous studies. For example, classical results based on equilibrium dialysis experiments give estimates for the charge inversion concentrations of 60 mM and 100 mM, respectively (13), which coincide with our own results. Classical electrophoretic mobility measurements obtained by McLaughlin et al. (17) in the presence of 0.1 M of NaCl give similar but slightly higher estimated values: 83 mM for Ca²⁺ and 125 mM for Mg²⁺. Hence, we can conclude that the affinities of PS⁻ lipids for Mg²⁺ and Ca²⁺ are very similar, with charge inversion concentrations (and hence affinities) differing only by a factor of ∼1.5–1.7 between these two cations.

Figure 1.

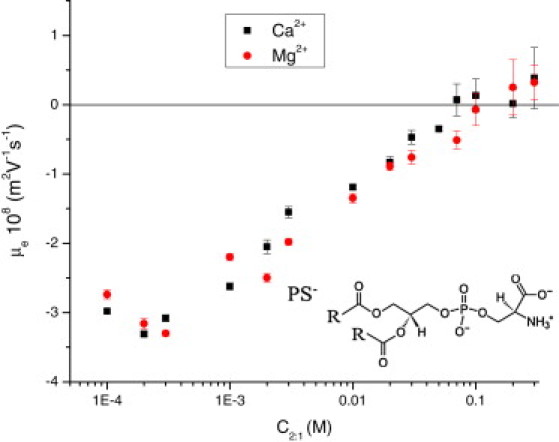
Electrophoretic mobility of PS⁻ liposomes as a function of Ca(NO₃)₂ and Mg(NO₃)₂. Squares and circles stand for Ca(NO₃)₂ and Mg(NO₃)₂, respectively. Inset: Molecular structure of PS⁻ lipids.

In Fig. 2 we show the stability rate of PS⁻ liposomes as a function of the salt concentration for the same electrolytes employed in electrokinetic measurements (Mg(NO₃)₂ and Ca(NO₃)₂). Again, very similar results are obtained for the two electrolytes, although small differences in the values of CCC are found. In particular, we estimate a CCC of ∼10 mM for Mg(NO₃)₂ and 8 mM for Ca(NO₃)₂. Hence, we need to employ slightly larger concentrations of Mg²⁺ (as compared with Ca²⁺) to induce aggregation of liposomes. These results indicate a higher affinity of PS⁻ for Ca²⁺ than for Mg²⁺, in line with the electrokinetic results. Also, these results are in agreement with the prevailing concept that larger concentrations of Mg²⁺ (as compared with Ca²⁺) are required to induce fusion of membranes containing PS⁻ (12).

Experimental aggregation of liposomes induced by Ca²⁺ and Mg²⁺

The aggregation process of liposomes induced by Mg(NO₃)₂ and Ca(NO₃)₂ can be characterized by turbidity measurements. Following the protocols described by Ohki (18), we measured the absorbance obtained 2 min after changing each ion concentration. Our results, presented in Fig. 3, extend the range measured by Ohki to higher salt concentrations to better illustrate the differences observed between Ca²⁺ and Mg²⁺. In general, we can see that in both cases the absorbance increases with the electrolyte concentration, indicating liposome aggregation. Absorbance increases until a maximum plateau is reached. However, clear differences are observed between measurements made in the presence of Ca²⁺ or Mg²⁺. The Mg²⁺ curve is clearly shifted to higher salt concentrations, and therefore a smaller concentration of Ca²⁺ is required to induce aggregation, in agreement with our previous CCC estimation. Fig. 3 also shows that the plateau of absorbance reached for Ca²⁺ is noticeably larger than that observed for Mg²⁺. This observation suggests that the volume corresponding to the PS⁻ aggregates induced by Ca²⁺ is larger than that corresponding to clusters induced by Mg²⁺.

Figure 3.

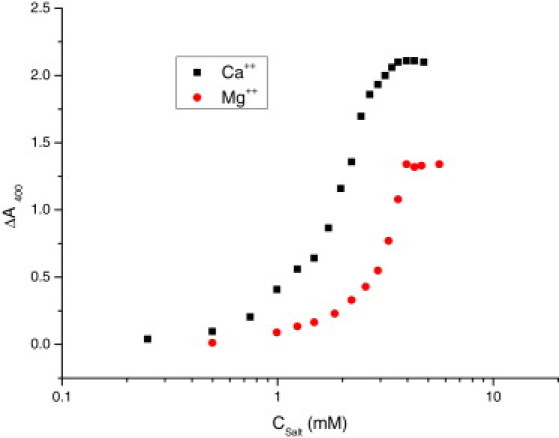
Relative absorbance at 400 nm of wavelength of PS⁻ liposomes as a function of Ca(NO₃)₂ and Mg(NO₃)₂. Turbidity at 2 min after the addition of the 2:1 electrolyte is plotted. Squares and circles stand for Ca(NO₃)₂ and Mg(NO₃)₂, respectively.

It is interesting to analyze the results of our turbidity measurements (Fig. 3) in view of the kinetic and structural parameters obtained for this system in previous works (24,25). In those studies, the fractal dimensions of the structures resulting from aggregating liposomes (d_f) were calculated by means of static light-scattering experiments. The results for a representative divalent salt concentration of 5 mM (corresponding to the plateau in absorbance observed in Fig. 3) are given in Table 1. The d_f values reported for the resulting clusters indicate substantial differences in the morphology of the aggregates induced by Ca²⁺ and Mg²⁺. Historically, two limiting regimes have been identified in colloidal aggregation: a rapid diffusion-limited cluster aggregation and a slow reaction-limited cluster aggregation. These limiting regimes are exemplified by salt-induced aggregation of electrically stabilized bare colloidal particles aggregating at low and high electrolyte concentrations. In the case of Ca²⁺, the fractal dimension of 1.75 reported in Table 1 is the well-established value for the diffusion-limited cluster aggregation regime, i.e., at 5 mM the liposomes have reached such a regime and form ramified open structures (classical mass-fractal structures) (24). In contrast, a singular surface- to mass-fractal transition is reported for the case of clusters induced by Mg²⁺, giving rise to values of d_f > 1.75 as the cation concentration increases. In particular, for a Mg(NO₃)₂ concentration of 5 mM, the value of d_f reported for PS⁻ liposomes is 3.46 (see Table 1). Such a high value implies that dense cluster morphologies are observed for PS⁻ aggregates induced by Mg²⁺. These dense structures were interpreted in terms of the ability of Mg²⁺ to allow internal restructuring of the lipid bilayers (25). This difference in the structure of the aggregates justifies the different absorbance reported in Fig. 3 for this concentration (5 mM).

Given the difference in the structures of the aggregates of liposomes induced in the presence of Ca²⁺ and Mg²⁺, it is natural to think that the kinetic processes that lead to these structures are also different. In this work, we followed the kinetics of aggregation in our experiments by employing a dynamic light-scattering technique. The variation of the translational diffusion coefficients of liposomes as a function of time was measured for different concentrations of Ca²⁺ and Mg²⁺, and its exponential decrease with time was characterized by a kinetic exponent (α) as shown in Table 1. Because α quantifies how fast the kinetic aggregation of PS⁻ liposomes occurs, we can deduce that the aggregation of PS⁻ induced by Ca²⁺ is faster than that induced by Mg²⁺. In other words, the formation of denser structures by Mg²⁺ proceeds more slowly than the formation of the branched structures induced by Ca²⁺. Altogether, the evidence discussed here shows that although PS⁻ has similar affinities for Ca²⁺ or Mg²⁺, the interaction of these ions with lipids gives rise to different structures. This suggests the possibility of substantial differences at the molecular-scale organization of the PS⁻ bilayer after incorporation of Ca²⁺ or Mg²⁺.

Results of MD simulations

Our MD simulations allow us to obtain an atomistic picture of the interaction between PS⁻ lipids and Mg²⁺ or Ca²⁺ cations. In both cases, the divalent counterions are observed to condense to the negatively charged bilayer membrane, i.e., all cations contain at least one oxygen atom from PS⁻ molecules in their first coordination shell (this is the usual definition for binding in MD simulations). In all cases, the oxygen atoms from PS⁻ lipids are of the O2 type. In the employed force field (37), the oxygen atoms assigned to the O2 type are the two oxygen atoms coming from the carboxylic moiety and the two oxygen atoms coming from the phosphate moiety, which are bonded to phosphorus atoms but not to carbon atoms (see the structure of PS lipids in the inset of Fig. 1). Hence, the more-internal oxygen atoms of the lipid molecule are not observed to be involved in ion binding.

The incorporation of cations into the membrane influences the area per lipid of the membrane. Previous simulations of PS⁻ bilayers with Na⁺ counterions (37) reported an area per lipid ∼53.7 ± 0.1 Å². Our simulations give a larger area per lipid: 55.55 ± 0.01 Å² for simulations with Ca²⁺ and 55.30 ± 0.01 Å² for simulations with Mg²⁺. In our previous simulations with La³⁺ (38), we obtained an area per lipid of 55.41 ± 0.01 Å². Hence, the area per lipid is almost identical for Ca²⁺, Mg²⁺, and La³⁺, but it is slightly larger than that obtained with Na⁺.

Of interest, our simulations show that both Ca²⁺ and Mg²⁺ are incorporated deep into the hydrophilic region of the membrane, but the two cations have different positions at the membrane. In Fig. 4, we show the density profiles averaged over the xy plane as a function of z. In both cases, the cations are typically embedded by oxygen atoms of the O2 type from lipids, as can be seen in the snapshots shown as insets in Fig. 4. The distribution of O2 atoms (responsible for the cation binding) is identical for simulations containing Ca²⁺ or Mg²⁺ cations. However, the distribution of cations is different in each case. In the case of Ca²⁺, the cations and O2 atoms have very similar distributions, with a peak at a distance of ∼2 nm from the center of the bilayer membrane. In the case of Mg²⁺, the distribution of cations has two distinct peaks, located at z-values of 1.8 nm and 2.2 nm (i.e., a few angstroms before and after the peak of the O2 distribution). These results are consistent with NMR results indicating that both cations are buried deep in the hydrophilic region of the membrane, with a slightly larger tendency of Mg²⁺ to be found in more superficial regions (45). In addition to the density profiles of cations, the different hydration of absorbed Ca²⁺ or Mg²⁺ cations and the hydration of lipid molecules are also included in Fig. 4. In bulk electrolyte, both Ca²⁺ and Mg²⁺ cations have ∼6 water molecules in their first coordination shell. After absorption at the lipid membrane, these cations become partially dehydrated. On average, the first coordination shell of absorbed Ca²⁺ cations contains 4.2 oxygen atoms from lipids and 2.8 oxygen atoms from water molecules. In the case of Mg²⁺, we obtain 2.7 oxygen atoms from lipids and 3 oxygen atoms from water molecules. Hence, these cations retain approximately half of their inner hydration water. In the case of the Ca²⁺ cations, their first coordination shell is slightly expanded by absorption because it replaces 3 oxygen atoms from water by ∼4 oxygen atoms from lipids. In the case of Mg²⁺, 3 oxygen atoms from water are replaced by ∼3 oxygen atoms from lipids. Concerning the hydration of the lipids, we computed the number of water molecules near the carbonyl ester group of the PS⁻ lipids because the (relative) hydration of this group of the lipid can be observed experimentally (25). We obtained a hydration of 7.5 water molecules per lipid in the simulations with Ca²⁺, and 9 water molecules per lipid in the case of Mg²⁺ simulations.

Figure 4.

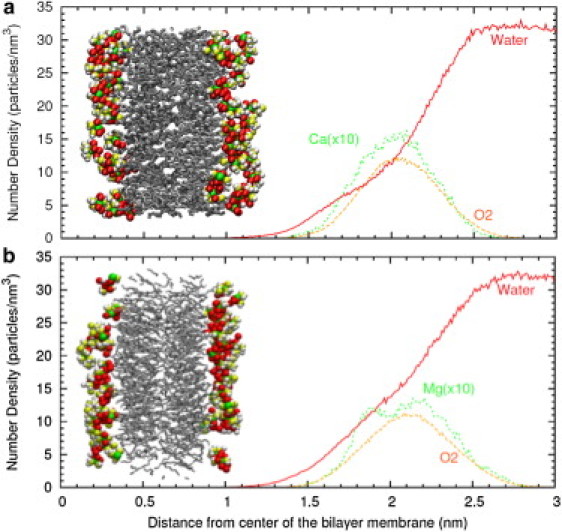
Average density profile of different species as a function of the z coordinate (perpendicular to the membrane) obtained from MD simulations. Solid line: water density (molecules/nm³); dashed line: oxygen atoms of O2 type from lipid molecules (atoms/nm³); dotted line: number density of divalent cations (ions/nm³) multiplied by a factor of 10 for clarity. Shown are simulations with (a) Ca²⁺ and (b) Mg²⁺. (Inset) Snapshot from MD simulations. Hydrocarbon tails are shown schematically as lines and divalent cations, oxygen atoms of O2 type from lipids and hydration water molecules are highlighted. To aid in interpretation of the figure, we also show schematically the hydrocarbon tails as lines.

These differences in the hydration behavior can be also observed from the differences in the density profiles of water inside the hydrophilic region of the bilayer. To facilitate this comparison, we plotted the density profiles of water shown in Fig. 4, a and b, in a single plot in Fig. 5, and also added the results for La³⁺ obtained in a previous work (38). As shown in Fig. 5, there is depletion in the water density profile in the region with z between 1.6 nm and 2.3 nm for the simulations with Ca²⁺, a feature that is not observed for Mg²⁺. Hence, our MD results point out the larger capability of Ca²⁺ to dehydrate the PS⁻ membrane, whereas an intermediate value of hydration between Ca²⁺ and Mg²⁺ cases was obtained for La³⁺. Hence, the dehydration efficiency of these cations follows the sequence Ca²⁺ > La³⁺ > Mg²⁺, which coincides with the sequence of sizes for these cations.

Figure 5.

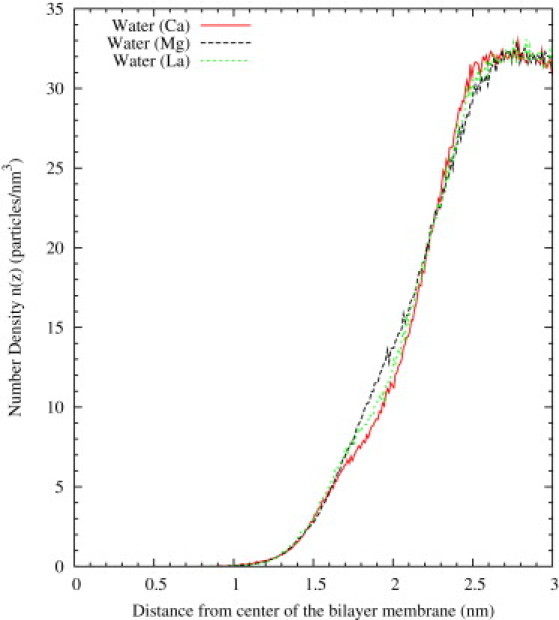
Hydration profiles of PS⁻ bilayers in the presence of Ca²⁺, Mg²⁺, and La³⁺. Data were obtained from Fig. 4 for Ca²⁺ and Mg²⁺, and Martín-Molina et al. (38) for La³⁺.

These results are also consistent with previous calorimetric experimental results (27) that were interpreted as indicating a larger dehydration of the PS lipids due to Ca²⁺ as compared with Mg²⁺. In addition, the origin of the dissimilar morphology experimentally found for PS⁻ liposome aggregates induced by Ca²⁺ and Mg²⁺ (see Table 1) was attributed to a different degree of hydration of liposomes in the presence of these divalent cations. This interpretation was supported by an analysis of FTIR spectroscopy spectra (26). The FTIR measurements indicated that, under equal concentrations, liposomes are more hydrated in the presence of MgCl₂ than in the presence of CaCl₂, as observed in our simulations. This feature agrees also with another study in which the destabilization of the lipid bilayers induced by Ca²⁺ (required for the membrane fusion) was related to its ability to dehydrate the lipid membrane (46).

Our simulations also show that the organization of the cations within the lipid bilayer is different for Ca²⁺ and Mg²⁺. To characterize in detail the binding of cations to lipids, we computed the number of oxygen atoms and its origin for all observed binding events. A histogram with the results is shown in Fig. 6 a, and illustrative snapshots of the most probable binding modes are shown in Fig. 6 b. In the case of Ca²⁺, the most probable case corresponds to binding to 2 oxygen atoms from phosphate and 2 from carboxyl (see Fig. 6 a). This binding mode involves two PS⁻ lipids and is illustrated in the snapshot of Fig. 6 b. This finding is consistent with the experimental expectation of a dominant 2:1 binding ratio for PS lipids and bound Ca²⁺ ions (30). Also, this finding emphasizes that both phosphate and carboxyl moieties are relevant in the binding process, and helps to reconcile the findings obtained from different experimental techniques (31,32). Other configurations also contribute significantly, and in general they tend to have more oxygen atoms from the carboxyl moiety than from phosphate. The average corresponds to 1.8 oxygen atoms from phosphate and 2.4 from carboxyl moieties. This gives a total of 4.2 oxygen atoms from lipids on the average first coordination shell of absorbed Ca²⁺ cations. Of interest, the distribution of binding modes shows significant differences between Ca²⁺ and Mg²⁺. In the case of Mg²⁺, the peak of the distribution is not clearly defined, and several different configurations are important (see Fig. 6 a). The two most probable cases correspond to binding involving 2 oxygen atoms from a single moiety (either phosphate or carboxyl) and 2 lipid molecules, as illustrated in the snapshot of Fig. 6 b. The binding mode involving 2 phosphate oxygen atoms implies a deeper penetration of the Mg²⁺ cation inside the membrane, whereas the binding to 2 oxygen atoms from carboxyl implies a more superficial or external location of bound Mg²⁺ cations. The different location of the cation in these two binding modes can be correlated with the two peaks appearing in the density profile of Mg²⁺ in Fig. 4 b, appearing at a distance of ∼1.8 nm and 2.2 nm from the center of the bilayer. Other configurations also contribute in addition to these two most probable cases, and the average binding for Mg²⁺ corresponds to 1.1 oxygen atoms from phosphate and 1.6 oxygen atoms from carboxyl. In this case, the total number of oxygen atoms on the average coordination shell of an absorbed Mg²⁺ cation is 2.7.

Figure 6.

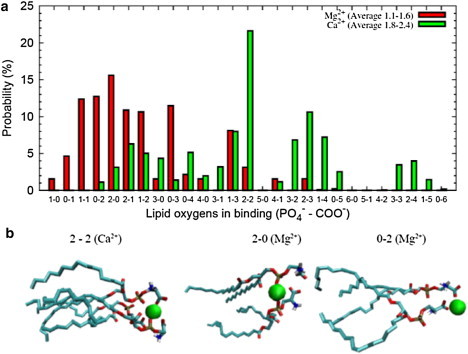
Different binding modes of Ca²⁺ and Mg²⁺ as observed in MD simulations. (a) Histogram showing the probability of different binding modes involving PO⁻₄ or COO⁻ groups of PS⁻ lipids. The first number indicates the number of oxygen atoms from PO⁻₄, and the second indicates the number of oxygen atoms from COO⁻. The most probable configurations for each cation are indicated by arrows. Snapshots of these configurations are shown in b. The snapshots were made with the use of the VMD program. Cations are shown as spheres and lipid molecules are shown in the bond representation of the VMD program.

Conclusions

In this work, we conducted experiments to examine the interaction between PS⁻ liposomes in the presence of Ca²⁺ and Mg²⁺. We observed similar electrokinetic and stability behaviors of PS⁻ liposomes in the presence of Ca²⁺ and Mg²⁺. However, the aggregation experiments showed specific ionic effects, i.e., different aggregation kinetic and morphologies for aggregates of PS⁻ induced by Ca²⁺ and Mg²⁺. To explain these experimental findings, we analyzed the interaction between PS⁻ phospholipids and Ca²⁺ and Mg²⁺ by means of all-atomic MD simulations. Our MD results show subtle but important differences at the molecular level regarding the manner in which cations (Ca²⁺ or Mg²⁺) interact with the bilayer. Both cations are incorporated deep into the hydrophilic region of the membrane. Adsorbed Ca²⁺ cations tend to be bound to two PS⁻ headgroups in a binding mode that involves both the carboxylic and phosphate moieties of the lipid headgroup. On the other hand, binding of Mg²⁺ typically involves two lipids through their phosphate or carboxylic moieties. As a consequence, the distribution of Mg²⁺ cations inside the membrane peaks at two different locations: one more superficial and one more profound than the most probable location found for the Ca²⁺ cation. Of interest, these different binding modes induce different hydration of the membrane containing Ca²⁺ or Mg²⁺ absorbed cations. Simulations show that the dehydration efficiency of cations follows the sequence Ca²⁺ > La³⁺ > Mg²⁺, which coincides with the sequence of sizes for these cations. In view of the structural differences (i.e., different lipid-cation organization and hydration content), it is natural to expect a different liposome–liposome interaction and aggregation behavior depending on the cation present in the membrane. Our main conclusion is that the similar affinities of Ca²⁺ or Mg²⁺ cations to PS⁻ lipids involve different molecular arrangements that become evident only when one studies the liposome–liposome interaction and aggregation behavior.

We thank the staff of the RES-Red Española de Supercomputación for providing computer resources and technical assistance.