Studies on the Dissociation and Urea-Induced Unfolding of FtsZ Support the Dimer Nucleus Polymerization Mechanism

Abstract

FtsZ is a major protein in bacterial cytokinesis that polymerizes into single filaments. A dimer has been proposed to be the nucleating species in FtsZ polymerization. To investigate the influence of the self-assembly of FtsZ on its unfolding pathway, we characterized its oligomerization and unfolding thermodynamics. We studied the assembly using size-exclusion chromatography and fluorescence spectroscopy, and the unfolding using circular dichroism and two-photon fluorescence correlation spectroscopy. The chromatographic analysis demonstrated the presence of monomers, dimers, and tetramers with populations dependent on protein concentration. Dilution experiments using fluorescent conjugates revealed dimer-to-monomer and tetramer-to-dimer dissociation constants in the micromolar range. Measurements of fluorescence lifetimes and rotational correlation times of the conjugates supported the presence of tetramers at high protein concentrations and monomers at low protein concentrations. The unfolding study demonstrated that the three-state unfolding of FtsZ was due to the mainly dimeric state of the protein, and that the monomer unfolds through a two-state mechanism. The monomer-to-dimer equilibrium characterized here (K_d = 9 μM) indicates a significant fraction (∼10%) of stable dimers at the critical concentration for polymerization, supporting a role of the dimeric species in the first steps of FtsZ polymerization.

Introduction

FtsZ is a 40.3 kDa protein that plays a key role in bacterial cell division. In vitro, FtsZ self-assembles upon GTP binding to form single filaments (1–3). FtsZ and tubulin display a remarkable structural similarity and are considered members of the same protein family (4). Investigators have characterized the interaction between subunits of FtsZ and tubulin in detail by resolving the crystal structure of the FtsZ homodimer and the α/β-tubulin heterodimer (5). The FtsZ subunit shows two domains: the N-terminal GTP/GDP-binding domain with a Rossmann fold, and the C-terminal domain with a chorismate mutase fold that interacts with other cell division proteins (6). The protofilament interaction is established by a head-to-tail association between two FtsZ subunits, where the T7-loop, located at the C-terminal domain and containing key catalytic residues, inserts into the GTP/GDP-binding pocket located at the N-terminal domain, completing the active site of FtsZ (5).

The GTPase activity and polymerization of FtsZ display a critical concentration below which no activity is detected (7–9). FtsZ self-assembles in the presence of both GTP and GDP, with the difference that GTP-induced assembly is cooperative, whereas GDP-induced assembly is an isodesmic process (10,11). These findings have prompted investigators to elucidate a cooperative mechanism that results in single filaments. In the proposed dimer nucleus model, the conversion of a monomer from a low-affinity conformation to a high-affinity conformation in the nucleation step allows dimer formation and the subsequent steps of polymerization (12–14). Although a conformational change between the monomer and polymer states has not been experimentally demonstrated for FtsZ, molecular-dynamics simulations suggested the existence of a switch close to the interface between both domains that may be related to the conformational change mediating activation of the monomer (15). In a different approach, a comparison of a set of FtsZ crystal structures bound to GDP or GTP revealed minor conformational changes in specific regions at the N- and C-terminal domains (16). In any case, there is no agreement regarding the specific conformational changes involved in FtsZ polymerization, or whether those changes are responsible for dimer formation.

The chemical unfolding of FtsZ is a three-state reversible process, unlike tubulin unfolding, which is also multistate but nonreversible. Refolded FtsZ fully regains its functional properties, whereas tubulin is unable to recover its native conformation and functionality after refolding (17,18). The three-state behavior of FtsZ unfolding has been attributed to different mechanisms considering a monomeric state of the protein. In one model, the first stage is ascribed to nucleotide release from the N-terminal domain, and the second stage is ascribed to the unfolding of the apoprotein (17). Alternatively, a strong interaction between the N- and C-terminal domains in FtsZ may explain the three-state unfolding reaction, in that the first stage is the rupture of the interaction between domains, and the second stage is the concerted unfolding of each domain (16). The structural details that are responsible for the appearance of the intermediate during the unfolding of FtsZ are still not clear.

In this work, we investigated the influence of the self-assembly on the unfolding pathway of GDP-bound FtsZ. Our aim was to relate the distribution of the oligomeric species present in FtsZ mixtures with unfolding data to elucidate the mechanism behind the three-state unfolding pathway. We also analyzed the results in the context of the dimer nucleation model for FtsZ.

Materials and Methods

Size exclusion chromatography

Size-exclusion chromatography (SEC) data were collected in a Waters 1525 HPLC pump equipped with a Waters 2487 detector, both controlled by Millennium software (Waters, Milford, MA). After centrifugation at 10,000 × g, 200 μL of the supernatant of the protein samples were loaded onto a Tosoh Bioscience G3000SW_XL column (300 × 7.8 mm). The elution (50 mM potassium phosphate buffer pH 6.5 and 0.3 M KCl) was carried out at 25°C at a flow rate of 1.0 mL min⁻¹ and monitored by the absorbance at 220 nm. Column calibration was performed using gel filtration molecular mass standards (Sigma, St. Louis, MO) previously equilibrated in the mobile phase at the working temperature.

Fluorescence anisotropy

Anisotropy measurements were performed in an ISS PC1 spectrofluorometer (ISS, Champaign, IL). The excitation wavelength (16-nm band-pass) was 490 nm for fluorescein isothiocyanate (FITC) and 360 nm for 5-(dimethylamino)-naphthalene-1-sulfonyl chloride (DNS). To block scattered light, the emission was observed through a 515-nm long-pass filter (Schott, Elmsford, NY) for FITC and through a 445-nm long-pass filter (Corning, Corning, NY) for DNS. The starting solution for dilution experiments was obtained by seeding unlabeled protein with the labeled protein. All measurements were made in 10 × 4 mm quartz cuvettes at 25°C.

Time-resolved fluorescence

Frequency domain time-resolved fluorescence measurements were performed in an ISS Chronos fluorometer (ISS, Champaign, IL) in analog mode. For sample excitation, a 471-nm LED passing through a 482-nm band-pass interference filter (Semrock, Rochester, NY) was used for FITC, and a 375-nm LED passing through a 375-nm band-pass interference filter (Semrock) was used for DNS. The emission was observed through two 515-nm long-pass filters (Schott) for FITC and through one 445-nm long-pass filter (Corning) for DNS. As the reference lifetime, fluorescein (4.05 ns; Sigma) dissolved in 0.01 M NaOH was used for FITC, and dimethyl POPOP (1.45 ns; Sigma) dissolved in 100% ethanol was used for DNS. Lifetime and dynamic polarization data were analyzed in GLOBALS for spectroscopy software (http://www.lfd.uci.edu/globals/). All measurements were performed in 10 × 4 mm quartz cuvettes at 22°C. Time-resolved fluorescence methods in the time domain have been successfully applied to Escherichia coli FtsZ (19).

Circular dichroism

Circular dichroism (CD) data were recorded in a Jasco-600 spectropolarimeter controlled by J-700 standard analysis software for Windows (Jasco, Tokyo, Japan). CD spectra were recorded between 200 and 260 nm (step resolution 0.4 nm; speed 50 nm/min; bandwidth 1 nm) using the signal at 260 nm for baseline correction. The CD signal at 222 nm for each sample was recorded for 10 min after 2 h of incubation at the indicated urea concentration at 25°C. Measurements were performed with cylindrical quartz cells of 1 cm, 1 mm, and 0.1 mm path length for protein concentrations of 1, 5.6, and 46.3 μM, respectively.

Fluorescence correlation spectroscopy instrumentation and sample handling

Fluorescence correlation spectroscopy (FCS) measurements were performed on an in-house-built confocal microscope. The system was based on a Zeiss (Jena, Germany) Axiovert S100 TV microscope equipped with a water immersion Zeiss objective. A Mai Tai HP titanium-sapphire laser at 790 nm was used as the two-photon excitation source with an average power of 40 mW. Fluorescence counts were detected with a hybrid HPM-100-40 detector from Becker & Hickl GmbH (Berlin, Germany). The output signal was recorded and analyzed with SimFCS software (http://www.lfd.uci.edu/globals/). Then 50 μL of sample containing FtsZ-Alexa488 (100 nM) at desired urea concentration were equilibrated for 2 h at room temperature and then loaded in a standard No. 1 coverslip glass (Corning) placed over the microscope objective using an in-house-made sample holder. Calibration of the observation volume was performed with rhodamine 110 using D = 430 μm² s⁻¹ (20).

Other methods

Protein purification, protein concentration determination, nucleotide content determination, protein modification with fluorescent probes, and data analysis are described in the Supporting Material.

Results

Characterization of the oligomerization state of wild-type FtsZ in solution

SEC was used to determine the oligomerization state of FtsZ bound to GDP (i.e., unpolymerized FtsZ). The chromatograms showed monomer and other oligomeric states of the protein (Fig. 1). Column calibration (not shown) indicated the presence of monomers, dimers, and tetramers of FtsZ depending on protein concentration. At 3 μM FtsZ, chromatogram integration showed that the monomer is the predominant species, accounting for 97% of the total population; the dimer and tetramer species represent 2% and <1%, respectively (Fig. 1, solid line). Approximately 0.2% of the total integrated absorbance corresponds to soluble high-molecular-mass oligomers that eluted in the void volume (Fig. 1, arrow). At 40 μM FtsZ (Fig. 1 dashed line), three elution peaks are evident in the chromatograms corresponding to monomer (73%), dimer (21%), and tetramer (6%) species as judged by retention times identical to the peaks detected in the sample at 3 μM FtsZ. Clearly, increasing the protein concentration induced the self-association of FtsZ. We tested the equilibrium reversibility of the system by reinjecting the monomer fraction collected from a concentrated sample loaded in the column (Fig. 1, inset). The protein concentration in the reinjected sample was 16 μM, with relative populations of 83% monomer, 12% dimer, 5% tetramer, and none eluted in the void volume. The presence of FtsZ in every elution peak was confirmed by silver-stained SDS-PAGE (see Fig. S1).

Figure 1.

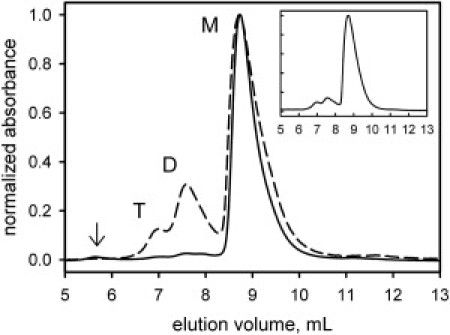
SEC profiles of FtsZ at 25°C monitored by the absorbance at 220 nm. The samples at 3 μM (solid line) and 40 μM (dashed line) were equilibrated in the mobile phase and then injected into the column. Elution peaks corresponding to monomer, dimer, and tetramer species are marked as M, D, and T, respectively. A small fraction (<1%) of high-molecular-mass aggregates eluted in the void volume, indicated by an arrow in the main plot. The inset shows reinjection of the monomer fraction.

Steady-state and time-resolved fluorescence measurements of FtsZ fluorescent conjugates

SEC experiments demonstrated the presence of monomers, dimers, and tetramers of FtsZ. Hence, the dilution of FtsZ at a high protein concentration may induce dissociation from tetramers to monomers through a dimer intermediate. To quantitatively determine FtsZ dissociation, the protein was covalently labeled with FITC or DNS to follow changes in anisotropy upon dilution. The labeling ratio was 10:1 (FITC) and 2:1 (DNS) protein/dye. The anisotropies of the fluorescent conjugates as a function of total protein concentration are depicted in Fig. 2 (solid symbols). In both cases the anisotropy decreased upon dilution, indicating dissociation of the oligomers. Assuming a three-state equilibrium for the self-association of FtsZ monomers into dimers and then into tetramers (2M↔D, 2D↔T), we fit the experimental anisotropy values to the theoretical curves shown in Fig. 2 (solid lines). The calculated limiting anisotropies for monomer (r_M), dimer (r_D), and tetramer (r_T) species, and the calculated equilibrium constants for tetramer-to-dimer (K_dT) and dimer-to-monomer (K_dD) dissociation are shown in Table 1. A statistical analysis of the fits revealed poor parameter accuracy for the FtsZ-FITC experiment, as judged by the χ²-value for this regression (Table 1), which was larger than unity. Nonetheless, the three-state model better described the FtsZ-DNS experiments, as indicated by a statistical analysis. Because of this discrepancy, the three-state model chosen to fit the experimental data was compared with dimer-to-monomer and tetramer-to-monomer equilibriums (Fig. S2). In both cases, a single transition could not improve the fits based on statistical analyses.

Figure 2.

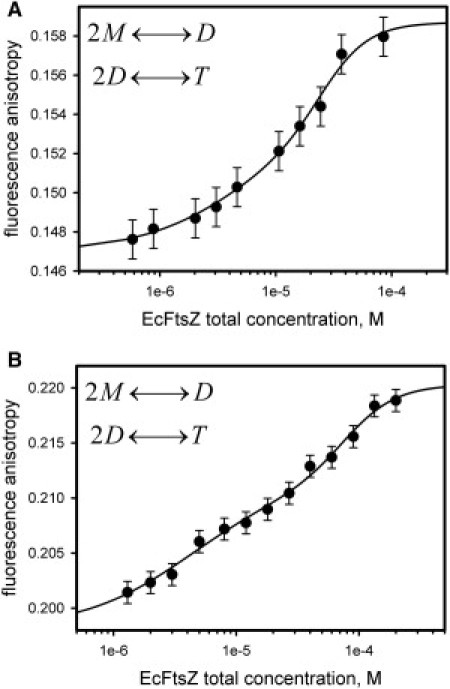
Fluorescence anisotropy of FtsZ conjugates as a function of protein concentration in 50 mM potassium phosphate buffer, pH 6.5, at 25°C. (A) Dilution of FtsZ-FITC conjugates. (B) Dilution of FtsZ-DNS conjugates. The experimental data (symbols) were fit to the equilibrium of dissociation of a tetramer into monomers through a dimer intermediate 2M↔D, 2D↔T (solid lines); limiting anisotropies and dissociation constants are summarized in Table 1. The error bars represent the standard deviation (SD) of the 20 iterations used to calculate the anisotropy.

Table 1.

Calculated equilibrium constants and limiting anisotropies for FtsZ dissociation

	KdDμM	KdTμM	rM	rD	rT
FITC∗	9 (8)†	152 (98)	0.147 (0.001)	0.153 (0.002)	0.159 (0.001)
DNS	8 (4)	1500 (600)	0.198 (0.002)	0.211 (0.001)	0.221 (0.001)

^∗Reduced χ²-values of the fits were 2.6 and 0.1 for FITC and DNS, respectively.

^†Values in parentheses are the standard errors of the fit parameters.

We performed fluorescence lifetime and dynamic polarization measurements to study the effect of changing the protein concentration (i.e., the oligomerization state of FtsZ) on the rotational rate of the fluorescent conjugates. Fluorescence lifetime data and detailed fit results for both conjugates are shown in Fig. S3 and Table S1. Although no changes were observed in the lifetime of FITC conjugates upon dilution, a 3 ns increase was observed in the average lifetime of DNS conjugates, which may be due to the environmentally sensitive fluorescent properties of the dansyl moiety. Dynamic polarization data for FtsZ fluorescent conjugates (Fig. S4, symbols) were fit using a two-component model (Fig. S4, solid lines). Fit results, including the average lifetimes (τ_ave = τ_i × f_i) used to calculate the rotational correlation times (θ) and fractional anisotropies (r), are shown in Table 2. The two rotations found in both cases can be referred as to local probe motion for short components (θ₁), and global protein rotation for longer components (θ₂) (21). On average, for the three concentrations tested, the amount of local motion accounted for 57% and 15% of the total anisotropy for FITC and DNS probes, respectively. In both cases, a decrease in the global rotation was observed with a decrease in the protein concentration, consistent with the dissociation of the oligomers.

Table 2.

Time-resolved fluorescence measurements of FtsZ conjugates

	FITC conjugates∗
FtsZ μM	τave.	θ1	r1	θ2	r2
31	3.68	0.57† (0.05)	0.16 (<0.01)	38.9 (5.7)	0.15 (<0.01)
6	3.68	0.48 (0.04)	0.18 (<0.01)	34.6 (5.0)	0.13 (<0.01)
1	3.58	0.29 (0.03)	0.19 (<0.01)	19.7 (1.9)	0.12 (0.01)
	DNS conjugates
FtsZ μM	τave.	θ1	r1	θ2	r2
45	15.2	0.54 (0.25)	0.07 (0.03)	147 (5)	0.27 (<0.01)
4	17.3	1.04 (0.23)	0.05 (<0.01)	67 (2)	0.29 (<0.01)
0.5	17.6	0.99 (0.24)	0.03 (<0.01)	46 (1)	0.31 (<0.01)

^∗Global reduced χ²-values of the fits were 0.67 and 0.35 for FITC and DNS conjugates, respectively.

^†Constant standard errors of 0.2° for phase angle and 0.004 for modulation were used for minimization. Values in parentheses are the standard errors of the fit parameters.

Unfolding pathway of FtsZ

We studied the dependence of the unfolding stability of FtsZ on total protein concentration by CD monitoring the loss of secondary structure induced by urea over a range of protein concentrations. At 1 μM FtsZ, the unfolding curve showed one smooth transition beginning at 0 M urea and stabilizing between 2.6 and 3 M urea with the absence of an evident intermediate (Fig. 3 A, circles). When the protein concentration was increased to 5.6 μM, the unfolding curve showed two transitions with the presence of an intermediate (Fig. 3 A, triangles). The first transition ended at 0.6 M urea and the second transition occurred between 0.7 and 3 M urea. At 46.3 μM, the unfolding curve also showed two stages (Fig. 3 A, squares): the first transition stabilized at 0.4 M urea, and the second transition occurred at 0.5–3 M urea. A stabilization of the signal at urea concentrations between 3 and 5 M (not shown) was observed in the three experiments, which corresponds to an unfolded state. The CD spectra of FtsZ at 1, 5.6, and 46.3 μM revealed minor differences with changes in the protein concentration (Fig. 3 A, inset). The only difference in the CD spectrum was observed at 1 μM FtsZ, showing a slight decrease in the ellipticity at 210 nm in comparison with the spectra at 5.6 and 46.3 μM FtsZ.

Figure 3.

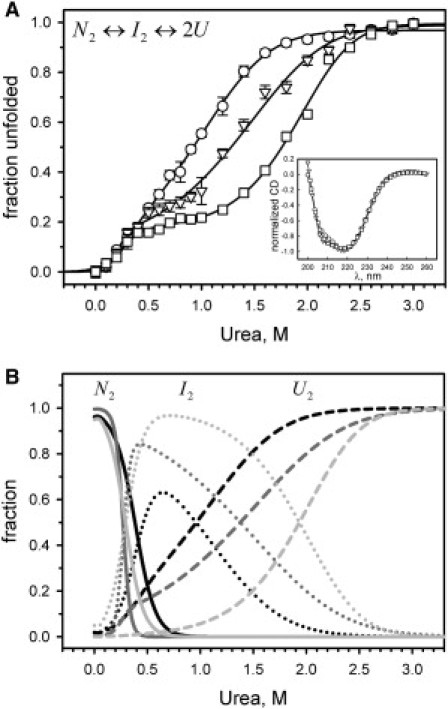
Urea-induced unfolding of FtsZ monitored by the CD at 222 nm in 50 mM potassium phosphate buffer, pH 6.5, at 25°C. (A) FtsZ unfolding at 1 μM (circles), 5.6 μM (triangles), and 46.3 μM (squares) of protein concentration. Data are displayed as an unfolded fraction, and the solid lines represent the fit to a three-state dimer unfolding with a dimer intermediate (N₂↔I₂↔2U). The inset in A shows the normalized ellipticity as a function of wavelength for FtsZ at 1 μM (circles), 5.6 μM (triangles), and 46.3 μM (squares). (B) Modeled fractions (from left to right) of native dimer (N₂, solid lines), dimer intermediate (I₂, dotted lines), and unfolded monomer (U, dashed lines) as a function of urea concentration at 1 μM (black), 5.6 μM (dark gray), and 46.3 μM (light gray), respectively. The modeled fractions were calculated using the data from the fits shown in panel A (see Table 3). The error bars in A show the SD of the CD signal at 222 nm.

The CD data were fit to the three-state unfolding equilibrium N₂↔I₂↔2U, where the first stage is the unfolding of the native dimer (N₂) into a dimer intermediate (I₂) followed by the coupled dissociation-unfolding of the intermediate into two unfolded monomers (U) in the second stage (Fig. 3 A, solid lines in the main plot). The total free-energy change for unfolding of the dimers in the absence of urea, ΔG_T°_H2O, and the m-values for the first and second stages of unfolding at the three protein concentrations used are shown in Table 3. Calculation of the transition midpoints for the first stage of unfolding (C_50%), as described in the Supporting Material and Materials and Methods, resulted in C_50% = 0.32, 0.24, and 0.25 M of urea for 1, 5.6, and 46.3 μM FtsZ, respectively (Table 3). Similar values of C_50% for the first transition were expected at the three concentrations tested. However, at 1 μM there was a relative increase in this value, which may be explained by the apparent two-state unfolding behavior that moved the transition midpoint to a larger value. Although a two-state unfolding mechanism (N↔U) was also used to analyze the data at 1 μM FtsZ (see below), the three-state model was maintained for comparison. For the second stage of unfolding, the calculated transition midpoints were C_50% = 1.2, 1.7, and 2.1 M of urea for 1, 5.6, and 46.3 μM FtsZ, respectively (Table 3). Clearly, as the protein concentration increased, there was a consistent increment in the midpoint of the second stage of unfolding that reflected the changes in the oligomerization state of the protein. Overall, the main changes in the free energy for unfolding were observed in the second stage, with average values 5.5 times larger than in the first stage, accounting for 84% of the calculated ΔG_T°_H2O for dimer unfolding (Table 3). Eftink (22) previously used global fitting to improve unfolding analyses by combining the data from different spectroscopic techniques as well as from different experimental conditions. Here, we simultaneously fit the data from the three unfolding experiments to the same model used before, and the resulting parameters confirmed the results previously observed (Table 3). Using the thermodynamic parameters from the global analysis given in Table 3, we performed a simulation of the results that would be obtained at different FtsZ concentrations. There was good overlap between the experimental data obtained at 1, 5.6, and 46.3 μM and the predicted values (Fig. S5, open symbols and solid lines, respectively). It is apparent that with an increase in the protein concentration, the precision of the model was diminished (Table 3, χ²-value). This disparity was attributed to the increase in the tetramer population. Specifically, the fraction of the tetramer species in solution is difficult to predict due to the discrepancy in K_d values calculated from the dissociation data. Nevertheless, our dimer model fits the experimental data with reasonable precision according to the statistical analysis. This result suggests that the tetramer has marginal stability in the presence of urea, such that its population decreases quickly at low urea concentrations.

Table 3.

Thermodynamic analysis of the unfolding of FtsZ using the three-state dimer model

FtsZ∗μM	$\Delta G_{H_{2}O,N_2\leftrightarrow I_2}^0$ kcal mol−1	$m_{N_2\leftrightarrow I_2}$ kcal mol-1M−1	$C_{50\%,N_2\leftrightarrow I_2}$ M†	$\Delta G_{H_{2}O,I_2\leftrightarrow 2U}^0$ kcal mol−1	$m_{I_2\leftrightarrow 2U}$ kcal mol-1M−1	$C_{50\%,I_2\leftrightarrow 2U}$ M	$\Delta G_{T{H}_{2}O}^0$ kcal mol−1
1	2.3 (1.9)‡	7.2 (4.2)	0.32	11.1 (0.8)	2.5 (0.4)	1.2	13.4 (2.6)
5.6	2.5 (1.8)	10.5 (6.6)	0.24	10.1 (0.2)	1.8 (0.1)	1.7	12.6 (2.1)
46.3	1.7 (0.9)	7.1 (3.1)	0.25	12.8 (0.3)	3.3 (0.1)	2.1	14.5 (1.3)
GA§	1.8 (0.6)	6.6 (2.0)	—	12.2 (0.4)	3.2 (0.1)	—	14.0 (1.1)

^∗Reduced χ²-values of the fits were 1.3, 1.5, 1.8, and 2.2, respectively.

^†C_50% values were calculated as described in the Supporting Material and Materials and Methods.

^‡Values in parentheses are the fit standard errors.

^§GA indicates the results obtained with the full data sets by global analysis.

Unfolding of FtsZ followed by FCS

The observation of an apparent single transition in the unfolding experiment of FtsZ at 1 μM suggested a low population of the dimer intermediate. Additionally, gel filtration analysis indicated that almost full dissociation of FtsZ dimers might occur at protein concentrations below 3 μM; therefore, a single unfolding transition is to be expected, due to the monomeric state of the protein. To test this hypothesis, we monitored the urea-induced unfolding of FtsZ labeled with Alexafluor-488 (labeling ratio 1:1 protein/dye) at 100 nM protein using FCS to measure the diffusion coefficient as a function of urea concentration. Fig. S6 depicts the normalized autocorrelation functions that were fit using one diffusion component. The effect of the addition of urea on FtsZ-Alexa488 diffusion coefficients (D) is plotted in Fig. 4 A. Values of D were corrected for changes in viscosity and refractive index due to the addition of urea, as described in the Supporting Material and Materials and Methods. A sharp decrease from D_FtsZ = 60 ± 1 μm² s⁻¹ to D_FtsZ = 40 ± 2 μm² s⁻¹ was observed with increasing urea from 0 to 1 M. A less pronounced decrease was observed from D_FtsZ = 40 ± 1 μm² s⁻¹ to D_FtsZ = 29 ± 1 μm² s⁻¹ with increasing urea from 1.2 to 3 M. The intensities remained nearly constant in the samples at all urea concentrations, confirming that urea was not affecting the fluorescence emission of the dye (Fig. 4 A, inset). To characterize the expansion of FtsZ polypeptide chain during urea-induced unfolding, we calculated the hydrodynamic radius from the diffusion coefficient using the Stokes-Einstein equation. The resulting values are plotted in Fig. 4 B together with the CD unfolding data of FtsZ at 1 μM for comparison. The fit to a two-state mechanism of unfolding (N↔U) for CD data (1 μM FtsZ) and FCS data (0.1 μM FtsZ) resulted in C_50% of 0.9 ± 0.2 M and 0.7 ± 0.2 M of urea, respectively.

Figure 4.

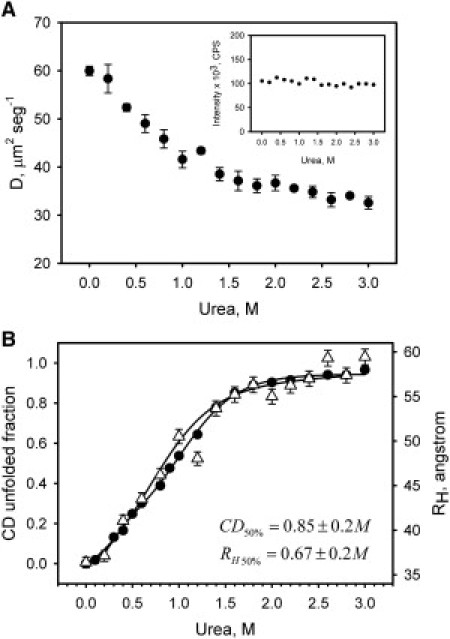
Urea-induced unfolding of FtsZ-Alexa488 conjugates at 100 nM of protein concentration monitored by FCS in 50 mM potassium phosphate buffer, pH 6.5, at room temperature. (A) The diffusion coefficient of FtsZ-Alexa488 conjugates as a function of urea concentration obtained from autocorrelation functions. The inset shows the fluorescence intensity as a function of urea concentration. (B) FtsZ-Alexa488 unfolding data from FCS measurements plotted together with unfolding data from CD measurements of FtsZ at 1 μM. FCS unfolding data are plotted as the hydrodynamic radius (R_H) calculated with the Stokes-Einstein equation from diffusion coefficients as described in Materials and Methods. The solid lines represent the two-state fits of the experimental data, and the inset displays the urea concentration required to obtain 50% of denaturation in each case. The error bars represent the SD of three measurements.

Discussion and Conclusions

FtsZ monomers self-assemble into dimers and tetramers

Previous studies on the subunit association of FtsZ using analytical ultracentrifugation and isothermal titration calorimetry indicated the presence of monomers in equilibrium with small oligomers (8,10,23,24). In this work, using SEC, we found that GDP-bound FtsZ consisted of monomers, dimers, and tetramers depending on the protein concentration, in agreement with other studies (see below). A change in total protein concentration from 3 to 40 μM increased the population of dimers eightfold and the population of tetramers 12-fold. Although SEC is a nonequilibrium method, for stable oligomers with association rates significantly faster than the column run times, the dissociation constants can be approximated with reasonable precision (25,26). Therefore, the results presented here suggest micromolar dissociation constants for FtsZ dimers and tetramers. Additionally, almost complete dissociation of dimers and tetramers was observed at 3 μM, strongly suggesting a predominantly monomeric state of FtsZ at submicromolar concentrations.

To quantitatively determine the dissociation constants for FtsZ dimers and tetramers, we labeled the protein with the fluorescent probes FITC or DNS. We selected the dyes based on their fluorescence lifetime to more accurately monitor the rotational rates of the monomer, dimer, and tetramer species (see below). The labeling reaction was performed at high protein concentration (∼150 μM) to ensure that oligomeric forms would be present and hence modification of the FtsZ subunit interface by the dyes would be minimized. This scenario was confirmed by SEC, which detected only a slight increase in the dimer proportion compared with the unlabeled protein (Fig. S1). Sossong et al. (8) reported FtsZ dimer and trimer dissociation constants of 0.15 and 2.7 μM, respectively. Mukherjee et al. (24) reported a tetramer dissociation constant of 2.5 μM. In the work presented here, the dilution experiments with both FITC and DNS dyes yielded similar dimer-to-monomer dissociation constants, but the values (∼K_dD = 9 × 10⁻⁶ M) are 60 and 3 times larger than the values mentioned above, respectively. However, the dimer dissociation constant agrees with the value for isodesmic assembly reported by Caplan and Erickson (10), K_D = 8 μM, regardless of the different experimental approaches used. In the case of tetramer-to-dimer dissociation, the FITC and DNS probes gave different dissociation constants, but weak interactions between dimers were predicted in both cases (Table 1). A discrepancy in K_dT values was not unexpected, because the dyes have different fluorescence lifetimes. FITC, a short-lifetime probe, tends to be more sensitive to the monomer-dimer equilibrium, whereas DNS, a long-lifetime probe, tends to be more sensitive to the dimer-tetramer equilibrium.

An aspect of the dilution experiments that deserves attention is the rather small change in anisotropy observed upon dissociation, i.e., 0.011 for FITC and 0.023 for DNS. This observation can be explained by considering the ratio of the lifetime to the correlation time (τ/θ). This ratio is smaller for a short-lifetime probe (e.g., FITC) and larger for a long-lifetime probe (e.g., DNS), and therefore the changes in anisotropy upon dissociation are expected to be smaller for FITC than for DNS. The anisotropy change upon dissociation may also be affected by changes in local probe mobility, as indicated by the time-resolved fluorescence measurements. Dynamic polarization measurements for FtsZ-FITC and -DNS conjugates revealed 57% and 15% of local motion contribution to the total anisotropy, respectively. The mobility of attached probes is attributed to rotations around the covalent linkage, which yield an additional depolarization process during the fluorescence lifetime. Because the amount of local motion found for FITC is higher than the local motion found for DNS, a smaller change in the anisotropy upon dissociation is expected. Nonetheless, for both dissociation experiments, the data fit well to the three-state dissociation model from tetramers to monomers through a dimer intermediate. Moreover, the data could not be well fit to the dissociation of tetramers to monomers or the dissociation of dimers to monomers (Fig. S2). In dimer-to-monomer dissociations a logarithmic span (i.e., 10–90% dissociation) of 2.86 log units is expected, whereas in tetramer-to-monomer dissociations a span of 1.59 log units is expected (27). In this study, the dissociation occurred over 2.66 and 2.33 log units for FITC and DNS conjugates, respectively (values in between the tetramer and dimer dissociation spans). Using the Perrin-Weber equation (28), for a spherical particle with the molecular mass of the FtsZ monomer (40 kDa), the calculated correlation time (θ₀) is 17 ns, and in the case of a tetramer the calculated correlation time is 68 ns. The observed global rotational correlation times for FtsZ-FITC and -DNS conjugates were 38.9 ns at 31 μM and 147 ns at 45 μM, respectively, supporting the concept that at high concentrations, the protein has oligomerization states higher than monomer. Lowering the protein concentration decreased the global rotation in both cases, which was interpreted as dissociation of the oligomers. Dilution of FtsZ-FITC from 31 to 1 μM decreased the global correlation time from 38.9 ns to 19.7 ns, a value comparable to the monomeric state of FtsZ. A comparison of the theoretical correlation time of FtsZ tetramer with the experimental value (θ_DNS = 147 ns) indicates that the tetramer behaves hydrodynamically as a prolate ellipsoid in solution (here it is assumed that the longer DNS lifetime permits a more accurate determination of the global correlation time; see above). This behavior was expected because the tetramer should be an elongated structure due to the longitudinal interaction described for FtsZ dimers (i.e., a head-to-tail interaction) (5).

The three-state unfolding of FtsZ is due to the presence of the dimer

Denaturant-induced unfolding of proteins has been used to understand the structural changes and stabilization of monomeric and oligomeric proteins. The free energy of unfolding (ΔG_T°_H2O), the slope of the unfolding transition (m-value), and the transition midpoint (C_50%) are all affected by changes in the degree of association of oligomeric proteins (29,30). Although the reversible unfolding of FtsZ was studied previously, it was always analyzed in terms of a monomeric system that was independent of the protein concentration used (16,17). Our study shows that FtsZ unfolds through a three-state process due to the oligomeric state of the protein, which clearly affects the second unfolding transition. CD data were fit to a three-state mechanism of unfolding wherein the first stage consisted of the unfolding of the native dimer into a dimer intermediate, followed by the coupled dissociation-unfolding of the intermediate into two monomers in the second stage. Global fitting with the full data sets resulted in ΔG_T°_H2O = 14 ± 1 kcal mol⁻¹, which is very similar to the average values from the individual fits. This value is in agreement with ΔG_T°_H2O reported for proteins of similar size and oligomeric state. For example, in the case of protein dimers showing a single transition between native and denatured states, ΔG_T°_H2O was found to increase with molecular mass from 10 to 27 kcal mol⁻¹ (29–31). The m-value for denaturant-induced unfolding reactions correlates well with the difference in accessible surface area (ΔASA) between the native and unfolded states (32). Our prediction of ΔASA for denaturation of FtsZ dimer by urea (∼44783 Å²), based on the ASA of individual residues for the native and unfolded states (33), allowed us to calculate a theoretical m-value for unfolding of 9.1 kcal mol⁻¹ M⁻¹. Global fitting of the full data sets resulted in m = 9 ± 2 kcal mol⁻¹M⁻¹ for denaturation of the dimer, which is consistent with the predicted value. The results indicate that 68% of the change in ΔASA takes place in the first stage of unfolding. In turn, this result suggests a highly hydrated dimeric intermediate relative to the native dimer, which is compatible with the expansion of monomers within the dimer at low urea concentrations before dissociation takes place. Modeling of the fractions of species as a function of urea concentration, using ΔG°_H2O and m-values obtained from the individual fits, indicated that the biphasic behavior of FtsZ unfolding is due to a high proportion of the dimer at low urea concentrations (Fig. 3 B, solid lines and dotted lines). Although the intermediate is not evident at low protein concentrations, its presence diminishes the cooperativity of the unfolding process compared with a two-state unfolding behavior (Fig. 3 B, dotted lines). The simulated curves calculated from thermodynamic parameters showed a good overlap with the experimental data (Fig. S3), predicting a biphasic behavior at high protein concentration and a monophasic behavior at low protein concentration. This supports the conclusion that a low proportion of the dimer may be responsible for the apparent two-state unfolding.

FtsZ monomer unfolds through a two-state transition

FCS provides information about the hydrodynamic properties of proteins in solution from measurements of diffusion coefficients. In previous studies, FCS was used to study the denaturant-induced unfolding of proteins (34–36). In these studies, an expansion of the polypeptide chain with increasing concentrations of denaturant was always observed. The expansion of globular proteins during the unfolding by urea is proposed to be due to weakening of the hydrophobic core caused by binding of urea to the backbone and residue side chains (37). To study the unfolding of the FtsZ monomer, we induced dissociation by lowering the protein concentration to ∼100 nM. According to the dimer dissociation constant calculated in this work, >99% of the species should be monomeric at 100 nM FtsZ. The predicted diffusion coefficient and hydrodynamic radius for the FtsZ monomer in the native state, based on the 3D structure and using HYDROPRO (38), are 81 μm² s⁻¹ and 29 Å, respectively. The experimentally obtained diffusion coefficient and hydrodynamic radius for FtsZ in the native state were 60 ± 1 μm² s⁻¹ and 36 ± 1 Å, respectively. This discrepancy may reflect an asymmetry in the protein subunit that is not represented in the 3D rigid structure, i.e., in solution, the behavior of the monomer deviates from that of a spherical particle. In the case of the unfolded state of FtsZ, a hydrodynamic radius of 66 Å was calculated (39). The experimental hydrodynamic radius for FtsZ in the denatured state was 57 ± 1 Å, which is lower than the theoretical value, indicating that the FtsZ monomer may further expand and bind urea above 3 M. A comparison of the FCS data with the unfolding at 1 μM FtsZ by CD (Fig. 4 B) showed a reasonable overlap, indicating that in the presence of urea, the expansion of the monomer at nanomolar concentration occurs concomitantly with the loss of secondary structure. Furthermore, in both cases a single transition with similar stability (C_50%) appears between the compact native state and the expanded unfolded state. These results indicate that negligible changes in the oligomerization take place at protein concentrations below 0.5 μM, confirming that the apparent two-state unfolding transition is due to the primarily monomeric state of the protein.

FtsZ assembly in the presence of GTP or GDP

Our experimental results demonstrate that polymerization of FtsZ can be detected only above 1 μM protein. Extrapolation of the protein concentration-dependent light-scattering data indicates a critical concentration C_c of 0.5 μM. (Fig. 5 A, open bars). Calculation of the fraction of dimers at the protein concentrations used in the polymerization assay (Fig. 5 A, closed bars) indicates that the dimeric form is only marginally present at total protein concentrations below the C_c. However, the monomer-to-dimer equilibrium characterized here (K_d = 9 μM) indicates a significant fraction (∼10%) of stable dimers at the C_c for polymerization, supporting a role of the dimeric species in the first steps of FtsZ polymerization. The observation of weak filament formation and weak oligomerization at submicromolar FtsZ concentrations, when bound to GTP or GDP, respectively, suggests that the nucleation step corresponds to the monomer-dimer equilibrium. This hypothesis is also supported by the finding that the oligomerization state of FtsZ bound to GTP or GDP did not change significantly at a total protein concentration ≤ C_c (Fig. 5 B). To summarize, all of our results support an FtsZ polymerization mechanism in which the dimer is the nucleus for filament formation.

Figure 5.

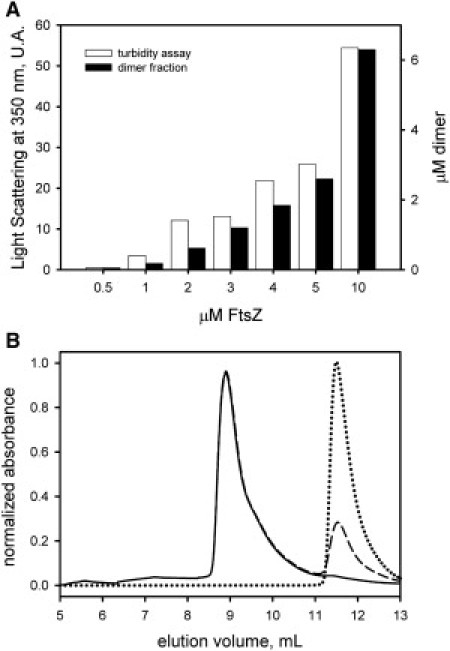
(A) GTP-induced polymerization assay of FtsZ as described previously (40). The polymerization was monitored by 90° light scattering at 350 nm (open bars). The fraction of dimers at every protein concentration (closed bars) was calculated based on a dimer dissociation constant K_dD = 9 × 10⁻⁶ M. (B) SEC profiles of FtsZ (0.5 μM) bound to GDP (solid line) or GTP (dashed line) in the same conditions as in Fig. 1. The peaks eluting at 8.9 mL correspond to monomeric FtsZ (see Fig. 1). The protein mixture was saturated with 500 μM GTP before it was injected into the column. The free nucleotide elutes in the internal column volume of 11.5 mL (dotted line).