Network-Based Model Weighting to Detect Multiple Loci Influencing Complex Diseases

Abstract

For genome-wide association studies it has been increasingly recognized that the popular locus-by-locus search for DNA variants associated with disease susceptibility may not be effective especially when there are interactions between or among multiple loci, for which a multi-loci search strategy may be more productive. However, even if computationally feasible, a genome-wide search over all possible multiple loci requires exploring a huge model space and making costly adjustment for multiple testing, leading to reduced statistical power. On the other hand, there are accumulating data suggesting that protein products of many disease-causing genes tend to interact with each other, or cluster in the same biological pathway. To incorporate this prior knowledge and existing data on gene networks we propose a gene network-based method to improve statistical power over that of the exhaustive search by giving higher weights to models involving genes nearby in a network. We use simulated data under realistic scenarios, including a large-scale human protein-protein interaction network and 23 known ataxia-causing genes to demonstrate potential gain by our proposed method when disease-genes are clustered in a network.

INTRODUCTION

High-throughput genotyping technology has made it possible to conduct genome-wide association studies, though it is still not clear how to analyze resulting data most effectively. The current practice seems to focus on locus-by-locus searches. However, accumulating data from model organisms and human studies suggest that complex traits are influenced by interactions among loci. A recent study by Marchini et al (2005) has clearly demonstrated potential gains in statistical power by considering multiple loci simultaneously over that of a locus-by-locus search. In particular, they have shown that an exhaustive search for logistic regression models that include 2- or 3-way interactions is computationally feasible, and after the Bonferroni adjustment for multiple testing, may yield higher statistical power than that of searching for only one locus. Nevertheless, as acknowledged by the authors, there is a higher adjustment cost for models including a larger number of loci because the number of such possible models increases exponentially with the number of loci included. Hence, it is natural to consider boosting statistical power by reducing the cost of multiple testing adjustment in searching for multiple loci. For this purpose a straightforward idea is to restrict the search to a subspace of more promising models, as in pathway-based approaches (Dinu et al 2007; Wang et al 2007). In the context of networks, as to be shown, there are some practical issues in implementing such an idea Therefore, we generalize this idea and propose that, rather than treating all possible models equally a priori in a typical adjustment for multiple testing, we would put more weights on those more promising ones. Now the key becomes how to judge the extent to which a multilocus model is promising. Our short answer is to use gene networks.

While many human genetic diseases are caused by multiple genes, it has been increasingly recognized that, because the mutations of these genes lead to the same or similar phenotype, these genes are likely to be functionally related, and such functional relatedness can be exploited to identify novel disease genes (Oti et al 2006). Protein-protein interactions (PPIs) are a strong manifestation of such functional relatedness among the genes. In fact, several genetically heterogeneous hereditary diseases, such as Hermansky-Pudlak syndrome and Fanconi anemia, are caused by mutations of the genes whose protein products interact to each other (Di Pietro et al 2005; Mace et al 2005); in breast cancer, more than a half of the proteins from about 100 mutated cancer genes formed a tight cluster in a PPI network (Lin et al 2007). Furthermore, it has been shown that the mutations of the genes whose protein products interact tend to lead to similar disease phenotypes (Gandhi et al 2006). In this paper, we will use data from a recent study (Lim et al 2006) that showed for the first time that the 23 genes causing human inherited ataxias were tightly linked in a PPI network involving 54 proteins.

The premise of our proposed method is the assumption that a PPI (or other genetic) network-neighbor of a disease-causing gene is more likely (than any randomly chosen gene) to be related to the disease. For simplicity, we also assume that a single most promising genetic marker (e.g. SNP) or haplotype from each gene has been identified; more discussions on relaxing this restriction are given later. Therefore, for a model involving multiple genes, we rate a priori its promisingness by the average distance of the genes in a network. This basic idea is related to the emerging literature on prioritizing or predicting disease-causing genes (for reviews see Oti et al 2006; Ideker and Sharan 2008). However, we emphasize that the goals are quite different: here we would like to use this information to reduce the cost of multiple testing and thus to increase statistical power while maintaining a rigorous control on a genome-wide error rate for multilocus searches in genome-wide association studies; in contrast, for prioritizing or predicting disease-causing genes, the goal is that, given one or more small genomic regions (e.g. as predicted by a linkage analysis), or some disease-causing genes, how to rank a small number of candidate genes based on their likelihood to be disease-causing. The motivation of our study also bears some similarity to the pathway-based approach of Wang et al (2007), including the “one marker per gene” restriction, though specific strategies are quite different. First, the pathway-based approach conducts a joint test on the significance of all the loci specified by a pathway; in contrast, our method discovers significant individual loci/genes. Second, the pathway-based approach treats all the loci/genes within a pathway identically, failing to account for their varying relationships, whereas ours takes into account the topological relationships of the genes in a network. Third, the pathway-based approach requires the user to supply sets of the genes in candidate pathways, while ours takes a genome-wide network as input. Because of incomplete knowledge on pathways, PPI or other experimental data-based networks may contain more information. In fact, our network can be a set of pathways. Finally, the pathway-based method restricts the search of multiple loci to only given pathways, which however may miss some novel relevant multiloci; in contrast, our method keeps the door open even for those less likely ones (as long as non-zero weights are assigned to them, as usual).

While the necessity of using multilocus models is well known when interactions among multiple loci or genes exist, it seems less emphasized otherwise. In this paper we emphasize the need for multilocus models even if there is no gene-gene interaction. Specifically, if a disease is caused by independent mutations from multiple genes while the effect of each gene is only moderate, there can be gains in statistical power when models involving multiple genes, rather than those with only single genes, are adopted. As suggested by empirical studies in humans, the effect of a single locus on complex disease phenotypes is typically weak or moderate with odds ratio (OR) in the range of 1.2–2.0 (Lohmueller et al 2003); for example, the estimated ORs for the associations between a common variant of the FTO gene and the overweight and obesity phenotypes for various study populations are often as low as 1.1–1.2 (Frayling et al 2007).

METHODS

Searching for Multiple Disease-Causing Genes

A straightforward way to detect one or more of multiple disease-causing genes is to consider each of possible models involving multiple genes, leading to an exhaustive search in a large model space. To be concrete, throughout this paper we assume that multiple or single logistic regression is used, and the exhaustive search considers all possible logistic models containing t ≥ 1 genes that are a subset of all the G genes; Marchini et al (2005) showed that using t = 3 is computationally feasible in genome-wide association studies. From each model M_i = M_i(t) involving t genes, i = 1, …, m, we have a p-value P_i indicating the statistical significance of M_i; a small P_i suggests that either some or all of the genes in M_i be associated with the disease phenotype. To account for multiple tests, we adopt the Bonferroni adjustment to control the family-wise error rate (FWER): for a specified genome-wide significance level α, we would reject the non-significance of M_i if P_i ≤ α/m.

For example, for a genome with G genes, if we consider models with t = 2 genes, we have m = C(G, 2) = G(G − 1)/2 possible models, where C(G, t) is the combination number of choosing t ≤ G items from G items. In contrast, if we consider only one gene at a time, we have m = G, which is much smaller than G(G − 1)/2 when G is typically large in genome-wide studies. In other words, for the Bonferroni adjustment, rather than using the cut-off α/G for one-gene models, we have to use a much more stringent cut-off α/(G(G − 1)/2) when searching for two genes, leading to possibly reduced statistical power. This is what we call the high cost of multiple test adjustment; the more genes to be included, the higher the cost. Although the Bonferroni adjustment is well known to be conservative, we argue here that our main point applies to other general multiple-test-control methods too; the key is that the cost of a multiple test adjustment goes up with the number of tests, m. For example, if the more popular Benjamini-Hochberg (BH) (1995) procedure to control the false discovery rate (FDR) is adopted, we still have to pay the price of multiple tests: suppose that the p-values are in ascending order as P_(i), then to control the FDR within α, one would reject the non-significance of the first T models with the smallest p-values with T = max{i: P_(i) < iα/m}; note that the threshold is inversely proportional to m. For clarity of presentation, we will focus on the Bonferroni adjustment.

To motivate our proposal to alleviate the effects of a multiple-test adjustment, we first look at a simple idea that is based on directly reducing m by restricting to a smaller search space, and point out its problems. Then we generalize the idea and propose a p-value weighting scheme to give higher weights to those models that are a priori more likely to be significant.

Gene Networks and kON

If we can restrict the search space of possible models to a smaller one while maintaining a high probability of its covering significant models, we can have improved power with a smaller m. Now the key question is how to do so. One possible way is based on gene networks. Recent studies have shown that disease-causing genes tend to be in the same pathways; for example, in cancer studies, in spite of hundreds of known cancer genes, “it is becoming increasingly clear that pathways, rather than individual genes, govern the course of tumorigenesis. Mutations in any of several genes of a single pathway can thereby cause equivalent increases in net cell proliferation” (Wood et al 2007). Because of incomplete biological knowledge on pathways and of possible involvement of several pathways, use of gene networks is an alternative. In fact, it has been found that the protein products of disease-causing genes tend to be closer to each other in a protein-protein interaction (PPI) network. For example, Lim et al (2006) identified 23 human inherited ataxias-causing genes and found unexpectedly that they are all tightly linked in a PPI network involving 54 proteins.

Because of disease-causing genes tend to be closer to each other in a network, we can restrict our attention to the nearby genes. A possible way is to consider for each gene its direct or 1st-order neighbors to be included in a multi-gene model; we denoted the 1st-order neighbors of a gene as 1ON. Compared to an exhaustive search over N_0t = C(G, t) models, the number of models in 1ON search, say N_1t, can be much smaller (Table 1), thus leading to improved power.

Table 1.

Ratio of the number of all possible models over that of kON based on the kth-order neighbors of each gene in the PPI network.

k	1	2	3	4	5
N02/Nk2	22.024	1.534	1.098	1.080	1.077
N03/Nk3	178.785	2.364	1.167	1.124	1.119

A severe limitation of the 1ON search is its strong restriction: for example, based on currently available PPI data, most of the 23 ataxia-causing genes do not interact to each other directly, thus a 1ON search may miss most of them. As an alternative, we may expand the search to 2ON: for each gene, in addition to its direct neighbors, we consider the direct neighbors of each of its direct neighbors, i.e., its 2nd-order neighbors. More generally, we can thus consider kON searches for kth-order neighbors. Computationally, a kON search is equivalent to considering only models containing the genes with their shortest path distance no greater than 2k. However, as shown in Tables 1–2, the number of models searched in 2ON may quickly approach that of the exhaustive search due to the small world property of biological networks (Barabasi and Oltvai 2004): most nodes can be reached from any others by traveling only short distances. As an alternative, we consider a more general method that covers a kON search as a special case.

Table 2.

Distribution of the numbers of the kth-order neighbors (in kON) of the genes in the PPI network. Q_j is the jth quartile.

k	min	Q1	Q2	Q3	max
1	1	2	4	10	1957
2	2	28	119	490	6567
3	2	652	2797	5332	10100

A Simple Example

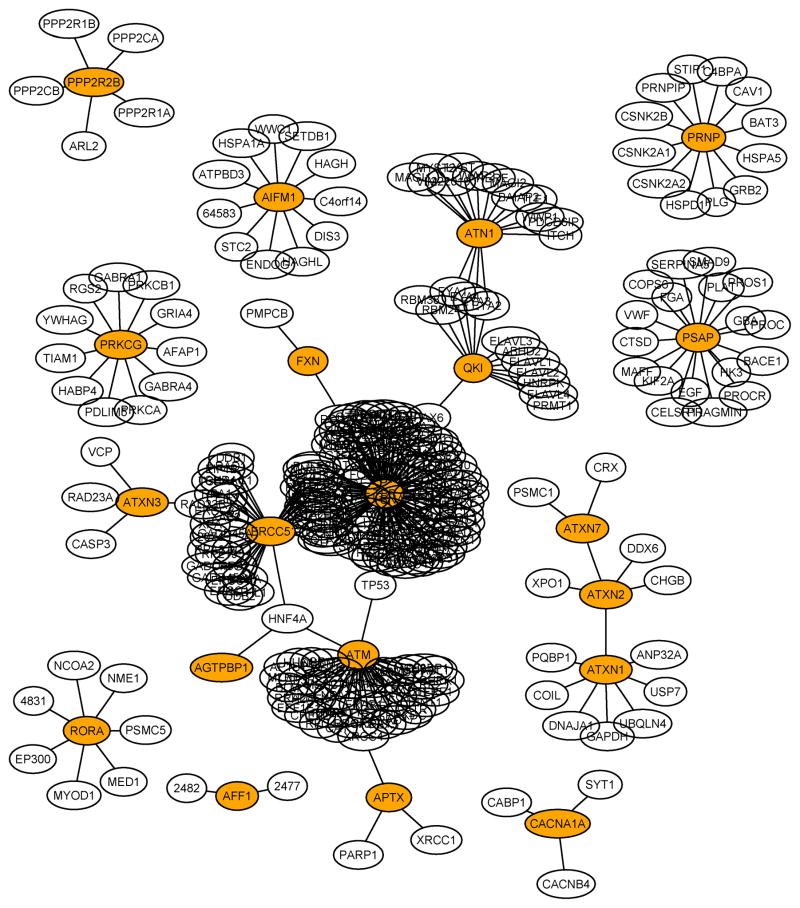
Before moving to more technical details, we give a simple example to illustrate the idea. Consider the subnetwork containing three ataxia genes, ATXN1, ATXN2 and ATXN7, and 12 other genes in Figure 1. If we consider only these 15 genes, an exhaustive search will identify N₀₂ = C(15, 2) = 105 models with two genes, and N₀₃ = C(15, 3) = 455 models with three genes. In contrast, a 1ON search will only identify N₁₂ = 55 models with two genes, and N₁₃ = 108 models with three genes, only a half and a fourth of those from the exhaustive search respectively. At the genome-wide significance level of α = 005, the p-value P_i of model i including two (or three) genes is considered to be significant if and only if P_i < 0.05/105 (or P_i < 0.05/455) for the exhaustive search, whereas it is significant if and only if P_i < 0.05/55 (or P_i < 0.05/108) for the 1ON search based on the Bonferroni adjustment. Hence, with a loose cut-off, the 1ON search will be more powerful if indeed disease-causing genes are in 1ON of at least one gene, as the three ataxia genes in the subnetwork of Figure 1; otherwise, the 1ON search will miss some disease-causing genes. A simple way to fix the problem is to expand the 1ON search to a kON search with k > 1. However, the number of models covered by a kON search approaches that of the exhaustive search rapidly as k increases; in the above example, a 2ON search is exactly the same as the exhaustive search because all the genes are in the 2ON of gene ATXN2.

Figure 1.

Twenty ataxia-causing genes (dark nodes) and their direct neighbors in a PPI network. Genes with no names are annotated with their Entrez numbers.

A more general method we discuss next is based on p-value weighting (Genovese et al 2006). The method assigns a weight w_i ≥ 0 to each model i, then model i is claimed to be significant if and only if its p-value P_i < 0.05w_i/m, where m is the total number of models being searched. It can be proved that, if ${\sum }_{i=1}^m{w}_i/m=1$, then the genome-wide Type I error rate is controlled at α = 0.05. The basic idea of our proposed method is to assign a larger weight to a model including the genes that are closer to each other in a network, giving the model a larger cut-off to claim statistical significance and thus boosting power (if indeed the disease-causing genes are closer to each other in the network).

P-value Weighting

P-value weighting has been proposed as a general method to improve power for multiple tests, and applied to incorporate prior linkage analysis or gene functional group information into genome-wide association studies (Genovese et al 2006; Roeder et al 2006, 2007; Ionita-Laza et al 2007). Here we incorporate the closeness of disease genes in a network into p-value weighting.

Suppose that a weight w_i is attached to each p-value P_i with the constraint that $\overline{w}={\sum }_{i=1}^m{w}_i/m=1$. The modified Bonferroni adjustment is to reject the significance of M_j if P_i < w_i α/m. It is obvious that if a larger weight w_i is given to a more likely model M_i, then the power will be improved. It can be seen that the Bonferroni adjustment is a special case of p-value weighting with all w_i = 1; that is, all the models are treated equally likely a priori. On the other hand, the kON search is another special case with weights equal to either 1 or 0, depending on whether the genes in a model are in kON of one gene. Finally, we note that the BH procedure to control FDR can be similarly modified (Roeder et al 2006), but again we focus on the Bonferroni adjustment to control FWER.

In the current context, given a gene network, we can calculate the shortest path (SP) distance between any two genes, say SP(j₁, j₂) for genes j₁ and j₂. Now for any model M_i(t) involving t genes, we can calculate the average SP distance between any of the two of the t genes in model M_i as

$${SP}_i(t)={\text{Ave}}_{j_1\ne j_2\in M_i}SP(j_1,j_2).$$

We consider two simple weighting schemes, called exponential (Exp) and inverse (Inv) probabilities: for model M_i(t), its weight is

$$w_i=w_i(t)=v_i(t)/\overline{v}(t),$$

where

$$v_i(t)=exp(-B\ast {SP}_i(t))\text{or}{v}_i(t)=1/{({SP}_i(t)-1)}^B$$

for the Exp or Inv weighting scheme with B ≥ 0 as a parameter to be specified, and v̄(t) = Σ_iv_i(t)/m. Roeder et al (2007) also proposed a data-driven method to estimate optimal weights, which however is computationally too demanding to be implemented in simulations due to the requirement for tens of thousands of replicated datasets in simulations.

RESULTS

Gene Network and Disease-Causing Genes

To be practical, we used a large-scale human PPI network involving G = 11203 genes and 57235 pairwise interactions/edges, integrated by Chuang et al (2007) from yeast two-hybrid experiments (Rual et al 2005; Stelzl et al 2005), predicted interactions via orthology and co-citation (Ramani et al 2005), and curation of the literature (Peri et al 2003; Alfarano et al 2005; Joshi-Tope et al 2005).

Again to be practical, we retrieved the 23 ataxia-causing genes (Lim et al 2006), and treated several subsets of the genes as true disease-causing genes in our simulations. Among the 23 ataxia-causing genes, only 20 appeared in the PPI network; these 20 ataxia-genes and their direct neighbors in the PPI network are depicted in Fig 1.

Denote N_0t as the number of all possible models involving t genes while N_kt as that based on kON. Table 1 gives their ratios for k = 1, …, 5 and t = 2, 3. It is clear that, the model space of 1ON was much smaller than that of the exhaustive search, and the difference between the two increased with t. However, for a fixed t, the ratio approached one rapidly as k increased. Table 2 summarizes the distribution of the numbers of the kONs of all the genes, from which it is confirmed that the number of the indirect neighbors increased very fast with k.

Table 3 summarizes the distribution of the average SP distances among t genes in a subset of nine ataxia-causing genes, in the set of 20 ataxia-causing genes, and in the whole PPI network. If two genes belong to two disconnected subnetworks, then their SP distance is defined to be ∞. It is evident that the ataxia-causing genes tended to be closer to each other in the network than were the other genes.

Table 3.

Distribution of the average shortest path lengths among t genes in one of the two ataxia-related gene subnetworks or the whole network.

t	Subnetwork	min	Q1	Q2	Q3	max
2	9-ataxia-gene	2.0	2.0	3.0	3.0	4.0
	20-ataxia-gene	1.0	3.0	4.0	4.0	∞
	All	1.0	3.0	4.0	5.0	∞
3	9-ataxia-gene	2.0	2.7	3.0	3.3	4.0
	20-ataxia-gene	1.3	3.3	3.7	4.0	∞
	All	1.3	3.7	4.0	5.7	∞
4	9-ataxia-gene	2.2	2.7	3.0	3.2	3.8
	20-ataxia-gene	2.2	3.3	3.7	4.0	∞
	All	1.5	3.7	4.2	4.8	∞
5	9-ataxia-gene	2.4	2.8	2.9	3.1	3.6
	20-ataxia-gene	2.4	3.4	3.7	∞	∞
	All	1.6	3.7	4.2	4.9	∞

Simulation Set-ups

We generated simulated data by mimicking real situations. For example, because the available data on the mutation frequencies for 227 cancer genes indicate their range from 0.2% to 64% with the mean at 4% (Cui et al 2007), we specified disease-causing gene mutations at the rates from 5% to 10% in the population. In addition, because it is well known that the association strength between a complex disease phenotype and a disease-associated DNA variant typically ranges from OR=1.2 to 2 (Lohmueller et al 2003), we specified ORs in this range. We also adopted the commonly used case-control study design for genome-wide association studies with the sample size in the range of 2000–4000 subjects in each of the case and control cohorts. Again there were G = 11203 genes, and we used the PPI network with 57235 edges.

We generated a binary disease status from a main-effect logistic regression model without interactions. Although interaction models could be equally adopted, we do not expect that our conclusion would change; furthermore, we want to emphasize the point that models with multiple genes can be beneficial even if there are no gene-by-gene interactions, which seems to be less emphasized than the epistatic effect in the literature. For simplicity, we assume a binary predictor indicating whether there is a disease-causing mutation for each gene as implied by a recessive or dominant genetic model, though the methodology and conclusions are expected to carry over to more general cases. In addition, we assume that the disease-causing genes are unlinked (as for unlinked loci in Marchini et al 2005) such that all the binary predictors are independent with each other. Specifically, for the first two set-ups, the disease status Y was generated from a multiple logistic regression model involving three binary predictors for three disease-genes:

$$\text{logit}Pr(Y=1)={\beta }_0+X_1{\beta }_1+X_2{\beta }_2+X_3{\beta }_3,$$

where β₀ = log 0.2/0.8 = − log 4 was the log odds of having disease as caused by other (e.g environmental) factors other than the three genes; the association strengths in terms of log OR between the disease and the mutations of the three genes were β₁ = log 1.5, β₂ = log 1.4 and β₃ = log 1.6; the disease-causing mutation frequencies were Pr(X₁ = 1) = 0.075, Pr(X₂ = 1) = 0.1 and Pr(X₃ = 1) = 0.05. Each simulated sample consisted of n cases (with Y = 1) and n controls (with Y = 0); we used n = 2000 for set-up 1 and n = 4000 for set-up 2.

In set-ups 3–4, we considered more disease-causing genes, each of which has only a moderate effect. To simplify presentation, we used five “similar” disease-genes:

$$\text{logit}Pr(Y=1)={\beta }_0+\sum _{i=1}^5{X}_i\beta ,$$

with β₀ = −log 4 and β = log 1.4. The binary predictors X_i’s were independent and identically distributed with Pr(X_i = 1) = 0.1 for i = 1, …, 5.

For each set-up, 10000 independent datasets were generated based on the true model.

Power Calculations

For each simulated dataset, we fitted a series of logistic regression models containing one or more disease-causing genes (without any interactions). The p-value P_i for each model M_i was based on the (asymptotic) likelihood ratio test to compare M_i to a null model (with the intercept only). Because each fitted model i contained at least one disease-causing gene, the empirical statistical power (ePower) of a method is simply the proportion of the tests correctly rejecting the null model. Specifically, for the exhaustive and 1ON searches for models including t genes, their empirical power was calculated by

$$\begin{array}{l}\text{ePower}(\text{Exhaustive})={\text{Ave}}_{i}Pr(P_i\le \alpha /N_{0t}),\\ \text{ePower}(1\text{ON})={\text{Ave}}_{i}Pr(P_i\le \alpha /N_{1t}),\end{array}$$

where N_0t and N_1t were the numbers of searched models with t genes by the two methods respectively.

For the weighted method with models containing t genes, first, we repeatedly drew a random sample of t genes from all of the genes, then we calculated the average SP distance between any two genes for each set of the drawn t genes. Second, we used a histogram to estimate the distribution of the average SP distances: we collapsed the calculated average SP distances into about 20 intervals I_j with mid-points L_j and proportions q_j. Third, for any model M_i(t), if the average SP distance of the genes included in M_i fell inside I_j then

$$v_j=exp(-B\ast L_j)\text{or}{v}_j=1/{(L_j-1)}^B,\overline{v}=\sum _j{q}_j{v}_j,$$

and w_j= v_j/v̄ was the weight assigned to M_i. For any two of the connected genes in our PPI network, their SP distance ranged between 1 and 15; we truncated any average SP distance larger than 15 at 16. Fourth if the proportion of average SP distances of the disease-causing genes falling inside I_j was q_0j, then the empirical power of the weighted method was

$$\text{ePower}(\text{Weighted})={\text{Ave}}_i\sum _j{q}_{0j}Pr(P_i\le w_j\alpha /N_{0t}).$$

Note that in practice, q_0j’s were unknown and thus ePower (Weighted) could not be calculated; however, in simulations, we assumed that disease-causing genes were known and thus q_0j’s could be estimated. Obviously the power of the weighted method depends on the topological relationships among the disease-causing genes through q_0j’s. Below, we considered three realistic scenarios 1) “3-ataxia-genes”: the 3 disease-causing genes were connected in a subnetwork as the three connected ataxia-causing genes, ATXN1, ATXN2 and ATXN7; 2) “9-ataxia-genes”: the 3 or 5 disease-causing genes were randomly drawn from the nine not-directly-connected but still tightly linked ataxia-causing genes, ATXN3, ATN1, QKI, FXN, TBP, BRCC5 ATM, AGTPBP1 and APTX; 3) “20-ataxia-genes”: the 3 or 5 disease-causing genes were randomly drawn from all the 20 ataxia-causing genes; see Fig 1. As for q_j’s we used Monte Carlo simulations to estimate q_0j’s: if our true model included t = 3 or t = 5 disease-causing genes, for any of the above three scenarios, we would randomly sample t genes from the candidate disease genes, and calculate their average SP distances for a large number of times; then used the same set of intervals I_j to estimate q_0j’s as the corresponding sample proportions (of average SP distances’ falling inside I_j).

Simulation Results

Table 4 compares the performance of the three methods, in which each column gives the power for detecting the disease-causing gene(s) when models with the corresponding number of the genes were searched. For example, column “X₁, X₂” refers to that of detecting the first two disease-genes when two-gene models (i.e., t = 2) were searched. First of all, the empirical powers for detecting one of three disease-causing genes based on searching only one-gene models were 0.138, 0.097 and 0.116 for set-up 1, and 0.641, 0.526 and 0.577 for set-up 2, respectively. It is confirmed that sometimes, as for set-up 2, searching for multi-gene models gave higher power than that of single genes. Second, it is clear that the 1ON search improved the power over that of the exhaustive search, as expected, because of the former’s reduced search space and thus lower cost for multiple test adjustment. Nevertheless, the 1ON search was only applicable to situations where a subset of disease-genes were all direct neighbors to each other, as for the 3-ataxia-gene situation, but not for the other two. Third, as expected, the performance of the weighted method depends on the topological relationships among the disease-causing genes in the network. If the disease-causing genes were well connected to each other, as for the 3-ataxia-gene scenario, there was a substantial power improvement. For the 9-ataxia-gene scenario, although none of them were directly connected to each other in the network, any one of them was connected to another through a common interacting partner; as a consequence of their closeness in the network, there were some gains in power. On the other hand, for the 20 ataxia-causing gene scenario, because some of them were not well connected, for example, AFF1 was not connected to any of the other (i.e SP = ∞), there could be some slight power loss.

Table 4.

Empirical power based on 10000 simulated datasets for set-ups 1 and 2. The genome-wide significance level was fixed at α = 0.05.

Method		Set-up 1, n = 2000				Set-up 2, n = 4000
		X1, X2	X1, X3	X2, X3	X1, X2, X3	X1, X2	X1, X3	X2, X3	X1, X2, X3
Exhaustive 1ON:		.057	.064	.048	.034	.654	.694	.610	.718
3-ataxia-gene Weighted:		.141	.160	.125	.128	.811	.848	.784	.900
3-ataxia-gene	Exp, B = 1	.116	.130	.100	.063	.775	.811	.741	.813
	Exp, B = 2	.171	.191	.151	.100	.837	.868	.812	.870
	Inv, B = 1	.084	.093	.069	.043	.720	.755	.675	.765
	Inv, B = 2	.113	.127	.097	.058	.769	.805	.733	.802
9-ataxia-gene	Exp, B = 1	.098	.110	.083	.042	.746	.781	.706	.757
	Exp, B = 2	.129	.144	.112	.047	.781	.815	.749	.766
	Inv, B = 1	.076	.084	.062	.037	.700	.736	.654	.734
	Inv, B = 2	.093	.104	.078	.039	.733	.770	.692	.746
20-ataxia-gene	Exp, B = 1	.056	.063	.046	.032	.606	.634	.561	.671
	Exp, B = 2	.048	.053	.040	.030	.561	.596	.517	.659
	Inv, B = 1	.059	.066	.048	.033	.655	.694	.609	.716
	Inv, B = 2	.059	.065	.048	.032	.647	.686	.601	.709

For simulation set-ups 3–4 with five “similar” disease-causing genes (Table 5), first, for the exhaustive search, searching only one gene at a time yielded higher power than searching for multiple genes for n = 2000; however for n = 4000, there was a clear trend that searching for more genes led to increased power. Second, for the weighted method, if the five disease-causing genes were among the 9 ataxia-causing genes, then there was power improvement; however, as for other set-ups, if they were equally likely to be among any of the 20 ataxia-causing genes, there was barely any improvement; again the Inv weighting seemed to be more robust with barely any power loss as compared to the Exp weighting, though the Inv weighting also gained less power for the 9-ataxia-gene case than did the Exp, which was consistent with the observation of Roeder et al (2006): A more extreme weighting scheme, such as Exp(B=2), can gain more if higher weights are correctly put on the p-values for true positives, but at the same time may lose more if incorrectly specified.

Table 5.

Empirical power based on 10000 simulated datasets for set-ups 3 and 4. The genome-wide significance level was fixed at α = 0.05.

Method		Set-up 3, n = 2000					Set-up 4, n = 4000
		X1	X1–2	X1–3	X1–4	X1–5	X1	X1–2	X1–3	X1–4	X1–5
Exhaustive Weighted:		.091	.038	.020	.009	.047	.507	.562	.608	.638	.899
9-ataxia-gene	Exp, B = 1		.070	.030	.013	.047		.662	.653	.699	.899
	Exp, B = 2		.096	.016	.015	.047		.707	.665	.709	.899
	Inv, B = 1		.051	.025	.011	.047		.609	.627	.670	.899
	Inv, B = 2		.065	.013	.012	.047		.648	.640	.687	.899
20-ataxia-gene	Exp, B = 1		.038	.020	.010	.047		.518	.564	.662	.899
	Exp, B = 2		.032	.018	.011	.047		.475	.551	.664	.899
	Inv, B = 1		.039	.020	.009	.047		.562	.606	.643	.899
	Inv, B = 2		.039	.020	.010	.047		.555	.598	.660	.899

DISCUSSION

Because of genetic heterogeneity, many complex diseases, including Parkinson’s disease, diabetes, hypertension and cancers, are caused by mutations of multiple genes while the effect sizes of the mutations may be small or moderate, for which the popular locus-by-locus or gene-by-gene search may have low power to discover any disease-susceptible genes. For such disorders, searching for multiple disease-causing genes simultaneously can be more productive. To counter the inherent high cost of the adjustment for multiple testing for such multilocus or multi-gene searches, we have proposed a weighting strategy to focus on more promising gene combinations. Based on the premise that the disease-causing genes are likely to be functionally related, such as manifested by their clustering in a PPI or other genetic network, we down-weight those gene combinations whose members are not close to each other in the network. As expected, the effectiveness of the proposed method depends on the extent of clustering among all or a subset of disease-causing genes in a network. For the 20 ataxia-causing genes and the currently available human PPI network, some subsets of the 20 ataxia-causing genes are tightly clustered while the others are less so. Because of the incomplete biological knowledge, with more PPI data accumulating, it may turn out that the 20 ataxia-causing genes are better connected to each other than characterized here by the current PPI network. In fact, it has been conjectured that many more ataxia-causing genes are likely to be identified among the interacting partners of the known 23 ataxia-causing genes (Lim et al 2006). In addition, we only tried two simple weighting schemes, whereas a more effective way is to estimate optimal weights for the p-value weighting (Roeder et al 2007). Hence, taken these factors into consideration, our proposed method may prove to be powerful when all or some of the underlying disease-causing genes are clustered in a given network.

We note that our results are applicable not only to the Bonferroni adjustment for FWER control, but also to the BH procedure to control FDR. Although we have emphasized the importance of searching for multiple genes for cases without gene-gene interactions, the main conclusion is applicable to that with gene-gene interactions. Computationally, our method is as demanding as the exhaustive search, which determines the maximum number of the genes/loci, t, to be included in a model; as shown by Marchini et al (2005), t = 3 is computationally feasible for genome-wide association studies, though a larger t is expected as computing power keeps improving. A useful extension of our method is to relax the “one marker per gene” restriction: we have assumed the availability and use of only one (most promising) locus or haplotype for each gene, but it is desirable to extend the proposed method to allow for multiple markers, e.g. SNPs, for each gene. A reasonable way is to first assign each locus to its nearest gene, or consider only those loci inside or in close vicinity to the genes as suggested by Wang et al (2007) and Dinu et al (2007) respectively, then treat all the loci within a gene equally: the multiple loci are treated as multiple copies of the same gene within which they reside and we disallow multiple loci from the same gene to appear together in the same model because these nearby loci can be handled by existing single-locus methods (Roeder et al 2005 and references therein). Alternatively, to be more flexible, e.g., to possibly treat loci outside or far away from coding regions differently from those inside, we may partition the genome-wide significance level into two parts: one for multilocus models, each of which consists of loci coming from different genes as we have discussed so far, and the other for remaining locus combinations; for the former, we can use our proposed weights based on their genes’ average SP distances in a network, while for the latter, we can simply use the usual Bonferroni adjustment. These issues, along with other ones, such as accounting for errors in a gene network, warrant further investigation in future studies with both simulated and real data.