BSMac: A MATLAB toolbox implementing a Bayesian spatial model for brain activation and connectivity

Abstract

We present a statistical and graphical visualization MATLAB toolbox for the analysis of functional magnetic resonance imaging (fMRI) data, called the Bayesian Spatial Model for activation and connectivity (BSMac). BSMac simultaneously performs whole-brain activation analyses at the voxel and region of interest (ROI) levels as well as task-related functional connectivity (FC) analyses using a flexible Bayesian modeling framework (Bowman et al., 2008). BSMac allows for inputting data in either Analyze or Nifti file formats. The user provides information pertaining to subgroup memberships, scanning sessions, and experimental tasks (stimuli), from which the design matrix is constructed. BSMac then performs parameter estimation based on Markov Chain Monte Carlo (MCMC) methods and generates plots for activation and FC, such as interactive 2D maps of voxel and region-level task-related changes in neural activity and animated 3D graphics of the FC results. The toolbox can be downloaded from http://www.sph.emory.edu/bios/CBIS/. We illustrate the BSMac toolbox through an application to an fMRI study of working memory in patients with schizophrenia.

1. Introduction

Functional magnetic resonance imaging (fMRI) is a powerful tool for identifying neural activity associated with emotional, cognitive, or behavioral tasks. By acquiring temporally and spatially localized measures of blood oxygen level dependent (BOLD) fMRI signals corresponding to various experimental tasks, one can determine distributed patterns of task-related changes in activity and evaluate associations in neural activity between spatially distinct brain regions. Activation studies generally seek to characterize the neural responses to experimental paradigms by detecting differences in patterns of brain activity between various experimental conditions (stimuli), different subgroups of subjects, or two or more scanning sessions, e.g. baseline and post-treatment. The objective of functional connectivity (FC) studies is to determine areas of the brain that share similar task-related (or resting-state) brain activity properties.

Typical fMRI analyses for activation studies use a two-stage procedure, in which the first stage involves subject-specific and voxel-specific models relating neural processing to experimental tasks (Purdon et al., 2001; Friston et al., 2002). The second stage specifies voxel-specific models for group (or population) level parameters (Worsley et al., 2002). Both stages fit separate models at each voxel. The voxel-by-voxel analysis employs estimation techniques that assume an improbable lack of correlation between voxel pairs. However, there is emerging recognition of the importance of modeling spatial correlations between voxels both for estimation and for statistical inferences.

Several software toolboxes have been published for fMRI analyses, making state-of-the art methods available to neuroimaging scientists. For example, AFNI (http://afni.nimh.nih.gov), Statistical Parametric Mapping (SPM) (http://www.fil.ion.ucl.ac.uk), and the Functional MRI of the Brain Software Library (FSL) (http://www.fmrib.ox.ac.uk/fsl/) are widely used comprehensive packages offering a range of functionality for image processing, analysis, and visualization. Numerous other toolboxes, such as Group ICA of fMRI Toolbox (GIFT) (http://www.nitrc.org/projects/gift), FMRISTAT (http://www.math.mcgill.ca/keith/fmristat/), and a range of SPM extensions, provide users access to specialized analysis tools for fMRI data. Moreover, specialized packages for EEG and MEG data are available, such as EEGLAB (Delorme and Makeig, 2004) and ERPWAVELAB (Morup et al., 2007). Collectively, these and other toolboxes provide users access to functional routines via graphical user interfaces (GUI), often for non-experienced users. The growing number of comprehensive and specialized toolboxes for neuroimaging analyses are vital for promoting sound statistical practices. Among the existing toolboxes, currently none implements analyses for combined (simultaneous) activation and FC analyses, nor do they provide techniques for modeling spatial correlations during estimation.

In this paper, we present a MATLAB toolbox for analyzing spatially correlated neuroimaging data. Our Bayesian Spatial Model for activation and connectivity toolbox (BSMac) is based on a Bayesian hierarchical statistical model (Bowman et al., 2008), and is released as an open source package under the GNU public license (http://www.gnu.org/licenses/gpl.html). The BSMac toolbox is intended to supplement existing packages such as SPM, FSL, and AFNI. In fact, BSMac assumes that preprocessing and preliminary analyses have been performed using one of these or alternative software packages.

BSMac implements a spatial model for making inferences regarding task-related changes in brain activity, while simultaneously identifying and accounting for prominent functional connections in the brain. In this way, BSMac combines the major objectives of both activation analyses and FC analyses. Additionally, BSMac provides a unified framework for investigating both voxel-level and region-level activation inferences. Hierarchical models are general tools for estimating and making inferences about quantities that can be conceptualized through a multi-level process. Bayesian methods offer inferential advantages over frequentist approaches by providing samples from the joint posterior probability distribution for all of the model parameters, rather than p-values, providing greater flexibility in the inferences that may be drawn from functional neuroimaging data.

The remainder of this paper is organized as follows. Section 2 describes the underlying theory of our two-stage Bayesian model and includes novel extensions to the model of Bowman et al. (2008), for instance, incorporating covariate effects into the spatial model and implementing analyses for small sample sizes. Section 3 discusses the functionality of the toolbox and illustrates its use via a data example from a study of working memory in patients with schizophrenia. Section 4 concludes the paper with a general summary and discussion of the BSMac toolbox, our Bayesian statistical methodology, and the results obtained from the study of working memory in schizophrenia patients.

2. Methods

BSMac is a software application written in MATLAB that is provided as a stand-alone executable GUI as well as an open-source MATLAB toolbox. BSMac consists of a collection of new functions and scripts, which make use of existing routines in the MATLAB distribution and other publicly available additions. The application allows the user to analyze brain imaging data saved in either Analyze (Biomedical Imaging Resource, Mayo Foundation) or Nifti (http://nifti.nimh.nih.gov/nifti-1) formats. BSMac is built as a GUI to implement a second state (group-level) modeling approach for fMRI data from a two-stage framework that emulates a random effects analysis. The toolbox can also be extended for applications to PET data. In this section, we present a brief description and the theoretical background of the methods used in the toolbox.

2.1. Stage I model

Let i = 1, …, K represent subjects, v = 1, …, V voxels, s = 1, …, S scans, and let Y_i(v) be an S × 1 vector measured at voxel v from the serial fMRI BOLD responses for subject i. The S × q design matrix X_iv includes independent variables of interests such as experimental conditions, and H_iv contains covariates that are not of substantive interest. The first-stage model is represented as:

$${\mathbf{Y}}_i(v)={\mathbf{X}}_{iv}{\mathit{\beta }}_i(v)+{\mathbf{H}}_{iv}{\mathit{v}}_i(v)+{\mathit{\epsilon }}_i(v),$$ (1)

where β_i(v) = (β_i1(v), …, β_iq(v))′, and β_ij (v) is the effect corresponding to stimulus j for subject i. The vector ε_i(v) denotes random errors representing characteristics of the measurement process that are unaccounted for by the statistical model, and the model assumes that the errors follow a zero-mean multivariate normal distribution $N(\mathbf{0},{\sigma }_i^2(v)\mathbf{I})$, where ${\sigma }_i^2(v)$ is the error variance at voxel v.

The first-stage accounts for temporal correlations between serial scans within one session using variants of an autoregressive model (Bullmore et al., 1996; Purdon et al., 2001) and is constructed as a general linear model (GLM) for each individual’s vector of serial responses at the voxel level. Here, scan to scan temporal correlations are addressed in standard ways. Standard approaches either implement prewhitening followed by application of the model with diagonal covariance structure (as indicated in model (1)) or by precoloring followed by application of a model with known covariance structure, up to an unknown scalar constant (Worsley, 2005; Worsley et al., 2002). This first-stage model is implemented prior to using BSMac and can be performed in available software such as FSL, SPM, and AFNI.

2.2. Stage II model

The statistical model underlying the BSMac toolbox leverages a parcellation of the brain into regions, for example, defined by the Automated Anatomical Labeling (AAL) (Tzourio-Mazoyer et al., 2002) or Brodmann (Garey, 1994) maps, with regions indexed by g = 1, 2, …, G. Let V_g represent the number of voxels in a particular brain region. The individualized Stage I regression estimates are denoted by β_igj = (β_igj(1), …, β_igj(V_g))′, concatenating the localized effects from all voxels in region g, and let x_iq denote the qth (q = 1, 2, …, Q) between-subject covariate for subject i.

The Stage II model has the following hierarchical structure:

$$\begin{array}{l}{\mathit{\beta }}_{\mathit{igj}}\mid {\mathit{\mu }}_{gj},{\alpha }_{\mathit{igj}},{\sigma }_{gj}^2~\text{MVN}\left({\mathit{\mu }}_{gj}+\mathbf{1}{\alpha }_{\mathit{igj}}+\sum _{q=1}^Q{\mathit{\eta }}_{\mathit{gjq}}{x}_{iq},{\sigma }_{gj}^2\mathbf{I}\right)\\ {\mathit{\mu }}_{gj}\mid {\lambda }_{\mathit{gjq}}^2~\text{MVN}(\mathbf{1}{\mu }_{0gj},{\lambda }_{gj}^2\mathbf{I})\\ {\mathit{\eta }}_{\mathit{gjq}}\mid {\tau }_{gj}^2~\text{MVN}(\mathbf{0},{\tau }_{\mathit{gjq}}^2\mathbf{I})\\ {\sigma }_{gj}^{-2}~\text{Gamma}(a_0,b_0)\\ {\mathit{\alpha }}_{ij}\mid {\mathit{\Gamma }}_j~\text{MVN}(\mathbf{0},{\mathit{\Gamma }}_j)\\ {\lambda }_{gj}^{-2}~\text{Gamma}(c_0,d_0)\\ {\tau }_{\mathit{gjq}}^{-2}~\text{Gamma}(e_{0q},f_{0q})\\ {\mathit{\Gamma }}_j^{-1}~\text{Wishart}({(h_0{\mathbf{H}}_{0j})}^{-1},h_0)\end{array}$$ (2)

where μ_gj = (μ_gj(1), …, μ_gj(V_g))′, η_gjq = (η_gjq(1), …, η_gjq(V_g))′, and α_ij = (α_i1j, …, α_iGj)′. The parameter μ_0gj is the global mean across all subjects and intra-regional voxels. The model assumes that each individual’s task-related neural activity at a voxel level is randomly distributed around a population (or group) parameter plus an individualized region-specific random effect, after adjusting for covariate effects through η_gjq. The voxel-level group parameters are conceptualized as stemming from a random process centered around the mean neural activity for the entire brain region. While some departures from the additive random effect assumption are likely, our model provides an improvement over a commonly used framework that assumes independence between voxels. The regional random effect contributes to short range intra-regional correlations and accounts for possibly long range inter-regional spatial correlations through the covariance matrix Γ_j. Specifically, the first level of the hierarchical model in (2) and the subject- and region-specific random effect, α_igj, imply the following conditional exchangeable correlation structure:

$$\mathit{var}({\mathit{\beta }}_{\mathit{igj}}\mid {\mathit{\mu }}_{gj},{\mathit{\eta }}_{gj})={\gamma }_{gg}^{(j)}\mathbf{J}+{\sigma }_{gj}^2\mathbf{I},$$ (3)

where ${\gamma }_{gg}^{(j)}$ is the gth diagonal element from Γ_j, and η_gj = (η_gj1, …, η_gjQ)′ accounts for variance of the covariate coefficients. This exchangeable model builds in equal correlations between all pairs of voxels within a defined anatomical region, given by:

$${\rho }_{gj}^{(w)}=\frac{{\gamma }_{gg}^{(j)}}{{\gamma }_{gg}^{(j)}+{\sigma }_{gj}^2},$$ (4)

representing a measure of the strength of task-related intra-regional connectivity. Thus, ${\rho }_{gj}^{(w)}$ reflects the coherence or the similarity in the paradigm-related neural activity between voxels within a given anatomical structure. Note that extending our model to voxel-level random effects is infeasible because it would introduce millions (perhaps billions) of new parameters and lead to prohibitive computations.

For the inverse-Wishart prior, the degrees of freedom must satisfy h₀ ≥ G to yield a proper prior distribution, with smaller values corresponding to more vague priors. We set h₀ = G as the default value to reflect the most diffuse proper prior that the data can support. We obtain H_0j based on the sample covariance matrix corresponding to the jth effect, calculated from the subject-and effect-specific mean activity levels in each of the anatomical regions. Specifically, we use:

$${\mathbf{H}}_{0j}=(1-\omega ){\mathbf{H}}_{oj}^{\ast }+\omega [\mathit{diag}({\mathbf{H}}_{oj}^{\ast })],$$ (5)

where ${\mathbf{H}}_{oj}^{\ast }$ is the sample covariance matrix and 0 ≤ ω ≤ 1. The user-specified parameter shrinks the covariances, hence correlations, toward zero. When ω = 1, H_0j has a diagonal structure, which coincides with a prior proposed by Kass and Natarajan (2006) in a generalized linear model, after adapting it to our setting using region-specific random intercepts and a normal link function. Our framework also includes the slight extension of accommodating heterogeneity across brain regions. Our structure for H_0j may be used to perform sensitivity analyses by varying the strength of correlations (covariances) used in the inverse Wishart prior. MCMC methods are employed for estimation, implemented with the Gibbs sampler. The full conditional distributions derived from our second-stage spatial model appear in Appendix A.

There are novel extensions included in our current formulation of the Bayesian hierarchical model (2). First, model (2) permits the inclusion of covariate effects x_iq, which is a very important extension in the context of functional neuroimaging analyses, e.g. to control for age, education, handedness, and other potentially confounding variables. Secondly, there is an implicit restriction on the number of brain regions considered, imposed by the sample size, to ensure that the covariance matrix Γ_j is well-estimated. With a sufficiently large sample, one can easily implement a whole-brain analysis in BSMac. However, many functional neuroimaging studies use limited sample sizes. We now extend our model to permit as many regions as one wishes, even with a limited sample size, but the number of inter-regional correlation estimates obtained is still constrained by the sample size.

3. Data example and results

3.1. Preprocessing

Functional neuroimaging data typically undergo preprocessing before statistical analyses. Our toolbox assumes that the user has already performed preprocessing and that the data have been normalized to the Montreal Neurological Institute (MNI) coordinate template, with 91 × 109 × 91 voxel dimensions, using FSL, SPM, AFNI, or another software package. The initial preprocessing steps may involve checking for anomalous images, e.g. images that are improperly reconstructed, extremely noisy, or not correctly oriented. Other commonly used preprocessing steps include slice timing correction, motion correction, co-registration, spatial normalization, and spatial smoothing. We provide specific recommendations concerning spatial smoothing in the next section.

3.2. Data example

To illustrate the utility of BSMac, we employ data from the Functional Imaging Research on Schizophrenia Test-bed (FIRST) Biomedical Informatics Research Network (BIRN) or fBIRN (Zou et al., 2005; Potkin et al., 2002). The functional scans were T2*-weighted gradient echo EPI sequences, with TR = 2 s, TE = 30 ms, flip angle 90°, acquisition matrix 64 × 64, 22 cm FOV, and 27 slices when possible (4-mm thick with 1 mm gap), oblique axial AC–PC aligned.

We consider data from one site of this multi-center study obtained while subjects performed a cognitive recognition task called the Sternberg Item Recognition Paradigm (SIRP). The SIRP is a continuous performance task that requires the use of working memory or the ability to store and manipulate multiple pieces of information simultaneously. Subjects are asked to memorize a set of target digits shown visually on a screen. They are then presented with probes (single digits) and asked to respond by pressing a button box with their index finger if the probe appeared as a target (a member of the memorized set) or with their middle finger if the probe is a foil (not a member of the memorized set). To provide a range of working memory load conditions, the SIRP task included three working memory loads, where subjects were shown a memory set consisting of 1, 3, or 5 target digits in red, followed by a series of probe digits in green. For each run, two memory sets for each of the three load conditions were presented. The sample included 15 schizophrenia subjects and 13 healthy controls, matched by age, gender, race, handedness, education, and early life adversity. All the subjects were scanned in two separate sessions between at least 24 h and no more than 3 weeks later.

We preprocessed the scans for each run and performed a first level analysis using FSL. Our preprocessing steps included brain extraction, correction of head motion, focal spatial smoothing with 6 mm full-width at half-maximum (FWHM) 3D Gaussian kernel, and registration to a common brain shape that transforms the images into a standard space defined by the MNI template. We recommend very focal smoothing, at most, because more dispersed smoothing may impact the interpretations of the spatial correlation estimates. The normalized images were interpolated using bilinear interpolation and resliced to 2 mm × 2 mm × 2 mm voxels. Three summary images were generated for each subject in each run after the first-level analysis, corresponding to the number of digits involved in the working memory tasks.

3.3. Software structure

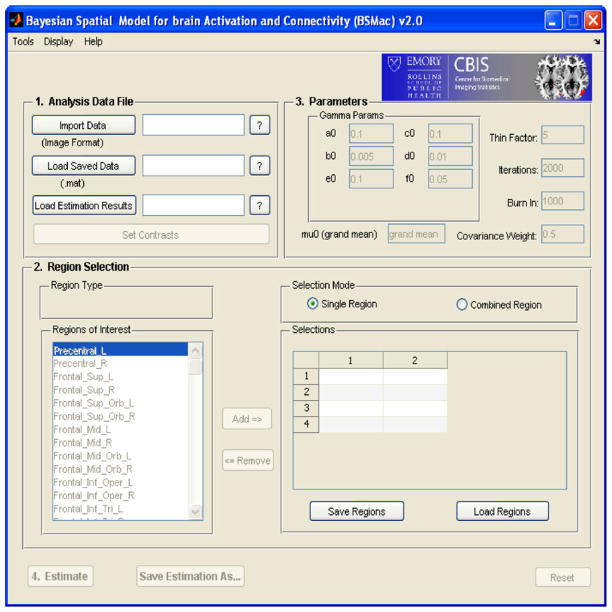
BSMac provides a GUI environment in which a user is able to implement advanced statistical concepts from an easy to use interface. Fig. 1 shows a screen capture of the BSMac GUI interface running under Windows. Five steps are included in the toolbox, namely (1) importing the data (“Analysis Data File(s)”), (2) selecting brain regions to be included in the analysis (“Region Selection”), (3) specifying the parameters for Gibbs sampler (“Parameters”), (4) executing the estimation (“Estimate”), and (5) visualization (“Plot”). We guide the reader through the main steps of the BSMac toolbox and provide illustrations using data from the study of working memory in individuals with schizophrenia.

Fig. 1.

BSMac GUI interface.

3.3.1. Analysis data file

BSMac allows the user to read in image files from either Nifti or Analyze formats, making use of a publicly available toolbox (Jimmy, 2010). Fig. 2 shows a BSMac screen shot of the interface for reading in the images, i.e. loading the input data.

Fig. 2.

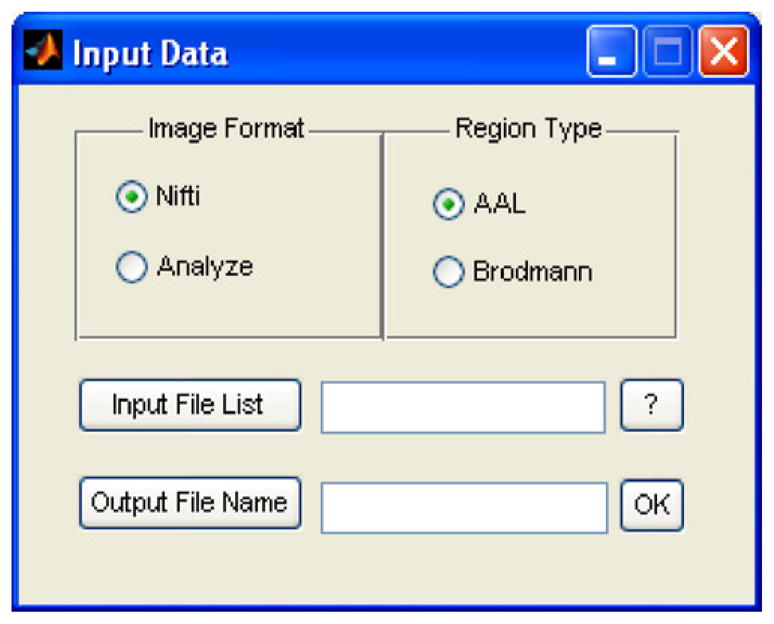
Interface for loading images.

As described in Section 2, the spatial model implemented in BSMac incorporates a neuroanatomic parcellation, and the user may select either the AAL or Brodmann parcellation templates. Alternatively, one could modify the source code to accommodate a preferred neuroanatomic or functional parcellation based on the analytic objectives and the intended interpretations. For example, the objectives of an analysis may prompt the use of small to moderately sized regions, functionally homogeneous regions, anatomically interpretable regions, or a sufficiently large number of regions to quantify graph theoretic connectivity metrics. AAL is defined neuroanatomically and the Brodmann parcellation is defined according to cytoarchitecture, and these serve as default options in BSMac. There are tradeoffs to using either functional or anatomical parcellations. Functionally defined parcellations should yield regions that are relatively homogeneous. However, only a subset of the functional regions may be interpretable anatomically, and several may reflect artifacts, e.g. related to preprocessing (Bowman, 2005). Brodmann and AAL parcellations contain regions that are easily interpretable, widely used in neuroscience, and that often have affiliated functions determined from previous research.

The user must provide a text file that includes descriptive information reflecting design variables and information regarding the locations and filenames for the data (see Table 1). The first line in the text file contains column headers, and no spaces are allowed in the header names. The subsequent lines contain the data corresponding to the column headings. The text file should include at least 5 columns separated by spaces, as shown in Table 1 (the first five columns), namely “Path”, “File-name”, “Group”, “Session” and “Stimulus”. “Path” and “File-name” specify the image files’ names and locations, “Group” separates the subjects into different groups, e.g. 1 and 2 represent healthy control and schizophrenia groups respectively. “Session” refers to time periods for which we wish to quantify and possibly compare effects, e.g. pre- and post-treatment sessions or serial baseline, 6 month, and 12 month sessions. “Stimulus” indicates the experimental task. The total number of columns depends on the number of additional covariates. Adding a large number of covariates may cause substantial increases in computing time and memory during estimation. After the information is extracted from the image data, the toolbox saves a MATLAB data file (.mat) under a folder named\data, which can be loaded directly in subsequent analyses, rather than repeating downloading of the image files.

Table 1.

Input file format.

Path	File-name	Group	Session	Stimulus	Age	…
C:/WM_data	subj1_HC_task1.nii	1	1	1	29	…
C:/WM_data	subj1_HC_task2.nii	1	1	2	29	…
C:/WM_data	subj1_HC_task3.nii	1	1	3	29	…
C:/WM_data	subj2_SP_task1.nii	2	1	1	45	…
C:/WM_data	subj2_SP_task2.nii	2	1	2	45	…
C:/WM_data	subj2_SP_task3.nii	2	1	3	45	…
…	…	…	…	…	…	…

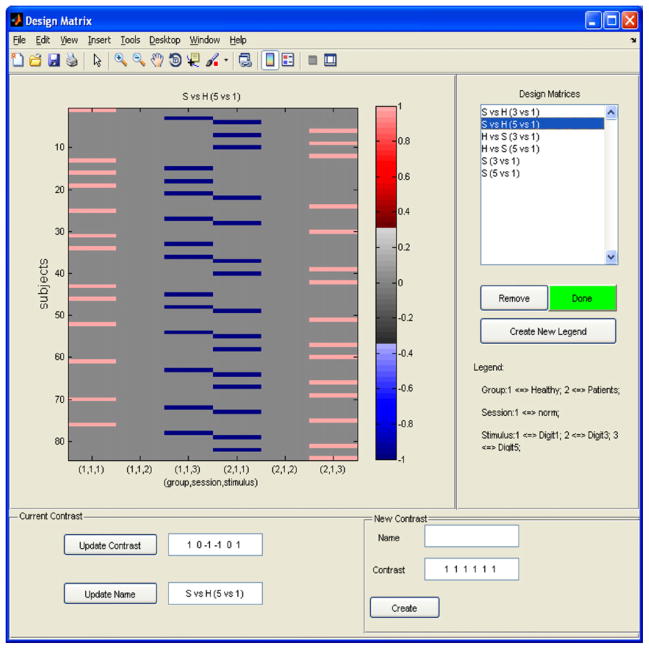
In practice, researchers are often interested in making inferences pertaining to the differences between sessions or groups. One common approach is to define, estimate, and perform hypothesis testing about a contrast of interest. Fig. 3 illustrates the BSMac interface for setting up contrast vectors. BSMac allows the user to define multiple contrasts, which will all be estimated during the subsequent estimation step.

Fig. 3.

Contrast matrix for the second-level analysis of the fBIRN data.

3.3.2. Region selection

The user may select particular anatomical regions to be included in an analysis, based on either the AAL map or the Brodmann map. The number of regions included in an analysis is unlimited. However, the number of regions for which we can estimate between-region correlations is limited to be less than the smallest sample size within any subgroup (Bowman et al., 2008). With an adequate sample size, one may easily include all regions in an analysis and estimate all of the associated between-region correlations, and our experience has shown that the estimation step still proceeds relatively quickly. So one rationale for selecting regions is that one is conducting an analysis based on a relatively small sample of subjects and is interested in the functional connectivity estimates and inferences. Another reason for selecting regions is that substantive interest largely targets particular brain regions. The user may combine up to 4 regions together to constitute a single larger region, if desired.

3.3.3. Parameters

BSMac employs a Bayesian hierarchical parametric structure for statistical modeling. The terminal levels of the modeling hierarchy require the user to specify hyper-prior parameter values, e.g. based on prior knowledge or beliefs or based on the data. We set the default values for these parameters that reflect weakly informative priors. The default parameters are: a₀ = 0.1, b₀ = 0.005, c₀ = 0.1, d₀ = 0.01, e₀ = 0.1 and f₀ = 0.01, and the parameter μ_0gj is obtained as the mean across all voxels in region g and across all subjects. We also set ω = 0.5 by default, reflecting our use of the sample covariance matrix with a 50% reduction in the covariances to construct H_0j. The values for a₀, b₀, c₀, d₀, e₀ and f₀ generate densities that place large probability masses on large variances. The rationale for using these vague priors is to ensure that the information in the data primarily governs the results. The user can set more informative values for these parameters if some additional information about the data is available. Note that the variance parameters were very well estimated in our analyses, and our results were not sensitive to the choice of either diffuse or more informative priors.

3.3.4. Estimation

BSMac uses the Gibbs sampler to perform estimation using MCMC methods. Applying MCMC methods in our context is complicated by the massive amount of data, the vast number of spatial locations, and the large number of parameters. However, the Gibbs-friendly model specification facilitates estimation by providing substantial reductions in computing time and memory. After discarding iterations included in the burn-in period, the computing time and memory can be further reduced with a thinning factor, which retains samples from the joint posterior distribution drawn at the specified interval. The estimation results are saved automatically (into a folder named\results) for further model diagnostics and visualization.

3.3.5. Plots

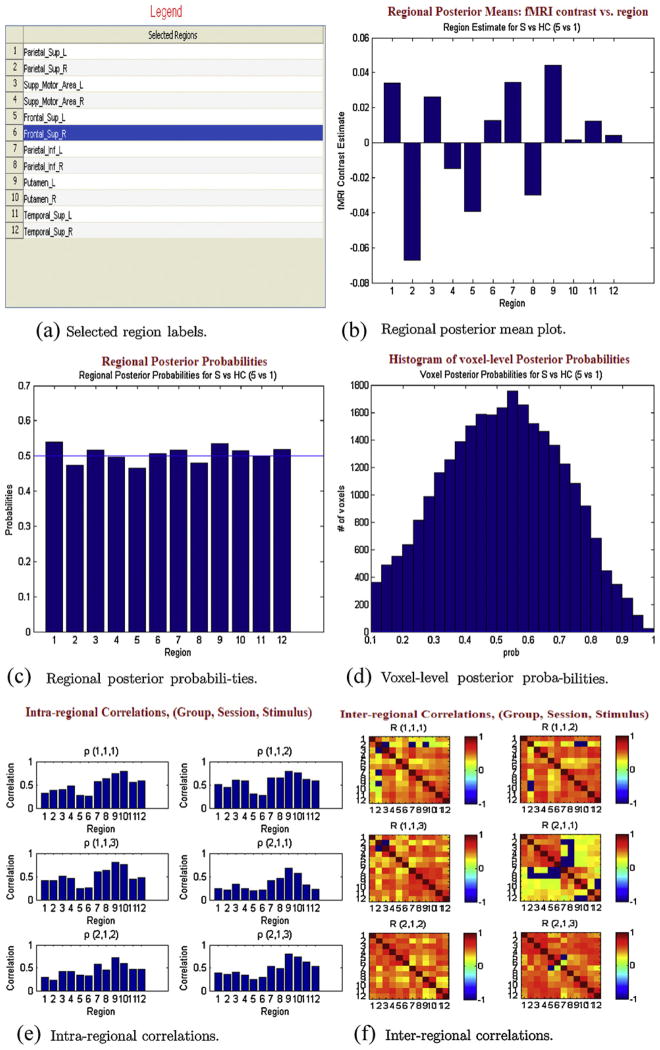
After estimation, BSMac has several graphical tools that can help to summarize the results. The graphical tools yield basic summary plots, dynamic activity maps, and rotating 3D functional connectivity maps. The “Basic summary plots” tab generates several results, either displayed in a web browser (HTML format) or in separate MATLAB figures. First, a legend of the selected regions (Fig. 4(a)) is displayed. A plot of the regional posterior mean estimates is generated (Fig. 4(b)), which shows the contrast estimate in each selected region, and the corresponding regional posterior probabilities appear in Fig. 4(c), e.g. reflecting posterior probabilities of group differences in working-memory related brain activity. A histogram of voxel-level posterior probabilities is also displayed (Fig. 4(d)). Fig. 4(e) shows intra-regional correlations, separately for each unique combination of subgroup, session, and task (e.g. patients/pre-treatment/task 1), and Fig. 4(f) shows the inter-regional correlation matrices, thresholded at 0.1 for ease of visualization. These basic plots convey general information about the results from an analysis. BSMac also generates advanced graphics that provide more anatomically relevant information about the results.

Fig. 4.

Basic summary plots: (a) selected region labels, (b) regional posterior mean plot, (c) regional posterior probabilities, (d) voxel-level posterior probabilities, (e) intra-regional correlations, and (f) inter-regional correlations.

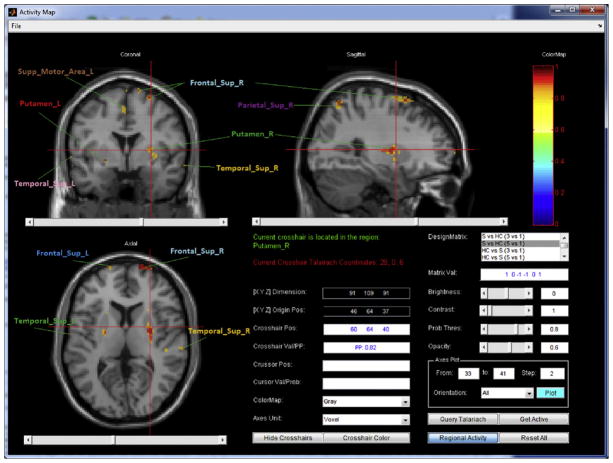
Fig. 5 shows activity maps reflecting probable alterations in localized brain activity. These activity maps display the posterior probabilities (of activation) associated with the selected contrast in axial, sagittal, and coronal views. The lower right area of the frame provides descriptive information, such as the crosshair/cursor position (both the coordinate values and the corresponding neuroanatomic label) and the posterior probability value. The user can set the posterior probability threshold and opacity for visualization. By selecting the “Regional Activity” button, the user can switch the activity map between the regional and the voxel-level results. The user may also display selected slices and orientations in a MATLAB figure window for printing or for further manipulation.

Fig. 5.

Voxel-level activity map. Region labels are obtained from the GUI and then added manually to this figure.

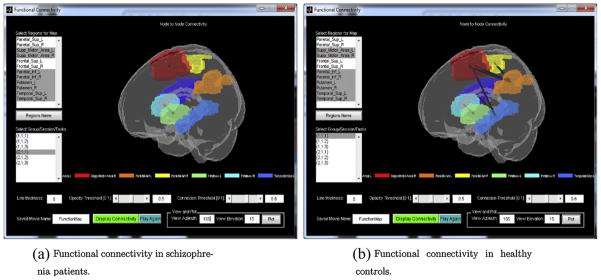
The BSMac toolbox also showcases dynamic 3D plots of inter-regional task-related functional connectivity results. The user can select a subset (or all) of the regions included in the analysis and specify the desired connectivity map for the display (e.g. corresponding to a subgroup, session, and task). The functional connectivity map displays all of the selected regions in a dynamically rotating brain, with lines connecting regions that have (posterior median) correlations exceeding a user-specified threshold. The connected regions have different line thicknesses, depending on the strengths of the functional connections between the regions. Fig. 6 shows the functional connectivity results for selected regions.

Fig. 6.

Functional connectivity: functional connectivity in (a) schizophrenia patients and (b) healthy controls.

3.4. Application to working memory study of schizophrenia

Schizophrenia is a devastating psychiatric disorder, which is associated with significant impairments in working memory (Park and Holzman, 1992). These deficits correlate with findings of abnormal fMRI activation and altered topological properties of complex brain networks (Bassett et al., 2008; Bullmore and Sporns, 2009). In this paper, we use the BSMac toolbox to compare both localized working-memory related neural activity and working memory related functional connectivity between the schizophrenia patients and healthy control subjects. We select 12 AAL regions, shown in Fig. 4(a), with particular interest in brain regions that are relevant to the SIRP task such as the parietal lobes, the superior temporal gyri, and the superior frontal gyri (Buchsbaum et al., 2003; Lynall et al., 2010). We use the default weakly informative prior parameters, i.e. a₀ = 0.1, b₀ = 0.005, c₀ = 0.1, d₀ = 0.01, e₀ = 0.1 and f₀ = 0.01, and the parameter μ_0gj is set to be the mean across all subjects and intra-regional voxels. We are interested in evaluating voxel-level and region-level differences in working memory related brain activity between schizophrenia patients and healthy control subjects. Thus, we define contrast vectors to compare working memory load levels (1 digit, 3 digit, and 5 digit) and then to contrast these working memory related changes between schizophrenia patients and healthy controls. For example, the vector [1 0 –1 –1 0 1] defines a contrast of the 5 digit versus 1 digit for schizophrenia patients relative to healthy controls (see Fig. 3).

Fig. 5 displays the activation map at the voxel level, associated with the selected contrast, with posterior probabilities of activation falling above the threshold of 0.8. There is a high probability that working memory related changes in neural activity are larger for schizophrenia patients than for healthy controls in the right and left putamen, the right and left superior temporal gyrus, the right and left superior frontal gyrus, the right superior parietal region, and the left supplementary motor area. The voxel-level changes shown in Fig. 5 do not extend to region level differences (not shown) in the two subject groups due to the fact that the activations at the voxel level are quite localized. Therefore, extending the inferences to a broader region level results in an apparent mitigation of the effect.

Fig. 6(a) and (b) reveals that the working-memory related connectivity is significantly reduced in the schizophrenic group, relative to the healthy controls, in the supplemental motor area, the parietal cortex, and the superior temporal gyrus. These findings are consistent with prior fMRI reports of reduced functional connectivity in patients with schizophrenia (Bluhm et al., 2007; Lynall et al., 2010). Our analysis also reveals highly coherent neural activity within both the right and the left putamen.

The MCMC runs were investigated in our data analysis to ensure the stability of the results. However, the volume of data prevents formal use of MCMC convergence tools for all model parameters. Instead, trace plots were used to assess convergence to stationarity for region specific univariate parameters, such as σ_gj. Trace plots for voxel specific parameters were investigated by taking a small random sample of voxels. All plots suggest rapid convergence to stationarity.

In cases where the regional activity is not uniform throughout the entire region, the within-region correlation estimate will reflect a certain degree of spatial smoothing. Although α is the same, we have μ_gj(v) to account for the cross subject non-uniform activity. We used data from the schizophrenia study to check empirically the impact of the region sizes on variance estimates and on inter-/intra-regional covariance (results not shown). For these data, the region sizes have little impact on the resulting variance/covariance estimates, with region sizes ranging roughly from 1000 to 4000 voxels. Very small regions may produce small variance estimates, but only if the neural activity in such regions is relatively uniform across voxels.

We conducted sensitivity analyses to examine the robustness of our findings to various specifications of the inverse gamma and inverse Wishart prior parameters. Specifically, we considered hyper-prior settings for the inverse gamma distributions with different combinations of a₀ = {0.1, 0.3, 1, 2.9}, b₀ = {0.005, 0.01, 0.5, 1}, c₀ = {0.1, 1, 2.9}, and d₀ = {0.01, 1, 6.4}. The results remain essentially identical to those obtained when specifying diffuse or weakly informative priors, and the posterior estimates are extremely consistent across these various prior specifications, namely for the posterior median estimates of ${\sigma }_{gj}^2,{\lambda }_{gj}^2$, γ_gg, and ρ_gj as well as the regional posterior mean estimates θ_gj. Correlations calculated from Γ_j are more variable, but still relatively consistent. We also considered various scale matrices H_0j for the inverse Wishart distribution obtained using ω = {0, 0.3, 0.5, 0.7, 1}. Again, the results show that the covariance matrix is very well estimated in our analyses.

4. Summary and discussion

We develop a new open source MATLAB toolbox, BSMac, which implements a spatial Bayesian hierarchical model designed to analyze functional neuroimaging data. This toolbox provides a unified framework to obtain activation inferences as well as functional connectivity inferences, rather than treating these as distinct analytic objectives, and investigates brain activity at both the voxel level and the regional level. The toolbox employs a parametric modeling approach based on a Bayesian paradigm and provides a range of flexible inferences. The Bayesian framework enables the user to formulate probabilistic statements that help to quantify the evidence provided by experimental data. Also, this model can be extended for application to PET data.

Our Bayesian hierarchical model is formulated based on a combination of data characteristics and mathematical convenience stemming from conjugate and conditionally conjugate priors. The normal assumption for β in the likelihood function, and hence for the mean μ, seems reasonable given that our (pseudo) data arise from effects in the Stage I linear model with normally distributed errors. Further, this normal likelihood is a standard assumption in practice for neuroimaging analyses targeting task-related changes in neural activity.

The gamma and Wishart distributions are assumed, in part, due to mathematical/computational convenience. However, these assumptions can lead to poor estimation in some settings (Natarajan and Kass, 2000; Kass and Natarajan, 2006; Gelman, 2006). We feel that the conditions on the assumed gamma priors typically leading to poor performance are unlikely in our setting. We generally have a substantial amount of data for estimating the variance parameters σ_gj and λ_gj. For example, we set a vague prior for σ_gj as the default, i.e. down weighting the impact of the prior, so there is sufficient data to estimate this variance well, with at least 1000 voxels contributing in the schizophrenia study. To avoid potential issues with the inverse Wishart prior in context of a generalized linear mixed model, Kass and Natarajan (2006) propose the use of an empirically based scale matrix that is determined from the first stage variance. Similarly, we set the hyper parameter values for the Wishart prior empirically. We include a covariance shrinkage parameter to adjust the prior beliefs regarding between-region correlations, specifically by optionally shrinking the correlations toward zero. Setting this shrinkage parameter (ω) to one in our framework produces a similar format to that proposed by Kass and Natarajan (2006), with our slight extension of accommodating heterogeneity across brain regions.

Our approach differs from methods that target standard interpretations of functional connectivity by calculating correlations directly from the BOLD time series or their spectral representations (Fiecas et al., 2010; Sun et al., 2004). It also differs from methods that seek to describe the directional influence that one brain region exerts on another, such as dynamic causal modeling (Friston, 2011) and structural equation modeling (McIntosh and Gonzales-Lima, 1994). Our Bayesian hierarchical model captures information regarding nondirectional paradigm-related FC both within and between pre-defined brain regions. The task-related FC broadly describes both long- and short-range spatial correlations between task-specific estimates of Stage I BOLD effects rather than directly measuring neuronal level associations. Through the Bayesian hierarchical model, our approach enables us to draw statistical inferences to examine differential task-related functional connectivity between sub-groups. By pursuing objectives of activation studies in a framework that accounts for task-related functional connectivity, our proposed method is complementary to these previous works.

We applied the BSMac toolbox to data from an fMRI study of neural correlates of a working memory task, the SIRP, in patients with schizophrenia and healthy control subjects. Despite the apparent complexity and rather rich formulation of our Bayesian hierarchical model as well as the high throughput nature of the data, computations for estimation are quite fast. It took around 23 min to run 6000 iterations for our 28 subjects on our PC with 2.4 GHz CPU and 2 GB memory.

The results from our analysis are consistent with prior findings based on different metrics, such as those based on graph theory (Bullmore and Sporns, 2009), functional disconnectivity (Bluhm et al., 2007; Meyer-Lindenberg and Weinberger, 2006), and functional hierarchy (Bassett et al., 2008). For example, our analysis revealed significant alterations in functional connectivity in the schizophrenia subgroup, which seems to correspond with previous observations of less efficient wiring in patients with schizophrenia (Bluhm et al., 2007; Catani and Mesulam, 2008). Specifically, our findings were consistent with recent studies that demonstrate altered functional connectivity in brain areas subserving working memory in patients with schizophrenia compared to healthy controls (Henseler et al., 2010; Meyer-Lindenberg et al., 2001; Perlstein et al., 2001; Walter et al., 2001).

Voxel-level subgroup differences in neural activity were seen at various loci. Numerous functional neuroimaging studies have demonstrated diminished activity in the frontal cortex in patients with schizophrenia compared to healthy controls (Barch et al., 2003; Cannon et al., 2005; Carter et al., 1998; Ragland et al., 1998). However, functional imaging studies of working memory in schizophrenia have also produced divergent findings of frontal cortical hyper-activation (Callicott et al., 2000; Manoach et al., 2000), suggesting a more complex relationship between brain activation and functional deficits in schizophrenia (Callicott et al., 2003; Glahn et al., 2005; Karlsgodt et al., 2009). This highlights the advantage of the growing trend to explore functional connectivity in addition to focusing on region-specific variability in activation.

Evidence of a functional relationship between connectivity strength and working memory performance suggests that functional connectivity may be an important neural correlate of the working memory deficit seen in schizophrenia (Henseler et al., 2010). Functional connectivity patterns in specific domains of executive functioning including working memory may represent novel endophenotypes for studying the pathophysiology of schizophrenia.

The tools available in the BSMac software have been developed to input data from commonly used neuroimaging formats, to perform spatial analysis of activation and functional connectivity parameters, and for visualization. These functions have been integrated into a simple and user-friendly GUI environment. This toolbox can be freely downloaded from http://www.sph.emory.edu/bios/CBIS under the GNU general public license. MATLAB literate researchers are also able to modify the code if desired.

Appendix A. Full conditional model

Using the definition in Section 2.2, and Eq. (2) for the Bayesian hierarchical model, we obtain:

$$\begin{array}{l}{\mathbf{D}}_j^{-1}=\mathit{diag}(V_1{\sigma }_{1j}^{-2},\dots ,V_G{\sigma }_{Gj}^{-2}),{\overline{\mathit{\beta }}}_{gj}=\frac{1}{K_j}\sum _{i=1}^{K_j}{\mathit{\beta }}_{\mathit{igj}},\\ {\overline{\mathit{\beta }}}_{ij}=\frac{1}{V_g}\sum _{v=1}^{V_g}{\mathit{\beta }}_{\mathit{igj}}(v),{\overline{\mathit{\mu }}}_j=({\overline{\mu }}_{1j},\dots ,{\overline{\mu }}_{Gj}),\\ {\overline{\mathit{\eta }}}_{jq}=({\overline{\eta }}_{1jq},\dots ,{\overline{\eta }}_{\mathit{Gjq}}),{\overline{\mu }}_{gj}=\frac{1}{V_g}\sum _{v=1}^{V_g}{\mu }_{gj}(v),\\ \mathit{and}{u}_{\mathit{igj}}^2={\left({\mathit{\beta }}_{\mathit{igj}}-{\mathit{\mu }}_{gj}-\mathbf{1}{\alpha }_{\mathit{igj}}-\sum _{q=1}^Q{\mathit{\eta }}_{\mathit{gjq}}{x}_{iq}\right)}^{\prime }\\ \left({\mathit{\beta }}_{\mathit{igj}}-{\mathit{\mu }}_{gj}-\mathbf{1}{\alpha }_{\mathit{igj}}-\sum _{q=1}^Q{\mathit{\eta }}_{\mathit{gjq}}{x}_{iq}\right).\end{array}$$

The full conditionals are given by:

$$\begin{array}{l}{\mathit{\mu }}_{gj}~\text{MVN}\left({\mathit{\Omega }}_{gj}\left\{{\lambda }_{gj}^{-2}{\mu }_{0gj}\mathbf{1}+K_j{\sigma }_{gj}^{-2}\left({\overline{\mathit{\beta }}}_{gj}-\mathbf{1}{\overline{\alpha }}_{gj}-\frac{1}{K_j}\sum _{i=1}^{K_j}\sum _{q=1}^Q{\eta }_{\mathit{gjq}}{x}_{iq}\right)\right\},{\mathit{\Omega }}_{gj}\right)\\ {\mathit{\eta }}_{\mathit{gjq}}~\text{MVN}\left({\mathit{\Phi }}_{\mathit{gjq}}\left\{{\sigma }_{gj}^{-2}\sum _{i=1}^{K_j}{x}_{iq}\left({\mathit{\beta }}_{\mathit{gji}}-{\mathit{\mu }}_{gj}-\mathbf{1}{\alpha }_{\mathit{igj}}-\sum _{q^{\prime }\ne q}^Q{\mathit{\eta }}_{gj{q}^{\prime }}{x}_{i{q}^{\prime }}\right)\right\},{\mathit{\Phi }}_{\mathit{gjq}}\right)\\ {\sigma }_{gj}^{-2}~\text{Gamma}\left\{a_0+\frac{K_j{V}_g}{2},{\left(\frac{1}{b_0}+\frac{1}{2}\sum _{i=1}^{K_j}{\mu }_{\mathit{igj}}^2\right)}^{-1}\right\}\\ {\mathit{\alpha }}_{ij}~\text{MVN}\left({\mathit{\Psi }}_j\left\{{\mathbf{D}}_j^{-1}\left({\overline{\mathit{\beta }}}_{ij}-\overline{{\mathit{\mu }}_j}-\sum _{q=1}^Q{\overline{\mathit{\eta }}}_{jq}{x}_{iq}\right)\right\},{\mathit{\Psi }}_j\right)\\ {\tau }_{\mathit{gjq}}^{-2}~\text{Gamma}\left\{e_{0q}+\frac{V_g}{2},{\left(\frac{1}{f_{0q}}+\frac{1}{2}\sum _{i=1}^{K_j}{\mathit{\eta }}_{\mathit{gjq}}{\mathit{\eta }}_{\mathit{gjq}}^{\prime }\right)}^{-1}\right\}\\ {\lambda }_{gj}^{-2}~\text{Gamma}\left\{c_0+\frac{V_g}{2},{\left(\frac{1}{d_0}+\frac{{({\mathit{\mu }}_{gj}-\mathbf{1}{\mu }_{0gj})}^{\prime }({\mathit{\mu }}_{gj}-\mathbf{1}{\mu }_{0gj})}{2}\right)}^{-1}\right\}\\ {\mathit{\Gamma }}_j^{-1}~\text{Wishart}\left\{{\left(h_0{\mathbf{H}}_0+\sum _{i=1}^{K_j}{\mathit{\alpha }}_{ij}{\mathit{\alpha }}_{ij}^{\prime }\right)}^{-1},h_0+K_j\right\}\end{array}$$ (6)

where we denoted ${\mathit{\Omega }}_{gj}={({\lambda }_{gj}^{-2}+K_j{\sigma }_{gj}^{-2})}^{-1}\mathbf{I},{\mathit{\Phi }}_{\mathit{gjq}}={({\tau }_{\mathit{gjq}}^{-2}+{{\sigma }_{gj}}^{-2}{\sum }_{i=1}^{K_j}{x_{iq}}^2)}^{-1}\mathbf{I}$, and ${\mathit{\Psi }}_j={({\mathit{\Gamma }}_j^{-1}+{\mathbf{D}}_j^{-1})}^{-1}$. For simplicity, we omitted the notation for conditional variables.