Novel metrics for evaluating improvement in discrimination: net reclassification and integrated discrimination improvement for normal variables and nested models

Summary

Net reclassification and integrated discrimination improvements have been proposed as alternatives to the increase in the AUC for evaluating improvement in the performance of risk assessment algorithms introduced by the addition of new phenotypic or genetic markers. In this paper, we demonstrate that in the setting of linear discriminant analysis, under the assumptions of multivariate normality, all three measures can be presented as functions of the squared Mahalanobis distance. This relationship affords an interpretation of the magnitude of these measures in the familiar language of effect size for uncorrelated variables. Furthermore, it allows us to conclude that net reclassification improvement can be viewed as a universal measure of effect size. Our theoretical developments are illustrated with an example based on the Framingham Heart Study risk assessment model for high risk men in primary prevention of cardiovascular disease.

Introduction

In the last several decades statistical models for binary or time-to-event outcomes have become essential tools in the quantification of risk. Their applications span numerous areas ranging from medicine (risk for adverse health outcomes) to finance (risk for default). Statistical techniques of choice evolved from discriminant analysis [1] to logistic regression [2] and survival analysis [3]. Rapid scientific progress in genetics and biochemistry has led to the proposal of numerous new variables as candidates to improve risk models. For example, the debate about the usefulness of C-reactive protein as predictor of cardiovascular disease is ongoing [4].

But before we can ascertain the usefulness any given additional variable may provide a risk prediction model, we need to define what we mean by “useful”. It is obvious we cannot rely merely on statistical significance-- since our interest lies in the variable’s added explanatory power. Thus we must ask whether the addition of the new variable improves the model at hand. This, in turn, requires us to establish some criteria for the determination of said improvement. One fundamental criterion expected from a “good” risk model is the assignment of higher probabilities for developing the event to those who actually develop events than to those who do not. This property is termed discrimination and historically quantified using the probability that given two randomly selected subjects, the subject with the event has a higher model-based probability of that event than the subject without the event. The key finding which led to the overwhelming popularity of this metric for models with binary outcomes was its equality to the area under the receiver operating characteristic (ROC) curve (AUC), a plot of the sensitivity vs. 1–specificity for all possible cut-offs [5]. More recently, several authors proposed extensions of the AUC to survival data [6-11] and Hand [12] introduced a modification of the AUC that allows for more flexible and objective weights for different misdiagnoses.

In recent years, several authors have criticized the pervasive reliance on the AUC, or its empirical estimator, often called the c-statistic, as the main measure of improvement in explanatory power in the field of risk assessment. The main objections stemmed from the observation that once the AUC reaches a certain level, it requires unrealistically large effect sizes from new variables to lead to any noticeable increase [13-17] when employing standard methods of model development and comparison, and, on a more conceptual level, that the ROC plot and its area are not the most intuitive measures in the field of risk assessment, the main focus in this field being on model-based event probabilities [18, 19].

In response to the above criticism, new measures of improvement in model performance have been developed. Cook et al. [15], Pencina and D’Agostino et al. [16] and Janes et al. [18] discussed the difficulties quantifying model improvement in the cases where meaningful risk cut-offs influence treatment decisions. Vickers et al. [20], Baker et al. [21] and Gail et al. [22] took the problem one step further, introducing utilities associated with correct and incorrect decisions related to patient management, based on risk assessment models.

However, any measures that rely on categories or utilities are only as good as the categories or utilities selected. For example, a probability cut-off of 0.20 is used to categorize patients as high-risk for coronary heart disease (defined as myocardial infarction and coronary death). However, the same cut-off is often used for a broader condition of cardiovascular disease which includes not only coronary events but also strokes and heart failure. As a result, the feasibility for comparison of effects across different studies and cohorts are limited. We believe that this more subjective, cut-off-based assessment, while necessary and valuable, should take place at a later stage in the model development process. Our focus is on immediate measures which will quantify the promise that the variable(s) offers, irrespective of the existence of meaningful risk categories or utilities.

With the objective narrowed in this manner, we focus on three measures of improvement in model performance: an increase in the AUC, the integrated discrimination improvement (IDI) and the continuous version of the net reclassification improvement (NRI). We briefly introduced the AUC in the paragraph above. The other two measures have been proposed by Pencina and D’Agostino et al. [16] as alternatives. The IDI can be defined as the difference in discrimination slopes between two models-- one with, and the other without, the added variable. Discrimination slope was first introduced by Yates [23] and D’Agostino et al. [24] suggested as a “useful performance measure for it quantifies in a simple manner the separation of positive and negative outcomes”. Recently Tjur [19] supported this argument calling it “a highly recommendable” measure of explanatory power for binary outcome models. It is defined as a difference in the means of the model-based event probabilities, that is, a subtraction of the nonevents from the events. D’Agostino et al. [24] suggested and Tjur [19] formally proved that it is closely related to the binary model coefficients of determination, the R-square, regardless which definition of the latter one has adopted (see Hu et al. [25] for a review of different definitions of the R-square in the context of binary outcome models). Furthermore, Tjur [19] showed that it can be viewed as the most natural way to summarize a plot of the empirical distributions of the model-based probabilities, displayed separately for events and nonevents. This plot offers a more relevant presentation than the ROC curve for risk estimation.

The continuous NRI generalizes a summary measure proposed for reclassification tables [26] by eliminating risk categories and calling any increase in model-based probability resulting from the addition of a new marker upward reclassification and any decrease a downward reclassification. The continuous NRI index is equal to twice the difference in the probabilities of upward reclassification for the events minus the nonevents. Naturally, if the new variable is useful, it should increase the model-based probabilities for events and decrease the model-based probabilities for nonevents, leading to a higher discrimination slope and IDI as well as a higher NRI.

One practical advantage the AUC enjoys lies in the familiarity of its scale. The value of 0.7 seems to be a common cut-off between acceptable and poor models. However, the interpretation of an increase in the AUC remains vague with statistical testing and p-values inserted in the place of conclusions regarding magnitude. This is unreasonable, as this measure is concerned with strength of effect and not with significance of association, which hopefully has been established beforehand— that is, when the variable was initially added to the model. By analogy, few statisticians would argue an increase in a linear model’s R-square is fully captured by the p-value associated with this increase. For the discrimination slope, IDI and NRI, the matter may be even more complicated; the magnitudes of these carry little familiarity, even though the slope has an intuitive interpretation. Nevertheless, it has been argued that magnitude of the slope might be one of its main limitations, as it is well known that models considered to be “good” based on the AUC tend to have slopes in the 0.1 to 0.2 range, far from the maximum of 1.0.

In this paper we attempt to give meaning and interpretation to changes in the AUC, discrimination slope and NRI. We have used a simple case where normal predictors satisfy the assumption of linear discriminant analysis (LDA) [1]. Mentioned earlier, LDA serves as a tool for risk assessment models, and despite its somewhat restrictive assumptions, it possesses several features that aid a straight-forward interpretation. In particular, the concept of a squared Mahalanobis distance [27] used by LDA as a multivariate measure of separation between points, reduces to a sum of squared effect sizes when there is no correlation between predictors. Hence an ‘x’ increase in the squared Mahalanobis distance corresponds to the addition of a new, uncorrelated variable with the effect size ‘square root of x’. When we combine this property with the relationships between the squared Mahalanobis distance and the three measures of interest, which are the focus of this paper, we see how appropriate intuition about the magnitude of increase in the AUC, IDI and NRI can be developed. Furthermore, the relationships between the squared Mahalanobis distance and the three measures show how they are connected under the LDA assumptions and allow us to investigate the degree to which improvement in model performance (being incurred by the addition a new variable) depends on the performance of the baseline model (without the new variable).

2. Increase in AUC, IDI and NRI as functions of squared Mahalanobis distance

Let X be a vector of p + q normal predictors and let D be an event indicator (1 for the events, 0 for the nonevents). Assume: X | D=1 ~ N(μ₁,∑₁) and X | D=0 ~ N(μ₀,∑₀), where μ₁,μ₀ are the vectors of means and ∑₁,∑₀ are the variance-covariance matrices. N denotes the normal distribution. Consistent with assumptions of linear discriminant analysis, let ∑ = ∑₁ = ∑₀ be the pooled variance-covariance matrix equal to the variance-covariance matrices of the two sub-groups. (The results that follow are easily generalized to proportional variance-covariance matrices; in the Appendix we show their form for both unequal and non-proportional matrices.) Let ∑⁻¹ denote its inverse. Because we are concerned with concepts, rather than exact relationships and inference, the developments presented below do not account for the uncertainties due to estimation; the approach outlined by Su and Liu [28] could be used to extend them.

Furthermore, let δ = μ₁ – μ₀ denote the vector of the mean difference between the events and nonevents which can be decomposed as $\delta =\left(\begin{array}{c}\hfill {\delta }_1\hfill \\ \hfill {\delta }_2\hfill \end{array}\right)$ for the first p (δ₁) and last q (δ₂) variables. Let a = ∑⁻¹ ·δ be a solution to the linear discriminant analysis problem with p + q variables and $b={\Sigma }_{11}^{-1}\cdot {\delta }_1$ as the corresponding solution for the first p variables, where ${\Sigma }_{11}^{-1}$ is the inverse of the variance-covariance matrix for the first p predictors. Define $M_{p+q}^2={\delta }^T\cdot {\Sigma }^{-1^T}\cdot \delta$ and $M_p^2={\delta }_1^T\cdot {\Sigma }_{11}^{-1^T}\cdot {\delta }_1$ the Mahalanobis distances for cases of p + q and p variables, respectively. Denote by $L_{p+q}^{\ast }\left(X\right)=a^{T}X-\frac{1}{2}{a}^T({\mu }_1+{\mu }_0)$ the linear discriminant analysis classification function based on all p + q variables. The corresponding function for the first p variables can be written $L_p^{\ast }\left(X\right)=b^{T}X-\frac{1}{2}{b}^T({\mu }_1+{\mu }_0)$. The predicted probability of an event based on p+q predictors is given as $p_{p+q}\left(X\right)=\frac{1}{1+r\cdot e^{-L_{p+q}^{\ast }\left(X\right)}}$, where r is the incidence or prevalence ratio of nonevents to events. The following 3 definitions describe the 3 measures of improvement in model performance.

1. Increase in AUC:

   $$\Delta \mathit{AUC}=\mathit{pr}\left(p_{p+q}\right(X\mid D=1)>p_{p+q}(X\mid D=0\left)\right)-\mathit{pr}\left(p_p\right(X\mid D=1)>p_p(X\mid D=0\left)\right)$$ (1)
2. IDI (difference of discrimination slopes):

   $$\begin{array}{cc}\hfill \mathit{IDI}& =\left\{E\right(p_{p+q}(X\mid D=1))-E(p_{p+q}(X\mid D=0)\left)\right\}-\left\{E\right(p_p(X\mid D=1))-E(p_p(X\mid D=0)\left)\right\}\hfill \\ \hfill & =E(\frac{1}{1+r\cdot e^{-L_{p+q}^{\ast }(X\mid D=1)}}-\frac{1}{1+r\cdot e^{-L_{p+q}^{\ast }(X\mid D=0)}})-E(\frac{1}{1+r\cdot e^{-L_p^{\ast }(X\mid D=1)}}-\frac{1}{1+r.e^{-L_p^{\ast }(X\mid D=0)}})\hfill \end{array}$$ (2)
3. Continuous NRI:

   $$\frac{1}{2}\mathit{NRI}=\mathit{pr}\left(p_{p+q}\right(X\mid D=1)>p_p(X\mid D=1\left)\right)-\mathit{pr}\left(p_{p+q}\right(X\mid D=0)>p_p(X\mid D=0\left)\right)$$ (3)

We observe interesting resemblances between the ΔAUC and IDI as well as ΔAUC and NRI. The first is demonstrated by the AUC’s calculation of the probability that the difference in model-based risks for events and nonevents is positive, as the slope similarly computes the expectation of this difference. On the other hand, the ΔAUC and NRI use the same building blocks but place them in a different order: ΔAUC involves the difference of the probabilities calculated between events and nonevents but within models, whereas NRI focuses on the difference of the probabilities between models but within the events and nonevents. NRI can be interpreted as a difference in the probabilities of increasing model-based risks between the events and the nonevents.

Of note, these definitions and observed similarities hold in general cases, without any recourse to linear discriminant analysis. Employing the LDA assumptions above, we make the following three Propositions:

$$\Delta \mathit{AUC}=\Phi \left(\sqrt{\frac{M_{p+q}^2}{2}}\right)-\Phi \left(\sqrt{\frac{M_p^2}{2}}\right)$$ (4)

$$\begin{array}{cc}\hfill & \mathit{IDI}={\int }_{-\infty }^{\infty }\frac{1}{\sqrt{2\cdot \pi \cdot M_{p+q}^2}}\exp \left(\frac{{-(x-0.5\cdot M_{p+q}^2)}^2}{2\cdot M_{p+q}^2}\right)\cdot (\frac{1}{1+r\cdot \exp (-x)}-\frac{1}{1+r\cdot \exp \left(x\right)})\cdot \mathit{dx}\hfill \\ \hfill & -{\int }_{-\infty }^{\infty }\frac{1}{\sqrt{2\cdot \pi \cdot M_p^2}}\exp (\frac{{-(x-0.5\cdot M_p^2)}^2}{2\cdot M_p^2}\cdot (\frac{1}{1+r\cdot \exp (-x)}-\frac{1}{1+r\cdot \exp \left(x\right)})\cdot \mathit{dx}\hfill \end{array}$$ (5)

$$\frac{1}{2}\mathit{NRI}=\Phi (\frac{\sqrt{M_{p+q}^2-M_p^2}}{2}-\Phi (\frac{-\sqrt{M_{p+q}^2-M_p^2}}{2})=2\cdot \Phi (\frac{\sqrt{M_{p+q}^2-M_p^2}}{2})-1$$ (6)

The proof of the first proposition can be found in [28]. The second relationship relies on the normality of $L_{p+q}^{\ast }(X\mid D=1),L_{p+q}^{\ast }(X\mid D=0),L_p^{\ast }(X\mid D=1),L_p^{\ast }(X\mid D=0)$ and the definition of expected value. We note that the integrals in 2 do not have a closed form solution and numerical integration is necessary. The proof of proposition 3 is new and presented in the Appendix, where we additionally extend it to both unequal and non-proportional variance-covariance matrices (Proposition 4).

The 3 propositions above lead to the following conclusions about our performance metrics of interest for LDA:

1. All 3 measures quantifying improvement in a model’s performance are functions of the Mahalanobis distances of models with p+q and p variables. Thus, they indeed measure the improvement in discrimination, or in other words, the degree to which an added variable helped increase the separation between the predictions of events and nonevents.

2. All 3 measures are bounded from above, reaching their respective maxima when the baseline model has no discriminatory power (that is, when the Mahalanobis distance approaches zero) and the new model has great discriminatory power (as the Mahalanobis distance approaches infinity). These maxima are 0.5 for ΔAUC and 1 for the IDI and NRI. The result for the IDI is empirical.

3. The NRI and ΔAUC rely only on Mahalanobis distances. Thus these two measures are not influenced by the prevalence/incidences of the event of interest and therefore may be compared across studies reporting differing event rates. Meaningful reference can be presented regardless of the event rates.

4. The IDI depends on the incidence/prevalence ratio of the nonevents to events, r, and thus remains study-specific and cannot be compared across studies with different event rates. Meaningful reference ranges for discrimination slopes and IDI have to be event rate-specific. Furthermore, the loss of calibration introduced by the application to a validation cohort might render this measure problematic if event rates differ.

5. The NRI is the only measure of the three that is a function of the difference in the Mahalanobis distances. Thus, the improvement it quantifies does not directly depend on the performance of the baseline model-- but solely on the characteristics of the new variable – its effect size and correlation with other predictors (this still might introduce an indirect relationship with the baseline model – the better the baseline model, the more variables it may contain and the greater the chances for correlation with the new variable, which would reduce the increase in the Mahalanobis distance).

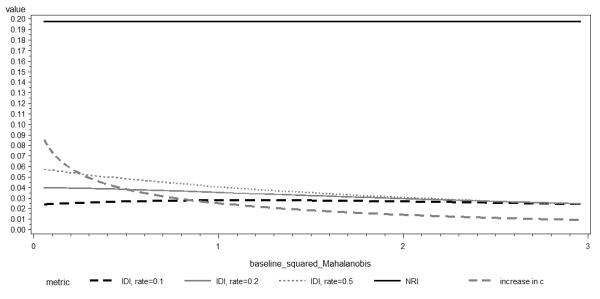
6. On the contrary, the ΔAUC and IDI depend directly on the performance of the baseline model. As the normal cdf asymptotically approaches 1, it is clear that a fixed improvement in squared the Mahalanobis distance translates into decreasing improvements in the ΔAUC as functions of the baseline models’ AUCs. The shape of this relationship for the IDI depends on the event rate as illustrated in Figure 1 for different choices of the event rate. It is (generally) more constant than the difference of AUCs. For both metrics, however, this dependence on the baseline model can lead to opposite conclusions about the same marker added to the same model, in two different settings. It is known that performance of the baseline model is a function of variability in the predictors. Hence if one group assesses their new marker on a sample with limited baseline age distribution and the other on a sample with broad baseline age distribution, the former is likely to conclude the new marker offers meaningful improvement whereas the latter may not make an identical conclusion. This suggests that NRI may be a preferable measure of incremental usefulness in this context.

   In addition, the following 3 Corollaries hold:

Figure 1.

Denoting LDA coefficients for the new q predictors added to a model with p predictors by a_p+1,a_p+2,…,a_p+q and assuming normality of all predictors, the following equivalence holds:

$$\Delta \mathit{AUC}=0\iff a_{p+1}=0,a_{p+2}=0,\dots ,a_{p+q}=0$$ (7)

$$\mathit{IDI}=0\iff a_{p+1}=0,a_{p+2}=0,\dots ,a_{p+q}=0$$ (8)

$$\mathit{NRI}=0\iff a_{p+1}=0,a_{p+2}=0,\dots ,a_{p+q}=0$$ (9)

Note that we do not require equality or proportionality of the variance-covariance matrices in the event and non-event groups for this proposition to hold.

Corollary 1 has been proven by Demler et al. [29] and relies on Proposition 1 (or its more general version given by Su and Liu [28]) and the fact that if the Mahalanobis $M_{p+q}^2$ based on p+q variables and $M_{p+q}^2$ based on the first p variables are equal, then the additional discriminant coefficients a_p+1,a_p+2,…,a_p+q must all be zero. The proof of Corollary 2 has been given by Pepe et al. [30] in a more general case, which does not require the assumptions of LDA. Proof of Corollary 3 mirrors that of Demler et al. [29] but uses Proposition 3 or Proposition 4 given in the Appendix instead of Proposition 1.

These three corollaries provide further justification against hypothesis testing for model performance metrics. Under sufficiently strong assumptions, it is shown that statistical significance of model improvement is the same as statistical significance of coefficients.

As recently pointed out by Hand [12], the AUC and hence the ΔAUC contain implicit weighting for the misclassification of events vs. nonevents. Since the NRI is composed of two pieces, one for events and one for nonevents— and the IDI as given in Definition 2 can be re-arranged to have a similar representation, we also have the option (or problem), with these two measures, to employ differential weights that could be applied to any event vs. event and any nonevent vs. nonevent comparisons. In the definitions introduced in this paper we proposed 1:1 weights for the event and nonevent pieces. This should not be misinterpreted as implying equal importance being given to increases in model-based probabilities for the events and decreases for the nonevents. This is only the case when the incidence or prevalence is 50%. When there are fewer events than nonevents, the improvement achieved for the events is weighted more highly, with the weight increasing as the proportion of events decreases (cf. [31]). This weighting is consistent with the weighting introduced by Youden’s index [32] and provides a simple option when no costs or utilities are available. It should be noted that the goal of the metrics we describe is to give researchers the “first impression” of the potential that their improved model might have and not to provide tools for a formal cost-benefit analysis. Nevertheless, if costs or utilities exist, they could be built into the NRI or IDI as weights [26].

3. Practical example

The Framingham Heart Study’s risk prediction functions are key tools for cardiovascular risk assessment and prevention. They were originally developed using discriminant analysis but more recently the use of logistic regression or proportional hazards modeling has become more popular. The most recent Framingham paper on the topic [33] focused on prediction of broadly defined cardiovascular disease (CVD) in people free of the condition at baseline and followed for 10 years. Separate models were developed for women and men and risk factors included baseline age, systolic blood pressure (SBP), total and HDL cholesterol and accounted for diabetes and smoking status. They also proposed another, simplified model which did not include lipids— and demonstrated only a small decrease in the AUC when compared to the full model. Simplification of risk prediction algorithms is an area of current focus in the field of CVD prevention, primarily because simpler models which do not require blood draws may be applied in a home setting or in countries where obtaining markers is prohibitively expensive or impossible. As an illustration of our developments we took a subset of data used by D’Agostino et al. [33] consisting of 1369 high risk men with either prevalent diabetes, smokers or treated with antihypertensive medications. We then compared two separate risk prediction tools: the first, based only on age and SBP, while the other additionally included total and HDL cholesterol. Normalizing Box and Cox [34] transformations were applied to these 4 predictors before employing linear discriminant analysis with the outcome defined as occurrence of CVD in 10 years. Full follow-up was available on the majority of participants; for simplicity we assumed that those who discontinued prematurely did not develop CVD in 10 years, resulting in an event incidence of 0.244. Of note, simplifications of this kind are not necessary in real applications as survival analysis equivalents exist for all three: the ΔAUC, the IDI and the NRI [9, 11, 26]. Poolability of covariance matrices was tested using a chi-square test proposed by Morrison [35] and could not be rejected for either model. For comparison, logistic regression models were fit as well, on the untransformed predictors. The goal was to assess the improvement in model-based predictions between the simpler model which included only baseline age and SBP and the larger model which added total and HDL cholesterol. We considered three ways of estimating: the ΔAUC, the IDI and the NRI:

1. Formula-based method estimated squared Mahalanobis distances from the sample and applied formulas given in propositions 1-3.

2. The Empirical Discriminant approach employed LDA on Box-Cox transformed predictors to obtain the probabilities of the event which were used to calculate the three measures of interest using empirical estimators given in [16].

3. The Empirical Logistic approach employed logistic regression models with untransformed predictors to obtain the probabilities of the event which were used to calculate the three measures of interest using empirical estimators given in [16].

We stress again that the developments presented in this paper are purely theoretical and are meant to provide a conceptual framework for the new performance metrics. In particular, they are not intended to provide new estimators for the NRI and the IDI, alternative to the ones presented by Pencina, D’Agostino et al. [16]. Thus even though the “formula-based” approach uses results from propositions 1-3, these are presented to illustrate the concepts and not recommended as alternatives to the empirical estimators. Focusing on the aim of our example we did not cross-validate our results, even though we strongly recommend it in all practical applications.

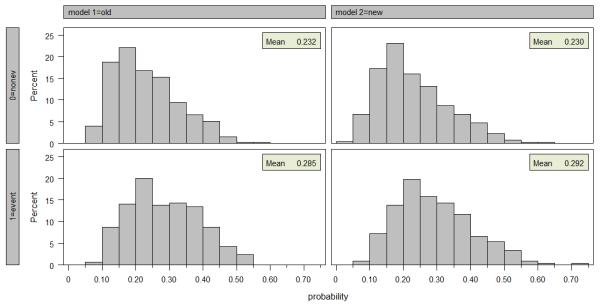
The results are summarized in Figure 2 and Table 1. The figure presents parallel histograms suggested by Tjur [19] for both the baseline and the full models. Ideally, we would see a clear separation between the model-based predicted probabilities: for the nonevents, the probability mass would be concentrated on the left of the graph, and for the events, on the right. Here we see some shift of the probability mass to the right going from the nonevent histogram to the event histogram. The shift is slightly improved for the new model, but we see in both models events occurring in people with low model-based probabilities and a substantial fraction of people with high probabilities do not experience events. This suggests further potential for model improvement. Our visual conclusion of a weak performance by the old model and the rather unimpressive improvement offered by the total and HDL cholesterols is further supported by the results in Table 1. The AUC improves from 0.65 to 0.66 with neither the original value nor the level of improvement being satisfactory. The ½ NRI falls between 0.10 and 0.11, depending on the method used. To gain better insight into the magnitude of the observed improvement, we apply proposition 3 to express quantities based on the predicted probabilities in terms of the corresponding effect sizes. We first translate ½ NRI into the increase in the squared Mahalanobis distance, assuming multivariate normality and employing the known LDA coefficients to obtain 0.063 to 0.074. In this data, the squared Mahalanobis distance can be estimated directly and yields 0.062. If the correlations of the new markers with those in the old model were zero, this would translate into an effect size of 0.25-0.27. Using effect size ranges introduced by Cohen [36], this would be categorized as small. For comparison, under the same assumptions, a medium effect size of 0.50 (a squared Mahalanobis distance of 0.25) would result in ½ NRI of about 0.20 and a large effect size of 0.80 (a squared Mahalanobis distance of 0.64) would yield ½ NRI of 0.31. The corresponding increases in the AUC from 0.65 in the baseline 2 model would be 0.70 and 0.75 for medium and large effect sizes, respectively. However, if the baseline AUC started at 0.80, the medium effect size marker would increase it only to 0.82 and the large effect size marker to 0.84. The ½ NRI s would remain at 0.20 and 0.31. In our example, the discrimination slope increased from 0.053 to 0.063, yielding an IDI = 0.010. Keeping the above assumptions and the event rate observed in our sample (0.244), the medium effect size marker would increase the slope of 0.053 to 0.097 yielding an IDI = 0.044 and the large effect size marker would produce an increase in slope to 0.160 with an absolute IDI = 0.107. Given the original model strength’s correspondence to a squared Mahalanobis distance of 0.29, which further corresponds to a medium effect size of 0.53, the relative doubling and tripling of the discrimination slope resulting from the addition of medium and large effect size markers seems reasonable. If we started with a better baseline model corresponding to an AUC of 0.80, we would have a slope of 0.228, much higher than the 0.053 observed in our case. Of interest, an AUC of 0.80 requires a very large effect size of 1.18. The addition of medium and large effect size markers would increase the slope to 0.263 (with an absolute IDI 0.035) and 0.312 (with an absolute IDI 0.084). Thus the IDI is attenuated, but not nearly as substantially as the increase in the AUC.

Figure 2.

Table 1.

Improvement in CVD risk prediction model after adding total and HDL cholesterol

Measure	Formula-based	Empirical discriminant	Empirical logistic
Mp2	0.295	0.289*	0.285*
Mp+q2	0.357	0.363*	0.345*
ΔM2	0.062	0.063**	0.074**
AUCp	0.649	0.648	0.647
AUCp+q	0.664	0.665	0.661
ΔAUC	0.014	0.017	0.014
slopep	0.053	0.053	0.051
slopep+q	0.063	0.063	0.060
IDI	0.010	0.010	0.009
P(up|D=1)	0.550	0.570	0.612
P(up|D=0)	0.450	0.470	0.504
½NRI	0.099	0.100	0.108

Formula-based refers to sample estimator for squared Mahalanobis distance used in place of M² in propositions 1, 2 and 3

Empirical discriminant refers to quantities calculated based on estimated probabilities from linear discriminant model

Empirical logistic refers to quantities calculated based on estimated probabilities from logistic regression model

^*based on inverting AUC (Proposition 1)

^**based on inverting NRI (Proposition 3)

4. Extensions to non-normal variables

Our presentation focused exclusively on normal variables. While continuous predictors can often be normalized, rendering our developments applicable, there is no reason to believe that any of our results extend to binary or categorical risk factors. On the contrary, it is possible to construct examples in which a binary risk factor with a low prevalence may have a very high relative risk but lead to only a miniscule improvement in the AUC or NRI. To illustrate this point, we conducted some simple simulations. First we generated two normal variables, with identity variance-covariance matrices within events and non-events. The first one had an effect size of 0.545, corresponding to an AUC of 0.65, roughly equal to what we observed in the example from section 3. The second had a medium effect size of 0.5. The fraction of events was set at 0.244 and sample size at 1369, following our practical example. Then we dichotomized the second predictor at three different points, corresponding to specificity equal to sensitivity, 0.85 and 0.99. Table 2 presents the median ΔAUC, IDI and NRI from 199 repetitions of the experiment.

Table 2.

Simulated improvement in risk prediction model with baseline AUC of 0.65 after adding binary predictors obtained by different dichotomizations of normal variable with effect size of 0.5

	Added Predictor
Metric	Continuous	Binary, Specificity=Sensitivity	Binary, Specificity = 0.85	Binary, Specificity = 0.99
Prevalence of “exposure”	N/A	45.1%	18.8%	1.6%
Odds ratio	1.64	2.23	2.31	3.46
ΔAUC	0.051	0.034	0.027	0.006
IDI*	0.044	0.027	0.023	0.007
½NRI	0.198	0.197	0.143	0.047

^*Event rate equals 0.244

We note that for the binary variables, the odds ratio increases with decreasing prevalence. The opposite is true for all three performance measures. When prevalence equals 1.6% and the odds ratio suggests a strong effect size, the ΔAUC, IDI and NRI all imply that the contribution is very weak. Of interest, at the point where specificity equals sensitivity, the NRI resulting from adding a variable obtained by a dichotomization of a normal predictor approaches the NRI obtained when adding this normal predictor. But in general, as expected, the effect of a dichotomized variable is weaker than that of its normal counterpart. Further research is needed to examine the non-normal cases in more detail.

5. Conclusions

In this paper we have applied the assumption of multivariate normality to provide direct links between three methods for quantifying improvement in model performance resulting from the addition of a set of new markers and the well-known metrics of the squared Mahalanobis distance and effect size. In addition to the reassurance provided by such relationships, they can also be used to express the magnitude of improvement in model performance in familiar effect size ranges for uncorrelated variables. For example, obtaining a ½ NRI of 0.20, the researcher can conclude that if s/he was working with uncorrelated normal variables, this ½ NRI value would correspond to a medium effect size of 0.50.

We have further observed that under LDA assumptions, the NRI is the only measure of the three that does not directly depend on the performance of the baseline model. Despite this singular strength, it has meaning only in the context of comparing two models. In this sense, the NRI can be interpreted as a performance measure of the marker or set of markers. It is also a simple, interpretable and uniformly applicable measure of effect size. It can be used for single or multiple markers, irrespective of their distribution. It will work for any risk algorithm: model-based or not— and it is not affected by model calibration. The presentation of the NRI as a difference of the probabilities of the increase in calculated event probabilities for events and nonevents allows interpretation of its meaning whereas the connection to the difference of the squared Mahalanobis distances provides a tool to interpret its magnitude. Hence the NRI may be the preferred measure of effect size in studies with binary outcomes.

On the other hand, the ΔAUC and IDI, defined as differences in specific measures of model performance, can be viewed as metrics tied to the two models in question. Their magnitude depends on the baseline model and it is generally harder to improve models that already perform well. However, reporting the parent values resulting in the ΔAUC and IDI provides additional information which the NRI does not offer: it gives the researcher a sense of how close to a perfect model s/he is. Discrimination slopes and IDI are based directly on event probabilities, and as such, may carry more information than the AUC in risk prediction. They are also more sensitive in judging improvement in model performance. On the other hand, the AUC does not depend on calibration and can more easily be compared across different studies. The broad research community is also familiar with its magnitude.

The arguments presented in this paper assumed nested models. However, all three measures are applicable to situations where we aim to compare any two models with possibly different predictors and different analytic techniques. All required inputs are limited to the event probabilities; meaningful comparisons using the NRI and IDI require that these probabilities are calibrated to the same incidence or prevalence. In this context, the NRI is not a measure of effect size for a set of markers but still remains meaningful as a difference of the probabilities of upward movement for events and nonevents. It can answer the question “what effect size is gained using the better model”. This gives it a dual nature as a measure of both effect size, and improvement in model performance.

Given the arguments above, we suggest reporting all three measures in studies with binary outcomes that relate to risk prediction and assessment. We recommend that appropriate confidence intervals are also provided and the external or cross-validation of results. When reporting the ΔAUC and IDI we strongly suggest reporting the AUC and discrimination slope of the baseline model.

Appendix.

Proof of Proposition 3

We adopt the notation of section 2 and assume equal variance-covariance matrices ∑ = ∑₁ = ∑₀. Let ∑ be decomposed into $\Sigma =\left(\begin{array}{cc}\hfill {\Sigma }_{11}\hfill & \hfill {\Sigma }_{12}\hfill \\ \hfill {\Sigma }_{21}\hfill & \hfill {\Sigma }_{22}\hfill \end{array}\right)$ where ∑₁₁ denotes the variance-covariance matrix for the first p variables, ∑₂₂ for the last q variables and ${\Sigma }_{12},{\Sigma }_{21}={\Sigma }_{12}^T$ are covariance matrices between the first p and last q variables and T denotes transposition. Let the inverse of ∑,∑⁻¹ be decomposed as follows: ${\Sigma }^{-1}=\left(\begin{array}{cc}\hfill {\Sigma }_{11}\hfill & \hfill {\Sigma }_{12}\hfill \\ \hfill {\Sigma }_{21}\hfill & \hfill {\Sigma }_{22}\hfill \end{array}\right)$ Moreover, let δ = μ₁ – μ₀ denote the vector of mean difference between events and nonevents which can be decomposed as $\delta =\left(\begin{array}{c}\hfill {\delta }_1\hfill \\ \hfill {\delta }_2\hfill \end{array}\right)$ for the first p and last q variables. Let a = ∑⁻¹ ·δ be a solution to the linear discriminant analysis problem with p + q variables and $b={\Sigma }_{11}^{-1}\cdot {\delta }_1$ the corresponding solution for the first p variables.

In the following we operate in the p+q dimensional setting, so it is of use to express b in a somewhat different form. In particular, we assume the coefficients are equal to zero for the last q variables. This can be accomplished by writing b as $b=\left(\begin{array}{cc}\hfill {\Sigma }_{11}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill {\delta }_1\hfill \\ \hfill {\delta }_2\hfill \end{array}\right)$. From Definition 3:

$$\frac{1}{2}\mathit{NRI}=\mathit{pr}\left(p_{p+q}\right(X\mid D=1)>p_p(X\mid D=1\left)\right)-\mathit{pr}\left(p_{p+q}\right(X\mid D=0)>p_p(X\mid D=0\left)\right).$$ (10)

Furthermore using definitions of $L_{p+q}^{\ast }$ and $L_p^{\ast }$ we can write:

$$\begin{array}{cc}\hfill & \mathit{pr}\left(p_{p+q}\right(X\mid D=1)>p_p(X\mid D=1\left)\right)=\mathit{pr}\left(L_{p+q}^{\ast }\right(X)>L_p^{\ast }(X)\mid D=1)=\hfill \\ \hfill & \mathit{pr}\left(\right(a^T-b^T)X>\frac{1}{2}(a^T-b^T\left)\right({\mu }_1+{\mu }_0)\mid D=1).\hfill \end{array}$$ (11)

.

We have E((a^T – b^T)X| D = 1) = (a^T – b^T)μ₁ and it can be shown (following Lemma) that: $\mathrm{var}\left(\right(a^T-b^T)X\mid D=1)=\mathrm{var}\left(\right(a^T-b^T)X\mid D=0)=\mathrm{var}\left(\right(a^T-b^T\left)X\right)=M_{p+q}^2-M_p^2$ Hence:

$$\begin{array}{cc}\hfill & \mathit{pr}\left(p_{p+q}\right(X\mid D=1)>p_p(X\mid D=1\left)\right)=\mathit{pr}(Z>\frac{\frac{1}{2}(a^T-b^T)({\mu }_1+{\mu }_0)-(a^T-b^T){\mu }_1}{\sqrt{M_{p+q}^2-M_p^2}}=\hfill \\ \hfill & \mathit{pr}(Z>\frac{-\frac{1}{2}(a^T-b^T)({\mu }_1-{\mu }_0)}{\sqrt{M_{p+q}^2-M_p^2}})=\mathit{pr}(Z>\frac{-(M_{p+q}^2-M_p^2)}{2\sqrt{M_{p+q}^2-M_p^2}}=\mathit{pr}(Z>\frac{-\sqrt{M_{p+q}^2-M_p^2}}{2}),\hfill \end{array}$$ (12)

where Z is the standard normal random variable.

By similar reasoning we get $\mathit{pr}\left(p_{p+q}\right(X\mid D=0)>p_p(X\mid D=0\left)\right)=\mathit{pr}(Z>\frac{\sqrt{M_{p+q}^2-M_p^2}}{2})$ Thus ½ NRI = $=\mathit{pr}(Z>\frac{-\sqrt{M_{p+q}^2-M_p^2}}{2})-\mathit{pr}(Z>\frac{\sqrt{M_{p+q}^2-M_p^2}}{2})=2\cdot ϴ\left(\frac{\sqrt{M_{p+q}^2-M_p^2}}{2}\right)-1$, where Θ() denotes the cumulative distribution function of the standard normal variable Z.

Lemma

Let a and b denote vectors of coefficients which provide solutions to linear discriminant analysis problems with p+q and p normal predictors (p being a subset of p+q), assuming identical variance-covariance structure within the event and nonevent groups (∑ = ∑₁ = ∑₀). Furthermore, let $b=\left(\begin{array}{cc}\hfill {\Sigma }_{11}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\cdot \left(\begin{array}{c}\hfill {\delta }_1\hfill \\ \hfill {\delta }_2\hfill \end{array}\right)$, where ∑₁₁ denotes the variance-covariance matrix for the first p variables and $\delta =\left(\begin{array}{c}\hfill {\delta }_1\hfill \\ \hfill {\delta }_2\hfill \end{array}\right)$ is the difference in means for the first p and remaining q variables. If D is an event indicator and $M_{p+q}^2,M_p^2$ are squared Mahalanobis distances, then:

$$\mathrm{var}\left(\right(a^T-b^T)X\mid D=1)=\mathrm{var}\left(\right(a^T-b^T)X\mid D=0)=\mathrm{var}\left(\right(a^T-b^T\left)X\right)=M_{p+q}^2-M_p^2.$$ (13)

.

Proof

We prove the relationship for D=1. The rest follows from the fact that ∑ = ∑₁ = ∑₀. Let $\Sigma =\left(\begin{array}{cc}\hfill {\Sigma }_{11}\hfill & \hfill {\Sigma }_{12}\hfill \\ \hfill {\Sigma }_{21}\hfill & \hfill {\Sigma }_{22}\hfill \end{array}\right)$ and ${\Sigma }^{-1}=\left(\begin{array}{cc}\hfill {\Sigma }_{11}\hfill & \hfill {\Sigma }_{12}\hfill \\ \hfill {\Sigma }_{21}\hfill & \hfill {\Sigma }_{22}\hfill \end{array}\right)$.

$$\begin{array}{cc}\hfill & \mathrm{var}\left(\right(a^T-b^T)X\mid D=1)=(a^T-b^T)\mathrm{var}(X\mid D=1)(a-b)=\hfill \\ \hfill & ={\delta }^T\cdot [{\left({\Sigma }^{-1}\right)}^T-{\left(\begin{array}{cc}\hfill {\Sigma }_{11}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)}^T]\cdot \Sigma \cdot [{\Sigma }^{-1}-\left(\begin{array}{cc}\hfill {\Sigma }_{11}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)]\cdot \delta =\hfill \\ \hfill & ={\delta }^T\cdot [I-\left(\begin{array}{cc}\hfill I\hfill & \hfill {\Sigma }_{11}^{-1}{\Sigma }_{12}\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)]\cdot [{\Sigma }^{-1}-\left(\begin{array}{cc}\hfill {\Sigma }_{11}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)]\cdot \delta =\hfill \\ \hfill & ={\delta }^T\cdot \left(\begin{array}{cc}\hfill 0\hfill & \hfill {\Sigma }_{11}^{-1}{\Sigma }_{12}\hfill \\ \hfill 0\hfill & \hfill I\hfill \end{array}\right)\cdot \left(\begin{array}{cc}\hfill {\Sigma }^{11}-{\Sigma }_{11}^{-1}\hfill & \hfill {\Sigma }^{12}\hfill \\ \hfill {\Sigma }^{21}\hfill & \hfill {\Sigma }^{22}\hfill \end{array}\right)\cdot \delta =\hfill \\ \hfill & ={\delta }^T\cdot \left(\begin{array}{cc}\hfill -{\Sigma }_{11}^{-1}{\Sigma }_{12}{\Sigma }^{21}\hfill & \hfill -{\Sigma }_{11}^{-1}{\Sigma }_{12}{\Sigma }^{22}\hfill \\ \hfill {\Sigma }^{21}\hfill & \hfill {\Sigma }^{22}\hfill \end{array}\right)\cdot \delta \hfill \end{array}$$ (14)

It can be shown (Mardia et al. [37]) that $-{\Sigma }_{11}^{-1}{\Sigma }_{12}{\Sigma }^{22}={\Sigma }^{12}$ and also ${\Sigma }^{21}=-{\Sigma }_{22}^{-1}{\Sigma }_{21}{\Sigma }^{11}$ and ${\left({\Sigma }^{11}\right)}^{-1}={\Sigma }_{11}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}$, or equivalently ${\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}={\Sigma }_{11}-{\left({\Sigma }^{11}\right)}^{-1}$. Hence: $-{\Sigma }_{11}^{-1}{\Sigma }_{12}{\Sigma }^{21}={\Sigma }_{11}^{-1}{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}{\Sigma }^{11}={\Sigma }_{11}^{-1}({\Sigma }_{11}-{\left({\Sigma }^{11}\right)}^{-1}){\Sigma }^{11}={\Sigma }^{11}-{\Sigma }_{11}^{-1}$. Finally:

$$\mathrm{var}\left(\right(a^T-b^T)X\mid D=1)={\delta }^T\cdot \left(\begin{array}{cc}\hfill {\Sigma }^{11}-{\Sigma }_{11}^{-1}\hfill & \hfill {\Sigma }^{12}\hfill \\ \hfill {\Sigma }^{21}\hfill & \hfill {\Sigma }^{22}\hfill \end{array}\right)\cdot \delta ={\delta }^T\Sigma \delta -{\delta }^T\left(\begin{array}{cc}\hfill {\Sigma }_{11}^{-1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\delta =M_{p+q}^2-M_p^2$$ (15)

Proposition 4

When we have unequal variance-covariance matrices for events and non-events, the following identity holds: $\frac{1}{2}\mathit{NRI}=\Phi \left(\frac{\sqrt{M_{p+q}^2-M_p^2}}{2\sqrt{2\alpha }}\right)-\Phi \left(\frac{-\sqrt{M_{p+q}^2-M_p^2}}{2\sqrt{2(1-\alpha )}}\right)$, where α is defined below.

Proof of Proposition 4

We adopt the notation of section 2 and the proof of Proposition 3 above but assume unequal variance-covariance matrices ∑₁ ≠ ∑₀. Let ∑ be the matrix corresponding to the best linear combination coefficients and let $M_{p+q}^2,M_p^2$ represent squared Mahalanobis distances based on ∑. From [28] we can take ∑ = ½(∑₁ + ∑₀).

Let $K={\Sigma }^{-1}-\left(\begin{array}{cc}\hfill {\Sigma }^{11}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)$. From Definition 3 we have:

$$\begin{array}{cc}\hfill & \frac{1}{2}\mathit{NRI}=\mathit{pr}\left(p_{p+q}\right(X\mid D=1)>p_p(X\mid D=1\left)\right)-\mathit{pr}\left(p_{p+q}\right(X\mid D=0)>p_p(X\mid D=0\left)\right)=\hfill \\ \hfill & \mathit{pr}\left(\right(a^T-b^T)X>\frac{1}{2}(a^T-b^T\left)\right({\mu }_1+{\mu }_0)\mid D=1)-\mathit{pr}\left(\right(a^T-b^T)X>\frac{1}{2}(a^T-b^T\left)\right({\mu }_1+{\mu }_0)\mid D=0)\hfill \end{array}$$ (16)

Following the same arguments as in the proof of Proposition 3, it can be shown that:

(a^T – b^T)X | D = 1 is distributed as N(δ^T Kμ₁, δ^T K∑₁Kδ) and

(a^T – b^T)X | D = 0 is distributed as N(δ^T Kμ₀, δ^T K∑₀Kδ)

This yields $\frac{1}{2}\mathit{NRI}=\mathit{pr}(Z>\frac{-\frac{1}{2}{\delta }^{T}K\delta }{\sqrt{{\delta }^{T}K{\Sigma }_{1}K\delta }})-\mathit{pr}(Z>\frac{\frac{1}{2}{\delta }^{T}K\delta }{\sqrt{{\delta }^{T}K{\Sigma }_{0}K\delta }})$.

Observe that ${\delta }^{T}K\delta =M_{p+q}^2-M_p^2$. Furthermore, δ^TK∑₁Kδ +δ^T K∑₀Kδ = 2δ^T K∑Kδ Following the logic used in the proof of Proposition 3 lemma it can be shown that ${\delta }^{T}K\Sigma K\delta =M_{p+q}^2-M_p^2$. Denoting $\alpha =\frac{{\delta }^{T}K{\Sigma }_{1}K\delta }{2(M_{p+q}^2-M_p^2)}$ we obtain:

$$\begin{array}{cc}\hfill & \frac{1}{2}\mathit{NRI}=\mathit{pr}(Z>\frac{-\sqrt{M_{p+q}^2-M_p^2}}{2\sqrt{2\alpha }}-\mathit{pr}(Z>\frac{\sqrt{M_{p+q}^2-M_p^2}}{2\sqrt{2(1-\alpha )}}=\hfill \\ \hfill & =\Phi \left(\frac{\sqrt{M_{p+q}^2-M_p^2}}{2\sqrt{2\alpha }}\right)-\Phi \left(\frac{-\sqrt{M_{p+q}^2-M_p^2}}{2\sqrt{2(1-\alpha )}}\right).\hfill \end{array}$$ (17)