Interactions between Core and Matrix Thalamocortical Projections in Human Sleep Spindle Synchronization

Abstract

Sleep spindles are bursts of 11–15 Hz that occur during non-rapid eye movement sleep. Spindles are highly synchronous across the scalp in the electroencephalogram (EEG) but have low spatial coherence and exhibit low correlation with the EEG when simultaneously measured in the magnetoencephalogram (MEG). We developed a computational model to explore the hypothesis that the spatial coherence spindles in the EEG is a consequence of diffuse matrix projections of the thalamus to layer 1 compared with the focal projections of the core pathway to layer 4 recorded in the MEG. Increasing the fanout of thalamocortical connectivity in the matrix pathway while keeping the core pathway fixed led to increased synchrony of the spindle activity in the superficial cortical layers in the model. In agreement with cortical recordings, the latency for spindles to spread from the core to the matrix was independent of the thalamocortical fanout but highly dependent on the probability of connections between cortical areas.

Introduction

Human sleep is associated with a profound modification of consciousness and the emergence of distinct sleep oscillations. In the early stages of non-rapid eye movement (NREM) sleep, the electroencephalogram (EEG) shows characteristic spindle oscillations. These sleep spindles are a hallmark of nonpathological stage 2 NREM sleep in mammals and are thought to play an important role in memory consolidation (Sejnowski and Destexhe, 2000). In humans, sleep spindles consist of waxing-and-waning bursts of field potentials oscillating at 11–15 Hz. These bursts last 0.5–3 s and recur every 5–15 s.

Although compelling evidence from decortication in vivo (Morison and Basset, 1945; von Krosigk et al., 1993) and spindle recordings in thalamic slices (Kim et al., 1995) demonstrate that spindles can be generated by the thalamus without cortical input, the neocortex is required for the long-range synchronization of spindles (Contreras et al., 1996a,b, 1997; Destexhe et al., 1998). Previous studies suggest that corticothalamic feedback projections to the thalamic reticular nucleus may be primarily responsible for this large-scale coherence (Destexhe et al., 1998).

Human sleep spindles measured by the EEG or MEG during simultaneous recordings exhibit different synchronization properties: the EEG signals from different channels have stronger cross-pair coherence than the MEG signal (Dehghani et al., 2010a). Although the relative spatial resolution of these modalities is a possible explanation, a more compelling one is that the EEG and MEG are generated from different cortical layers. The evidence comes from current source density (CSD) profiles of cortical depth electrode recordings of sleep spindles during presurgical exploration of human epileptic patients, consistent with spatially coherent spindles generated by upper cortical layers and spatially incoherent spindles generated in middle cortical layers (Cash et al., 2010).

To confirm this hypothesis, we have investigated the synchronization properties of spindle oscillations in a biologically plausible computational model using two parallel thalamocortical pathways (core and matrix), which were suggested from studies in primates, but whose functional role has remained elusive (Jones 2001, 2002).

This study reconciles the differences in the EEG or MEG recorded during sleep spindles in humans (Dehghani et al., 2010a,b, 2011) and in vivo data from anesthetized animals (Destexhe and Sejnowski, 2003), with a model in which (1) human sleep spindle oscillations are initiated in the specific projecting thalamocortical core pathway, with focal projections to the middle cortical layers, and that (2) the thalamocortical matrix pathway underlies the synchronization of the oscillatory activity through the distributed thalamocortical projections to the upper cortical layers. The activities in thalamocortical core and matrix pathways dominate the MEG and EEG recordings, respectively.

Materials and Methods

Although faithful in capturing the most salient features of spindle oscillations, the computational models developed thus far have been limited to a unique thalamocortical pathway (Dextexhe et al., 1994, 1998; Bazhenov et al., 1999, 2000). To adequately investigate the propagation and synchronization of spindle oscillations, we needed to construct a spatially extensive four-layer model, comprising two main distinct but interconnected thalamocortical pathways based on nonhuman primate observations (Jones, 2002; Zikopoulos and Barbas, 2007): (1) the core pathway, in which thalamic efferents project to the middle layers of the cortex (mostly to layers III and IV), and (2) the matrix pathway, which has thalamic afferents to superficial layers of the cortex (mainly to layer I). The matrix thalamocortical pathway has more diffuse connections than the core, the latter being more topologically compact and specific (Jones, 2002; Fig. 1A). We incorporated these specific connectivity and topographic features into our thalamocortical network model.

Figure 1.

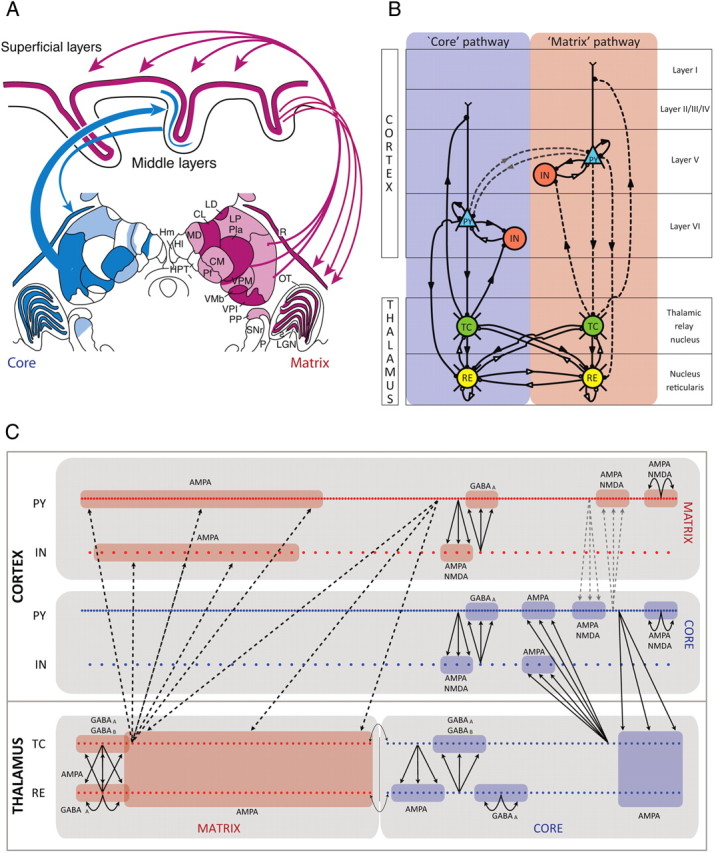
Model topology. A, Thalamocortical system with the distribution of matrix cells (red) and core cells (blue) indicated in a frontal section through the middle of a macaque monkey thalamus. The core thalamic projections are topographically ordered to the middle layers of a single cortical field. The matrix thalamic projections collectively project diffusely to the superficial layers of dispersed cortical fields [modified from Jones (2001)]. CL, Central lateral nucleus; CM, center median nucleus; HI, lateral habenular nuclei; Hm, medial habenular nuclei; LD, lateral dorsal nucleus; LGN, lateral geniculate nucleus; LP, lateral posterior nucleus; MD, mediodorsal nucleus; OT, optic tract; P, color-code retinal ganglion cells; Pla, anterior pulvinar nucleus; PP, peripeduncular nucleus; R, reticular nucleus; s, s laminae; SNr, substantia nigra, pars reticulata; VMb, basal ventral medial nucleus; VPI, ventral posterior inferior nucleus; VPM, ventral posterior medial nucleus. B, Schematic diagram showing the topology of the thalamocortical computational model, where both the matrix and core systems are depicted. The network connectivity shows the projections between the thalamus and the cortex (bottom and top, respectively) and between the core and matrix networks (left and right sides, respectively). Excitatory (inhibitory) connections are indicated by solid (open) circles at the end of a directed path (represented by the arrows). The black dotted lines indicate the projections in the matrix network whose fanout is a variable parameter for the purpose of this study. The gray dotted lines indicate the corticocortical connections between the matrix and core systems whose connectivity fanout is fixed at 5 but whose probability p of each connection existing varied from 0 to 50% (default value of 2%). C, Schematic connectivity showing the structure of the core and matrix thalamocortical networks distributed into four interconnected layers. Each cell is represented by a dot, and the area to which it projects is depicted as a shaded area for a representative cell. Intrathalamic connections were topographic with a divergence (fanout) of four cells. For these connections only, the cells at the boundary between the thalamic core and matrix networks are neighboring cells (indicated by the gray arrows). Thalamocortical and corticothalamic projections in the matrix pathway (black dashed lines) were made more expansive than in the core pathway. The fanout values for all connections are summarized in Table 1. Connections between the core and matrix PY layers (gray dashed lines) are topographic with a fanout of 5 with a low probability (2% for simulations in which this value was not varied).

The thalamic relay (TC) cells and reticular (RE) neurons were based on compartment models with Hodgkin-Huxley kinetics (Hodgkin and Huxley, 1952) used in previous models of sleep oscillations (Bazhenov et al., 2002). The cortical model included two-compartment excitatory cortical pyramidal (PY) neurons and inhibitory interneurons (IN) with Hodgkin-Huxley kinetics. The TC and RE cells had low-threshold calcium, fast sodium, and potassium currents. The h-type and potassium A currents were also included in the TC model cells. The PY and IN cells had high-threshold calcium, fast, persistent sodium, calcium-dependent potassium, and potassium M currents in the dendrites; and fast potassium, fast sodium, and persistent sodium currents in the soma. Calcium pumps that extruded calcium were embedded in all the neurons. The details of the synaptic kinetics and parameters are included below (see Modeling details).

Network structure

A schematic of the model thalamocortical network geometry is shown in Figure 1B. Our model incorporated two populations of TC cells: matrix TC neurons forming diffuse projections to matrix PY cortical neurons with cell bodies in layer V and core TC neurons forming specific, focused projections to the core PY neurons with cell bodies in layer VI. The apical dendrites of all PY cells extended to supragranular layers. The termination of matrix TC neurons was in cortical layer I, and those of core TC neurons were in cortical layer IV. We have not explicitly modeled supragranular cortical neurons; instead, we focused on the contacts made by matrix thalamic projections to the apical dendrites of the layer V pyramidal cells. This simplification allowed varying easily the main anatomical features of the matrix and core subsystems, such as radius of thalamocortical projections that was in the focus of our study. Also incorporated were matrix and core RE neurons interconnected with matrix and core PY and TC neurons, respectively. Each cortical layer included a layer-specific population of inhibitory IN also receiving thalamocortical inputs from the respective thalamic areas. The thalamocortical model was structured as a one-dimensional, six-layer array of cells: (1) a four-layered cortex of matrix PY, matrix IN, core PY, and core IN cells, and (2) a two-layered thalamus of TC and RE cells, core, and matrix being equally divided (Fig. 1C). Core and matrix pathways were connected at the thalamic and cortical levels: (1) along one of the boundaries in the thalamus (TC and RE layers), and (2) additional “long-range” cortical connections between the matrix and core pathways were made between their respective PY layers, with a 2% probability (p = 0.02) corticocortical connection. We also tested the effect of increasing probability up to p = 0.25. This choice of long-range intracortical probability was essentially determined by the average size of the presynaptic population; probability p = 0.02 corresponded to only few (zero to one) long-range connections, and probability p = 0.25 corresponded to approximately seven long-range connections for an average footprint of 30 neurons. Within thalamus, interactions between core and matrix subsystems were provided through thalamic reticular neurons. Specifically, we tested the effect of the varying overlap between reticular neurons of two subsystems on the development and synchronization of spindles.

We performed one-dimensional multilayer simulations consisting of 200 PY neurons and 50 IN neurons per cortical core and matrix networks and 50 TC neurons and 50 RE neurons in each of the thalamic core and matrix networks, totaling 700 cells. The widths of the fanout of the thalamocortical and corticothalamic projections of the matrix were initially focal and equal to those of the core fanout widths. In subsequent simulations, matrix fanouts were progressively widened while keeping the corresponding focal connections in the core system constant (Fig. 1B,C, dashed lines). The maximal values of synaptic connectivity radiuses were determined by the network size; to avoid limitations of “all-to-all” connectivity, we limited connectivity by 50 cells in any direction so that the system would be able to display complex spatiotemporal dynamics (e.g., propagating waves). The total synaptic strength per cell was scaled accordingly to maintain constant the overall synaptic strength of a given pathway. The maximal conductances for individual synapses were the maximal conductance per synaptic release scaled by the number of synapses. These connectivity properties are summarized in Table 1 and visualized in Figure 1C. The matrix PY cells were also slightly more hyperpolarized than the core PY cells (by adjusting the potassium leak conductance: g_KL = 0.0025 mS/cm² for core PY cells and 0.003 mS/cm² for matrix PY cells; see below, Modeling details). Otherwise, all parameters in the two subsystems were modeled identically.

Table 1.

Connectivity properties

	PY→TC	PY→RE	TC→PY	TC→IN	PY→PY	PY→IN	IN→PY	RE→RE	TC→RE	RE→TC
Matrix pathway fanout	5, 9, 13, 17, 21, 25	5, 9, 13, 17, 21, 25	5, 14, 23, 32, 41, 50	1, 3, 5, 7, 9, 11	5	1	5	4	4	4
Core pathway fanout	5	5	5	1	5	1	5	4	4	4
Synaptic current	AMPA	AMPA	AMPA	AMPA	AMPA, NMDA	AMPA, NMDA	GABAA	GABAA	AMPA	GABAA, GABAB

Top two rows show fanouts used for connections in the matrix and core thalamocortical network model. Multiple numbers within a single cell represent parameter changes with increased fanout. Bottom row shows synaptic currents of network connectivity.

Most simulations were initiated by a brief external stimulus to five cells at the edge of the core RE layer modeled by AMPA synapses that had a maximal conductance of 20 μS, but spindle sequences also occurred spontaneously within the network.

To quantify the synchrony in the system, we used an all-to-all, zero-time-lag cross-correlation of the estimated local field potential (LFP) during the spindle activity. The measure of the synchrony in the cortical activity, R, was found by taking the weighted sum of the dot products of all possible pairs of LFP spindle activity time courses within a cortical layer. This metric is related to the Schreiber reliability measure (Schreiber et al., 2003):

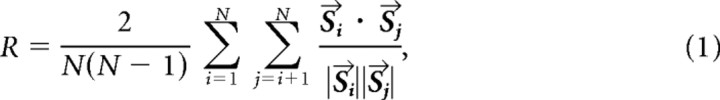where N is the number of LFP points in the population and ${\overrightarrow{S}}_i$ is the time course of the LFP at location i. Equation 1 captures the similarity of the LFP spindle activity across a cortical layer.

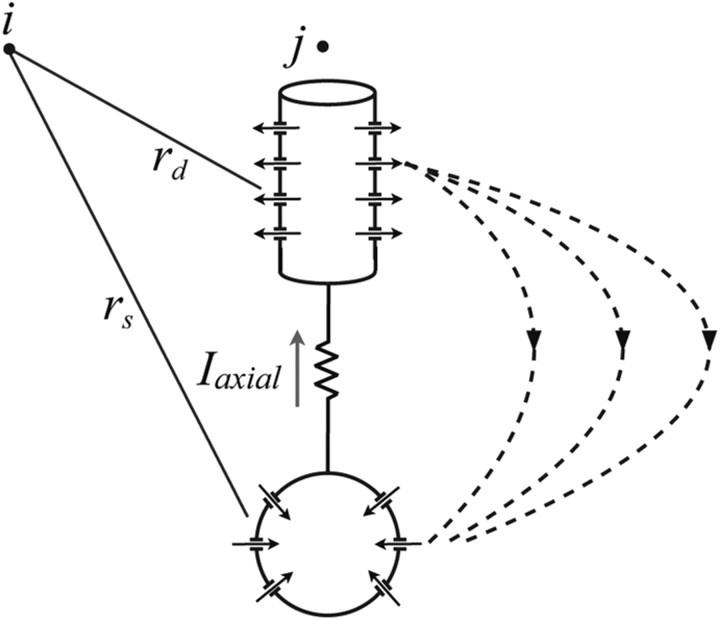
The LFP was estimated using the axial current between dendritic and somatic compartments of the cortical cells by an approximate dipole measure. For each subsystem, the LFP at a cortical location i, ${\overrightarrow{S}}_i$, was computed by the following equation:

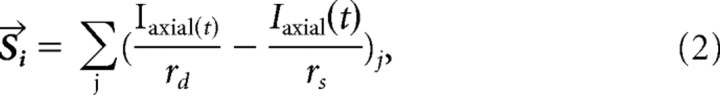where the sum is taken over all excitatory cortical neurons within the subsystem, I_axial is the axial current from the dendritic compartment (source) to the soma compartment (sink) for the model cortical pyramidal cells, and r_d and r_s are the distances from the dendrite and soma, respectively, to the location of the LFP measurement (Fig. 2.) This equation approximately reduces to a dipole field, as described by Nunez and Srinivasan (2006, their Eq. 5.7; modulo a scaling factor), when r_d, r_s ≫ 1. The distance between the dendrite and the soma (from layer I to layer V in the matrix and from layer II to layer VI in the core) was assumed to be 2 mm. The distance between cortical cells was estimated to be 100 μm based on the assumption that the synaptic footprint (equal to twice the fanout plus 1), within which there were ∼10 cells, was ∼1 mm. The LFP signal was bandpass filtered between 5 and 20 Hz to extract spindle activity.

Figure 2.

Local field potential. Schematic of the contribution of pyramidal neuron j to the local field potential calculated at location i. Arrows indicate the flow of current through ionic channels, the axial current (I_axial) between the dendritic (cylindrical) and somatic (spherical) compartments, and the resulting dipole current in the extracellular space (dashed lines.) The distances from the dendritic and somatic compartments to the location of the LFP calculation point i are r_d and r_s, respectively.

Modeling details

Intrinsic currents: thalamus.

TC and RE cells were modeled as single compartment cells with voltage- and calcium-dependent currents described by Hodgkin-Huxley kinetics:

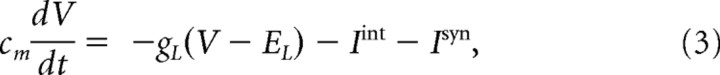where C_m = 1 μF/cm² is the membrane capacitance, g_L is the leakage conductance (g_L = 0.01 mS/cm² for TC cells and g_L = 0.05 mS/cm² for RE cells), and E_L is the reversal potential (E_L = −70 mV for TC cells and E_L = −77 mV for RE cells). I^int is the sum of active intrinsic currents (I_j^int), and I^syn is the sum of synaptic currents (I_j^syn). The area of a TC cell was S_TC = 2.9 × 10⁻⁴ cm², and S_RE = 1.43 × 10⁻⁴ cm² for an RE cell. Both TC and RE cells included a fast sodium current, I_Na; a fast potassium current, I_K (Traub and Miles, 1991); a low-threshold Ca²⁺ current, I_T [for RE cells (Huguenard and Prince, 1991); for TC cells (Huguenard and McCormick, 1992)]; and a potassium leak current, I_KL, where I_KL = g_KL(V − E_KL), with E_KL = −95 mV. TC cells also included a hyperpolarization-activated cation current, I_h (McCormick and Pape, 1990; Destexhe et al., 1996). A potassium A-current is also included in the TC cell compartment. The expressions for voltage- and Ca²⁺-dependent transition rates for all currents are given by Bazhenov et al. (1998). The maximal conductances were g_K = 10 mS/cm², g_Na = 90 mS/cm², g_T = 2.2 mS/cm², g_h = 0.017 mS/cm², g_Ca = 2.7 mS/cm², and g_KL = 0.0142 mS/cm² for TC cells and g_K = 10 mS/cm², g_Na = 100 mS/cm², g_T = 2.3 mS/cm², g_Ca = 2.3 mS/cm², and g_KL = 0.005 mS/cm² for RE cells. See Table 2 for a list of parameters.

Table 2.

Parameters

Parameter	Value
Cm	1 μF/cm2
Cm;dendrite	1 μF/cm2
Thalamic cells
STC	2.9 × 10−4 cm2
SRE	1.43 × 10−4 cm2
GL	0.01 mS/cm2 (TC)
	0.05 mS/cm2 (RE)
EL	−70 mV (TC)
	−77 mv (RE)
EKL	−95 mV
gK	10 mS/cm2 (TC;RE)
gNa	90 mS/cm2 (TC)
	100 mS/cm2 (RE)
gT	2.2 mS/cm2 (TC)
	2.3 mS/cm2 (RE)
gh	0.017 mS/cm2 (TC)
gCa	2.7 mS/cm2 (TC)
	2.3 mS/cm2 (RE)
gKL	0.0142 mS/cm2 (TC)
	0.005 mS/cm2 (RE)
Cortical cells
Ssoma	1.0 × 10−6 cm2
ρ	165 (PY)
	50 (IN)
EL	−68 mV (PY)
	−70 mV (IN)
EKL	−95 mV
gNa	3000 mS/cm2 (PY)
	2500 mS/cm2 (IN)
gK	200 mS/cm2
gNa(P)	15 mS/cm2
	3.5 mS/cm2 (dendrites)
gL	0.06 mS/cm2
gKL	0–003 mS/cm2
gHVA	0.01 mS/cm2
gK[Ca]	0.3 mS/cm2
gK,m	0.01–0.02 mS/cm2

Low-threshold Ca²⁺ current, I_T, and hyperpolarization-activated cation current, I_h play particularly important roles in spindles (Destexhe et al., 1996; Bazhenov et al., 2002). The model used in this study for computing I_h follows a single-variable kinetic scheme proposed by Destexhe et al. (1996), modified after a version introduced previously by Destexhe et al. (1993). The present model assumes that the voltage dependence and conductance is influenced by Ca²⁺ to a regulating factor, P, which itself binds to the open form of the channel and blocks its transition to the closed form. The dependence of the amplitude of I_h with the intracellular Ca²⁺ concentration is captured by the parameter k. All parameters used in the computation of I_h were taken from previously published papers (Destexhe et al., 1996; Bazhenov et al., 2002) and were kept constant throughout the simulations. Therefore, the influence of I_h on spindle oscillations in our model was, in all aspects, comparable to previous observations, both in computational models and in in vitro experiments (Bal and McCormick, 1996; Luthi and McCormick, 1998). In vitro characterization of spindles revealed a slowly decaying afterdepolarization, which is strongly pronounced in thalamocortical cells.

Intrinsic currents: cortex.

Each PY and IN cortical neuron was modeled by two compartments coupled by a somato-dendritic resistance of r = 10 MΩ. The ionic currents followed Hodgkin-Huxley kinetics (Mainen and Sejnowski, 1996) with the addition of a persistent sodium current, I_Na(p), in the PY cells to increase bursting propensity. The firing pattern depends on the coupling conductance between the axosomatic and dendritic compartments (g = 1/R) and the parameter ρ, which is the ratio of the surface area of the dendritic compartment to the somatic compartment (Mainen and Sejnowksi, 1996). The area of the soma was S_soma = 1.0 × 10⁻⁶ cm² for the axosomatic compartment and S_dend = ρS_soma for the dendritic compartment. For the cortical PY cells, ρ = 165 to match intrinsic bursting responses observed in the majority of pyramidal cells in cortical slabs, and ρ = 50 for IN to obtain fast spiking firing patterns.

The membrane potentials of PY and IN cells were governed by the following equations:

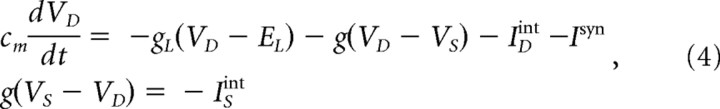where C_m is the membrane capacitance, g_L is the leakage conductance of the dendritic compartment, E_L is the reversal potential (E_L = −70 mV for IN and −68 mV for PY cells), V_D and V_S are the membrane potentials of the dendritic and axosomatic compartments, I^D_int and I^S_int are the sums of active intrinsic currents in dendritic and axosomatic compartments, I_syn is a sum of synaptic currents, and g is the conductance between dendritic and axosomatic compartments. To increase simulation speed, the axosomatic compartment had no capacitance, as already described in a previous study (Bazhenov et al., 2002). The capacitance of the dendritic compartment was C_m = 0.075 μF/cm².

Both IN and PY cells included fast Na⁺ channels, I_Na, of a high density in the axosomatic compartment and of a low density in the dendritic compartment. A fast delayed rectifier potassium K⁺ current, I_K, was present in the axosomatic compartment. A slow voltage-dependent noninactivating K⁺ current, I_Km; a slow Ca²⁺-dependent K⁺ current, I_KCa; a high-threshold Ca²⁺ current, I_HVA; and a potassium leak current, I_KL, where I_KL = g_KL(V × E_KL), E_KL = −95 mV, were included in the dendritic compartment. A persistent sodium current, I_Na(p), was included in the axosomatic and dendritic compartments of the PY cells (Alzheimer et al., 1993; Kay et al., 1998). The voltage- and Ca²⁺-dependent transition rates for all currents followed kinetics given by Timofeev et al. (2000). The maximal conductances were g_Na = 3000 mS/cm² (2500 mS/cm² for IN), g_K = 200 mS/cm², and g_Na(p) = 15 mS/cm² for axosomatic compartments and g_L = 0.033 mS/cm² (0.06 mS/cm² for PY cells), g_KL = 0–0.0025 mS/cm² (0.0025 for core PY cells and 0.003 for matrix PY cells), g_HVA = 0.01 mS/cm², g_Na = 0.8 mS/cm², g_KCa = 0.3 mS/cm², g_Km = 0.01 mS/cm² (0.02 mS/cm² for PY cells), and g_Na(p) = 3.5 mS/cm² for dendritic compartments.

Synaptic currents.

All synaptic currents were calculated according to the following:

where g_syn is the maximal conductance, E_syn is the reversal potential, and [O](t) is the fraction of open channels. For AMPA and NMDA receptors, E_syn = 0 mV; for GABA_A receptors, E_syn = −70 mV in the RE and PY cells and −80 mV for the TC cells (Ulrich and Huguenard, 1997); and for the GABA_B receptors, E_syn = −95 mV.

The maximal conductance was multiplied by a depression variable, E ≤ 1, representing the amount of available “synaptic resources.” E was nonunitary for the GABA_A intercortical connections and the thalamocortical AMPA connections to describe short-term depression for these connections (Bazhenov et al., 2002.) A simple phenomenological model was used: E = 1 − (1 − E_i(1 − U))e^{−(t − ti)/τ}, where U is the fraction of resources used per action potential, τ = 700 ms is the time constant of recovery of the synaptic resources, E_i is the value of E immediately before the ith event, and (t − t_i) is the time after the ith event. For IN GABA_A synaptic conductance, U = 0.07, and for TC thalamocortical AMPA synaptic conductance, U = 0.073.

The GABA_A, NMDA, and AMPA synaptic currents were modeled by first-order activation schemes (Destexhe et al., 1994; Golomb and Amitai, 1997). For the NMDA receptors, the dependence on postsynaptic voltage was 1/[1 + exp(−(V_post − V_th)/σ)], where V_th = −25 mV and σ = 12.5 mV (Traub et al., 1991; Destexhe et al., 1994; Golomb and Amitai, 1997). A higher-order reaction scheme that took into account the G-protein-activated K⁺ channels modeled the GABA_B receptors (Bazhenov et al., 2002). The equations for all synaptic currents were given by Bazhenov et al. (1998) and Timofeev et al. (2000). The maximal conductances per synaptic release were g_AMPA(PY-PY) = 150 μS, g_NMDA(PY-PY) = 10 μS, g_AMPA(PY-IN) = 50 μS, g_NMDA(PY-IN) = 8 μS, g_AMPA(PY-TC) = 25 μS, g_AMPA(PY-RE) = 50 μS, g_GABAA(IN-PY) = 50 μS, g_AMPA(TC-PY) = 100 μS, g_AMPA(TC-RE) = 4.00 μS, g_GABAA(RE-TC) = 30 μS, g_GABAB(RE-TC) = 80 μS, and g_GABAA(RE-RE) = 175 μS.

The maximal conductances for individual synapses were the maximal conductance per synaptic release scaled by the number of synapses. The exception to this was for the synapses onto edge neurons in the TC and RE layers, where they were scaled by the number of synapses as in the center of the layers, and for connections between the core and matrix PY layers, in which they were scaled by the number of synapses within a connectivity footprint.

Computational methods.

All simulations described in the study were performed using a forth-order Runge-Kutta integration method. The time step was 0.02 ms. Source C++ code was compiled on a Linux server using the GCC compiler.

Results

Human spindles have divergent EEG and MEG synchronization properties

Typical simultaneous recordings of the EEG and MEG during sleep spindles obtained from six normal human subjects in stage 2 of nonpathological NREM sleep are displayed in Figure 3. The high-density EEG confirmed widespread synchrony across the scalp during spindles (Fig. 3A), whereas the MEG was highly variable across the head (Fig. 3B) with widely varying phase and amplitude in different sensors. Furthermore, the simultaneously recorded EEG and MEG had low coherence and little discernable relationship with each other (Fig. 3C). Spindles were generated somewhat independently in different cortical areas (Fig. 3D). Overall, the average coherence between pairs of MEG gradiometers was only ∼0.3 during spindles, in contrast to the coherence value of ∼0.7 for EEG sensor pairs. The variability of spindles across MEG sensors suggested that the signal may be formed by multiple partially independent cortical generators, in contrast to the EEG, which may instead be dominated by a weak but widespread spindle generator.

Figure 3.

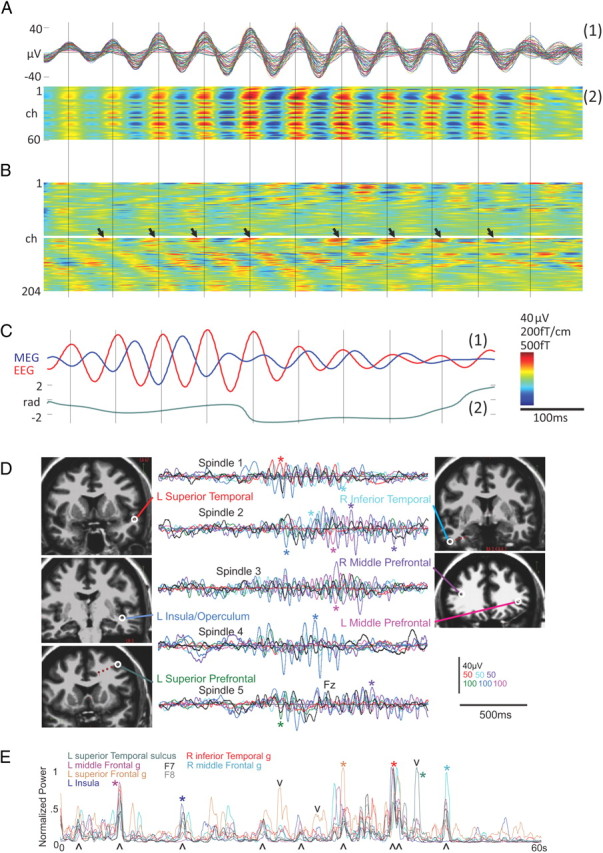
Spindle recordings with EEG versus MEG sensors. A, Referential EEG waveforms from 60 scalp channels during a single spindle (superimposed) in a healthy subject during natural sleep (1) and shown with voltage color coded (2). The EEG appears highly synchronous across the scalp. B, MEG spindle recorded by 204 gradiometers at the same time as A in the same healthy human subjects. The MEG appears highly variable and asynchronous across the scalp. The EEG peaks, marked with vertical lines, show no regular relationship with MEG peak activity. The arrows mark the peaks of a particular MEG channel that initially precedes and later follows the EEG peaks. C, Superposition of two of the largest amplitude EEG and MEG waveforms during a single spindle (1) also shows that the EEG and the MEG have variable relationships during spindles. The instantaneous phase lag, found via the Hilbert transform, varies considerably (2) [modified from Dehghani et al. (2010a)]. D, Spindles generated simultaneously in multiple regions of the cortex show variable phase relationships and relative amplitudes. In each of the five spindles recorded in patients underlying presurgical epileptic mapping, six depth sites with locally generated spindles (colored traces) and one scalp site (Fz, black trace) are superimposed. Different cortical generators are relatively larger in different spindles or portions of spindles (colored asterisks). Local generation was assured by choosing transcortical bipolar depth recordings (e.g., with one lead in white matter and one in CSF), with spindles that were larger and polarity inverted from adjacent leads. E, Participation by different cortical areas varies across spindles. Power from 7 to 14 Hz was calculated for moving 0.5 s epochs, and each channel was normalized to its peak amplitude in the 60 s epoch. Although most, but not necessarily all, cortical locations participate in the larger spindles (^), the relative amplitudes of different locations varies across spindles (*), and there are times where spindles are being generated in many cortical locations in both hemispheres but are not recorded at the scalp (v). Plastic screw guides were used so the scalp EEG remained insulated from the brain by the skull, as in controls.

When simultaneously recorded in the MEG and EEG, the spindle onset in the MEG preceded the EEG activity by one to two cycles (Dehghani et al., 2011). The current sinks and sources generating spindles (identified with linear microelectrode arrays) were either in middle layers when spindles were focal in the overlying subdural grid or in superficial layers when spindles were coherent in the grid (Cash et al., 2010).

Spindle oscillations are reproduced in a thalamocortical network model using two segregated pathways

Previous models have reproduced regular spindle oscillations using a simplified, single thalamocortical pathway with a unique layer for each cell type (Destexhe et al., 1998; Bazhenov et al., 2002). To faithfully address the role of matrix and core thalamocortical pathways, we reproduced spindle oscillations in a spatially extensive four-layer model comprising two main distinct but interconnected thalamocortical networks based on primate literature (Jones, 2001, 2002; Zikopoulos and Barbas, 2007; see Materials and Methods for details). Each pathway initially followed the parameters and topology of the thalamocortical model proposed in an earlier model (Bazhenov et al., 2002); however, we subsequently allowed the fanout of thalamocortical projections to be up to five times wider in matrix versus core pathways. As in previous models, the spindle oscillations were maintained by interactions between TC and RE neurons. Sequences of spindle oscillations alternated with localized patterns of spike-burst activity propagating inside the RE network. New sequences of spindle oscillations were initiated by input from the RE nucleus onto the TC cells after removal of I_h-mediated depolarization. RE activation was either mediated by intrinsic activity of the RE nucleus, as in the study by Bazhenov et al. (2000), or by spontaneous cortical activity, as in the study by Destexhe et al. (1998).

An example of the typical neuronal activity for simulated spindle oscillations using the entire thalamocortical network with both interconnected core and matrix pathways is shown in Figure 4 (left column, core pathway; right column, matrix pathway). Some of the most salient properties of spindles known from animal data (Steriade and Llinas, 1988) were reproduced in this simulated activity, such as the waxing and waning of the membrane potential and the subharmonic firing (∼5 Hz) observed in individual TC cells.

Figure 4.

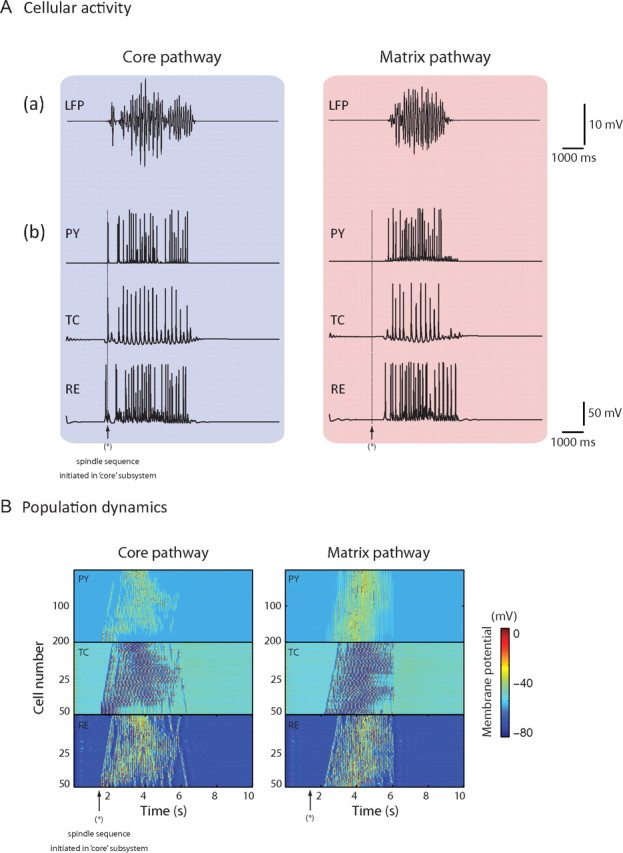
Canonical spindles. A, Top, Local field potentials in the cortical domains of the core and matrix networks during a 10 s simulation of spindle activity. Bottom, Voltage traces of individual neurons (PY, TC, and RE) in each layer of core and matrix networks (blue and red backgrounds, respectively). The time of spindle initiation in the core system is indicated by the vertical arrows. B, Space–time plot representing the activity of the whole model for 10 s, showing the pattern of wave propagation within core and matrix networks. Individual membrane potential activity from A corresponds to the cell in the middle of each respective layer (cell 100 of PY, and 25 of TC and RE) of B. The value of the membrane potential for each neuron is coded by the false color scale. The time of spindle initiation in the core network is indicated by the arrows. (Results are shown for the case with matrix TC→PY fanout is 41, whereas the core TC→PY fanout is 5).

A single spindle sequence was usually observed during the 10 s simulation, although multiple spontaneous spindles recurred for longer simulations. Once the sequence initiated in the core pathway, it spread to the matrix pathway within ∼700 ms (Fig. 4A, dotted vertical bars). Both LFPs and neuronal firing were dominated by ∼10 Hz oscillatory rhythms lasting, on average, 2.9 ± 0.45 s during the subsequent autonomously organized spindle discharge, values within the physiological range (Steriade and McCarley, 2005). The LFPs of the underlying activity for both core and matrix were characterized by a typical waxing-and-waning envelope (Fig. 4A, top traces), as did the membrane potentials for the cellular activity of TC cells during rebound spike bursts (Fig. 4A, second to fourth traces; IN not displayed).

The population dynamics of each subsystem confirmed that the site of initiation of spindles occurred in the core and preceded, by a few hundreds of milliseconds, the occurrence of spontaneous spindles in the matrix subsystem (Fig. 4B). Although the initiation and the first cycle of oscillation were qualitatively similar in the two distinct pathways, the spatial propagation of the spindle sequence was more synchronous in the matrix than in the core (Fig. 4B), a fundamental property of these pathways, as shown later. In each network, the spindle oscillation started from one edge of the layer and propagated to the opposite edge at a velocity close to 2.5 mm/s (Fig. 4B). The termination of the spindle sequence was also well defined temporally in the matrix pathway, as opposed to the core where the oscillation waned asynchronously, suggesting that the spread and strength of corticothalamic feedback influences spindle termination (Bonjean et al., 2011).

These data suggest that the focused corticothalamic projections of the core pathway facilitate spindle initiatioņ whereas the diffuse connections that characterize the matrix pathway are conducive to creating synchronization. We investigate below the impact of the breadth of thalamocortical connectivity in the synchronization properties of spindles.

Matrix and core pathways exhibited different degrees of synchrony during spindle generation

The breadth of connectivity in the core and matrix was investigated by performing simulations in which the matrix thalamocortical and corticothalamic connections became increasingly diffuse, whereas connections in the core pathway remained focal (see Materials and Methods). The two pathways only differed in their respective connectivity profiles and otherwise shared the same properties. Although the core thalamic cell afferents terminate with large boutons and the matrix projections terminate in a dense matrix of small boutons (Zikopoulos and Barbas, 2007), structural characteristics that are useful for anatomically differentiating the two pathways, these features were not included in the model.

When the profiles of the matrix and core connections (i.e., TC→{PY,IN} and PY→{TC,RE} connections) were identical (Fig. 5A, top), the characteristics of spindle activity were similar in both networks (Fig. 5A, bottom). After being initiated in the core, the spindle propagated to the matrix by a latency of ∼700 ms. The degree of synchrony in the two pathways during a spindle sequence was indistinguishable (Fig. 5A). Similarly, the termination of the sequence could not be qualitatively distinguished between the core and matrix.

Figure 5.

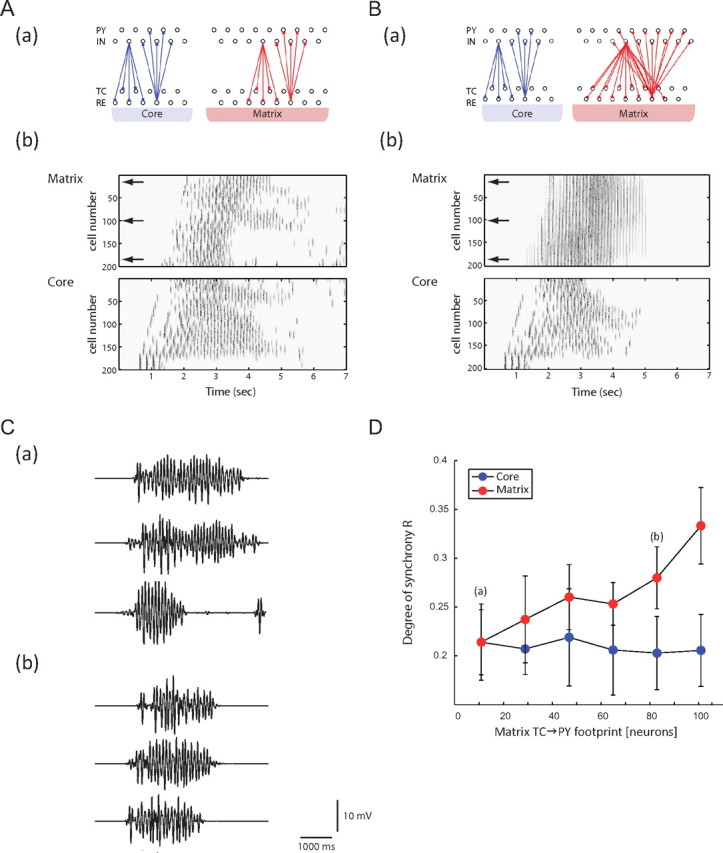
Spindle synchronization measure. A, Top, Schematic diagram illustrating the connection profile used for the core and matrix networks (situation of equal and focal fanout for both pathways). Bottom, Space–time plots of cortical core and matrix pathways using the connection profile (top) during a 7 s simulation of spindle activity. B, Top, Schematic diagram illustrating the connection profile used for the core and matrix networks (situation of focal fanout for the core pathway only). The matrix fanout is now diffuse. Bottom, Space–time plots of cortical core and matrix pathways using the connection profile (top) during a 7 s simulation of spindle activity. C, LFP traces for cortical neurons in the matrix pathway under the connectivity profiles used in A and B. The three virtual recording sites are indicated by the horizontal arrows in B. D, Quantification of the degree of synchrony of cortical activity in both core (blue dots) and matrix (red dots) as a function of different thalamocortical and corticothalamic footprints in the matrix pathway (footprints in the core are kept identical). Each dot represents the average of 10 simulations ± SD. Letters a and b correspond to the LFPs represented in Ca and Cd, respectively.

We next analyzed and quantified how the fanout of thalamocortical connections affected the degree of synchrony during spindle generation within the core and matrix pathways. When the fanout of the thalamocortical (TC→{PY;IN}) and corticothalamic (PY→{TC;RE}) matrix connections significantly increased while maintaining constant focal core connectivity (Fig. 5B, top), the cortical spindle activity appeared more synchronous in the matrix compared with the spindle activity in the core (Fig. 5B, bottom). As before, the spindles were initiated in the core and propagated to the matrix with a delay. A striking difference between the degree of synchrony in the two networks was observed in such circumstances. Whereas the core network population activity was qualitatively identical as in Figure 5A, the matrix network population had a significantly higher degree of synchrony, with nearly simultaneous cortical firing within the whole layer on each burst cycle. These synchrony differences were quantified by the Schreiber measure (see text below).

Sample LFP traces from three different virtual recording sites of the matrix network were simulated for both focal (Fig. 5Ca) and diffuse (Fig. 5Cb) fanouts. The three virtual sites were, respectively, located at the top, center, and bottom of the matrix layer and were equally separated from each other (compare Fig. 5A, bottom, horizontal arrows). In agreement with the spatiotemporal plots, the three LFPs recorded from a single cortical layer were incommensurate when the fanout was focal and topographically limited (Fig. 5Ca). Conversely, the LFP traces were better phase locked and showed very similar spindle duration when the cortical layer had a diffuse fanout (Fig. 5Cb).

We quantified the degree of synchrony of the cortical LFPs using the Schreiber reliability measure R as a metric (Schreiber et al., 2003; see Materials and Methods). We varied the thalamocortical and the corticothalamic fanouts of the matrix, whereas the connectivity profile of the core remained focal and constant (compare Fig. 1B,C, dashed lines). In so doing, we observed that the synchrony value increased as a function of the fanout width of the thalamocortical connectivity in the matrix pathway. Indeed, synchronous activity in the superficial cortical layers became more prevalent as the fanout of the projections broadened (from the matrix pathway). The red (Fig. 5, respectively blue) dots denote the degree of synchrony value for the matrix (respectively core) pathway with error bars for the SD (n = 10 simulations). When both the core and matrix footprints were focal and equal to 11 (i.e., each TC cell projected to 11 PY cells), the two pathways had the same measure of synchrony (∼0.21). As the matrix footprint increased from 11 to 101, the degree of synchrony R for this pathway reached 0.34 (ANOVA; F = 51; df = 19′ p < 10⁻⁵), a 62% increase compared with the initial value (Fig. 5D, red dots). In contrast, the cortical core synchrony was unaffected by a change in the matrix fanout (Fig. 5D, blue dots).

Impact of feedforward versus feedback and probability of intercortical connections

Both feedforward thalamocortical and feedback corticothalamic projections may affect the degree of synchrony observed in the core and matrix networks. To unravel the specific role of each projection type, we performed simulations varying the fanout of one projection of the matrix while keeping the fanout of the other pathway focal (see model; Fig. 1B,C, black dashed lines). As before, the core network had constant focal connectivity for all simulations. The diffuse feedforward thalamocortical connections of the matrix were primarily responsible for producing more synchronous spindles in the matrix cortical layers than in the core, and, accordingly, the degree of synchrony in the spindle activity was significantly higher in the matrix than in the core (Fig. 6Aa; ANOVA, F = 58, df = 19, p < 10⁻⁶). In contrast, increasing only the footprint size of the feedback connections from the cortex to the thalamus in the matrix system did not significantly affect the synchrony of spindle activity (Fig. 6Ab; ANOVA, F = 1.42, df = 19, p > 0.1).

Figure 6.

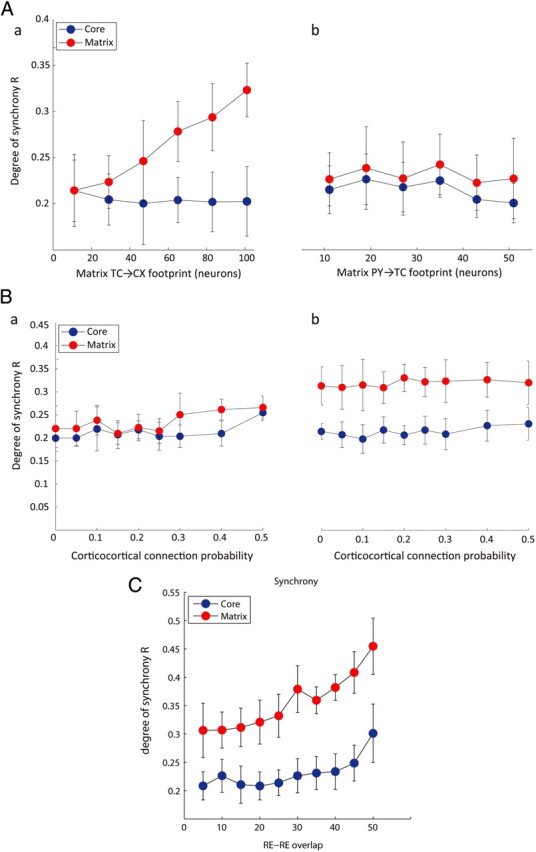
Roles of increased connectivity between different neuronal populations in corticocortical synchrony of spindle discharges. A, Impact of feedforward versus feedback footprints in the matrix pathway. a, Evolution of the degree of synchrony R as a function of the feedforward thalamocortical connections. b, Evolution of the degree of synchrony R as a function of the feedback thalamocortical connections. (Core connections remained focal for Aa and Ab). B, Impact of the probability of corticocortical connections between core and matrix networks. a, Both core and matrix networks have an equal focal fanout. b, Core fanout was focal whereas matrix fanout was more diffuse. C, Impact of the overlap between the two reticular layers (core and matrix) on the spindle synchrony.

We also examined how the interconnectivity density between the core and matrix cortical layers affected the degree of synchrony (see model; Fig. 2B,C, gray dashed lines). We maintained the footprint for cortical connections between layers the same as that of connections within a given cortical layer; however, each intercortical connection between the matrix and core cortical layers was made with probability p within the footprint. The default probability in previous simulations was p = 0.02. Varying the probability of connectivity from p = 0 to p = 0.5, we saw no significant influence on the degree of synchrony of the core and matrix pathways (Fig. 6B). That observation held whether the matrix footprint was focal (Fig. 6Ba) or diffuse (Fig. 6Bb), with the core footprint remaining constant (TC→PY = 11) throughout. From this, we can conclude that the only major architectural parameter that significantly affected the synchrony measure was the spread of the feedforward thalamocortical footprint, whereas neither the cortical feedback projections to the thalamus nor the corticocortical connectivity significantly impacted spindle synchrony.

Impact of the intrathamic connections on spindle synchronization

Although the core and matrix pathways have been clearly identified, the extent of reticulo-reticular connections between these two pathways yet remained unknown. In our initial model, we used a limited connectivity profile between the core and matrix reticular nuclei. Here, we wanted to assess the impact of a progressive overlap between the two reticular layers on the spindle synchrony. We found that, as the degree of RE–RE overlap increased up to 50 cells per layer, so did the synchrony degree for both core and matrix pathways (Fig. 6C).

We also tested the hypothesis of a lesion at the reticular level, thereby isolating core and matrix reticular nuclei from each other. In this case, we found that although the spindle was still initiated and sustained in the core, the thalamic lesion prevented the matrix from being recruited in the spindle oscillatory activity. A progressive increase in the density of intercortical connections did not succeed in recruiting the matrix, confirming that reticular neurons, which can be recruited by cortical cells, are critical in the initiation of spindle oscillation.

Latency and duration of spindles in the core and matrix systems

Finally, we addressed the impact of corticocortical connectivity on the latency of spindle initiation between the core and the matrix, as well as the duration of spindle sequences in both networks. To ensure similar initial states for different simulations, the initial spindle was always initiated by external stimulation to the core.

Surprisingly, the breadth of connections in the core and matrix did not reliably affect the latency of spindle initiation between these two thalamocortical pathways, as shown by the absence of significant difference in the spindle latency when the fanout diffusiveness in the matrix was varied under fixed intercortical connectivity probability (Fig. 7A; p = 0.02). However, the degree of interconnection alone between the core and matrix greatly impacted the spindle latency between these pathways (Fig. 7B). As the probability p of intercortical connections increased, the propagation delay between the two pathways decreased under fixed thalamocortical footprints (Fig. 7B). For example, the spindle initiation latency was 817 ms for a low cortical interconnection probability (p = 0.02) but decreased to 150 ms for higher probability values (p = 0.3) under constant thalamocortical footprints, as illustrated by membrane potential traces in Fig. 7, Ca and Cb, respectively.

Figure 7.

Connectivity factors affecting the delay from spindle onset in the core versus matrix systems. A, Latency of spindle propagation between core and matrix networks as a function of the matrix thalamocortical fanout (core fanout kept constant). B, Latency of spindle propagation between core and matrix networks as a function of the probability p of corticocortical connections between the two networks (core and matrix fanout kept constant). C, Example of individual voltage traces for pyramidal cells in the core and matrix pathway illustrating the latency of spindle propagation between the two pathways. a, For p = 0.02 (compare vertical arrow in Ba). b, For p = 0.3 (compare vertical arrow in Bb).

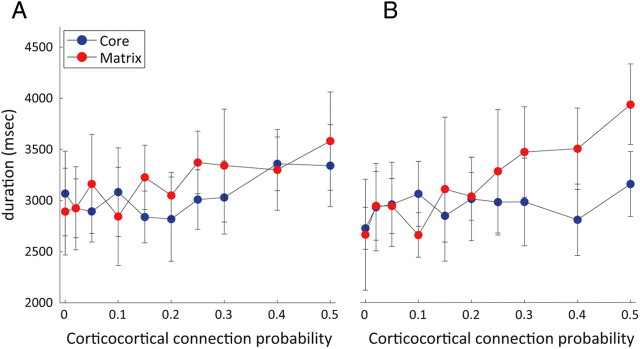
The duration of spindle sequences in the core and matrix was quantitatively comparable when the footprints in both networks were equal and focal (Fig. 8A). But increasing the corticocortical probability between the two pathways slightly increased the spindle duration from an average of 2.9 s in both networks for p = 0.02–3.3 (resp. 3.6) seconds in the core (resp. matrix) for p = 0.5 (Fig. 8A).

Figure 8.

Spindle duration as a function of connectivity between and within systems. The average spindle duration of a spindle sequence in both core (blue dots) and matrix (red dots) networks is shown. Each dot represents mean value ± SD. A, With both core and matrix fanouts equal and focal. B, With focal core fanout and diffuse matrix fanout.

The same assessment for the influence of interconnection probability on spindle duration was performed under a more diffuse footprint for the matrix pathway (TC→PY = 83), whereas the core remained constant and focal (TC→PY = 11). Under these different conditions, we similarly found no statistically significant differences in the average spindle sequence duration between the two thalamocortical pathways [2.9 s for p = 0.02; 3.2 s (core) and 3.9 s (matrix) for p = 0.5, n.s.; Fig. 8B).

Together, these results indicate that, on the one hand, the breadth of connections (matrix fanout) neither statistically influence the average spindle latency between core and matrix nor the average spindle sequence duration, at odds with its role in spindle synchronization as shown previously and in line with the literature (Contreras et al., 1996b, 1997; Destexhe et al., 1998). On the other hand, although the cortical interconnection probability played no significant role in spindle synchrony, it was, however, the key factor to constrain spindle initiation latency between the core and matrix.

Discussion

This study was motivated by recent findings that human spindles simultaneously recorded by EEG and MEG sensors have strikingly different characteristics (Dehghani et al., 2010a,b, 2011). Here, we have explored a mechanism to explain the spatiotemporal properties and synchronization differences found in human spindle oscillations. Implementing a computational model incorporating the known anatomical properties of two separate thalamocortical networks (“core” and “matrix”) found in nonhuman primates (Jones, 2001), we have shown that the difference between core and matrix pathways in the fanout of thalamocortical projections best explains the discrepancies in spindle synchronization between scalp EEG and MEG recordings.

Specifically, we have shown that whereas the spindle activity was initiated in the core pathway, the matrix pathway contributed to the widespread spindle synchronization across the network. Surprisingly, we found that the spread of corticothalamic connections, unlike thalamocortical ones, had little significance on spindle coherence. Finally, we found that the latency of spindle propagation between the core and the matrix pathways was constrained by the probability of corticocortical connections between the two systems.

Synchrony divergence between electroencephalography or magnetoencephalography

In simultaneous EEG/MEG recordings, spindle activity was sometimes detected in one of the modalities only (Hughes et al., 1976; Nakasato et al., 1990; Yoshida et al., 1996; Manshanden et al., 2002; Dehghani et al., 2011). Recently, Dehghani et al. (2010a) reported that the MEG signal was asynchronous and varied strongly in amplitude and phase across locations and across spindles, unlike the simultaneously recorded EEG, which was spatially and temporally highly coherent across the scalp and across spindles. Overall, the average coherence between pairs of MEG gradiometers was only ∼0.3 during spindles, in contrast to the coherence value of ∼0.7 for EEG sensor pairs. Moreover, many spindle epochs were visible in the MEG but not in the EEG (Dehghani et al., 2011). When they did appear in both modalities, the spindle in the MEG led that in the EEG by ∼190 ms on average (Dehghani et al., 2010a).

The variability of spindles across MEG sensors may reflect multiple partially independent cortical generators, whereas EEG recordings may instead be dominated by a weak but widespread unique spindle generator. These empirical observations led to the hypothesis that the MEG and EEG primarily record spindles from different thalamocortical pathways, specifically the core and matrix pathways, respectively. This interpretation suggests that spindles occur first in the core pathway and then quickly spread to the matrix pathway, which contributes to the widespread synchronization of spindles across the cortical network, an interpretation that was observed and confirmed in the present study.

The volume conduction effects that smear the EEG, relative to MEG, may explain the differences in global versus focal coherence during spindle activity. In other words, the lead fields associated with EEG are smoother and more distributed than those of the MEG. As a consequence, focal synchrony will appear to be more globally coherent over sensors. However, this is not a sufficient explanation for the synchrony differences between the EEG and MEG because (1) intracranial recordings acquired at the same time as noninvasive electromagnetic measures suggest that EEG and MEG signals are generated in different cortical layers. It is this fact that motivates the current study, in which we propose that both local and global synchrony could coexist and that the EEG is selectively sensitive to global synchrony, and (2) the existence of the relatively large phase delays between MEG signals in vivo that commonly exceed the period of spindle oscillations (Fig. 3) suggests that the averaging of the MEG signal over the larger volume would only lead to the loss of periodicity.

Core mediates multiple focal generators, whereas matrix mediates large-scale synchrony

Previous models of spindle oscillations did not consider the differences between core and matrix thalamocortical pathways. Our model is the first to incorporate these two thalamocortical networks and to investigate the impact of their topological differences on spindle activity. Specifically, our model captures the distinct thalamocortical projections between the core and the matrix pathways found in nonhuman primates (Jones, 2001). Relay cells from the core project to a highly restricted target domain, typically terminating with large boutons in layer IV, which transmit focal sensory information via ionotropic receptors (Zikopoulos and Barbas, 2007). In contrast, relay cells from the matrix project very diffusely, often to multiple cortical areas, and terminate in a dense matrix of small boutons in layer I, associated with the slow modulatory NMDA and metabotropic transmission (Rubio-Garrido et al., 2009).

Although some of the differences in glutamate receptors and synaptic morphology between matrix and core were not included in the model, its architecture critically incorporated the essential differences between the focal thalamocortical connections in the core and the more diffuse and widespread connectivity of the matrix. This difference of thalamocortical fanout was in itself sufficient to explain the synchrony mismatch between the core and matrix pathways.

Our results can explain the discrepancies outlined above between the EEG and MEG recorded during sleep spindles. Cortical anatomy combined with the biophysics of signal propagation (i.e., the so-called “forward solution”) predicts that the MEG would be more sensitive to focal activity and the EEG more sensitive to distributed sources (Dehghani et al., 2010a, 2011). Using models incorporating the subcranial CSF, the calculated leadfields, i.e., the cortical areas projecting to each sensor, were ∼25 times larger for referential EEG sensors than for MEG gradiometers (A. Irimia, E. Halgren, personal communication). Furthermore, when a distributed current generator was active, <30% of the referential EEG signal was canceled, unlike up to 90% for the MEG. We can conclude that the EEG is therefore more biased toward diffusely synchronous spindle generators, as produced by the cortical matrix pathway, whereas the MEG is more likely to pick up the activity from focal asynchronous spindle generators, as produced by the cortical core pathway.

Asynchronous activation of various core thalamocortical domains may be visible in the varying location, frequency, and synchrony of spindles in the MEG. The local generation of spindles could be found in many cortical locations, including ventrolateral frontal and temporal areas, such as in the left middle frontal gyrus, left inferior frontal sulcus, left middle temporal gyrus, left cingulate sulcus, right inferior frontal gyrus, right superior frontal gyrus, right precentral sulcus, and right middle temporal gyrus (Cash et al., 2010).

Synchronization of focal thalamocortical domains during spindles by the matrix pathway into coherent discharge may be visible in the EEG (Dehghani et al., 2010a, 2011).

We gained additional insight as to the differential role of the two thalamocortical networks via laminar recordings during spindle oscillations. CSD analysis of multielectrode depth recordings during spindles obtained in five subjects recorded during natural stage 2 sleep suggested that spindle generation involved multiple systems. CSD profiles showed two patterns of laminar spindle activity (Cash et al., 2010). The first pattern was generated by widely separated source/sink current pairs in deep and superficial layers, and the second pattern was generated by adjacent source/sink pairs in the middle layers. The first pattern of spindle activity, consistent with an input from the matrix cells in the thalamus, had low spatial coherence, whereas the second, consistent with input from the core thalamocortical projections, had high spatial coherence (S. Cash and E. Halgren, unpublished observations). From this, we can draw a conclusion on the different roles for the matrix and the core thalamocortical pathways.

Interactions between the core and matrix networks

In our model, spindle activity, which initiated in the core, was transmitted to the matrix with a delay that was inversely proportional to the density of corticocortical connections between the two networks. This transfer of spontaneous activity from the core to the matrix could lead to the large-scale synchronization of multiple focal, scattered spindle generators. It was shown recently that sleep spindles are predominantly local and occur separately in specific regions, mostly confined to local circuits (Nir et al., 2011; see also Fig. 3D). Our results, in line with this study, suggest that the local, distributed core pathways underlie local spindles, whereas global spindle activity is a result of the synchronization by the matrix pathway.

The delay in the spread of activity from one system to another explains the loose linkage between spindles recorded with the MEG and EEG experimentally. Our model shows that intercortical connectivity between the matrix and core can tune the value of this delay. The propagation latency in the model that best matched the experimental results (the MEG leads the EEG by ∼190 ms; cf. Dehghani et al., 2011) was obtained with an intercortical connection probability between the core and the matrix of ∼0.25.

In our study, although the involvement of the thalamocortical circuitry was required for synchronization, varying the range of corticothalamic feedback did not significantly influence the synchrony when the fanout of feedforward (thalamocortical) connections was small. This predicts that in the brain, only the fanout of the feedforward thalamocortical and not the corticothalamic feedback affects spindle synchronization. One possible explanation is that corticothalamic feedback onto the population of inhibitory reticular thalamic neurons reduces the synchronizing effects of corticothalamic input through lateral inhibitory interactions among the reticular thalamic neurons.

The modeling results support a mechanism whereby the spread of spindle discharges from the core to matrix occurs by intercortical coupling, as well as through thalamocortical loops, but without the involvement of interthalamic synchronizing mechanisms. In the model, the corticocortical connectivity had little impact on the spindle coherence within core and matrix, in agreement with Contreras et al. (1996b). In contrast, the probability of corticocortical connections between these two pathways did influence the latency and duration of spindle sequences.

The ultimate test of our hypothesis would be a selective inactivation of neurons in the thalamus where the cells in the matrix and core systems are somewhat segregated. Our model predicts that the core cells would engage in spindles rather independently of each other and with spotty cortical synchronization, whereas the matrix cells would tend to engage synchronously in spindles, synchronously with each other and across the cortical areas. Therefore, inactivation of the core (resp. matrix) thalamic populations should decrease (resp. increase) the appearance of spindles in deep versus superficial cortical layers and affect the overall level of spindle synchronization. The techniques for such manipulations currently become available (e.g., optogenetic stimulation); however, these experiments are only feasible in rodents, and we currently have no data to evaluate the spatiotemporal properties of spindles across cortical layers in such settings. The other prediction is that the core pattern spindles with current sinks and sources concentrated in middle cortical layers would tend to be focal and asynchronous, whereas the matrix, generated in superficial cortical layers, would tend to be synchronous and widespread. In other words, the prediction is that there would be a correlation between the cortical layer generating the spindle and the degree of synchrony it exhibits with other cortical areas. These recordings are possible in humans using depth electrodes and could provide a valuable test of our model.

Conclusion

The thalamocortical model described herein explains the empirical results from simultaneous recordings of the EEG and MEG during spindles, and supports the working hypothesis that more synchronous, spatially coherent spindle activity is generated in the matrix pathway because of the broad and widespread thalamocortical projections pertaining to this network. In contrast, spindle activities in the core pathway are less spatially coherent because the thalamic projections are more focal. Surprisingly, the corticothalamic feedback projections are ineffective in supporting greater spindle synchrony. Although core spindles are mostly independent across the cortical surface, functionally related cortical columns may be synchronized by the matrix even if they are not adjacent. Synchronization between distant columns arises mainly because the thalamocortical feedforward projections of the matrix pathway are widespread. This study reconciles the discrepancies observed in simultaneous recordings of the MEG and EEG during spindles, and proposes a principle mechanism based on anatomical observations from the primate. This sheds new light onto the different mechanisms of thalamocortical and corticothalamic projections underlying local and global spindles.