Abstract
A recent study in South Africa has confirmed, for the first time, that a vaginal gel formulation of the antiretroviral drug Tenofovir, when applied topically, significantly inhibits sexual HIV transmission to women [10]. However the gel for this drug, and anti-HIV microbicide gels in general, have not been designed using full understanding of how gel spreading and retention in the vagina govern successful drug delivery. Elastohydrodynamic lubrication theory can be applied to model such spreading of microbicide gels, which are inherently non-Newtonian [13,15]. A yield stress is emerging as one of the important properties of microbicide gel vehicle deployment, as this may improve retention within the vaginal canal. On the other hand, a yield stress may decrease the initial extent of the coating flow. Here, we first explain a certain yield stress paradox observed generally in many lubrication flows. Four conditions are determined, via scaling analysis, which mitigate the inconsistency in the use of lubrication theory to analyze the specific problem of elastic wall squeezing flow of yield stress fluid. Parameters characterizing these conditions are obtained experimentally for a test gel. Using them, it is shown that the lubrication approximation may be applied to the elastic wall-squeezing problem for this gel.
Keywords: Yield stress, Carreau fluid, Lubrication flow, Anti-HIV microbicide, Squeezing flow, Biviscosity model
1. Introduction
Elastohydrodynamic flow theory can be used to model a number of flows of biomedical interest [1–5]. In this regard, a relatively recent and compelling problem is application of vaginal gels for delivery of mucosal antigens or of topical ‘microbicide’ molecules to inhibit infection by sexually transmitted pathogens such as HIV [2,6–9]. This low-cost modality could have substantial biomedical and epidemiological importance, enabling women to control their susceptibility to infection. Very recently, use of a vaginal gel formulation of the antiretroviral drug Tenofovir has shown significant reduction in HIV transmission in a clinical trial [10]. This is the first time that a topical microbicide gel has shown significant efficacy, and comes after failures of several other gels in prior trials. This initial success not with standing, there is widespread agreement that more effective microbicide delivery vehicles must be developed. This should be based, in part, upon a better understanding of how gel spreading and retention in the vagina govern successful anti-HIV drug delivery. Once that understanding is developed, specific gels can be created with characteristics designed to optimize their spreading, retention and drug delivery [11].
The vaginal gel coating flow problem involves: significant deformation of tissue accompanying the flow; little alteration of gel physical properties associated with pressure and temperature changes [12]; non-Newtonian gel behavior; and oftentimes yield stress behavior (depending upon the composition of the gel [11]). There are multiple mechanisms by which current microbicides act to prevent infection by genital pathogens. For all of these, a deeper physical understanding and mathematical modeling of vaginal coating flow is clearly needed. Recently, we developed a framework for understanding the transluminal flow (along the vaginal canal) of microbicide vehicles driven by combined elastic squeezing and gravitational sliding [13]. These are believed to be the primary forces acting to drive such flow [14]. We then enhanced our model with a convective-diffusive transport equation to characterize water transport into the gel and, thus, spatially inhomogeneous gel dilution [15]. Neither of these initial studies took into account yield stress behavior of the fluids, despite the fact that many current microbicide gels do exhibit such behavior. The goal of the present work is to incorporate such yield stress behavior into the biomechanics of vaginal coating by non-Newtonian gels.
Coating by a microbicide vehicle is a physically diverse process in which several factors interact to govern the flow. Among these are gravity, transvaginal pressure gradients due to contractility of the supporting viscera, the transverse squeezing forces from the distended epithelium, the possible yield stress as a rheological property of the microbicide gel, and the dilution by vaginal fluids being exuded from the boundaries (i.e. tissue surfaces). There have been initial fluid mechanical studies of intravaginal vehicle flows; these have focused on the individual effects of gravity or epithelial squeezing [16–18]. These initial studies are instructive in developing a physical understanding of the mechanisms of intravaginal vehicle deployment flows. The model developed in [13] incorporates simultaneous effects of a longitudinally directed force along the vaginal canal, e.g., gravity, and transversely directed epithelial squeezing in a lubrication flow analysis. Both non-Newtonian (in the form of Carreau constitutive model) and Newtonian fluid behaviors were considered. The Carreau model was chosen because microbicide gels (which are highly hydrated) are shear thinning and typically exhibit a plateau at low shear strain rates in a log–log plot of shear stress vs. shear strain rate. Because vaginal coating flows are slow flows in which much of the flow field experiences low shear strain rates, it is important to employ a constitutive equation that embodies such plateau behavior. The Carreau model does precisely this, while the Power Law model overestimates shear stress at the biologically relevant low shear strain rates. In our prior analysis, a single dimensionless number, independent of viscosity, was derived to characterize the relative influences of squeezing and gravitational acceleration on the coating flow in the Newtonian case. A second scale, involving viscosity, was used to determine the spreading rate. In the case of a shearthinning fluid, the Carreau number also played a role. More recently, we extended this analysis, incorporating the effects of gel dilution due to contact with vaginal fluid produced at the gel-tissue interface [15]. Here, the model developed in [13] was supplemented by a convective-diffusive transport equation to characterize water transport into the gel, and, thus, local gel dilution. The problem was solved using a multi-step numerical scheme in a moving domain. The association between local dilution of the gel and its rheological properties was obtained experimentally, delineating the way constitutive parameters of a shear thinning gel were modified by dilution.
In the present study, we add yield stress behavior of microbicide vehicles to the elastohydrodynamic lubrication model of [13]. A microbicide gel can be designed to have a yield stress, e.g. by including derivatives of polyacrylic acid such as Carbopol and/ or polycarbophil in its composition. In a limiting case, a yield stress fluid is a viscoplastic material that behaves as a rigid body at low applied stress but flows as a viscous fluid at higher stress, i.e. behaving as a Bingham fluid [19]. The physical basis of such behavior is that the liquid contains particles (e.g., clay), or large molecules (e.g., polymers) that interact, creating a weak solid structure; a certain amount of stress is required to break this structure. Yield stress fluids are used, for example, as mathematical models of the flow of mud in offshore engineering, and in the analysis of slurries.
The flows of yield stress fluids have been investigated under a range of conditions in the literature [20,21]. It is common for flows of these fluids to exhibit complex, spatially inhomogeneous behavior, i.e., mixed flows of rigid body and viscous flow simultaneously. Details depend upon the absolute value of local stress throughout the fluid. This suggests the concept of the yield surface, over which the value of stress is equal to the yield stress. A yield stress fluid follows a different constitutive equation when the absolute value of stress exceeds the yield stress, delineated by the location of the yield surface. Due to such rheological behavior, yield stress fluids can be analyzed in separate domains of validity for each constitutive equation, as determined by the absolute local value of stress. As an alternative, Smyrnaios et al. used a continuous rheological model for yield stress fluids [22], which spans the entire domain with a single constitutive model [23]. Here, the yield surface does not have to be placed within the domain [24]. Such an approach was originally proposed by Papanastasiou [25]. In the present work, we employ another continuous rheological model, i.e. the biviscosity model [26], implemented for a Carreau-like fluid.
Although fundamental, the developments here will be useful to the microbicide community. The concept of a yield stress fluid as the gel delivery vehicle for an intravaginal microbicide is attractive because such a material may tend to stay in place after coating vulnerable surfaces (when shear stresses are sufficiently small) and not be prone to leakage from the vagina. In addition to being more cosmetically acceptable to users, this may be an important factor in sustaining drug delivery, and also providing a physical barrier to HIV migration from semen to tissue [27].
2. Problem formulation
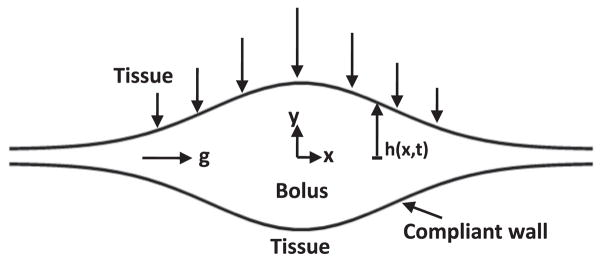
In this section, we first discuss the physics of the flow problem, and then explain a certain yield stress paradox observed in lubrication flows. We then determine conditions that render the lubrication theory of elastic wall squeezing flow consistent with the study of a yield stress fluid, using scaling analysis. We present a biviscosity model of a Carreau-like fluid with a yield stress, and the Reynolds lubrication equation as an evolution equation for the shape of a bolus of non-Newtonian fluid. The equations are developed in the symmetric domain –h(x,t) ≤ y ≤ h(x,t) and a body force is included in the x-direction. The physical problem and computational domain are sketched in Fig. 1. The model is formulated in a 2D Cartesian domain. The simplification of two-dimensional flow is quite relevant anatomically; the cross-section of the undistended human vaginal canal is “H” shaped, with the transverse dimension large compared to the vertical openings on its two sides [28].
Fig. 1.
Definition sketch of the vaginal canal, emphasizing the longitudinal direction. The introitus is to the right. The transverse direction has an “H” shaped cross-section; see text.
2.1. Physics of the flow problem
The elastohydrodynamic flow of microbicide gels is driven by initial distention of elastic surfaces (squeezing) and potentially, gravitational acceleration which depends on the woman’s posture. Following the placement of a gel into the vagina, the vaginal walls distend and this creates an elastic restoring force and leads to a pressure-gradient along the vaginal canal in the longitudinal direction. For the absence of a yield stress, for a non-Newtonian fluid, we make use of the lubrication approximation, obtaining the governing equation as [13],
| (1) |
where is the Carreau number and W = Eρ̃g̃/M̃ is a dimensionless group comparing gravitational and squeezing effects which drive the flow. The sign of b is chosen so as to render absolute value of τ̃xy positive. The constitutive model relates the shear-rate and the shear stress, , where for a Carreau-like fluid. This features shear thinning with a plateau at low shear rates, leading to a finite viscosity at zero-shear rate. The highly hydrated gels applied vaginally tend to exhibit such behavior. In the case of a Newtonian fluid, F(τ̃) = 1/m̃0 (or n = 1 in the Carreau-like model), and the governing equation reduces to,
| (2) |
Details of these derivations can be found in [13]. Note that dimensional variables were indicated with a tilde in [13]. Here and in the model that we present below, we have made use of the one dimensional constrained continuum model [29] approximation to account for the elastic forces of the vaginal walls. In this approximation, the fluid pressure near a compliant wall is linearly related to the local deformation of that wall. In general, for a deformation h, the fluid pressure is given by p = (E/T)h ≡ Mh. Here, E is the elastic (Young’s) modulus of the compliant layer, T is its thickness, and M is termed the compliance of the elastic wall.
The presence of a yield stress complicates the problem in the form of a yield stress paradox, which is discussed in the next section. In solving the yield stress case we again make use of the lubrication approximation. In this analysis, we seek a method of reasonable and consistent approximation for the fluid mechanics, which will be amenable to rapid solutions, such as one would need in microbicide gel design. The constrained continuum model has been previously used by Lighthill and colleagues in the analysis of deformation effects in lubrication theory based blood flow [1,30]. Given our limited understanding of vaginal wall mechanics, we believe it is reasonable to use that model here. As an improved understanding of those mechanics emerges, then more accurate numerical approaches to solution of the fluid mechanics will become appropriate.
2.2. Yield stress paradox
Previous analyses of squeezing flows of Bingham fluids with the lubrication approximation have produced conflicting results [31]. One must expect an un-yielded region of the yield stress fluid near the plane of symmetry, which would not flow; that is, this region should behave like a solid according to the rheological properties of a yield stress fluid, (e.g., Bingham fluid, Herschel–Bulkley fluid). However, owing to the fact that the apposed walls are approaching one another, there must be a corresponding flow, in the longitudinal direction. This paradox originates in the neglect of the normal stresses compared with the shear stresses while following the lubrication approximation. Hence, normal stresses should be considered for the squeeze flow of a Bingham fluid, i.e., lubrication theory might not be applicable when the behavior of a yield stress fluid is analyzed [22].
The presence of the rate of strain in the denominator of the constitutive equation of a Bingham fluid renders this model singular as the yield surface is approached. The biviscosity model is one of the models proposed in order to remove this singularity [32,26]. That model allows for the determination of certain conditions under which lubrication theory may be applied to the squeezing flow of the yield stress fluid. The constitutive equation of the biviscosity model of a Newtonian fluid with yield stress is written,
| (3) |
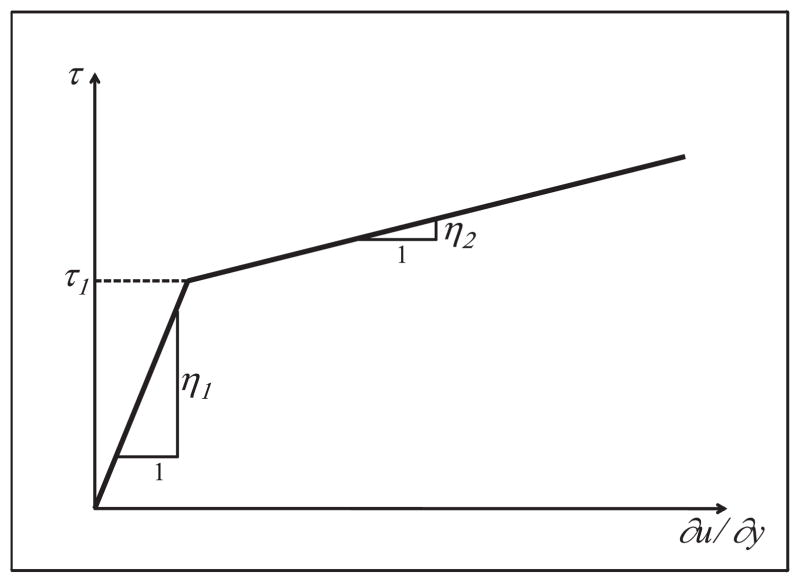
where, τy = τ1(1 − δ) and δ is the viscosity ratio, δ = η2/η1. Fig. 2 shows the stress–strain-rate curve of the biviscosity model of a Newtonian fluid. The simple Newtonian case is recovered when δ = 1. The case of a Bingham fluid [19] is approached in the limit δ → 0. Wilson [32] determined conditions that make use of lubrication theory consistent with the analysis of a biviscosity yield stress fluid, by using scaling analysis. The condition is derived for the fluid squeezed between two solid disks. An analogous set of conditions consistent with the elastic wall squeezing flow is required for use in the problem of interest here.
Fig. 2.
Stress–strain-rate curve of the biviscosity model of a Newtonian fluid.
2.3. Elastohydrodynamic lubrication theory with a biviscosity yield stress fluid
We begin by sketching what may be called standard lubrication theory. The balance of linear momentum for the x- and the y-directions is written as,
| (4) |
| (5) |
Hence, with appropriate boundary conditions,
| (6) |
Yield surfaces, where the fluid starts yielding, can be located with Eq. (6). For the surface in the interval 0 < y ≤ h(x, t), the result is y1, where
| (7) |
Eq. (3), the constitutive equation of the biviscosity model with constant viscosity, is used here, with appropriate boundary and interface conditions. This leads to an expression for the axial velocity u:
| (8) |
The order of the axial normal stress τxx can be obtained from the axial velocity u.
| (9) |
The group of scales of the axial normal stress τxx is calculated in terms of other known scales, with careful manipulation of Eqs. (8) and (9).
| (10) |
Here, H and L are length scales for the transverse (thickness) and longitudinal directions, respectively, and G = ∂p/∂x. On the other hand, the scale of shear stress τxy is obtained from Eq. (6).
| (11) |
In order to neglect normal stress, i.e., for the lubrication approximation to be valid, O(τxx) should be much smaller than O(τxy). This leads to the requirement
| (12) |
where ε = H/L, and δ = η2/η1.
Hence, it is self-consistent to analyze a biviscosity yield stress fluid with the lubrication approximation when Eq. (12) is satisfied. In particular, we require τy to be small enough and δ to be not too small.
2.4. A constitutive equation of a Carreau-like model with a yield stress
The ‘purest’ representative rheological model of a yield stress fluid is the Bingham model [33]:
| (13) |
As noted above, we have found it useful to work with a Carreau-like model to account for details of shear-thinning behavior evident in most gel delivery vehicles [13]. The original Carreau model can be written as . Here, η is viscosity, η0 is the zero shear viscosity, λ is the relaxation time of the fluid, γ̇ is the shear rate invariant and n is the power index. The parameters of the Carreau model can be converted into those of Carreau-like model asymptotically [13] in the relationship m0 = η0 and m = η0/λ1−n. We can alter the constitutive equation of a Carreau-like model to include a true yield stress through simple modification, as based on the Bingham model. This constitutive equation of a Carreau- like model with a yield stress would then read,
| (14) |
Here,
| (15) |
The Carreau-like model is effective in the region where |τxy| > τy. When |τxy| < τy, the fluid behaves like a solid.
2.5. Biviscosity model of a Carreau-like fluid with a yield stress
Now we follow the lead of Wilson [32], and define a biviscosity model of a Carreau-like fluid with a yield stress. As we shall show, the biviscosity captures more realistic yield stress behavior for the specific types of fluids we are considering. The model (cf. Eq. (3)) may be written
| (16) |
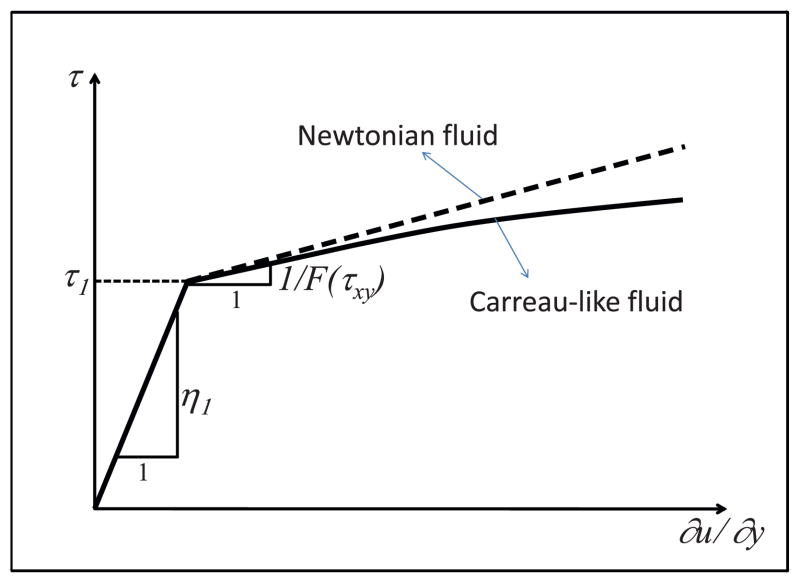
where, such that τy is yield stress, and τy = τ1(1 − δ). Here, δ is the viscosity ratio, δ= 1/η1F(τxy). We plot the stress–strain curve of the biviscosity model of a Carreau-like fluid at Fig. 3. Here, the exponent n of the function F(τxy) is assumed to be less than one, which means that a Carreau-like fluid is a shear-thinning fluid. F(τxy) can be written through modification of Eq. (15).
Fig. 3.
Stress–strain curve of the biviscosity model of a (shear-thinning) Carreau-like fluid.
| (17) |
Next, we present the Reynolds lubrication equation into which our constitutive model is substituted:
| (18) |
where,
| (19) |
We have developed the governing equations accounting for the gravitational forces. However, in further developments here we shall neglect gravity for the following reasons. There is no standard way of inserting these microbicide gels. Gravitational effects can therefore be transient and act in any direction, as determined by the user’s posture during and after gel insertion.
In the present analysis, the elastohydrodynamic flow is driven by initial distention of elastic surfaces and the resultant squeezing of the fluid bolus, which is initially at rest. This distention leads to pressure gradients and, eventually, fluid flow. We first integrate the x-momentum equation in the y-direction to obtain the shear stresses. Neglecting gravity and using the lubrication approximation, this equation becomes (∂p/∂x = ∂τ/∂y). Here, shear stress can be obtained as, (τ = y∂p/∂x = yM∂h/∂x). Note that at y = 0, τ = 0 due to symmetry. Then by substituting shear stresses into Eqs. (17) and (19), m2 values are obtained. Integrating the x-momentum equation in the y-direction twice, u1 values are obtained. Velocities in the y-direction (u2) are easily extracted from the in compressibility condition. In the mean time, m2 values are substituted into the Reynolds lubrication equation, Eq. (18), and new height profile is obtained. Iteration proceeds and updated height profile is used to evaluate new shear stresses. The Reynolds lubrication equation, Eq. (18) is solved explicitly. As a partial check on accuracy, an asymptotic analysis of a closely related problem was given in our previous study [13]. Another check on accuracy was presented in [34] which tracks the integral balance of linear momentum. Stability also should be checked because the Reynolds lubrication equation is solved explicitly in time. A stability analysis including the influence of the Deborah number was presented in [34].
The representative viscosity of the Carreau-like model with a yield stress, m0, can be used in the scaling analysis. Hence, the ratio of the yielded fluid viscosity to the un-yielded fluid viscosity, δ, is written in δ = m0/η1. Applying the condition, ε/δ≪1, one of Eq. (12), the use of lubrication theory is self-consistent in the case when
| (20) |
The pressure scale should also be considered here. Given the limitations on magnitude of the Reynolds number and the thin layer assumption, pressure is made dimensionless by use of a scale constructed from the shear stress, P = (m0U/H)/ε.
The velocity scale U is chosen to be the centerline velocity for flow due only to the compliance of the surfaces, i.e., the velocity scale when gravity is zero [13]. For Newtonian fluids with viscosity μ, the centerline velocity of pressure driven flow is , where is pressure gradient, h is the height of the channel in which fluid is flowing. The equation of the compliance of the elastic wall, p = (E/T)h ≡ Mh, can be applied to here, which leads to . Hence, the velocity scale is U = MH3/(2μL) for Newtonian fluids. In the case of a Carreau-like model, this can be written U = MH3/(2m0L).
The pressure scale is found to be P = (MH)/2 for the elastic wall boundaries with compliance, M. Hence, one of the conditions for the neglect of the normal stresses is obtained from Eq. (12), which is
| (21) |
The last term of Eq. (12) can be written,
| (22) |
The normal stresses of the fluid should be considered when (20)– (22) are not satisfied. The first condition of Eq. (12) must be satisfied in all cases due to the use of lubrication theory here.
3. Results and discussion
Overall, the use of lubrication theory in the analysis of elastohydrodynamic flow of a Carreau-like fluid with a yield stress is self-consistent, provided that four conditions are satisfied: ε ≪ 1 and (20)–(22). However, five rheological parameters: yield stress τy, first viscosity η1, power index n, zero shear viscosity of Carreau-like model m0, modified viscosity of Carreau-like model m, must be known in order to evaluate these conditions.
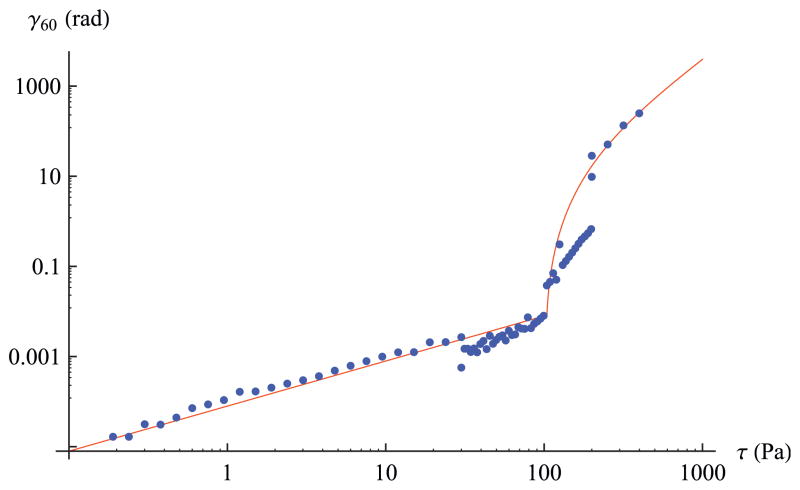
The measurement of yield stress has been historically problematical [20,21,35,36]. In the present study, we used the method given by Kulicke et al. [37] as applied to a test gel that was constructed using hydroxyethylcellulose and Carbopol. The presence of the latter macromolecule is what gives rise to yield stress behavior in this gel [11]. This is a relatively high viscosity gel, in the context of prototypes for use as vaginal microbicide vehicles. Fig. 4 illustrates results of application of the Kulicke method to this gel. In the method, a plot is created of stress vs. strain (not strain rate) for a gel, during unidirectional rotation in a rheometer with a parallel plate configuration. We used a TA Instruments (New Castle, DE) 1500ex rheometer, and measurements were performed at body temperature (37 °C). The yield stress is defined as the value of stress in which there is an abrupt change in slope of the stress vs. strain curve. This point was found by stepwise numerical computation of the slope of the plot of stress vs. strain. This same rheometer was used to obtain viscosity as a function of shear rate (at 37 °C), using a controlled stress protocol that enabled measurements at shear rates down to about 10−3 s−1. These data were processed to obtain the values of the parameters in the Carreau model [38], after first subtracting the value of measured yield stress from the set of stress measurements obtained by the rheometer.
Fig. 4.
Strain at 60 s as a function of applied stress. The dots show experimental data; the solid line shows the best-fit rheological parameters in Eq. (23).
The data in Fig. 4 are the superposition of results from two experiments. In the first, we acquired individual data over a larger time step than in the second experiment (apparent in Fig. 4). Our intent in the second experiment was to obtain a more refined picture of the change in slope. However, this second rheometric protocol created a different time history of mechanical conditions for the gel. Denn [35] has pointed out that this can lead to differences in configuration of the gel microstructure which give rise to differences in quantitative macro-scale stress vs. strain data. In both rheometric experiments there are abrupt changes in the slope of the curve and these occur at points that are relatively close. The distinction is not important to the theoretical developments of the analyses presented here. We have shown both sets of experimental results to illustrate the challenges of measuring yield stress.
We now propose a means by which to extract the five constitutive parameters from the experimental data. The thickness of the gel, h, in the rheometer is small compared to the length scale in the direction of applied stress. Therefore, the lubrication approximation can be employed to model the flow in the rheometer. Hence, we assume that pressure gradients are negligible in the direction of applied stress, and consequently a linear velocity profile is obtained, i.e. Couette flow. This is a good approximation because the strain at 60 s, γ60, has a linear dependence on applied stress for small values of stress. Note that any significant pressure gradient would result in at least a quadratic change in velocity, leading to a curved relation between γ60 and applied stress for a Newtonian fluid. Substitution of the biviscosity model of a Carreau-like fluid with a yield stress, Eq. (16), into the velocity profile enables us to determine the velocity profile and, thus total strain at 60 s, γ60, as follows, Experimental data obtained following the methods of [11] and the fit of (23) into the experimental data are shown in Fig. 4. The fitted values of the rheological parameters are given in Table 1.
Table 1.
Parameters of the constitutive equation for undiluted test gel.
| τy (Pa) | η1 (Pa s) | n | m(Pa sn) | m0 (Pa s) |
|---|---|---|---|---|
| 109.35 | 37268.1 | 0.4222 | 44.43 | 742.43 |
| (23) |
Now that we have determined the constitutive parameters from the straightforward analysis of the rheometer flow, we can turn to examining the validity conditions for lubrication analysis of the vaginal flow. Table 2 shows the resulting values after the parameters in Table 1 are substituted into the conditions: ε ≪1 and (20)– (22). In keeping with the need to develop a rapidly solvable approximation to this flow for use in design calculations, we shall accept as reasonably well-satisfied the criteria of Eq. (12).
Table 2.
Conditions given by (20)–(22) and the resulting values after the parameters given in Table 1 are substituted.
| ε ≪ 1 | ||||||
|---|---|---|---|---|---|---|
| 0.0125 | 0.6275 | 0.0044 | 0.2196 |
Two of the conditions, and are more critical. The first and third conditions, ε ≪ 1 and , are satisfied as long as the second and fourth conditions are satisfied separately, owing to the small value of δ = m0/η1, i.e. δ ≪ 1.
Given these experimental results, and having addressed (at least approximately) the conditions of validity of the lubrication approximation, we now consider a simulation of the coating flow of this gel driven by squeezing from the distended vaginal walls.
The initial condition for the shape of the bolus is taken as,
| (24) |
The fluid volume of such a bolus (above the offset h∞) is , where c is the vaginal width, i.e. 2 cm. The volume of the bolus here is 3 mL. As a scale for the height H, we choose 0.5 cm; this scale is of the order of magnitude of the maximum height of the bolus at time zero. Here we choose h∞ = 0.05H and b = 0.45H, and obtain .
The boundary conditions at the outlets of the channel far from the gel bolus are given as:
| (25) |
Here, L is the half of the vaginal length, and taken as 20 cm.
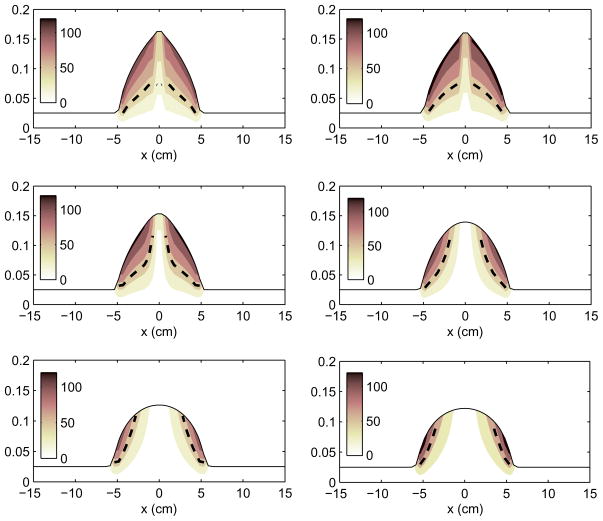
The applied stress depends on several parameters such as the pressure gradient and gel rheological properties. As the gel bolus coats the vaginal surface, gradients in height (i.e. thickness), and thus pressure gradients, become smaller. Therefore the shear stress, which is proportional to the pressure gradient, decreases. This enlarges the un-yielded region within the bolus and affects the coating process. Fig. 5 illustrates the growth of the un-yielded region within the gel over time. The contours of the shear stresses (Pa) are plotted in Fig. 5 at 10 s, 1, 5, 30, 90, and 120 min (left-to-right, top-to-bottom). Here, the yield surface (dashed line) within the bolus is defined by Eq. (7). According to Eq. (7), an un-yielded zone occurs below the dashed line, while the yielded region is located between the dashed line and the surface of the bolus (solid line). The graphs are plotted only for the upper half of the bolus because the domain is symmetric with respect to the x-axis. Thus, the coating flow of the gel bolus begins as a flow of mostly yielding material. There is a gradual transition to un-yielded material which, in this biviscosity model, flows much more sluggishly. The gel in this study (termed a “bolus gel”) was designed with the intent that it does not spread appreciably along the vaginal canal. This design goal derives from the hypothesis that such limited gel flow could improve retention within the canal over time. The present analysis demonstrates this theoretically. However, the spatial extent of gel spreading may be quite limited if the yield stress is excessive.
Fig. 5.
Contour plots of the shear stresses (Pa) along the channel (cm) at 10 s, 1, 5, 30, 90, and 120 min (from left-to-right, top-to-bottom). Yield surfaces, Eq. (7), are plotted as dashed lines. The un-yielded zone occurs below the dashed line, while the yielded region is located between the dashed line and the surface of the bolus (solid line). Note that dashed lines are exaggerated. In reality, they are simply lines of infinitesimal thickness, and represent the interface between the yielded and the un-yielded regions.
4. Conclusions
In summary, we have studied an important biological problem with significance related to efforts to prevent infection by HIV. The problem reduces to flow of a shear thinning fluid, with a yield stress, along a two-dimensional channel, as driven by the elastic squeezing forces of the distended channel walls. This problem is in the spirit of a large body of work on flows of yield stress fluids, but has a number of features not previously considered and/or combined, for example: (1) the constitutive equation is an alternative to the Power Law model (we used the Carreau model) to account for the low shear rate behavior of the types of fluids relevant to this specific problem; and (2) the elastic forces driving the flow are coupled to the flow. We investigated conditions under which lubrication analysis is valid for the flow, and developed four conditions for self-consistency of our approach, two of which dominate: and , when δ = m0/η1 ≪1. In addition, we illustrated the extraction of five rheological parameters from rheometric data for a test gel which is an actual prototype gel for vaginal delivery of anti-HIV molecules: yield stress τy, first viscosity η1, power index n, zero shear viscosity of Carreau-like model m0, and modified viscosity of the Carreau-like model m. We presented reasonable validation of the self-consistency conditions in the model, in keeping with the goals of the effort to obtain a rapidly solvable model suitable for use in design calculations. Finally, the yield surface and height profile of a spreading bolus of the gel were obtained. These showed growth of the un-yielded region of gel due to the decreasing pressure gradients that accompany the flow. Beyond the application to vaginal coating by microbicide gel vehicles, this work represents, more generally, extension of the work of Wilson [32] to resolve the yield stress paradox, here for elastohydrodynamic squeezing flows of a yield stress fluid.
Acknowledgments
The authors acknowledge support from NIH Grant No. AI 077289 (D.F.K.), including a subaward to the University of California, and from California HIV/AIDS Research Program Grant No. ID07-B-135 (A.J.S).
References
- 1.Lighthill MJ. Pressure-forcing of tightly fitting pellets along fluid-filled elastic tubes. J Fluid Mech. 1968;34:113–143. [Google Scholar]
- 2.Jin ZM, Dowson D. Elastohydrodynamic lubrication in biological systems. Proc Inst Mech Eng J: J Eng Tribol. 2005;219:367–380. [Google Scholar]
- 3.Holly FJ, Holly TF. In: Lacrimal Gland, Tear Film, and Dry Eye Syndromes. Sullivan DA, editor. Plenum; New York: 1994. [Google Scholar]
- 4.Jones MB, Fulford GR, Please CP, McElwain DLS, Collins MJ. Elastohydrodynamics of the eyelid wiper. Bull Math Biol. 2008;70:323–343. doi: 10.1007/s11538-007-9252-7. [DOI] [PubMed] [Google Scholar]
- 5.Gouldstone A, Brown RE, Butler JP, Loring SH. Elastohydrodynamic separation of pleural surfaces during breathing. Respir Physiol Neurbiol. 2003;137:97–106. doi: 10.1016/s1569-9048(03)00138-1. [DOI] [PubMed] [Google Scholar]
- 6.Stone A. Microbicides: a new approach to preventing HIV and other sexually transmitted infections. Nat Rev Drug Discov. 2002;12:977–985. doi: 10.1038/nrd959. [DOI] [PubMed] [Google Scholar]
- 7.Vermani K, Garg S. The scope and potential of vaginal drug delivery. Pharm Sci Technol Today. 2000;3:359–364. doi: 10.1016/s1461-5347(00)00296-0. [DOI] [PubMed] [Google Scholar]
- 8.Harrison PF, Rosenberg Z, Bowcut J. Topical microbicides for disease prevention: status and challenges. Clin Infect Dis. 2003;36:1290–1294. doi: 10.1086/374834. [DOI] [PubMed] [Google Scholar]
- 9.DCruz OJ, Uckun FM. Clinical development of microbicides for the prevention of HIV infection. Curr Pharm Des. 2004;10:315–336. doi: 10.2174/1381612043386374. [DOI] [PubMed] [Google Scholar]
- 10.Abdool Karim QA, et al. Effectiveness and safety of Tenofovir gel, an antiretroviral microbicide, for the prevention of HIV infection in women. Science. 2010;329:1168–1174. doi: 10.1126/science.1193748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mahalingam A, Smith E, Fabian J, Damian FR, Peters JJ, Clark MR, Friend DR, Katz DF, Kiser PF. Design of a semisolid vaginal microbicide gel by relating composition to properties and performance. Pharm Res. 2010;27:2478–2491. doi: 10.1007/s11095-010-0244-1. [DOI] [PubMed] [Google Scholar]
- 12.Skotheim JM, Mahadevan L. Soft lubrication: the elastohydrodynamics of nonconforming and conforming contacts. Phys Fluids. 2005;17:092101. [Google Scholar]
- 13.Szeri AJ, Park SC, Verguet S, Weiss A, Katz DF. A model of transluminal flow of an anti-HIV microbicide vehicle: combined elastic squeezing and gravitational sliding. Phys Fluids. 2008;20:083101. doi: 10.1063/1.2973188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Katz DF, Henderson M, Owen DH, Plenys AM, Walmer DK. What is needed to advance vaginal formulation technology? In: Rencher WF, editor. Vaginal Microbicide Formulations Workshop. Lippencott-Raven; Philadelphia: 1998. [Google Scholar]
- 15.Tasoglu S, Peters JJ, Park SC, Verguet S, Katz DF, Szeri AJ. The effects of inhomogeneous boundary dilution on the coating flow of an anti-HIV microbicide vehicle. Phys Fluids. doi: 10.1063/1.3633337. Submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kieweg SL, Geonnotti AR, Katz DF. Gravity-induced coating flows of vaginal gel formulations: in vitro experimental analysis. J Pharm Sci. 2004;93:2941–2952. doi: 10.1002/jps.20194. [DOI] [PubMed] [Google Scholar]
- 17.Kieweg SL, Katz DF. Squeezing flows of vaginal gel formulations relevant to microbicide drug delivery. J Biomech Eng. 2006;128:540–553. doi: 10.1115/1.2206198. [DOI] [PubMed] [Google Scholar]
- 18.Kieweg SL, Katz DF. Interpreting properties of microbicide drug delivery gels: analyzing deployment due to squeezing. J Pharm Sci. 2007;96:835–850. doi: 10.1002/jps.20774. [DOI] [PubMed] [Google Scholar]
- 19.Bingham EC. An investigation of the laws of plastic flow. US Bur Stand Bull. 1916;13:309–353. [Google Scholar]
- 20.Barnes HA. The yield stress – a review or ‘παντα ρει’ – everything flows? J Non-Newtonian Fluid Mech. 1999;81:133–178. [Google Scholar]
- 21.Barnes HA, Nguyen QD. Rotating vane rheometry – a review. J Non- Newtonian Fluid Mech. 2001;98:1–14. [Google Scholar]
- 22.Smyrnaios DN, Tsamopoulos JA. Squeeze flow of Bingham plastics. J Non- Newtonian Fluid Mech. 2001;100:165–189. [Google Scholar]
- 23.Florides GC, Alexandrou AN, Georgiou G. Flow development in compression of a finite amount of a Herchel–Bulkley fluid. J Non-Newtonian Fluid Mech. 2007;143:38–47. [Google Scholar]
- 24.Ellwood KRJ, Georgiou GC, Papanastasiou TC, Wilkes JO. Laminar jets of Bingham-plastic liquids. J Rheol. 1990;34:787–812. [Google Scholar]
- 25.Papanastasiou TC. Flows of materials with yield. J Rheol. 1987;31:385–404. [Google Scholar]
- 26.O’Donovan EJ, Tanner RI. Numerical study of the Bingham squeeze film problem. J Non-Newtonian Fluid Mech. 1984;15:75–83. [Google Scholar]
- 27.Lai BE, Geonnotti AR, DeSoto MG, Montefiori DC, Katz DF. Semi-solid gels function as physical barriers to human immunodeficiency virus transport in vitro. Antiviral Res. 2010;88:143–151. doi: 10.1016/j.antiviral.2010.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Roy S. Barrier Contraceptives: Current Status and Future Prospects. Wiley; New York: 1994. [Google Scholar]
- 29.Coyle DJ. Forward roll coating with deformable rolls: a simple one dimensional elastohydrodynamic model. Chem Eng Sci. 1998;43:2673–2684. [Google Scholar]
- 30.Fitzgerald JM. Mechanics of red-cell motion through very narrow capillaries. Proc R Soc Lond B. 1969;174:193–227. doi: 10.1098/rspb.1969.0088. [DOI] [PubMed] [Google Scholar]
- 31.Lipscomb GG, Denn MM. Flow of Bingham fluids in complex geometries. J Non-Newtonian Fluid Mech. 1984;14:337–346. [Google Scholar]
- 32.Wilson SDR. Squeezing flow of a Bingham material. J Non-Newtonian Fluid Mech. 1993;47:211–219. [Google Scholar]
- 33.Bird RB, Armstrong RC, Hassager O. Fluid Mechanics. Vol. 1. Wiley-Interscience; 1987. Dynamics of Polymeric Liquids. [Google Scholar]
- 34.Park SC. PhD Dissertation. University of California; Berkeley: 2009. Fluid mechanics of delivery of a non-Newtonian anti-HIV microbicide. [Google Scholar]
- 35.Bonn D, Denn MM. Yield stress fluids slowly yield to analysis. Science. 2009;324:1401–1402. doi: 10.1126/science.1174217. [DOI] [PubMed] [Google Scholar]
- 36.Nguyen QD, Boger DV. Measuring the flow properties of yield stress fluids. Annu Rev Fluid Mech. 1992;24:47–88. [Google Scholar]
- 37.Kulicke WM, Arendt O, Berger M. Characterization of hydroxypropylmethylcellulose- stabilized emulsions Part II: the flow behaviour. Colloid Polym Sci. 1998;276:1024–1031. [Google Scholar]
- 38.Lai BE, Xie YQ, Lavine M, Szeri AJ, Owen DH, Katz DF. Dilution of microbicide gels with vaginal fluid and semen stimulants: effects on rheology and coating flow. J Pharm Sci. 2008;97:1030–1038. doi: 10.1002/jps.21132. [DOI] [PubMed] [Google Scholar]