Flip Angle Profile Correction for T1 and T2 Quantification with Look-Locker Inversion Recovery 2D SSFP Imaging

Abstract

Fast methods using balanced steady-state free precession (SSFP) have been developed to reduce the scan time of T1 and T2 mapping. However, flip angle (FA) profiles created by the short RF pulses used in SSFP deviate substantially from the ideal rectangular profile, causing T1 and T2 mapping errors. The purpose of this study was to develop a FA profile correction for T1 and T2 mapping with Look-Locker 2D inversion recovery SSFP and to validate this method using 2D spin echo as a reference standard. Phantom studies showed consistent improvement in T1 and T2 accuracy using profile correction at multiple FAs. Over six human calves, profile correction provided muscle T1 estimates with mean error ranging from excellent (−0.6%) at TR/FA = 18 ms/60° to acceptable (6.8%) at TR/FA = 4.9 ms/30°, while muscle T2 estimates were less accurate with mean errors of 31.2% and 47.9%, respectively.

INTRODUCTION

Inversion recovery spin echo (IR-SE) is an accurate method for T1 mapping but is limited in clinical application due to its prohibitively long acquisition time. To overcome this limitation, a number of fast T1 mapping methods using gradient echo (GRE) sequences have been proposed. These methods follow the transient magnetization after an inversion or saturation pulse, such as the Look-Locker method (LL) (1–4), or utilize the steady-state magnetization, such as the driven equilibrium single pulse observation of T1 (DESPOT1) method (5), or they are a combination of both (6,7). 2D inversion recovery balanced SSFP (IR-SSFP) is a promising approach due to the higher SNR efficiency of SSFP when compared to spoiled GRE (8) and can provide T2 estimations in addition to T1 (7). IR-SSFP has been used to perform fast T1 mapping in skeletal muscle (9).

There are a number of inherent challenges in these fast T1 mapping methods. Short radiofrequency (RF) excitation pulses are often used to reduce the repetition time (TR), especially for time-sensitive applications such as breath-hold myocardial T1 mapping (4,10–12). It is well known that the flip angle (FA) profile of a short slice-selective RF pulse can deviate substantially from the ideal rectangular profile. Because MR signal depends on the FA, the non-ideal FA profile introduces a bias in the estimated relaxation times when not properly accounted for in the signal fitting. This problem has been addressed for T1 mapping using dual FA 2D spoiled GRE imaging (13). In addition, FA profile correction has been investigated for T1 mapping using 3D spoiled GRE LL imaging (14,15). However, this method is specific to 3D imaging and assumes that the signal of a voxel is generated by a single FA determined by the position of that voxel along the slice direction. FA profile correction has not been investigated for 2D IR-SSFP, where a range of different FAs contribute to the signal of each voxel. Therefore, the purpose of this study was to develop and validate a signal fitting algorithm that takes into account the non-ideal FA profile for 2D LL IR-SSFP T1 and T2 mapping.

METHODS

Effective FA profile

Given a shaped RF pulse with magnitude B₁(t) and phase ϕ(t) in the rotating frame and a constant slice-select gradient G_z(t) = G, the resultant magnetization along the slice direction M(z) can be calculated by using the hard pulse approximation (16,17) as follows:

$$\begin{array}{l}\mathbf{M}(\text{z})\cong \left(\prod _{\text{i}=0}^{\text{N}-1}{\mathbf{R}}_{\mathbf{z}}(\psi ){\mathbf{R}}_{\mathbf{z}}({\varphi }_{\text{i}}){\mathbf{R}}_{\mathbf{x}}({\vartheta }_{\text{i}}){\mathbf{R}}_{\mathbf{z}}(-{\varphi }_{\text{i}})\right){\mathbf{M}}_{\mathbf{0}}(\text{z})\\ \psi =\gamma \text{Gz}\mathrm{\Delta }\text{t}{\varphi }_{\text{i}}=\varphi (\text{i}\mathrm{\Delta }\text{t}){\vartheta }_{\text{i}}=\gamma {\text{B}}_1(\text{i}\mathrm{\Delta }\text{t})\mathrm{\Delta }\text{t}\end{array}$$ [1]

where M(z) = [M_x M_y M_z]^T represents the magnetization vector, N is the number of discretizing hard pulses, Δt is the interval between hard pulses, R_x and R_z denote the rotation matrices around x and z axis, respectively, and M₀(z) = [0 0 1]^T is the initial equilibrium magnetization. Note that off-resonance and relaxation effects are ignored in Eq.1 (this simplification is justified when the RF pulse width is short as in this study). The transverse magnetization M_xy(z) at the end of the excitation and the corresponding effective FA profile α(z) are then given by:

$$\begin{array}{l}{\text{M}}_{\text{xy}}(\text{z})={({\text{M}}_{\text{x}}^2+{\text{M}}_{\text{y}}^2)}^{1/2}\\ \alpha (\text{z})=arcsin({\text{M}}_{\text{xy}}(\text{z}))\end{array}$$ [2]

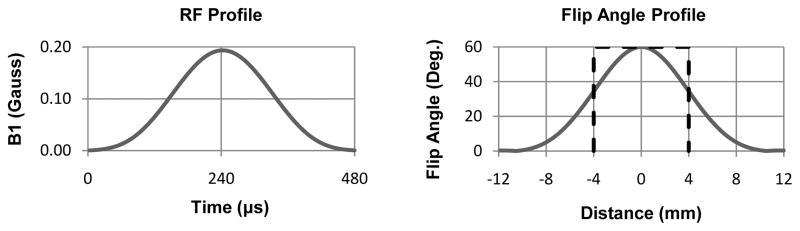
As an example, Fig. 1 shows a Hamming filtered half-sinc RF pulse (17) with a 60° nominal FA and its effective FA profile.

Figure 1.

RF profile of a half-sinc excitation pulse (apodized with a Hamming window) with a 60° nominal FA (left) and corresponding effective FA profile calculated using Bloch simulation (right). The dashed line shows the ideal rectangular FA profile over the slice thickness used in our imaging experiments (8 mm).

Look-Locker IR-SSFP T1 and T2 mapping with FA profile correction

This study implemented a 2D IR-SSFP sequence for LL T1 mapping. One LL period of this sequence consists of a non-selective hard inversion pulse and spoiler gradients, followed by 6 Kaiser-Bessel-ramped RF pulses prior to uninterrupted SSFP readout, and concluded by a sufficiently long time delay to allow the excited magnetization to return to equilibrium before the next period. The Kaiser-Bessel ramp provided a short and effective magnetization preparation for subsequent SSFP readout (18,19). A short hard pulse was used for longitudinal magnetization inversion instead of a long adiabatic pulse as it is difficult to quantify the inversion efficiency of an adiabatic pulse for short T2 tissues such as muscle (20). Given T1, T2, M₀ and pertinent sequence parameters (including the shapes of the imaging RF pulses), Bloch simulation can be used to follow the evolution of the magnetization over the course of the experiment and to calculate the transverse SSFP signal S (10,21) as follows (ignoring off-resonance effects):

$$\text{S}(\text{n},{\text{T}}_1,{\text{T}}_2,{\text{M}}_0)=\underset{\text{z}}{\int }[({\text{S}}_0(\text{z})-{\text{S}}_{\text{ss}}(\text{z}))\lambda {(\text{z})}^{\text{n}}+{\text{S}}_{\text{ss}}(\text{z})]\text{dz}$$ [3]

where

$$\lambda (\text{z})=\frac{cos(\alpha (\text{z}))({\text{E}}_1-{\text{E}}_2)+\sqrt{cos{(\alpha (\text{z}))}^2{({\text{E}}_1-{\text{E}}_2)}^2+4{\text{E}}_1{\text{E}}_2}}{2},$$ [4]

and the steady state transverse magnetization is given by

$${\text{S}}_{\text{ss}}(\text{z})={\text{M}}_0\frac{\sqrt{{\text{E}}_2}(1-{\text{E}}_1)sin(\alpha (\text{z}))}{1-({\text{E}}_1-{\text{E}}_2)cos(\alpha (\text{z}))-{\text{E}}_1{\text{E}}_2}$$ [5]

Here n is the index of the SSFP readouts, S₀(z) is the transverse signal at time TE in the first readout that follows the inversion pulse, spoiler gradients and the 6 Kaiser-Bessel ramp-up preparation, E₁ = exp(−TR/T₁), E₂ = exp(−TR/T₂), M₀ is a scaling factor (which includes then proton density and receiver sensitivity), α(z) is the flip angle at position z along the slice direction, and λ denotes the relaxation rate of the SSFP signal evolution (10,21). Note that Eq.3 is similar to Eq.6 in (21) or approach 2 in (10) (with a more generalized S₀(z) due to the use of a 6 Kaiser-Bessel ramp in this work), where the length of the SSFP readout is assumed to be long enough to allow the transverse magnetization to reach steady state, and the time delay between the end of the SSFP readout and the start of the next inversion pulse is long enough to allow a full relaxation of the longitudinal magnetization. Both of these conditions were met in our study. Eq.4 is the same as Eq. 5 in (21) except for the factor of 2 in the denominator, which was missing in (21). For TR ≪ T1, T2, the formula for λ can be simplified as in Refs (10) and (21) (this simplification was not used in this study).

It is important to note the dependency of S₀(z), S_ss(z) and λ(z) on the position z along the slice direction. Given the measured noisy SSFP data, denoted by S^*(n), T1, T2 and M₀ can be obtained by minimizing the sum of squared differences between the measured and expected signals:

$${\text{T}}_1,{\text{T}}_2,{\text{M}}_0=argmin\sum _{\text{n}}{(\text{S}\ast (\text{n})-\text{S}(\text{n},{\text{T}}_1,{\text{T}}_2,{\text{M}}_0))}^2$$ [6]

Imaging experiments

All experiments were performed at 1.5T (GE HDxt 15.0). For phantom imaging, four water tubes were doped with manganese chloride (MnCl₂) at 0.4, 0.2, 0.1, and 0.04 mM concentrations. For the volunteer study, the calf muscles of six healthy volunteers (4 male, 2 female, mean age of 26 years ± 3 [standard deviation (SD)]) were scanned. The study was approved by the local IRB and informed consent was obtained from all subjects prior to imaging.

IR-SSFP imaging parameters were as follows: TR = 5–5.4 ms (phantoms)/4.9 (humans); TE = TR/2 (symmetric full echo); nominal FA = 30°, 60°, 90° (phantoms)/30°, 60° (humans); FOV = 25 cm (phantoms)/26–30 cm (humans), partial phase FOV factor = 0.5, matrix = 256×128, slice thickness = 8 mm, readout bandwidth = ±62.5 kHz. To investigate the magnetization transfer (MT) effect of TR and FA on the SSFP signal of skeletal muscle tissue as suggested previously (22), subjects were also scanned with a long TR of 18 ms and FA of 30° and 60°. In addition, one volunteer was scanned using a FA of 90°. An 8-channel cardiac phased-array receive coil was used for all experiments. A Hamming filtered half-sinc pulse (17), which is the standard RF excitation pulse for the product 2D SSFP sequence on our system, was used in all experiments. Each scan consisted of multiple LL periods, and the length of each period is the time between consecutive inversion pulses and consisted of 1) an SSFP readout following the inversion pulse consisting of either 1024 SSFP TRs when using TR ~5 ms or 512 TRs when using TR = 18 ms to allow the transverse magnetization to reach steady state, and 2) a time delay between the end of the SSFP readout and the next inversion pulse (about 9 sec for phantoms and 5–6 sec for human imaging) to allow a full relaxation of the longitudinal magnetization. For 128 phase encodes and 0.5 partial phase FOV, 16 LL periods were required to complete the scan. The length of one LL period was 14 sec for phantoms and 10/15 sec (TR = 4.9/18 ms) for humans, with corresponding scan times of 3.7 min and 2.7/4 min, respectively. For comparison, standard 2D single-echo IR-SE and SE imaging with matching FOV and spatial resolution were performed to obtain the reference standard T1 and T2 values, respectively. B1 maps were also obtained in humans using the double FA method (23) for nominal FA error correction in LL data fitting.

Data analysis

A look-up table method was used to correct for signal bias due to Rayleigh noise in sum-of-squares magnitude images obtained with a multiple receiver coil (Fig. 2 in Ref (24)). This correction is particularly important for data points near the zero-crossing where the signal amplitudes are low. The negative polarity of the data points before zero-crossing was then restored by using the method proposed in (25). B1 correction was performed before fitting for T1 to account for imperfections in the inversion and imaging flip angle. In human subjects, an ROI was selected in the soleus muscle with uniform signal intensity and free of image artifacts. Signals were averaged over a 3×3 neighborhood before fitting to reduce noise effects. Bloch simulation was used to calculated the flip angle profile obtained directly from the scanner, which was a Hamming windowed half-sinc pulse. LL data fitting without FA profile correction was also implemented by assuming a rectangular FA profile in Eqs.3–5. In addition, voxel-wise T1 and T2 maps were obtained from all subjects. Processing was performed in MATLAB (Mathworks, Natick, MA) using a Dell PowerEdge R910 computer with 32 cores. The Nelder-Mead unconstrained non-linear solver was used for fitting and a non-linear least-squares fitting was used to obtain the reference T1 and T2 values from the spin echo data. Relative fitting residual, defined as ||Signal_measured−Signal_fitted||₂/||Signal_measured||₂×100, was calculated to measure the quality of the fit. Relative T1 and T2 errors were defined as ||T1_IR-SSFP−T1_IR-SE||₂/||T1_IR-SE||₂×100 and ||T2_IR-SSFP−T2_SE||₂/||T2_SE||₂×100. A two-tailed paired sample t-test was used to assess the differences in T1 and T2 values obtained with IR-SSFP and reference methods. A P value of less than 0.05 was considered statistically significant.

RESULTS

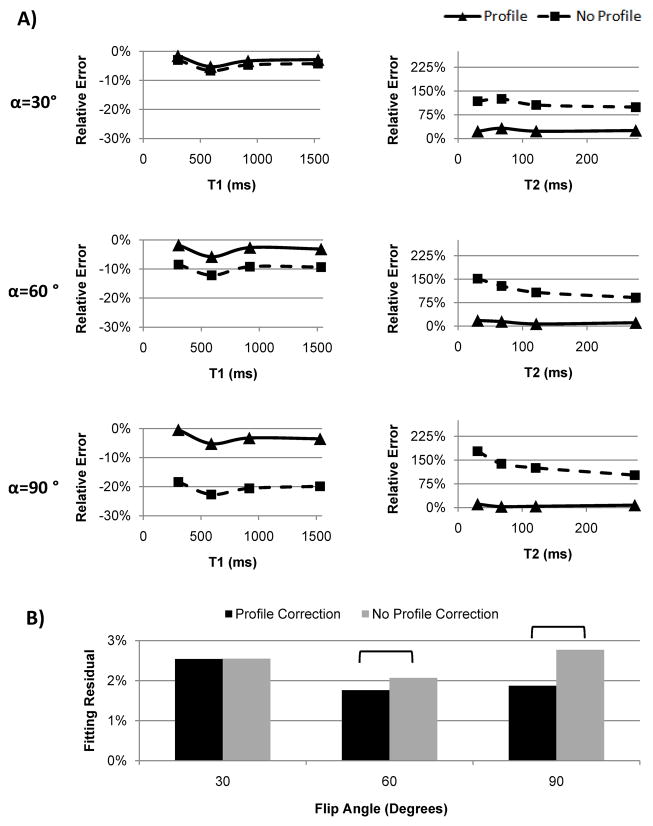
T1/T2 values of the four MnCl₂ phantoms obtained with reference standard SE methods were 304/30, 589/67, 919/121, 1532/275 ms. Figure 2a shows the relative T1 and T2 errors in the phantoms obtained with 2D LL IR-SSFP with and without FA profile correction, demonstrating consistently improved accuracy with the profile correction method for both T1 and T2, as well as increasingly larger T1 errors at higher FAs when profile correction was not used. Overall T1 errors were less than 5.8% when fitting with profile correction for FA range of 30°–90°, while T1 error could be as high as 22.7% when fitting without profile correction. Fitting with profile correction provided relative T2 error magnitudes in the range of 2.7–32.3%, while fitting without profile correction yielded much larger T2 error ranging from 91.1% to 177.9%. The differences in T1 and T2 errors obtained with and without profile correction were statistically significant for all FAs (P<0.005). Fitting residuals obtained without profile correction for FA of 60° and 90° were significantly higher than those obtained with profile correction, indicating poorer fits between the measured data and the signal model when FA profile is ignored (Fig. 2b).

Figure 2.

(A) Relative T1 and T2 errors obtained with Look-Locker 2D IR-SSFP with (solid line) and without (dashed line) FA profile correction at 30°, 60° and 90° nominal FAs on four MnCl₂ phantoms. Reference T1 and T2 values were obtained with reference standard spin echo methods. (B) Comparison of relative fitting residuals averaged over all four phantoms obtained with and without profile correction. Brackets indicate statistical significance (P<0.05). Note the increasingly larger fitting residuals obtained without profile correction as FA becomes larger than 60°, indicating that the assumption of constant FA profile becomes less adequate for this FA regime.

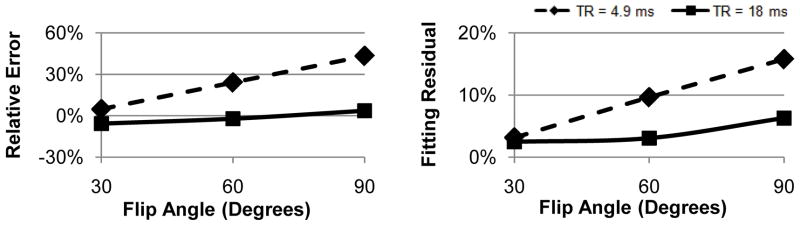
Figure 3 shows the effects of FA and TR on T1 error and fitting residual obtained in the calf muscle of one subject with FA profile correction. Note the small error and good fits obtained with a long TR of 18 ms or a small FA of 30°; however, unlike the trend observed in water phantoms (Fig. 2), shortening TR to 4.9 ms and employing a FA larger than 60° lead to much larger errors and poorer fits.

Figure 3.

Relative T1 error (left) and fitting residuals (right) obtained with FA profile correction in the calf muscle of one volunteer with a short TR of 4.9 ms (dashed line) and a long TR of 18 ms TR (solid line) at different FAs. Note the increasingly larger errors and worse fits at shorter TR or higher FA, most likely due to larger magnetization transfer effect in the muscle tissue in this regime (see Discussion).

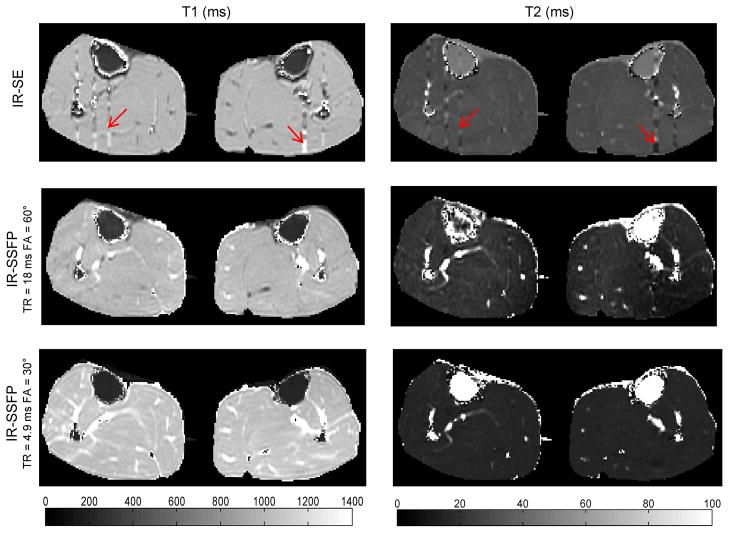
Table 1 summarizes T1 and T2 values obtained with Look-Locker 2D IR-SSFP and reference standard SE methods in human calves (N=6) using ROI analysis. FA profile correction at 60° with an 18 ms TR provided excellent T1 estimates (−0.6 ± 1.8% error) and T2 estimates with moderate accuracy (−31.2 ± 5.0% or −9.5 ± 1.2 ms error), representing a 94% and 80% improvement in accuracy for T1 and T2, respectively, when compared with results obtained without profile correction. Profile correction at 30° with a short 4.9 ms TR yielded less accurate results with a relative error of 6.8 ± 2.2% for T1 and −47.9 ± 2.3% for T2. Interestingly, fitting without profile correction at this FA and TR provided more accurate T1 (4.8 ± 2.1% error) and T2 (25.8 ± 4.1% error) estimates. Figure 4 shows voxel-wise T1 and T2 maps generated by the proposed fitting method with profile correction. Average fitting time was 23 msec per voxel.

Table 1.

T1 and T2 values of human calf muscle obtained with Look-Locker 2D IR-SSFP based methods with and without FA profile correction using ROI analysis. Two combinations of short TR/low FA and long TR/high FA were chosen for SSFP to minimize potentially confounding MT effect in muscle. Also shown are values obtained with reference standard SE based T1 and T2 mapping methods (N=6).

T1
	IR-SE	IR-SSFP FA=30° TR=4.9 ms		IR-SSFP FA=60° TR=18 ms
		Profile	No Profile	Profile	No Profile
Mean ± SD	985 ± 6	1052 ± 16	1033 ± 15	979 ± 20	874 ± 19
P		<.001	.002	.44	<.001

T2
	SE	IR-SSFP FA=30° TR=4.9 ms		IR-SSFP FA=60° TR=18 ms
		Profile	No Profile	Profile	No Profile
Mean ± SD	31 ± 2	16 ± 1	39 ± 3	21 ± 2	78 ± 5
P		<.001	<.001	<.001	<.001

Figure 4.

Example of T1 and T2 maps obtained with reference standard SE methods (top row) and with Look-Locker IR-SSFP and FA profile correction in the calf of one volunteer using TR/FA=18 ms/60° (middle row) and 4.9 ms/30° (bottom row). T1 maps were very similar between the reference standard and IR-SSFP at 18 ms/60° except in the areas affected by blood flow (red arrows). The T1 map obtained with 4.9 ms/30° appears more noisy. T2 maps are generally less accurate than T1 maps.

DISCUSSION

Our preliminary phantom and human results demonstrate that FA profile correction can greatly reduce errors in T1 and T2 mapping using the Look-Locker 2D IR-SSFP sequence. The improvement in both T1/T2 accuracy and fitting agreement is most obvious on water phantoms covering a wide range of T1/T2 values. In human calf muscles, the proposed method provided T1 estimates with accuracy ranging from excellent (−0.6% error) to acceptable (6.8% error) depending on the combination of TR and FA, while the T2 estimates were generally less accurate. While the effect of a non-ideal FA profile on T1 mapping has been studied in the context of spoiled GRE imaging (13), the method developed here confirms the importance of FA profile correction for Look-Locker 2D SSFP based T1 mapping with a shaped RF pulse, which is often ignored (4,10).

In this study, we observed increased T1 errors and larger fitting residuals in the calf muscle when a short TR of 4.9 ms was used in combination with a FA higher than 60° (Fig. 3). However, this trend was not present in water phantoms (Fig. 2). This discrepancy between phantom and in vivo results suggests the presence of on-resonance MT effect in muscles described previously by Bieri and Scheffler (22). Specifically, unlike the free water in phantoms, skeletal muscle tissue can be modeled with a binary spin-bath model with energy exchange between the two spin compartments. This exchange is a function of sequence TR and FA and leads to signal deviating from that derived from the Bloch equation for a single compartment. For our T1/T2 mapping application, employing a lower FA lessens this effect, but also reduces the dynamic range of the transient signal curve, making T1/T2 quantification more sensitive to noise. Using a longer TR also helps mitigate the MT effect, allowing for higher FAs to be used (Fig. 3) for improved robustness against noise, but at the cost of increased SSFP off-resonance artifacts. The long TR/high FA and short TR/low FA acquisitions demonstrated the effects of MT and FA profile. We should note that the IR-SSFP experiment with TR =18 ms was performed purely to validate our hypothesis regarding the MT effect. Off-resonance effects were minimized by performing a volume shim targeting the small imaging volume and accordingly only minor banding artifacts were observed in one leg which was excluded from ROI analysis. For general T1 mapping, however, the use of a low FA to mitigate the MT effect is recommended.

As MT tends to suppress SSFP signal, the non-ideal FA profile tends to increase the SSFP signal, and these opposite effects may accidently cancel each other out, resulting in good T1/T2 estimate even if both effects are ignored in the signal model. Our fairly accurate in vivo T1 results obtained without profile correction using a 4.9 ms TR and 30° FA demonstrate this phenomenon. Accordingly, care should be exercised when changing these sequence parameters to avoid errors or when applied to different tissues. We should note that while the MT effect has been shown to have a detrimental effect on spoiled GRE based T1 quantification (26), previous works on IR-SSFP based T1 mapping often utilized a high FA (e.g., 50°) and ignored this effect in their signal models (4,7,10). A method has been proposed (27) for a multi-component relaxometry method which accounts for MT effect in the SSFP signal model. However, this method requires multiple FAs (up to 15), potentially leading to long scanning times. Other authors have used small FAs (10° in (28) and 35° in (29)) for IR-SSFP based T1 mapping, but did not consider the MT effect. Finally, we should note that shortened tissue T1 will reduce the MT effect (22), thereby increasing the need for FA profile correction in post-contrast T1 mapping.

Although both T1 and T2 mapping can be obtained simultaneously with our method, T2 accuracy was found to be limited. For in vivo imaging with a 30° nominal FA, the relaxation is primarily dominated by T1 effect and becomes less dependent on FA profile (see Fig. 2 in Ref 17). As T2 mapping is sensitive to off-resonance effects in IR-SSFP (7), the limited T2 accuracy may also be explained by the omission of B₀ correction in the signal fitting algorithm. Despite these challenges, improved T2 accuracy was obtained with FA profile correction in this work.

T1 quantification using Look-Locker 2D IR-SSFP has been investigated previously. Our work follows the approach in (10), in which a Bloch equation based SSFP signal fitting algorithm was implemented for post-contrast myocardial T1 mapping. Here, we introduced FA profile correction and provided an in vivo comparison with reference standard T1 and T2 mapping methods. A three-parameter mono-exponential curve fitting was proposed in (4) to obtain an apparent relaxation rate T1^* which is then corrected using a formula originally proposed in (3) for IR spoiled GRE (FLASH) acquisition. The applicability of this correction to IR-SSFP has not been elucidated. The average T1 value of skeletal muscle obtained in normal volunteers reported in (4) was 780 ms, which corresponds to a 22% underestimation compared to other relaxometry studies (30,31). A SSFP-based correction formula for T1 was introduced in (7) which was derived from prior work on SSFP transient signal behavior in (21). This method only applies to an IR-SSFP acquisition prepared with a half-alpha RF pulse. In our study, we found that a half-alpha preparation led to severe ghosting artifacts and accordingly decided to use a 6 Kaiser-Bessel ramp preparation which has been shown to be more robust against off-resonance effects (18,19).

The proposed fitting algorithm requires SSFP signal integration over the FA profile (Eq.3) at each iteration step and accordingly the computational demand is higher than previous methods (13,32). Parker et al proposed a fast look-up table technique for T1 mapping using dual FA 2D spoiled GRE imaging, but this approach becomes non-trivial when multiple parameters (T1, T2, M₀) need to be estimated such as in IR-SSFP. We have explored several venues to reduce the fitting time. First, the number of points required for discretizing the FA profile was optimized and as few as 11 points along the profile was found to provide accurate results. Since the FA profile is symmetric for the RF pulse used in this study, signal computation only needs to be carried out for half of the profile. Second, as the fitting of multiple voxels is highly parallelizable, a multi-core version of our algorithm was implemented, achieving an average fitting time of 23 msec per voxel. Further optimization and implementation of the fitting algorithm using a general-purpose programming language such as C may offer further reduction in fitting time.

This study has several limitations. The effects of B₀ inhomogeneity, which may not be ignored at higher field strengths or in other organs such as the heart, were not considered. However, B₀ maps can be acquired and incorporated into the Bloch equation based signal fitting algorithm. Additionally, while B₁ mapping can improve T1 and T2 accuracy against FA error of the inversion and imaging RF pulses (e.g., due to imperfect prescan), this method requires extra scan time. Also, we only investigated the half-sinc pulse, which is the standard RF excitation pulse for the product 2D SSFP sequence on our scanner. The effect of other RF pulses can be calculated similarly using the hard pulse approximation approach.

In conclusion, FA profile correction significantly improves T1 and T2 quantification with 2D LL IR-SSFP relaxometry and the MT effect in skeletal muscle tissues needs to be considered during pulse sequence design and/or signal fitting for accurate results.