Abstract
This work is the fifth in a series of papers on the thermodynamically constrained averaging theory (TCAT) approach for modeling flow and transport phenomena in multiscale porous medium systems. The general TCAT framework and the mathematical foundation presented in previous works are used to develop models that describe species transport and single-fluid-phase flow through a porous medium system in varying physical regimes. Classical irreversible thermodynamics formulations for species in fluids, solids, and interfaces are developed. Two different approaches are presented, one that makes use of a momentum equation for each entity along with constitutive relations for species diffusion and dispersion, and a second approach that makes use of a momentum equation for each species in an entity. The alternative models are developed by relying upon different approaches to constrain an entropy inequality using mass, momentum, and energy conservation equations. The resultant constrained entropy inequality is simplified and used to guide the development of closed models. Specific instances of dilute and non-dilute systems are examined and compared to alternative formulation approaches.
Keywords: Averaging theory, TCAT, Averaged thermodynamics, Model formulation, Species transport, Porous media
1 Introduction
This paper is the fifth in a series of efforts intended to yield complete, rigorous, closed models that describe transport phenomena in multiscale porous medium systems using the thermodynamically constrained averaging theory (TCAT) approach. The first paper [5] provided an overview of the general TCAT approach, which is built on averaged conservation and thermodynamic equations that constrain the entropy inequality. The second paper provided the mathematical fundamentals and theorems that are used to generate needed macroscale equations [15]. The third paper illustrated the application of the method for single-fluid-phase, single-species flow in a porous medium [6]. The fourth paper formulated multiphase conservation and balance equations for species, advanced averaged thermodynamic relations for species, and detailed conditions that must hold at equilibrium [16]. Here we consider the formulation of models to describe single-fluid-phase flow and multiple species transport in a porous medium system.
Modeling of species transport involves determining the velocity of each species relative to the barycentric velocity of the flow. At the microscale, the Fickian approximation whereby the diffusive flux of a chemical is modeled as being proportional to the gradient of mass or mole fraction has been very successful for dilute solutions. However, when the solution is not dilute, the interaction of the various species with each other requires that this simple expression be expanded to account for these interactions.
At the macroscale, the most commonly used model for diffusion and dispersion mimics the Fickian form and requires a proportionality between the total dispersive flux, which includes the effects of diffusion as well as subscale velocity variations, and the species mass fraction. This traditional approach has been successful in describing the movement of a dilute species in homogeneous macroscale porous medium systems. Such systems are straightforward to create at the laboratory scale and typical of many engineered systems. This success is responsible for the widespread use in practice of the common advective-dispersive model.
It is now widely recognized that most natural systems are not sufficiently homogeneous at the macroscale for the common Fickian dispersion model to provide an accurate description of species transport over all length scales [e.g., 1, 3, 18]. This is especially true for non-dilute and highly heterogeneous systems where the length scale of concern is of the same order of magnitude as the scale of spatial variability. This failure has led to many alternative models, including multiple domain models, time and space variable dependence modifications of the standard dispersion model, continuous time random walk approaches, fractional derivative models, and general non-local approaches. Such non-local models are not the focus of this work.
Although some approaches to non-Fickian dispersion have been proposed [e.g., 8, 9, 13], an apparent void exists in deriving macroscale species transport models based upon a microscale flow and transport equations, appropriate microscale thermodynamics, rigorous averaging of conservation and thermodynamic equations that maintains consistency across scales, and a general, consistent procedure for closing the models at the macroscale. In fact, no such macroscale models with a strong theoretical foundation have been derived for either the non-dilute situation or the dilute limit. The development of such models would provide a sound means upon which a hierarchy of models of increasing sophistication could be built. The TCAT approach provides the path for derivation of this sort of model.
Some open issues are important in relation to building better macroscale species transport models. First, the standard macroscale model proceeds directly by analogy with the microscale Fickian law. This approach requires that subscale contributions to dispersion be accounted for by a dispersion coefficient or tensor. Second, since quantities such as chemical potential have not been carefully averaged to the macroscale, no direct correspondence is available between microscale and macroscale driving forces for dispersion. Third, Gray and Miller [6] have indicated some extensions to Darcy's law, but the current state of dispersion modeling only builds on the traditional use of Darcy's law, with its limitations, as a surrogate for the momentum equation. Fourth, the commonly used model does not emerge as a special case of a more general theory with an explicit list of assumptions needed to reduce to this case indicated. In the present exposition, we seek a self-consistent theory in which mass and momentum transport are both modeled from first principles.
The overall goal of this work is to formulate a rigorous theory of multispecies transport for single-fluid-phase flow in porous media. The specific objectives of this work are: (1) to develop a general, consistent and rigorous theory for deriving macroscale species transport models; (2) to formulate classical irreversible thermodynamics expressions for species in fluids, solids, and interfaces; (3) to examine two alternative approaches for modeling the momentum transport of a species; (4) to detail assumptions needed to arrive at the standard advective-dispersive transport model; (5) to formulate a model to describe non-dilute systems based upon the general theory; and (6) to comment on potential further uses of the general model derived.
2 General Approach
The system under consideration in this work is similar to that considered in Gray and Miller [6] but extended to include modeling of chemical species. An averaging volume, indicated as Ω, is associated with each point in space. Within that averaging volume is a region occupied by a solid phase, Ωs; a region occupied by the fluid phase, Ωw; and the interfacial region between the solid and fluid phases, Ωws. These different types of regions are generally referred to as entities. Conservation equations for each chemical species within each entity may be written. Specifically, equations of mass, momentum, and energy conservation for each species may be written at the microscale within each entity and then integrated over its corresponding entity within Ω to obtain a complete set of macroscale equations. These equations are used in their own right and as constraints on the entropy inequality that is obtained as a macroscale expression. Of importance is the fact that the sum of a type of conservation equation over all the species in the entity of interest yields the corresponding total conservation equation for the entity.
The set of entities for the system under consideration is denoted as
| (1) |
where Ωι represents the domain of the ι entity, ℑ = {w, s, ws} = ℑP ∪ ℑI is the index set of entity qualifiers or identifiers, ℑP = {w, s} is the index set of phases, ℑI = {ws} is the index set of interfaces, and w, s, and ws are specific qualifiers that indicate the wetting phase, the solid phase, and interfacial area between the wetting and solid phases.
The connected entity sets for this system are 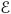 cw = {Ωws},
cw = {Ωws}, 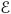 cs = {Ωws}, and
cs = {Ωws}, and 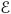 cws = {Ωw, Ωs} with corresponding connected entity index sets ℑcw, ℑcs, and ℑcws. Connected entity sets represent the set of entities in the domain Ω that share an internal boundary with a specified entity.
cws = {Ωw, Ωs} with corresponding connected entity index sets ℑcw, ℑcs, and ℑcws. Connected entity sets represent the set of entities in the domain Ω that share an internal boundary with a specified entity.
We describe the composition of the system as consisting of a set of species 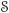 with index set ℑs. The set of species in entity Ωι is
with index set ℑs. The set of species in entity Ωι is  ι with index set ℑsι. Thus, the set of species can be represented as
ι with index set ℑsι. Thus, the set of species can be represented as  = ∪ι∈ℑ
= ∪ι∈ℑ ι and ℑs = ∪ι∈ℑℑsι. Since ℑsι ⊂ ℑs, ∀ι, summation over ℑs will generally be an acceptable representation of a process summed over all species in an entity, since it is an inclusive set.
ι and ℑs = ∪ι∈ℑℑsι. Since ℑsι ⊂ ℑs, ∀ι, summation over ℑs will generally be an acceptable representation of a process summed over all species in an entity, since it is an inclusive set.
In the approach employed here, the length scale of Ω is taken to be sufficiently large that it contains a representative sample of all species in all entities in the system. The intention is that the averaged values obtained from integration of the conservation equations over their respective regions will be representative averages that are independent of variations in the size of the averaging volume. Such an averaging volume is referred to as a representative elementary volume (REV), and formulation of the governing equations at this length scale does not require detailed knowledge of the pore morphology and topology.
The formulation of macroscale models of single-fluid-phase transport follows the TCAT approach [5, 15] and represents an extension of the approach employed to model single-phase flow involving a single chemical species [6]. The fundamentals needed to initiate the model building process for the multi-species cases of concern follow from Miller and Gray [16]. This previous work will allow us to concisely approach the model building process. Specifically, we will not detail the fundamental averaging operator, the types of averages, the formulation of macroscale conservation and balance equations, the precise mathematical definition of all variables, or the formulation of macroscale thermodynamical relations and equilibrium conditions that have previously been presented. These details are important if one wishes to understand all aspects of the TCAT approach, but to focus on the novel aspects of the present work, we do not repeat these details that are available elsewhere.
3 Thermodynamic Considerations for Species
The averaged macroscale classical irreversible thermodynamics (CIT) Euler equations for the internal energy of a fluid phase w, a solid phase s, and the ws interface are, respectively [4, 7, 16]
| (2) |
| (3) |
| (4) |
where E is the internal energy density, η͘ is the entropy density, θ͘ is the temperature, ει is the measure of the quantity of entity ι per macroscale volume, pw is the pressure of the wetting fluid phase, ρ is the mass density, ωkῑ is the mass fraction of species k in the ι entity, μ͘ is the chemical potential, σs̿ is the Lagrangian stress tensor, Cs is the Green's deformation tensor, js is the solid-phase Jacobian, and γws if the interfacial tension of the ws interface.
These relations are employed in considering the behavior of entities as a whole. However, when the species that constitute an entity are being modeled, it is important to have thermodynamic relations for those species. These are obtained making use of partial mass quantities. Because a fluid, a solid, and an interface have distinct thermodynamic behavior, the macroscale partial mass relations for species in these entities will be developed separately.
3.1 Fluid Phase
We begin with the microscale Euler form for the w phase energy
| (5) |
where 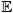 is the internal energy,
is the internal energy, 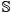 is the entropy,
is the entropy, 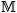 is the mass,
is the mass, 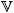 is the volume, and k is a species qualifier.
is the volume, and k is a species qualifier.
The differential expression with respect to 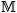 iw while holding pw, θw, all other masses, denoted
iw while holding pw, θw, all other masses, denoted 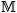 kw, constant yields
kw, constant yields
| (6) |
The partial derivatives in this expression are partial mass quantities. We therefore can write Eq. (6) as
| (7) |
Then multiplication by ρwωiw yields
| (8) |
where
| (9) |
| (10) |
and
| (11) |
The sums of Eiw and of ηiw over all species i yield Ew and ηw, respectively. Additionally, the sum of Xiw over all species i is equal to 1. The differential of Eq. (8) is
| (12) |
The Gibbs-Duhem equation is
| (13) |
We now obtain the macroscale version of Eq. (8) by averaging over the portion of the averaging volume occupied by the w phase. The macroscale variables that arise that are neither volume averages nor mass-weighted averages are
| (14) |
| (15) |
| (16) |
| (17) |
Note that a macroscale temperature is defined for each species because of the presence of the species-dependent weighting factor in the averaging process. We will assume that this effect is small within an averaging volume and therefore set for all i. With these definitions employed, the macroscale version of Eq. (8) is
| (18) |
3.2 Solid Phase
The manipulations required to obtain the Euler form of the macroscale internal energy relation for a species in a solid phase are similar to those for a fluid phase. Here, we highlight the differences due to the different thermodynamic description of an elastic solid. The Euler form for the s phase internal energy is
| (19) |
where 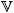 0s is the initial, or reference, volume of the solid phase.
0s is the initial, or reference, volume of the solid phase.
The differential expression with respect to 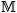 is while holding σs, θs, and all other masses, denoted by
is while holding σs, θs, and all other masses, denoted by 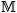 ks, constant yields
ks, constant yields
| (20) |
The partial derivatives in this expression are partial mass quantities. We therefore can write Eq. (20) as
| (21) |
Then multiplication by ρsωis yields
| (22) |
where
| (23) |
| (24) |
and
| (25) |
where
| (26) |
The differential of Eq. (22) is
| (27) |
The Gibbs-Duhem equation is
| (28) |
We now obtain the macroscale version of Eq. (22) by averaging over the portion of the averaging volume occupied by the s phase. The macroscale variables that arise that have definitions different from those for the w phase are
| (29) |
| (30) |
With these definitions employed, the macroscale version of Eq. (22) is
| (31) |
3.3 Interface
We begin with the Euler form for the ws interface energy
| (32) |
where  ws is the area of the fluid-solid interface. The differential expression with respect to
ws is the area of the fluid-solid interface. The differential expression with respect to  iws while holding γws, θws, and other masses, denoted by
iws while holding γws, θws, and other masses, denoted by  kws, constant yields
kws, constant yields
| (33) |
The partial derivatives in this expression are partial mass quantities. We therefore can write Eq. (33) as
| (34) |
Then multiplication by ρwsωiws yields
| (35) |
where
| (36) |
| (37) |
and
| (38) |
The sums of Eiws and of ηiws over all species i yield Ews and ηws, respectively. Additionally, the sum of Xiws over all species i is equal to 1. The differential of Eq. (35) is
| (39) |
The Gibbs-Duhem equation is
| (40) |
We now obtain the macroscale version of Eq. (35) by averaging over the portion of the averaging volume occupied by the ws interface. The macroscale variables that arise that are neither area averages nor mass-weighted averages are
| (41) |
| (42) |
| (43) |
| (44) |
Note that a macroscale temperature is defined for each species because of the presence of the species-dependent weighting factor in the averaging process. We will assume that this effect is small within an averaging volume and therefore set for all i. With these definitions employed, the macroscale version of Eq. (35) is
| (45) |
4 Entity-Based Momentum Equation Model
4.1 Overview
The TCAT approach requires the formulation of an augmented entropy inequality (AEI) wherein conservation equations and thermodynamic conditions are employed as constraints on the entropy inequality; solution for the Lagrange multipliers used to apply the constraints [5, 14]; simplification of the result through algebraic rearrangement to produce a constrained entropy inequality (CEI); imposition of restrictions and approximations consistent with the physical system of interest to yield a simplified entropy inequality (SEI); and the formulation of approximate closure relations that are consistent with the SEI and with the behavior of the physical system to produce closed models. One approach to formulating a TCAT model for species transport in a single-fluid-phase system is to consider only entity-based internal energy and momentum, but species-based conservation of mass when formulating the AEI. This primary restriction on the form of the AEI will influence the form of the models that result. We summarize the results following this general formulation approach in the subsections that follow.
4.2 Augmented Entropy Inequality
The AEI for the case in which entity-based internal energy and momentum equations are used to constrain the EI can be given as
| (46) |
where  ι,
ι, 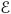 ι,
ι, 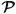 ι, and
ι, and 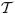 ι represent the balance of entropy, the conservation of energy, the conservation of momentum, and a themodynamic-based equality for the material derivative of internal energy all for entity ι;
ι represent the balance of entropy, the conservation of energy, the conservation of momentum, and a themodynamic-based equality for the material derivative of internal energy all for entity ι; 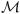 iι is a conservation of mass equation for species i in entity ι; λ's are Lagrange multipliers, where the subscript denotes the corresponding equation and the superscript denotes the corresponding entity or species-entity combination; and Λ is the entropy production for the system.
iι is a conservation of mass equation for species i in entity ι; λ's are Lagrange multipliers, where the subscript denotes the corresponding equation and the superscript denotes the corresponding entity or species-entity combination; and Λ is the entropy production for the system.
When working with the entity-based momentum equation formulation, the individual species macroscale velocities, , and their derivatives do not appear explicitly in the conservation equations. Rather the formulation is in terms of the macroscale entity velocities, vῑ, and the dispersion velocities defined as
| (47) |
The conservation, balance, and thermodynamic equations represented by shorthand notation in Eq. (46) have been previously derived [16]. With the definition of the non-advective entropy flux vector for an entity, ϕι̿, expressed in terms of its species summed components, the balance of entropy is expressed as
| (48) |
where ηι̿ is the macroscale entropy of entity ι per volume, t is time, dι̿ is the rate of strain tensor, I is the identity tensor, is the species non-advective entropy flux vector, bι is the entropy source density, and the material derivative is defined as
| (49) |
The conservation of energy equation for entity ι may be written as
| (50) |
where ι is an entity qualifier; i is a species qualifier; Eι̿ is the internal energy density; ρι is the mass density; is the macroscale kinetic energy per unit mass due to microscale velocity fluctuations; t is time; ωiῑ is the mass fraction of species i in the ι entity; is the body force potential restricted to gravity for the present study; tι̿ is the stress tensor; is a non-advective heat flux vector; hι̿ is a heat source density; riι represents reactions that produce species i in entity ι; represents the transfer of energy from entity κ to entity ι due to mass exchange of species i, with mass exchange accounted for as ; represents the transfer of energy associated with momentum transfer from entity κ to entity ι, where the momentum transfer is represented as ; and represents the exchange of heat from the κ to the ι entity.
The product rule may be applied to the material derivatives in Eq. (50) to obtain a rearranged form of the energy conservation equation that will be useful subsequently
| (51) |
The conservation of momentum equation for entity ι may be written as
| (52) |
where is the body force, represents the momentum exchange from the κ to the ι entity due to mass exchange of species i and the other quantities have been defined previously.
The conservation of mass equation for species i in entity ι is stated as
| (53) |
or after referencing the material derivative to vῑ as
| (54) |
where riι represents the rate of production of mass of species i in entity ι per unit measure of the entity resulting from reactions involving all other species in entity ι.
The material derivative of macroscale internal energy of fluid phase w can be related to the material derivatives of other thermodynamic quantities based upon CIT for conditions of microscale local equilibrium giving [16]
| (55) |
where μ is the chemical potential with the pair of indices indicating the species i and the w phase, p is the fluid pressure, and the subscripts indicate microscale quantities while the superscripts indicate macroscale variables.
Under conditions of microscale local equilibrium, the material derivative of the macroscale internal energy of an elastic solid phase, s, is [16]
| (56) |
for
| (57) |
where ts is the microscale stress tensor for the solid phase, Cs is the Green's deformation tensor, js is the Jacobian, ∇Xx is the gradient of a spatial location vector relative to its initial location, and the solid surface is denoted by Ωss = {Ωκ, ∀κ ∈ ℑcs} = Ωws. The Lagrangian stress tensor σs is defined as a partial derivative of the internal energy with respect to the Green's deformation tensor multiplied by the initial volume. This particular stress tensor is equal to one half the second Piola-Kirchhoff stress tensor.
When microscale local equilibrium is assumed, the material derivative of macroscale internal energy for the ws interface is [16]
| (58) |
for
| (59) |
and
| (60) |
where ns is the outward unit normal vector from the bounday of the solid phase, and γ is the interfacial tension.
The averaged CIT expression for the ws interface can be written in an alternative form following some manipulation. These manipulations involve application of averaging theorems, elimination of macroscale interfacial tensions, and changing the form of the material derivative forms. The resulting form is convenient for use in the subsequent derivation of closure relations.
The thermodynamic relationship for the ws interface that is obtained does not require any further assumptions and is expressed
| (61) |
We wish to use the EI to guide the formulation of closure relations for dissipative processes due to flow and transport within phases and across interfaces. To facilitate this we employ the conservation equations as constraints on the system entropy balance equation by use of Lagrange multipliers. The Lagrange multipliers are free parameters that can be selected arbitrarily without altering the validity of the balance of entropy expression. We select these Lagrange multipliers to eliminate some of the material derivative terms from the AEI, since our focus is on closure relations for the dissipative processes. To enhance the focus on the targeted material derivatives, we rewrite the balance and conservation equations in shorthand notation. The expression for the balance of entropy, Eq. (48), is
| (62) |
The alternative form of the energy equation given by Eq. (51) is chosen for expression in shorthand form because it employs individual material derivatives making use of entity velocities that appear in the other conservation and thermodynamic equations. The expression for this equation is
| (63) |
The conservation of momentum, Eq. (52), is expressed
| (64) |
The equation for conservation of mass of a chemical species, Eq. (53) is written
| (65) |
In these equations, , , , and are residual portions of the respective equations that account for terms in addition to the explicitly stated material derivatives.
A shorthand notation is also employed for the thermodynamic equations. The ACIT expression for the w phase, Eq. (55) is
| (66) |
For the s phase, ACIT Eq. (56) becomes
| (67) |
The ACIT expression for the ws interface, Eq. (61) is written
| (68) |
where , , and are residual portions of the wetting phase, solid phase, and wetting-solid interface thermodynamic expressions that account for terms in addition to the explicitly stated material derivatives.
Eqs. (46), (62), (63), (64), (65), (66), (67), and (68) can be combined to give a final AEI of the form
| (69) |
4.3 Constrained Entropy Inequality
Examination of Eq. (69) shows that the material derivatives that appear explicitly may be made to cancel with a judicious choice of Lagrange multipliers, although some other material derivatives remain in the residual terms. A unique solution for the λ's is then accomplished as outlined in Gray and Miller [6] by considering only the material derivatives that are explicit in Eq. (69). Such a solution yields
| (70) |
Substituting Eq. (70) into Eq. (69) and simplifying by cancelling out material derivatives gives
| (71) |
Reinsertion of the expressions for , , , , and leads to the expanded form of the constrained entropy inequality (CEI) given by
| (72) |
Eq. (72) can be placed into a more convenient form with some manipulation. We will consider these manipulations systematically and show intermediate results along the way for clarity. Our overall goal is to end up with a formulation that has groupings of variables related to non-dissipative processes and groupings of variables related to dissipative processes, which are arranged in flux-force pairs and satisfy the axiom of objectivity.
Non-dissipative processes are identified to relate the flux and source of entropy in a system to the flux and source of heat and other thermodynamic quantities. The non-advective heat flux term may be rearranged using the product rule to obtain
| (73) |
Additionally, the heat transfer due to species dispersion may also be rearranged using the product rule to obtain the identity
| (74) |
One other application of the product rule that will prove convenient involves rearrangement of the dispersion term that arises from the species mass conservation equation
| (75) |
To reference the surviving material derivatives to the solid-phase velocity recall
| (76) |
which allows for
| (77) |
or
| (78) |
For the like term applied to an interface, we restrict the material derivative to the interface by noting
| (79) |
and
| (80) |
Employing these relations, we obtain
| (81) |
so that
| (82) |
Consider the gravitational acceleration term arising from the product of the Lagrange multiplier and the conservation of momentum equation for the wetting phase and reference the velocity to the solid-phase velocity
| (83) |
where
| (84) |
Use has been made of the fact that giw = −∇ψiw and of the definitions of the averages to construct the last term that makes use of the averaging operator. The partial derivative with respect to time of the body force term originating from the energy equation can be added into Eq. (83) and rearranged in material derivative form to yield
| (85) |
Similar manipulations and combination of terms for the solid phase results in the identity
| (86) |
Manipulations similar to the preceding may be performed for the gravitational term on the ws interface. If the material derivative is restricted such that it follows the interface, the result obtained is
| (87) |
where
| (88) |
Eq. (72) can be rearranged while making use of the identities Eqs. (73)–(75), (78), (82), (85), and (87) and also collecting terms that multiply the rates of strain and the temperature gradients to give
| (89) |
Further simplification of Eq. (89) is facilitated by use of the thermodynamic relations. Eqs. (2)–(4), which provide the entity-based macroscale thermodynamic relations, may be substituted into Eq. (89). Additional manipulation makes use of the microscale Gibbs-Duhem equation for the w phase
| (90) |
This equation allows the following elimination of terms in the expression appearing in Eq. (89)
| (91) |
Then after explicit evaluation of the terms in the averaging operator on the right side, this equality simplifies to
| (92) |
Insertion of this identity, macroscale thermodynamic relations Eqs. (2)–(4), and the species thermodynamic relations given by Eqs (18), (31), and (45) into Eq. (89) and some additional collection of terms that appear into groups with common characteristics gives
| (93) |
The terms involving the material derivatives of pw − pw and εw can be eliminated using a previously derived averaging theorem for multiscale fluctuations [15] giving
| (94) |
The final set of terms that require some expansion and rearrangement are the inter-entity exchange terms. The manipulations performed are similar for the various collections so they will not be presented in detail here. The objectives of these expansions are to ensure that all velocities that appear are expressed relative to the solid phase velocity and to gather terms that are appropriately impacted by temperature differences between entities.
For example, consider the expansion performed for the exchanges of momentum. All the terms involving momentum exchange in Eq. (93) can be collected and then expanded directly to obtain
| (95) |
A cancellation of the terms on the right, where possible, and collection of the remaining terms so that all velocities are relative to the solid yields
| (96) |
It will be desirable to have the term containing vw̄,s̄ divided by rather than . This can be accomplished by adding and subtracting the appropriate term to obtain
| (97) |
Similar manipulations can be performed for the terms involving heat exchange to obtain
| (98) |
For the collection of mass exchange quantities, the expansion and regrouping of terms leads to
| (99) |
Eqs. (94), (97), (98). and (99) can be substituted into Eq. (93) to yield, after expanding some of the summations over entities and regrouping of terms to give
| (100) |
4.4 Simplified Entropy Inequality
Eq. (100) is the final form CEI for the entity-based momentum equation. Given the choices of the system being considered, the restrictions on an REV, and the use of CIT, this equation does not include any approximations, and it is arranged, where possible, in force-flux form. Careful examination of Eq. (100) reveals that the several lines of this equation include terms that are not strictly in the flux-force form as they include some combination of material derivatives and microscale quantities in integral form. Approximations are needed to transform Eq. (100) into a final form of an EI that can be used to derive closed models to describe species transport in the porous medium system being considered. We refer to this desired form as a simplified entropy inequality (SEI), and emphasize that the final form depends upon the approximations made. If better approximations, or exact expressions, are developed in the future, then they need only be applied at this stage to the CEI, which does not change form.
Averaging of thermodynamic relations from the microscale to the macroscale in multiphase systems leads to integrals of the dyadic products of orientation vectors. We term such quantities geometric orientation tensors. The geometric orientation tensor of interest for single-fluid systems is
| (101) |
While Eq. (101) is exact and is an accessible quantity given detailed knowledge at the microscale, examination of Eq. (100) shows that the microscale geometric tensor for the ws interface appears as a product involving other terms in several places. We approximate these geometric product terms by assuming independence among certain groupings of variables, which allows for integrals of products to be expressed as products of integral expressions. To be specific, the following approximations are used
| (102) |
| (103) |
| (104) |
| (105) |
| (106) |
and
| (107) |
In addition to the geometric approximations, an approximation to express solid mechanics terms as a product of mass exchange is of the form
| (108) |
Eq. (100) can be combined with Eqs. (94)–(108) to derive an SEI of the form
| (109) |
This equation will be used subsequently to obtain closed models for flow and transport. However, before developing the closure relations, we will provide a parallel derivation to the preceding that makes use of a species-based momentum equation, rather than an entity-based momentum equation. Then closure forms for these alternative derivations can be juxtaposed and the results compared.
5 Species-Based Momentum Equation Model
5.1 Overview
The TCAT formulation for species transport models can be approached in a variety of ways. In §4, species information was retained for the conservation of mass equations but entity-based formulations were used for all other conservation and balance equations. In this section, a species form of both the conservation of mass and conservation of momentum equations will be used, while entity-based forms will be used for all other conservation and balance equations. This alternative approach will lead to forms of the AEI, CEI, and SEI different from those previously derived, and ultimately to differences in closure relations and final closed models.
5.2 Augmented Entropy Inequality (AEI)
The AEI for the case in which species-based equations are used for both the conservation of mass and momentum and entity-based forms are used for all other equations has the general form
| (110) |
where doubly superscripted variables denote species and entity qualifiers. The λ's are Lagrange multipliers that must be determined. As before, 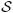 represents the entropy equation with the production term on the right side of Eq. (110). The symbols
represents the entropy equation with the production term on the right side of Eq. (110). The symbols 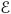 ,
, 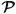 ,
, 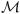 , and
, and 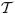 represent the conservation equations and thermodynamic relations. An important implication of using the species-based rather than an entity-based momentum equation is that neither dispersion velocities nor entity velocities are retained in the entropy inequality. Rather, all velocities can be expressed in terms of
with the barycentric entity velocity expressed as a mass fraction weighted sum of the entity species velocities.
represent the conservation equations and thermodynamic relations. An important implication of using the species-based rather than an entity-based momentum equation is that neither dispersion velocities nor entity velocities are retained in the entropy inequality. Rather, all velocities can be expressed in terms of
with the barycentric entity velocity expressed as a mass fraction weighted sum of the entity species velocities.
Throughout this development, velocities will be referenced to a common velocity, taken to be the mass-averaged macroscale velocity of the solid phase, vs̄. This may be expressed in a form analogous to Eq. (76) as
| (111) |
The balance of entropy has previously been stated in Eq. (48), written making use of the entity velocity, vῑ, and the diffusion velocity, . For the species-momentum formulation considered here, it is necessary to express the velocities and rate of strain tensors in terms of species constituents to allow connection to other quantities in the AEI. Toward this end, it may be noted that
| (112) |
| (113) |
and
| (114) |
Eqs. (112)–(114) can be substituted into Eq. (48) to obtain the balance of entropy as
| (115) |
Formulating the AEI in terms of the species momentum equation requires that the conservation equations be expressed in an alternative form compared to the entity-momentum formulation previously detailed. This is so because of the desire to maintain consistent forms of the terms that appear across the set of conservation equations. For example, the species momentum equation is written in terms of a mass-averaged species velocity and a species stress tensor. This suggests that these terms must also appear in the conservation of energy equation in species form; thus the starting point must be a species conservation of energy equation. However, we will still connect the material derivative of internal energy to the entropy balance equation using an entity-based thermodynamic expression. This suggests that manipulation of the conservation of energy equation for a species is needed as detailed below.
The conservation of energy equation for a species in an entity was derived in [16] and may be written as
| (116) |
where
| (117) |
| (118) |
Since an entity-based internal energy equation appears in Eq. (110), it is useful to note
| (119) |
| (120) |
With these conditions employed, the total energy equation for the entity, Eq. (116), may be rearranged so that the material derivative of the internal energy is with respect to the entity velocity while the species velocity appears in all other terms. Also, because a CEI will be constructed to eliminate certain material derivatives in the usual manner, it is useful to express the material derivative involving in a form in which components match material derivative expressions arising in other conservation equations. The necessary manipulations are similar to those performed in deriving Eq. (51) and lead to the expression
| (121) |
Eq. (121) is convenient because it expresses the material derivative of the internal energy in a form that allows connection to thermodynamic expressions for an entity while retaining species information needed to connect to other conservation and balance equations. It is exactly equivalent to Eq. (51), but some properties appear as related specifically to individual species rather than simply summed over all species to obtain entity-based quantities.
The conservation of momentum equation for a species in an entity may be written as [16]
| (122) |
with representing the intra-entity momentum transfer rate from all other species in entity ι to the i species per unit measure of the entity.
The general macroscale conservation of mass equation for species i in entity ι
| (123) |
Recall the thermodynamic relation for internal energy of the wetting phase based upon the ACIT given previously as Eq. (55) and now written with k as the species summation index
| (124) |
For the species-based momentum formulation, it is useful to express the material derivative of εwρwωiw̄ referenced to rather than vw̄. This is easily accomplished making use of the general relation
| (125) |
where the entity indicator, ι is replaced by w when considering the w entity. Additionally the last four material derivatives in Eq. (124) can be referenced with respect to the solid entity velocity so that we obtain
| (126) |
Recall the microscale Gibbs-Duhem equation for fluid phase w
| (127) |
Eq. (127) can be used to eliminate some terms in Eq. (126) to give
| (128) |
Performing a similar set of manipulations, one obtains a material derivative of the internal energy for the solid phase of the form
| (129) |
Lastly, introducing species velocities into the ws interface thermodynamic equation yields
| (130) |
As with the entity-based momentum equation case, we wish to derive an EI expression to guide the formulation of closure relations. In so doing, our focus is on the closure relations for dissipative processes. Through the use of products of Lagrange multipliers and conservation equations summed to the EI, some material derivatives can be eliminated. Again, the shorthand notation will be employed to sharpen the focus on the material derivatives that are to be eliminated.
The shorthand form of entropy balance Eq. (115) is
| (131) |
Conservation of energy as given by Eq. (121) can be written
| (132) |
The compressed form of conservation of momentum Eq. (122) is
| (133) |
The macroscale species conservation of mass given in Eq. (123) may be compressed to
| (134) |
The compressed thermodynamic expression for entity ι is
| (135) |
In this expression, the terms that make up are of a different form for each entity but can be easily extracted from Eq. (128) for the w entity, Eq. (129) for the s entity, or Eq. (130) for the ws entity.
Eqs. (110), (132), (133), (134), and (135) are combined to give a final form of the AEI for the present formalism involving species-based momentum and mass conservation equations
| (136) |
This equation may be solved for the values of the Lagrange multipliers that eliminate the material derivatives giving
| (137) |
Substitution of Eq. (137) into Eq. (136) and simplifying leaves the entropy inequality in terms of the shorthand residual contributions
| (138) |
Insertion of the expressions for the residuals , , , , and into Eq. (138) gives an expanded form CEI
| (139) |
A series of manipulations analogous to those that transformed Eq. (93) into Eq. (100) may be applied to Eq. (139) to obtain the final form of the species-based momentum equation form of the CEI
| (140) |
5.3 Simplified Entropy Inequality
The convention employed is that a CEI is free of any approximations beyond the assumption of the existence of an REV and the use of CIT at the microscale. The final form given in Eq. (140) nevertheless reflects the choices made in selecting the entity and species conservation equations used to constrain the system EI. Approximations can be applied to Eq. (140) to arrive at a form that is convenient for use in obtaining closure relations. The resultant form is an SEI, and the form of this equation is subject to the approximations applied here to the CEI as stated explicitly below.
If dispersion of a species within the solid phase is neglected so that the solid phase composition is considered invariant with respect to space at both the microscale and macroscale then
| (141) |
and
| (142) |
As was the case with the entity-based momentum equation, geometric tensor terms arise in product forms in formulating the species-based EI. The following approximations are made
| (143) |
| (144) |
| (145) |
| (146) |
| (147) |
and
| (148) |
Also recall Eq. (108)
| (149) |
Eqs. (140)–(149) can be combined and rearranged to yield an SEI for the species-based momentum equation constraint form
| (150) |
This equation is different from Eq. (109) primarily because the species momentum is explicitly modeled rather than the momentum of the entity as a whole. Additionally, some small differences exist in the assumptions made to convert the respective CEI's to SEI's. The latter model should allow for more complete modeling of the system physics but at a cost of the need for some species-based closure relations. In the next section, the closure of both models will be accomplished so that comparisons can be made in the descriptions of the system physics.
6 Model Closure
Eqs. (109) and (150) are SEI expressions that can be used to derive closed, thermodynamically consistent models to describe species transport in a single fluid phase porous medium system. Either of these SEI equations can be used to constrain a family of models that depend upon the way in which the EI is enforced. Put another way, the SEI provides a basis for the selection of closure relations that is non-unique. As a general approach, one should choose the level of sophistication needed to describe the systems of interest.
The generality of the SEI's derived make it possible to derive model closures for a wide range of applications. Here we will restrict attention to a specific application within the family of possible models. The application of concern is the movement of a potentially concentrated solution consisting of a dense brine. This application has been the focus of significant recent research [e.g., 9, 12, 13, 19–21] with the appropriate model for flow and transport considered an open question. In addition, interesting aspects of this application can be considered and ultimately compared to laboratory data, while ignoring certain complicating aspects of closure that would emerge in the most general model. The restrictions, approximations, and model closure approaches are detailed in the subsections that follow with emphasis on obtaining the closed flow and transport equations within the fluid phase, or w entity.
6.1 Restrictions and Formal Approximations
The derivation of TCAT models requires that some choices be made that affect the final form of the model derived. We divide these choices into three categories: primary restrictions, secondary restrictions, and formal approximations. Primary restrictions are decisions made about the system being considered prior to the derivation of the EI. These restrictions determine the type of system of concern and the physical processes that are to be modeled. Secondary restrictions are applied after the derivation of the SEI and limit the system to a subset of the more general system originally considered. The key feature of secondary restrictions is that they are relatively easy to relax and only involve how the SEI is used to close models. Formal approximations are introduced first to transform the CEI to an SEI and second to produce closure relations that are consistent with the SEI. In neither process are the manipulations performed exact, but the desire is to construct these approximations such that the resulting models are of utility. The TCAT approach relies upon comparison to highly resolved microscale simulations and experimental results to arrive at a determination of the utility of any given model. To put the approach taken thus far into perspective and focus the model closure work that follows, we summarize in turn the restrictions and approximations invoked here in developing the particular model of interest.
The primary restrictions employed here are:
The system of concern contains a well-defined REV, and the macroscale model is developed at a scale consistent with the size of the REV.
The system consists of three entities: a water phase, a solid phase, and a water-solid interface.
Species composition is of concern and is modeled through a species conservation of mass equation.
An entity-based momentum equation or a species-based momentum equation composition may be developed, leading to two different CEI's and SEI's and two different approaches for model closure.
Classical irreversible thermodynamics applies to the systems of concern at the microscale.
The secondary restrictions that will be applied to the SEI's for the current example are:
Diffusion within the solid phase is ignored.
The water-solid phase interface can be ignored.
The system is isothermal.
The system is non-reactive.
The porous medium is isotropic.
The gradient of the body force potential vector is equivalent to the acceleration due to gravity and is invariant with respect to species.
Compositional effects are limited to a single species A dissolved in solvent B within the w phase.
The formal approximations imposed are:
A set of integral product breaking approximations needed for geometric tensors and other terms and which are used to derive the SEI's from the CEI's as detailed above are sufficiently accurate to produce useful models.
The system behaves thermodynamically such that the entropy, heat flux, and diffusion velocity vectors can be related.
Entropy source, heat source, and some other fluctuation terms can be related.
Kinetic energy due to microscale velocity fluctuations is negligible.
A closure scheme that is at most first-order and consistent with the SEI is adequate to describe the systems of concern.
Inertial terms can be neglected in the conservation of momentum equations.
Macroscale stress tensors are independent of the macroscale rate of strain tensors.
Cross-coupling of behavior between entities may be ignored.
6.2 Entity-Based Momentum Approach for a Binary System
The restrictions and formal approximations noted above allow the species mass conservation equation, Eq. (53), for the fluid phase, w, to be written as
| (151) |
The entity-based conservation of momentum equation for the w entity simplifies from Eq. (52) to
| (152) |
The model represented by Eqs. (151) and (152) contains more unknowns than equations, thus requiring closure approximations for a well-posed model. These closure relations are derived from the entity-based SEI given in Eq. (109) which simplifies in light of the above-noted secondary restrictions and formal approximations to
| (153) |
where use has been made of the fact that
| (154) |
The flux-force form of Eq. (153) provides information that can be used to guide closure relations, which are related to the interfacial transfer of momentum, the stress tensor, and the diffusion velocity.
A first-order closure for the force term whose conjugate flux is the relative velocity of the phase gives
| (155) |
where R̂w is a scalar resistance for the isotropic medium.
The zero-order closure for the stress tensor, as obtained based on Formal Approximation (7) yields
| (156) |
For the diffusive flux of species A, a first order closure scheme is also employed so that
| (157) |
where D̂ABw is a second-rank symmetric dispersion tensor for the binary, isothermal system and is the mole fraction of species i in entity w.
The closure relations given by Eqs. (155)–(157) provide additional information consistent with the SEI that can be used to derive a closed model.
First, we will obtain the closed momentum equation for the w entity. Substitution of Eqs. (155) and (156) into Eq. (152) gives
| (158) |
Summation of Eq. (151) over species A and B gives the total mass balance equation
| (159) |
which facilitates reduction of Eq. (158) to
| (160) |
The inertial term in this equation is negligibly small for typical slow flows in porous media so that Eq. (160) reduces further to
| (161) |
The macroscale Gibbs-Duhem equation for an isothermal fluid entity provides the identity
| (162) |
Additionally, since the body force is gravity, the body force potential satisfies the relation
| (163) |
Substitution of these last two equations into Eq. (161) yields
| (164) |
The term that appears explicitly in the averaging operator will be proportional to the gradient in porosity at equilibrium, where the coefficient of proportionality will be related to gw̄·∇εw. The average of the terms can be non-zero away from equilibrium and thus is taken to be proportional to the velocity. Thus we make use of the constitutive relation
| (165) |
where R̂p and R̂d are closure coefficients related to variations in pressure and density, respectively, as well as the scale of the averaging. With this relation, Eq. (164) becomes
| (166) |
We note, in passing, that if Formal Approximation (7) had not been applied such that the stress tensor of the fluid was considered to be linear in the rate of strain tensor, the Darcy-Brinkman equation would result with the set of approximations imposed rather than the simpler Darcy-like equation that appears here. The two terms involving R̂w and R̂p arise because of the transformation of the flow equation from its more natural form in terms of potentials in Eq. (160) to a form that is predominantly in terms of the average pressure.
For the two-species case, we can model the system using either species conservation equations for both species or a species conservation equation for one species with a mass conservation equation for the entity. These approaches are equivalent, but we choose the latter. Summation of Eq. (151) over species A and B eliminates the diffusion term consistent with Eq. (154). Then expansion of the material derivative yields the conservation of mass equation for the w entity
| (167) |
A full analysis to combine Eqs. (166) and (167) for a homogeneous fluid where the solid deformation is accounted for was previously provided in [6]. A slightly simpler form may be obtained for the case where vs̄ = 0 and taking R̂p∇εw = 0 by substituting Eq. (166) directly into Eq. (167). With the result expressed in terms of the dynamic viscosity μ̂w and the intrinsic permeability for the momentum equation in terms of pressure, k̂ = μ̂w / (R̂w − R̂d), the flow equation obtained is
| (168) |
where ρw and μ̂ depend upon the chemical composition.
Next we will obtain the closed mass conservation equation for species A in the w entity. Substitution of Eq. (159) into Eq. (151) and applying the product rule gives the distribution form of the species conservation equation
| (169) |
Manipulations that follow are first concerned with an expansion of Eq. (157) to eliminate the chemical and gravitational potentials that appear explicitly. For the isothermal case, the macroscale version of the microscale Gibbs-Duhem relation given by Eq. (13) is
| (170) |
Additionally, the gravitational potential satisfies the relation
| (171) |
Combination of these last two equations provides
| (172) |
With this information, and treatment of the deviation terms as in Eq. (165), Eq. (157) may be expressed
| (173) |
where
| (174) |
If the macroscale activity coefficient, , consistent with a reference state is defined such that
| (175) |
the macroscale chemical potential may be expressed as:
| (176) |
where is a reference chemical potential for species i in the w entity, R is the ideal gas constant, and MWi is the molecular weight of species i, which enters the formulation because chemical potentials are here defined on a unit mass basis. From this expression, we obtain
| (177) |
Substitution into Eq. (173) for the dispersive flux yields
| (178) |
where use has been made of the facts that for the binary system
| (179) |
and
| (180) |
where MWw is the molecular weight of the w entity obtained from [2]
| (181) |
Substitution of Eq. (178) into Eq. (169) then provides
| (182) |
In the limit of small mass fraction ωAw̄, the terms involving ∇pw and in Eq. (182) become very small and the equation simplifies to:
| (183) |
where use is made of the fact that [2]
| (184) |
and
| (185) |
Eqs. (182) and (183) can supplemented with equations of state of the forms
| (186) |
| (187) |
and
| (188) |
to yield a closed model. In addition, complete closure also requires functional forms for R̂p and R̂d, which while scalars in this formulation may be tensors under certain circumstances.
6.3 Species-Based Momentum Approach
The restrictions and formal approximation noted above reduce the conservation of species relation, Eq. (123), for entity w to
| (189) |
In light of the restrictions and formal approximations, the species-based conservation of momentum equation, Eq. (122), for a species in the w entity may be written
| (190) |
The model represented by Eqs. (189) and (190) contains more unknowns than equations, thus requiring closure approximations for a well-posed model. These closure relations are derived from the entity-based SEI.
Application of the above-noted secondary restrictions and approximations to the SEI given as Eq. (150) for the binary, isotropic system under consideration yields
| (191) |
The flux-force form of Eq. (191) provides information that can be used to guide closure relations, which are related to the interfacial transfer of momentum, the stress tensor, and the species velocities.
A first-order closure for the species mass flux in relation to its conjugate force in Eq. (191) gives
| (192) |
where R̂ijw is a resistance tensor. Cross-coupling of the velocities can be ignored by setting R̂ABw = R̂BAw = 0.
The zero-order closure for the stress tensor yields
| (193) |
Substituting Eqs. (192) and (193) into Eq. (190) gives
| (194) |
which may be simplified by making use of the conservation of mass equation to
| (195) |
Because the inertial term is typically small for porous media flows, it will be neglected here. With this approximation and with expansion of the summation in Eq. (195), we obtain
| (196) |
Substitution of the macroscale Eq. (172) based on the Gibbs-Duhem relation into Eq. (196) yields
| (197) |
The averages of the deviation terms are approximated similarly to the approach in the last section so that this equation simplifies further to
| (198) |
Elimination of the remaining gradient of chemical potential using Eq. (177) then gives momentum equations for each species
| (199) |
Recall that
| (200) |
Expansion of Eq. (199) for the two-species system, and elimination of the gradients of the activity coefficient and mole fraction of the B species using Eq. (200), provides momentum equations for each species. With one possible approximation of the resistance tensors, Eq. (199) for each species becomes
| (201) |
| (202) |
and the resistance tensors have been assigned the forms R̂iiw = μ̂ωiw̄(I − Ẑ)/k̂, R̂ABw = μ̂ωBw̄Ẑ/k̂, and R̂BAw = μ̂ωAw̄Ẑ/k̂ where Ẑ is a coupling tensor for the velocities with Ẑ = 0 corresponding to no coupling.
For the binary system, a species mass conservation equation with the form of Eq. (189) and the two species momentum Eqs. (201) and (202) are supplemented with equations of state of the general form
| (203) |
| (204) |
| (205) |
and
| (206) |
to yield a closed model that does not make use of a dispersion coefficient.
It is interesting to note that summation of the Eqs. (201) and (202) yields a momentum equation for the w phase
| (207) |
Although a more complex analysis can be done, we can consider the implications of a special case where coupling between species in considered unimportant such that Ẑ = 0. Then Eq. (201) may be combined with Eq. (207) to obtain
| (208) |
A comparison of this result with Eq. (178) obtained using the entity-based momentum formulation indicates that the results will be the same if
| (209) |
It is important to remember that this equivalence was obtained with the interaction between species neglected. The result indicates that in the absence of the interaction, the dispersion process will be isotropic in an isotropic medium. This suggests that the interaction term is important such that Ẑ ≠ 0 is necessary if the dispersion is to be modeled as anisotropic.
7 Discussion
Modeling of non-dilute systems in porous medium systems has received considerable attention in the literature both because of intrinsic interest [e.g., 9, 12, 13, 19–21] and also because of the many important applications that fall into this category of model [e.g., 10, 11, 17]. A rich, recent experimental literature has contributed as well to helping better understand the physicochemical phenomena of interest in these complex systems. Much of this recent experimental work has involved the investigation of factors that affect dispersion in non-dilute systems and how such dispersion compares to dispersion in similar systems in the non-dilute limit.
Multiple attempts have been made to model dispersion in non-dilute systems with mixed results. These efforts have included posited non-linear dispersion relationships [9] and multiscale models based upon homogenization [13]. None of the models advanced to date appear to provide a first-principles based approach capable of fitting the observed data for dispersion in a non-dilute system under varying velocities, mass fractions, and media conditions. None of the porous medium models advanced for non-dilute systems account for non-ideal effects using activity coefficients, which seems to be a fundamental flaw.
The models developed in this work are complete based upon a rigorous upscaling of conservation principles and closed in a thermodynamically consistent manner. The available experimental data provides a means to test these new models and evaluate their usefulness compared to existing models. If these models provide a good description of the data, then the models used will be set on a solid theoretical foundation and can be used for many applications. If these models do not prove useful, then the manner in which these models were developed provides a means to evaluate and alter assumptions and restrictions made in their development and produce increasingly complex, and hopefully more realistic, models. We advocate the comparison of the simple models developed in this work as a first priority, and extending these models to more complex forms only if necessary to describe high fidelity experimental observations.
Beyond the simple non-dilute dispersion application, this work may be extended to produce families of models to describe more complex systems. In doing so, a large fraction of the work presented here could be used as a basis for considering such systems. This is so because the CEI expressions are approximation free and the SEI expressions can be used in their current form to examine more complex systems, such as those with deformable solids and non-isothermal systems. Many such applications and a wide range of model closures could be developed based upon the fundamental aspects of this work.
8 Conclusions
The TCAT approach has been extended significantly in this work for application to chemical species transport in a single-fluid-phase porous medium system. Species-based thermodynamics have been derived and averaged to the macroscale in Section 3. An entity-based momentum equation approach was employed in Section 4 to obtain a general constrained entropy inequality the CEI of Eq. (100), that does not make use of mathematical approximations. Thus this form can be used as a starting point for subsequent analysis. The CEI was also reduced to a simplified entropy inequality, the SEI of Eq. (109). The approximations that went into obtaining the SEI from the CEI are such that the SEI will serve as a reasonable jumping off point for a wide range of transport problems.
If one wishes to consider modeling different systems containing chemical species where the momentum of each entity can be treated as a whole, Eq. (109) will be applicable such that the detailed calculations that led to this form do not have to be repeated. If one wishes to model the momentum of each species within an entity, as well as its concentration in that entity, then the formalism described in Section 5 can be followed. The resulting general CEI is given as Eqn (140). Note that in this CEI, the independent variable set includes the velocity of each species in each entity. In the entity-based-momentum formulation, the set of independent variables includes the entity velocities while constitutive closure relations have to be developed for the dispersive fluxes of each species in each entity. An SEI that can be used as the starting point for the development of closure relations when a set of restrictions can be applied to the CEI is obtained as Eq. (150). The closure obtained based on this equation will differ from that obtained with the entity-based-momentum form in that stress tensors for each species in each entity must arise for the species momentum equation. This form is more general than that of Eq. (109), but the price of this generality is the complication of closed momentum equations for each species as opposed to closed dispersive fluxes for each species.
Although the two SEI's are very valuable equations, their main function is to serve as guides for the development of closure relations. Although simplifications have been applied to their respective CEI antecedents to obtain these forms, they are still extremely general and carry the potential to model a wide range of flow velocities, fluid types, solid, and thermal exchange processes for multi-species systems. What we have presented in Section 6 are examples of use of the SEI's to obtain closure for case of binary dispersion in an isothermal system. This simple system is presented to provide an instance of the implementation of the method, not to demonstrate the wide range of systems that the derived SEI's describe. In fact, in generating the closed forms, the restrictions and approximations employed listed illustrate that what we have examined is a very restricted physical case. For the entity-based momentum approach, the SEI reduces to Eq. (153). This equation is exploited to obtain a species mass transport equation appropriate for non-dilute systems, Eq. (182), and a further simplified form suitable for modeling dilute systems, Eq. (183). For the species-based momentum formulation, the mass conservation equations for each species do not require any closure relations. Rather the momentum equations for each species are developed. The SEI Eq. (150) reduces to Eq. (191) for the isothermal binary system. Then momentum equations are obtained for each of the two species in the respective forms Eq. (201) and Eq. (202). Although the example cases are limited in scope, the derivation of CEI's and SEI's provides the foundational work for examining a wide-range of additional models.
Even though restricted to an isothermal binary system, the production of a complete set of closed models is of special significance. This set provides the first complete transport formulations based upon the TCAT approach. These models can be evaluated and compared to experiments as well as existing models. If the models presented in this work are unsatisfactory, a rigorous means exists to extend these models to incorporate incrementally more sophisticated representations of the physics through examination of the restrictions and assumptions employed that may not be applicable.
Acknowledgments
This work was supported by National Science Foundation grant DMS-0327896 and by National Institute of Environmental Health Sciences grant P42 ES05948. We appreciate the efforts of Amber B. Sallerson Jackson, who reviewed and commented on a draft of this work. Interest in the non-dilute case considered in this work was motivated in part by the work of collaborators of CTM on brine-based remediation, including J.A. Pedit, D.N. Johnson Wright, P.S. Birak, Y.C. Chang, G. Brubaker, and T.J. McHale.
Abbreviations
- ACIT
averaged classical irreversible thermodynamics
- AEI
augmented entropy inequality
- CIT
classical irreversible thermodynamics
- EI
entropy inequality
- REV
representative elementary volume
- TCAT
thermodynamically constrained averaging theory
Notation
Roman letters
| area | ||
| Ā | partial mass area | |
| b | entropy source density | |
| C | Green's deformation tensor | |
| D̂ | dispersion tensor | |
| D̂ABwe | effective dispersion tensor for binary system | |
| d | rate of strain tensor | |
| E | internal energy density | |
| internal energy | ||
| Ē | partial mass internal energy | |
| ET | total energy density | |
| the set of entities | ||
 I I
|
the set of interface entities | |
 P P
|
the set of phase entities | |
| conservation of energy equation | ||
 c c
|
connected set of entities | |
| eiι | microscale intra-entity internal energy transfer rate from all other species in entity ι to the i species per unit measure of the ι entity | |
| eTiι | total macroscale energy transfered intra-entity from all other species in entity ι to the i species per unit measure of the ι entity | |
|
|
total macroscale energy transfered intra-entity from all other species in entity ι to the i species per unit measure of the ι entity | |
| g | acceleration vector due to an external force, such as gravity | |
| h | heat source density | |
| I | identity tensor | |
| I′ | surface identity tensor | |
| ℑ | index set of entities | |
| ℑc | index set of connected entities | |
| ℑI | index set of interface entities | |
| ℑP | index set of phase entities | |
| ℑs | index set of species | |
| ℑsι | index set of species in entity ι | |
| js | solid-phase Jacobian | |
| k̂ | intrinsic permeability | |
| KE | macroscale kinetic energy per unit mass due to microscale velocity fluctuations | |
| mass | ||
| conservation of mass equation | ||
|
|
transfer of mass of species i in the κ entity to the i species in the ι entity per unit volume per unit time | |
|
|
transfer of energy from the κ entity to the ι entity due to inter-entity mass transfer of species i per unit volume per unit time | |
|
|
transfer of momentum from the κ entity to the ι entity due to inter-entity mass transfer of species i per unit volume per unit time | |
| MW | molecular weight | |
| nι | outward unit normal vector from entity ι | |
| conservation of momentum equation | ||
| p | fluid pressure | |
| piι | microscale intra-entity momentum transfer rate from all other species in entity ι to the i species per unit measure of the entity | |
|
|
macroscale intra-entity momentum transfer rate from all other species in entity ι to the i species per unit measure of the entity | |
|
|
transfer of energy from species in the κ entity to the i species in the ι entity resulting from heat transfer and deviation from mean processes per unit volume per unit time | |
| q | non-advective heat flux density vector | |
| R | ideal gas constant | |
| R̂ | resistance tensor | |
| R̂d | closure relation due to variations in density | |
| R̂p | closure relation due to variations in pressure | |
| riι | microscale intra-entity reaction rate resulting in the production of species i in entity ι from all other species per unit measure of the entity | |
| riι | macroscale intra-entity reaction rate resulting in the production of species i in entity ι from all other species per unit measure of the entity | |
| entropy balance equation | ||
| entropy | ||
| S̄ | partial mass entropy | |
| set of all species | ||
| CIT-based thermodynamic equation for material derivative of internal energy | ||
|
|
transfer of momentum from species in the κ entity to the i species in the ι entity due to stress and deviation from mean processes per unit volume per unit time | |
|
|
transfer of energy from species in the κ entity to the i species in the ι entity due to work and deviation from mean processes per unit volume per unit time | |
| t | stress tensor | |
| t | time | |
| u | diffusion velocity | |
| volume | ||
| V̄ | partial mass volume | |
 0s 0s
|
initial volume of the solid phase | |
| v | velocity | |
| X | partial mass ratio | |
| X | partial mass tensor | |
| X | material coordinate position vector | |
| x͘ | mole fraction | |
| x | position vector in the solid phase | |
| Ẑ | velocity coupling tensor |
Greek letters
| Γ | boundary of domain of interest | |
| γ | interfacial tension | |
|
|
activity coefficient | |
| ει | measure of quantity of entity ι per macroscale volume | |
| η | entropy density | |
| θ | temperature | |
| Λ | entropy production rate density | |
| λ | vector of Lagrange multipliers | |
| λ | Lagrange multiplier | |
| μ | chemical potential | |
| μ͘0 | reference chemical potential | |
| μ̂ | dynamic viscosity | |
| ρ | mass density | |
| σ | Lagrangian stress tensor for the solid phase | |
| ϕ | entropy density flux vector | |
| ψ | acceleration potential (e.g., gravitational potential) | |
| Ω | spatial domain | |
| Ω̄ | closed spatial domain | |
| Ωss | solid surface spatial domain | |
| ω | mass fraction of a species in an entity |
Subscripts and superscripts
| A | species qualifier |
| B | species qualifier |
| energy equation qualifier | |
| i | general index denoting a species |
| j | general index denoting a species |
| k | general index denoting a species |
| mass equation qualifier | |
| momentum equation qualifier | |
| r | residual portion of specified equation |
| s | index that indicates a solid phase |
| thermodynamic equation qualifier | |
| w | entity index corresponding to the wetting phase |
| ws | entity index corresponding to the wetting-solid interface |
| ι | entity qualifier |
| κ | entity qualifier |
Other mathematical symbols
| _ | closure of set (overline) |
| 〈 〉 | averaging operator |
| Dῑ/Dt | material derivative |
| ∂′/∂t | partial derivative of a point on a potentially moving interface |
| ∇′ | microscale surficial del operator on an interface |
| ∇(·)|_ | spatial derivative of the thermodynamic function (·) taken with the quantities listed following the vertical bar held constant |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
William G. Gray, Email: GrayWG@unc.edu.
Cass T. Miller, Email: casey_miller@unc.edu.
References
- 1.Berkowitz B, Scher H. On characterization of anomalous dispersion in porous and fractured media. Water Resources Research. 1995;31(6):1461–1466. [Google Scholar]
- 2.Bird RB, Stewart WE, Lightfoot EN. Transport Phenomena. 2nd. Wiley; New York: 2002. [Google Scholar]
- 3.Cushman JH. The Physics of Fluids in Hierarchical Porous Media: Angstroms to Miles. Kluwer Academic Publishers; Dordrecht, The Netherlands: 1997. [Google Scholar]
- 4.Gray WG. On the definition of derivatives of macroscale energy for the description of multiphase systems. Advances in Water Resources. 2002;25(8–12):1091–1104. [Google Scholar]
- 5.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 1. Motivation and overview. Advances in Water Resources. 2005;28(2):161–180. doi: 10.1016/j.advwatres.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gray WG, Miller CT. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 3. Single-fluid-phase flow. Advances in Water Resources. 2006;29(11):1745–1765. doi: 10.1016/j.advwatres.2008.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gray WG, Schrefler BA. Analysis of the solid phase stress tensor in multiphase porous media. International Journal for Numerical and Analytical Methods in Geomechanics. 2007;31:541–581. [Google Scholar]
- 8.Hassanizadeh SM. On the transient non-fickian dispersion theory. Transport in Porous Media. 1996;23(1):107–124. [Google Scholar]
- 9.Hassanizadeh SM, Leijnse A. A non linear theory of high-concentration-gradient dispersion in porous media. Advances in Water Resources. 1995;18(4):203–215. [Google Scholar]
- 10.Hill EH, Moutier M, Alfaro J, Miller CT. Remediation of DNAPL pools using dense-brine barrier strategies. Environmental Science & Technology. 2001;35(14):3031–3039. doi: 10.1021/es001891d. [DOI] [PubMed] [Google Scholar]
- 11.Johnson DN, Pedit JA, Miller CT. Efficient, near-complete removal of DNAPL from three-dimensional, heterogeneous porous media using a novel combination of treatment technologies. Environmental Science & Technology. 2004;38(19):5149–5156. doi: 10.1021/es0344765. [DOI] [PubMed] [Google Scholar]
- 12.Landman AJ, Johannsen K, Schotting R. Density-dependent dispersion in heterogeneous porous media Part I: A numerical study. Advances in Water Resources. 2007;30(12):2467–2480. [Google Scholar]
- 13.Landman AJ, Schotting R, Egorov A, Demidov D. Density-dependent dispersion in heterogeneous porous media Part II: Comparison with nonlinear models. Advances in Water Resources. 2007;30(12):2481–2498. [Google Scholar]
- 14.Liu IS. Method of Lagrange multipliers for exploitation of the energy principle. Archive for Rational Mechanics and Analysis. 1972;46:131–148. [Google Scholar]
- 15.Miller CT, Gray WG. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 2. Foundation. Advances in Water Resources. 2005;28(2):181–202. doi: 10.1016/j.advwatres.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Miller CT, Gray WG. Thermodynamically constrained averaging theory approach for modeling flow and transport phenomena in porous medium systems: 4. Species transport fundamentals. Advances in Water Resources. 2008;31(3):577–597. doi: 10.1016/j.advwatres.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Miller CT, Hill EH, Moutier M. Remediation of DNAPL-contaminated subsurface systems using density-motivated mobilization. Environmental Science & Technology. 2000;34(4):719–724. [Google Scholar]
- 18.Rubin Y. Applied Stochastic Hydrogeology. Oxford University Press; New York: 2003. [Google Scholar]
- 19.Schotting RJ, Moser H, Hassanizadeh SM. High-concentration-gradient dispersion in porous media: Experiments, analysis and approximations. Advances in Water Resources. 1999;22(7):665–680. [Google Scholar]
- 20.Watson SJ, Barry DA, Schotting RJ, Hassanizadeh SM. Validation of classical density-depedent solute transport theory for stable, high-concentration-gradient brine displacements in coarse and medium sands. Advances in Water Resources. 2002;25(6):611–635. [Google Scholar]
- 21.Watson SJ, Barry DA, Schotting RJ, Hassanizadeh SM. On the validity of Darcy's law for stable high-concentration displacements in granular porous media. Transport in Porous Media. 2002;47(2):149–167. [Google Scholar]


