Three-dimensional residual strain in midanterior canine left ventricle

Abstract

All previous studies of residual strain in the ventricular wall have been based on one- or two-dimensional measurements. Transmural distributions of three-dimensional (3-D) residual strains were measured by biplane radiography of columns of lead beads implanted in the midanterior free wall of the canine left ventricle (LV). 3-D bead coordinates were reconstructed with the isolated arrested LV in the zero-pressure state and again after local residual stress had been relieved by excising a transmural block of tissue. Nonhomogeneous 3-D residual strains were computed by finite element analysis. Mean ± SD (n = 8) circumferential residual strain indicated that the intact unloaded myocardium was prestretched at the epicardium (0.07 ± 0.06) and compressed in the subendocardium (−0.04 ± 0.05). Small but significant longitudinal shortening and torsional shear residual strains were also measured. Residual fiber strain was tensile at the epicardium (0.05 ± 0.06) and compressive in the subendocardium (−0.01 ± 0.04), with residual extension and shortening, respectively, along structural axes parallel and perpendicular to the laminar myocardial sheets. Relatively small residual shear strains with respect to the myofiber sheets suggest that prestretching in the plane of the myocardial laminae may be a primary mechanism of residual stress in the LV.

IT IS NOW WELL RECOGNIZED that the resting left ventricular wall contains residual stress in the absence of luminal or pericardial pressure or any other external loads (2, 14, 25). Transmural distributions of the associated residual strains have been measured in short-axis rings of isolated left ventricle (LV), which spring open into an arc when residual stress is relieved by a radial cut (14). The stress-free configuration has been characterized by the “opening angle” of this arc, which is ~45° in the adult rat (14, 19). The opening angle is species dependent (16), changes during development of the embryonic chick heart (25), and may be altered by ventricular growth and hypertrophy (17).

When residual strain is included in mechanical models of LV filling (4, 12, 24), the resulting residual stress is compressive at the endocardium and tensile at the epicardium, helping to reduce the endocardial stress concentrations that might otherwise occur during diastole. At the myocyte level, Rodriguez et al. (19) found that residual stress causes sarcomeres to be a mean of 0.13 μm shorter at the endocardium than at the epicardium in the unloaded rat LV. The implications of this finding for systolic fiber stress can be appreciated when one considers the steepness of the isometric tension-sarcomere length relation (1, 26). Hence, the presence of residual stress and strain may significantly influence ventricular mechanical function throughout the cardiac cycle.

To date, measurements of ventricular residual strain have been one dimensional (19) or two dimensional (14), but myocardial deformations in the intact heart are three dimensional (8, 27). Therefore, to obtain a complete description of the stress-free state of the myocardium, we arrayed radiopaque beads across the anterior wall of the canine LV and recorded their motion when residual stress was relieved locally. The measured deformations were used to compute transmural distributions of three-dimensional residual strain. The components of residual strain were referred to structural axes constructed from histological measurements of the three-dimensional myocyte and connective tissue organization. The analysis showed that there are substantial three-dimensional components of residual strain not previously described and that the primary residual stress-bearing structures tend to align with the local myocardial sheet orientation.

METHODS

All animal studies were performed according to the National Institutes of Health (NIH) “Guide for the Care and Use of Laboratory Animals.” All protocols were approved by the Animal Subjects Committee of the University of California, San Diego, which is accredited by the American Association for Accreditation of Laboratory Animal Care.

Experimental protocol

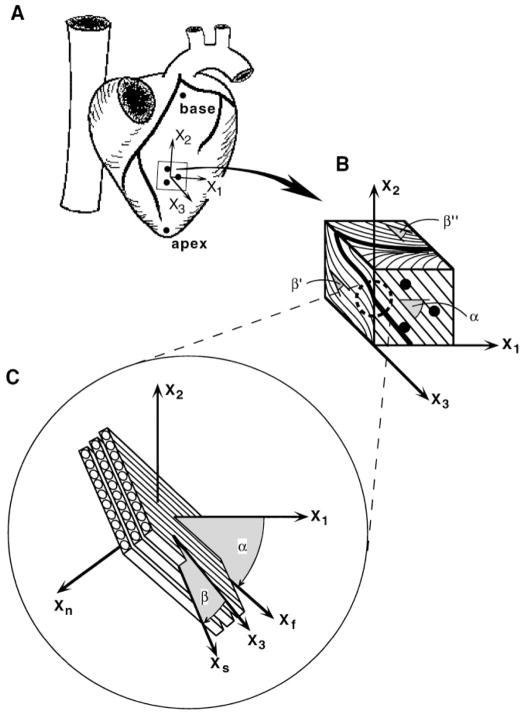
Eight adult mongrel dogs (21–41 kg) were pretreated with 10 mg oral nifedipine the day before the study. Each dog was anesthetized to a surgical plane with pentobarbital sodium (25–30 mg/kg), intubated, and ventilated with positive pressure. The heart was exposed by a median sternotomy and bilateral thoracotomy and supported in a pericardial cradle. Three columns of four to six lead beads (1 mm diam) were inserted 10 mm apart in a triangular array into the midanterior LV free wall at approximately two-thirds the distance from base to apex. A larger (2 mm) surface bead was sutured to the epicardium over each column. Long-axis reference markers were sutured at the apical dimple and at the first bifurcation of the left main coronary artery (Fig. 1A). The five surface markers were later used to define a local system of “cardiac coordinates” aligned with the circumferential (x₁), longitudinal (x₂), and radial (x₃) axes of the LV (10).

Fig. 1.

Schematic diagram of method for defining structurally based coordinate systems used to study 3-dimensional (3-D) residual strain. A: isolated heart in its intact unloaded state showing 5 surface markers used to define cardiac coordinates (x₁, x₂, x₃) aligned with local circumferential (x₁), longitudinal (x₂), and radial (x₃) axes of left ventricle. B: excised stress-free block of tissue containing transmural bead set. Bold lines indicate intersection of a hypothetical sheet with each of 3 orthogonal cardiac coordinate planes. Fiber angle, α, is measured in epicardial tangent (1–2) plane (x₁ = 0°). Cleavage plane angles, β′ and β″, are measured in (2–3) and (1–3) transverse planes, respectively (x₃ = 0°). For all 3 angle measurements, a clockwise rotation relative to 0° represents a negative angle. C: at each transmural depth, a sheet angle, β, is computed from 3 intersection angles and is used to define a local system of fiber-sheet coordinates (x_f, x_s, x_n) aligned with structural axes of myocardial laminae. Fiber axis x_f is obtained by a rotation about radial x₃ axis through fiber angle α. A subsequent rotation about x_f through sheet angle β yields sheet axis x_s, which is normal to x_f and lies in sheet plane. x_n is mutually orthogonal sheet normal axis.

Each animal was heparinized (3 mg/kg), the great vessels were ligated, and the heart was arrested by coronary perfusion with a hypothermic cardioplegic solution containing (in g/l) 60.0 dextran, 9.0 NaCl, 4.48 KCl, 3.0 2,3-butanedione monoxime (BDM), and 0.0002 nifedipine. The heart was excised and rinsed, and at this point, four of the hearts were used for a separate isolated heart study that involved passively inflating the LV several times with and without coronary perfusion (8). After this study, all testing devices were removed, and the heart was allowed to float in a bath of room temperature cardioplegic solution. In this unloaded state, the positions of the lead beads in the LV were recorded with biplane fluoroscopy on standard 30-Hz VHS videotape using charge-coupled device videocameras (Cohu, 4915–2000). In the four hearts used for the perfusion study, the unloaded configuration was obtained an average of 114 min after arrest. In the remaining experiments, the unloaded state was measured immediately after isolation of the heart, at an average of 27 min after arrest.

Next, an extra reference marker was attached near one epicardial bead to facilitate column identification in the radiograms. A block of tissue spanning the LV wall thickness and containing the entire transmural bead array, ~2.5 cm square (Fig. 1B), was then cut from the LV free wall with a scalpel to locally relieve residual stress. The tissue block was suspended in fluid so that all of the beads were visible in both views of the biplane X-ray, and video was recorded. At the end of the experiment, a three-dimensional geometric phantom was recorded and later used to compute the transformations needed to reconstruct the three-dimensional coordinates of the beads in the unloaded and stress-free configurations (8).

Morphological studies

After radiography, the tissue block was fixed by immersion with 10% formaldehyde in phosphate buffer for at least 48 h. A transmural sample of the block was dehydrated, embedded in paraffin, and used to measure muscle fiber orientation in the circumferential-longitudinal (1–2) plane. At 8–11 points across the wall, 20-μm-thick sections were obtained parallel to the epicardium and stained with hematoxylin. By use of a video camera (Sony, DXC-151) mounted on a light microscope (Nikon, Optiphot-2), low-power (×20) images of the serial tissue sections were acquired onto a microcomputer (Apple, Macintosh Quadra 900) using NIH Image software. At each transmural depth, the mean fiber angle was obtained from at least five measurements in each image. Angles were measured relative to one edge of the tissue section, and transformed so that 0° coincided with the circumferential (x₁) cardiac axis (Fig. 1B).

Canine ventricular myocardium has recently been shown to have a laminar organization (6, 20) in which myocytes are grouped by the perimysial collagen matrix into branching sheets approximately four cells thick. These myocardial laminae give rise to the cleavage planes that have long been described in long- and short-axis transmural sections of the mammalian heart (3, 22). To examine the relationship of this laminar architecture to residual stress and strain, we used the method of LeGrice et al. (7) to measure the orientations of myocardial cleavage planes. Briefly, 1-mm-thick sections were cut from the fixed stress-free tissue block parallel to the longitudinal-radial (2–3) and the circumferential-radial (1–3) transverse cardiac coordinate planes. Each of these slices spanned the entire wall thickness, and the cleavage planes were visible with low-power reflected light microscopy. Images of the tissue sections were captured onto a Macintosh computer, and cleavage plane angles in each of the two transverse sections were measured at 1-mm increments from epicardium to endocardium, with 0° aligned with the radial x₃-axis perpendicular to the epicardial boundary (Fig. 1B).

Following the observations of LeGrice et al. (7), we interpret the cleavage plane angles as projections of a sheet angle (β), which, together with the fiber angle (α), defines the orientation of myocardial laminae in three dimensions (Fig. 1C). These angles would therefore satisfy the following trigonometric relationships

$$tan\beta =tan{\beta }^{\prime }cos\alpha$$ (1a)

$$tan\beta =-tan{\beta }^{″}sin\alpha$$ (1b)

where β′ is the cleavage plane angle measured in the (2–3) plane, β″ is the cleavage plane angle from the (1–3) plane, and α is the fiber angle from the (1–2) plane. Each of the two cleavage plane measurements (β′ and β″) was used to calculate the sheet angle β from the appropriate equation (1a or 1b), with α interpolated at the corresponding relative wall depth from linear least-squares fits to the measured fiber angles. Equations 1a and 1b indicate that when α = 90° (typical near the endocardium), β is independent of β′, and when α = 0° (typical near midwall), β equals β′ and is independent of β″. Therefore, a best estimate of the transmural distribution of sheet angle β was obtained from a quadratic least-squares fit to the combined data set, with individual points weighted by the sine or cosine of α to reflect the accuracy of the cleavage plane angle projection based on the local fiber orientation. A system of local “fiber-sheet coordinates” (x_f, x_s, x_n) was then defined by two consecutive rotations of the cardiac coordinate axes. First, a rotation about the radial x₃-axis through the interpolated fiber angle α yields the fiber axis x_f aligned with the local muscle fiber orientation in the epicardial-tangent (1–2) plane. A second rotation about x_f through the sheet angle β yields the sheet axis x_s, which lies within the sheet plane and is normal to x_f, and the mutually orthogonal sheet-normal axis x_n, which is perpendicular to the local sheet plane (Fig. 1C).

Strain analysis

The two-dimensional pixel coordinates of the marker centroids were digitized from images acquired with an 8-bit frame grabber (Data Translation DT2651) on a VAXstation 3200. Images of the stationary bead set from three consecutive video frames were digitized and averaged in both the unloaded and stress-free states. The three-dimensional bead coordinates were computed from the camera transformations found with the geometric phantom (8). The coordinates of the markers in each configuration were then transformed into the local cardiac coordinate system (x₁, x₂, x₃) defined in the intact, unloaded state using the apical and basal reference markers.

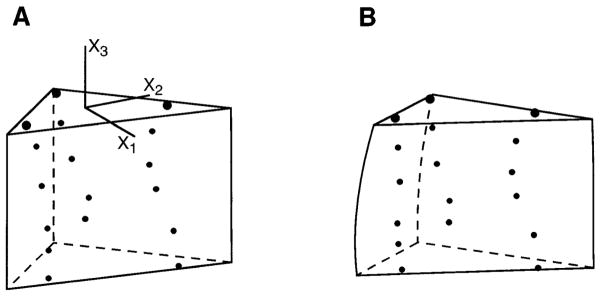
Continuous nonhomogeneous transmural distributions of three-dimensional finite strain were computed using a modification of the least-squares finite-element technique described by McCulloch and Omens (9). A three-dimensional bilinear-quadratic finite element was used to model the deformation of the bead set. Bead positions in the unloaded configuration were computed inside a triangular prismatic element (Fig. 2A), which enclosed the entire bead set and extended transmurally to span the measured wall thickness in each heart. The deformed element configuration was then obtained by a least-squares fit to the projected material coordinates of the beads in the stress-free configuration (Fig. 2B). Hence, components of the Lagrangian strain tensor, E^exp, could be computed along the transmural centerline of the element from epicardium to endocardium as previously described (9). E^exp describes the experimentally observed deformation from the isolated unloaded heart to the stress-free block of tissue, referred to initial segment lengths in the unloaded intact state. However, because residual strain is defined by the inverse deformation from the stress-free state to the unloaded residually stressed state (14), we computed e^res = −E^exp, which is equal to the residual strain measured with respect to deformed coordinates (Eulerian definition).

Fig. 2.

Finite element analysis of 3-D residual strain. A: bead set in unloaded configuration inside a high-order finite element, which matches measured wall thickness. B: updated element configuration obtained from a least-squares fit to projected bead coordinates in stress-free state (actual bead coordinates and element geometries from a representative heart). Lagrangian 3-D finite strains are computed from A to B and are used to calculate Eulerian residual strains which describe inverse deformation from B to A.

The six components of the symmetric residual strain tensor include three normal strains, which describe extension or shortening along each coordinate axis, and three shear strains, which describe changes in the angle between pairs of coordinate axes that are mutually perpendicular in the unloaded configuration. The strains were computed at 10% increments of relative wall depth in each heart (starting at the epicardium) and averaged. Although strains could be computed throughout the finite element (i.e., 100% of wall thickness), we did not extrapolate beyond the subendocardial extent of the transmural bead array. The strain tensors were also transformed at each depth to compute components of residual strain with respect to fiber-sheet coordinates. Relative volume changes in the myocardium contained within the bead set were found from the determinant of the deformation gradient tensor, detF^exp, which represents the local ratio of stress-free to unloaded tissue volume.

Statistical analysis

Data are presented as means ± SD for n = 8 animals unless otherwise specified. Statistical analyses were performed using the software Superanova (version 1.1, Abacus Concepts, Berkeley, CA). Statistical significance was accepted at P < 0.05.

RESULTS

Myocardial fiber and sheet morphology

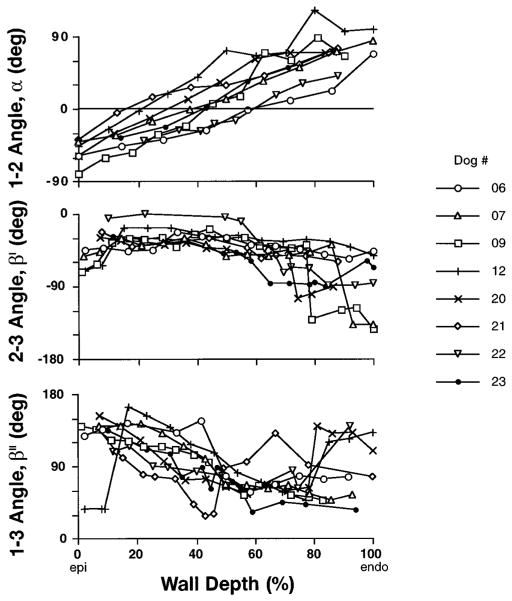
The measured fiber and cleavage plane angles (α, β′, β″) are shown in Fig. 3 vs. relative wall depth for all eight animals. Fiber angle α and the (1–3) cleavage plane angle β″ both exhibited a gradient from epicardium to endocardium, whereas the (2–3) angle β′ was more uniform, especially in the outer half of the wall. In several animals, discontinuities in β′ and β″ were observed in the subendocardium (>80% depth), where papillary muscle and trabeculae caused abrupt changes in the laminar connective tissue structure. A sudden change in subepicardial β″ was also observed in one animal. Mean local wall thickness before fixation was 12.8 ± 1.3 mm.

Fig. 3.

Individual transmural distributions from epicardium (Epi) to endocardium (Endo) of fiber angle α, measured in (1–2) cardiac coordinate plane, and 2 cleavage plane angles, β′ and β″, measured in (2–3) and (1–3) coordinate planes, respectively, from midanterior left ventricular free wall myocardium fixed in stress-free state. Discontinuities in β′ and β″ reflect abrupt changes in sheet structure, such as endocardial trabeculae. β′ and β″ are plotted in ranges of 0 to −180° and 0 to 180°, respectively.

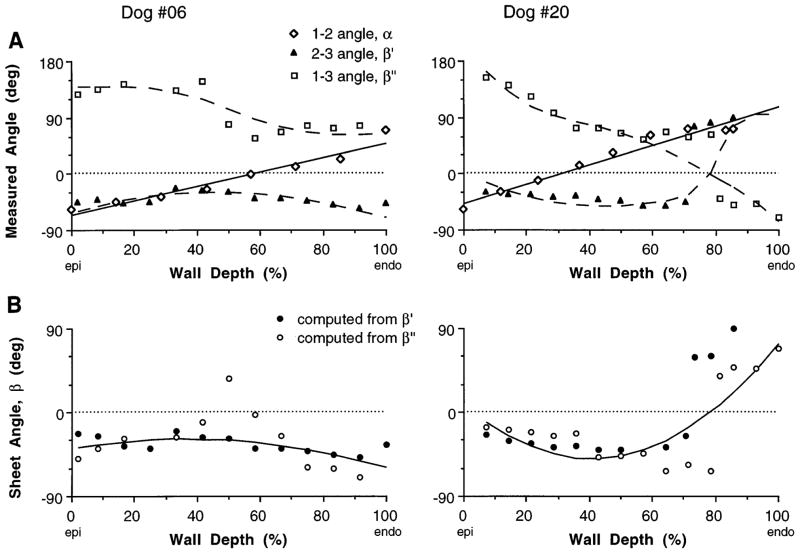
Measurements of α, β′, and β″ for two animals are shown in Fig. 4A, together with the fiber angle regression line. The two distributions of sheet angle β computed from these data with Eqs. 1a and 1b showed general agreeement through most of the wall (Fig. 4B). To check the validity of the mathematical model, the fitted distributions of β and α were substituted back into Eqs. 1a and 1b, which were then solved for the corresponding cleavage plane angles. These estimates of β′ and β″ showed good consistency with the measurements (Fig. 44A, dashed lines), including the higher-order transmural variations.

Fig. 4.

Distributions from Epi to Endo of 3 measured angles (A) and calculated sheet angle (B) for 2 individual animals. A continuous transmural distribution of fiber angle α was obtained from a linear least-squares fit to data (solid line in A). Each measurement of 2–3 cleavage plane angle β′ was then used to compute a sheet angle β, using an interpolated value of α at matching wall depth. This was repeated using (1–3) angle β″, yielding 2 sets of sheet angle data in B. A continuous transmural distribution of β was then obtained from a weighted quadratic least-squares fit to combined data set (solid line in B). To test for self-consistency, sheet angle equations were solved in reverse for values of β′ and β″ using fitted fiber and sheet angle distributions, and these results agreed with actual cleavage plane measurements (dashed lines in A)

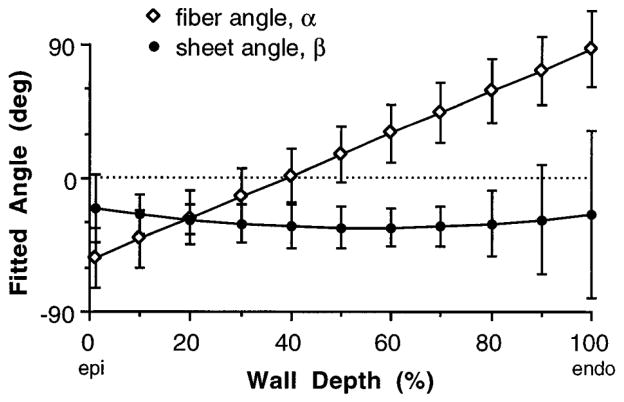
The average fitted fiber and sheet angle distributions (α and β, respectively) from the eight animals are shown in Fig. 5. Fiber angle α varied linearly from −53 ± 20° at the epicardium to 87 ± 25° at the endocardium, whereas mean values of β were −20 ± 23°, −33 ± 14°, and −25 ± 56° at the epicardium, midwall, and endocardium, respectively. For six of the eight animals, the reconstructed sheet angle was negative across the wall, but in two hearts, β crossed zero at ~80% wall depth to yield positive values in the subendocardium, giving rise to the larger standard deviations in that region. The average root-mean-squared (rms) errors in the least-squares fits were 9 ± 4° for α and 23 ± 12° for β.

Fig. 5.

Mean (±SD) fitted transmural distribution of fiber angle α and sheet angle β from 8 animals.

Three-dimensional residual strain

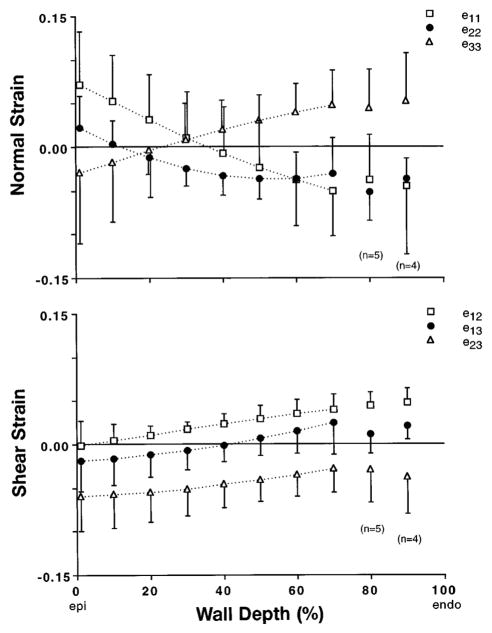
The average transmural distributions of the six components of three-dimensional Eulerian residual strain referred to cardiac coordinates are shown in Fig. 6. In all eight experiments, the bead set spanned at least 70% of the wall thickness. Mean results deeper in the subendocardium are also reported, with n = 5 at 80% depth and n = 4 at 90% depth. One-factor analysis of covariance (ANCOVA), with the strain component treated as a nominal factor, revealed a significant interaction of component and depth on the variation of residual strain (P< 0.001). Therefore, post hoc linear regression analysis was performed to help characterize the transmural distribution of each strain component. All residual cardiac strain components showed significant transmural gradients (P < 0.002). Mean circumferential strain ( $e_{11}^{\text{res}}$) indicated residual extension at the epicardium with subendocardial shortening (slope = −0.0014/%depth), whereas radial strain ( $e_{33}^{\text{res}}$) had a slope of similar magnitude but opposite sign. Longitudinal strain ( $e_{22}^{\text{res}}$) indicated small residual shortening across most of the wall, and the average transmural value (50% intercept of linear regression) of −0.03 was significant (P = 0.0001). Two of the residual shear strains ( $e_{12}^{\text{res}}$ and $e_{13}^{\text{res}}$) had a similar small transmural gradient (slope = 0.0005/%depth), and $e_{12}^{\text{res}}$ was consistently positive, indicating a small net residual torsion of 0.03 (P = 0.0001). However, the mean transverse residual shear strain in the longitudinal-radial plane ( $e_{23}^{\text{res}}$) was predominant, with an average transmural value of −0.04 (P = 0.0001).

Fig. 6.

Transmural distributions from Epi to Endo of 6 components of 3-D Eulerian residual strain tensor, e^res, referred to cardiac coordinates. Circumferential, $e_{11}^{\text{res}}$, and radial, $e_{33}^{\text{res}}$, strains showed opposing transmural gradients, consistent with published 2-D residual strain studies. Longitudinal strain, $e_{22}^{\text{res}}$, was small but significant (P < 0.0001), as were $e_{12}^{\text{res}}$ and $e_{13}^{\text{res}}$ shear strains. A substantial residual transverse shear strain, $e_{23}^{\text{res}}$, was found in longitudinal-radial plane. Symbols represent mean values (n = 8 except as noted), with error bars indicating ±SD.

The distribution of detF^exp (not shown) indicated the change in overall average tissue volume within the bead set from the unloaded intact state to the stress-free state was not significant [H_o: mean (detF^exp − 1) ≠ 0; P = 0.50]. However, the transmural gradient was significant (slope = 0.0011/%depth, P = 0.0001) and indicated a 6% decrease in local tissue volume at the epicardium, with a reciprocal increase in subendocardial volume when residual stress was relieved.

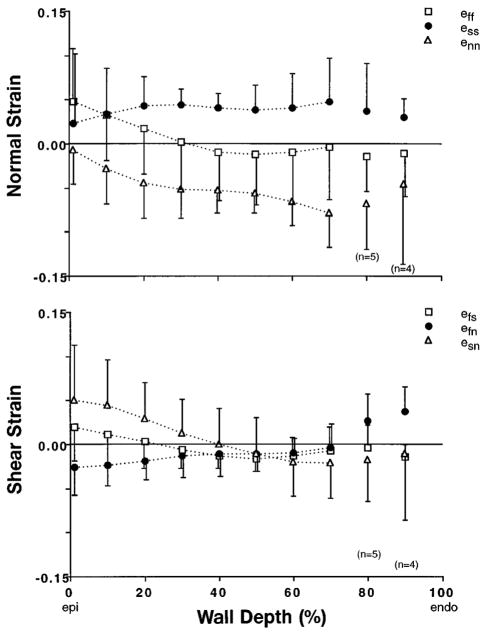
When residual cardiac strains were transformed into fiber-sheet coordinates (Fig. 7), mean residual strain in the fiber direction ( $e_{\text{ff}}^{\text{res}}$) indicated ~5% extension at the epicardium with smaller subendocardial shortening (slope = −0.0007/%depth, P = 0.002). Sheet-normal strain was negative and relatively uniform across the wall ( $e_{\text{nn}}^{\text{res}}\approx -0.05$), whereas residual strain within the sheet plane showed uniform extension transverse to the fiber axis with $e_{\text{ss}}^{\text{res}}\approx 0.04$ (neither slope was significant, P> 0.06). All three shear components ( $e_{\text{fs}}^{\text{res}},e_{\text{fn}}^{\text{res}}$, and $e_{\text{sn}}^{\text{res}}$) exhibited a small but significant transmural gradient (P < 0.005). However, none was different from zero on average (P> 0.06), and except in the inner and outer 20% of the wall, none of the mean shear strains exceeded values of ±0.02. Therefore, the principal deformations due to residual stress may act primarily along sheet structural axes across most of the LV wall.

Fig. 7.

Transmural distributions from Epi to Endo of 6 components of 3-D Eulerian residual strain, e^res, referred to sheet coordinates. Residual stress gives rise to compression of adjacent myocardial laminae ( $e_{\text{nn}}^{\text{res}}<0$) and stretching within sheet plane, particularly transverse to fiber axis ( $e_{\text{ss}}^{\text{res}}>0$). With exception of subepicardial $e_{\text{sn}}^{\text{res}}$, all 3 shear strains were small. Gradient in fiber strain, $e_{\text{ff}}^{\text{res}}$, was consistent with previously measured changes in sarcomere length due to residual stress in rat heart. Symbols represent mean values (n = 8 except as noted), with error bars indicating ±SD.

DISCUSSION

We have presented the first measurements of fully three-dimensional residual strains in the heart. The findings were consistent with earlier one- and two-dimensional studies but revealed other significant components, including substantial negative transverse shear strains. From measurements of myocyte fiber orientations and cleavage plane orientations, we defined a local coordinate system based on these anatomic structures in the tissue. By referral of the strain components to these microstructural axes, the mechanics of residually stressed myocardium could be interpreted relative to the underlying tissue architecture. The relation between the observed residual deformations and the fibrous, laminar connective tissue organization of the ventricular wall suggests structural pre-stressing of myocardial laminae in the unloaded intact LV myocardium.

Myocardial fiber and sheet morphology

The three-dimensional nonhomogeneous fibrous architecture of the myocardium has been well documented (13, 23), and our transmural fiber angle data from the midanterior LV free wall are consistent with previous measurements in this region (8, 15). A laminar connective tissue organization of the myocardium has also long been recognized (3, 22), and quantitative measurements of the structure of these myocardial sheets have recently become available (6, 7). Our cleavage plane angle measurements (Fig. 3) were similar to these previous measurements, although LeGrice et al. (6, 7) reported a steeper transmural gradient in the (2–3) cleavage plane angle β′, which may reflect regional variations between our measurement site and theirs. It is also possible that cleavage plane morphology is different in the stress-free state than in the unloaded (6) or inflated (7) states studied previously.

Three-dimensional residual strain

Residual strains describe the deformation from the stress-free state to the unloaded state of a body (from B to A in Fig. 2). We have chosen to present Eulerian residual strains, e^res, because the deformed (intact, unloaded) state of the myocardium represents a well-defined reproducible reference configuration in which the cardiac coordinates are easily related to the LV geometry. However, Lagrangian residual strains, E^res, referred to the undeformed (stress-free) configuration are equally valid and are more consistent with previous studies. So, for comparison, we also computed E^res for each heart (21), which was straightforward once the deformation gradient tensor was extracted from the finite element analysis. In both the cardiac and sheet coordinate systems, the Lagrangian normal strain profiles were shifted upward (indicating greater lengthening and smaller shortening) compared with the corresponding Eulerian strain profiles, whereas the trend was inconsistent for the shear strains. The difference between the mean Lagrangian and Eulerian strain profiles was typically ~0.02 or less for the normal strains and <0.01 strain units for the shear components. These small differences were always within 1 SD of the mean Eulerian strains and hence would not affect our conclusions.

The distributions of circumferential ( $e_{11}^{\text{res}}$) and radial ( $e_{33}^{\text{res}}$) residual strains agree with previous two-dimensional measurements from the study by Omens and Fung (14), in which equatorial rings of isolated rat heart sprang open into an arc after being radially transected to relieve residual stress. On the basis of their mean principal stretch ratios in the anterior portion of the rat LV, Eulerian residual strains in the subepicardial and subendocardial one-thirds of the heart wall would be 0.07 and −0.09 (circumferential) and −0.09 and 0.12 (radial), respectively. We found similarly opposing transmural gradients of $e_{11}^{\text{res}}$ and $e_{33}^{\text{res}}$ (Fig. 6), characteristic of the opening angle experiments. The somewhat smaller magnitudes of residual strain in this study suggest a smaller opening angle in the dog than in the rat, consistent with measurements from our laboratory (unpublished data, 1994) of an opening angle of 25 ± 4° (mean ± SD, n = 3) for an equatorial section of the potassium-arrested dog heart, compared with 45 ± 10° in the rat (14). Residual stress was also found to cause small but significant longitudinal shortening, $e_{22}^{\text{res}}$, which has been neglected in previous two-dimensional studies. In addition, the three-dimensional measurements revealed a small positive torsional residual shear strain, $e_{12}^{\text{res}}$. This is consistent with measurements in the normal mouse LV (16), in which an opening angle of 25 ± 9° was accompanied by an out-of-plane warp angle of 3.4 ± 1.2° so that the anterior side of the LV moved toward the apex when residual stress was relieved. The three-dimensional measurements also revealed a substantial negative longitudinal-radial transverse residual shear strain, $e_{23}^{\text{res}}$, which had not previously been reported.

Residual strain referred to fiber-sheet coordinates indicated subepicardial stretching of muscle fibers in the presence of residual stress, with subendocardial fiber shortening. This is consistent with the study of Rodriguez et al. (19), who reported sarcomere extension in the subepicardium and sarcomere shortening in the subendocardium due to residual stress in an equatorial ring of rat LV, with no measurable change in midwall sarcomere lengths compared with the stress-free state. Using the stress-free sarcomere length distribution reported in that study combined with our mean values of $e_{\text{ff}}^{\text{res}}$, we calculated a transmural gradient of sarcomere length in the unloaded canine heart of −0.13 μm/normalized wall thickness, which compares with the value of −0.114 ± 0.054 μm reported for the rat (19). Considering the smaller opening angle in the dog than in the rat, one might have expected a smaller gradient in sarcomere length as well. However, Rodriguez et al. (19) commented that they may have underestimated the actual sarcomere length gradient in the intact unloaded rat heart because the effects of longitudinal residual stress were neglected, which presumably would have the greatest influence in the epicardial and endocardial regions where muscle fiber orientations have a substantial longitudinal component. Our mean values of $e_{22}^{\text{res}}$ indicated that, relative to the stress-free state, the intact unloaded myocardium was stretched longitudinally at the epicardium and compressed in the subendocardium, supporting the hypothesis of a steeper transmural sarcomere length gradient in the intact residually stressed LV than would be measured in a partially stress-relieved equatorial ring of myocardium.

Residual strains in cardiac coordinates indicated substantial shearing deformations in transverse planes of the LV wall, the same planes in which we measured the orientation of cleavage planes separating adjacent layers or “sheets” of myocardium. In light of the observations of LeGrice et al. (7), these cleavage planes were interpreted as two-dimensional projections of a fully three-dimensional laminar connective tissue organization of the myocardium. Individual myocardial sheets are about four cells thick and are bounded by a dense perimysial connective tissue matrix, which provides tight coupling within the sheet, with adjacent sheets connected by a loose network of collagen fibers (5, 6). It has been postulated that such an organization facilitates rearrangement of cell bundles, providing a mechanism for the large changes in ventricular wall thickness that occur during the cardiac cycle (3, 22). Such sliding or slippage of myocardial sheets would be consistent with macroscopic transverse shearing deformations, as recently demonstrated in the subendocardium during systole (7). However, when residual strains were referred to a coordinate system based on the local three-dimensional structural axes of the myocardial laminae, small sheet shear strains through most of the LV wall implied little relative motion of adjacent layers of myocardium due to residual stress. Instead, the residual strains indicated compression normal to the sheets ( $e_{\text{nn}}^{\text{res}}<0$), which may reduce the gaps or clefts between adjacent myocardial laminae or may reflect thinning of the sheets themselves. Reciprocal extension along the sheet axis ( $e_{\text{ss}}^{\text{res}}>0$) indicated muscle fibers may be transversely stretched or separated within the sheet plane in the presence of residual stress. Therefore, the measured transverse shear strains in cardiac coordinates arose from shortening and extension along oblique structural axes oriented parallel and perpendicular to the myocardial laminae. Because of its organization relative to the myocardial sheets, the perimysial extracellular connective tissue matrix may be an important residual stress-bearing structure in the myocardium. Because the myocytes themselves are by definition aligned with the myocardial sheets, intracellular load-bearing components of the cytoskeleton may also play a role; further research is needed to determine the contributions of these individual structures to residual stress in the ventricular wall.

The residual strains measured in this study are smaller than typical strains during ventricular filling (15) and ejection (27). This, together with the fact that the stiffness of resting myocardium is lowest around the zero-stress state due to the material nonlinearity, suggests that associated residual stresses may be substantially smaller than ventricular wall stresses under physiological loading conditions. Nevertheless, the effects of residual stress and strain on ventricular mechanical function can be significant. Several model studies suggest residual compression may help to decrease subendocardial stresses during LV filling (4, 12, 24). Furthermore, because it affects sarcomere length (19), residual stress may influence systolic mechanics due to the strong dependence of peak active tension on sarcomere length in vitro (1, 26). For example, a stress-free sarcomere length of 1.84 μm (19) would decrease by 0.03 μm in the residually stressed subendocardium according to our measurements of residual fiber strain. From the data from ter Keurs et al. (26) in isolated rat trabeculae at an extracellular calcium concentration of 0.5 mM, this change would correspond to a decrease in peak isometric tension of ~5 mN/mm², representing 5–10% of the expected peak tension for end-systolic sarcomere lengths in the range of 2.2–1.9 μm (18).

Effects of edema due to perfusion

The first four of the eight experiments were conducted after a separate isolated heart perfusion study (8) in which a mean 14% change in tissue volume was reported due to edema. To assess whether there was a statistically significant difference in residual strain between the perfused and nonperfused groups, one-factor ANCOVA was performed for each strain component, using the perfusion state as a nominal factor. Differences in transmural gradients between the two groups were quantified by post hoc linear regression, and Scheffé’s S procedure was used for post hoc comparison of means. In the fiber-sheet coordinate system, four of the six residual strain components ( $e_{\text{ff}}^{\text{res}},e_{\text{nn}}^{\text{res}},e_{\text{fn}}^{\text{res}}$, and $e_{\text{sn}}^{\text{res}}$) differed significantly between the perfused and unperfused groups (P ≤ 0.05). Of these, perfusion only altered the transmural gradient of $e_{\text{fn}}^{\text{res}}$ (P = 0.005). The mean transmural gradient of $e_{\text{fn}}^{\text{res}}$ in the four unperfused hearts was ~40% lower than that shown for the entire group in Fig. 7. Moreover, the mean values of the residual shears, $e_{\text{fn}}^{\text{res}}$ and $e_{\text{sn}}^{\text{res}}$, were even smaller in the unperfused group. This provides more support to our conclusion that residual stress gives rise to negligible shear strains in sheet coordinates, implicating sheet axes as principal axes of residual strain. The average value of $e_{\text{nn}}^{\text{res}}$ was −0.03 for the nonperfused hearts compared with −0.05 for the combined group. The average value of $e_{\text{ff}}^{\text{res}}$ was −0.03 in the nonperfused hearts compared with 0.00 for the combined data. Thus, although the effects of edema due to perfusion had some significant effects on the measured residual strains, the conclusions based on the combined data were supported or strengthened by the results from the four hearts that were not perfused.

We also found a significant effect of perfusion on the mean value of detF^exp, which changed slightly from 1.00 for the nonperfused hearts to 0.97 for the perfused hearts (P = 0.008), indicating a small net loss of volume from the edematous tissue when it was cut out of the heart to relieve residual stress. However, there was no effect of perfusion on the transmural gradient of detF^exp (P = 0.24). In both groups, there was a small but significant gradient of detF^exp, which suggests that compressive endocardial residual stress and tensile epicardial residual stress may shift the balance of volume in the wall. If this volume is attributed to the relatively mobile intracoronary fluid, this finding may explain why the endocardium has a higher apparent capacitance than the epicardium (8).

Sources of error

LeGrice et al. (7) have discussed the limitations of measuring projections of the three-dimensional sheet structure in three separate two-dimensional planes. Accurate reconstruction of the sheet orientation requires structural homogeneity throughout the region of the measurements. Agreement between sheet angles computed from β′ and β″ indicated that this assumption was reasonable, and self-consistency between the measured and calculated cleavage plane angles (Fig. 4A) further supports this notion. Some specific discrepancies between the two sets of sheet angle data were anticipated on the basis of the mathematical model of the cleavage planes. Therefore, reliability of the projected cleavage plane angles was incorporated into the analysis. In two animals, a systematic difference of ~40° existed between the sheet angles calculated from β′ and β″ across the wall, indicating relatively rapid changes in sheet structure within the local measurement volume. In these cases, the quadratic fit fell between the two distributions of β and was assumed to be a reasonable estimate of the average sheet angle distribution in the region of the bead set.

Several measures were taken to minimize experimental artifacts that might influence the measured residual strains. To reduce the effects of gravity on the experimental preparation, the intact hearts and tissue blocks were suspended in a bath of fluid. To delay the onset of ischemic contracture, the animals were pretreated with oral nifedipine, and the heart was arrested in vivo, and the coronary circulation was briefly perfused with a hypothermic, hyperkalemic cardioplegic solution containing 2,3-BDM, which protects the isolated tissue from cutting injury (11). Thus the use of this preparation should eliminate any residual physiological cross-bridge formation and preserve passive material properties. Although progressive contracture would cause the calculated residual strain to change with time, differences between the reported strains and those measured during the subsequent 2–3 min were within the accuracy of our experimental methods (9). We thus infer that ischemic contracture did not adversely affect the results of this study.

Accuracy of the residual strains requires that the excised tissue block represents the true zero-stress state of the tissue. Previous two-dimensional residual strain studies in ventricular cross sections have shown no significant change in the zero-stress state subsequent to the first radial cut (14). By comparison, in the present study, the zero-stress state was effectively approximated as the state following two closely spaced radial cuts in the ventricular cross section. Thus it may not be the same as the stress-free state used in previous studies, but it should be a better approximation to it.

Finally, accuracy of the computed residual strains obtained by nonhomogeneous finite element analysis was improved by projecting the actual three-dimensional marker coordinates in the unloaded reference state directly into the initial finite element, thus eliminating errors due to the initial approximation of the reference configuration required by our previous strain analysis method (9). Additionally, rms errors in the least-squares fit to the deformed (stress free) bead set coordinates were reduced, ranging from 0.05 to 0.24 mm for the eight hearts, compared with errors as large as 0.34 mm obtained using the previous method. Despite these improvements, differences in strain between the two techniques were typically <0.02, which is similar to the estimated variation due to the measurement accuracy (9).

In conclusion, three-dimensional residual strains in passive midanterior canine LV myocardium were consistent with earlier one- and two-dimensional studies. However, the presence of substantial transverse shear strains with small torsional and longitudinal strains reveals a more complex distribution of residual stress and strain than previously identified. When referred to a coordinate system based on the underlying fibrous and laminar architecture of the myocardium, the residual strains suggest epicardial fiber tension and endocardial fiber compression in the unloaded intact LV, although myocytes in much of the midwall may experience relatively little residual stress along the muscle fiber axis. The residual strains also indicated both tension and compression normal to the local fiber axis, with residual stresses being borne mainly by structures lying parallel and perpendicular to the laminar bundles of myofibers. For example, the perimysial extracellular connective tissue matrix may be a primary residual stress-bearing structure in passive myocardium. Therefore, pathological conditions, such as fibrosis or matrix degradation during stunning, may alter residual stresses in the heart and hence may provide useful models for future studies of the structural basis of residual stress and strain.