Abstract
In native apomyoglobin, His-24 cannot be protonated, although at pH 4 the native protein forms a molten globule folding intermediate in which the histidine residues are readily protonated. The inability to protonate His-24 in the native protein dramatically affects the unfolding/refolding kinetics, as demonstrated by simulations for a simple model. Kinetic data for wild type and for a mutant lacking His-24 are analyzed. The pKa values of histidine residues in native apomyoglobin are known from earlier studies, and the average histidine pKa in the molten globule is determined from the pH dependence of the equilibrium between the native and molten globule forms. Analysis of the pH-dependent unfolding/refolding kinetics reveals that the average pKa of the histidine residues, including His-24, is closely similar in the folding transition state to the value found in the molten globule intermediate. Consequently, protonation of His-24 is not a barrier to refolding of the molten globule to the native protein. Instead, the normal pKa of His-24 in the transition state, coupled with its inaccessibility in the native state, promotes fast unfolding at low pH. The analysis of the wild-type results is confirmed and extended by using the wild-type parameters to fit the unfolding kinetics of a mutant lacking His-24.
His-24 plays a remarkable role in the structure and pH titration behavior of apomyoglobin (apoMb). His-24, which is in the B helix, is completely buried, and its neutral imidazole ring is hydrogen bonded to that of His-119 in the G helix (1–3), thus providing a strong link (4) between the B and G helices. Although His-119 can be protonated at low pH, His-24 remains neutral and cannot be protonated in the native form (N) of apoMb (2). The charged guanidinium group of Arg-118 sits directly above the imidazole ring of His-24 in N (5). Consequently, protonation of His-24 occurs only when N forms a stable molten globule intermediate (I) at pH 4. Only a subdomain of N containing the A, G, and H helices of apoMb is stably folded in I (6).
His-48, His-64, His-113, and His-119 have low pKa values in N (2, 7), but only His-24 is entirely resistant to being protonated in N; and protonation of His-24 at pH 4 forces the conversion of N to I. All histidine residues are protonated in the molten globule at and below pH 5, where I is formed (2); thus, the pKa values of all histidines in the molten globule are close to normal.
Because His-24 cannot be protonated in N, the question arises of whether His-24 can be protonated in the folding transition state (I‡) of the N to I reaction. Barrick et al. (4) pointed out that, if His-24 is inaccessible in the folding transition state, this will present a serious kinetic barrier to the refolding of I to N at pH values where I is protonated. To answer this question, we first determine the average pKa value of the histidine residues in the molten globule, from the pH-dependent equilibrium between N and I, using data from ref. 8, combined with the pKa values of histidine residues in the native state, determined earlier (2, 7). The N ⇌ I equilibrium depends on pH through ΔQ, the difference between the number of protons bound to N vs. I, and the pH dependence of its standard free energy is given by −2.303∫ΔQdpH. This integral is calculable from the pKas of the histidines in N and I (9) when unfolding occurs in the pH range in which only histidines are titrating. We use the extensive data of Barrick and Baldwin (8) on the pH dependence of the equilibrium [N]/[I] ratio.
After determining the average pKa value of histidines in the molten globule intermediate, the average pKa value of histidines in the folding transition state may be calculated from the plot of log kobs vs. pH (9, 10), because the pKa values in N and I are known. Simulations reveal that, if any histidine has a pKa in the folding transition state that differs markedly from the average value, this fact will be apparent in the pH dependence of the unfolding/refolding kinetics.
The double mutant H24V/H119F (4) provides an important control for this analysis of the unfolding/refolding kinetics of wild type (WT). The double mutant is stably folded: the double replacement of His-24 and His-119 with Val and Phe is found commonly in the globin family, and the nonpolar Val-Phe link between the B and G helices makes the double mutant more stable to urea unfolding at neutral pH than WT (4). The single mutants H24V and H119F are both considerably less stable than WT (4). The main cause for the WT native state's becoming unstable at low pH is the protonation of His-24 in I, and, because the double mutant lacks His-24, its N ⇌ I unfolding transition is shifted down near pH 3, where the Asp and Glu residues undergo protonation (2, 4). The unfolding transition of the less stable mutant H36Q, which also is studied here, is shifted in the opposite direction to a higher pH range because protonated His-36 stabilizes WT through side chain interactions (4).
Experimental Procedures
Protein Expression and Purification.
A synthetic gene for sperm whale myoglobin was expressed and purified as described (2, 11). The heme was removed by acid-acetone precipitation (12). Protein concentration was determined by absorbance in 6 M GdmCl as described (13) using ɛ280 nm = 15,200 M−1⋅cm−1 and ɛ288 nm = 10,800 M−1⋅cm−1.
Fluorescence Stopped-Flow Experiments.
Data were collected on an Applied Photophysics (Surrey, U.K.) model DX17 MV instrument, using a 2-mm pathlength cell. Excitation was at 288 nm, and measurements of emission were made by using an optical cutoff filter. Kinetic traces from the stopped-flow experiments were fitted to single, double, and triple exponential time courses with the software provided by Applied Photophysics.
Modeling the pH Dependence of the Rate Constants.
All simulations were performed with sigmaplot (Jandel, San Rafael, CA). The rate constants for folding (kf) and unfolding (ku) are expressed as functions of pH by assuming that the proton binding sites are independent, using the following equations.
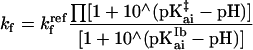 |
1a |
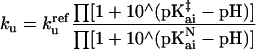 |
1b |
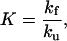 |
2 |
where k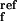 and
k
and
k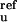 are the reference rate constants for
the Ib → N and N → Ib reactions, respectively, at pH 9;
K is the folding equilibrium constant; and the
pKai values refer to residue i in the N, Ib, and
I‡ forms.
are the reference rate constants for
the Ib → N and N → Ib reactions, respectively, at pH 9;
K is the folding equilibrium constant; and the
pKai values refer to residue i in the N, Ib, and
I‡ forms.
Results
Average pKa of Histidines in the Molten Globule.
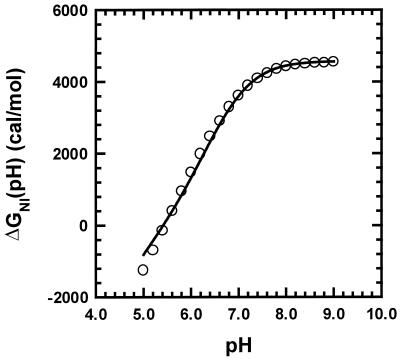
Fig. 1 shows ΔGNI(pH), the difference in standard Gibbs free energy between N and I, calculated from data given by Barrick and Baldwin (8), who used circular dichroism to measure the pH-induced and urea-induced unfolding transitions of apoMb at 0°C from pH 1 to 8 and from 0 to 8 M urea. They fitted the results to a simplified three-state model (N ⇌ I ⇌ U) using a minimal number of parameters. The urea- and pH-induced unfolding results are fitted closely by the three-state model, and the fitting parameters can be used to give reasonably accurate values of ΔGNI(pH) as a function of pH.
Figure 1.
Determination at 0°C of the average pKa of histidines in the molten globule (see text for details). Values of ΔGNI, the change in Gibbs energy for unfolding from N to I, are taken from ref. 8. The fitted curve is given by −2.303 ∫ΔQ dpH, where ΔQ is the difference in number of protons bound to N vs. I; ΔQ is computed from the pKa values in N measured by chemical shift titration (2,7) and from the average pKa in I, treated as the sole unknown.
In Fig. 1, ΔGNI(pH) is plotted against pH, and the fitted line is −2.303 ∫ΔQdpH, where ΔQ is computed from the known individual pKa values of the histidines in N and from the average pKa of the histidines in I, treated as the sole unknown. The pKa values in N are corrected to 0°C [the temperature used by Barrick and Baldwin (8)] from the 35°C values of Geierstanger et al. (2) by using the heat of protonation of free histidine, −6.9 kcal/mol (14), in the van't Hoff relation. The average pKa in I is found by least-squares fitting to be 6.8 (0°C). His-36 is omitted from the calculation of ∫ΔQdpH in Fig. 1 because its protonated form stabilizes N, contrary to the assumptions of the simple three-state model, and as a result the contribution of His-36 to the experimental N ⇌ I data is smoothed out in fitting the data to the model of ref. 8. The native pKa determinations of histidine residues were made in 10 mM acetate buffer (2) whereas data for the N ⇌ I unfolding transition (8) were obtained in 2 mM citrate buffer. We show below that, although there is a significant difference in ΔGNI in these two buffers, the same pKa values apply in both buffers.
Unfolding and Refolding Kinetics vs. pH.
Although the nature of the rate equation for protein folding is still under discussion (15), there is general agreement that the transition state approximation provides the basis for the rate equation: it specifies that the folding transition state I‡ is in equilibrium with the denatured protein in refolding and with the native protein in unfolding. There are two forms of the apoMb molten globule, Ia and Ib, which coexist in a pH-dependent equilibrium, and the kinetics of the overall folding reaction indicate that the pathway is N ⇌ Ib ⇌ Ia ⇌ U, in which N is formed directly from Ib, not Ia (16); U is the acid-unfolded form. The designation “I” is used here as a collective term for (Ia,Ib) when both forms are present and no further specification is needed.
In refolding to N, I‡ equilibrates with Ib, and the pH dependence of the folding rate kf is attributed to this equilibrium:
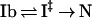 |
3a |
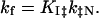 |
3b |
KI‡ is the equilibrium constant for equilibration between Ib and I‡, and k‡N is the rate constant with which I‡ breaks down to give N. Likewise, in unfolding to Ib, N equilibrates with I‡, and the unfolding rate ku is written
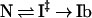 |
4a |
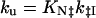 |
4b |
In fitting the experimental curve of log kobs vs. pH, KI‡ is pH dependent in refolding experiments, and KN‡ is pH dependent in unfolding experiments because these equilibrium constants depend on the pKa values of residues that titrate in this pH range. For a two-state reaction, the observed rate constant kobs is the sum of the unfolding and refolding rate constants.
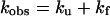 |
5 |
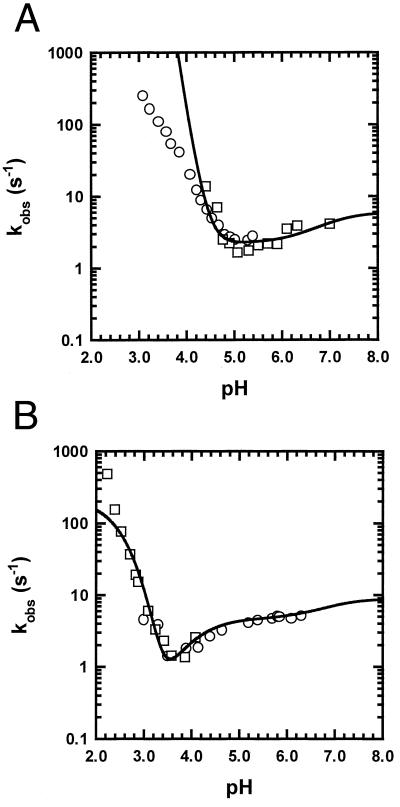
Fig. 2 shows kobs plotted against pH at 4.5°C, in citrate buffer, for WT (Fig. 2A) and for the double mutant H24V/H119F (Fig. 2B). The average pKa of histidine residues in the folding transition state, determined from the WT curve, is 6.7, almost the same as in the molten globule (6.8, Table 1). Simulations presented below show that, if His-24 had an abnormally low pKa in I‡ as it does in N, this would be readily observable from the shape of the curve of log kobs vs. pH. Exactly the same parameters are used to fit the WT curve and the H24V/H119F curve (Fig. 2B), whereas the pKa values of His-24 and His-119 are omitted in the latter. The pKa values used to fit these curves (Table 1) are discussed below.
Figure 2.
The plot of log kobs vs. pH for pH-induced unfolding/refolding in a citrate buffer (2 mM citrate/30 mM NaCl) at 4.5°C for WT (A) and the double mutant H24V/H119F (B). Both mutant and WT curves are fitted by using the same pKa values (Table 1), with reference values ku = 0.001 and kf = 6 (A) or with ku = 2 × 10−5 and kf = 9 (B). The rate constants are given in units of s−1 and the reference values refer to pH 9.
Table 1.
pKa values used to fit the pH-dependent unfolding/refolding kinetics
| Residue | pKa, N* | pKa, I‡† | pKa, I§ | No. |
|---|---|---|---|---|
| His-24 | >3.5 | 6.7 | 6.8 | 1 |
| His-36 | 8.5 | 6.7 | 6.8 | 1 |
| His-48 | 6.0 | 6.7 | 6.8 | 1 |
| His-64 | 5.5 | 6.7 | 6.8 | 1 |
| His-113 | 6.5 | 6.7 | 6.8 | 1 |
| His-119 | 6.5 | 6.7 | 6.8 | 1 |
| Acidic I | 3.4 | 4.0 | 4.0 | 9 |
| Acidic II | 3.4 | 3.5 | 3.6 | 13 |
All pKa values refer to 4.5°C, the temperature of the experiments reported here. The estimated uncertainty of the histidine pKa values is ±0.1. See text for the procedure used to fix pKa values of the acidic residues (Asp and Glu): group I corresponds to the unfolded CDEF subdomain of the apoMb molten globule, and group II corresponds to the structured A[B]GH subdomain of the molten globule.
The pKa values of histidine residues in native apoMb are taken from table 2 of ref. 2, determined at 35°C and corrected to 4.5°C (see text). No correction has been made for the possible influence of D2O on the histidine pKa values determined by chemical shift titration.
The average pKa value of histidine residues in the folding transition state, determined by fitting the plot of log kobs versus pH for wild type in citrate buffer (Fig. 2A), when the pKa values in N and in Ib are known.
The average pKa of the histidine residues in the molten globule, determined as shown in Fig. 1.
Results in Acetate Buffer.
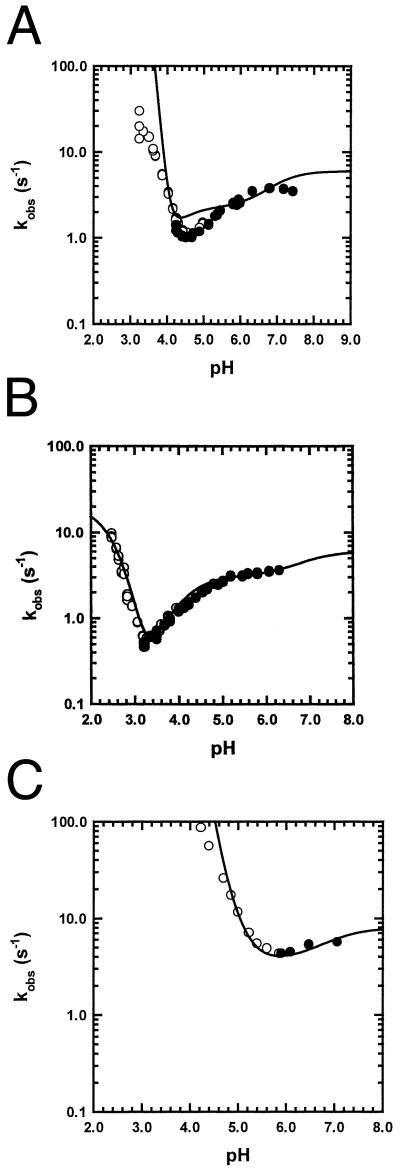
Because citrate buffer causes the Ia ⇌ Ib equilibrium to be more strongly dependent on pH than acetate buffer (ref. 16 and unpublished results), and because we thought this behavior might affect the pH dependence of the unfolding/refolding kinetics, we also determined the unfolding/refolding kinetics in 10 mM acetate buffer. Fig. 3 shows the results for WT (Fig. 3A) and two mutants (H24V/H119F), whose unfolding curve is shifted to lower pH (Fig. 3B), and H36Q (Fig. 3C), whose unfolding curve is shifted to higher pH. These curves are fitted by the same pKa values determined in citrate (Table 1), whereas the altered stability of I in acetate (Table 2) is taken into account by adjusting the values of ku and kf.
Figure 3.
The plot of log kobs vs. pH in 10 mM acetate buffer at 4.5°C for WT (A), H24V/H119F (B), and H36Q (C). All three curves are fitted with same pKa values (Table 1), which are also used to fit the data in citrate buffer (Fig. 2), with reference values ku = 2 × 10−5, kf = 6 (A), ku = 2 × 10−6, kf = 6 (B), ku = 5 × 10−4, and kf = 8 (C). The rate constants are given in s−1, and the reference values refer to pH 9.
Table 2.
Properties of the pH-induced unfolding reactions in citrate vs. acetate buffer
| Citrate | Acetate | |||
|---|---|---|---|---|
| Protein | pHm | ΔGNI | pHm | ΔGNI |
| WT | 4.7 | 4.8 | 4.4 | 7.0 |
| H24V/H119F | 3.5* | 7.2 | 3.2† | 8.2 |
| H36Q | n.d. | n.d. | 5.3 | 5.3 |
Determined at 4.5°C in either 10 mM acetate or 2 mM citrate, 30 mM NaCl buffer. pHm is the pH midpoint of the unfolding transition monitored by the final fluorescence values obtained in unfolding/refolding experiments, as in Fig. 4 A and B. ΔGNI is the Gibbs energy difference between the native and molten globule forms at pH 9, in kcal/mol, computed from the values of ku and kf used to fit the curve of log kobs vs. pH.
A lower value than the one given here is obtained if the baseline found for the WT protein is used.
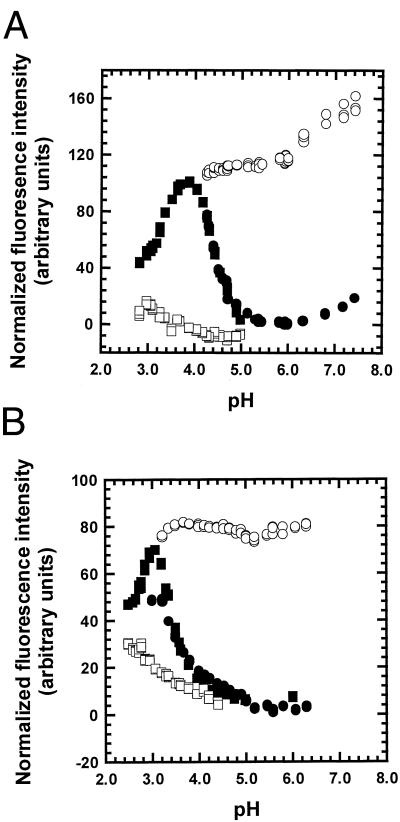
In analyzing the kinetics of a folding reaction, it is necessary to examine the kinetic amplitudes as well as the rates. The kinetic amplitudes in acetate buffer are shown in Fig. 4A for WT and in Fig. 4B for H24V/H119F. The unfolding or refolding reactions start at pH values where either N (unfolding) or I (refolding) is present in the initial conditions, and the pH-jump typically ends at pH values inside the unfolding transition zone, so that the final fluorescence value follows the equilibrium unfolding transition if the reaction is two-state. The fluorescence attributed to the two Trp residues in apoMb increases when N unfolds to I because of specific fluorescence quenching in N. The open and filled circles show the initial and final fluorescence values in refolding, whereas the open and filled squares show the initial and final values in unfolding. The final fluorescence values follow the equilibrium unfolding curve of N to I at pH values where only N and I are present, but, at lower pH values, U is also formed and the fluorescence again decreases. U has a lower fluorescence than I because the two Trp residues of apoMb are partially sequestered from solvent in I but are solvent exposed in U (16). The equilibrium pH unfolding curve obtained by monitoring fluorescence is subject to some uncertainty because of the difficulty of determining the correct unfolded and native base lines.
Figure 4.
The kinetic amplitudes of the unfolding and refolding experiments shown in Fig. 3 A and B. Open symbols are initial values, filled symbols are final values. Circles are refolding starting from pH 4.2, and squares are unfolding starting from pH 6.0. The fluorescence data are normalized so that the final fluorescence is 0 at pH 6.0 and 100 at pH 4.2. The fitted curves are equilibrium pH unfolding curves, which yield two of the pHm values shown in Table 2
Quality of the Data Fitting.
By using a single set of pKa values to fit the pH-dependent unfolding/refolding kinetics not only of WT but also of the two mutants that unfold in different pH ranges (Fig. 3 B and C), we have a further test of the pKa values. Likewise, using the same pKa values to fit the kinetic data taken in both acetate and citrate buffers provides an additional test of the pKa values, because the location of the pH unfolding curve shifts significantly between acetate and citrate for both WT and H24V/H119F (Table 2). By insisting that a single set of pKa values should fit all of the data, and by determining, one step at a time, the average pKa values of the histidine residues in the Ib intermediate and in the folding transition state, we have a severe test of the assumptions made in this analysis as well as of the pKa values. The fact that the fitted curve appears to be better for the double mutant (Figs. 2B and 3B) than for WT (Figs. 2A and 3A) probably reflects the fact that only one pKa (the average pKa of I‡) is an adjustable parameter in fitting the WT data, whereas the acidic pKa values of both subdomains (Table 1) are adjusted in fitting the H24V/H119F data. The fitted curves for WT (Figs. 2A and 3A) diverge from the data points at low pH. The divergence can be eliminated by abolishing the carboxylate pKa differences between different forms of the protein (I, I‡, and N), but then it becomes impossible to fit the pH-dependent unfolding refolding kinetics of H24V/H119F. The divergence occurs at pH values where unfolding ceases to be a two-state process, as the acid-unfolded form U becomes populated (compare Figs. 3A and 4A), and we tentatively assign the divergence to failure of the two-state assumption in this pH range. A second assumption that likely affects the quality of the fitted data is that the pKa values are independent of the extent of titration of neighboring groups.
Simulation of the Effect of His-24 on the Unfolding/Refolding Kinetics.
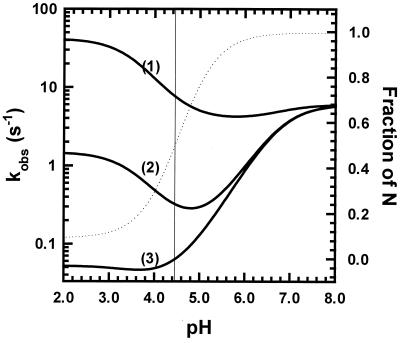
The fact that His-24 cannot be protonated in N gives this residue a unique role in the unfolding/refolding kinetics of WT, as shown by simulations for a simple model with only one ionizing residue. The pKa of this residue in N is so low that its protonation cannot be observed. The rate curves in Fig. 5 are simulated for three different pKa values in I‡: either 6.6 (curve 1), 5.15 (curve 2), or 3.7 (curve 3). The pKa of the single residue is set at 3.5 in N and at 6.8 in I. The assigned pKa of 3.5 in N does not allow this residue to be observably protonated in N because I is formed before N is protonated. The equilibrium transition curve for pH unfolding (dotted line in Fig. 5) is given by the ratio kf/ku, containing the rate constants for folding and unfolding, and pHm, the pH midpoint of the equilibrium unfolding curve, is near 4.4, close to the experimental pHm for WT in acetate. The unfolding transition does not go to completion at low pH because the assigned pKa difference between N and I is not large enough to accomplish this when only a single residue is involved. The part of each simulated rate curve (Fig. 5) that lies below pHm contributes to the unfolding rate whereas the part that lies above pHm contributes to the refolding rate. The simulated curves show that the presence of a single residue whose pKa differs substantially between N and I will have a large effect on the pH dependence of the unfolding/refolding kinetics.
Figure 5.
Simulation of the values of kobs vs. pH for a simple model (see text) in which only one ionizing group has pKa values that differ in I, I‡, and N. The pKa value in I‡ differs in the three cases shown: case 1, 6.6 (close to I); case 2, 5.15 (intermediate); case 3, 3.7 (close to N). The pKa value in N is 3.5 and in I is 6.8 in all three cases. The fraction unfolded is shown on the right y axis, and the dotted line is the equilibrium unfolding curve (unfolding does not go to completion at low pH) calculated from the values of ku and kf vs. pH (see Experimental Procedures). Their values at pH 9 are ku = 0.001 s−1 and kf = 6 s−1.
The main qualitative features of the simulated results can be understood by noting two properties of the folding rate equation. First, at pH values below pHm, the unfolding rate typically dominates the overall rate (the sum of the unfolding and refolding rates), whereas above pHm the reverse is true. Second, the pKa difference between N and I‡ controls the unfolding rate whereas the refolding rate is controlled by the pKa difference between I and I‡. Thus, the refolding rate is nearly pH independent in case 1 (pKa of I‡ is close to I), whereas the unfolding rate is nearly pH independent in case 3 (pKa of I‡ is close to N). In case 2, (pKa of I‡ intermediate between N and I) both the unfolding and refolding rates are strongly pH dependent. In experiments on pH-induced unfolding, the minimum value of the observed rate normally falls near the midpoint of the transition curve, as in denaturant-induced unfolding. The rate curve becomes independent of pH when the difference in number of protons bound becomes pH independent: for N versus I‡ if unfolding is being measured, and for I versus I‡ if refolding is being measured.
Discussion
Histidine pKa Values Are Close to Model Compound Values in both I and I‡.
The average pKa of the histidine residues in the transition state (6.7) is close to the average pKa in the molten globule (6.8; Table 1), and both pKa values are determined by procedures in which only a single adjustable parameter is determined. The average histidine pKa value determined for the molten globule is reasonably close to values measured in small peptides [6.8–6.9 at 25°C (17) or 7.2–7.3 at 4.5°C], considering that histidine pKa values are affected significantly by neighboring charged residues (17, 18). In native apoMb, the range of pKa values covers 3 pH units even when His-24 is excluded (see Table 1). Presumably the histidine residues in the molten globule are well exposed to solvent and do not make strong interactions with neighboring side chains, unlike histidine residues in the native protein. The effect of net charge on the pKa values of the molten globule intermediate should be small at the pKa of the histidine residues in I because the net proton charge is small: there are 15 basic groups, including histidines, and 13 acidic groups in the A[B]GH subdomain of apoMb. On the other hand, the pKa values of His residues in holomyoglobin are affected by neighboring charged residues (17, 18), and they increase measurably with NaCl concentration (18).
Nature of the pH-Dependent Unfolding Kinetics of H24V/H119F.
The double mutant H24V/H119F lacks His-24, and so its curve of log kobs vs. pH might be expected to have a different shape from that of WT. Surprisingly, the two curves are similar in shape (Figs. 2 and 3). The Asp residues of native apoMb were studied by chemical shift titration of 13C-labeled protein; 5 of 7 Asp residues could be observed and were found to titrate with normal pKa values (2). No data for the Glu residues are available. The double mutant kinetic data can be fitted by assigning average pKa values to the 9 Glu and Asp residues in the unfolded CDEF subdomain that are 0.6 pH units lower in N than in I‡ (Table 1). The effect on the pH-dependent unfolding rate is similar to that produced by the large (>3 pH) displacement of the pKa of a single residue, His-24, in WT. The smaller increase in the refolding rate of H24V/H119F above pHm can be fitted by assigning an average pKa in I‡ to the 13 acidic groups in the A[B]GH subdomain that is only 0.1 pH units less than the average value in I.
The pKa values assigned to the Asp and Glu residues (Table 1) are chosen on the basis of an earlier study of the acid-induced unfolding of the apoMb molten globule (19) that found that the Linderstrøm-Lang smeared-charge model describes reasonably well the effect of net positive charge on the stability of the molten globule, with w (the sole adjustable parameter of the model) = 0.05 and with an average value of 4.0 assigned to the intrinsic pKa values of Asp and Glu. In that study, a set of single mutants, each with one basic residue mutated to alanine, consistently increased the stability of the molten globule if the positively charged group was inside the A[B]GH subdomain. Some additional mutants were studied later, and consistent results were found (20). The pKa value of 3.6 assigned to 13 acidic residues (6 Asp, 7 Glu) in the A[B]GH subdomain is the value found from the Linderstrøm-Lang equation with w = 0.05. It agrees with the value (pKa = 3.54) found by fitting data for the I ⇌ U unfolding transition in figure 2 of ref. 21, by using equation 6 of ref. 2. The CDEF subdomain is treated as being unfolded, and its 9 acidic residues (1 Asp, 7 Glu and 1 C-terminal carboxylate included as being unfolded) are assigned a pKa = 4.0. Then the values assigned to the average pKa values in I‡ and N are obtained by fitting the experimental results.
The shift in pHm between acetate and citrate (Table 2) is observed both with WT, whose unfolding occurs in a pH range where His-residues are titrating, and with H24V/H119F, whose unfolding occurs in a pH range where Asp and Glu residues are titrating. The similar behavior found in these two pH ranges indicates that the effect of anion binding is not restricted to one class of ionizing groups, and is consistent with the effect being one of net charge on molten globule stability. Preferential binding of the citrate anion, which would stabilize the molten globule by reducing its net positive charge (22), may account for the smaller value of ΔGNI found in citrate versus acetate. Goto and Nishikori (23) carried out partial acetylation of lysine amino groups in cytochrome c and separated the partially reacted species by net charge using isoelectric focusing; they found that molten globule stability at pH 1.8 varies with net positive charge as expected if anion binding stabilizes molten globules.
Comparison with Related Work.
The effect of protonating one residue (Asp 93) on the pH dependence of the unfolding rate of barnase was studied by Oliveberg and Fersht (10). They found a large rise in unfolding rate below pHm and also a comparably large rise in refolding rate above pHm, implying that the pKa of Asp 93 in I‡ is roughly half way between its values in the native and denatured states. Our results are quite different, probably because there are important structural differences between barnase and apoMb. Charged Asp-93 in barnase forms part of a buried salt link with Arg-69, and its pKa is strongly shifted in N, down to 0.7 in 50 mM KCl. The fact that the pKa of Asp-93 in the folding transition state is intermediate between its values in the native and denatured states indicates that the ion pair interaction is formed but not fully developed in the transition state. In contrast to charged Asp 93 in barnase, neutral His-24 in apoMb forms a hydrogen-bonded interaction with His-119.
Concluding Comment.
Residues with depressed pKa values in the acid range are found commonly in studies of the pH dependence of stability of native proteins (24). They are thought to be a main contributor to the behavior, commonly observed in globular proteins, in which thermal stability drops sharply at acid pH (25). Our results suggest that the type of pH dependence found here for the N ⇌ Ib reaction of apoMb, with a sharp rise in unfolding rate below pHm and a smaller rise in refolding rate above pHm, is likely to be found commonly in the kinetics of pH-dependent unfolding reactions of small proteins at acid pH, although the barnase results of Oliveberg and Fersht (10) show that this situation will not always occur.
Acknowledgments
This work was supported in part by research grants from the National Institutes of Health (GM 19988 to R.L.B.) and from the Deutsche Forschungsgemeinschaft (Ge 868/1-1 to B.H.G.).
Abbreviations
- N
native form
- I
folding intermediate
- I‡
folding transition state
- U
acid-unfolded form
- WT
wild type
- ΔQ
difference in number of protons bound to N and I
- pHm
pH midpoint of unfolding transition
- ΔGNI
difference in standard Gibbs free energy between N and I
- apoMb
apomyoglobin
References
- 1.Bashford D, Case D A, Dalvit C, Tennant L, Wright P E. Biochemistry. 1993;32:8045–8056. doi: 10.1021/bi00082a027. [DOI] [PubMed] [Google Scholar]
- 2.Geierstanger B, Jamin M, Volkman B F, Baldwin R L. Biochemistry. 1998;37:4254–4265. doi: 10.1021/bi972516+. [DOI] [PubMed] [Google Scholar]
- 3.Hennig M, Geierstanger B. J Am Chem Soc. 1999;121:5123–5126. [Google Scholar]
- 4.Barrick D, Hughson F M, Baldwin R L. J Mol Biol. 1994;237:588–601. doi: 10.1006/jmbi.1994.1257. [DOI] [PubMed] [Google Scholar]
- 5.Takano T. J Mol Biol. 1977;110:537–568. doi: 10.1016/s0022-2836(77)80111-3. [DOI] [PubMed] [Google Scholar]
- 6.Hughson F M, Wright P E, Baldwin R L. Science. 1990;249:1544–1548. doi: 10.1126/science.2218495. [DOI] [PubMed] [Google Scholar]
- 7.Cocco M J, Lecomte J T. Protein Sci. 1994;3:267–281. doi: 10.1002/pro.5560030211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Barrick D, Baldwin R L. Biochemistry. 1993;32:3790–3796. doi: 10.1021/bi00065a035. [DOI] [PubMed] [Google Scholar]
- 9.Tanford C. Adv Protein Chem. 1970;24:1–95. [PubMed] [Google Scholar]
- 10.Oliveberg M, Fersht A R. Biochemistry. 1996;35:6795–6805. doi: 10.1021/bi9529317. [DOI] [PubMed] [Google Scholar]
- 11.Loh S N, Kay M S, Baldwin R L. Proc Natl Acad Sci USA. 1995;92:5446–5450. doi: 10.1073/pnas.92.12.5446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rossi-Fanelli A, Antonini E, Caputo A. Biochim Biophys Acta. 1958;30:608–615. doi: 10.1016/0006-3002(58)90108-2. [DOI] [PubMed] [Google Scholar]
- 13.Edelhoch H. Biochemistry. 1967;6:1948–1954. doi: 10.1021/bi00859a010. [DOI] [PubMed] [Google Scholar]
- 14.Edsall J T, Wyman J. Biophysical Chemistry. New York: Academic; 1958. [Google Scholar]
- 15.Eaton W A, Muñoz V, Hagen S J, Jas G S, Henry E R, Hofrichter J. Annu Rev Biophys Biomol Struct. 2000;29:327–359. doi: 10.1146/annurev.biophys.29.1.327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jamin M, Baldwin R L. J Mol Biol. 1998;276:491–504. doi: 10.1006/jmbi.1997.1543. [DOI] [PubMed] [Google Scholar]
- 17.Takahashi T, Nakamura H, Wada A. Biopolymers. 1992;32:897–909. doi: 10.1002/bip.360320802. [DOI] [PubMed] [Google Scholar]
- 18.Kao Y-H, Fitch C A, Bhattacharya S, Sarkisian C J, Lecomte J T, Garcia-Moreno B. Biophys J. 2000;79:1637–1654. doi: 10.1016/S0006-3495(00)76414-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kay M S, Baldwin R L. Biochemistry. 1998;37:7859–7868. doi: 10.1021/bi9802061. [DOI] [PubMed] [Google Scholar]
- 20.Ramos C H I, Kay M S, Baldwin R L. Biochemistry. 1999;38:9783–9790. doi: 10.1021/bi9828627. [DOI] [PubMed] [Google Scholar]
- 21.Jamin M, Antalik M, Loh S N, Bolen D W, Baldwin R L. Protein Sci. 2000;9:1340–1346. doi: 10.1110/ps.9.7.1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Goto Y, Takahashi N, Fink A L. Biochemistry. 1990;29:3480–3488. doi: 10.1021/bi00466a009. [DOI] [PubMed] [Google Scholar]
- 23.Goto Y, Nishikori S. J Mol Biol. 1991;222:679–686. doi: 10.1016/0022-2836(91)90504-y. [DOI] [PubMed] [Google Scholar]
- 24.Anderson D E, Lu J, McIntosh L, Dahlquist F W. In: NMR of Proteins: Topics in Molecular and Structural Biology. Clore G M, Gronenborn A M, editors. Boca Raton: CRC; 1993. pp. 258–304. [Google Scholar]
- 25.Privalov P L. Adv Protein Chem. 1979;33:167–241. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]