Targeting the dynamics of complex networks

Abstract

We report on a generic procedure to steer (target) a network's dynamics towards a given, desired evolution. The problem is here tackled through a Master Stability Function approach, assessing the stability of the aimed dynamics, and through a selection of nodes to be targeted. We show that the degree of a node is a crucial element in this selection process, and that the targeting mechanism is most effective in heterogeneous scale-free architectures. This makes the proposed approach applicable to the large majority of natural and man-made networked systems.

Complex networks are mathematical objects with the ability to neatly encode relevant information on the irregular structure of interactions among coupled dynamical units, thus serving as useful models of large-scale systems of biological, physical and social interest¹. For a given coupling scheme, an issue of the utmost importance is how to make the network abandon its current time evolution (as defined by its equations of motion and initial condition) and approach a goal dynamics. Traditionally, this has been the subject of the theory of chaos control and targeting of dynamical systems, whose methods have laid the basis for a judicious manipulation of a nonlinear dynamics, cleverly directing it towards a desired one. The idea behind control² is that of stabilizing one of the infinite number of unstable orbits embedded in chaotic attractors by the application of small time-dependent perturbations. The targeting procedure³,⁴,⁵,⁶, instead, seeks to steer the dynamics of the system in the shortest possible time towards another trajectory fully compatible with the equations of motion of the system, but originating from a different initial condition.

There is, therefore, a subtle and yet deep difference between the two processes. While control aims to stabilize an otherwise unreachable trajectory, targeting allows to pursue a goal dynamics out of the set of those achievable by the natural evolution of the system from the attractor basin, and, as such, it can be interpreted as forcing the system to forget its initial condition.

While applications of both procedures to low dimensional chaotic (and spatially extended⁷,⁸,⁹) systems have been one of the fields of major interest within the last 20 years¹⁰, only recently has the issue of network controllability been approached¹¹,¹²,¹³,¹⁴. Imagine a network of N m-dimensional units, such that a generic trajectory meanders in an m × N-dimensional phase space. When the goal is having the network realize a desired evolution 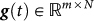, then tertium non datur: either i) one has to set the network to the initial condition producing g(t), or ii) one has to target a generic initial condition towards g(t). Clearly, the first case is fully impracticable: the extremely high dimensionality (linearly growing with the network size) of the phase space renders the selection of the specific initial state almost impossible, especially in those applications where noise or any kind of other disturbance are present. Here, we address the as yet unexplored issue of targeting the dynamics of a complex network.

Results

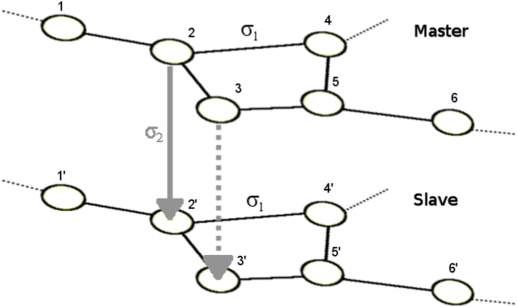
The feasibility of targeting a general goal dynamics g(t), compatible with the natural evolution of the graph, is tantamount to demonstrating that a suitable perturbation may have a network leaving its current state, and attaining another one that would be naturally produced by a different initial condition. Therefore, the effect of the perturbation can be understood as removing the sensitivity of the network to the initial condition. A way of engineering such a perturbation is to consider two identical networks (configured in a master-slave scheme), and specify when they identically synchronize¹⁵,¹⁶, when starting from different initial conditions. Therefore, our approach consists in: i) considering two identical graphs, both producing a turbulent regime (i.e., a generic dynamics not showing any particular global or local order), but starting from different initial conditions [a master network (MN) providing us the specific g(t), and a slave network (SN)], and ii) properly engineering a unidirectional pinning action from MN to SN, as shown in Fig. 1, which ultimately leads to the synchronization of their dynamics.

Figure 1. The targeting procedure.

The MN and SN are initially disconnected. Each targeting step establishes a new unidirectional connection between both networks. At the current step, a subgraph of the MN is connected to its counterpart in the SN (see gray continuous line). The searching step establishes a further connection via that node (see gray dotted line) that minimizes the associated MSF.

We analytically assess the stability of the solution corresponding to the synchronization between the two networks, as unidirectional links are sequentially created from nodes in MN to their images in SN. To do so, we introduce the associated Master Stability Function (MSF)¹⁷ (see the Methods Section), giving the maximum Lyapunov exponent (MLE) for each pinning configuration (PC) between the two networks. Eventually, after a given fraction of nodes has been pinned, we show that the MLE becomes negative, indicating that SN attained the goal dynamics g(t). Notice that the MLE is an ensemble average over all possible attractor's trajectories, and therefore, assessing synchronizability by the negativity of MLE independently of the initial state for a given sequence of pinned nodes corresponds to addressing the targetability of the slave network into one of its possible natural evolutions.

A relevant issue is optimizing the search of the best PC, i.e., that PC requiring the minimal number of pinning actions from the MN to the SN. It is evident that, as the network size grows, the problem becomes intractable. This is because one would have to apply the MSF approach (equation (5) in Methods Section) to all possible N! permuting sequences of nodes susceptible to be pinned, and look for the shortest one that renders the MLE negative. Here we pursue a suboptimal solution, provided by the outcome of a greedy algorithm that sequentially selects the best pinning action (i.e. the one minimizing the MLE) at each step.

For a given PC, the changes in the MLE brought about by temporarily establishing an additional link from the MN to the SN are exhaustively explored. The best link at decreasing the MLE is eventually created. When iterated (see Methods section), the procedure leads to a specific targeting sequence, or node ranking, which we call suboptimal ranking.

For very large networks, however, this suboptimal strategy can also be computationally demanding. To overcome this limitation, we extend recent results on criticality of network resilience to perturbations on the highly connected nodes¹¹,¹⁸. Namely, we show that the node pinning sequence minimizing the MSF largely coincides with the sequence of decreasing degrees for small size networks (and can therefore be replaced to a good approximation by such a sequence), thus allowing for the use of the MSF approach also for very large graphs, and compare different graph structures in terms of their targetability.

As an illustration of both the greedy search procedure and the correlation with the node degree, we consider a network made of N = 50 Rössler oscillators¹⁹ (see the Methods Section). It is important to remark that the MSF approach is in principle applicable to any continuous time dynamics, and not necessarily limited to a specific kind of oscillator (like the Rössler case we are here considering), nor to a specific dimension of the phase space containing the dynamics' attractor of each network's unit. As for the network structure, we use the topology resulting from a realization of the configuration model²⁰ based on a degree sequence taken from a random generation of N integers uniformly distributed between 5 and 45. This will provide us with a suitable statistics to compare our suboptimal sequence with the degree sequence of the graph. In Fig. 2 we report λ_max (the MLE, as obtained from the MSF), when starting from disconnected MN and SN, until the case where they are fully (unidirectionally) coupled, each step following the suboptimal ranking procedure (blue circles). It can be seen that each additional targeting action results in about the same decrease of λ_max, and that the targeting of 12 nodes is enough to reach a negative λ_max, indicating the achievement of the goal dynamics g(t).

Figure 2. Suboptimal vs. degree ranking.

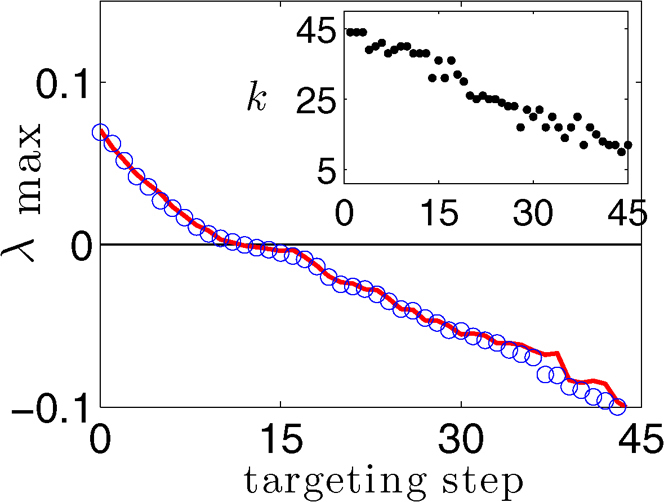
Targeting procedure applied to a N = 50 network of Rössler oscillators (see the main text and the Methods section for details on the graph construction and on the ranking procedure). λ_max extracted from the MSF as a function of the targeting step, for the suboptimal sequence (blue open circles), and with the node degree sequence (red continuous line). The inset shows the degree k of each pinned node in the suboptimal sequence, vs. the targeting step.

The degree of the nodes in the suboptimal ranking is shown in the inset of Fig. 2. There is a striking correlation between such a ranking and the inverse of the degree sequence. Indeed, the values of λ_max obtained with a targeting based on the degree ranking are also shown in Fig. 2 (red continuous line), and are almost identical to those obtained with the suboptimal ranking. This raises the possibility that a targeting procedure based on the degree ranking produces quite similar results in a much shorter computation time (N vs. N(N + 1)/2 computations), thus allowing for the application of our MSF approach to networks of considerably greater size. Qualitatively identical results were obtained by varying the initial conditions and configuration model realization, as well as with more familiar topologies (Erdös-Rényi (ER) random graphs²¹, or Barabási-Albert scale-free (SF) networks²²) of N = 50. Nevertheless, we remark that our results, though obtained with a somewhat uncommon topology, are the ones that best illustrate the correlation between suboptimal and degree ranking (due to their including nodes of almost all possible degrees). Indeed, for the specific network size used, both the SF and the ER topologies result in a less precise correspondence of degree and suboptimal ranking, due to the strongly reduced degree variability.

The ability to study large-sized networks opens up the way for an exploration of different topological ensembles, and a quantification of their propensity to be targeted. On the other hand, it is still an open question how different the results would be if based on a less judicious ranking, such as a random ranking, or, generically, a ranking not aiming at reaching the imposition of the MN's dynamics upon SN.

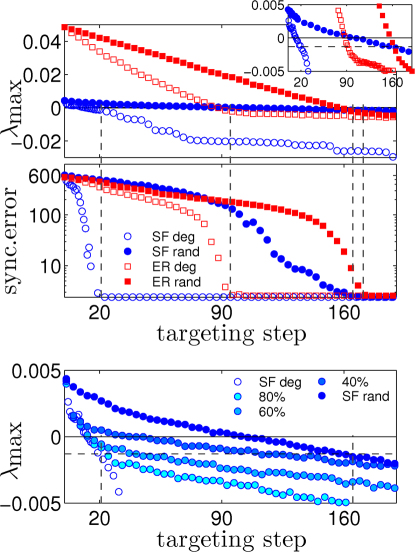
To address both issues, we apply the targeting procedure to a network of N = 500 Rössler oscillators (see, again the Methods Section), with Erdös-Rényi (ER)²¹ and Barabási-Albert scale-free (SF)²² topologies. In Figure 3 (top and middle panels) we show the results of the first 200 targeting steps [sufficient, in all cases, for the attainment of g(t)]. Both the degree ranking (the solution proven to greatly approximate the suboptimal ranking) and a random ranking (in which the order of appearance of each node is fully random) are inspected, thus allowing a comparison between both ends of the spectrum of possible targeting strategies. The results are ensemble averages over 40 different graph realizations, and over 40 different ranking realizations for the random ranking case. Aside from λ_max, we also report the synchronization error (see the Methods Section), which vanishes for the same targeting step at which λ_max gets slightly negative. Notice, indeed, that the negativity of the MLE is a necessary, but not sufficient condition for synchronization, as the MLE is by definition an ensemble average over all the attractor's trajectories. In our case, the dynamics g(t) is a turbulent one, and as such it is spanning the entire phase space. As a result, having a negative (yet very small in absolute value) MLE does not prevent that, in some areas of the phase space, expanding events will take place that will locally separate the trajectories of the two networks. This, in its turn is reflected in a not perfectly vanishing value of the time averaged synchronization error, which will instead vanish perfectly when the negative MLE will have a sufficiently high absolute value to warrant contraction in the whole phase space.

Figure 3. Targetability of different topologies.

(Top and middle panels) Targeting scheme for ER and BA networks of size N = 500. λ_max (top panel) and synchronization error (middle panel, see Methods Section for definition) as functions of the targeting step, for the degree and random rankings. The legend applies to both panels, and contains the symbol codes for the specific topologies considered, as well as for the specific ranking used for the targeting. The vertical dashed lines originating in the middle panel mark the targeting step at which the synchronization error vanishes. The inset of the top panel is a zoom around λ_max = 0. The horizontal dashed line in the inset of the top panel marks the negative value at which the vertical lines intersect the λ_max curves. (Bottom panel) Robustness of the targeting strategy against networks' uncertainties. The panel reports the λ_max curves vs. the targeting step for the BA network used in the top and middle panels. The different curves refer to the degree ranking (empty circles), the random ranking (full circles with the darkest blue intensity), and a degree ranking based on the knowledge of the degrees of only 80%, 60% and 40% of randomly selected nodes in the network. These latter three curves are coded as full circles with increasing blue intensities.

While in the top and middle panels of Fig. 3 it is evident that, in all cases, the degree ranking leads to a much better targeting, as compared to the random scheme, there is an additional feature that deserves the utmost attention: the relative improvement in SF networks results to be much more evident than that of the ER case, indicating that the dynamics of heterogeneous structures, like the ones encountered in real world networks, are much easier to be manipulated and targeted. Regarding the application of the method to real networks, one should prove the robustness of the degree sequence criterion in cases where only partial information on the network is available. To this purpose, we have considered the same scale-free topology of the top and middle panels of Fig.3, and artificially screened out the information on the degree of a higher and higher percentage of randomly selected nodes in the network. We then took the remaining nodes (whose degree is supposed to be known), and constructed the corresponding degree sequences to be used for the targeting. This process is equivalent to a mixed-strategy, in which part of the information on the network degree is lost in favor of a random selection of nodes. The bottom panel of Fig. 3 reports λ_max vs. the targeting steps for the cases in which the percentage of nodes with available degree is 80%, 60% and 40%. For comparison, the same panel contains also the two curves already shown in the top panel of the same Figure, and referring to the pure degree and random rankings. It is evident that, while the targeting procedure is still effective and robust for a relatively high fraction of nodes with unknown degrees (the curves labeled with 80% and 60% are still very close to that of the pure degree ranking), as the uncertainty is further increased, the λ_max curve approaches that of the pure random ranking.

Discussion

While a relevant part of the research on complex networks concentrated on their response (as, e.g. vulnerability) to various types of external interference, recently the attention has shifted towards methods for engineering a set of perturbations for a network to feature a particular behavior. In this paper, we have shown the feasibility of targeting a general goal dynamics g(t) compatible with the natural evolution of a network, and we have given a rigorous treatment of the necessary conditions for attaining such a dynamics by just pinning a limited number of nodes in the graph. By further comparing the targetability of different topological structures, we demonstrated that the dynamics exhibited by heterogeneous topologies are easier to be targeted. Our conclusion is, therefore, that the vast majority of real world networks are easily manageable from a targeting point of view with our approach, as most of them (from transportation networks in technology, to networks of acquaintances in social science, to metabolic and genetic networks in biology) display a scale free topology, with some nodes concentrating most of the connections.

Methods

Master stability function approach

We consider a master network (MN) composed of N identical diffusively coupled chaotic units, and we call 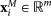the vector state of the i^th node. The MN evolution is ruled by:

where 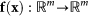and 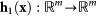are, respectively, a local evolution and an output vectorial function. σ₁ is a coupling strength, and 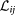are the elements of the corresponding zero row-sum Laplacian matrix of the interaction network. f and h₁ are chosen such that the networked units are of class I, with a monotonically increasing trend of the master stability function associated to the synchronous state ¹, which is, therefore, always unstable, regardless of the choice of σ₁.

Let now

be the slave network (SN), obtained as a copy of the MN.

As long as both networks remain uncoupled and start from different initial conditions, each one will sustain a different turbulent state, such that 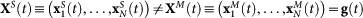, and the SN will never realize the desired goal dynamics. At this stage, we implement a pinning strategy to target g(t), that consists in sequentially establishing unidirectional links between nodes in the MN and their copies in the SN. The dynamical evolution of the SN is now described by:

where 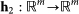is the coupling function between MN and SN [with the condition that h₂(0) = 0], and χ_i encodes the pinning procedure, i.e. χ_i = 1 if there is a link from the ith node of the MN to the ith node of the SN, and 0 otherwise. Furthermore, σ₂ is the parameter ruling the inter-network link strength (see Fig. 1).

It follows that the equation for the vector describing the difference between the networks' dynamics 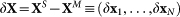can be written (in terms of its component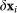s ) as

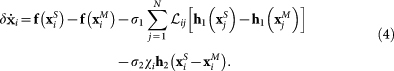A stable fixed point of Eqs. (4) at δX = 0 is a necessary condition for networks (1) and (3) to display the synchronized state X^M = X^S. The synchronization error is then defined as .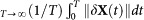

The linear stability of this solution can be assessed rigorously by the analysis of the linearized system for small δX, which reads:

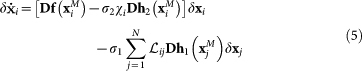being Df, Dh₁, and Dh₂ the Jacobian functions, and X^M = g(t) the MN state to be targeted. This equation represents the master stability function (MSF) for the stability of the solution corresponding to the identical synchronization between MN and SN. Each of the linear equations (5), solved in parallel to the N nonlinear equations for the MN defined in (1), corresponds to a set of m conditional Lyapunov exponents at each pinning configuration (PC). Therefore, each peculiar PC that renders negative the largest of all such exponents makes the synchronous state X^M = X^S stable.

Targeting procedure

Unidirectional MN-to-SN links are always established between analogous nodes, so it is natural to denote them by the label i of the corresponding node in both networks (2, in the example of Fig. 1). To refer to a generic link established at a given step t, we use n_t (evidently, 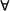t, 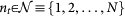, but also 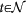, as there are as many possible steps as nodes in the networks). At the targeting step t, we suppose to have already established a PC represented by the sequence of links 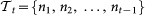, where n_i ≠ n_j, and we seek to identify the next pair of MN-SN nodes to be pinned, i.e., the specific integer n_t. Obviously, at t = 1 we start from the scenario where MN and SN are disconnected, and thus 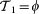, and the issue is to identify n₁, whereas at t = N, the only disconnected pair of nodes is eventually coupled by the link n_N.

As for the sequence search, we use the following procedure. At step t, we go through all possible PC comprising 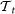and one extra link between the not yet connected pairs. Denoting each configuration by 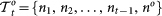(where o {1, 2, …, N − (t − 1)} and 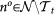) and calling 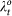the maximum Lyapunov exponent (MLE) associated with the corresponding MSF, we choose n_t to be the specific n^o that corresponds to the smallest 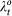, and include it in 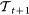for the next step. A typical computation of the MLE for a given configuration includes the integration of the full system from a random initial condition across a time window of 50,000 time units (about 7,960 cycles of the Rössler oscillator). As the system is integrated, the MLE value is updated and saved once every 5 time units. At the end of the entire simulation, we ended up with a sequence of 10,000 MLE estimations, which is generically observed to converge to an asymptotic value with very small fluctuations. The MLE values reported in the text correspond to the average taken across the second half (5,000 estimations) of this sequence. Repeated tests with several hundreds of such computations show that the standard deviations (the absolute error in the evaluation of the MLE) are always between 10⁻⁵ and 10⁻⁴, the largest value ever observed being 4.87 × 10⁻⁴.

Network model

The equations of the network of Rössler oscillators that are considered in the main text, written for simplicity in their scalar form, are:

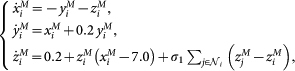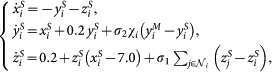where, at targeting step t, χ_i = 1 if 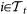and 0 otherwise. This corresponds, in our notations, to x^M ≡ (x^M, y^M, z^M), x^S ≡ (x^S, y^S, z^S), h₁(x) = (0, 0, z), h₂(x) = (0, y, 0), f = [−y − z, x + 0.2y, 0.2 + z(x − 7.0)], and with 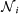being the set of neighbors of node i. All our results refer to the case σ₁ = σ₂ = 1.

Author Contributions

R.G., I.S.N. and S.B. derived the analytical results. R.G. and I.S.N. carried out the numerical simulations. R.G., M.Z. and D.P. analyzed the data and prepared the figures. R.G., I.S.N. and S.B. wrote the main manuscript text. All authors reviewed the manuscript.