Analysis of high-affinity assembly for AMPA receptor amino-terminal domains

Abstract

Analytical ultracentrifugation (AUC) and steady-state fluorescence anisotropy were used to measure the equilibrium dissociation constant (K_d) for formation of dimers by the amino-terminal domains (ATDs) of the GluA2 and GluA3 subtypes of AMPA receptor. Previous reports on GluA2 dimerization differed in their estimate of the monomer–dimer K_d by a 2,400-fold range, with no consensus on whether the ATD forms tetramers in solution. We find by sedimentation velocity (SV) analysis performed using absorbance detection a narrow range of monomer–dimer K_d values for GluA2, from 5 to 11 nM for six independent experiments, with no detectable formation of tetramers and no effect of glycosylation or the polypeptide linker connecting the ATD and ligand-binding domains; for GluA3, the monomer–dimer K_d was 5.6 µM, again with no detectable tetramer formation. For sedimentation equilibrium (SE) experiments, a wide range of K_d values was obtained for GluA2, from 13 to 284 nM, whereas for GluA3, the K_d of 3.1 µM was less than twofold different from the SV value. Analysis of cell contents after the ∼1-week centrifuge run by silver-stained gels revealed low molecular weight GluA2 breakdown products. Simulated data for SE runs demonstrate that the apparent K_d for GluA2 varies with the extent of proteolysis, leading to artificially high K_d values. SV experiments with fluorescence detection for GluA2 labeled with 5,6-carboxyfluorescein, and fluorescence anisotropy measurements for GluA2 labeled with DyLight405, yielded K_d values of 5 and 11 nM, consistent with those from SV with absorbance detection. However, the sedimentation coefficients measured by AUC using absorbance and fluorescence systems were strikingly different, and for the latter are not consistent with hydrodynamic protein models. Thus, for unknown reasons, the concentration dependence of sedimentation coefficients obtained with fluorescence detection SV may be unreliable, limiting the usefulness of this technique for quantitative analysis.

INTRODUCTION

Dynamic protein–protein interactions play a key role in the function of glutamate receptor ion channels (iGluRs), the membrane proteins that mediate excitatory synaptic transmission in the brain of vertebrates (Traynelis et al., 2010). For these proteins, both the initial assembly mechanism and the stability of different conformational states for the mature tetrameric protein are controlled by the strength of interactions between large extracellular domains. Because these domains can be genetically excised and expressed as soluble proteins, it is possible to measure the equilibrium dissociation constant of oligomers corresponding to assemblies found in the intact protein, independent of the membrane-embedded ion channel segment. Although a variety of techniques could in principle be used to measure the equilibrium constant for formation of iGluR oligomers, including isothermal calorimetry, surface plasmon resonance, and fluorescence anisotropy, all published studies have used analytical ultracentrifugation (AUC). In contrast to isothermal calorimetry, AUC is equally suitable for analysis of homo- and hetero-oligomerization and lends itself well to these studies, as it is traditionally operated label-free and allows in a variety of approaches the characterization of affinities spanning many orders of magnitude (Schuck et al., 2010).

The extracellular domains of iGluRs, which form 85% of the mass of the receptor, can be subdivided into discrete amino-terminal (ATD) and ligand-binding (LBD) domains of ∼380 and 280 residues, respectively (Mayer, 2011). The initial group of AUC studies on iGluRs targeted the LBDs expressed as soluble proteins in Escherichia coli. The results of these experiments gave important insight into the mechanisms of desensitization and allosteric modulation of iGluRs by drugs and endogenous ions, and revealed that although the wild-type proteins interact weakly, with K_d values for LBD dimer assembly >5 mM, mutations in the dimer interface that attenuate desensitization resulted in K_d values as low as 30 nM (Sun et al., 2002; Furukawa et al., 2005; Weston et al., 2006; Chaudhry et al., 2009a,b; Nayeem et al., 2009). More recent work has targeted the ATD expressed as a glycosylated protein using insect or mammalian cell culture. In contrast to the low affinity for assembly of the LBD, monomer–dimer K_d values as low as 0.5 nM have been reported for wild-type ATDs, but there is no consensus on whether the ATD dimer pairs assemble to form tetramers in solution (Clayton et al., 2009; Jin et al., 2009; Kumar et al., 2009, 2011; Karakas et al., 2011; Rossmann et al., 2011). For the four AMPA receptor subunits, members of the iGluR family that mediate fast synaptic transmission at the majority of synapses in the brain (Traynelis et al., 2010), an unusually broad range of monomer–dimer K_d values has been reported for ATD assembly. For the GluA1 subtype expressed in insect cells, a monomer–dimer K_d of 270 nM (95% confidence interval of 163–432 nM) was measured by sedimentation equilibrium (SE) AUC at 4°C; for GluA2, the monomer–dimer K_d measured by the same approach was 152 nM (95% confidence interval of 89–265 nM), with no species of size larger than dimer detected by equilibrium runs with loading concentrations as high as 5 mg/ml, at a concentration of ∼100 µM (Jin et al., 2009). However, when GluA2 was expressed in human embryonic kidney (HEK)293T cells, the differential sedimentation coefficient distribution c(s) measured by sedimentation velocity (SV) AUC at 20°C showed peaks at s-values of 4.3, 5.9, and 7.9 S, which were interpreted as corresponding to monomer, dimer, and tetramer species, respectively. Modeling these c(s) peaks as Gaussians to estimate species populations led to an estimated K_d of 4.3 µM for monomer–dimer assembly and 50 µM for dimer–tetramer assembly (Clayton et al., 2009). More recently, SV AUC measurements at 10°C for the GluA2 ATD also expressed in HEK cells, but labeled with 5,6-carboxyfluorescein succinimidyl ester (FAM), gave a monomer–dimer K_d of 1.8 nM, derived from measurements of SV profiles using fluorescence detection optics (FDS-SV AUC) of the FAM label, whereas for GluA1, GluA3, and GluA4, the monomer–dimer K_d values obtained were 98, 1,200, and 10 nM, respectively (Rossmann et al., 2011). Finally, using GluA2 labeled with an oxazine fluorophore, translational diffusion times measured by fluorescence correlation spectroscopy at a protein concentration of 1 nM were consistent with entirely monomeric protein, apparently at conflict with the monomer–dimer K_d of 1.8 nM measured by FDS-SV (Jensen et al., 2011).

The 2,400-fold range of monomer–dimer K_d values reported for the GluA2 ATD, 4.3 µM, 152 nM, and 1.8 nM, is without precedent and could have multiple origins. Possibilities include differences in the design of the GluA2 ATD construct; different extents of glycosylation in insect cells and HEK cells; different errors intrinsic to SE and SV AUC; and different limitations unique to absorbance, interference, and fluorescence detection systems. In this study, we prepared the GluA2 and GluA3 ATDs under conditions that allowed the effects of glycosylation to be examined; we also made different GluA2 ATD constructs to test whether this influenced dimer assembly. In addition, we have directly compared results from different AUC methods, and as an independent method of analysis, we performed steady-state fluorescence anisotropy experiments. Our analysis confirms the nanomolar K_d for GluA2 ATD dimer assembly reported by Rossmann et al. (2011) and establishes that this can be accurately determined using absorbance detection SV AUC. Although the resolving power of fluorescence detection greatly exceeds that of conventional absorbance and interference optical systems at low nanomolar and picomolar concentrations (Kroe and Laue, 2009), and is especially useful for analysis of heteromeric assemblies of two homodimerizing molecules, we find that GluA2 ATD sedimentation coefficients measured using FDS-SV AUC are inconsistent with calculated hydrodynamic properties. The underlying cause(s) is presently unknown and requires further investigation.

MATERIALS AND METHODS

Protein expression and purification

Constructs for the GluA2 and GluA3 ATDs with their native signal peptides were cloned into the pRK5-IRES-EGFP expression vector, with a C-terminal thrombin cleavage site and affinity tag (LVPRGS-His₈), as described previously (Kumar et al., 2009). For GluA2, we prepared short (GluA2S) and long (GluA2L) versions, last native residue Ser380 and Glu388, as reported by Jin et al. (2009) and Clayton et al. (2009), respectively. The GluA2L construct includes the linker that connects the ATD with the LBD; the construct reported by Rossmann et al. (2011), last native residue Thr376, has a four-residue deletion compared with GluA2S. For GluA3, only the short version was prepared. Protein expression and purification were performed as reported previously (Kumar et al., 2011). In brief, HEK293T and GnTI⁻ cells grown in suspension culture were transiently transfected with plasmids encoding the selected cDNAs; the secreted glycoproteins were then purified by affinity chromatography and digested sequentially with thrombin and in some experiments endoglycosidase H (EndoH), followed by ion exchange chromatography. Final yields were 1 and 3–5 mg of purified protein per liter for GluA2 and GluA3, respectively.

Protein characterization by light scattering and mass spectrometry

Size-exclusion chromatography, coupled with multi-angle light-scattering and refractive index detectors (SEC-UV/RI/MALS), was performed using a size-exclusion column (Superdex 200 HR 10/300) equilibrated with 20 mM HEPES, 200 mM NaCl, and 1 mM EDTA, pH 7.4. The protein loading concentration was 2 mg/ml unless stated otherwise. Detection was performed using a triple-angle light-scattering detector (Mini-DAWN TREOS; Wyatt Technology) and a differential refractometer (Optilab rEX; Wyatt Technology). Mol wts and hydrodynamic radii were determined using ASTRA software (Wyatt Technology). Dynamic light-scattering analysis was performed using a DynaPro with DYNAMICS software (Wyatt Technology). Electrospray ionization (ESI) mass spectra were acquired on a Q-TOF micro spectrometer (Micromass; Waters); MALDI spectra were acquired on an AB SCIEX 5800 spectrometer.

SV AUC with conventional optics

SV experiments were performed using analytical ultracentrifuges (ProteomeLab XL-A or XL-I; Beckman Coulter) according to the protocols outlined in Brown et al. (2008). All instruments were temperature calibrated relative to a pool of eight AUC instruments on the National Institutes of Health (NIH) campus using the monomer s-value of BSA measured from the same sample solutions without cell disassembly, in the identical rotor. Run-to-run instrument-dependent variations were highly reproducible and assigned as empirical correction factors, with an average magnitude of 0.8%, compatible with the temperature-calibration specifications of the manufacturer. Glutamate receptor ATD protein samples in a buffer containing 20 mM NaH₂PO₄/Na₂HPO₄, 150 mM NaCl, and 1 mM EDTA, pH 7.50 (in some experiments without EDTA), were loaded into double-sector charcoal-filled epon centerpieces with either 3- or 12-mm pathlengths and either quartz or sapphire windows. Incubation time before the start of sedimentation was generally in excess of 2 h. Sedimentation at 50,000 rpm was monitored using absorbance optics at 210, 230, and 280 nm, either alone or in combination with interference optics, at 20°C unless otherwise stated. The buffer density and viscosity at 20°C were calculated using SEDNTERP (provided by J. Philo), and at 10°C, they were measured using a densitometer (DMA5000M) and a micro viscometer (AMVn; both from Anton Paar).

SV samples were prepared by serial dilution of chromatographically purified stocks. For example, for the GluR2 ATD with complex glycosylation, 11 samples were prepared with concentrations ranging between 0.51 µg/ml and 1.56 mg/ml. Because of surface adsorption and some variability in the experimental statistical noise, the lowest useable concentration for which sedimentation can be measured is difficult to predict but can be determined from data analysis. To precisely determine the effective loading concentrations, extinction coefficients at 210, 230, and 280 nm were calculated from the absorbance signal relative to the interference signal, using refractive index increments predicted from the amino acid composition in SEDFIT (Zhao et al., 2011), corrected for contributions of glycosylation, assuming an average dn/dc value of 0.13 ml/g for carbohydrates. The effective loading concentration of sedimenting protein in each experiment was then determined from integration of the c(s) peaks, corresponding to the height of the sedimentation boundary in the raw data. The absorbance signal at 230 nm was found superior in utility over the interference system. Although the latter often has a better signal/noise ratio and wider dynamic range, signal offsets from imperfect optical buffer match became limiting at low protein concentrations. We found 210 nm data to exhibit significantly higher noise, offsetting the advantage of higher absorbance than at 230 nm, which is consistent with a lower lamp intensity at 210 than at 230 nm.

The sedimentation profiles were analyzed with the standard c(s) model as described previously (Brown et al., 2008), using maximum entropy regularization (Schuck, 2000). The c(s) distributions were used to create weighted-average s-value (s_w) isotherms (Schuck, 2003) by integration of the c(s) peak in the distribution between 2 and 7 S for the data at 20°C and 1 and 6 S for the data at 10°C, respectively. Error estimates of s_w were calculated using the Monte Carlo approach for distributions in SEDFIT; to account for cross-correlation with the meniscus parameter, this was conducted with meniscus values at both of its predetermined confidence limits, taking the maximal range of s_w as the confidence interval for each value. Confidence limits of the meniscus were determined either graphically, or, where possible, from nonlinear regression of c(s). The resulting s_w isotherm was loaded into SEDPHAT for weighted nonlinear regression, using the experimental s-values and the following monomer–dimer model:

$$s_w\left(c_{tot}\right)=\frac{{\eta }_{20,w}\left(1-{\stackrel{-}{v}}_x{\rho }_x\right)}{{\eta }_x\left(1-{\stackrel{-}{v}}_{20,w}{\rho }_{20,w}\right)}\times \frac{c_1{s}_1+2K_{12}{c}_1^2{s}_2}{c_{tot}}\times \left(1-k_s{M}_1{c}_{tot}\right),$$ (1)

with c₁ and c_tot denoting molar monomer and total loading concentrations, respectively; K₁₂ is the equilibrium association constant (K₁₂ = K_d⁻¹); s₁ and s₂ are the monomer and dimer sedimentation coefficients under standard conditions of water at 20°C, respectively; η_x and η_20,w are the solvent viscosity under experimental and standard conditions, respectively; ρ_x and ρ_20,w are the solvent density under experimental and standard conditions, respectively; ${\stackrel{-}{v}}_x$ and ${\stackrel{-}{v}}_{20,w}$ are the protein partial-specific volumes at experimental and standard conditions, respectively; M₁ is the monomer molar mass; and k_s is the hydrodynamic nonideality coefficient fixed at 10 ml/g. The first term represents a correction factor from standard to experimental conditions, which for the experiments at 20°C amounts to 0.948. K₁₂, s₁, and s₂ were refined in nonlinear regression of the isotherms, with both s-values constrained to a range of physically possible values. All experimental SV data and best-fit values are presented in units of experimental s-values. The reported error intervals represent the upper and lower limits at a 95% confidence level, as determined using error surface projection method and F-statistics (Johnson, 1992).

FDS-SV AUC

For FDS-SV experiments, GluA2S expressed in GnTI⁻ cells and digested with EndoH was labeled by coupling to primary amines. In brief, 56 µg of 5(6)-FAM (Biotium, Inc.) was added to 500 µl of a 10-µM GluA2S stock solution in a buffer containing 20 mM NaH₂PO₄/Na₂HPO₄, 150 mM NaCl, and 1 mM EDTA, pH 7.0, at room temperature (22°C). The protein solution was mixed well and then incubated at room temperature for 20 min to yield a dye to protein molar labeling ratio of 1.1:1. The mixture was then dialyzed against 500 ml of dye-free buffer in a 15-kD MWCO dialysis membrane for 1.5 h, followed by a second dialysis with 500 ml of fresh buffer for another 1.5 h. The labeled protein was then purified through a Superdex 75 (10/300) gel filtration column at 4°C. Before use, the solution was centrifuged at 10,000 rpm for 10 min to precipitate any aggregates. Supernatants were taken out as working stocks, from which dilutions were prepared using filtered buffer. Concentrations and labeling efficiency were determined by a UV-VIS spectrophotometer using ε₂₈₀ of 55,720 M⁻¹cm⁻¹ for unlabeled protein and ε₂₈₀ of 15,050 M⁻¹cm⁻¹ and ε₄₉₅ of 70,000 M⁻¹cm⁻¹ for the dye. For control experiments, enhanced green fluorescent protein (EGFP) was used, prepared as described in the supplemental Materials and methods.

Before preparing the concentration series for the FDS-SV run, BSA (Sigma-Aldrich) was dissolved in the same buffer to create a stock of 36.7 mg/ ml, and then added to each sample to reach a final concentration of 0.10 mg/ml. Two sets of samples were made to construct different concentration series. For the first set, FAM-GluA2S stock was diluted to generate samples with a concentration range of 0.22–74.30 nM. For the second set, for each sample, FAM-GluA2S at a final concentration of 0.74 nM was mixed with unlabeled GluA2S, the concentration of which varied over the range of 1–99 nM. FDS-SV was performed in an analytical ultracentrifuge (Optima XLI; Beckman Coulter) equipped with a fluorescence optical system (Aviv Biomedical) with fixed excitation at 488 nm and fluorescence detection at >505 nm. This ultracentrifuge instrument was a different machine from those used for the absorbance and interference SV experiments. Samples were prepared and loaded into 12-mm pathlength double-sector graphite-filled epoxy centerpieces (SedVel60K; Spin Analytical), with centrifugation at 50,000 rpm at 20°C started ∼3 h after sample dilution. The data acquisition was conducted with uniform PMT voltage and gain settings for all cells. Data analysis proceeded in the same way as for absorbance and interference detection SV AUC, except that because of the nonlinearity of the fluorescence detection at high protein concentrations, the effective loading concentration was calculated based on dilution factors of the stock, assuming that the BSA carrier protein prevents any adsorption to the windows and centerpieces.

SE AUC

SE experiments were performed following the protocol described in Balbo et al. (2007). In brief, long solution columns (6 mm) were obtained by loading 170 µl of sample prepared by dilution of a concentrated stock with buffer. SE data were acquired using multiple wavelengths and interference detection at rotor speeds of 8,000, 12,000, and 18,000 rpm at either 4 or 10°C (Table 1). Experiments probing for pressure effects were conducted with ∼4-mm lamellas of mineral oil overlaid onto the sample solution columns (Josephs and Harrington, 1968; Marcum and Borisy, 1978). Data acquired at multiple loading concentrations, rotor speeds, and wavelengths were modeled globally in SEDPHAT using a standard monomer–dimer association model following Boltzmann distributions linked by mass action law (Schuck et al., 2010), coupled with implicit or soft mass conservation constraints, treating the baselines and the bottom of the solution columns as floating parameters (Vistica et al., 2004; Ghirlando, 2011). The loading concentrations used for EndoH-digested GluA2 ranged in different experiments from 37 nM to 26.5 µM, and for GluA3 293T from 0.58 to 4.8 µM.

Table 1.

K_d values determined for GluA2 constructs by different techniques

Technique	Temperature	GluA2S	GnTI−	EndoH	GluA2L	GluA2S-FAM	EndoH-FAM	EndoH-DyLight
SV	10°C	6.0 [2.1–22]a				14.9b [7.6–47]
	20°C	8.3 [2.0–22]	11 [0.8–43]	5.6 [2.3–23]	5.5 [2.8–43]
				8.3 [5.1–27]
				9.7 [4.4–16]
FDS-SV	20°C						5.3c [3.0–14]
							26d [10–57]
SE	4°C			160 [83–268]
				284 [159–461]
				30e [ND–260]
	10°C			13f [0.14–50]
				17 [ND–74]
				244f [46–643]
FAI	20°C							10.8 [2.4–29]
								11.3 [ND–68]
								8.43 [ND–50.8]

K_d values for individual experiments are reported in nanomolar; errors represent the 95% confidence interval using an automated surface projection method, unless indicated otherwise. 10 independent AUC experiments were performed for GluA2S digested with EndoH, as indicated by replicate entries for the mean and 95% CI. SV, sedimentation velocity with absorbance and interference optics; FDS-SV, sedimentation velocity with fluorescence detection optics; SE, sedimentation equilibrium with absorbance optics; FAI, fluorescence anisotropy.

^a68.3% confidence interval.

^bThe data obtained after FAM labeling of GluA2 led to the highest best-fit value, but the labeling does not significantly affect binding within the 95% confidence interval of this assay.

^cAnalysis of FDS-SV data only.

^dAnalysis of FDS data with single high concentration data point measured by absorbance at 488 nm.

^eAnalysis of data with low loading concentration and 210-nm detection.

^fAnalysis of data with oil layer to increase pressure.

Steady-state fluorescence anisotropy

GluA2S expressed in GnTI⁻ cells and digested with EndoH was labeled by adding 50 µg N-hydroxysuccinimide ester–activated DyLight405 (Thermo Fisher Scientific) to 500 µl of a 34-µM GluA2S stock solution at room temperature. The protein solution was mixed well and then incubated for 1 h to yield a molar labeling ratio of 1.4:1.6 in individual experiments. Free dye was then removed by dialysis followed by size-exclusion chromatography as described above for FAM-labeled GluA2S. Before use, the protein solutions were centrifuged at 10,000 rpm for 10 min to remove possible aggregates. Supernatants were taken out as the working stocks, from which dilutions were prepared using filtered buffer. Concentrations and labeling efficiency were determined by a UV-VIS spectrophotometer using ε₂₈₀ of 55,720 M⁻¹cm⁻¹ for unlabeled protein and ε₂₈₀ of 16,920 M⁻¹cm⁻¹ and ε₄₀₅ of 30,000 M⁻¹cm⁻¹ for the dye. Steady-state fluorescence was measured in a steady-state fluorimeter (Photon Technology International) at 20°C. The absorbance was <0.1 at the wavelength of excitation to avoid inner filter effects. To measure the equilibrium constant of GluA2S homodimerization, steady-state fluorescence anisotropies were measured as a function of protein concentration by titrating 2 nM of DyLight405-labeled GluA2S with unlabeled GluA2S aliquots at a range of concentrations, using λ_ex of 400 nm and λ_em of 420 nm, with time intervals of 10–15 min between change of concentration. Each intensity value was corrected by subtracting the buffer intensity from the observed signal, and for each titration point, three replicate readings were taken. The grating factor was determined using 2 nM DyLight405-GluA2S. As a control to probe for the possible quenching of fluorescence from dimerization, the fluorescence emission spectrum was measured (using 400 nm as λ_ex and 410–500 nm as λ_em) under similar conditions, with 2 nM of labeled GluA2 in the presence of varying concentrations of unlabeled GluA2S (2, 20, and 200 nM). No significant change in the spectrum was observed. The steady-state fluorescence anisotropy, r, was calculated from its intensity components, correcting sensitivity of the detection system for vertically and horizontally polarized light (Lakowicz, 1999), and the anisotropy isotherm was fit using a monomer–dimer model in SEDPHAT as a weighted average determined by the equilibrium dimerization constant and species’ anisotropy values, which were all refined in the analysis (i.e., with a form analogous to Eq. 1 without the standardization and nonideality terms).

Online supplemental material

The online supplemental material contains Fig. S1, which shows the c(s) distributions for GluA2L, and Figs. S2 and S3, which depict a global hydrodynamic analysis of all s_w isotherms shown in Fig. 3 D after ad hoc “temperature correction” of the FDS-derived data points. In addition, it contains a brief description of the preparation of EGFP. The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201210770/DC1.

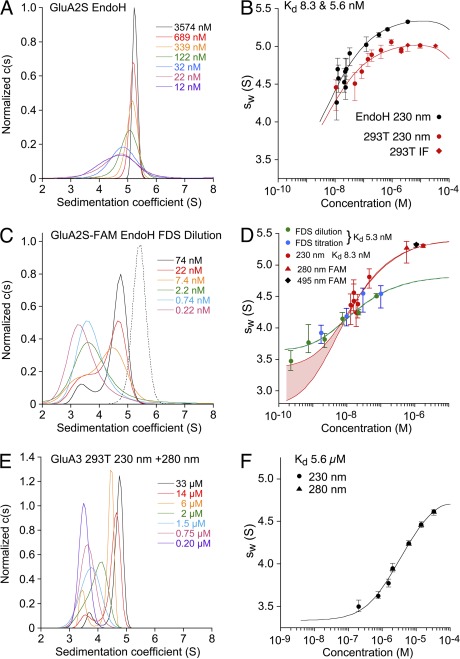
Figure 3.

SV AUC analysis for the GluA2 and GluA3 ATDs performed with different optical systems. Shown as pairs are the normalized sedimentation coefficient c(s) distributions (A, C, and E) and the s_w isotherm (B, D, and F) derived by integration. All SV data and isotherm models are shown in units of experimental s-values. (A) c(s) distributions for EndoH-digested GluA2S measured at 230 nm. (B) Comparison of s_w isotherms for the same data (black) and for GluA2S with complex glycosylation (red) acquired by absorbance at 230 nm (circles) and interference detection (diamonds). Fits for a monomer–dimer association were calculated with hydrodynamic constraints for monomer s-values of 2.75–3.37 S; the best-fit dimer s-values were 5.31 S (EndoH) and 5.07 S (293T), with K_d values of 5.6 and 8.3 nM, respectively. (C) Fluorescence-detected c(s) distributions for EndoH-digested FAM-labeled GluA2S (solid lines); the dotted line shows the c(s) distribution for absorbance detection at 495 nm of EndoH-digested FAM-labeled GluA2S. (D) s_w isotherms for EndoH-digested GluA2S derived from integration of fluorescence-detected c(s) profiles for a dilution series (green) and a titration series with unlabeled protein (blue), with the global best-fit isotherm in the absence of hydrodynamic constraints (blue-green line). For comparison, s_w isotherms were measured by absorbance at 230 and 280 nm for the same preparation before (red circles) and after FAM labeling (red triangle), respectively, and by absorbance at 495 nm from a different FAM-labeled preparation (black diamond). The best-fit s-value of the dimer was 5.44 S, but the monomer s-value was undefined, with a range from 2.75 to 3.37 S yielding statistically indistinguishable fits, indicated by the red lines for the extreme values, with the shaded area highlighting the range. (E and F) GluA3 c(s) distributions and the isotherm of s_w values fit with a monomer–dimer K_d of 5.6 µM.

RESULTS

Preparation and characterization of proteins with different extents of glycosylation

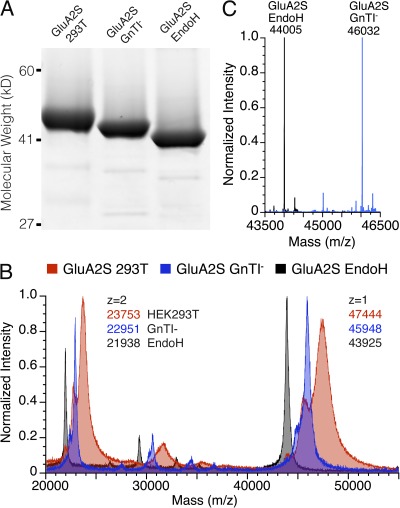
To address the issue of whether differences in glycosylation have any influence on AMPA receptor ATD oligomerization, we prepared proteins using both HEK293T cells, which produce proteins with complex N-linked glycans, and HEK293S GnTI⁻ cells that produce high mannose N-linked glycans (MAN5GlcNAc2), which can be trimmed to single GlcNAc residues by digestion with EndoH (Reeves et al., 2002). To determine if the presence of the ATD–LBD linker accounts for the different oligomerization properties reported by Clayton et al. (2009), we prepared short (GluA2S) and long versions (GluA2L) of the GluA2 LBD. Before analysis by AUC, the proteins were assessed for purity by SDS-PAGE, which revealed shifts in mol wt consistent with changes in the extent of glycosylation (Fig. 1 A). N-terminal Edman sequencing for the GluA2 ATD constructs used in our experiments established cleavage of the native signal peptides between Ser24 and Asn25, giving predicted masses from the cDNA sequence of 43,600 and 44,132 D for the short (GluA2S) and long (GluA2L) constructs after proteolytic removal of the affinity tag. Analysis by MALDI-TOF for GluA2S gave mass values (calculated from the 2⁺ species) of 47,504, 45,902, and 43,878 D for the HEK293T, GnTI⁻, and EndoH-digested GnTI⁻ samples, respectively, corresponding to glycosylation extents of 3.9, 2.3, and 0.3 kD, respectively, with detection of both single and doubly ionized species (Fig. 1 B). More accurate mass values of 46,032 and 44,005 D were obtained for the GnTI⁻ and EndoH-digested GnTI⁻ samples using an ESI-QTOF spectrometer (Fig. 1 C). For the undigested GnTI⁻ sample, the mass difference of 2,432 D from the value predicted from the amino acid sequence establishes that both consensus N-linked glycosylation sites (NXS/T) are coupled to a MAN5GlcNAc2 glycan; for the EndoH-digested protein, the mass increase of 405 D from the value predicted from the amino acid sequence establishes complete digestion to single GlcNAc residues. For the GluA2L construct expressed in GnTI⁻ cells and then digested with EndoH, the ESI mass spectrum gave a single peak of mass 607 D greater than that predicted from the amino acid sequence, consistent with the presence of an additional consensus N-linked glycosylation site in the ATD–LBD linker. Interpretable ESI mass spectra were not obtained for proteins expressed in HEK293T cells, probably because of heterogeneity in glycosylation (Crispin et al., 2009), but for the GluA2S construct, the MALDI-TOF result suggests the presence of 2 GlcNAc residues and 9–10 hexose sugars at each site. For the GluA3 ATD, N-terminal Edman sequencing revealed cleavage between Gly22 and Gly23, giving a predicted mass of 45,208 D after proteolytic removal of the affinity tag. For EndoH-digested GnTI⁻ samples, ESI mass spectral analysis revealed a single species of mass 45,815 D, corresponding to the addition of GlcNAc residues at each of the three N-linked glycosylation sites predicted from the cDNA sequence.

Figure 1.

Analysis of GluA2 preparations varying in extent of glycosylation. (A) SDS-PAGE showing approximate masses of 45.3, 44, and 41.5 kD for GluA2S expressed in 293T cells (left lane), GnTI⁻ cells (middle lane), and after digestion with EndoH (right lane). (B) Overlay of MALDI-TOF spectra for the same preparations illustrating singly (z = 1) and doubly (z = 2) charged species. (C) Overlay of deconvoluted ESI spectra for GluA2S GnTI⁻ samples before and after digestion with EndoH.

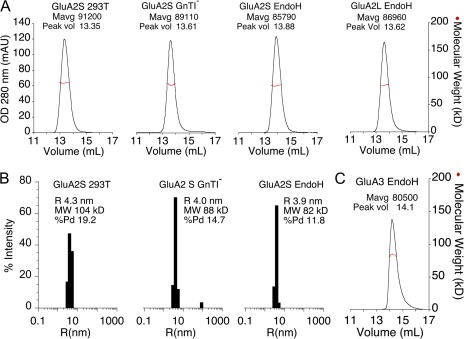
Before performing AUC experiments, the solution behavior of the GluA2 and GluA3 ATDs was assessed by SEC-UV/RI/MALS. The SEC-UV/RI/MALS results establish that when injected at a concentration of ∼45 µM, the GluA2 proteins elute with mol wts of 97–98% of that calculated for the dimeric species, and that the peak profiles are not altered by different extents of glycosylation nor by the different lengths of the GluA2S and GluA2L constructs (Fig. 2 A). Analysis by dynamic light scattering at a concentration of 2 mg/ml, yielding a concentration of ∼45 µM, also revealed a relatively monodisperse population of size and mass corresponding to formation of dimers in solution, with no evidence of aggregation (Fig. 2 B). For the GluA3 ATD construct, the SEC-UV/RI/MALS profile yielded a peak mass of only 88% of that calculated for the dimer (Fig. 2 C), which most likely reflects a lower affinity for dimer assembly than for GluA2, and dissociation into monomers at low micromolar protein concentrations.

Figure 2.

Light-scattering analysis of GluA2 and GluA3 ATD preparations. (A) SEC-MALS analysis for GluA2 ATD constructs differing in length and extent of glycosylation. UV absorbance at 280 nm is shown as a black trace; red circles indicate mol wt calculated from light-scattering and refractive index signals. (B) Size distributions by dynamic light scattering for the three GluA2S constructs with the mol wt and radius of each sample; no evidence of aggregation or higher ordered assemblies is apparent. (C) SEC-MALS analysis for the EndoH-digested GluA3 ATD expressed in GnTI⁻ cells.

SV analysis of GluA2 and GluA3 self-association

We conducted SV AUC experiments on multiple preparations of the GluA2 and GluA3 ATDs (Figs. 3 and 4, and Table 1). Boundary element hydrodynamic predictions (Aragon, 2011), as well as bead shell modeling (García De La Torre et al., 2000), were used to estimate the likely range of sedimentation coefficients that would be expected based on crystal structures of the GluA2S ATD for which extended glycan chains and disordered residues at the amino and carboxy termini were modeled in COOT (Emsley et al., 2010). Based on this structure, under our experimental conditions the dimer would be expected to sediment at ∼4.5–4.9 S, from which a hydrodynamic power law of compact molecules would predict the monomer s-value to be in the range of ∼2.8–3.1 S, and that of a putative tetramer to be ∼7.2–7.9 S; higher monomer and dimer s-values were calculated for GluA2 without glycan chains, with s-values in the range of 2.9–3.3 and 4.6–5.3 S, respectively, dependent on the assumed conformation of the disordered N and especially C termini. Fig. 3 (A and E) shows typical c(s) distributions of GluA2 and GluA3, displaying concentration-dependent peaks, consistent with monomer and dimer species with interconversion on the time scale of sedimentation (Gilbert, 1959; Dam et al., 2005). It can be discerned that, even at the highest concentration (3.6 µM for GluA2S and 33 µM for GluA3), no species larger than the dimer is detectable, in agreement with SE results for GluA1 and GluA2 reported by Jin et al. (2009). In some experiments, there was a small peak at 8 S for 11 nM GluA2, which was not present for higher concentrations (e.g., Fig. 4 C). At face value, this could be interpreted as resulting from a larger species at low protein concentrations, but such behavior often appears at extremely low signal/noise ratios and is an artifact of the regularization process that penalizes zero c(s) values; the exclusion of s-values >6 S from the model does not result in a statistically significant change in the quality of fit, and in subsequent experiments, such species were not observed by FDS-SV for even lower protein concentrations. Analogous families of concentration-dependent c(s) distributions for EndoH-digested GluA2L are shown in Fig. S1. The absence of nontrivial higher oligomers and aggregates (>6 S) in our data is in contrast with the data of Clayton et al. (2009), who detected major c(s) peaks at 7.9 S and higher for GluA2L at 0.6 mg/ml, and indicates that the ATD–LBD linker does not mediate formation of tetramers in solution, consistent with the lack of interaction of the ATD–LBD linkers observed in the GluA2 crystal structure (Sobolevsky et al., 2009).

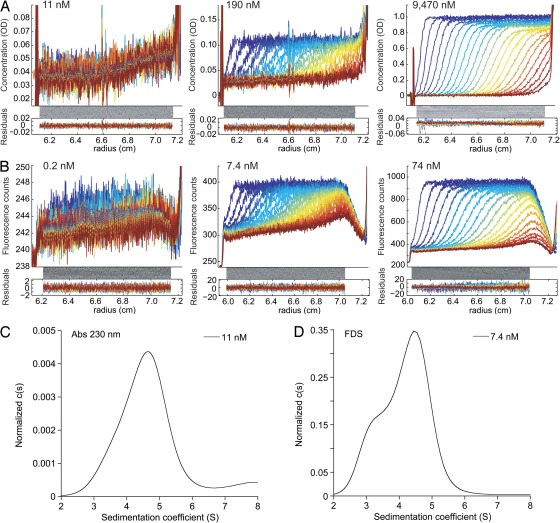
Figure 4.

Representative raw SV data at different GluA2 concentrations measured using absorbance and fluorescence detection. (A) Data for GluA2S measured by absorbance at 230 nm. (B) Data for EndoH-digested FAM-labeled GluA2S measured using fluorescence detection; the data shown form part of the s_w isotherm shown in Fig. 3 D. In both panels, the radial signal distributions are shown at equidistant time points after start of the centrifugation, with later times indicated by higher color temperatures on a blue < green < red scale. (C) c(s) distribution obtained from the analysis of the 11-nM data of GluA2S shown in A. Integration and Monte-Carlo analysis leads to an s_w value of 4.46 S (4.16–4.56 S). (D) For comparison, analogous c(s) distribution of FAM-labeled GluA2S at 7.4 nM derived from FDS data, leading to an s_w value of 4.14 S (4.06–4.26 S).

At equivalent concentrations, the c(s) peaks reveal much larger dimer populations for GluA2 (Fig. 3 A) than for GluA3 (Fig. 3 E). To dissociate the GluA2 dimer, it was necessary to extend the dilution series to lower concentrations than those typically used in AUC experiments with absorbance or interference optics. Theoretical simulations reveal that, as a result of the large number of data points (10⁴–10⁵) generated in the experiment, which can all be incorporated in the c(s) analysis, the initial signal amplitude of the sedimentation boundary can be as low as 0.6 times the noise of the data and still allow determination of a weighted-average s-value (s_w) with statistical errors sufficiently small to allow defining the binding isotherm (Fig. 4 A). Fig. 4 C shows an example of the c(s) traces corresponding to low signal/noise data obtained for GluA2S at 11 nM; the data at 12 nM of EndoH-digested GluA2S in Fig. 3 A and the distribution obtained at 11 nM of EndoH-digested GluA2L in Fig. S1 show other examples. However, the ability to hydrodynamically distinguish different macromolecular species is substantially less at a lower signal-to-noise ratio because of the peak broadening induced by regularization. Although this can be counteracted by applying Bayesian knowledge of the expected range of sedimentation coefficients (Brown et al., 2007), this option was not used in the present work because it was aimed only at extracting s_w, for which the resolution of monomer and dimer species is not relevant. This allowed us to reproducibly analyze data at a loading concentration as low as ∼10 nM using absorbance optics.

For the quantitative analysis of binding affinity, s_w values were determined from the integration of sedimentation coefficient distributions, c(s). These are rigorously rooted in second-moment mass balance considerations and are essentially independent of conversion kinetics (Schuck, 2003). Their isotherm as a function of loading concentration was modeled based on mass action law, and parameter estimates for the binding constants and monomer and dimer s-values were refined using nonlinear regression (Fig. 3, B and F). For GluA3, the best fit results in a K_d of 5.6 µM (95% confidence interval [CI], 1.7–14 µM) and s-values of 3.34 S (95% CI, 2.94–3.65 S) and 5.05 S (95% CI, 4.83–5.40 S) for monomer and dimer, respectively. This K_d is in good agreement with the results obtained subsequently from SE analysis performed using absorbance optics (Fig. 6 A) but more than fourfold larger than the value of 1.2 µM derived from fluorescence detection SV analysis by Rossmann et al. (2011). For GluA2, the high affinity leaves the value for the monomer s-value essentially undetermined from the s_w isotherm and in strong correlation with the estimated value of K_d. However, hydrodynamic predictions can be used to very effectively constrain possible monomer s-values, which, in turn, allow for determining K_d (Fig. 3 D). Allowing for a wide range of possible translational friction ratios for the monomer between 1.3 and 1.6, translating to possible s-values of 2.75–3.37 S, a best-fit binding constant of 8.3 nM at 20°C was determined for GluA2S expressed in 293T cells (Fig. 3 B), where the extreme values of s₁ contribute a factor of two to the 95% confidence interval that ranges from 2.0–22 nM. The dimer s-value in the best-fit isotherm was 5.07 S, slightly above the hydrodynamically predicted range for GluA2S with extended complex glycan chains (Fig. 3 B). The K_d for dimer assembly for the GluA2 ATD is an order of magnitude less than that obtained in previous experiments by SE studies (Jin et al., 2009), and approximately three orders of magnitude lower than that estimated from SV analysis for a GluA2 construct that includes the ATD–LBD linker (Clayton et al., 2009). However, the presence of the ATD–LBD linker does not account for this difference, because for GluA2L, we measured a K_d of 5.5 nM (95% CI, 2.8–43 nM) by SV analysis (Table 1) comparable to the K_d of 1.8 nM determined by fluorescence detection SV for GluA2S (Rossmann et al., 2011).

Figure 6.

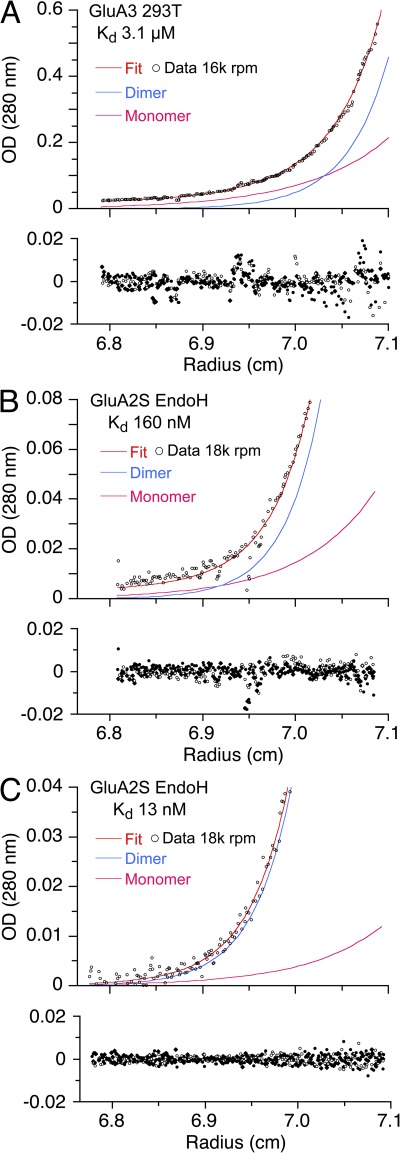
SE AUC analysis for the GluA2 and GluA3 ATDs. A wide range of K_d values is illustrated by representative data for GluA3 (A) and two replicate experiments for EndoH-digested GluA2S with high (B) and low (C) K_ds. In each panel, the top section shows the raw data and best-fit distribution (red line) and calculated monomer (magenta) and dimer (blue) species; the bottom section shows the radial distribution of residuals from three different rotor speeds recorded from the same cell. Traces shown are at initial loading concentrations of 4.8 (A), 7.4 (B), and 5.8 µM (C), respectively, after establishing an equilibrium concentration gradient at 16,000 (A) and 18,000 rpm (B and C), all taken from the global analysis of data from multiple cells at a range of different loading concentrations, recorded using multiple signals. In B and C, only a subset of the SE profile is shown to highlight the low concentration region close to the meniscus, which provides information on dimer dissociation.

To study the potential influence of glycosylation on the binding affinity, we analyzed analogously the sedimentation behavior of both GluA2S expressed in GnTI⁻ cells and EndoH-digested GnTI⁻ samples and obtained similar K_d estimates between 6 and 11 nM, with overlapping 95% confidence intervals (Table 1). The data do not indicate any effect of glycosylation on binding affinity. Based on the hypothesis that the binding affinity of all GluA2 constructs studied is the same, we can average the results of the individual measurements and arrive at a K_d at 20°C of 7.1 nM.

GluA2 dimerization studied by fluorescence detection SV

To explore the benefits of the high sensitivity of fluorescence detection at low nanomolar protein concentrations demonstrated for FAM-labeled GluA2 (Rossmann et al., 2011), we embarked on SV experiments with the FDS detection system. Labeling was conducted with EndoH-digested GluA2S at micromolar concentrations where the protein is largely dimeric, making it unlikely that the amine-reactive label would attach into the dimer recognition interface. We confirmed by SV with absorbance detection at 230 nm that the FAM-labeled material was binding competent, yielding an estimated K_d at 10°C of 14.9 nM (95% CI, 7.6–46 nM), within error consistent with the value for unlabeled material (Table 1). As shown in Fig. 4 B, FDS-SV data of GluA2-FAM exhibits an ∼50-fold higher sensitivity than absorbance data at 230 nm (Fig. 4 A), but a distinct nonlinearity in the signal magnitude can be discerned from the comparison of the boundary amplitude at 7.4 and 74 nM. Although the FDS-SV data also showed artifactual features close to the bottom of the cell, as described previously (Kroe and Laue, 2009), these were excluded from the analysis, and changing the fitting limit did not significantly influence the results. Interestingly, consistent with the prior analysis by FDS-SV (Rossmann et al., 2011), the c(s) profiles analysis (Fig. 3 C) reveals peaks for monomer and dimer, apparently indicating moderately slow interaction with a dimer complex lifetime on the order of tens of minutes (Dam et al., 2005). In parallel to the dilution series for GluA2-FAM (Fig. 3 D, green circles), we conducted a titration experiment in which increasing concentrations of unlabeled GluA2 were added to 0.74 nM of FAM-labeled GluA2 (Fig. 3 D, blue circles). Both s_w isotherms clearly show dissociation of the dimer in the expected concentration range, and the results of the titration and dilution isotherms are consistent. When analyzed globally, without any hydrodynamic constraints for the dimer s-value, the s_w isotherms lead to a best-fit K_d of 5.3 nM (95% CI, 3.0–14 nM; Fig. 3 D, blue/green line), consistent with the results from conventional SV. Absorbance SV experiments with 230- and 210-nm detection, conducted in parallel on the same GluA2 preparation before labeling with FAM (Fig. 3 D, red circles), resulted in an absorbance-based s_w isotherm with a best-fit K_d of 8.3 nM (95% CI, 5.1–27 nM).

However, the dimer peak location in c(s) plots for the FDS-SV data, which after temperature correction is consistent with the results reported by Rossmann et al. (2011), has a significantly lower s-value than the dimer s-value determined in a parallel experiment on FAM-labeled GluA2 using absorbance optics (Fig. 3, C and D). When the s_w isotherm is examined in detail, the best-fit dimer s-value extrapolated from modeling the isotherm of the FDS-SV experiment is ∼9% lower than the corresponding value determined using absorbance optics for the same protein preparation before FAM labeling (Fig. 3 D), and the ratio of the dimer s-value to the monomer s-value from the FDS-derived isotherm is less than expected given the relatively globular shape of both the monomer and dimer species (Fig. 3, C and D). When absorbance data for 1.1 µM of FAM-labeled protein recorded at 495 nm (Fig. 3 D, black diamond) is included in a global isotherm analysis for the FDS-SV data, the fit is of poor quality and the K_d increases to 26 nM (95% CI, 10–57 nM); however, when the data at 495 nm for the labeled protein data are included in a global analysis for unlabeled protein recorded using absorbance optics at 230 nm (Fig. 3 D), the fit was good. Thus, although the K_d values obtained using absorbance and fluorescence detection systems are in good agreement, for unknown reasons the s-values from the FDS-SV experiments are incompatible with those from conventional optics and from hydrodynamic predictions.

Fluorescence quenching in the dimer form could potentially bias the detection of monomer and dimer and thereby lead to misleading s_w values; this was excluded by the overlapping titration and dilution isotherms (Fig. 3 D). Furthermore, we confirmed in a benchtop fluorometer that the fluorescence spectrum was unchanged when adding unlabeled GluA2 to GluA2-FAM. Consistent with this, crystal structures for GluA2 ATDs reveal that the N termini, the likely site of modification by FAM, are separated by 7.7 nm in the dimer assembly, and thus dye quenching is unlikely based on proximity effects (Clayton et al., 2009; Jin et al., 2009; Rossmann et al., 2011). Next, we performed control SV experiments with absorbance and interference optics to examine the influence of 0.1 mg/ml BSA that was used as a carrier protein in the FDS experiments on FAM-GluA2. We found the difference of the s-value in the presence or absence of BSA to be only 0.025 S, demonstrating BSA to be inert.

To explore the differences in s-values between the FDS data and the absorbance data, we performed a series of SV runs with an EGFP that does not dimerize in the concentration range used. Replicate dilution series of EGFP were run in the FDS instrument using fluorescence detection, in the FDS instrument using conventional absorbance detection, and separately in five conventional AUCs not modified for FDS using absorbance and interference detection. The experimental s-value at 20°C from the conventional AUCs was 2.87 ± 0.03 S. Unexpectedly, s-values from the FDS instrument were approximately ∼10% lower: 2.54 ± 0.02 S for fluorescence detection and 2.62 ± 0.02 S with the absorbance detector, both measured in the same FDS instrument. Hypothesizing that an instrument-related technical factor may cause a uniform underestimate by 10% of all s-values, we applied ad hoc an increase by 10% to all s_w values from the FDS dilution and titration experiments to test whether this would lead to a consistent interpretation with the conventional SV data. The global fit of the so “corrected” FDS data with the absorbance data acquired in conventional AUC instruments at 230 and 210 nm still showed systematic deviations, but now with FDS-derived s_w values at low concentrations that were consistently too high (Figs. S2 and S3). In principle, this could be explained by incomplete equilibration before the SV run caused by the apparent slow reaction kinetics suggested by FDS-SV–derived c(s) for FAM-GluA2S, but this would be associated with an underestimate of the monomer population and the underestimate of K_d, which was indicated neither by the FAM-GluA2S isotherm experiments using conventional AUC (Table 1) nor by the FDS-SV data.

GluA2 dimerization studied by steady-state fluorescence anisotropy

To pursue an independent biophysical method to verify the binding constant of fluorescently labeled GluA2, we used steady-state fluorescence anisotropy. Unfortunately, although a clear decrease of anisotropy was observed with decreasing total concentration of labeled protein, FAM-labeled GluA2S did not exhibit a sufficiently strong fluorescence signal for anisotropy measurement at low nanomolar concentrations. Therefore, we used DyLight405 as an alternative label. We established the absence of aggregates for EndoH-digested, labeled GluA2S preparations by SV with absorbance optics. Also, we established that the fluorescence emission spectrum was invariant when adding unlabeled GluA2S at a final concentration of 0.1 µM to 2 nM of labeled GluA2S, consistent with the absence of dimerization-induced quenching of fluorescence signals. To probe the time scale of dimer dissociation, which potentially impacts the analysis of SV experiments, we studied the time dependence of the anisotropy signal after dilution from dimeric stock to a low concentration where the monomer population should dominate. The first measurements were made 1–2 min after dilution, and thereafter the signal was stable for over an hour, indicating that dimer dissociation of DyLight405-labeled, EndoH-digested GluA2S is rapid, in apparent conflict to the greater dimer stability of GluA2-FAM suggested by c(s) analysis during FDS-SV (Fig. 3 C).

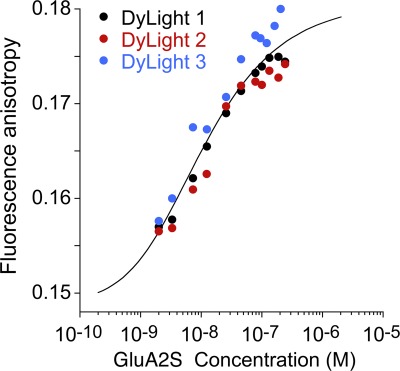
Next, anisotropy experiments were conducted with a constant 2-nM concentration of DyLight405-labeled GluA2S, which was titrated with unlabeled GluA2S. A distinct, concentration-dependent increase in the anisotropy was observed (Fig. 5). Although the isotherm does not cover the range of full dissociation, lower concentrations of GluA2S could not be easily studied because of the degrading signal/noise ratio at low protein concentrations. The global analysis of the three isotherms led to a best-fit K_d of 9.7 nM (95% CI, 0.35–41 nM), with best-fit results well reproducible across different protein batches (Table 1). These data are consistent within error with those obtained by SV.

Figure 5.

Steady-state fluorescence anisotropy isotherms of DyLight405-labeled, EndoH-digested GluA2S measured in three independent experiments (circles) and the best-fit global isotherm (black solid line).

Quantifying the dimerization of GluA2 and GluA3 by SE

To explore the potential impact of errors that differ for SE and SV experiments, we performed SE experiments using unlabeled material (Fig. 6). For GluA3, we obtained a monomer–dimer K_d of 3.1 µM (95% CI, 2.6–3.7 µM) at 10°C (Fig. 6 A), in good agreement with the value of 5.6 µM at 20°C from SV, considering the 10°C temperature difference. In contrast, a 20-fold range of K_d was obtained from analysis of six independent SE experiments for GluA2S expressed in GnTI⁻ cells and digested with EndoH (Table 1). In three experiments, the K_d value was 160–284 nM (Fig. 6 B), consistent with the value of 152 nM obtained in SE experiments for GluA2 reported by Jin et al. (2009). However, in another three experiments, much higher affinities were obtained (Fig. 6 C), with a K_d value of 13–17 nM, within error not statistically different from the value of 7.1 nM obtained by SV experiments with absorbance optics.

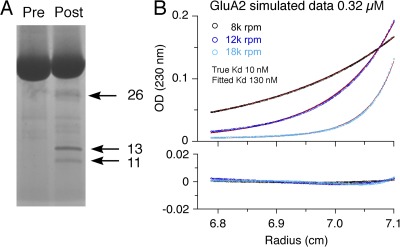
In initial experiments, before discovery of the wide range in variation of K_d values obtained by SE, we explored whether higher pressures, which occur in SV experiments, could potentially explain differences in K_d of the two methods, and performed experiments in the presence of a mineral oil layer to increase the pressure on the solution column, but without consistent results. Similarly, temperature differences between SV and SE experiments did not account for the discrepancy (Table 1). However, we noted that data acquired using the interference optical system from the SE experiment shown in Fig. 6 B yielded a K_d of 570 nM compared with the value of 160 nM for data acquired using the absorbance system. This difference is suggestive of the presence of breakdown products from proteolytic degradation during the long time of the experiment, producing fragments lacking aromatic amino acids. Indeed, silver-stained SDS gels of GluA2S samples taken out of the ultracentrifuge cell after completion of replicate SE experiments frequently showed the presence of small degradation products with bands at 11, 13, and 26 kD (Fig. 7 A). It is typical of proteolytic degradation in AUC cells to be poorly reproducible, even from cell to cell in the same run with the same preparation. Thus, we hypothesize that proteolytic degradation during the several days required for SE experiments is a possible origin of the elevated apparent K_d observed in some experiments.

Figure 7.

Proteolytic breakdown products lead to artificially high K_d estimates for EndoH-digested GluA2 ATD dimer assembly. (A) Silver-stained gel for the same preparation before SE (Pre) and for material recovered after the SE experiment (Post), showing degradation products at 11, 13, and 26 kD. (B) Subset of theoretical SE signal profiles simulated for conditions mimicking the experiment shown in Fig. 6, assuming a hypothetical K_d of 10 nM, superimposed with signals from 11-, 13-, and 26-kD fragments, each at 2% of the total loading concentration and with signals from 2% of binding-incompetent monomer. The corresponding global fit to the simulated data is shown as solid lines, leading to an apparent K_d of 130 nM. The residuals are shown in the bottom panel, with the same radials scale. The root-mean-square deviation is 0.0011 OD.

To examine this hypothesis, we simulated SE profiles for GluA2 at representative high and low loading concentrations, with three rotor speeds and all other conditions taken from the experimental data, assuming a monomer–dimer K_d of 10 nM. Superimposed on the theoretical profiles were signals from species the size of the detected breakdown products, each at 2% of the total loading concentration. We then globally reanalyzed the simulated data with a standard monomer–dimer model, not accounting for the signals from the breakdown products; this led to an apparent K_d of 85 nM, with residuals within the noise typical for experimental data, confirming the sensitivity of SE toward low degrees of protein degradation. In repeated simulations, the apparent K_d varied with the molar fraction of the breakdown products. Another degradation effect could come from the presence of nicked polypeptides of similar mol wt to the intact protein that have been rendered binding incompetent and which would not be detected by a difference in mol wt in both SE and on the SDS gel. Simulations in which in addition to breakdown products 2% of the protein is unable to form dimers increased the apparent K_d to 130 nM, again with residuals below those commonly encountered in experimental data (Fig. 7 B).

DISCUSSION

Previous work has shown that mutations that alter the monomer–dimer equilibrium for iGluR ATDs profoundly impact assembly of full-length AMPA and kainate receptors (Kumar et al., 2011; Rossmann et al., 2011). The three orders of magnitude discrepancy of K_d values reported in the literature for homodimerization of the GluA2 ATD raises serious questions about what limits the accuracy of these measurements. This naturally led us to examine in detail the methodology used in prior work in order to identify potential problems in different experimental designs, and to compare different fluorescence and ultracentrifugation techniques in their performance for studying high-affinity interactions. Comparison of our results with those from prior analysis of oligomerization of the GluA2 ATD reveals important differences in experimental design and data analysis, which impact the accuracy of the results obtained and limit our ability to interpret the data. The most important are that (a) SV experiments should be performed with a range of loading concentrations spanning the expected K_d, and not for just a single concentration (Clayton et al., 2009); (b) differential sedimentation coefficient distributions c(s) combined with weighted-average s-value (s_w) isotherms should be used to determine the K_d from such experiments, instead of Gaussian fits to c(s) profiles (Clayton et al., 2009; Rossmann et al., 2011); (c) global analysis over multiple datasets, recorded using different optical systems, is preferable to averaging individual K_d values derived from a cell-by-cell analysis (Rossmann et al., 2011); and (d) when SE experiments are performed, useful information on species populations can be obtained from parallel SV runs (Jin et al., 2009).

The GluA2 and GluA3 ATDs assemble as dimers in solution

Using these approaches, we have obtained strong evidence for reproducible high-affinity GluA2 ATD dimerization with a K_d in the 5–10-nM range. Support for such a low nanomolar K_d comes from the combination of far-UV absorbance detection SV, which relies entirely on unlabeled molecules, as well as steady-state fluorescence anisotropy results for DyLight405-labeled GluA2. The nanomolar K_d is also qualitatively confirmed by SV data collected with FAM-labeled GluA2 with the fluorescence detection system, but with caveats because of apparent changes in sedimentation coefficients (see below), which prevent a global analysis of this data with that obtained using absorbance optics. Compared with data published in the literature, a K_d in the 5–10-nM range is within error of the K_d of 1.8 nM derived previously by FDS-SV (Rossmann et al., 2011), but more consistent with the monomeric state of 1 nM of oxazine-labeled GluA2 reported by Jensen et al. (2011). Because Rossmann et al. (2011) did not report an analysis of s_w isotherms or sedimentation coefficients for monomers and dimers, further comparison is not possible.

We believe that the 150-nM K_d reported by Jin et al. (2009), similar to our own SE experiments (Fig. 6), was an artifact caused by protein degradation, to which we found this technique to be particularly susceptible when studying high-affinity systems. We were able to rule out effects of glycosylation and the presence of the ATD–LBD linker to be major factors contributing to the 4.3-µM K_d estimate for GluA2L (Clayton et al., 2009); in the absence of other obvious causes, and based on observations reported by Rossmann et al. (2011), it appears that AMPA receptor ATDs can apparently lose the ability to dimerize, although this was never apparent in our series of experiments, giving rise to a large monomer population and hence an overestimate of the monomer–dimer K_d. This would easily be detected by analysis of SV experiments conducted at multiple concentrations, followed by calculation of c(s) distributions and s_w isotherms. For GluA3, from both conventional SE and SV AUC, we observed sedimentation behavior much different from GluA2, with monomer–dimer K_d estimates of 3.1 and 5.6 µM, respectively. These values are close to the K_d estimate of 1.2 µM obtained by FDS-SV (Rossmann et al., 2011), although in this work, the value was not well defined, with a 95% CI of 0–4.7 µM calculated from the reported mean and standard error of the mean of 1.2 ± 0.5 µM (n = 12). Provided that the SV experiments were performed at multiple GluA3 concentrations, analysis of s_w isotherms, instead of the reported cell-by-cell average of individual K_d values (Rossmann et al., 2011), would be expected to give a more precise estimate. Likewise, analysis of s_w isotherms is important for the high-affinity interaction observed for GluA2 (Rossmann et al., 2011), because strong error amplification can be expected when averaging individual K_d values arrived at cell by cell.

Of significance for the role of the ATD in the assembly and modulation of AMPA receptors, we did not detect the formation of tetramers at the highest protein concentrations for GluA2 nor GluA3. From SE experiments for GluA3, for which the maximum fitted protein concentrations exceeded 12 µM at the maximum speed, statistical analysis for a fit of a monomer–dimer–tetramer equilibrium indicates that the dimer–tetramer K_d has a lower 95% CI limit of 162 µM but could be much weaker. For GluA2, from a dataset for which the maximum fitted protein concentrations reached 22.6 µM, the dimer–tetramer K_d has a lower 95% CI limit of 2.5 mM.

Comparison of SE and SV AUC

Collectively, our results combined with those from previous reports raise several important methodological issues concerning the use of SE experiments for analysis of protein oligomerization at low nanomolar concentrations, as was required for GluA2 but not GluA3. Previous SV and SE experiments from our laboratory, for an extensive series of AUC experiments on glutamate receptor ATD and LBD mutants, which formed dimers over a wide range of low to moderately high affinities, gave monomer–dimer K_d values consistent within a factor of two (Chaudhry et al., 2009b; Kumar et al., 2009, 2011). This was the case in the present study for GluA3, but not for the much higher affinity GluA2 ATD. In our previous work, the K_d estimated by SV for 11 different wild-type and mutant proteins was consistently lower, by a factor of 1.8, than the value obtained by SE. However, in the highest affinity system studied previously, for the GluR6/KA2 ATD heterodimer, the K_d estimated by SV was 6.9 times less than the value estimated by SE, and for GluA2, the ratio increases to a discrepancy of >15, but with a high variance for individual SE experiments (Table 1). Typical sources of slight discrepancies, such as the temperature and pressure at which the experiments are usually conducted, have been ruled out. We believe that the differences are intrinsic to the methodology used for SE experiments when studying high-affinity self-association. Although the largest oligomers can usually be easily identified at high concentrations, the measurement of a K_d requires experiments at low protein concentrations where the monomeric state is significantly populated. This raises difficulties in both the time scale and the concentration scale of the experiments, which we discuss below.

SE AUC and protein degradation

In principle, far-UV detection in conjunction with global modeling, including mass conservation constraints, can provide sufficient sensitivity for low nanomolar-binding constants to be determined, as demonstrated previously in several applications (Philo et al., 1996, 2000; Hsu et al., 1997). However, in practice the duration of the experiments requires protein stability for several days. In our SE experiments with GluA2, we attribute the adventitious overestimation of the K_d by SE to the effects of protein degradation during the long time required to successively establish SE at different rotor speeds. This was supported by the appearance of degradation products visible by SDS-PAGE in conjunction with computer simulations of the effect of their signal offsets, which are hidden by experimental noise. The higher sensitivity of high-affinity systems to protein degradation and incompetent monomer formation has long been theoretically recognized (Yphantis et al., 1978), but experimental examples are rarely reported. It arises from the need to quantify very low free monomer concentrations from the information contained in the slope and curvature of the sedimentation profiles near the meniscus of the centrifugal solution column, where the larger species are relatively depleted. Unfortunately, close to the meniscus is also where binding-incompetent small species are relatively enriched. Therefore, the estimate of the apparent free monomer concentration is derived from the sum of locally reversible monomer species, plus signals from smaller unresolved degradation products that correlate to some extent with the monomer signal. In addition, the presence of monomer species that have been chemically modified and are incompetent to form dimers (see below) further complicates the analysis. Even though different experimental designs could be applied to significantly reduce the experimental time for SE, for example the use of shorter solution columns or fewer rotor speeds, as has been applied to tubulin dimerization (Sackett and Lippoldt, 1991), these would also lead to significantly reduced information content and limit the opportunity for detailed modeling, including the application of implicit mass conservation constraints in SEDPHAT (Vistica et al., 2004), thereby increasing the detection limit for free monomer and increasing the lowest K_d that can be resolved.

A back-of-the-envelope calculation would suggest that if 1% of the material is binding incompetent, the estimate of an apparent K_d from SE cannot arrive at a value <0.01-fold the total molar-loading concentration, regardless of the true K_d. This does not appear to pose a serious problem in techniques such as SV, where the analysis is based on isotherms of observables generated by different fixed dilutions of a stock, which will also dilute the degradation products proportionally, and where these dilutions can be chosen in the vicinity of K_d. In contrast, SE relies on a concentration gradient to be established within a solution column that can span two to three orders of magnitude of observable concentrations at a single loading concentration. This allows one to use much higher loading concentrations, especially in meniscus depletion SE conditions that always cause a significant fraction of the data points to be close to or below the detection limit. This can be useful for characterizing well the dimer state and deriving from that the protein density increment, and also for constraining the exponential model in the more dilute regions of the solution column. In light of the potential degradation problem, the inclusion of low loading concentrations seems advantageous, but low concentrations alone may not allow for statistically precise estimates.

Considerations of the time scale of the reaction for SV experiments

The time scale of the experiment also plays an important role for SV. Typically, SV experiments do not allow chemical equilibration on the time scale of sedimentation if the complex dissociation rate constant is 10⁻⁴/s or slower (Dam et al., 2005), and thus it is important that samples be allowed to reach equilibrium after preparing a dilution series before starting the centrifuge; in practice, this is usually achieved while waiting for the rotor to reach thermal equilibrium. Some clues about the kinetics of dimer dissociation can be determined from analysis of the c(s) sedimentation coefficient distributions, which for systems with slow dissociation show distinct peak positions for monomer and dimer, virtually independent of sample concentration, as opposed to peak positions that shift with concentration, reflecting a time-average migration velocity of interconverting species (Gilbert, 1960; Schuck, 2003). Unfortunately, at the low protein concentrations required for high-affinity interactions, such as those in the present study of GluA2, the signal/noise ratio of the UV detection system is not sufficient to allow the diagnosis by c(s) peaks, which tend to broaden strongly from regularization, mimicking the pattern expected for fast interactions. In this context, the result of the control experiment we performed to estimate the time dependence of fluorescence anisotropy is significant. It suggested that the dissociation kinetics, at least for DyLight405-labeled GluA2, were fast on the experimental time scale of an SV experiment. For unknown reasons, c(s) profiles for FAM-labeled GluA2 (Fig. 3 C), as well as data shown in Figs. S1 and S2 in the study by Rossmann et al. (2011), appear to indicate much slower kinetics.

The question of reaction kinetics also arises in the choice of SV data analysis method. Supported by the apparent hydrodynamic separation of FAM-GluA2 monomer and dimer species at different concentrations, Rossmann et al. (2011) assumed the approximation limit of very slow reactions for which c(s) peaks correspond to species concentrations. The interpretation of the 7.9- and 10.3-S c(s) peaks measured by Clayton et al. (2009) at a single concentration of GluA2 is more ambiguous, as it is well established that the sedimentation coefficient distribution at a single concentration does not permit the distinction between reaction boundaries of dynamically interconverting species and stable species boundaries. However, the strong underestimate of the molar mass associated with the 7.9-S peak is a telltale sign for the presence of a concentration-dependent aggregation process with relatively rapid equilibration (Dam et al., 2005; Schuck, 2010). In this case, species concentrations are not reflected in the peak amplitudes of the reaction boundaries, and using their integrals to estimate binding constants via mass action law would be incorrect. A valid data analysis method that is independent of conversion kinetics, provided that chemical equilibrium before sedimentation is established, is the isotherm of overall signal weighted-average s-values for data measured over a wide range of concentrations, which can be derived rigorously from directly integrating c(s) over all peaks (Schuck, 2003). For the purpose of integration, poor peak separation caused by regularization at low signal/noise ratios can be effectively avoided using Bayesian regularization (Brown et al., 2007). Using the approach of fitting c(s) peaks to Gaussians as a tool for integration, as performed by Clayton et al. (2009) and by Rossmann et al. (2011), departs from the theoretical foundation of the relationship between this method and the second-moment considerations of s_w, and is prone to introduce errors and bias especially for partially merging peaks. It is possible that this is the cause of the large spread of K_d values reported by Rossmann et al. (2011), although complications caused by substantial fractions of labeled proteins that failed to form dimers at high concentrations likely played a role as well. Indeed, in some of the c(s) distributions, it appears that >20% of the labeled protein is unable to form dimers (Fig. S2 A; Rossmann et al., 2011). The presence of even higher fractions of dimerization-incompetent monomer could theoretically explain the presence of a significant monomer peak in the c(s) distribution obtained by Clayton et al. (2009) at 0.6 mg/ml in SV and would be consistent with the apparent slow kinetics leading to baseline resolution of the monomer and dimer peaks, and thus explain the discrepancy in the resulting K_d. In principle, such a possibility could be ruled out in SV experiments performed at a range of concentrations, which have fundamental value in confirming the reversibility of all assembly steps observed, while a global isotherm analysis of s_w data from different concentrations may reveal the presence of incompetent monomer by an implausibly low ratio of extrapolated best-fit dimer and monomer s-values.

Detection limits in high-affinity systems and use of the FDS detection

A third and obvious key limitation of AUC or most methods for the study of high-affinity systems is the requirement for the accurate detection of low protein concentrations, typically on the order of or lower than the K_d, such as to allow for a significant fraction of the protein to dissociate into monomers. Our present data indicate that in the absence of proteolysis, far-UV absorbance optical detection can be used to determine K_d values for GluA2 in the 10-nM range by SE, consistent with previous reports on other molecules (Philo et al., 1996; Hsu et al., 1997). In the present work, we show that such low homodimerization K_d values can be much more reliably resolved using SV with far-UV absorbance detection, based on the high precision of sedimentation coefficients in SV and the high noise tolerance of the c(s) method for which total loading signals on the order of the statistical noise in the data acquisition are sufficient. (With regard to the numerical value assigned to the lowest useable signal/noise ratio for c(s), it should be noted that a different definition of signal/noise ratio as 20 log(S/N) was applied in Kroe and Laue, 2009, and in Kingsbury et al., 2008.) Recently, K_d values of 11 nM for the mixed homo-/heterodimerization of GluR6 and KA2 have been measured by SV using this approach (Kumar et al., 2011). However, significantly lower K_d values in the picomolar range would certainly exceed the capabilities of this approach.

The modern implementation of the fluorescence detection method FDS-SV (MacGregor et al., 2004; Kroe and Laue, 2009) thus appears particularly attractive for the study of high-affinity systems because of the potential for substantially enhanced sensitivity compared with absorbance or interference optics, dependent on the fluorophore and its local environment. Unfortunately, this increase in sensitivity comes at a price of several potential problems and pitfalls, some of which are already well known in the literature for other fluorescence techniques, for example, related to oligomeric-state–dependent quantum yields (Eftink, 1997; Lakowicz, 1999) and some that appear specifically in conjunction with AUC. Because of the limited number of studies in the last decade applying FDS-SV to the quantitative determination of binding constants (Kingsbury et al., 2008; Bailey et al., 2009; Mok et al., 2011; Ryan et al., 2011), and because of the lack of comprehensive methodological comparisons, the advantages and disadvantages of FDS-SV in general have not yet become entirely clear. A key requirement of this detection system for most proteins is that an extrinsic fluorophore be attached. That the fluorescent label is inert is not obvious, as exemplified most dramatically by the recent discovery in SE experiments of unexpected binding between FITC and a DNA repair enzyme (Melikishvili et al., 2011). For GluA2, we performed control experiments with conventional absorbance SV and fluorescence anisotropy, as well as mixing experiments of labeled with unlabeled molecules, to establish that both the FAM and DyLight labels do not significantly affect the gross structure and dimer affinity. We believe that such control experiments should be performed routinely for FDS-SV.

Qualitatively, the velocity of the sedimentation boundary of FAM-labeled GluA2S in FDS-SV showed the expected concentration dependence, confirming the dissociation of dimers into monomers in the low nanomolar range. Furthermore, the quantitative analysis of the s_w isotherm of the FDS data yielded a K_d estimate of 5.3 nM, consistent within error with the K_d from absorbance SV on FAM-labeled and unlabeled GluA2S and fluorescence anisotropy. However, in addition to the apparent hydrodynamic separation of species suggesting unexpectedly slow reaction kinetics, the dimer s-value estimated by either the s_w isotherm or the dimer c(s) peak was too low. The c(s) data from FDS-SV by Rossmann et al. (2011) appear consistent with both of these observations, after accounting for the different water viscosity at the experimental temperature of 10°C chosen in that study. Surprisingly, our control experiments with a nonself-associating EGFP molecule conducted with either absorbance or fluorescence detection in the same FDS-capable instrument used for analysis of FAM-labeled GluA2 also revealed ∼10% lower s-values. The reason for the difference of the hydrodynamic results is unknown at present. Even though unrecognized temperature calibration errors, of magnitude slightly larger than those reported previously (MacGregor et al., 2004), could potentially be a contributing factor, the s_w isotherm of FAM-GluA2S would still not be in satisfactory quantitative agreement with the absorbance data. In a separate theoretical study, we show that nonlinearity in the detection can systematically impact the s_w isotherms analysis and result in low s-values with only a slightly overestimated K_d, but for the present data this can account only for 2–3% of errors in s-values (unpublished data). A large fraction of the application of FDS-SV has been qualitative, and the study of AMPA receptor ATD oligomerization by FDS-SV reported by Rossmann et al. (2011) was the most extensive use to date of this approach for measuring binding constants at low nanomolar protein concentrations. Kingsbury and Laue (2011) have stated previously that “In the absence of other estimates for comparison, association strengths determined by NUTS must be interpreted with caution”, a finding that the present study reinforces (“NUTS” is being used as an acronym for “normal use tracer sedimentation” by FDS-AU).

Conclusions

In this study, we have performed multiple replicate SV and SE experiments on the same protein, which provides information on the precision of the estimated K_d values for GluA2 ATD monomer–dimer assembly (Table 1) independent of confidence intervals estimated in independent experiments. Because of the time needed to complete sedimentation experiments this is rarely undertaken, except for model systems. The present work demonstrates that the high accuracy of s-values in conventional far-UV SV can partially compensate for the lower signal/noise ratios, trading larger statistical errors of the determined K_d values for the chance to circumvent potential complexities arising from the use of fluorescently labeled proteins and fluorescence detection. A comparison with the results of previous AUC studies on GluA2 ATD oligomerization leads to an analysis of the design principles for AUC experiments, which should facilitate more accurate work in the future. For example, recent work indicates that NMDA receptors also present challenging targets for the quantitative measurement of ATD oligomerization (Karakas et al., 2011); indeed, the high affinity for heterodimer formation by the GluN1 and GluN2 ATDs prevented accurate measurement of the dimer K_d in the presence of ifenprodil. As for the present study on AMPA receptors, we suggest that a combination of orthogonal methods is the best approach to gain confidence in the binding affinity for NMDA receptor ATDs and for other proteins with tight homo- and heterodimerization. Fluorescence anisotropy, in particular, is a widely used and well-established technique, requiring only a benchtop fluorometer, which can lend itself very well for characterizing high-affinity binding and was used previously to supplement FDS-SV data in the study of GFP–antibody interactions (Kroe and Laue, 2009). Whereas SV relies on translational diffusion, anisotropy depends on changes in the rotational diffusion of the fluorescently tagged molecule caused by dimer assembly (Jameson and Seifried, 1999; Lakowicz, 1999). Despite some differences, such as potential complications in the anisotropy assay caused by local flexibility, and much lower size-dependent resolution than SV, both methods should have similar opportunities with regard to sensitivity and the measurement of binding constants. In principle, other fluorescence techniques could be applied as well, including fluorescence correlation spectroscopy (Jensen et al., 2011), if conducted as a function of protein concentration, or fluorescence cross-correlation spectroscopy (Boukari and Sackett, 2008). A challenging problem for future work is the measurement of the rate constants for formation and dissolution of AMPA receptor ATD dimer assemblies. Because this will substantially impact the process of subunit exchange during the biosynthesis of heteromeric receptor assemblies (Greger and Esteban, 2007), further investigations are warranted into the mechanism underlying slow exchange suggested by FDS-SV.