Phenotype Prediction by Integrative Network Analysis of SNP and Gene Expression Microarrays

Abstract

A long-term goal of biomedical research is to decipher how genetic processes influence disease formation. Ubiquitous and advancing microarray technology can measure millions of DNA structural variants (single-nucleotide polymorphisms, or SNPs) and thousands of gene transcripts (RNA expression microarrays) in cells. Both of these information modalities can be brought to bear on disease etiology. This paper develops a Bayesian network-based approach to integrate SNP and expression microarray data. The network models SNP-gene interactions using a phenotype-centric network. Inferring the network consists of two steps: variable selection and network learning. The learned network illustrates how functionally dependent SNPs and genes influence each other, and also serves as a predictor of the phenotype. The application of the proposed method to a pediatric acute lymphoblastic leukemia dataset demonstrates the feasibility of our approach and its impact on biological investigation and clinical practice.

I. Introduction

Modern microarray technologies have revolutionized biomedical investigations through the parallel assessment of structural or functional information of hundreds of thousands of biomolecules on a single chip. Various types of microarrays have been invented to study genomics from different aspects. Single-nucleotide polymorphism (SNP) microarrays interrogate DNA at a specific nucleotide, allowing genome-wide association studies to identify SNPs associated with disease formation in a hypothesis-free manner [1]. Gene expression chips record RNA transcripts from DNA, allowing differential expression analysis [2–3] to identify genes active or repressed in disease processes. While the techniques of analyzing each individual type of data have been well established, much work remains to usefully aggregate SNP and gene expression data to explain how genetic mutations and aberrant transcription result in disease formation.

Integrative analysis of SNP and gene expression microarrays has gained substantial attention in the past few years. Several novel statistical methods were developed to identify genetic variants associated with gene expression traits (called expression quantitative trait loci, or eQTLs) [4–6]. However, the identification of eQTLs does not reveal their functional association with disease formation, which has lead to difficulty translating eQTL findings to clinical practice. Furthermore, eQTL analysis only accounts for SNP-gene interactions, and is unable to explain SNP-SNP and gene-gene interactions.

This paper proposes the following strategies to perform integrative analysis of SNP and gene expression data:

1. To capture three types of molecular interactions (i.e., SNP-SNP, SNP-gene, and gene-gene interactions), we conduct a network analysis of the data.

2. To relate the eQTL findings to disease states, we treat the disease phenotype as a variable and measure association between it and the SNPs and genes.

3. To infer the influence of SNPs and genes on disease formation, we include the phenotype variable in the network analysis and model phenotype-SNP and phenotype-gene interactions along with the three types of molecular interactions.

4. To facilitate the clinical usefulness of our network analysis, the resultant network is also an accurate predictor/classifier of phenotypes.

Microarray data are usually noisy and experimental samples always present biological variability, thus we model the data by random variables. A SNP takes one of three possible genotypic states (i.e., homozygous major, homozygous minor, or heterozygous), which are described by a multinomial variable. A gene expression level is a continuous measurement of the abundance of the gene transcript in the cell, which is described by a log-normal variable. From the many approaches to biological network analysis [7], we choose a Bayesian network (BN) framework, due to the ease of handling random variables and making predictions based on the inferred networks. However, most existing BN methods for microarray analysis consider a single type of variable only [8–10]. When encountering mixed types of data, these BN methods quantize expression levels to simplify the analysis, but unfortunately lose much information during quantization. To avoid problems arising from quantization, this paper describes the application of a new BN method to process both discrete and continuous variables, resulting in an able tool for SNP-expression analysis. We then demonstrate how our approach can study transcription mechanisms in pediatric acute lymphoblastic leukemia (ALL).

II. Method Development

A. Phenotype-Centric Network

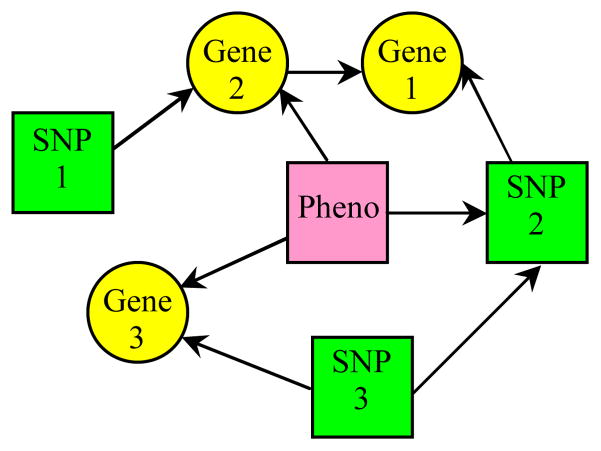
A Bayesian network is a directed graph, where a node represents a variable and a directed arc linking a pair of nodes records the probability of the child (target) node conditional on the parent (source) node. Figure 1 illustrates an example BN.

Fig. 1.

An example BN. Circle and square nodes denote continuous and discrete variables, respectively.

Our ultimate goal is to find genes and SNPs associated with disease phenotypes. Therefore, we model the SNP-gene network as a phenotype-centric network. With reference to Figure 1, the phenotype is a root node of the network, and all nodes are directly or indirectly linked to the phenotype. This structure allows us to predict the value of the phenotype given values for the other SNPs and genes in the network. Furthermore, we can find eQTLs from this network: SNP1 influences expression levels of Gene2, SNP2 of Gene1, and SNP3 of Gene3. Besides eQTL findings, we can explain other SNP-gene relations: The expression of Gene1 is simultaneously modulated by SNP2 and Gene2, implying Gene1 and Gene2 have some functional relationship; the genotype of SNP2 is dependent on SNP3, usually an indicator of linkage disequilibrium in the genome.

Given an integrative genomic database, our task is to infer the directed links between variables. However, modern microarray datasets contain more than 500,000 SNPs and more than 50,000 genes, so it is computationally infeasible to learn the network directly from the whole data set. To overcome this difficulty, we design a learning algorithm in the following steps.

B. Step 1: Variable Selection

Let X_s and Y_g be multinomial and Gaussian random variables representing the SNP genotypes and gene expression levels, respectively. The phenotypes are described by a multinomial random variable C indicating disease states. We use uppercase to denote random variables and lowercase to denote their values.

The genes and SNPs statistically dependent on the phenotype are filtered in the first step. The filtering can be accomplished by computing Bayes factors (BF), as follows:

$$BF(X_s)=\frac{p(X_s\mid C)}{p(X_s)}\stackrel{?}{>}{\tau }_X,$$

and similarly for Y_g with threshold τ_Y. For each gene or SNP, the Bayes factor evaluates the ratio of its likelihood of being dependent on the phenotype to its likelihood of being independent of the phenotype. Equivalently, we also can consider log Bayes factors LBF for variable selection. For thresholds τ greater than or equal to 1, the BF indicates that the gene or SNP is statistically associated with the phenotype, however in practice other values of τ can be chosen, generally for computational reasons.

C. Step 2: Network Learning

Without loss of generality, we assume that S SNPs and G genes were selected by the preceding step, and the microarray data under consideration turns out to be D= {c, x₁, …,x_S, y₁,…, y_G}. The task now is to search for a network topology that connects each variable to the parent variable(s) with strongest modulation of its values, where the best set of parents is determined by likelihood computation. More formally, our objective is to choose from a set of candidate network models Ω = {M₁, …, M_K} the optimal network M̂ that best explains the data D. Equivalently, we look for the highest posterior probability p(M_K | D). Applying Bayes’ theorem to p(M_K | D) results in p(M_k|D) ∝ p(M_k) p(D|M_k), where p(M_K) is the prior probability of model M_K and p(D | M_K) is the marginal likelihood. The computation of p(D | M_K) is accomplished by averaging out parameters, denoted by a vector θ_K, from the likelihood function p(D | M_K,θ_K). The vector θ_K contains the values of the random vector Θ_K parameterizing the distribution of C, X₁,…, X_S,Y₁,…,Y_G conditional on M_K. We can exploit the local Markov properties encoded by the network M_K to rewrite the joint probability p(D | M_K,θ_K) as

$$p(D\mid M_k,{\theta }_k)=\prod _{s=1}^{S}p(x_s\mid pa(x_s),{\theta }_{ks})\prod _{g=1}^{G}p(y_g\mid pa(y_g),{\theta }_{kg}),$$

where pa(z) denotes the values of the parents Pa(Z ) of random variables Z, and θ_kz is the subset of parameters used to describe the dependence of variable Z on its parents.

As a general rule, information flows from DNA to RNA; accordingly we allow genes in the network to have as parents SNPs, the phenotype, other genes, or any combination. In contrast, we allow SNPs to only have other SNPs or the phenotype, or their combination, as parents. We further assume the J samples in the database are independent. The likelihood function becomes

$$p(D\mid M_k,{\theta }_k)=\left[\prod _{j=1}^J\prod _{s=1}^{S}p(x_{sj}\mid pa(x_{sj}),{\theta }_{ks})\right]\times \left[\prod _{j=1}^J\prod _{g=1}^{G}p(y_{gj}\mid pa(y_{gj}),{\theta }_{kg})\right]$$

where the subscript j indicates the j -th sample. The first term can be estimated by sample frequencies, and the second term can be derived using a linear Gaussian model [10]. The marginal likelihood function is the solution of the integral

$$p(D\mid M_k)=\int p(D\mid M_k,{\theta }_k)p({\theta }_k)d{\theta }_k.$$

Due to limited space, in this paper we do not present the detailed computations, which can be derived from [10]. Finally, the best Bayesian network model is determined by $\widehat{M}=arg\underset{k}{max}p(M_k)p(D\mid M_k)$.

D. Phenotype Prediction

Once the network is learned, we can use it to predict the phenotypes. The SNPs and genes used to predict the phenotype variable C are those in the Markov blanket of C. The Markov blanket of a node consists of the node’s parents, its children, and its children’s other parents (Figure 1). To predict the phenotype of a patient, we substitute the values of each variable in the Markov blanket from the patient’s data into the network model, and then use a local propagation algorithm [11] to compute the most probable phenotype value.

III. Experiments

Acute lymphoblastic leukemia (ALL) is primarily considered a childhood cancer, although it can occur in individuals of any age. Due to different responses to chemotherapy, ALL can be classified into different subtypes, two of which are B-cell precursor ALL (BCP-ALL) and common ALL (C-ALL). Although physicians can follow the guidelines provided by the World Health Organization to distinguish BCP-ALL from C-ALL by lymphocyte analysis, the genetic and transcriptional difference between these two subtypes is still obscure [12]. Using our proposed network analysis, we demonstrate what SNPs and genes lead to the distinct ALL subclasses.

We used pediatric ALL data from the Gene Expression Omnibus GSE10792 [12]. In this data, 28 patients were genotyped at 100,000 SNPs using Affymetrix Human Mapping 100K Set microarrays, and the expression patterns of 50,000 genes were profiled using Affymetrix HG-U133 Plus 2.0 platforms. Eight of the patients were BCP-ALL while the rest were C-ALL. In the variable selection step of our analysis, by selecting genes with log Bayes factors > 0 and SNPs with log Bayes factors > 5, we obtained 14 genes and 109 SNPs for network analysis. In the network learning step, we restrict the maximum number of parents of each node to be 3, and implement the learning by the step-wise K2 algorithm [10].

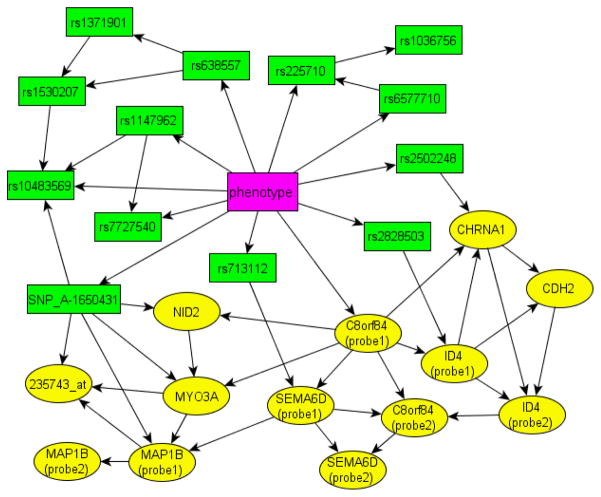
Figure 2 shows the network inferred from our analysis. The ALL subclasses dependency network consists of 13 transcript probes and 13 SNP probes. Enrichment study shows that the 13 transcript probes are mapped to 9 genes, listed in Table 1. We validated the network by predicting the phenotypes. The ALL network achieves 100% predictive accuracy for classifying BCP-ALL and C-ALL. To test the robustness of this network model, we performed leave-one-out cross validation, which reaches 96.5% accuracy.

Fig. 2.

The SNP-gene network of ALL subclasses

Table 1.

The signature SNPs and genes for ALL subclasses prediction. Nameless SNPs and genes are shown their probe IDs in brackets.

SNP/Gene Symbol	Chromosome Location	Function
MAP1B	5q13	Cell signaling, Cell morphology, Cellular assembly
C8orf84	8q21.11	Cancer, Genetic disorder
SEMA6D	15q21.1	Cellular movement,
ID4	6p22-p21	Cellular growth
CDH2	18q11.2	Cell morphology, Cellular assembly, Cellular movement
CHRNA1	2q24-q32	Cell morphology
MYO3A	10p11.1	Genetic disorder
NID2	14q21-q22	Cell signaling
[235743_at]	n/a
rs2828503	21q21.2
rs713112	21q22.2
rs10483569	14q21.3
rs1036756	1p35.1
rs225710	6q24.1
rs2502248	6q12
rs1530207	3q26.1
rs1371901	3q26.1
rs638557	3q26.1
rs7727540	5p15.31
rs1147962	10q11.21
rs6577710	8q24.23
[SNP_A1650431]	n/a

We now illustrate how to use the result to perform eQTL identification. In Figure 2, for instance, the SNP rs2502248 is a parent of genes CHRNA1, implying that rs2502248 is an eQTL of CHRNA1. Moreover, the network can identify genes jointly regulated by eQTLs and other genes. For example, the expression of CHRNA1 is co-regulated by SNP rs2502248 and genes C8orf84 and ID4; this finding is uniquely discovered by our network analysis that takes into account SNP-gene interactions in the interpretation of microarray data. Comparing Table 1 and Figure 2, we observe that genes and their eQTLs are located in different chromosomes. This observation suggests that there is a transcription mechanism across chromosomes, and that a more detailed study to investigate the biology is warranted.

We further performed a functional study on the network using Ingenuity Pathway Analysis (www.ingenuity.com). The known biological functions of the SNPs and genes are listed in Table 1. The genes SEMA6D, CHRNA1, CDH2, ID4, MYO3A and C8orf84 are involved in cellular movement and genetic disorders, and their relationship to leukemia have previously been reported [13–14]. Although MAP1B, NID2 have not yet been associated with leukemia, they participate in the cell signaling pathways; this finding implies that alterations in cell signaling is a mechanism characterizing the difference between BCP-ALL and CALL.

In the ALL network, the Markov blanket of the phenotype consists of 11 SNPs and 1 transcript, which are the only variables needed to predict ALL subclasses. To demonstrate that the transcript-SNP combination assembles the optimal signature, we examine the prediction accuracy of individual signatures. The results are summarized in Table 2. The table shows that none of the signature SNPs or transcript reaches 100% accuracy alone. Except rs2828503 which achieves 95% accuracy, all other signatures achieve no more than 88.1% accuracy. Rs2828503 is a SNP located on chromosome 21, far from known genes, but it is identified as an eQTL for the ID4 gene in our network, indicating a possible regulatory role in cell growth. Although the combination of SNPs seen in Figure 2 achieves better classification of BCP-ALL and C-ALL, the single SNP rs2828503 has remarkable performance.

Table 2.

The prediction accuracy of individual signature SNPs/genes.

SNP/Gene Symbol	Prediction Accuracy
C8orf84	58.1%
rs2828503	95.6%
rs713112	76.2%
rs10483569	87.5%
[SNP_A1650431]	78.7%
rs225710	85.6%
rs2502248	80.0%
rs1530207	88.1%
rs638557	88.1%
rs7727540	81.9%
rs1147962	85.6%
rs6577710	85.6%

IV. Conclusions

A long-term goal of biomedical research is to decipher how genetic processes influence disease formation. With the advent of microarray technologies, we can genotype hundreds of thousands of SNPs and assess expression of tens of thousands of genes. The large amount of data causes difficulty in integrating two types of genomic data. This paper develops a Bayesian network-based method to integrate SNP and gene expression microarrays. The proposed network model describes the data as a phenotype-centric network. The algorithm consists of variable selection and network learning. We used a pediatric ALL data to demonstrate the feasibility of the approach. The ALL study illustrates how to conduct eQTL investigation and predict phenotypes using the inferred network. Extending our approach to other datasets can lead to advances in biomedical study and clinical practice.