Detection of Neuron Membranes in Electron Microscopy Images using Multi-scale Context and Radon-like Features

Abstract

Automated neural circuit reconstruction through electron microscopy (EM) images is a challenging problem. In this paper, we present a novel method that exploits multi-scale contextual information together with Radon-like features (RLF) to learn a series of discrimi-native models. The main idea is to build a framework which is capable of extracting information about cell membranes from a large contextual area of an EM image in a computationally efficient way. Toward this goal, we extract RLF that can be computed efficiently from the input image and generate a scale-space representation of the context images that are obtained at the output of each discriminative model in the series. Compared to a single-scale model, the use of a multi-scale representation of the context image gives the subsequent classifiers access to a larger contextual area in an effective way. Our strategy is general and independent of the classifier and has the potential to be used in any context based framework. We demonstrate that our method outperforms the state-of-the-art algorithms in detection of neuron membranes in EM images.

1 Introduction

Electron microscopy (EM) is an imaging technique that can generate nanoscale images that contain enough details for reconstruction of the connectome, i.e., the wiring diagram of neural processes in the mammalian nervous system [4, 11]. Because of the large number and size of images, their manual analysis is infeasible and in some cases may take more than a decade [3]. Hence, automated image analysis is required. However, fully automatic reconstruction of the connectome is challenging because of the complex intracellular structures, noisy texture, and the large variation in the physical topologies of cells [5]. Therefore, a successful automated method must overcome these issues in order to reconstruct the neural circuit with high accuracy.

Many supervised and unsupervised techniques have been proposed to solve the connectome reconstruction problem. Macke et al. [9] proposed a contour propagation model that minimizes an energy function to find the cell membranes. However, this active contour model can get stuck in local minima due to the complex intracellular structures and may find false boundaries [10]. Vu and Manjunath [12] proposed a graph-cut framework that minimizes an energy defined over the image intensity and the intensity gradient field. But, the graph-cut method might be misled by the complex intracellular structure of the EM images and requires the user to correct segmentation errors. Kumar et al. [7] introduced a set of so-called Radon-like features (RLF), which take into account both texture and geometric information and overcome the problem of complex intracellular structures but only achieve modest accuracy levels due to the lack of a supervised classification scheme.

Supervised methods that use contextual information [2] have been proven successful to solve the reconstruction problem. Jain et al. [5] proposed a convolutional neural network for restoring membranes in EM images. Convolutional networks take advantage of context information from increasingly large regions as one progresses through the layers. To capture context from a large region, however, convolutional networks need many hidden layers, adding significant complexity to training. Jurrus et al. [6] proposed a framework to detect neuron membranes that integrates information from the original image together with contextual information by learning a series of artificial neural networks (ANN). This makes the network much easier to train because the classifiers in the series are trained one at a time and in sequential order.

Even though these approaches improve the accuracy of the segmentation over unsupervised methods, they don’t utilize the context information in an effective way. In [6], Jurrus et al. utilize context locations that are selected by a stencil and use them as input to a neural network. The performance of the classifier can be improved by using context from a large neighborhood; however, it is not practical to sample every pixel in a very large context area because of computational complexity and the overfitting problem. To address this problem, we develop a multi-scale strategy to take advantage of context from a larger area while keeping the computational complexity tractable and avoiding overfitting. We apply a series of linear averaging filters to the context image consecutively to generate a scale-space representation [1] of the context. Thus the classifier can have as input a small neighborhood, i.e., a 5 × 5 patch, at the original scale as well as the coarser scales. While scale-space methods are well known, to our knowledge their use for modelling context in classification problems is novel. Combining scale-space representation and contextual information leads to a novel segmentation framework that provides more information from the context for the classifiers in the series. This extra information from the contexthelps the later classifiers to correct the mistakes of the early stages and thus improves the overall performance.

In addition to the above problem with existing context based methods that we address in this paper, we also note that none of the existing methods make use of textural and geometric features specifically designed for connectome images. We also address this by incorporating the recently proposed Radon-like features [7] in our method. RLF, which can be efficiently computed, provide our classifier discriminative information in addition to that present in the grayscale micrograph. It must be emphasized that [7] proposes that RLF be used only at a single scale with certain set of parameters. We sidestep this parameter tuning problem by computing RLF at various scales and using them all in our classifier.

2 Sequential Training with Context

Given a set of training images and corresponding groundtruth labels for each pixel, we learn a set of classifiers in sequential order as in [6]. The first classifier is trained only on the input image features. The output of this classifier, the probability image map, is used together with the input image features to train the next stage classifier. The algorithm iterates until the improvement in the performance of the current stage is small compared to the previous stage.

Let X = (x(i, j)) be the input image that comes with a ground truth Y = (y(i, j)) where y(i, j) ∈ {−1, 1} is the class label for pixel (i, j). The training set is T = {(X_k, Y_k); k = 1, …, M} where M denotes the number of training images. A typical approximation of the MAP estimator for Y given X is obtained by using the Markov assumption that decreases the computational complexity:

$${\widehat{y}}_{\mathit{MAP}}(i,j)=\mathrm{argmax}p\left(y\right(i,j)\mid X_{N(i,j)}),$$ (1)

where N (i, j) denotes all the pixels in the neighborhood of pixel (i, j). Instead of using the entire input image the classifier has access to a limited number of neighborhood pixels at each input pixel (i, j).

In the series-ANN [6], a classifier is trained based on the neighborhood features at each pixel. We call the output image of this classifier C = (c(i, j)). The next classifier is trained not only on the neighborhood features of X but also on the neighborhood features of C. The MAP estimation for this classifier is:

$${\widehat{y}}_{\mathit{MAP}}(i,j)=\mathrm{argmax}p\left(y\right(i,j)\mid X_{N(i,j)},C_{N^{\prime }(i,j)}),$$ (2)

where N’ (i, j) is the set of all neighborhood pixels of pixel (i, j) in the context image. Note that N and N’ can be different neighborhoods. The same procedure is repeated through the different stages of the series classifier until convergence. It is worth mentioning that Eq. 2 is closely related to the CRF model [8]; however in our approach multiple models in series are learned, which is an important difference from standard CRF approaches.

According to Eq. 2, context provides prior information to solve the MAP problem. Even though the Markov assumption is reasonable and makes the problem tractable, it still results in a significant loss of information from global context. However, it is not practical to sample every pixel in a very large neighborhood area of the context due to the computational complexity problem and overfitting. Previous approaches [6] have used a sparse sampling approach to cover large context areas as shown in Fig. 2(a). However, single pixel contextual information at the finest scale conveys only partial information about its neighborhood in a sparse sampling strategy while each pixel at the coarser scales conveys more information about its surrounding area due to the use of averaging filters. Furthermore, single pixel context is noise prone whereas context at coarser scales is more robust due to the averaging. In other words, while it is reasonable to sample context at the finest level at a distance of a few pixels, sampling context at the finest scale tens to hundreds of pixels away is error prone and presents a non-optimal summary of its local area. We argue that more information can be obtained by creating a scale-space representation of the context and allowing the classifier access to samples of small patches at each scale. Conceptually, sampling from scale-space representation increases the effective size of the neighborhood while keeping the number of samples small.

Fig. 2.

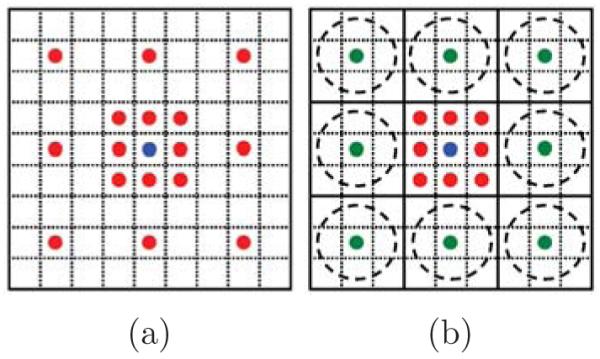
Sampling strategy of context: Sampling at (a) single-scale (b) multi-scale. Green circles illustrate the summary of pixels in dashed circles.

3 Multi-scale Contextual Model

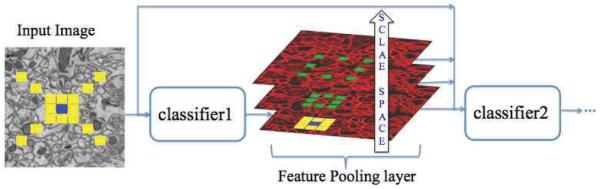
Multi-scale contextual model is shown in Fig. 1. Each stage is composed of two layers: a classifier layer and a feature pooling layer. Classifier: Different types of classifiers can be used in series architecture such as AdaBoost and neural networks. The first classifier operates only on the input image while the later stages are trained on both the input image and the context from the previous stage. Feature Pooling: In the conventional series structure, the feature pooling layer simply takes sparsely sampled context as in Fig. 2(a) and combines them with input image features. In the proposed method, the feature pooling layer treats each feature map as an image and creates a scale-space representation by applying a series of Gaussian filters. This results in a feature map with lower resolution that is robust against the small variations in the location of features and noise. Fig. 2 shows our sampling strategy versus single space sampling strategy. In Fig. 2(b) the classifier can have as an input the center 3 × 3 patch at the original scale and a summary of 8 surrounding 3 × 3 patches at a coarser scale. The green circles in Fig. 2(b) are more informative and less noisy compared to their equivalent red circles in Fig. 2(a). The summaries become more informative as the number of scales increases. For example, in the first scale the summary is computed over 9 pixels (3 × 3 neighborhood) while it is computed over 25 pixels (5 × 5 neighborhood) in the second scale. In practice, we use Gaussian averaging filters to create the summary (green circles in Fig. 2(b)). Other methods like maxpooling can be used instead of Gaussian averaging. The number of scales and the Gaussian filter size are set according to the application characteristics.

Fig. 1.

Illustration of the multi-scale contextual model. Each feature map is sampled at different scales (green rectangles). The blue rectangles represent the center pixel and the yellow rectangles show the selected context locations at original scale.

Taking multiple scales into account, Eq. 2 can be rewritten as:

$${\widehat{y}}_{\mathit{MAP}}(i,j)=\mathrm{argmax}p\left(y\right(i,j)\mid X_{N(i,j)},C_{N_0^{\prime }(i,j)}(0),\dots ,C_{N_l^{\prime }(i,j)}(l\left)\right),$$ (3)

where C(0), … , C(l) denote the scale-space representation of the context and $N_0^{\prime }(i,j),\dots ,N_l^{\prime }(i,j)$ are corresponding sampling structures. Unlike Eq. 2 that uses the context in a single scale, Eq. 3 takes advantage of multi-scale contextual information. Although in Eq. 3 we still use the Markov assumption, the size of the neighborhood is larger, and thus we lose less information compared to Eq. 2.

4 Radon-like Features

As mentioned earlier, the overall performance of our method can be improved by extracting RLF from the input image in addition to pixel intensities. It has been shown empirically that trying to segment the structures in connectome images using only geometric or textural features is not very effective [7]. RLF were proposed as a remedy to this problem as they are designed to leverage both the texture and the geometric information present in the connectome images to segment structures of interest. As a first step, RLF use the edge map of a connectome image as a means to divide it into regions that are defined by the geometry of the constituent structures. Next, for each pixel, line segments with their end points on the closest edges are computed in all directions. Finally, for each pixel, a scalar value is computed along each direction using the information in the original image along these line segments using a so-called extraction function. Extraction functions tuned to extract cell boundaries, mitochondria, vesicles, and cell background have been defined in [7].

In this paper, we are interested in obtaining the cell boundaries from the connectome images. Moreover, we intend to define a supervised scheme to automatically segment the cell boundaries while [7] presented an unsupervised, and consequently less accurate, framework. Both of these objectives allow us to use the RLF in a more targeted manner towards cell boundary segmentation. Foremost, we use not just the cell boundary extraction function but also the mitochondria extraction function since we train our classifier to not select mitochondria boundaries as cell boundaries. Secondly, we use what we call multi-scale RLF by computing RLF at multiple scales and for different edge threshold settings. This richer set of features allow for correct detection of cell boundaries in the regions that cannot be detected by the original RLF as proposed in [7] and avoids the need for extensive parameter tuning.

Combining these set of features and the multi-scale contextual model, the update equation for the framework can be written as:

$$\begin{array}{cc}\hfill {\widehat{y}}_{\mathit{MAP}}^{k+1}(i,j)=\mathrm{argmax}& p\left(y\right(i,j)\mid X_{N(i,j)},f(X_{N(i,j)}),\hfill \\ \hfill & C_{N_0^{\prime }(i,j)}^k\left(0\right),\dots ,C_{N_l^{\prime }(i,j)}^k\left(l\right)),\hfill \end{array}$$ (4)

where C^k(0), … , C^k(l) are the scale-space representation of the output of classifier stage k, k = 1, … , K – 1, ${\widehat{y}}_{\mathit{MAP}}^{k+1}(i,j)$ is the output of the stage k + 1 and f(.) is the RLF function. In turn, the k + 1’st classifier output as defined in Eq. 4 creates the context for the k + 2’nd classifier. The model repeats Eq. 4 until the performance improvement between two consecutive stages becomes small.

5 Experimental Results

We test the performance of our proposed method on a set of 70 EM images of a mouse cerebellum with corresponding groundtruth maps. The groundtruth images were annotated by an expert who marked neuron membranes with a one-pixel wide contour. 14 of these images were used for training and the remaining images were used for testing. In this experiment, we employed MLP-ANNs as the classifier in a series structure, as in [6]. Each MLP-ANN in the series had one hidden layer with 10 nodes.

To optimize the network performance, 5.5 million pixels were randomly selected from the training images such that there are twice the number of negative examples, than positive as in [6]. Input image feature vectors were computed on a 11 × 11 stencil centered on each pixel. The same stencil was used to sample the RLF for cell boundaries (at two scales) and mitochondria. The context features were computed using 5 × 5 patches at four scales (one at original resolution and three at coarser scales). The classifier then gets as input the 5 × 5 patch at the original resolution ($C_{N_0^{\prime }(i,j)}\left(0\right)$) and 5 × 5 patches at three coarser scales ($C_{N_l^{\prime }(i,j)}\left(0\right)$). The ROC curves for pixel-wise membrane detection are shown in Fig. 3(a). It can be noted that our method outperforms the state-of-the-art methods proposed in [6] and [7]. The average $F-\text{value}=\frac{2\times \text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}$ at zero threshold for different stages and different methods is shown in Fig. 3(b). The performance of the multi-scale contextual model without RLF is 2.65% better than using a single-scale context [6]. This improvement increases to 3.76% when we use RLF in addition to multi-scale contextual information. Fig. 4 shows some examples of our test images and corresponding membrane detection results for different methods. As shown in our results, the approach presented here performs better in membrane detection compared to [6], and it is more successful in removing undesired parts (green rectangles) from inside cells.

Fig. 3.

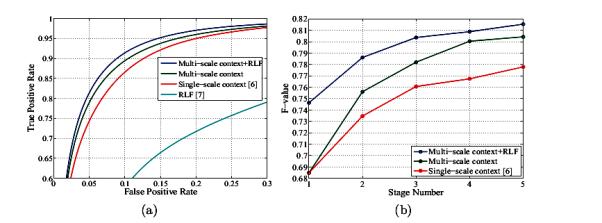
(a) The ROC curves for test images and for different methods. (b) The F-value at different stages for different methods. The F-value for RLF method [7] is 59.40%.

Fig. 4.

Test results for the membrane detection for two different input images: (a) Input image, the remaining columns show the output results (probability maps) for (b) RLF [7] (c) single-scale context [6] (d) multi-scale context (e) multi-scale context+RLF, and (f) shows the manually marked groundtruth.

6 Conclusion

This paper introduced an image segmentation algorithm using a multi-scale contextual model. The main idea of our method is to take advantage of contextimages at different scales instead of a single scale, thereby providing the classifier with a richer set of information. We also modified the RLF to extract more information from different structures of the input image. The proposed method is very general and does not depend on any particular classifier or any specific scale-space method.

We applied our method to membrane detection in EM images. Results indicate that the proposed method outperforms state-of-the-art algorithms while maintaining nearly identical computational complexity. We used linear averaging filters to generate the scale-space representation of the context. In future work, we will conduct a full study of the effect of scale-space depth and the advantage of using other linear or nonlinear scale-space methods.