Generation of a novel phase-space-based cylindrical dose kernel for IMRT optimization

Abstract

Purpose: Improving dose calculation accuracy is crucial in intensity-modulated radiation therapy (IMRT). We have developed a method for generating a phase-space-based dose kernel for IMRT planning of lung cancer patients.

Methods: Particle transport in the linear accelerator treatment head of a 21EX, 6 MV photon beam (Varian Medical Systems, Palo Alto, CA) was simulated using the EGSnrc/BEAMnrc code system. The phase space information was recorded under the secondary jaws. Each particle in the phase space file was associated with a beamlet whose index was calculated and saved in the particle’s LATCH variable. The DOSXYZnrc code was modified to accumulate the energy deposited by each particle based on its beamlet index. Furthermore, the central axis of each beamlet was calculated from the orientation of all the particles in this beamlet. A cylinder was then defined around the central axis so that only the energy deposited within the cylinder was counted. A look-up table was established for each cylinder during the tallying process. The efficiency and accuracy of the cylindrical beamlet energy deposition approach was evaluated using a treatment plan developed on a simulated lung phantom.

Results: Profile and percentage depth doses computed in a water phantom for an open, square field size were within 1.5% of measurements. Dose optimized with the cylindrical dose kernel was found to be within 0.6% of that computed with the nontruncated 3D kernel. The cylindrical truncation reduced optimization time by approximately 80%.

Conclusions: A method for generating a phase-space-based dose kernel, using a truncated cylinder for scoring dose, in beamlet-based optimization of lung treatment planning was developed and found to be in good agreement with the standard, nontruncated scoring approach. Compared to previous techniques, our method significantly reduces computational time and memory requirements, which may be useful for Monte-Carlo-based 4D IMRT or IMAT treatment planning.

INTRODUCTION

Intensity-modulated radiation treatment (IMRT) planning systems optimize 3D dose distributions based on dose constraints prescribed for the target and normal tissues. Pencil beam (PB) algorithms are generally used to calculate dose distributions in optimization loops because of their high computation speed. However, in accounting for electron transport in low density regions, like the lung, these algorithms are inaccurate in comparison to Monte Carlo (MC) computed doses.¹ MC simulations are often performed to verify dose distributions once the plan is optimized;^{2, 3, 4, 5} however, if the simulation shows large discrepancies in the planned dose, the physicist is left with few options to make the necessary corrections. The development of more accurate dose algorithms in the optimization process is likely to improve IMRT planning accuracy.

MC simulations have been used in IMRT optimization. For example, Jeraj et al.⁶ performed MC simulations of all bixels for inverse treatment planning. Shepard et al.⁷ used EGS4/DOSXYZ to calculate pencil beams to optimize aperture shapes. Bergman et al.⁸ calculated a beamlet-to-dose kernel matrix to optimize the positions of multileaf collimators (MLCs). Bogner et al.⁹ derived inverse kernels and optimized fluence maps utilizing a gradient method. To generate phase-space-based MC beamlets, Bush et al.¹⁰ developed a novel method of tagging each particle in the phase space file with its corresponding beamlet index. They sorted the tagged particles and saved them in separate files to compute dose from the corresponding beamlets using the standard DOSXYZnrc program. Bogner et al.¹¹ calculated inverse kernels by deriving all elements of the beamlet matrix within a single MC simulation using XVMC instead of performing individual calculations for each beamlet. As pointed out by Bush et al.,¹⁰ this approach requires a large RAM to store dose and uncertainty scoring arrays. To improve their computation efficiency, Bogner et al. truncated the kernels based on given thresholds and then used the truncated kernels to optimize fluences and aperture shapes.^{9, 11}

As the complexity of treatment techniques such as 4D IMRT or IMAT increases, so does the number of beamlets; thus, the time and memory requirements may become prohibitive. It is important that beamlets be generated more efficiently with less computer memory required in order to shorten computation time and improve computation efficiency. Here we present a new method of generating phase-space-based cylindrical beamlets for IMRT treatment planning and demonstrate the feasibility of using these beamlets to improve computation efficiency. The method was verified using an optimized treatment plan developed on a simulated lung phantom.

MATERIALS AND METHODS

A planning framework was developed using C++/QT in Linux to incorporate radiation beams and dose constraints. Beam configuration, intermediate variables, and final results are saved in text files for plan verification, and the formats of the I/O files used in this program are compatible with EGSnrc and the Pinnacle treatment planning system.

Source modeling and beamlet generation

Using the EGSnrc/BEAMnrc code system,¹² we modeled the treatment head components of a Varian 21EX linear accelerator (including the secondary jaws) for a 6 MV photon beam. The electron source distribution was modeled assuming a Gaussian function with 1.4 mm FWHM in both X- and Y-directions. A phase space file containing approximately 165 million particles was generated with BEAMnrc on a plane 45 cm from the linac source. A virtual plane was positioned 50 cm from the source, and partitioned into a N × N beamlet grid with N = 10 and 20, respectively. If a particle’s path intersected this grid, the index of the intersected beamlet was then calculated from the particle’s positional parameters specified in the phase space file. This index was saved in the particle’s 32-bit LATCH variable where 23 of these bits were overwritten by the beamlet’s index. The tagged particles from all the beamlets of a particular beam were saved in a single phase space file.

Suppose for each particle p in the phase space file, the line of p(x,y) in the direction (u,v,w) intersects with the target plane (that is, at Z = 0 in the machine coordinate system) at the point S₁. S₁ is named the virtual origin of the particle p. Suppose the Gaussian model of the electron source is centered at the point S. The coordinates s and t of the origin S₁(s, t) can be calculated by

$$s=x-\frac{{\mathit{ul}}_0}{w},t=y-\frac{{\mathit{vl}}_0}{w},$$ (1)

where u, v, and w are the cosine vector magnitudes of this particle in the x, y, and z directions, and l₀ (=45) is the distance from the phase plane to the beam source [see Fig. 1a]. The coordinates of the virtual origin were averaged over all the particles of a beamlet and saved into a file that was used to generate a cylindrical kernel for this beamlet.

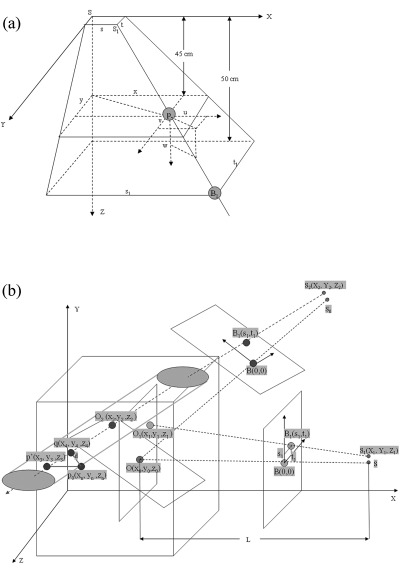
Figure 1.

(a) Orientation of a particle represented in the machine’s coordinate system; (b) truncation of a beamlet illustrated in the patient’s coordinate system.

The DOSXYZnrc code was modified to tally energy deposited according to each particle’s LATCH variable. Note, this is a unique approach and is different from that reported by Bush et al.,¹⁰ where all particles were sorted based on their beamlet indices and saved in individual phase space files for input to DOSXYZnrc for computation of 3D dose distributions. The modified DOSXYZnrc code enables computation of all the beamlet doses of each field within one single MC simulation, circumventing the need for hundreds of output files and the associated postprocessing requirements for standard IMRT, as well as 4D and adaptive planning. One issue with this approach is that each beamlet is associated with a 3D dose distribution; computing all the beamlets of each field within a single MC simulation over the entire 3D spatial dose range therefore requires considerable amounts of computer memory and computational time. To improve the computation efficiency and reduce the memory requirement burden, we needed to examine possible means of generating truncated kernels.

Generation and representation of cylindrical dose kernels

Beamlet dose falls off quickly in the off-axis regions, with the majority of the dose being distributed in a region corresponding to a cylinder. We proposed that the 3D beamlet dose distribution can be truncated such that energy deposited only within a cylinder is scored, without a significant loss of accuracy. Figure 1b illustrates the orientation of the beamlet in the patient coordinate system.

Assume that the isocenter of a treatment beam lies at O(x₀, y₀, z₀) in the patient coordinate system, and the distance of the source to the isocenter is denoted by L in the x-axis (as shown in Fig. 1). Suppose there is a beamlet that passes a point O₁(x₁, y₁, z₁) in the YZ-plane that is centered at the isocenter, O(x₀, y₀, z₀). The origin of the beamlet is assumed at S₁(X₁, Y₁, Z₁), where the coordinates of X₁, Y₁, and Z₁ can be determined by

$$X_1=x_0+L{Y}_1=y_0+s{Z}_1=z_0+t,$$ (2)

where (s, t) is the beamlet’s origin computed previously, and L is the source-to-isocenter distance, which was set to 100 in this study. The coordinates of O₁ can be calculated as follows:

$$x_1=x_0{y}_1=y_0+s+(s_1-s)\frac{\Vert \mathit{OS}\Vert }{\Vert \mathit{BS}\Vert }{z}_1=z_0+t+(t_1-t)\frac{\Vert \mathit{OS}\Vert }{\Vert \mathit{BS}\Vert },$$ (3)

where s₁ and t₁ are the coordinates of bixel B₁ in the B-plane centered at the B, and B is the intersection of the beam axis OS with the beamlet plane, which is 50 cm from the isocenter. After rotating the gantry ϕ degree, the beamlet’s axis O₁S₁ is rotated to O₂S₂ with the origin S₂(X₂, Y₂, Z₂), satisfying

$$X_2=x_0+L\cos (\varphi )+s\sin (\varphi )Y_2=y_0+L\sin (\varphi )-s\cos (\varphi )Z_2=z_0+t,$$ (4)

and with the point O₂(x₂,y₂,z₂), satisfying

$$x_2=x_0+(y_1-y_0)\sin (\varphi )y_2=y_0-(y_1-y_0)\cos (\varphi )z_2=z_1.$$ (5)

The equation of the beamlet axis O₂S₂ can be represented as

$$\frac{x-x_2}{X_2-x_2}=\frac{y-y_2}{Y_2-y_2}=\frac{z-z_2}{Z_2-z_2}.$$ (6)

Suppose a particle incident is located within a voxel centered at p₀(x_n, y_n, z_n). It is possible that two incident particles, with different absolute positions, could intersect a single voxel and, thus during rotation, could be rotated into different voxels in the cylinder. In order to avoid these rotation-induced dose scoring errors, all the incident particles intersecting within the bounds of a voxel are automatically counted at the center p₀ of that voxel. The distance of the center p₀ to the axis O₂S₂ can be calculated by

$$d=\frac{|O_2{S}_2\otimes p_0{O}_2|}{\left|O_2{S}_2\right|}.$$ (7)

To reduce memory requirements, the cylinder around the axis O₂S₂ is represented as a three dimensional vector. If the angle between the lines OS and O₂S₂ is greater than π/4, the XZ plane of y = y_n and the axis O₂S₂ have an intersection point p′(x₃, y₃, z₃), satisfying

$$x_3=x_2+(X_2-x_2)\frac{y_n-y_2}{Y_2-y_2}{y}_3=y_n{z}_3=z_2+(Z_2-z_2)\frac{y_n-y_2}{Y_2-y_2}.$$ (8)

Consequently, an array of dimension $(2\left[\sqrt{2}r\right],N_y,2\left[\sqrt{2}r\right])$ can be defined in DOSXYZnrc such that the energy deposited at the voxel p₀ is recorded in the entry $g_0:=([x_n-x_3+\sqrt{2}r],\left[y_n\right],[z_n-z_3+\sqrt{2}r])$, where the bracketed values represent integers, r is the radius of the cylinder, and N_y is the y-dimension of the 3D dose grid. A look-up table was created to establish the correlation between the entry g₀ and the voxel p₀.

If the angle between the lines OS and O₂S₂ is less than or equal to π/4, we have

$$x_3=x_n{y}_3=y_2+(Y_2-y_2)\frac{x_n-x_2}{X_2-x_2}{z}_3=z_2+(Z_2-z_2)\frac{x_n-x_2}{X_2-x_2}.$$ (9)

Similarly, an array of dimension $(N_x,2\left[\sqrt{2}r\right],2\left[\sqrt{2}r\right])$ was defined in DOSXYZnrc to record the dose deposited by this beamlet. If the distance from the voxel’s center p to the beamlet axis O₂S₂ is greater than r, the incident released energy is not counted, and thus the DOSXYZnrc code only saves the energy deposited within the cylinder of radius r. When a particle traverses a voxel within the cylinder, the index of this voxel is added into the corresponding look-up table based on the particle’s beamlet number.

RESULTS AND DISCUSSION

The CT images used in this study were converted into an EGS-phantom file using the CTCREATE program.¹³ The dose at each voxel was scored for each beamlet and normalized to the average dose of the corresponding beam. Region-of- interest (ROI) contours were imported from Pinnacle to an in-house developed optimization framework with the maximum and minimum dose constraints prescribed for each ROI. The phase space file generated under the jaws for a 10 × 10 cm² field size was used as an input into the code for testing purposes. The tests were performed on both a water phantom and a simulated, lung-type, anthropomorphic phantom.

Validation of source modeling and beamlet generation

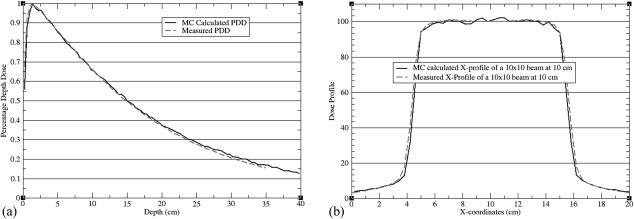
A simulated 40 × 40 × 40 cm³ water phantom was used to validate source modeling. Dose profile and percentage depth doses computed with BEAMnrc/DOSXYZnrc for a 10 × 10 cm², 6 MV beam were compared with clinical data measured with an ion chamber in a water tank. Average differences between measurements and calculations were less than 1.5% (see Fig. 2). The same phase space file was also used to compute dose kernels on the simulated anthropomorphic phantom.

Figure 2.

Calculated and measured (a) PDD and (b) profile of a 10 × 10 cm² field on a 40 × 40 × 40 cm³ water phantom.

Each beam was divided into 400 beamlets. Figure 3a provides an illustration of the simulated lung phantom in axial view. Figure 3b shows an example of a beamlet from a beam at angle 30°. Figure 3c shows the 20 central beamlets of the beam at angle 0°. These results provide examples of qualitative validation of our modified code system. The sum of the deposited energy scored from all beamlets was found to be equivalent to the energy deposited by the original DOSXYZnrc code, confirming that no particles were lost during the beamlet splitting operation.

Figure 3.

(a) Simulated lung phantom; (b) beamlet from a beam at angle 30°; (c) beamlets from the central Y leaf for the zero-degree beam.

Validation of the cylindrical kernel computation

After validating the beam rotation and particle tagging operations, kernel truncation was verified using the simulated lung phantom. Figure 4a shows the 3D dose distribution of a single beamlet without cylindrical truncation, and Fig. 4b represents the corresponding truncated dose distribution. Figure 4c shows their difference map. Since the path length of electrons scattered from a beamlet increases in low-density materials, the resultant dose distribution in Fig. 4a widens in the lung region but narrows in the central tumor area. As shown in Fig. 4c, the truncation-induced dose errors are higher in the anterior and posterior regions of the right lung [see Fig. 3a]. Note that the maximum dose difference in Fig. 4c, which occurs in the dose falloff region, is approximately 2.5% of the maximum dose in Figs. 4a, 4b.

Figure 4.

(a) A central beamlet of the zero-degree beam; (b) truncated central beamlet of the zero-degree beam; (c) difference map between (a) and (b); (d)–(f) correspond to a 150° beam.

The diameter of the cylinder implemented in this study is an even number $2\left[\sqrt{2}r\right]$. The central axis of this beamlet is one voxel wide. This results in the truncated cylinder having an asymmetric number of source elements on either side of the central axis. Consequently, the errors in Fig. 4c are not symmetric with respect to the beamlet’s central axis.

Figures 4d, 4e, 4f correspond to a peripheral beamlet from a beam at 150°. These figures provide a qualitative validation of the origin and orientation of the beamlet, as well as the truncation-induced dose errors.

While the dose accumulated from all beamlets was shown to be equal to the original dose calculated by the DOSXYZnrc code, the dose accumulated from all the truncated beamlets will differ from the original dose because of the truncation errors. Table TABLE I. shows the truncation-induced absolute errors averaged over all voxels in the phantom, relative to the maximum dose in the cylinder. For the case of r = 5, 53.1%, 17.2%, 10.7%, and 7.6% of voxels have errors less than 0.1%, 0.2%, 0.3%, 0.4%, respectively, and 11.4% of voxels have errors greater than 0.4%. It should be mentioned that these errors could also depend on other factors such as the material of the truncated region and the energy of the beam, in addition to the volume of the truncated cylinder.

TABLE I.

The dose errors averaged in the phantom for different truncation cylinders.

Cylinder radius (in voxels)	r = 3	r = 5	r = 7
Average error (%)	0.42	0.22	0.14

Impact of cylindrical truncation on plan optimization

A treatment plan created with five 6 MV beams incident on the simulated lung phantom was used to provide an initial evaluation of the impact of the cylindrical truncation on plan optimization. Using the modified DOSXYZnrc code, cylindrical beamlets were calculated on a dose grid with resolution 0.5 × 0.5 × 0.5 cm³. The standard deviation of the MC simulation was 2%. Bixel resolution projected on a plane 100 cm from the source was 0.5 × 0.5 cm². The full-range MC-based dose kernel K_F and the truncated dose kernel K_T were substituted into the plan optimization framework to generate the full-range dose kernel-based fluence vector F_F, and the truncated dose kernel-based fluence vector F_T, respectively.

Dose distributions optimized with the full-range dose kernel K_F and with the truncated, cylindrical dose kernel K_T can be calculated by $K_F·F_F$ and $K_T·F_T$ with their results shown in Figs. 5a, 5b, respectively. On average, their differences are less than 0.6% of the prescribed target dose. To estimate the influence of the cylindrical kernel truncation on the optimized dose distribution, we multiplied the truncated kernel K_T by the vector F_F to generate a 3D dose [Fig. 5c]. Comparison of the 3D dose to the dose optimized from the full-range MC kernel revealed differences of 0.3%, on average. Next, we multiplied the full-range MC-based kernel K_F by the vector F_T to derive a 3D dose distribution [Fig. 5d]. This distribution was within 0.9% of the dose derived from the full-range MC kernel-based optimization.

Figure 5.

Transverse slices of (a) dose distributions optimized with the full-range MC dose kernel ($K_F·F_F$) and (b) dose distributions optimized with the truncated, cylindrical kernel ($K_T·F_T$), (c) the dose calculated by $K_T·F_F$, and (d) the dose generated by $K_F·F_T$.

In fluence-based IMRT plan optimization, significant computation time is spent in multiplication of the dose kernel matrix with the fluence vector for evaluating the plan’s objective function. For a cylindrical kernel matrix, the ratio between the voxel number of the entire dose region and that of the truncated cylinder is on the order of O(k)² with k = N/r, so the computation efficiency can be improved substantially as k increases. The optimization time with the truncated kernel was found to be reduced by 78% relative to the time required for the full-range MC kernel-based optimization. The optimization program was tested on a 2.6GH workstation with 24 GB RAM.

DISCUSSION AND CONCLUSIONS

An IMRT plan typically requires more than five beams, with each beam consisting of at least 60 × 60 beamlets. A dose grid may contain more than 100 × 100 × 100 dose elements. Furthermore, the number of beamlets may increase 10 times for four-dimensional (4D) IMRT and 1800 times for 4D IMAT (intensity-modulated arc therapy) where 180 control points are assumed for optimization.^{14, 15} Due to the extremely large number of dose elements, calculation and management of all beamlets in MC-based 4D IMRT or IMAT plans demand not only a vast amount of computer memory but also require significant computation time. Kernel truncation may be a valuable tool to reduce memory requirements and improve efficiency if MC beamlets are to be used in these complex planning techniques. In this study, we have developed a new method of generating phase-space-based cylindrical dose kernels. This method may help reduce the memory requirement and improve computational efficiency in treatment plan optimization, while preserving MC dosimetry accuracy especially in heterogeneous regions.

For a beamlet-based plan optimization, Bogner et al.⁹ showed that the low dose elements of the inverse kernel matrix can be compressed with a threshold value. However, before compression, these elements still need to be calculated using MC simulation, which demands significant computing resources. Furthermore, dose computed in low dose regions often has large uncertainties. This may induce uncertainties in the truncated kernel and consequently compromise the final optimization results. The cylindrical method presented in this study scores radiation dose in a truncated, cylindrical region. Regions with low dose have been excluded prior to the MC scoring operation. Although primary beam radiation is divergent at the distal edge of the beamlet, and appears more representative of a conically shaped dose array, secondary electrons can travel relatively long distances in low-density regions like the lung. We circumvent this issue in our implementation by making the cylinder’s radius large enough so that primary radiation dose deposited in low-density regions is not cutoff, and thereby scored within the truncated cylinder.

The cylindrical truncation operation reduces kernel size to less than 6% (in the case of N = 40, r = 5) while increasing optimization speed four-fold compared to full-range 3D dose kernels. The dose distribution optimized with the cylindrical kernel is within 1% of that optimized with the full-range 3D dose kernel, which demonstrates, for the examples shown, that kernel truncation induces minimal errors. Efficiency and unreasonable memory requirements may be a significant problem in 4D IMRT or IMAT where the size of the kernel matrix may increase as much as a thousand-fold. With the cylindrical dose kernel, it may be possible to develop more efficient 4D treatment planning techniques without a significant loss of accuracy.

It should be mentioned that the quality of beamlet-based plan optimization may be compromised by the presence of a MLC or other beam modulating modifiers. To address this issue, fluences optimized from finite-size pencil beams can be combined with Monte Carlo simulations including the MLC to minimize MLC-induced dose delivery errors.^{16, 17} Analogously, fluences optimized from the phase-space-based beamlets can also be integrated with MLC-included MC simulations to derive more accurate dose distributions. In this study, we multiplied dose kernels by the fluence vectors that were generated with and without kernel truncations, respectively, demonstrating that the truncation operation has limited impact on the resultant dose distributions. Compared with pencil-beam kernels, the phase-space-based cylindrical dose kernel can achieve high dosimetric accuracy in heterogeneous regions and may have the potential to be integrated with modifier-included MC simulations for 4D IMRT or IMAT treatment planning.