Increasing the oscillation frequency of strong magnetic fields above 101 kHz significantly raises peripheral nerve excitation thresholds

Abstract

Purpose: A time-varying magnetic field can cause unpleasant peripheral nerve stimulation (PNS) when the maximum excursion of the magnetic field (ΔB) is above a frequency-dependent threshold level [P. Mansfield and P. R. Harvey, Magn. Reson. Med. 29, 746–758 (1993)]. Clinical and research magnetic resonance imaging (MRI) gradient systems have been designed to avoid such bioeffects by adhering to regulations and guidelines established on the basis of clinical trials. Those trials, generally employing sinusoidal waveforms, tested human responses to magnetic fields at frequencies between 0.5 and 10 kHz [W. Irnich and F. Schmitt, Magn. Reson. Med. 33, 619–623 (1995), T. F. Budinger et al., J. Comput. Assist. Tomogr. 15, 909–914 (1991), and D. J. Schaefer et al., J. Magn. Reson. Imaging 12, 20–29 (2000)]. PNS thresholds for frequencies higher than 10 kHz had been extrapolated, using physiological models [J. P. Reilly et al., IEEE Trans. Biomed. Eng. BME-32(12), 1001–1011 (1985)]. The present study provides experimental data on human PNS thresholds to oscillating magnetic field stimulation from 2 to 183 kHz. Sinusoidal waveforms were employed for several reasons: (1) to facilitate comparison with earlier reports that used sine waves, (2) because prior designers of fast gradient hardware for generalized waveforms (e.g., including trapezoidal pulses) have employed quarter-sine-wave resonant circuits to reduce the rise- and fall-times of pulse waveforms, and (3) because sinusoids are often used in fast pulse sequences (e.g., spiral scans) [S. Nowak, U.S. patent 5,245,287 (14 September 1993) and K. F. King and D. J. Schaefer, J. Magn. Reson. Imaging 12, 164–170 (2000)].

Methods: An IRB-approved prospective clinical trial was performed, involving 26 adults, in which one wrist was exposed to decaying sinusoidal magnetic field pulses at frequencies from 2 to 183 kHz and amplitudes up to 0.4 T. Sham exposures (i.e., with no magnetic fields) were applied to all subjects.

Results: For 0.4 T pulses at 2, 25, 59, 101, and 183 kHz, stimulation was reported by 22 (84.6%), 24 (92.3%), 15 (57.7%), 2 (7.7%), and 1 (3.8%) subjects, respectively.

Conclusions: The probability of PNS due to brief biphasic time-varying sinusoidal magnetic fields with magnetic excursions up to 0.4 T is shown to decrease significantly at and above 101 kHz. This phenomenon may have particular uses in dynamic scenarios (e.g., cardiac imaging) and in studying processes with short decay times (e.g., electron paramagnetic resonance imaging, bone and solids imaging). The study suggests the possibility of new designs for human and preclinical MRI systems that may be useful in clinical practice and scientific research.

INTRODUCTION

Magnetic resonance imaging (MRI) systems employ gradient coils that expose subjects to spatially dependent and time-dependent magnetic gradient fields. Increasing the amplitude of the applied magnetic gradient field or increasing the speed of gradient switching (i.e., increasing the overall gradient slew rate) can potentially improve spatial resolution and/or reduce overall scan time. Consistent with Maxwell’s equations that relate changing magnetic fields (i.e., dB/dt) with induced electromotive forces, the switching of magnetic gradient coils can result in the local induction of electrical currents in the human body, leading to peripheral nerve stimulation (PNS), which can be unpleasant or even painful if sufficiently strong. Experiments concerning the relationship between the maximal dB/dt that can be applied without causing PNS have been shown to follow the spatially extended nonlinear node (SENN) model,¹ adapted from the original work of McNeal.² The SENN model is a lumped electrical circuit representing nodes of Ranvier (described by the nonlinear electrodynamics of the myelinated neuron), separated by neuronal sections with insulating myelin sheaths (the SENN model is available free of charge and free of copyright restrictions).³

According to prior experiments in the literature (and described by the SENN model), electrostimulation thresholds for excitable tissue (nerve and muscle) follow strength–duration (SD) curves that relate the threshold of excitation to the duration of a monophasic stimulus.⁴ For magnetic stimulation by a monophasic dB/dt pulse, the SD relation can be expressed in terms of the induced electric field within the biological medium (in situ) in which the neuron resides

$$E_t=E_0\frac{1}{1-\exp (-t_p/{\tau }_e)},$$ (1)

where E_t is the threshold magnitude of the in situ electric field (E-field) in a direction aligned with the long axis of the nerve fiber, E₀ is the minimum threshold at long pulse durations (t_p ≫ τ_e), t_p is the pulse duration, and τ_e is the SD time constant. The SD time constant (τ_e) is a function not only of the electrical parameters of the excitable membrane but also of the distribution of the excitatory E-field over the length of the excited nerve fiber (pp. 48–49 and 132–134 in Ref. 5). The SD time constant approximates the “chronaxie” parameter, which is often used in other literature referring to nonmagnetic (e.g., electrical) nerve stimulation (pp. 28–30 in Ref. 5). With magnetic stimulation, the induced E-field is proportional to dB/dt, where B is the magnetic flux density; the proportionality constant depends on the size of the induction coil, and the dimensions, shape, and internal conductivity details of the biological subject. Consequently, with magnetic stimulation, one could replace the parameters E_t and E₀ in Eq. 1 with ${\stackrel{·}{B}}_t$ and ${\stackrel{·}{B}}_0$, respectively, where $\stackrel{·}{B}$ = dB/dt, ${\stackrel{·}{B}}_t$ is the threshold value at t_p, and ${\stackrel{·}{B}}_0$ is the minimum (rheobase) value at t_p ≫ τ_e.

The SENN model predicts a nonlinear relationship between the PNS threshold and the magnitude and waveshape of dB/dt.⁶ For brief (t_p ≪ τ_e) monophasic dB/dt pulses, the SENN model predicts that nerve excitation thresholds converge to a minimal excursion (ΔB) of magnetic flux density, corresponding to an asymptotic physiological threshold for ΔB at short stimulation durations (for monophasic functions of dB/dt).⁶ This expectation of asymptotic threshold has been codified in European Union regulations,^{7, 8} based on the conservative assumption of monophasic dB/dt waveforms. For brief biphasic pulses, the SENN model predicts excitation thresholds that may be substantially higher than for monophasic pulses.⁶

A sine wave is an example of a biphasic function that has been used for the switched magnetic gradient field in MRI systems. SENN model simulations predict several features that are relevant to such switched magnetic gradient fields: (a) a stimulus consisting of a single cycle of a sine wave is associated with a neural excitation threshold substantially above that for a single half-cycle, (b) the threshold gradually drops as the number of cycles increases, reaching a minimum plateau after an exposure period of roughly a millisecond, and (c) the threshold exhibits a sawtooth pattern as the number of half-cycles of stimulation is alternated between even and odd numbers (pp. 134–136 in Ref. 4). These predictions have been verified in human⁹ and animal¹⁰ experiments.

The PNS threshold value for ΔB is important because the spatial resolution of an MRI system is governed by gradient strength. Based on perceived theoretical limits, MRI designers had avoided increasing the speed of magnetic gradient coils, since the probability for PNS (at any given magnetic field strength) was expected to increase at high frequencies.^{11, 12} However, considering the possibility of increased ΔB thresholds with brief biphasic pulses, we tested human PNS responses with biphasic stimulation at frequencies above those traditionally used in MRI devices.

METHODS

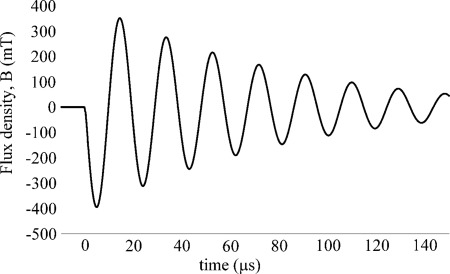
An apparatus was constructed to evaluate magnetostimulation in human volunteers for frequencies from 2 to 183 kHz. The experimental configuration was modeled after a classic dB/dt bioeffects study,¹³ employing a 3.5-cm-diameter coil placed below the subject’s wrist (Fig. 1). Capacitors were discharged into the coils to yield damped sinusoidal currents (Fig. 2), whose resulting magnetic field strengths were measured prior to the clinical trial with calibrated dB/dt probes. The stimulus consisted of a sinusoidal pulse train with exponential decay

$$B=k\exp (-t/{\tau }_s)\sin (2\mathrm{\pi }\mathit{ft}),$$ (2)

where k is a magnitude that was adjusted by the experimenter, τ_s was the stimulus decay time constant, and f was the frequency of the sinusoid. Note that the function responsible for stimulation is the time derivative of flux density (i.e., dB/dt).

Figure 1.

Apparatus for exposure to magnetic gradients. (a) Gradient coil in box. (b) Forearm resting above coil with box cover on.

Figure 2.

Typical flux density waveform for sinusoidal stimulation experiment (in this case, 59 kHz, 0.4 T magnitude). The stimulus waveform is proportional to the time derivative of the plotted function.

Circuit values were set to yield frequencies of 2, 25, 59, 101, and 183 kHz, with τ_s for each sine wave adjusted to include approximately 12–20 cycles at each frequency. Exposure frequencies were presented in descending order. For each frequency, the maximum magnetic field strength was varied as follows: 0.05, 0.1, and 0 T (“sham” pulses) and 0.2, 0.3, and 0.4 T. Each stimulus consisted of a sinusoidal pulse train, as defined by Eq. 2. The number of cycles was selected based on prior experiments showing little change in threshold when the number of cycles was increased above 12 cycles per stimulus pulse.⁹

The clinical trial, approved by an investigational review board (New England IRB, Newton, MA) prior to seeking informed consent, involved 26 adult subjects. Criteria for exclusion from the study were cardiac arrhythmia, short distance from sternum to wrist (in order to avoid cardiac-related bioeffects), visible tattoos or metallic objects on the hand selected for the study, and vital signs that would have made it difficult to assess potential cardiovascular distress (i.e., irregular or imperceptible pulse, heart rate below 50 or above 100, diastolic blood pressure below 50 mm Hg, or resting respiratory rate over 25 per minute).

Out of 26 subjects tested, 11 (42.3%) were male and 15 (57.7%) were female. The males were from 18 to 59 yr old with average age of 36 and median of 33. The females were from 19 to 60 yr old with average age of 43 and median of 47. The degree of sensation was reported by each subject immediately after exposure to each pulse, using a five-point scale as follows: 0 (“no sensation”), 1 (“barely noticed”), 2 (“easily noticed”), 3 (“unpleasant”), and 4 (“distress/very unpleasant”).

RESULTS

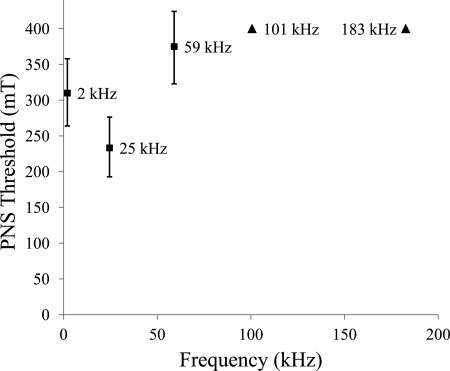
For 0.4 T pulses at 2, 25, 59, 101, and 183 kHz, stimulation (i.e., responses with 1 or more on the five-point sensation scale) was reported by 22 (84.6%), 24 (92.3%), 15 (57.7%), 2 (7.7%), and 1 (3.8%) subjects, respectively. These numbers indicate that the probability of PNS (i.e., all responses with a sensation score of 1 or higher) is markedly reduced at and above 101 kHz (i.e., p < 0.04 at 180 kHz) as compared to the probability of PNS at lower frequencies (i.e., p = 0.92 at 25 kHz). Results of the study are shown as a probability chart for sensory stimulation (i.e., sensation score of 1 or higher) in Fig. 3. The threshold for which 50% of subjects would experience PNS is shown in Fig. 4 (with lower limits indicated for frequencies of 101 kHz or higher).

Figure 3.

Probability of PNS sensation at various frequencies, at magnitude 0.4 T. Error bars correspond to exact confidence intervals with 95% power. Data points are labeled with frequency values.

Figure 4.

Magnetic field thresholds for PNS. Thresholds are shown for values of magnetic fields that would cause 50% of population to experience PNS. Error bars for frequencies below 101 kHz (squares) show 95% confidence intervals. At and above 101 kHz, triangles show the lower limit for 50% thresold, with 99% confidence. Data points are labeled with frequency values.

Each subject in the study was exposed to zero-magnitude (“sham”) pulse trains a total of five times. “No sensation” was reported in 120 (96.1%), “barely noticed” in 4 (3.1%), and easily noticed in 1 (0.8%) cases out of 125 “sham” pulse trains.

The clinical trial coordinator occasionally discerned hand twitching in four subjects, synchronized with the stimulus onset. Of four subjects who experienced twitching, each had only one case of twitching, and none of them exhibited it above 101 kHz. Two subjects twitched with no reported sensation (one subject at 25 kHz and one at 101 kHz, both at 0.4 T), two twitched with a “barely noticed” sensation (one subject at 25 kHz and 0.2 T and one subject at 59 kHz and 0.4 T). Due to the low incidence of twitching, we did not analyze this phenomenon statistically.

CONCLUSIONS

The goal of the study was to experimentally test the trending behavior of ΔB PNS threshold for brief high-frequency pulses. As shown in Fig. 3, for 0.4 T stimulations, the probability of sensation was markedly reduced at frequencies of 101 and 183 kHz when compared to the probability of sensation at 2 and 25 kHz. This reduction in sensation shows that the ΔB threshold for PNS is significantly higher at frequencies at or above 101 kHz than the threshold in the 2 to 25 kHz range. The results show that the probability for PNS will be lower at high frequencies (i.e., ≥101 kHz) than at lower frequencies for a given maximum magnetic gradient strength, when the sinusoidal pulse duration is brief. We conclude that the maximum tolerable magnetic gradient field strength may be increased by utilizing biphasic dB/dt pulses of high frequency and brief duration.

Since the study was limited to local (wrist) stimulation, additional studies may be needed to confirm that the threshold for PNS increases for high frequencies in the case of whole-body exposure. Although the specific ΔB and dB/dt PNS thresholds tested in this study may not be valid for all pulse trains, coil sizes, and geometry, we would expect that the physiological trend of increased threshold for PNS at high frequencies would hold for any given experimental setup.

The findings of this study suggest that magnetic gradient systems could deliver brief high-strength pulses at high frequency without causing PNS. As an example, it should be possible to deploy localized gradient systems that achieve magnetic field strengths ten or more times higher than conventional systems, using rise- and fall-times below 5 μs (i.e., half the period), corresponding to dB/dt values exceeding 160 000 T/s. High-strength gradient systems have been called for in local planar systems.¹⁴

Factors other than gradient speed are involved in determining overall pulse sequence duration. Some fast spin-echo type scans (e.g., fast or turbo spin-echo) are limited by RF heating.¹⁵ However, other pulse sequences (e.g., echo-planar imaging, spiral, diffusion) are gradient limited and could potentially be accelerated using faster and stronger gradients.¹⁵

More work is needed to better understand the tradeoffs involved in high-frequency high-strength gradient systems, and to examine physiological behavior more comprehensively (e.g., at more frequencies than were tested in this study, and with different waveforms).

As in prior clinical trials relating to PNS,^{9, 11, 13, 16} this study focused on sinusoidal waveforms instead of the trapezoidal waveforms more commonly used in conventional MRI. Sinusoidal waveforms are often used in functional MRI (fMRI) and where high patient throughput is desired, for example, with spiral scanning of the breast.¹⁷ The relevance of sinusoidal waveforms is further evident when we consider that some gradient amplifiers employ quarter-sinus resonance circuits in order to generate the most rapid portions of trapezoidal waveforms (i.e., where dB/dt would be highest).¹⁸

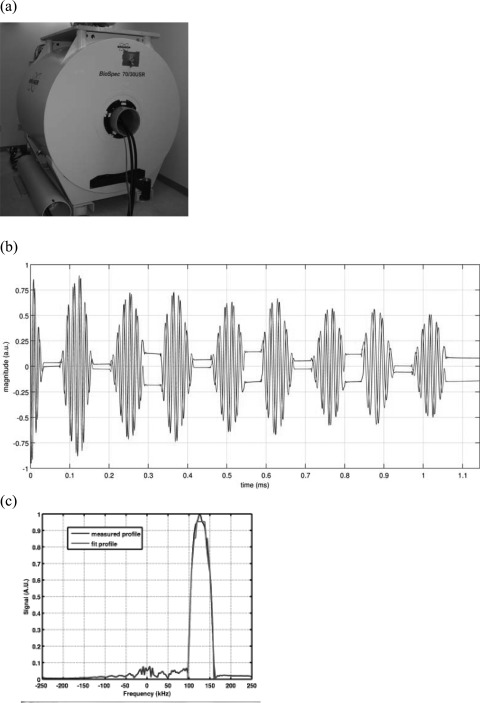
It should be noted that commercial clinical MRI gradient coils would not hold the voltages required to achieve magnetic fields with capacitor voltages at the magnitudes used in our experiments (e.g., 10 kV). The amplifier system used to power the experimental setup in this trial was used to drive a custom-built one-axis gradient coil constructed using standard winding techniques (Resonance Research, Inc.). This gradient coil was mounted in a 7 T 30-cm-bore research MRI (BioSpec 70/30 USR, Bruker BioSpin, Billerica, MA) to produce frequency-encoded echo-planar imaging (EPI) type pulse sequences with 14 μs gradient rise/fall-times and 64 μs flat top gradient pulses as shown in Fig. 5.

Figure 5.

MRI pulse sequence with 14 μs rise-time gradients. (a) Gradient coil rated to 10 kV was inserted into Bruker 7-T MRI. (b) Eight gradient echoes in 1 ms. (c) One-dimensional profile of NMR tube filled with silicone oil shown in frequency domain.

Ultrafast gradient subsystems without PNS could be valuable in preparing ultrashort pulse trains for high-resolution MRI of rapidly moving structures (e.g., the heart or fetus) or for collecting functional images of animals or humans without concomitant stimulation. Potentially, such techniques could facilitate MRI of short-lived species such as free-radicals (i.e., for electron paramagnetic resonance imaging applications) or MRI of materials with short transverse relaxation times (i.e., cortical bone). A possible benefit of high-frequency gradient coil operation might be a reduction in perceived noise, due to frequencies being above the human hearing range. An additional expected benefit of brief, high-frequency waveforms is that thresholds of excitation of both cardiac tissue and unmyelinated fibers (C-fibers) should increase by margins even greater than those for stimulation of myelinated peripheral nerve fibers (A-fibers) due to the differences in the equivalent membrane time constants among those tissue types (pp. 65–74 in Ref. 5). As a consequence, it appears possible to increase safety margins against cardiac arrhythmias or painful C-fiber responses to the gradient fields of ultrafast MRI devices.