CT based computerized identification and analysis of human airways: A review

Abstract

As one of the most prevalent chronic disorders, airway disease is a major cause of morbidity and mortality worldwide. In order to understand its underlying mechanisms and to enable assessment of therapeutic efficacy of a variety of possible interventions, noninvasive investigation of the airways in a large number of subjects is of great research interest. Due to its high resolution in temporal and spatial domains, computed tomography (CT) has been widely used in clinical practices for studying the normal and abnormal manifestations of lung diseases, albeit there is a need to clearly demonstrate the benefits in light of the cost and radiation dose associated with CT examinations performed for the purpose of airway analysis. Whereas a single CT examination consists of a large number of images, manually identifying airway morphological characteristics and computing features to enable thorough investigations of airway and other lung diseases is very time-consuming and susceptible to errors. Hence, automated and semiautomated computerized analysis of human airways is becoming an important research area in medical imaging. A number of computerized techniques have been developed to date for the analysis of lung airways. In this review, we present a summary of the primary methods developed for computerized analysis of human airways, including airway segmentation, airway labeling, and airway morphometry, as well as a number of computer-aided clinical applications, such as virtual bronchoscopy. Both successes and underlying limitations of these approaches are discussed, while highlighting areas that may require additional work.

INTRODUCTION

Airway related diseases (e.g., asthma and chronic bronchitis) are extremely common in the United States and worldwide.^{1, 2} This is not surprising when considering that lung airways are the primary conductive structure for gas exchange between the human body and the external environment. Because the airways are directly exposed to chemicals, viruses, pollutants, and allergens present in the environment, every individual, regardless of age, gender, or race, is susceptible to the development of airway diseases, albeit smoking and prolonged exposure to pollutants increases the risk of developing airway diseases. In the past two decades, the prevalence of airway diseases has been increasing. For example, the prevalence of asthma alone has doubled and it now affects approximately 25 million individuals in the United States and 300 million individuals around the world.³ Hence, there has been a great interest and effort in investigating factors that could cause airway diseases.

Anatomically, human airways appear as a treelike branching network of tubes that enable airflow into the lungs through the trachea. From the trachea to the terminal bronchioles, an airway tree consists of approximately 17 generations of branches,⁴ beyond which alveoli begin to appear and ultimately terminate at the alveolar sacs where most gas exchange occurs. Due to the specific structural characteristic of the airway tree, airway diseases are typically associated with morphological changes that may affect the ability of the lungs to exchange gas. For example, a reduction in airway lumen size may result in an overall decrease in pulmonary function.⁵ Whether specific airway diseases are caused by well recognized possible genetic factors, or not, remains unknown.^{6, 7} Yet, it is widely recognized that accurate quantitative measurements of airway morphometry may be helpful for clinically relevant assessments of different pathological conditions associated with airway diseases and for monitoring therapeutic efficacy of interventions.⁸ Whereas computed tomography (CT) technology enables the visualization of lung anatomical structures in significant detail, it has been widely used in pulmonary clinical practice for noninvasively assessing lung abnormalities, in general, and airway related abnormalities, in particular, Refs. ^{9, 10, 11}. However, in clinical practice, a single CT examination typically consists of a large number of CT images, ranging from 100 to 600 slices, depending on the reconstructed slice thickness. Hence, it is a very tedious and time consuming task to manually trace and analyze the airways depicted on CT images. Sonka et al. reported¹² that manual segmentation of the airway tree in a single CT examination (slice thickness in their study was 3.0 mm) required approximately 7 h of analysis. At the same time, large variability in performance exists among human experts,¹³ and it is almost impossible for an expert or different experts to manually delineate consistently and repeatedly the boundaries of a region-of-interest on large sets of images. This variability could lead to different diagnoses and thereby clinical decisions. In particular, Sonka et al.¹² noted that computer-based methods may actually achieve a higher degree of accuracy than a manually generated “gold standard.” Hence, it is extremely desirable to develop fully- or semiautomated computerized schemes aimed at performing these tasks.

In the past decade, computerized identification and analysis of the airways depicted on CT images has become an active research area. Technically, it covers a number of related topics, including: (1) airway segmentation; (2) airway identification, matching, and labeling; and (3) airway morphometry. Whereas airway morphometry may provide important information related to pulmonary physiology and pathophysiology, these techniques may also lead to, or aid in, other clinical investigations and applications, such as virtual bronchoscopy (VB) and investigations of the development and/or prognosis assessment of specific airway diseases. An overview of these topics and their current state of development follows.

AIRWAY TREE SEGMENTATION

Accurate, automated identification of the human airway tree as depicted in CT examinations is a building block for most computerized airway related analyses. Because there is a relatively high contrast between the airway lumen and the airway wall, a straightforward way of extracting an airway tree from CT images is to use a three-dimensional (3D) region-growing procedure specifically designed to identify lumen regions. However, in the presence of partial volume effects and/or image noise (artifacts), a purely region-growing based operation frequently leads to leakage into the lung parenchyma (i.e., a sudden explosion) under a given (fixed or constant) threshold (Fig. 1). This leakage often occurs in small airways and in cases with severe lung disease (e.g., emphysema), thereby leading to an early termination of the progressive airway tree detection process. Although schemes (e.g., front propagation¹⁴) have been developed to prevent leakage associated with region growing, there is no strategy available that can completely prevent it from occurring.

Figure 1.

An illustration of leakage that frequently occurs during region-growing operations. (b) shows the image after application of a thresholding operation. When an improper threshold is selected and applied as shown in (b), there may be leakage into the parenchyma (a sudden explosion) at the leakage site. (c) shows a segmented airway tree with leakage.

When applying a region-growing approach, a threshold and a seed location needs to be specified. Given the fact that CT examinations may be acquired under different scanning conditions and/or depict different diseases, it is difficult, if not impossible, to determine an optimal threshold for all cases. To determine an appropriate threshold, Mori et al.¹⁵ proposed an intuitive approach of gradually increasing the threshold until a sudden “explosion” appears, indicating the occurrence of a leakage. Similarly, Nakamura et al.¹⁶ proposed to adaptively change the threshold based on CT values [Hounsfield (HU)] of the seed area projected from adjacent images. When specifying a seed for region growing, the general idea is to locate the trachea regions that are typically defined as regions with low intensity and circular shapes.^{15, 17, 18} Whereas it is difficult to guarantee that the regions satisfying these criteria are always representative of the trachea, robust and efficient identification of the trachea region is not always an easy task. Hence, an interactive selection of a seed is often implemented for this purpose.^{16, 19, 20, 21}

Despite these limitations, the region-growing approach is very simple and efficient in implementation. Hence, many of the available airway segmentation methods^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 38} employ this procedure as an initial step for large airway identification and thereafter implement additional procedures to identify smaller airways while preventing potential leakage. According to their primary characteristics in terms of methodology, available airway segmentation methods can be roughly classified into five categories (Table TABLE I.): (1) morphological based methods,^{17, 22, 23, 24} (2) knowledge or rule based methods,^{12, 21, 25, 26} (3) template matching based methods,^{19, 27, 28, 29, 30} (4) machine learning classifiers based methods,^{31, 32, 33} and (5) shape analysis based methods.^{20, 34, 35, 36, 37, 38} A brief description of these methods follows.

TABLE I.

Summary and comparison of several airway segmentation methods.

Studies	Case#	Section thickness	Method	2D/3D	Auto	Performance
Aykac et al. (Ref. 17)	8	3 mm	Morphological reconstruction	2D	Fully	1) Sensitivity: 73%
						2) Total 364 branches
Bartz et al. (Ref. 19)	22	1.0 mm	3D region growing, 2D wave propagation, and 2D template matching	2D + 3D	Semi	2) 7th generation
						2) 20∼100 s
Fabijańska (Ref. 23)	10	0.625 mm	Region growing and morphological operation	3D	Fully	1) ∼9th generation
						2) ∼10 min
Fetita et al. (Ref. 24)	30	0.6 mm	Energy based reconstruction	3D	Fully	1) Sensitivity is ∼91%
Graham et al. (Ref. 20)	23	N/A	3D region growing and graph optimization	3D	Semi	1) ∼3 min
						2) >7th generations
Kiraly et al. (Ref. 22)	30	0.6 mm	3D region growing and mathematical morphology	3D	Fully	1) 2∼25 min
						2) 12 generations per case
						3) 182 branches per case
Mayer et al. (Ref. 27)	22	1.25 mm	3D region growing, 2D wave propagation, 2D template matching	2D + 3D	Fully	1) Sensitivity: 86%∼ 94%
						2) 27 s
Pu et al. (Ref. 38)	75	0.6–2.5 mm	Differential geometry method	3D	Fully	1) ∼11 generations
						2) 30 min
Sonka et al. (Ref. 13)	44	3.0 mm	3D region growing, rules, anatomical knowledge	2D + 3D	Fully	1) Sensitivity: 69%∼87%
Tschirren et al. (Ref. 28)	22	0.6 mm	Fuzzy connectivity	3D	Fully	1) 27.0 ± 4.4 segments

Morphological methods

Whereas the tubular characteristic of an airway tree makes it often appear as circular regions on CT image slices, identification of an airway tree may be transformed into a task of detecting two-dimensional (2D) circular structures and then reconstructing them as a 3D airway tree. In nature, the morphological method aims to explore the specific shape, size, and intensity of the airways, as well as their spatial relationship on neighboring slices for airway identification. This type of method generally consists of two primary steps: (1) identification of 2D candidate airway locations in a slice-by-slice manner and (2) 3D airway reconstruction using various morphological operations. The initial airway candidate identification can be either achieved by using a region-growing operation or other methods. For example, Aykac et al.¹⁷ identified the original airways by applying a threshold to the difference between the reconstructed image and the original image and locating the local extrema. The reconstruction step may work on the gray-scale CT image²² or its transformation (e.g., gradient image²³). The most basic morphological operations are dilation and erosion. However, the reconstruction performance based on basic morphological operations largely depends on the continuous detection of the detected airway candidates in space. Otherwise, there will be discontinuity when stacking the segmented 2D slices for the reconstruction of a 3D airway tree. Rather than using a traditional morphological operation, Fetita et al.²⁴ derived a mathematical morphology operator based on the concept termed “connection cost,” namely, the selective marking and depth-constrained connection cost (SMDC connection cost), for a complete airway reconstruction. The connection cost considers three types of regions related to airways, including (1) lumen, (2) airway walls, and (3) adjacent parenchyma tissue.

Knowledge or rule based methods

To take advantage of known properties specific to the airways, various anatomical knowledge or rule based approaches have been utilized for airway identification. The explored rules include (1) adjacency to vessels,^{12, 21} (2) low airway intensity,^{12, 21} (3) the degree of airway wall existence,²¹ (4) no existence of a closed loop among airway branches,²⁵ (5) no abrupt change in branching angle,²⁵ and (6) a progressive decrease in diameter.²⁶ In practice, the combination of these rules may be used to achieve a better performance. Considering that airways are adjacent to vessels, Sonka et al.¹³ defined a set of rules with regard to the spatial relationship between airways and vessels to aid in the detection of airways in a slice-by-slice manner. The assessment of this approach on five CT examinations showed a sensitivity ranging from 69% to 84% when compared with a sensitivity of 48% as achieved by the conventional region-growing approach. However, as pointed out in Ref. 21, this method results in a large number of false positive identifications, because the predefined rules do not necessarily correspond to the existence of actual adjacent airways. Park et al.²¹ improved this method using a set of fuzzy rules that increased the specificity of the method²⁵ without compromising its sensitivity. An example of the rules is, “If (BRIGHTNESS is LOW) and (ADJACENCY is HIGH) and (DEGREE_OF_WALL_EXISTENCE is HIGH), then the region is an airway with a VERY HIGH confidence.”²⁶ The fuzzy rules are organized using a table to determine the confidence-level of actually detected airways. In practice, it is very difficult to numerate all rules associated with airways, and these rules may not give acceptable confidence-levels of actually being airways. Such a limitation makes it difficult to use solely these rules for a robust identification of airways, but the rules may be used along with other approaches for removing potential false positive identifications.

Template matching methods

Template matching methods use a set of 2D/3D predefined masks (templates) to search for airway regions with similar shapes. Because of the tubular shape of airways, the commonly used masks are 2D circular templates with a range of sizes and intensity levels.^{19, 27} In order to identify airways in each image slice, shape matching is typically used. However, airways appear circular in cross sections only when the airways travel perpendicular to the scanning plane. Otherwise, there will be a variety of generally elliptical shapes, thereby making it difficult to use a limited number of templates to fully describe the airways in a cross-sectional form. At the same time, the variability in airway sizes also imposes a challenge when one defines a limited number of templates. These limitations may lead to inaccurate detection of airways. In particular, the frequent attachment of the airways with other surrounding structures (e.g., blood vessels) and the presence of lung diseases (e.g., emphysema) may result in inaccurate detection. In attempt to overcome the limitations associated with 2D circular templates, investigators^{28, 29, 30} used a 3D cylindrical shape to progressively obtain the airways starting from the trachea by adaptively predicting the orientation, size, and position of the airway tree branches. The use of a 3D cylindrical shape as a template may keep the segmentation in a small area and may also prevent leakage.

Machine learning methods

The motivation for using machine learning methods is to capture the underlying probability distribution of specific airway characteristics by automatically summarizing the possible patterns and determining if these represent true airways. To identify candidate airway regions, Lo et al.^{31, 32} developed a classifier that used several image appearance based features and a K-nearest neighbor (KNN) classification approach to differentiate airways from nonairways at varying scales. Only the features that maximize the area under the receiver operating characteristics (ROC) curve of the KNN classifier were regarded as optimal. The involved training procedure is based on a cost function that considers several measures, including airway shape, airway orientation, and an airway probability map. Recently, Lo et al.³³ improved the approach using a combination of an airway appearance model and a vessel orientation similarity measure. The appearance model uses a classifier that is trained with a set of easily acquired incomplete airway tree segmentations and is used to differentiate airways and nonairways. Whereas a training process is involved, the selected features and the diversity of the prelabeled data play a critical role in the ultimate performance of the airway tree identification.

Geometric shape analysis methods

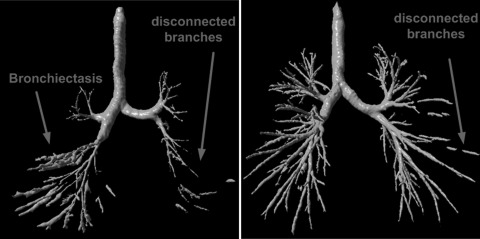
Since the human airways appear as a tubularlike shape, a number of shape based analysis methods have been developed to identify airways. The eigen-value analysis of the Hessian matrix at each voxel, or pixel, in image space has been widely used for distinguishing nodules, vessels, and airway walls from each other.^{34, 35, 36} However, due to the use of second derivatives, this Hessian matrix based filter is quite sensitive to the existence of image noise and presence of disease. In addition, when computing the derivatives, a Gaussian convolution filter is often applied to the CT images. Due to its blurring effect, the Gaussian convolution filter may reduce the contrast between the airway wall and the airway lumen, ultimately leading to the possible misses of small airways. To alleviate the blurring effect caused by Gaussian filtering, Bauer et al.³⁷ proposed to replace the multiscale computation of the gradient vectors by the gradient vector flow (GVF). As claimed by Bauer et al.,³⁷ the advantage of the GVF is the avoidance of diffusion of nearby structures into one another. In the past, Pu et al.³⁸ developed an approach for airway segmentation from a different perspective. The method first models the lung anatomical structures using the well-known marching cubes algorithm and then uses both principal curvatures and principal directions in differentiating airways from other structures (tissues) in geometric space. Unlike previous methods, this approach identified the airways in geometric space rather than in image space. Because it does not require the tracing of the airways paths, as do region-growing strategies, there are virtually no leakage or obstruction issues associated with this method. Disconnected airways due to obstructions may be detected using this approach (Fig. 2). In addition, as demonstrated in Ref. 38, this approach can also be used to identify the vascular tree. Recently, Graham et al.²⁰ developed a progressive approach to identify airway trees. The approach uses an elliptic shape analysis on 2D transverse, coronal, and sagittal views, for the identification of the regions with a high probability of being airways.

Figure 2.

Examples illustrating the performance of the method in Ref. 39 in identifying airway trees.

Summarization

Although we classified the available approaches into different categories, we note that the majority of the approaches are actually not based on a single strategy. Rather, the schemes often combine two or more of the above strategies to achieve better performance. For example, the method developed by Bartz et al.¹⁹ involved several different procedures, including 3D region growing, 2D wave propagation, and 2D template matching. A comparison of performance levels of several, albeit not all, of these methods is summarized in Table TABLE I.. We emphasize that comparisons should not be made simply based on the listed measures, as different datasets and different criteria were used for testing, in addition to different references or gold standards. However, these performance measures provide an overall perspective of the performance levels of these schemes in identifying the airways. In order to directly compare the performances of the different approaches, the second international workshop on pulmonary image analysis provided 40 publicly available cases for developing, training, and testing purposes.³⁹ A total of 15 teams participated in a competition, testing their schemes against this common dataset. Detailed information regarding the results of the competition was reported in Ref. 39. Unfortunately, the generated “reference standard” is not publicly available. Hence, there is no way for the community to preliminarily test newly developed airway segmentation schemes using this dataset as a “standardized” benchmark.

AIRWAY ANATOMICAL LABELING, SKELETONIZATION, AND MATCHING

Given a 3D segmented airway tree, it is not easy to visually locate or follow a specific region, because of the involved large number of generations and branches and the associated self-occlusion in space.^{40, 41} A possible solution is to assign names to the corresponding airway regions. The labeled information may act as a “map” or a “scout” for visual navigation purposes. This information also enables a relatively efficient and easy way to skip (“jump”) directly to the targeted diagnostic sites and thereby help with the semantic registrations of multiple airway trees, as well as provide a better understanding of the lung anatomy. In addition, for advanced computer-aided diagnostic applications, the labeled information may be used in the assessment of disease state and progression.

To assign predefined labels to the airway tree, a straightforward solution is to automatically match a segmented tree to a prelabeled airway model (i.e., a reference airway tree). Whereas the airways appear as a treelike structure, it is natural and useful to have the curved skeletons (centerlines) of the airways before performing a matching procedure. Hence, computerized airway labeling typically involves the following basic steps:⁴² (1) the airway skeletonization and (2) tree-structure matching.

Skeletonization

Skeletonization, frequently referred to as medial axis extraction or the thinning operation, is widely used in shape analysis for specific emphasis of the topological property of an object to describe low-level shape. There have been a large number of general methods developed for skeletonization of an arbitrary shape in the field of computer graphics and computer vision.^{43, 44, 45, 46} Although in theory these general skeletonization algorithms may be applied directly to obtain the centerlines of the airways, most of these require high computational cost in space and time, and are typically sensitive to noise. In practice, some characteristics specific to the airways are often explored to improve efficiency and robustness of the skeletonization approach being used.

Considering that the airways appear as a bifurcation tree, Aykac et al.¹⁷ used a linked list data structure to identify the branching points by assessing the changes of airway connectivity in neighboring image slices. If a list node had no “children,” it represents a branch endpoint; if a list node had two or more children, it represents a bifurcation point. Mori et al.⁴⁰ applied the Euclidean distance transform to obtain the centerlines of an airway tree and then represented these as a graph. The voxels (nodes) of the graph were classified into three types of voxels according to the number of voxels connected to the one in question. For example, a connecting voxel has exactly two connected voxels, a branching voxel has more than two connected voxels, and a terminating voxel has only one connected voxel. Alternatively, considering that the magnitude of the GVF vanishes at medial curves of a tubular region, Bauer et al.³⁷ proposed a medial curve extraction method in their attempt to identify the centerlines. In methodology, it is similar to identifying the ridges in a vector field. The regions with GVF values less than a predefined threshold were regarded as the ridges, as the magnitude of the GVF may decrease toward the medial lines of an object, but never to zero. Ma et al.⁴⁷ developed a parallel 3D thinning algorithm and demonstrated its efficacy in airway skeletonization. The underlying idea was to erode the volume in question from the outermost surface in a layer-by-layer manner until only a centerline remains. A total of 38 erosion templates were designed and any voxel that fit one of the templates was removed. At the same time, preservation conditions were designed to prevent the removal of the end points of the skeleton. An iterative operation of this removal procedure would result in a skeleton of a given volume. Whereas there could be disconnected regions due to high sensitivity of Ma et al.’s algorithm⁴⁷ to small perturbations, Chaturvedi et al.⁴⁸ improved the approach by using a simple dilation operation with a 5 × 5 × 5 spherical kernel at the break regions in order to assure connectivity. In addition, Swift et al.⁴⁹ proposed a semiautomated axes-generation algorithm that consisted of two stages. They first computed a discrete model to capture top-level topological structures of the airway tree and then used this model to obtain detailed smooth airway axes. Although the semiautomated method may be an optional methodology for identifying the centerlines of the airways, in practice, it is typically not feasible, and, in reality, fully automated methods are extremely desirable for this purpose.

Tree matching

To date, only a limited number of investigations have been performed in regard to airway tree matching (labeling). Given the centerlines of a reference airway tree with labeled information and a target airway tree to be labeled, an intuitive approach to tree matching is to traverse the airway tree from the “root” node to the “leaves” nodes in a depth-/width-first search manner. The dynamic programming based algorithm used in Ref. 50 followed this strategy for tree matching. However, additional false positive skeleton segments caused by noise and anatomical variability among different subjects could lead to incorrect branch matching. Another example that used a depth-/width-first search method is the Kitaoka et al.’s branch-point labeling algorithm,⁴² in which a mathematical phantom was used as a reference. Labels were assigned by matching the target tree against the phantom. However, this method was also not able to automatically manage false branches and these had to be pruned manually.

Different variations of graph theory have also been developed in order to match and label an airway tree. Tschirren et al.⁴¹ first performed a pruning step in order to improve their comparability and subsequently imposed a rigid registration in order to map the trees onto the same coordinate system. Thereafter, a hierarchical approach using an association graph was applied to the data to accomplish the matching. While this approach performs well for some trees, there are two major drawbacks: (1) the method requires robust detection of airway branch points of the trees, and (2) it relies on the invariance of the topological distance. The former may be possible in the case of major branching points, but difficult for small ones, and the latter is extremely susceptible to erroneous skeletonization due to possible false positive/negative identification of small airways. Experiments showed an accuracy of 92.9% in branch point matching when applied to 17 pairs of CT examinations. Each pair was acquired on the same subject at different expiration stages. Similarly, Kitaoka et al.⁴² proposed to match two trees by searching for subtrees with maximum similarity on the basis of a tree association graph (TAG). This algorithm was originally developed by Pelillo et al.⁵¹ as a tree-structure matching algorithm that had been applied successfully in the matching of shock trees and shape-axis trees. Details of the definition of similarity between subtrees and the searching algorithm can be found in Refs. ^{41, 51}. When applied to nine CT examinations, 95% of the detected airways could be accurately labeled. Bartoli et al.⁵² proposed an extension of the association graph approach to achieve both many-to-one and many-to-many matching of attributable trees.

To leverage the knowledge that airway trees always start from the trachea and usually appears in a bifurcation form, Mori et al.⁴⁰ labeled anatomical names to the airway tree using a knowledge based approach that has a set of predefined rules for assigning names. The knowledge based approach contained information of the tag name of a branch, the anatomical name, the parent branch name, the position, and the direction. Similarly, Kawai et al.⁵³ described an automated anatomical labeling algorithm of the bronchial branches. However, information regarding the procedure was not described in detail in Ref. 53. These proposed algorithms were applied specifically to incomplete trees with about 30 branches, and the built-in knowledge base did not include anatomical variations.

AIRWAY MORPHOMETRY ANALYSIS

As a conductive structure, morphological changes of the airways can affect airflow and thus change the gas exchange ability of the lungs. Therefore, the airway morphometry is particularly important. Changes in airway morphometry may also serve as an index for disease progression over time, as well as for assessment of response to specific treatments.⁵⁴ As Berger et al.⁵⁵ found, mean airway internal area (IA) was significantly different in smokers with chronic obstructive pulmonary disease (COPD) than in those without COPD. As explained in Ref. 56, COPD is defined as lung disease that has the co-occurrence of chronic bronchitis and emphysema, and its characteristic is the association of narrowed airways. In principle, given an airway tree with an individual branch labeled, it would be relatively easy to measure some global parameters, such as airway generation and/or branch number, airway length/volume, cross-sectional areas or circularity of the airway lumen, and airway bifurcation angles. Wood et al.⁵⁷ developed an approach that measured the branch length, angle, and diameters of an airway tree on the basis of airway segmentation and centerline extraction. However, in order to measure some parameters, such as the remodeling of the airway wall and/or the bronchoarterial ratio,^{58, 59, 60} additional efforts are needed to detect the outer airway wall, because available airway segmentation algorithms described in Sec. 2 are designed primarily for airway lumen identification.

Investigations showed that bronchial wall thickening is a well described sign of COPD and remodeling of the airway wall may be used to classify the severity of disease.^{61, 62, 63} Originally, airway wall measurements were performed manually by properly adjusting image intensity values using window levels.^{64, 65, 66} Repeatedly using manual-tracing techniques is very challenging and time-consuming to perform accurately, due to the large number of slices involved in a single examination. Therefore, there have been a number of computerized algorithms developed to aid in the identification and measurement of airway walls depicted on CT images, including the following.

Full-width at half maximum (FWHM) or half-max method

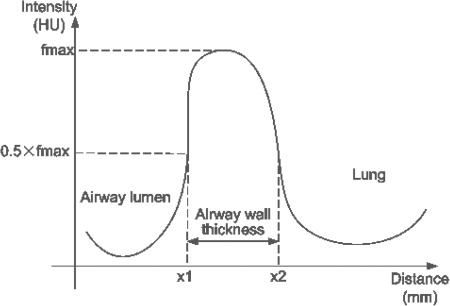
By shooting a number of rays from the center of the airway lumen outward to the parenchyma, the FWHM method estimates the inner and outer wall locations by studying intensity profiles along these rays.⁶⁷ Specifically, FWHM assumes that the outer and inner airway wall is located halfway between the local minimum value within the lumen and the maximum value within the wall (i.e., the FWHM location) as shown in Fig. 3. As mentioned in these studies,^{68, 69} this method depends solely on the gray-scale profile along a ray, which may be affected by different factors, such as a partial volume effect or the blurring introduced by the reconstruction method, as well as the orientation of the airways, thus leading to a potential overestimation of the airway wall measures. For small airways, the half-max method may result in an obvious estimation bias. Specifically, King et al.⁷⁰ found that the accuracy of this method depends on an object’s shape and the scanner’s point-spread function (PSF).

Figure 3.

An illustration of the FWHM method as used in airway wall identification. The curve denotes the intensity profile from a point located in the airway lumen outward.

2D model-based method

Reinhardt et al.⁶⁹ developed a 2D model-based method to estimate the airway inner and outer walls by matching a predicted ray profile with an actually observed profile in the data set. Typically, a calibration step was needed to estimate the parameters of the 2D PSF $S(x,y)$ of the scanner, and Gaussian blurring was the de-facto model for the point-spread function. This calibration was implemented by modeling the response $R(x,y)$ of an ideal scanner as a 2D convolution between $S(x,y)$ and the density function $D(x,y)$ of an ideal airway model [Eq. 1]. A maximum-likelihood method (i.e., a nonlinear optimization technique) was used to minimize the difference between the model and the observed data. The developed model was intended to simulate the scanning process of an ideal airway, and it assumed that the airway is circular in a plane and its axis is perpendicular to the scan plane. If the airway is scanned off-axis, the model could lead to errors in the measurement. Also, the PSF of a scanner may not be a Gaussian function in practice and may vary among different manufacturers

$$R(x,y)=C+A{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }D(x,y)S(x-t,y-t)\mathit{dxdy},\text{where}A\text{and}C\text{are constants}.$$ (1)

3D model-based method

To overcome the limitations of 2D model-based methods,⁶⁹ Saba et al.⁷¹ used an elliptical rather than a circular model and a full 3D PSF rather than a 2D PSF for this purpose. A least squares approach was used to fit ellipses to the inner and outer airway walls, and the tilt angle was then estimated using the major and minor axes. The resulting airway model was then convolved with the 3D scanner PSF to generate a predicted image. After a nonlinear optimization procedure, the parameters of the resulting airway model were used to estimate the inner and outer airway walls. This improved strategy allows for measuring airways that are nonperpendicular to the scanned plane. Similar to the 2D version,⁶⁹ the computational complexity of this method was relatively high.

Integral based method

When measuring relatively thin structures depicted on CT images, Weinheimer et al. assumed that the integral of a CT system’s PSF is equal to 1 in all directions, eliminating the need to approximate the PSF using a Gaussian function. For the airway walls, the authors modeled the intensity profile along a path using a linear system as shown in Eq. 2, where a is the path length within the lumen, b is the path length within the airway wall, c is the path length outside the airway, γ denotes the airway wall intensity, and δ denotes the nonairway wall intensity. For computing the profile integral along a path, the authors used the 10% value of the rising edge and the 10% value of the trailing edge as the start and end points. Solving this linear system leads to a unique solution for airway wall thickness estimation. To compensate for potential errors resulting from the finite integration, a correction factor λ was introduced. However, this approach is scanning parameters dependent (e.g., reconstruction kernel); hence, it requires a proper manual adjustment (a correction factor) and a proper estimation of the density of the material being measured. The performance of this integral (or summation) based method was initially evaluated using a phantom with difference sizes of tubes. The method was also tested by Achenbach et al. when studying correlation between airway wall thickness in COPD patients and pulmonary function tests (PFTs) (Ref. ⁶²)

$$\{\begin{array}{c}a·0+b·\gamma +c·\delta =\lambda {\int }_{10\%\mathit{rising}\mathit{edge}}^{10\%\mathit{trailing}\mathit{edge}}f(t)\mathit{dt}\\ a+b+c=|10\%\mathit{rising}\mathit{edge},10\%\mathit{trailing}\mathit{edge}|\\ a-c=0\end{array}.$$ (2)

Phase congruency method

Unlike methods that depend on a specific model of the airway (e.g., circular or elliptical) or a specific function of the scanner in question (e.g., PSF), Estépar et al.⁷² used phase congruency to detect the inner and outer airway walls by taking advantage of the fact that phase congruency is present at the scanner level when reconstructing data with different reconstruction kernels, is a normalized measure of phase variance across scales, and appears as a smooth function with local maxima at locations where the local phase is consistent across scales. Hence, under phase congruency, the inner/outer airway wall edge related features may be located at the regions where local phase exhibits maximal coherence. This method defined the wall boundaries by considering the point with half intensity with respect to the peak intensity inside the wall. In implementation, Estépar et al.⁷² introduced a feature dependent congruency ${\psi }_{\theta }$ and located the inner/outer airway wall by maximizing ${\psi }_{\pi /2}$ and ${\psi }_{3\pi /4}$, respectively. As noted in Ref. 72, the advantage of this method was a lower sensitivity to different reconstruction kernels and noise levels. The scheme is able to locate the airway walls relatively accurately.

Contour matching method

In order to overcome some of the segmentation difficulties that stem from vessels adjacent to airways, as well as wall irregularities, Saragaglia et al.⁷³ developed a method based on mathematical morphology combined with energy-based contour matching. To reduce the dependence on pixel value variations, this algorithm first used the FWHM to normalize the native image. Thereafter, with the aid of the airway centerlines, the outer airway wall is computed in a slice-by-slice manner by progressively extending an initial “closed” contour (e.g., a set of connected pixels) until a predefine energy reaches a state of equilibrium. In implementation, the energy function is defined as a combination of several morphological measures, such as grayscale gradient and distance to the neighborhood. In this method, the inner wall contours are used as the initial closed contour to automatically identify the outer wall. This method depends on the accuracy of the central axes of the airways, as these are used to generate the cross-sectional images at specific bronchial locations.

3D geometric deformable model

In most of the methods described above for airway morphometry analysis, measurements are typically restricted to airways that are largely perpendicular to the scanning plane. This may lead to obvious bias in the airway measurement, as the majority of airways depicted on axial images are actually oblique to the axial plane. In addition, these methods primarily focus on the identification of airway wall regions that are directly attached to the parenchyma while ignoring regions between the bronchial wall and adjacent vessels. Due to the similar intensity of the bronchial wall and the adjacent vessels, it is quite complicated to correctly identify the boundaries between the structures. To overcome these limitations, Ortner et al.⁷⁴ described a novel geometric method based on an explicit 3D triangle mesh surface model. The model deforms in a deformation force field defined by gradient vector flow according to simplified Lagrangian dynamics. In particular, the model allows for local adaptive time step integration, has no self-intersections during deformation, is independent to the airway orientation with respect to the scanning plane, and can deal with adjacent vessels automatically. However, this approach⁷⁴ requires a balloon force based on the image intensity to prohibit the surface stopping at the inner surface of the airway wall. While the image intensity of an airway wall may vary substantially, it is hard to select a constant parameter for the balloon force.

According to Estépar et al.,⁷² these methods can also be classified into two categories, namely, parametric methods and nonparametric methods, based on whether any mechanism/model (e.g., the PSF) is used to alleviate the blurring affect caused by a scanner. It is not easy to reliably measure some airway features, and the measurement process is hindered by variations in airway caliber, wall thickness, and orientation. Nonhomogeneous airway surroundings, such as adjacent airways, lung parenchyma, blood vessels, heart, and chest wall, further complicate the process. Of equal importance are the partial volume effects which are the result of the finite size of the image voxel. Due to partial volume effects, fine details and small objects (relative to pixel size) can be largely lost. Many of the mentioned techniques designed to assess airway wall thickness were validated using phantom studies, and all seem to work better for airways with a diameter larger than 2 mm. However, in reality, small airways play an important role in COPD and other respiratory related diseases caused by heavy smoking.

VIRTUAL BRONCHOSCOPY

As an approach to visually examine the airways, bronchoscopy is widely used for diagnostic and therapeutic assessment purposes in current clinical practice, allowing for inspection of abnormalities (e.g., tumors, inflammation, and foreign bodies) for diagnosis, as well as for performance of biopsies and surgical planning. However, the invasive nature of the conventional rigid/flexible bronchoscopy is associated with some risk to the patients and may not be suitable for all patients (e.g., young children or severely ill patients). In addition, due to physical limitations, conventional bronchoscopy can only reach the first few generations of an airway tree, and there is no guarantee that the exact designated site of the lung will be reached. The advent of sophisticated computational techniques in computer graphics, combined with high resolution CT imaging in a volumetric data acquisition mode, led to the development of VB techniques. As a result, it is now possible to noninvasively, efficiently, and safely perform a bronchoscopy in a clinical setting for all types of patients through a virtual “fly through” of the centerlines of the airway branches. With this approach, a clinician is able to study suspicious lesions from any desired direction and viewpoint without any time limit, albeit, without the ability to biopsy identified anomalies or suspicious areas. The applications of VB in studying a number of lung diseases in clinical settings have been described in detail in several reviews.^{75, 76, 77, 78}

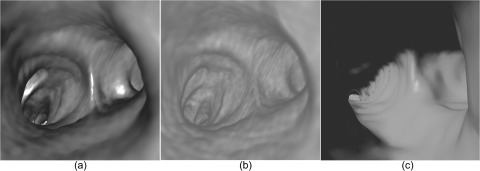
In terms of technique, a VB system can be comprised of two primary components:⁷⁷ (1) robust airway tree identification and centerline extraction for path planning and (2) interactive virtual navigation along the path. Initially, due to limitations in computer graphical techniques, it was relatively difficult to perform the virtual navigation in real time, and as a result, clinical applications and the actual use of VB were quite limited.⁷⁹ With advances in computer techniques (both hardware and software), it became relatively easy to have either a real-time surface rendering or a real-time volume rendering (Fig. 4). Hence, VB has been widely accepted and is now in routine clinical use. There have been a number of studies⁷⁹ investigating the feasibility and usefulness of VB in clinical practices, and all studies verified that VB is a promising and feasible approach for studying a number of diseases, but there remains a limitation in identifying subtle lesions. For example, after reviewing the findings in 18 consecutive patients, Dheda et al.⁸⁰ found that VB missed mucosal and infiltrative changes despite its adequate capability in identifying suspicious lung cancer and laryngotracheal pathology, as well as in determining the size of stenosis. Similarly, Finkelstein et al.⁸¹ compared findings using VB with fiberoptic bronchoscopy on 32 consecutive patients and concluded that with the use of VB one was not able to detect subtle lung lesions. In particular, Haliloglu et al.⁸² investigated the usefulness of VB in assessing suspected foreign body aspirations in children and concluded that VB should be performed only in specific situations, namely, where chest radiograph is negative but the clinical indication is highly suggestive of an aspirated foreign body.

Figure 4.

Examples of different presentation approaches to virtual bronchoscopy: (a) volume rendering with lighting, (b) volume rendering without lighting, and (c) surface rendering with lighting.

In order to develop an easy-to-use and practical VB system, there are primarily three issues that need to be addressed:

• (1)Accurate identification of small airways: As mentioned, small airways always constitute a region-of-interest for investigating various lung airway diseases, but full advantage of the approach cannot always be reached due to unreliable CT based segmentation of smaller airways.
• (2)Efficient and natural human–computer interface for performing the needed navigational tasks: With a proper user interface, the strengths of real-time rendering techniques could be better exploited for achieving optimal performance in visualization of the airways and the surrounding lung tissues. For example, Seemann et al.⁸³ compared different surface models (i.e., a triangle-surface rendering model, a shaded-surface rendering model, and a transparent shaded-surface rendering model) and found that each of the models had strengths and weaknesses. In principle, these models can be switched freely in implementation by incorporating a toggling function into the user interface. Also, an interactive adjustment of the transfer function for volume rendering, or the thresholding for surface rendering, may reveal additional details of a specific region-of-interest. In addition, the existence of a mechanism for interactive measurement during navigation may be helpful in studying the characteristic of a lesion.²² Unfortunately, there are few investigations on the design of a natural and efficient user interface for VB systems. In the future, special efforts should be made to improve the clinical utility through improving VB interpretation, in combination with automated morphometry techniques for aiding in the identification of small lesions (e.g., mild stenosis or small tumors).
• (3)A seamless conjunction with a real bronchoscope: One of the main challenges of VB when used in an interventional setting in conjunction with a real bronchoscope is to robustly estimate the current position of the true bronchoscope (TB) using a direct comparison between TB and VB. If this registration issue could be robustly resolved for real time use, perhaps with additional tracking devices, it would constitute an important step toward a possible wider clinical utilization of VB.

CORRELATION ANALYSES AMONG AIRWAY MORPHOMETRY, AIRWAY DISEASES, AND PULMONARY FUNCTION

The primary goal in developing computational techniques as described herein is to accelerate knowledge discovery of the underlying mechanisms of specific lung diseases. It has been widely recognized that lung structures and their morphological variations may be highly correlated with pulmonary function. In the past, there have been numerous investigations on the relationship, if any, between airways morphological characteristics in vivo and pulmonary function, or disease status in order to assess structural abnormalities and track changes over time or in response to treatment. Despite extensive effort in this regard, only a limited number of airway morphological features were investigated, including airway wall thickness, lumen area, trachea dimensions, and branch counts.

Many of these^{61, 62, 84, 85, 86, 87, 88} demonstrated that measurements of airway wall thickness on CT images were reasonably predictive of lung function and thicker airway walls tended to be found in subjects with reduced airflow. For example, Hogg et al.⁶³ showed that COPD progression was strongly associated with an increase in the volume of tissue in the wall and with accumulation of inflammatory mucus exudates in the lumen of airways less than 2 mm in diameter. By studying the central airway wall dimensions in the apical segmental bronchus of the upper right lobe in smokers, Nakano et al.⁶⁷ found that the percentage of total airway (lumen plus wall) that represented airway wall area [wall area percent (WA%)] correlated with forced expiratory volume in 1 second (FEV1), forced expiratory vital capacity (FVC), and the ratio between residual volume (RV) and total lung capacity (TLC), but not with a diffusing capacity of lung for carbon monoxide (DLCO). Multiple logistic regression analyses performed by Arakawa et al.⁸⁸ showed that air trapping and bronchial wall thickening were significant independent determinants of obstructive PFTs. Leader et al.⁸⁹ studied the association between lung function and airway wall computed attenuation (“density”) in 200 COPD screening subjects. For the purpose of this study, the presence of COPD was defined as FEV1/FVC < 0.7 with the presence of emphysema or airway obstruction (remodeling), or both. Airway morphometry parameters (i.e., lumen area, lumen perimeter, and wall area percent) had a slightly stronger correlation with lung function as compared with airway wall density (i.e., mean and maximum HU). In particular, there was a significantly stronger association for measurements computed from small airways when compared to larger airways in the investigated population. Achenbach et al.⁶² correlated wall thickness of large and small airways with functional parameters related to airflow obstruction in COPD patients using a new quantification procedure from a 3D approach of the segmentation of the bronchial tree. When compared with proximal airways, a higher correlation between function and distal airways was observed.

In addition to the airway wall, there are a limited number of investigations that considered other morphological airway features, such as lumen area, trachea dimensions, and airway branch numbers, during investigations of possible correlations, if any, with lung function. Bokov et al.⁹⁰ found that inspiratory airway resistance correlated with lumen area of the sixth bronchial generation of the right lung and peak expiratory flow (PEF) correlated with the area of the third generation. Considering that emphysema and emphysematous lungs tend to have fewer visible small airways than those with less parenchyma destruction, Diaz et al.⁹¹ studied the relationship between airway branch number and severity of emphysema and found that the total airway count was lower in subjects with more severe emphasematous destruction, suggesting that airway branch numbers might be a predictor of severity of COPD in smokers. To evaluate the correlation between measured tracheal features in emphysema patients and PFT before and after a lung volume reduction surgery (LVRS), Leader et al.⁹² computed a set of tracheal features (e.g., tracheal length, axial plane area, circularity index, tracheal length, and volume) and compared these with PFT results. Experiments on a dataset of 43 patients showed that combining PFT and anatomical features, such as tracheal features, could potentially provide a more accurate assessment of disease status, as well as disease progression. Handa et al.⁹³ verified this observation in a different study and showed that there was a positive correlation between tracheal area corrected for body surface area and peak expiratory flow (%PEF), and a negative correlation between airway wall area (WA%)/total airway area and %PEF. However, trachea measures may be affected by the scanning position, and as a result, the computed trachea measures may be over or under estimated.

Although the correlation between extent of emphysema and severity of airflow obstruction is well recognized, Coxson et al.⁹⁴ pointed out that “none of the studies published to date show ‘excellent’ correlations between lung function and CT measures of emphysema and airway wall remodeling.” Specifically, Hasegawa et al.⁸⁵ did not show a correlation between the right apical segmental bronchus and FEV1 but did show an improved correlation with FEV1 when more distal airways were considered. Coxson et al.⁹⁴ verified in an independent study that there was no correlation between airway wall dimensions and the segmental bronchi except in the airways of the fifth generation. It is not difficult to infer that the conclusions reached by these investigations are largely determined by the robustness and accuracy of the computational techniques used for segmenting and measuring airway structures. Available relevant computational techniques are still not mature enough for the purpose of accurately measuring small airways, while in fact it is these very regions that may alter airflow and may actually play an important role in airway obstruction as observed in COPD. We note that as a “global” measure of lung function, PFT results that are used in many of the studies as referenced are actually influenced by a large number of factors/variables than solely the airways.

DISCUSSION AND CONCLUSIONS

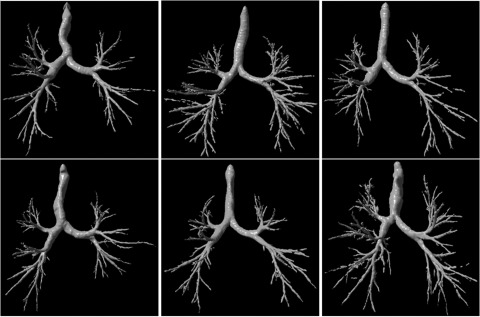
In this review, we attempted to provide an overview of available computational techniques as related to the airways depicted on CT examinations. Despite intensive effort, virtually none of the problems we describe have been adequately addressed, thereby limiting significantly the possible clinical use of these techniques. First, available airway tree segmentation schemes still miss a large fraction of small airways. Whereas airway segmentation is the underlying technical basis for a number of purposes (e.g., morphometry analysis and airway labeling) and different applications (e.g., VB), further improvements in the quality and accuracy of airway segmentation will be necessary before associated techniques can be confidently used in routine clinical practice. Second, airway labeling is not sufficiently robust due to the presence of false positive and false negative identifications. When compared with the level of effort in airway tree segmentation, relatively minor effort has been dedicated to other technical developments, such as airway labeling and morphometry analysis. For example, many of the investigations related to airway morphometry focus exclusively on thickness measurements of the airway wall while ignoring other parameters, such as the branching patterns of the airway tree (e.g., the global shape of an airway tree) and the spatial relationships, if any, between various airway measures and other anatomical structures (e.g., the distribution of airways in individual lobes). Although airway trees typically appear as bifurcation trees, there are significant differences in their global shape and branching patterns as shown in the examples in Fig. 5. Accurate description of these shapes may actually be useful for gaining a deeper understanding of the underlying mechanisms of airway disease progression, as well as the potential impact on lung function. Also, available airway measures are typically computed as mean values for the entire lung. This approach may not adequately represent the heterogeneous depiction of patterns, in particular, as related to airway abnormalities. Therefore, a more detailed investigation of various morphological features may be required.

Figure 5.

Examples demonstrating the variability in morphology of airway trees.

During the development of the techniques described in this survey, an unavoidable and unresolved problem is the difficulty in robust and reproducible performance validation, as unavailability of a gold standard results in the majority of investigations typically using phantoms, or manually delineating the boundaries of lung airway structures, and then performing a comparison of results to those obtained by different computerized schemes. Indeed, phantom studies could provide an alternative solution to this problem, but the artificial characteristics of these phantoms, as related to variations in these studies that are not comparable to variability in human lungs, make these assessments relatively simplistic in nature, in particular, as related to the presence of lung diseases. In addition, for a manually generated “gold standard,” a large effort is needed, as a very large and diverse dataset is required for this purpose, and each examination contains a large number of CT images. This requirement may limit the number of examinations used for this purpose leading to a serious limitation of the “gold standard.” For an example, Table TABLE I. lists the number of lung CT examinations collected for testing purposes and generally these numbers are relatively small compared with the diversity of lung airways in normal and abnormal subjects. A future possible solution to this problem may be the public sharing of datasets ascertained by different research groups. To the best of our knowledge, there is no accepted and available “gold standard” related to lung airways that is openly shared in the research community. We note that EXACT’09 (Ref. ³⁹) did assemble a “gold standard;” however, this “gold standard” is not available to the public. Manual delineation also typically suffers from a relatively large inter- and/or intrareader variability, in particular, as related to small airways. Hence, performance assessments that are based on manual results are not reliable in a strict sense.

One very important issue, namely, the human–computer user interface, has been largely ignored in the past. In fact, many of the problems we face in medical image analysis are highly interactive in nature and typically need a user friendly interface before any of the approaches described in this paper could be practically and widely used by most clinicians. For example, when characterizing morphological features (e.g., airway wall) in the airway tree, it would be desirable to display the computed results directly, superimposed on the CT images while allowing the user to interactively specify the region-of-interest, as well as the types of features he/she is interested in. Although some studies attempted to address several of the issues highlighted here in an implicit manner, specific investigational effort may be needed in order to enable optimal use of these approaches in clinical practice.