Isotope Effects and Heavy-Atom Tunneling in the Roush Allylboration of Aldehydes

Abstract

Intermolecular ¹³C kinetic isotope effects (KIEs) for the Roush allylboration of p-anisaldehyde were determined using a novel approach. The experimental ¹³C KIEs fit qualitatively with the expected rate-limiting cyclic transition state, but they are far higher than theoretical predictions based on conventional transition state theory. This discrepancy is attributed to a substantial contribution of heavy-atom tunneling to the reaction, and this is supported by multidimensional tunneling calculations that reproduce the observed KIEs.

Tunneling allows reactive trajectories that do not adhere to the classical limitation of the transition state energy, so that conventional transition state theory (TST) underestimates the reaction rate. Large kinetic isotope effects (KIEs) in hydrogen transfer reactions have often been interpreted as a diagnostic for tunneling through the reaction barrier.^1,2 The extent of tunneling is mass dependent and decreases with increasing mass of the atom. The much larger mass of carbon decreases its tunneling probability and consequently the effect of carbon tunneling on reaction rates is often ignored. As a result, carbon tunneling is much less understood and has been addressed for only a handful of chemical reactions.² It has been observed that allowance for tunneling improves the prediction of heavy-atom isotope effects, but tunneling corrections in most reactions not involving hydrogen transfer are very small. As a result, heavy-atom KIE predictions based solely on TST, not allowing for tunneling, are still usually reasonably accurate³ and sufficient for mechanistic interpretation.

We describe here a ¹³C isotope effect study of the Roush allylboration reaction. The experimental KIEs in this reaction are much larger than expected from TST, and theoretical analysis suggests that the large KIEs result from a surprisingly large contribution of tunneling to the reaction. The results provide several insights into the role of heavy-atom tunneling in ordinary organic reactions.

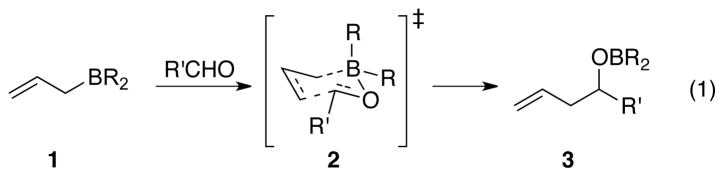
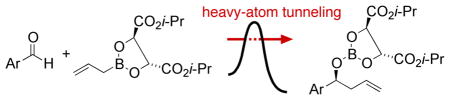
The allylboration of aldehydes (eq 1) affords homoallylic alcohols and formally accomplishes an aldol reaction when coupled with oxidative cleavage of the alkene. Enantioselective versions of this reaction have proven to be particularly useful because the stereochemical and regiochemical outcome is readily predictable and is consistent with a formal ene reaction proceeding by the chair-like transition state 2.⁴

Mechanistically, these are well-behaved reactions with straightforward bimolecular kinetics.⁵ Gajewski observed a significantly inverse secondary deuterium kinetic isotope effect (KIE) in the addition of the Roush allylboronate^4a to benzaldehyde, consistent with rate-limiting addition to the carbonyl and inconsistent with rate-limiting single-electron transfer.⁶ Theoretical studies have supported the basic mechanistic picture derived initially from experimental observations⁷ and have identified stereochemical control elements in the enantioselective reactions.⁸ From our perspective, the reaction provided a special opportunity to measure a series of differing ¹³C KIEs at low temperature.

The reaction of the Roush (+)-diisopropyl L-tartrate-modified allylboronate 4 with 5 proceeds smoothly at −78 °C and affords the homoallylic alcohol 6 in quantitative yield and 52% ee based on NMR analysis using Eu(hfc)₃ after basic hydrolysis (eq 2). In principle the ¹³C KIEs in the reaction could be obtained from either analysis of recovered starting materials or analysis of the product, but in practice the difficulty of recovering the allylboronate quantitatively precludes a starting material analysis. Product analysis is also subject to a problem that is common in KIE measurements, that is, the isotopic composition of products from reactions taken to low conversion must be compared to product in which no isotopic fractionation has occurred, most commonly product taken from reactions taken to “100%” conversion. This method is subject to error because small departures from a true 100% conversion lead to relatively large errors in the KIEs, and 100% conversion of both reactants is difficult to achieve in a bimolecular stoichiometric reaction. To avoid this problem, multiple reactions forming isotopic standards would be required. The experimental design used here, as shown in Scheme 2, requires only two reactions, the key idea being that the low-conversion reaction for one of the starting materials serves as the 100%-reaction standard for the other starting material, and vice versa. Using this design, the ¹³C KIEs for both components in the allylboration reaction were determined by NMR analysis at natural abundance.⁹ The results are summarized in Figure 1.

Scheme 2.

Design of allylboration KIE experiment

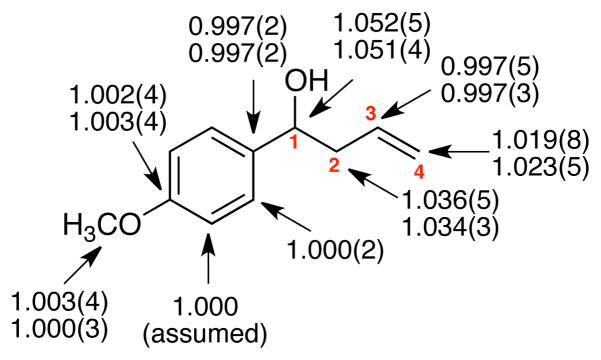
Figure 1.

Experimental ¹³C KIEs (k_12C/k_13C, −78 °C) for the reaction of 4 with 5. The two sets of KIEs represent two independent experiments, and the standard deviations from six measurements are indicated in parentheses. A second measurement at the ortho carbon was precluded by interference from solvent C₆D₆.

C1, C2, and C4 all exhibit substantial ¹³C KIEs, and their normal qualitative interpretation is that all three carbons are undergoing σ-bonding changes in the rate-limiting transition state. This is not an unexpected result, as it fits with the conventional cyclic mechanism in the qualitative transition state 2. The KIEs notably suggest that the transition state is relatively synchronous - for comparison the ¹³C KIEs in asynchronous Diels-Alder reactions are more uneven¹⁰ - though the larger KIEs at C1 and C2 versus C4 suggest that C-C bond formation is more advanced than C-B bond breaking. This argument assumes that the transition state is not late, as seems reasonable for a one-step exothermic reaction. Although aldehydeboronate complexes are surely intermediates in these reactions, the large KIEs show that complex formation must be reversible. Additionally, the slightly inverse KIE for C3 is also consistent with its restricted environment at the transition state.

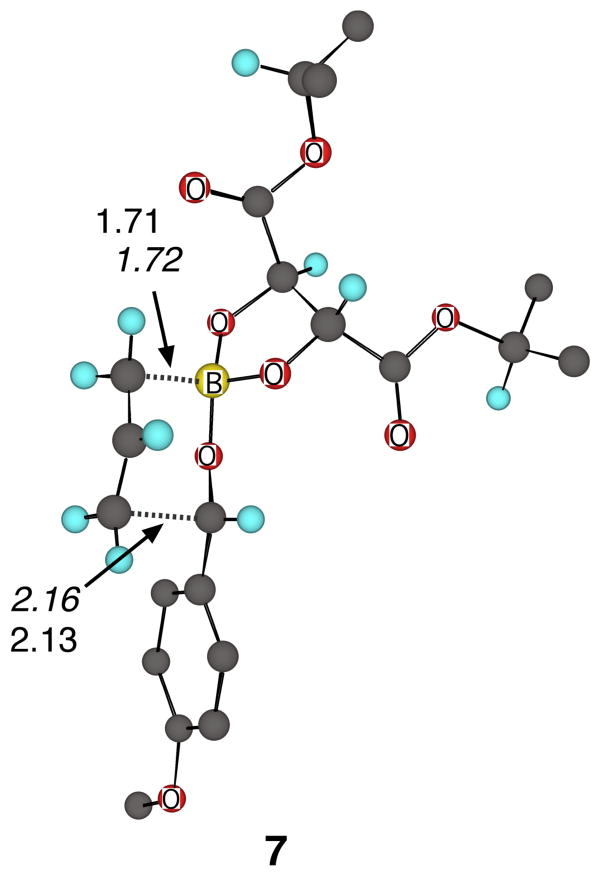
As a first step in the quantitative interpretation of the experimental KIEs, fully-optimized transition structure geometries for the reaction of 4 with 5 were obtained in M06-2X/6-31+G** calculations,¹¹ both in the gas phase and using a PCM solvent model¹² for dichloromethane. The lowest-energy PCM transition structure 7 (Figure 2) involves attack of the allyl moiety on the si face of the aldehyde (given the L-tartrate-derived 4). An alternative structure for the re addition (see the Supporting Information) was found to be 0.5 kcal/mol higher in energy (M06-2X/6-31+G**/PCM + zpe), fitting well with the experimental enantioselectivity (with a ΔΔG^‡ of 0.45 kcal/mol).

Figure 2.

Lowest-energy transition structures for the reaction of 4 with p-anisaldehyde (5). The distances in italics are M06-2X/6-31+G** (gas phase) while non-italicized distances are M06-2X/6-31+G**/PCM. Some hydrogens have been removed for clarity.

The ¹³C KIEs predicted from conventional TST for transition structure 7 were calculated from the scaled theoretical vibrational frequencies¹³ by the method of Bigeleisen and Mayer (Table 1).¹⁴ The first key observation from Table 1 is that irrespective of the calculational method, the predicted KIEs based on TST are significantly lower than the experimental values. This discrepancy is most pronounced for C1 and C2, the two carbon atoms that are most intimately associated with motion along the reaction coordinate at the transition state. Since conventional TST predictions have no allowance for either tunneling or recrossing, we have also generated KIE predictions based on canonical variational transition state theory¹⁵ (CVT) with the effect of multidimensional tunneling on the reaction dynamics computed using the small-curvature tunneling¹⁶ (SCT) approximation.

Table 1.

Predicted versus Experimental ¹³C KIEs (k₁₂/k₁₃, −78 °C) from conventional TST and from CVT/SCT.

method	C1	C2	C3	C4
conventional TST KIEsa
gas phase	1.038	1.026	0.997	1.018
PCM	1.041	1.025	0.998	1.016
CVT/SCT corrections
gas phase	1.008	1.010	1.001	1.003
PCM	1.010	1.013	1.001	1.002
CVT/SCT KIEsb
gas phase	1.047	1.036	0.998	1.020
PCM	1.052	1.038	0.999	1.019
experimental KIEs
	1.052(5)	1.036(5)	0.997(5)	1.019(8)
	1.051(4)	1.034(3)	0.997(3)	1.023(5)

^aThe conventional TST KIEs shown are based on 7. The corresponding KIEs for the lowest-energy transition structure leading to the minor enantiomer, 24% of the reaction, are within 0.0012 of those shown in each case.

^bThe CVT/SCT KIEs were obtained by multiplying the conventional TST KIEs by corrections obtained from model-system CVT/SCT calculations.

The prediction of small KIEs by the CVT/SCT method has the problem that tight convergence criteria and small step sizes are required for sufficient numerical convergence. This made a CVT/SCT study of the full system with the best calculational level and solvent model impractical. Instead, the CVT/SCT study was carried out for a simplified model of 4 in which the ester groups were replaced with hydrogen atoms. These calculations were performed using GAUSSRATE¹⁷ as the interface between POLYRATE¹⁸ and Gaussian 09.¹⁹ The semi-classical rate constants were computed using the Page-McIver method²⁰ to follow the minimum energy path (MEP) with a step size of 0.001 Bohr. The Hessian matrix was recalculated and a mode analysis performed every 0.01 Bohr. The predicted TST and CVT/SCT KIEs for each carbon atom were computed from the rate constants obtained from the parent calculation (all carbon atoms being ¹²C) and calculations with a ¹³C label at each carbon atom of interest. The ratios of the CVT/SCT and TST KIEs for the model system at −78 °C are listed in Table 1. These ratios were then applied as corrections to the TST KIEs for the full systems.²¹ Upon inclusion of the contributions from tunneling and statistically predictable recrossing,²² the predicted KIEs are in excellent agreement with the experimental KIEs (Table 1). This agreement with the inclusion of heavy-atom tunneling versus the disagreement when not including it strongly supports the role of heavy-atom tunneling in the reaction.

A number of observations in the results provide notable new insights. First, tunneling increases all of the ¹³C KIEs, even the inverse KIE at C3. The effect at C3 is obviously small, only 0.1%, but C3 is moving as the reaction coordinate progresses this leads to a tunneling effect on the KIE. Second, the contribution of tunneling to the KIEs is a large part of their observed values. The KIEs consist of three parts:^14b,c a part due to changes in the reduced isotopic partition function between the starting material and transition state (which tends to be dominated by zero-point energy effects), a part due to the ratio of imaginary frequencies for parent versus substituted isotopologs (which is largely the entropic part of the KIE), and a part due to tunneling. For the KIE at C2, the parts are 18%, 48%, and 34% of the isotope effect, respectively. Heavy-atom tunneling is more important to the KIE at C2 than is zero-point energy! A third observation is that the largest impact of tunneling on the KIEs does not occur at the position with the largest KIE. C2 is the atom moving the greatest amount in the transition vector, and the CVT/SCT correction at C2 is larger than that at C1 despite the KIE at C1 being larger. This shows that the magnitude of the KIE by itself is not a good indicator of the impact of tunneling. A final observation is that heavy-atom tunneling is having a substantial and, to our view, surprisingly large effect on the absolute rate of the reaction. Based on the ratio of CVT/SCT versus CVT rate constants, the acceleration due to tunneling is a factor of 1.36.

It is understood that tunneling contributes to the rates of all reactions passing though a barrier. Outside of reactions at exceedingly low temperatures,² however, the role of heavy-atom tunneling in organic reactions has been generally been assumed to be trivial. In the case of the ring-opening of cyclopropylcarbinyl radical, we recently demonstrated that there were relatively large effects of heavy-atom tunneling at −100 °C,^2h but the cyclopropylcarbinyl radical system has been postulated to be an exceptional case owing to an unusually narrow barrier in the reaction.²³ The allylboration reaction here is a perfectly ordinary organic reaction and the temperature, while low, is one that is commonly used in organic chemistry. The effect of tunneling on the ¹³C KIEs is not as large as it was with the cyclopropylcarbinyl radical case, but it is large enough that the experimental observations cannot be understood without allowing for heavy-atom tunneling.

The rate acceleration due to tunneling by a factor of 1.36 is not directly recognizable in the rate of the reaction; an Arrhenius plot of the rate versus temperature between −78 ° and 0 °C would not be detectably nonlinear, and there is never a theory-independent way of knowing what the rate would be in the absence of tunneling. In this respect, the heavy-atom tunneling is hidden from chemists, and we only know about it from its effect on the KIEs. Despite the hidden character of this acceleration, it has a substantial effect on how long the reaction takes. Heavy-atom tunneling plays a role in simple everyday organic reactions.

Scheme 1.

Chair-like transition state for allylboration reaction