Grapevines growing in Australia suffer from high temperatures which have major effects on photosynthesis and transpiration. To learn more, gas exchange was measured over several seasons and then modelled across temperatures from 20 to 45°C and validated with independent data.
Abstract
Background and aims
Grapevines growing in Australia are often exposed to very high temperatures and the question of how the gas exchange processes adjust to these conditions is not well understood. The aim was to develop a model of photosynthesis and transpiration in relation to temperature to quantify the impact of the growing conditions on vine performance.
Methodology
Leaf gas exchange was measured along the grapevine shoots in accordance with their growth and development over several growing seasons. Using a general linear statistical modelling approach, photosynthesis and transpiration were modelled against leaf temperature separated into bands and the model parameters and coefficients applied to independent datasets to validate the model.
Principal results
Photosynthesis, transpiration and stomatal conductance varied along the shoot, with early emerging leaves having the highest rates, but these declined as later emerging leaves increased their gas exchange capacities in accordance with development. The general linear modelling approach applied to these data revealed that photosynthesis at each temperature was additively dependent on stomatal conductance, internal CO2 concentration and photon flux density. The temperature-dependent coefficients for these parameters applied to other datasets gave a predicted rate of photosynthesis that was linearly related to the measured rates, with a 1 : 1 slope. Temperature-dependent transpiration was multiplicatively related to stomatal conductance and the leaf to air vapour pressure deficit and applying the coefficients also showed a highly linear relationship, with a 1 : 1 slope between measured and modelled rates, when applied to independent datasets.
Conclusions
The models developed for the grapevines were relatively simple but accounted for much of the seasonal variation in photosynthesis and transpiration. The goodness of fit in each case demonstrated that explicitly selecting leaf temperature as a model parameter, rather than including temperature intrinsically as is usually done in more complex models, was warranted.
Introduction
Models of photosynthesis have been in vogue since Farquhar et al. (1980) first published their biochemical model and much progress in the biochemical understanding of photosynthesis has followed (von Caemmerer 2000; Farquhar et al. 2001). Photosynthesis is recognized to be limited by the two processes of ribulose 1,5-bisphosphate (RuBP) carboxylation and RuBP regeneration, and many models of photosynthesis incorporate these limitations as an intrinsic part (Amthor 1994; Hikosaka 1997; Le Roux et al. 1999; Bown et al. 2007). Other photosynthetic models are based on the photosynthetic light response curve for individual leaves (Battaglia et al. 1996; Pachepsky and Acock 1996; Thornley 1998; Gómez et al. 2005) while other models are extended to the whole canopy using the physics of light attenuation to extend the photosynthetic light responses (Reynolds et al. 1992; Sands 1995; Cannell and Thornley 1998; Kull and Kruijt 1998; Raulier et al. 1999). Further still, the canopy has been partitioned into sun and shade leaves for some models (De Pury and Farquhar 1997; Dai et al. 2004; Greer et al. 2004). Although the effect of temperature is usually inherent in these models, it is less common for the effect of leaf temperature over the wide range that plants can experience to be explicitly investigated in the models.
The processes of photosynthesis are intrinsically related to temperatures, photon flux densities (PFD) and CO2 concentrations (both ambient and internal) prevailing at the time and including stomatal conductance, these parameters have been incorporated into some dynamic models of photosynthesis (Lieth and Pasian 1990; Kim and Lieth 2003; Noe and Giersch 2004; Caballé et al. 2011). These models often also couple photosynthesis with stomatal conductance and transpiration (Collatz et al. 1991; von Stamm 1994; Kim and Lieth 2003; Keenan et al. 2010). In turn, there are various ways to model stomatal conductance, notably that of Ball et al. (1987) relating stomatal conductance to assimilation, relative humidity (RH) and the CO2 mole fraction of the air, and the modification by Leuning (1995) involving replacing the RH term with a hyperbolic function of vapour pressure deficit (VPD). In addition, a multiplicative model relating stomatal conductance to RH, water status, PFD and air temperature has also been proposed (Fernández et al. 2006; Op de Beeck et al. 2010b) and to PFD and VPD (Noe and Giersch 2004). In contrast, transpiration is simply modelled as a function of stomatal conductance and leaf-to-air VPD and the effect of leaf temperature is essentially encapsulated in determining the saturated vapour pressure of the leaf (Kim and Lieth 2003; Yu et al. 2004).
Semillon grapevines are grown in many parts of Australia and are an economically important crop for the different regions (Australian Bureau of Statistics (ABS) 2005). This cultivar is known to have high rates of transpiration (Rogiers et al. 2009) and, therefore, irrigation is sometimes required for growth of the vines. The vines are also grown in climates where summer air temperatures readily exceed 35 °C (Gladstones 1992). These high-temperature exposures, sometimes >40 °C, are known to reduce photosynthesis of grapevine leaves (Kriedemann 1968; Ferrini et al. 1995; Yu et al. 2009; Zsófi et al. 2009). In part, these reductions in photosynthesis are related to stomatal limitation and, generally, photosynthetic recovery occurs within a few days after a heat treatment (Sepúlveda and Kliewer 1986; Ferrini et al. 1995; Soar et al. 2009). A pot trial on Semillon vines (Greer and Weston 2010) showed a reduction in photosynthesis after a heat event was caused by stomatal limitation but photosynthesis also recovered over a 10- to 12-day period. However, it is not known if stomata limit photosynthesis to the same extent in vineyard conditions, especially at the high temperatures to which the vines are exposed.
Thus, the objective of the present study was to measure gas exchange of Semillon leaves throughout the growing season under the prevailing high-temperature conditions and then to model photosynthesis and transpiration in relation to stomatal conductance, internal CO2 concentration, PFD, VPD and leaf temperature. The approach adopted was to use a statistical general linear model to assess which of these effects, as well as physical and biological effects such as time of day, day of season, leaf position, shoot position and vine, were significant. Temperature-dependent coefficients derived from the model for each parameter were then applied to independent datasets to assess the goodness of fit and validation of the model over a range of leaf temperatures.
Materials and methods
Plant material and growth conditions
This project was undertaken in a commercial vineyard in the Riverina, NSW, Australia, over the growing season of 2008/09. Some additional measurements were collected in the 2007/08 and 2009/10 growing seasons. The vines (Vitis vinifera L. cv. Semillon) were not grown on a rootstock and were planted in north–south rows with 3.5 m spacing between rows and 1.8 m spacing between the vines. The vines were grown with a vertical shoot position trellis and catch wires were lifted from about canopy closure to constrain the shoots semi-vertically. Apart from a fungicide spray programme, the selected vines had no other management practices imposed. Drip irrigation was used, with drippers at 0.6-m spacing supplying water and nutrients at a rate of 2.4 L h−1 for 12 h per week prior to ripening and 24 h per week after ripening started. Midday water potentials in midsummer averaged −1.6 ± 0.3 MPa and no indications of water stress were evident. Budbreak occurred at about 25 September and harvest of the grapes occurred on 12 February.
Gas exchange measurements
Throughout the growing season, commencing on 9 October 2008 (14 days after budbreak, DAB) and finishing on 18 March 2009 (174 DAB), photosynthesis and associated gas exchange measurements (stomatal conductance, gs; transpiration, E; internal CO2 concentration, ci) were made at 7- to 14-day intervals with an open gas exchange system (LCA4, ADC BioScientific, Hoddesdon, UK). On each occasion, measurements were conducted on all leaves of each of two selected shoots of three vines in each of six whole panels (three vines per panel), totalling 36 shoots. In each case, all leaves present that were >25 mm were measured on each occasion; thus, an increasing number of leaves were measured, starting with about five leaves and finishing with over 30 leaves at the end of the measurements. In all cases, gas exchange was measured between 0900 and 1600 h on the leaves in their natural orientation, and the PFD, leaf temperature and leaf-to-air vapour pressure deficit (VPDL) were measured concurrently. Leaf temperature was measured with a thermocouple appressed to the lower leaf surface within the gas exchange chamber.
Modelling procedure
Once all the data were collected and assembled into a spreadsheet, leaf temperatures and all associated data were selected using a sorting procedure with SAS 9.13 (SAS Institute, Inc., Cary, NC, USA) into 5 ± 2.5 °C bands from 20 to 45 °C. Photosynthesis (A) was modelled as a function of stomatal conductance (gs), internal CO2 concentration (ci) and PFD for each temperature band. A general linear modelling approach using the GLM procedure of SAS 9.1 (SAS Institute) was used to model photosynthesis to equation (1):
| (1) |
Similarly, transpiration (E) was modelled as a function of stomatal conductance and VPDL as:
| (2) |
The models were fitted to all data across the growing season and coefficients for each parameter (Ti, Tg, Tc, Tp, Tv), including an intercept term (Ti), were derived from these analyses for each temperature band. These coefficients were then analysed as a function of leaf temperature, using the GLM procedure in SAS.
A second dataset of photosynthetic and transpiration rates, stomatal conductances, internal CO2 concentrations, PFDs, VPDs and leaf temperatures were measured over the 2009/10 growing season from 22 October 2009 until 2 February 2010. The same numbers of vines and shoots (although different plants) were used and the same methods of measuring gas exchange. These data were then used to independently evaluate the model in equations (3) and (4) using the model parameters and encompassing their specific temperature coefficients derived from the comparable dataset in 2008/09.
Results
Seasonal changes in gas exchange along the shoot
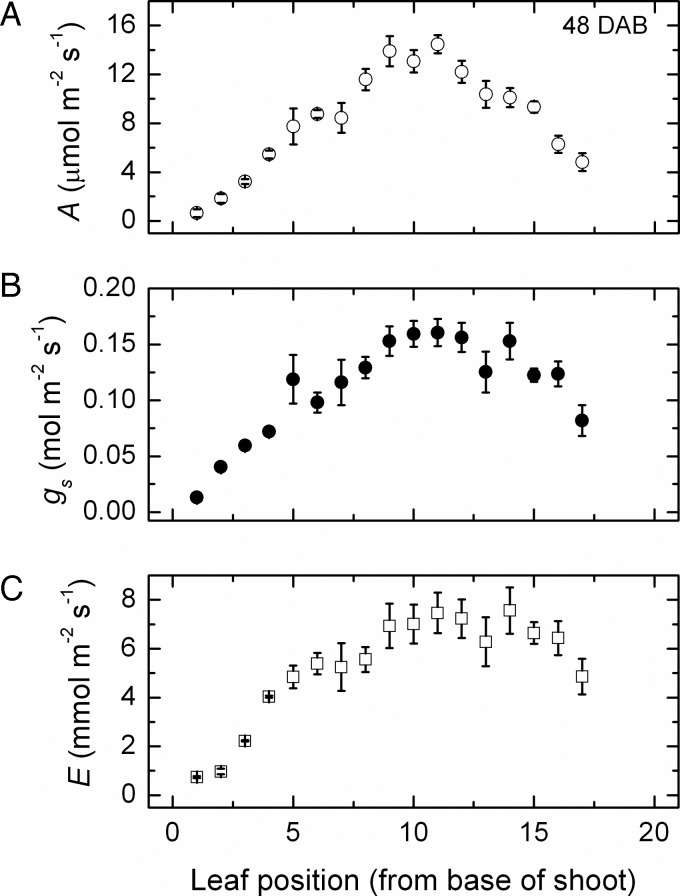
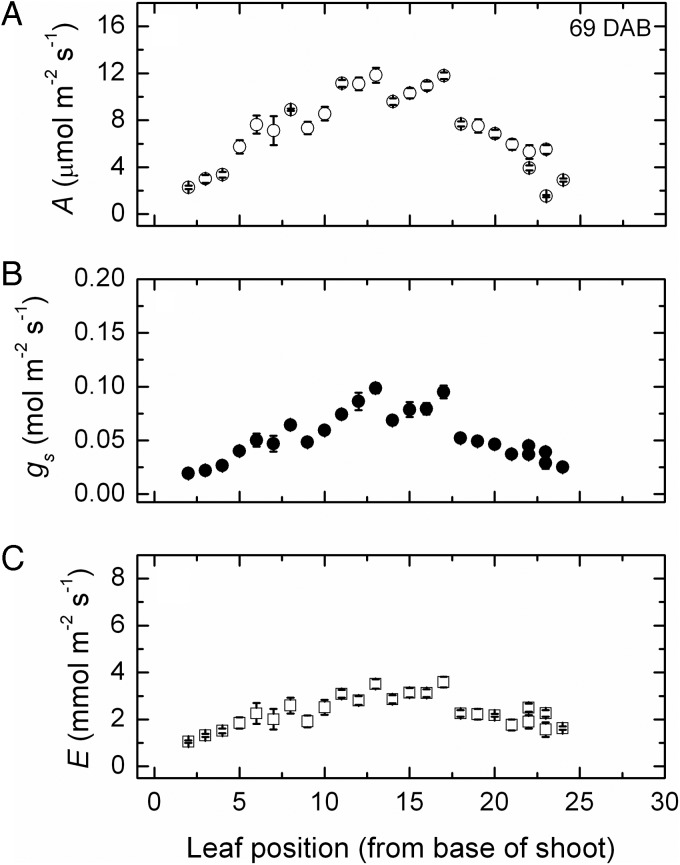
Early in the growing season, photosynthesis, transpiration and stomatal conductance (Fig. 1) all increased in leaves along the shoot, at least to position 10–12, where net photosynthesis was maximal at ∼15 μmol m−2 s−1 while conductance peaked at ∼0.16 mol m−2 s−1 and transpiration at 8–9 mmol m−2 s−1 at similar shoot positions. Reduced rates in each leaf at the higher shoot positions up to about position 17 probably reflected leaves not being completely developed. This was confirmed later in the season (Fig. 2), when leaves up to about this same position had the highest rates, although in all cases these had declined to about12 μmol m−2 s−1 of CO2 fixation, 0.10 mol m−2 s−1 of stomatal conductance and 4 mmol m−2 s−1 of water transpired.
Fig. 1.
Changes in gas exchange after 48 days. Net photosynthesis (A), stomatal conductance (B) and transpiration (C) along the shoot (mean ± SE, N = 36) of Semillon vines growing in an irrigated vineyard at 48 DAB, which was about the time of flowering.
Fig. 2.
Changes in gas exchange after 69 days. Net photosynthesis (A), stomatal conductance (B) and transpiration (C) along the shoot (mean ± SE, N = 36) of Semillon vines growing in an irrigated vineyard at 69 DAB, which was about the time when vegetative growth was terminating.
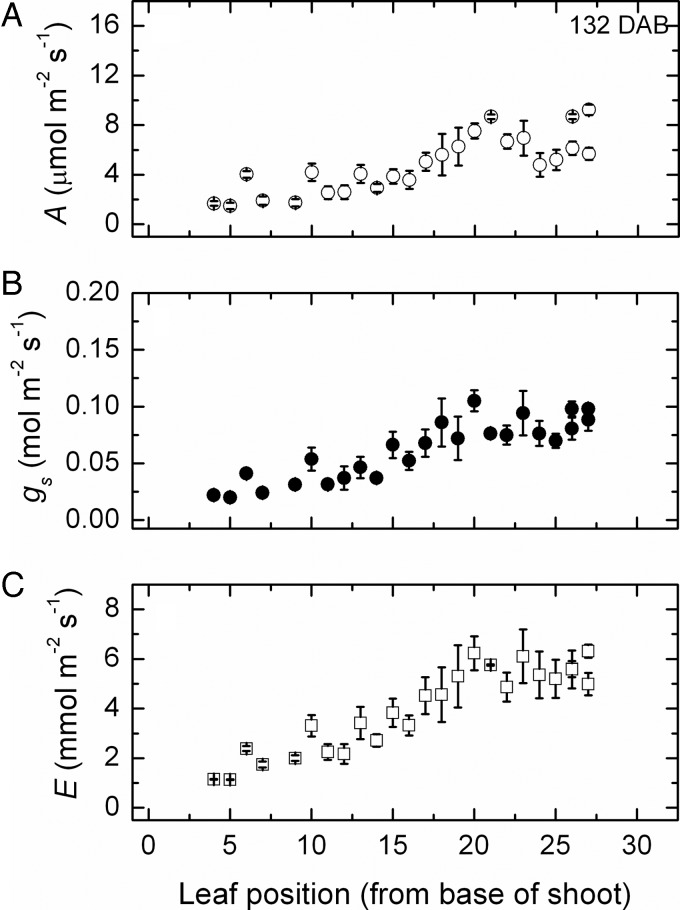
Again, rates in leaves at higher positions (20–25) declined because of incomplete development and yet again, later in the season, this same cohort of leaves now had the highest rates (Fig. 3). Nevertheless, the maximum rates of photosynthesis in these leaves were lower than in the mid-season and across the whole shoot rates had declined markedly, presumably from some senescence now occurring. In contrast, stomatal conductance and transpiration, especially, did not show a comparable decline in these late-emerging leaves and, in fact, had the highest rates for the whole shoot.
Fig. 3.
Changes in gas exchange after 132 days. Net photosynthesis (A), stomatal conductance (B) and transpiration (C) along the shoot (mean ± SE, N = 36) of Semillon vines growing in an irrigated vineyard at 132 DAB, which was just after the grape harvest.
Temperature dependency of gas exchange attributes
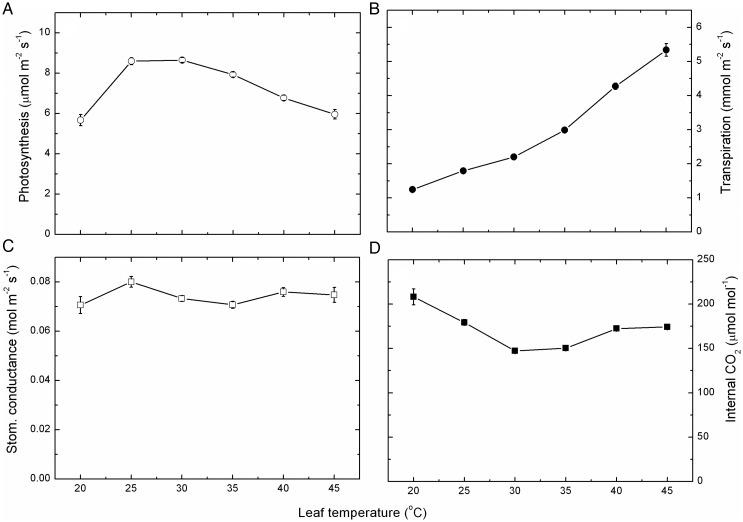
Averaged net photosynthesis over all leaves from throughout the growing season but divided into the six leaf temperature bands (Fig. 4A) showed an optimum between 25 and 30 °C. With further increases in leaf temperature, there was a linear decline in rates such that at 45 °C, net photosynthesis was reduced by 30 %. It was also notable that a sharper decrease in photosynthesis occurred when the leaf temperature decreased to 20 °C and, at 35 % reduction, was greater than occurred with the high temperatures.
Fig. 4.
The effect of leaf temperature on gas exchange. Net photosynthesis (A), transpiration (B), stomatal conductance (C) and internal CO2 concentration (D) of Semillon leaves (mean ± SE, N > 1000; see Table 1) measured over the whole growing season and averaged across all leaves, shoots and vines. These data were separated into the different leaf temperatures from 20 to 45 °C in ±2.5 °C bands and then analysed into least squares means using SAS 9.13.
By contrast, mean transpiration rates increased exponentially with increasing leaf temperature (Fig. 4B), particularly above 35 °C, and the increase in rates of transpiration between 20 and 45 °C was >4-fold. Thus, transpiration was strongly temperature dependent. However, it was not related to mean stomatal conductance, which was not especially temperature dependent (Fig. 4C) over the whole temperature range. Nevertheless, there were significant differences in stomatal conductance between the different leaf temperatures.
Internal CO2 concentration did vary with temperature (Fig. 4D) and highest at the low temperatures and lowest at 30–35 °C (by 30 %) with a slight (16 %) increase thereafter at the highest temperatures. Thus, the internal CO2 concentration was also strongly temperature dependent.
Assessing the model: assimilation
From the GLM procedure, neither leaf position along the shoot, shoot position on the vine, vine number, time of day nor day of season was significant in any of the analyses. Consequently, all these were excluded from further analyses and the full fit to equation (1) but with leaf temperature initially included indicated a highly significant temperature effect (P < 0.0001). Thus, the data were re-analysed by fitting equation (1) to each cohort of data in the separate leaf temperature bands. In all cases, stomatal conductance, internal CO2 concentration and PFD were all highly significant where the r2 for the fit to an additive model for each leaf temperature ranged from 0.75 to 0.90 (Table 1). By contrast, a multiplicative model, assuming interactions between all parameters, gave r2 from 0.15 to 0.58. Though all highly significant, the model accounted for much less of the variance in assimilation than the additive model and, therefore, was not adopted. Similarly, a model incorporating the non-linear hyperbolic tangent relationship between photosynthetic assimilation and PFD (Greer and Halligan 2001) gave no additional account of the variance in assimilation. Thus, the simpler additive model was adopted:
| (3) |
where Afit was the fitted rate of photosynthetic assimilation to the temperature-dependent function.
Table 1.
Statistics of fitting the model to photosynthetic data. The percentage of the error mean square accounted for by each of the three terms of the model is included. In all cases, the model was highly significant (P < 0.0001). The number of measurements (n) used in parameterizing the model for each temperature band is also shown.
| Leaf temperature (°C) | r2 | gs (%) | ci (%) | PFD (%) | n |
|---|---|---|---|---|---|
| 20 | 0.843 | 59 | 39 | 2 | 934 |
| 25 | 0.747 | 63 | 34 | 3 | 2179 |
| 30 | 0.804 | 54 | 38 | 8 | 2407 |
| 34 | 0.782 | 60 | 33 | 7 | 1714 |
| 40 | 0.811 | 81 | 15 | 4 | 974 |
| 45 | 0.905 | 81 | 18 | <1 | 222 |
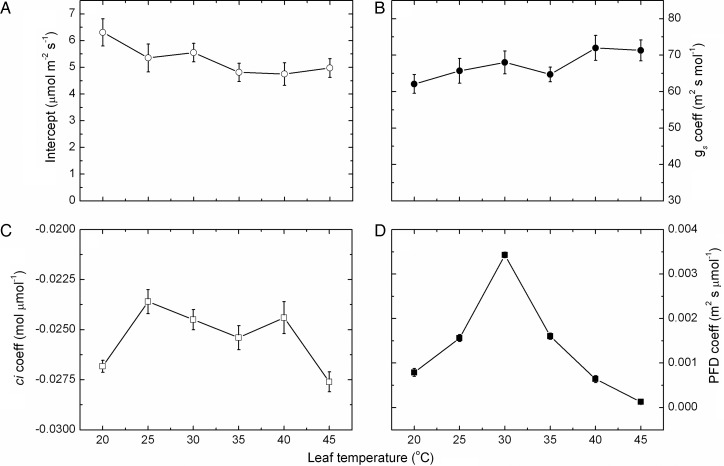
The coefficients, including an intercept term, for each parameter in the model across the different leaf temperatures (Fig. 5) were not uniform in their response. The intercept coefficient declined in a general linear pattern with increasing leaf temperature. The coefficient for stomatal conductance increased in a more or less linear pattern to leaf temperature, with a slight drop at 35 °C but significantly (P < 0.001) higher at high than low temperatures. The coefficient for internal CO2 concentration decreased from 20 to 25 °C (become less negative) and varied only slightly up to 40 °C but then increased sharply at 45 °C and again there were significant differences between temperatures. In contrast, the coefficient for PFD was the most responsive to temperature, increasing markedly between 20 and 30 °C, but thereafter declining more or less consistently with increasing leaf temperature and differences were significant.
Fig. 5.
Impact of temperature on intercepts and coefficients. The intercept (A) and coefficients for stomatal conductance (B), internal CO2 concentration (C) and photon flux density (D) as a function of leaf temperature (mean ± SE, N = 9). These coefficients were derived from a general linear additive model fitted to the seasonal rates of photosynthesis for all Semillon leaves, shoots and vines growing in an irrigated vineyard during the 2008/09 growing season for each separate temperature band between 20 and 45 °C. The model used stomatal conductance, internal CO2 concentration and the PFD that was measured concurrently with each photosynthetic rate as the parameters in the general linear model. The model was fitted separately to the data for each vine and replicate, and the coefficients were then averaged accordingly.
Model fitting: assimilation
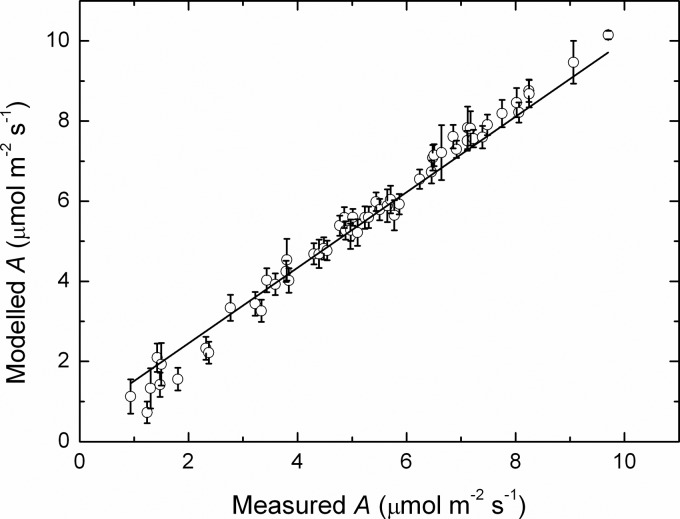
The application of the additive assimilation model and coefficients to a separate dataset from the 2009/10 growing season indicated that a highly significant (P < 0.0001) linear relationship occurred between the measured and modelled rates (Fig. 6). This relationship accounted for 80 % of the variance in modelled assimilation. The fitted line had a slope of 1.104 ± 0.008 μmol μmol−1, thus very close to a 1 : 1 relationship, suggesting a good fit to the model. A smaller dataset from the 2007/08 growing season was also evaluated and the fitted line had a slope of 0.981 ± 0.019 μmol μmol−1 and an r2 of 0.817 (not shown), thus a comparable fit of the model to the 2009/10 dataset. These analyses suggest that the overall fit was very good, demonstrating that the parameters and temperature coefficients were readily translatable to independent datasets.
Fig. 6.
Modelled rates of photosynthesis as a function of the measured rates. Rates were averaged over each vine and replicate (mean ± SE, N = 9) of Semillon vines growing in an irrigated vineyard during the 2009/10 growing season. The line is a linear regression fitted to the whole dataset (slope 1.104 ± 0.008 mol mol−1, r2 = 0.82, P < 0.0001).
Assessing the model: transpiration
The GLM procedure was applied to all the transpiration data from the 2008/09 growing season and no effect of leaf position, time of day or day of year was significant. There was, however, a significant effect of temperature (P < 0.001) and, therefore, a separate fitting of the model was applied to each temperature. An additive model fitting stomatal conductance and VPDL to the transpiration data was highly significant in all cases and accounted for 96–98 % of the variance. However, an interactive model, whereby transpiration was modelled with the product of stomatal conductance and VPDL, gave an r2 > 0.99 in all cases and was, therefore, adopted. The specific model used was as follows:
| (4) |
where Efit was the fitted estimate of transpiration and Tgv was the coefficient for an interaction between stomatal conductance and VPDL in the model.
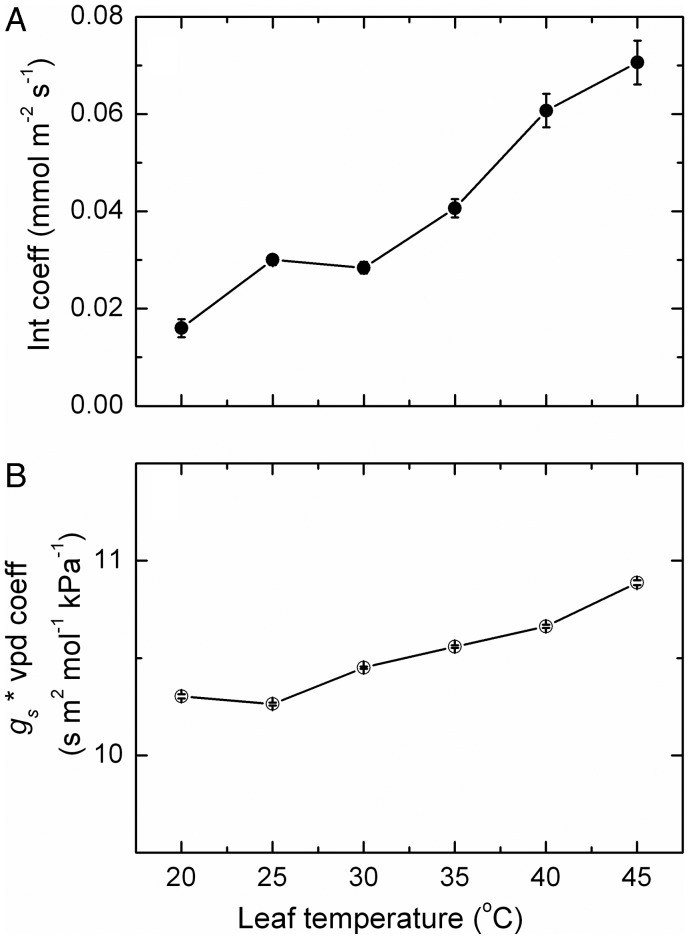
The coefficients, including the intercept term, were strongly affected by leaf temperature (Fig. 7), both increasing in a generally linear pattern as leaf temperature increased.
Fig. 7.
The intercept (A) and a combined stomatal conductance × VPD coefficient (B) as a function of leaf temperature. These coefficients (mean ± SE, N = 9) were derived from a general linear multiplicative model fitted to the seasonal rates of transpiration for all Semillon leaves, shoots and vines growing in an irrigated vineyard during the 2008/09 growing season for each separate temperature band between 20 and 45 °C. The model used stomatal conductance and the VPD that was measured concurrently with each transpiration rate as the parameters in the general linear model. The model was fitted separately to the data for each vine and replicate, and the coefficients were then averaged accordingly.
Model fitting: transpiration
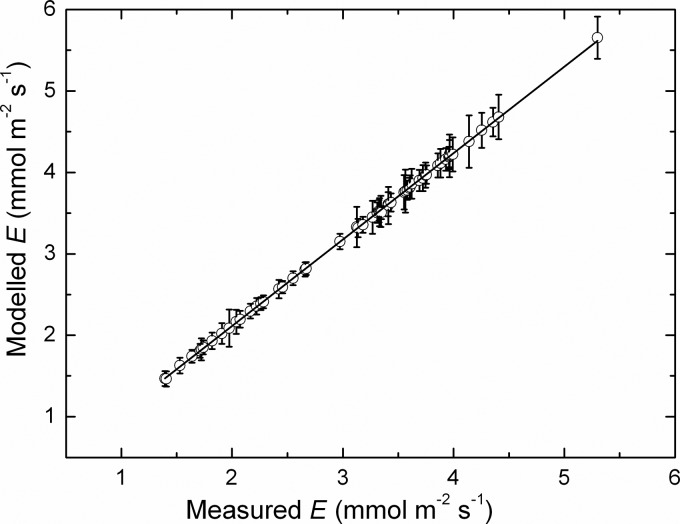
The application of the interactive transpiration model to the 2009/10 dataset indicated a highly significant (P < 0.0001) linear relationship between the measured and modelled rates (Fig. 8), with an overall slope of 0.981 ± 0.002 mmol mmol−1, that is close to 1 : 1 and accounting for 97 % of the variance. Thus, the model appeared to account extremely well for the changes in transpiration across the 2009/10 growing season.
Fig. 8.
Modelled rates of transpiration as a function of the measured rates, averaged over each vine and replicate. Semillon vines were growing in an irrigated vineyard during the 2009/10 growing season. The line is a linear regression fitted to the whole dataset (slope 1.08 ± 0.0002 mol mol−1, r2 = 0.999, P < 0.0001) (mean ± SE, N = 9).
Discussion
The present study of gas exchange of Semillon leaves over the growing season revealed that both photosynthesis and transpiration varied along the shoots in accordance with their expansion and development. Earliest emerging leaves had the highest rates of photosynthesis and transpiration, and these were achieved early in the growing season. As the season progressed, rates of photosynthesis declined in the basal leaves and increased in leaves towards the apical meristem. It was notable, however, that the leaves appearing in the mid- and late season did not reach the highest rates of photosynthesis and transpiration that were observed in the early emerging leaves. This suggested that some ontogenetic factor might have been at play, where the early-forming leaves are photosynthetically most active because of vines being heterotrophic at this stage and dependent on carbon reserves (Goffinet 2004; Field et al. 2009). A similar conclusion was reached for the early-emerging leaves on Actinidia deliciosa vines and elsewhere (Catský and Šesták 1996; Greer and Jeffares 1998; Suriyagoda et al. 2010). Although transpiration followed a pattern similar to photosynthesis, it is much harder to suggest a reason for this except that high transpiration rates might support transport of carbon assimilates from the roots to the leaves and shoot apical meristem. However, it was also clear that all changes in photosynthesis and transpiration were highly correlated with stomatal conductance. Stomatal conductance is also known to change with leaf development, increasing initially but generally declining with leaf age (Bogaert and Lemeur 1994; Suriyagoda et al. 2010; Salmon et al. 2011) as shown here for the Semillon leaves.
However, from the modelling of photosynthesis it was uncertain in statistical terms that there was a role of leaf development in photosynthetic capacity of the leaves. Leaf position, time of day and day of season were not significant terms in the model, which suggested that differences in photosynthesis along the shoot and during the season were almost entirely accounted for by leaf temperature, stomatal behaviour, internal CO2 concentration and PFD. The model generally accounted for 80–90 % of the variance in photosynthesis across the various temperature bands, but it was noteworthy that stomatal conductance accounted for ∼55 % of the variance at lower temperatures but 80 % at very high temperatures. This conforms to the well-established linear dependence of photosynthesis on stomatal conductance (Wunsche et al. 2000; Caballé et al. 2011), although at high gs the response can be non-linear (Williams 2012). In contrast, although photosynthesis was negatively correlated with internal CO2 concentration (see also Caballé et al. 2011), the percentage of the variance accounted for declined from ∼35–45 % at 20–25 °C to 15–20 % at 40–45 °C. Across all leaf temperatures, the PFD accounted for <10 % of the variance in the model and suggesting that the leaves were generally exposed to saturating PFDs during measurements, even though basal leaves were exposed to PFDs of ∼200–400 µmol m−2 s−1 from mid-season. This might also explain why a more complex model incorporating the non-linear relationship between photosynthesis and PFD did not improve the fit of the model. Nevertheless, the simple three-parameter model was successfully applied to the independent datasets of the 2007/08 and 2009/10 growing seasons, and the fit accounted for 80 % of the variance. Furthermore, the slope of the line fitted between the measured and modelled rates of photosynthesis gave a slope close to 1 : 1, which was another indication of the goodness of fit. This compares with the multiplicative PFD model of Fernández et al. (2006) for Festuca pallescens, which accounted for 86.5 % of the variance, and the PFD-based model of Caballé et al. (2011) for the same species and which accounted for 82 % of the variance. Similarly, the more extensive biochemical model of Kim and Lieth (2003) for rose leaves gave a similar slope and accounted for 96 % of the variance, while for a range of crops, shrubs and trees, both more extensive biochemical and leaf models gave variances from 50 to 85 % (Gao et al. 2004). The biochemical-leaf model of Gouasmi et al. (2009) and Op de Beeck et al. (2010a) also had a 1 : 1 slope between measured and predicted photosynthesis. Thus, the simple model presented here gave consistent results with the more complex models.
Photosynthesis of Semillon grape leaves is sensitive to temperature with an optimum around25–30 °C and rates declining by 30 % with leaf temperatures around40–45 °C, consistent with that for other grapevine varieties (Kriedemann 1968). The response is also well in keeping with the generally understood effect of temperature on photosynthesis (Berry and Björkman 1980). Underlying this temperature response are those of the stomata, internal CO2 concentration and PFD and their response to temperature. Although there were effects of temperature on stomatal conductance, across the whole temperature range, there was only a small overall change. This is in contrast to stomatal conductance of Eucalyptus leaves, which were markedly affected by temperature (Battaglia et al. 1996), especially towards the higher temperatures where the VPD increases markedly and thus closed the stomata (Reynolds et al. 1992; Battaglia et al. 1996). In contrast, for a range of warm- and cool-climate herbaceous species (Bunce 2000), stomatal conductance increased with increasing temperatures, which may be the response when the increase in VPD is prevented from occurring. Similar results were observed by Fischer et al. (1998) and Lu et al. (1994). In contrast, in a simulation, Reynolds et al. (1992) have suggested that stomatal conductance peaks at ∼12–15 °C and declines markedly at higher temperatures. A similar response was observed for spinach (Yamori et al. 2006). Stomatal conductance of two cool-temperature Poa species also declined with an increase in temperature from 7 to 12 °C (Medek et al. 2010), while in Pisum sativum, gs increased from 15 to 25 °C and in Chenopodium album, gs remained about constant between 20 and 30 °C (Hamilton et al. 2008).
Relative to other grapevine cultivars such as Campbell Early and Kyoho (Yu et al. 2009), Kékfrancos (Zsófi et al. 2009), Zinfandel and White Reisling (Schultz 2003), Temperanillo (Maroco et al. 2002) and Thompson Seedless (Williams 2012), the average stomatal conductances for the Semillon vines in the present study were towards the lower end of the reported ranges. In addition, the values reported here are lower than those reported for this variety in a cultivar comparison (Rogiers et al. 2009). This reflects the fact that many leaves and days of measurements were used to determine the overall gas exchange response to temperature in the present study. It does appear, however, that the temperature response of stomatal opening in other grapevine cultivars has not been assessed.
For the Semillon leaves, the internal CO2 concentration (ci) varied strongly with temperature, especially below 30 °C where the concentration increased markedly in a trend opposite to photosynthesis. In contrast, over a near similar range of temperatures, ci of Eucalyptus leaves changed only slightly, rising at high and low temperatures (Battaglia et al. 1996). Similarly, Caballé et al. (2011), Yamori et al. (2006) and Eamus et al. (2008) found no effect of temperature on ci, but Caballé et al. (2011) suggested that ci should change in the same direction as photosynthesis when stomata are dominating photosynthesis. The coupled changes in photosynthesis and stomatal conductance accompanied by an increase in ci that occurred in Coffea arabica plants (Gómez et al. 2005) conforms with this hypothesis. For the present study, however, the temperature dependency of ci was close to a mirror image of the temperature dependency of photosynthesis and, given that stomatal conductance was not strongly temperature dependent, suggests that non-stomatal limitations also played a part in regulating Semillon leaf photosynthesis (Greer and Weedon 2012).
The model of photosynthesis of Semillon leaves was constructed with three parameters, namely stomatal conductance, internal CO2 concentration and PFD, but determined separately for the different leaf temperatures. This model was similar to that of Kim and Lieth (2003), who used PFD, ci and leaf temperature to determine photosynthesis, and to that of Caballé et al. (2011), who used leaf temperature, ci and gs in a multiplicative model. A multiplicative model was also used by Fernández et al. (2006), involving RH, air temperature and gs and PFD-dependent responses. Thus, it would appear that the model used in the present study was one of a few to focus on leaf temperature explicitly and to ascertain the specific effect of temperature on each parameter of the model. In fact, all the coefficients of the parameters were temperature dependent although all varied in different ways, but the differences in the coefficients at the different temperatures were significant and warranted the approach. When combined, and taking into account the coefficients at the different temperatures, the model applied to new datasets gave an excellent fit and this confirmed the approach of determining the temperature sensitivity of the parameters of the model and indeed validated the model.
Transpiration of the Semillon leaves more than doubled when leaf temperatures increased from 20 to 45 °C, in keeping with the need for increased evaporative cooling at the higher temperatures (Bunce 2000; Keenan et al. 2010). This cultivar is known to have high transpiration rates among common wine grape cultivars (Rogiers et al. 2009) and this cooling capacity can maintain leaf temperatures several degrees cooler than air temperature (Greer et al. 2010). In contrast, transpiration rates of the grape variety Trincadeira preta declined markedly above about35 °C (Correia et al. 1995) and similarly transpiration rates of Eucalyptus haemastoma leaves declined markedly above about 35 °C (Eamus et al. 2008). For Vigna unguiculata, however, rates were maximal between 36 and 40 °C (Hall and Schulze 1980). There are clearly differences in the temperature dependency of transpiration and the response may well depend on the growth conditions of each species.
The modelling of transpiration over the growing season indicated that a multiplicative model of stomatal conductance and VPDL (leaf to air) gave the best fit, and accounted for almost 100 % of the variance in transpiration (Cowan and Farquhar 1977; Hall and Schulze 1980; Meinzer et al. 1995; Zhu et al. 2011). Using a similar relationship, Op de Beeck et al. (2010a) had comparable results between measured and modelled transpiration, with 93 % of the variance accounted for and a 1 : 1 slope. The same multiplicative model used here was also used by Meinzer et al. (1995), but compared with whole tree transpiration. It is noteworthy that an additive model in the present study, where gs and VPDL were included separately in the model, accounted for 93–98 % of the variance in transpiration over all temperatures, but significantly, gs accounted for most of the variance even though the effect of VPDL was highly significant. Transpiration has been commonly reported to be linear function of stomatal conductance, as has been shown for V. vinifera x V. labrusca cv. Campbell's Early and Kyoho (Yu et al. 2009) and sugarcane (Meinzer and Grantz 1989). Likewise, from diurnal changes in transpiration and stomatal conductance, a linear function was evident for Anacardium excelsium leaves (Meinzer et al. 1993). In contrast, Bunce (1997) showed an inverse relationship between stomatal conductance and transpiration for Abutilon leaves.
The role of temperature in transpiration is explicitly in the determination of VPDL and calculating the saturated vapour pressure of the leaf (Collatz et al. 1991), but also through the effect of temperature on gs. Fredeen and Sage (1999) have shown for white spruce seedlings that gs increased with increasing leaf temperature but only if the VPD was 2–3 kPa. Hall and Schulze (1980) had observed a similar response, except that the temperature effect on conductance was greatest at low rather than at high VPDs. For well-watered grapevines, in contrast, gs declined with increasing leaf temperature (Correia et al. 1995). However, Peak and Mott (2011) concluded that a direct effect of temperature on gs is relatively small when the VPDL is kept constant. With the approach adopted in the present study, it was not possible to exclude a direct temperature effect on gs in relation to transpiration from that of the effect on VPDL. Nevertheless, the model including leaf temperature responses of the gs × VPDL interaction was warranted, given the extremely high-quality fit of the model prediction of the independent datasets and, therefore, validated the approach.
Conclusions and forward look
The modelling of photosynthesis and transpiration from measurements made over whole growing seasons using a statistical regression approach successfully accounted for much of the seasonal variation that occurred. The model was underpinned by the temperature response of the various parameters, including stomatal conductance, internal CO2 concentration, leaf-to-air water vapour difference and PFD. In contrast to other more complex biochemically based models, the present model was relatively simple and accounted for a high percentage of the variance in independent datasets. It is common to include temperature in various photosynthetic models but more typically as an intrinsic property of various biochemical processes (Farquhar et al. 1980), whereas the temperature responses in the present study were explicitly encapsulated by the parameter coefficients and central to the model. This focus on temperature is related to the high-temperature climate in which the vines are grown and these models will contribute to more extensive models of vine growth and development in relation to the climate that are currently under development.
Sources of funding
This project was funded by the Winegrowing Futures, a Grape and Wine Research and Development Corporation-funded initiative to the National Wine and Grape Industry Centre at Charles Sturt University.
Conflict of interest statement
None declared.
Acknowledgements
I wish to thank Mr Mark Weedon, Research Associate, and Mr Chris Weston, Technical Officer, at the National Wine and Grape Industry Centre for assistance with collecting the data. I also thank the Vineyard Owner for allowing me to conduct this study on their property. I am also indebted to SAS Australia for providing further support.
References
- Amthor JS. Scaling CO2–photosynthesis relationships from the leaf to the canopy. Photosynthesis Research. 1994;39:321–350. doi: 10.1007/BF00014590. [DOI] [PubMed] [Google Scholar]
- Australian Bureau of Statistics. 2005. Australian Bureau of Statistics Yearbook 1301.0www.abs.gov.au .
- Ball JT, Woodrow IE, Berry JA. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. Dordrecht, The Netherlands: Martinus-Nijhoff Publishers; 1987. [Google Scholar]
- Battaglia M, Beadle C, Loughhead S. Photosynthetic temperature responses of Eucalyptus globulus and Eucalyptus nitens. Tree Physiology. 1996;16:81–89. doi: 10.1093/treephys/16.1-2.81. [DOI] [PubMed] [Google Scholar]
- Berry J, Björkman O. Photosynthetic response and adaptation to temperature in higher-plants. Annual Review of Plant Physiology and Plant Molecular Biology. 1980;31:491–543. [Google Scholar]
- Bogaert G, Lemeur R. Ontogenetic effects on the stomatal apparatus of four Belgian sugar beet (Beta vulgaris subsp. vulgaris L.) cultivars. Photosynthetica. 1994;30:333–339. [Google Scholar]
- Bown HE, Watt MS, Clinton PW, Mason EG, Richardson B. Partititioning concurrent influences of nitrogen and phosphorus supply on photosynthetic model parameters of Pinus radiata. Tree Physiology. 2007;27:335–344. doi: 10.1093/treephys/27.3.335. [DOI] [PubMed] [Google Scholar]
- Bunce JA. Does transpiration control stomatal responses to water vapour pressure deficit? Plant, Cell and Environment. 1997;20:131–135. [Google Scholar]
- Bunce JA. Acclimation of photosynthesis to temperature in eight cool and warm climate herbaceous C3 species: temperature dependence of parameters of a biochemical photosynthesis model. Photosynthesis Research. 2000;63:59–67. doi: 10.1023/A:1006325724086. [DOI] [PubMed] [Google Scholar]
- Caballé G, Fernández ME, Gyenge J, Aparicio A, Schlichter T. Modeling leaf maximum net photosynthetic rate of Festuca pallescens, the dominant perennial grass of Patagonian pine-based silvopastoral systems. Agroforestry Systems. 2011;83:13–24. [Google Scholar]
- Cannell MGR, Thornley JHM. Temperature and CO2 responses of leaf and canopy photosynthesis: a clarification using the non-rectangular hyperbola model of photosynthesis. Annals of Botany. 1998;82:883–892. [Google Scholar]
- Catský J, Šesták Z. Photosynthesis during leaf development. New York: Marcel Dekker; 1996. [Google Scholar]
- Collatz GJ, Ball JT, Grivet C, Berry JA. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer. Agricultural and Forest Meteorology. 1991;54:107–136. [Google Scholar]
- Correia MJ, Pereira JS, Chaves MM, Rodrigues ML, Pacheco CA. ABA xylem concentrations determine maximum daily leaf conductance of field-grown Vitis vinifera L. plants. Plant, Cell and Environment. 1995;18:511–521. [Google Scholar]
- Cowan IR, Farquhar GD. Stomatal function in relation to leaf metabolism and environment. Symposia of the Society for Experimental Biology. 1977;31:471–505. [PubMed] [Google Scholar]
- Dai Y, Dickinson RE, Wang YP. A two-big-leaf model for canopy temperature, photosynthesis, and stomatal conductance. Journal of Climate. 2004;17:2281–2299. [Google Scholar]
- De Pury DGG, Farquhar GD. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant, Cell and Environment. 1997;20:537–557. [Google Scholar]
- Eamus D, Taylor DT, Macinnis-Ng CMO, Shanahan S, De Silva L. Comparing model predictions and experimental data for the response of stomatal conductance and guard cell turgor to manipulations of cuticular conductance, leaf-to-air vapour pressure difference and temperature: feedback mechanisms are able to account for all observations. Plant, Cell and Environment. 2008;31:269–277. doi: 10.1111/j.1365-3040.2007.01771.x. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, von Caemmerer S, Berry JA. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta. 1980;149:78–90. doi: 10.1007/BF00386231. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, Von Caemmerer S, Berry JA. Models of photosynthesis. Plant Physiology. 2001;125:42–45. doi: 10.1104/pp.125.1.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández ME, Gyenge JE, Schlichter TM. Growth of Festuca pallescens in silvopastoral systems in Patagonia, Part 2: parameterization of models of stomatal conductance and leaf photosynthesis. Agroforestry Systems. 2006;66:271–280. [Google Scholar]
- Ferrini F, Mattii GB, Nicese FP. Effect of temperature on key physiological responses of grapevine Leaf. American Journal of Enology and Viticulture. 1995;46:375–379. [Google Scholar]
- Field SK, Smith JP, Holzapfel BP, Hardie WJ, Emery RJN. Grapevine response to soil temperature: xylem cytokinins and carbohydrate reserve mobilization from budbreak to anthesis. American Journal Enolology and Viticulture. 2009;60:164–172. [Google Scholar]
- Fischer RA, Rees D, Sayre KD, Lu ZM, Condon AG, Larque Saavedra A. Wheat yield progress associated with higher stomatal conductance and photosynthetic rate, and cooler canopies. Crop Science. 1998;38:1467–1475. [Google Scholar]
- Fredeen AL, Sage RF. Temperature and humidity effects on branchlet gas-exchange in white spruce: an explanation for the increase in transpiration with branchlet temperature. Trees—Structure and Function. 1999;14:161–168. [Google Scholar]
- Gao Q, Zhang X, Huang Y, Xu H. A comparative analysis of four models of photosynthesis for 11 plant species in the Loess Plateau. Agricultural and Forest Meteorology. 2004;126:203–222. [Google Scholar]
- Gladstones J. Viticulture and environment. Underdale, South Australia: Winetitles; 1992. [Google Scholar]
- Goffinet MC. Relation of applied crop stress to inflorescence development, shoot growth, and cane starch reserves in ‘Concord’ grapevine. Acta Horticulturae. 2004;640:189–200. [Google Scholar]
- Gómez LF, López JC, Riaño NM, López Y, Montoya EC. Diurnal changes in leaf gas exchange and validation of a mathematical model for coffee (Coffea arabica L.) canopy photosynthesis. Photosynthetica. 2005;43:575–582. [Google Scholar]
- Gouasmi M, Mordelet P, Demarez V, Gastellu-Etchegorry JP, Le Dantec V, Dedieu G, Menaut JC, Calvet JC, Lamaze T. Photosynthesis of a temperate fallow C3 herbaceous ecosystem: measurements and model simulations at the leaf and canopy levels. Photosynthetica. 2009;47:331–339. [Google Scholar]
- Greer DH, Halligan EA. Photosynthetic and fluorescence light responses for kiwifruit (Actinidia deliciosa) leaves at different stages of development on vines grown at two different photon flux densities. Australian Journal of Plant Physiology. 2001;28:373–382. [Google Scholar]
- Greer DH, Jeffares D. Temperature-dependence of carbon acquisition and demand in relation to shoot growth of kiwifruit (Actinidia deliciosa) vines grown in controlled environments. Functional Plant Biology. 1998;25:843–850. doi: 10.1071/FP03111. [DOI] [PubMed] [Google Scholar]
- Greer DH, Weedon MM. Modelling photosynthetic responses to temperature of grapevine (Vitis vinifera cv. Semillon) leaves on vines grown in a hot climate. Plant, Cell and Environment. 2012 doi: 10.1111/j.1365-3040.2011.02471.x. (in press). doi:10.1111/j.1365-3040.2011.02471X. [DOI] [PubMed] [Google Scholar]
- Greer DH, Weston C. Heat stress affects flowering, berry growth, sugar accumulation and photosynthesis of Vitis vinifera cv. Semillon grapevines grown in a controlled environment. Functional Plant Biology. 2010;37:206–214. [Google Scholar]
- Greer DH, Seleznyova AN, Green SR. From controlled environments to field simulations: leaf area dynamics and photosynthesis of kiwifruit vines (Actinidia deliciosa) Functional Plant Biology. 2004;31:169–179. doi: 10.1071/FP03151. [DOI] [PubMed] [Google Scholar]
- Greer DH, Weston C, Weedon M. Shoot architecture, growth and development dynamics of Vitis vinifera cv. Semillon vines grown in an irrigated vineyard with and without shade covering. Functional Plant Biology. 2010;37:1061–1070. [Google Scholar]
- Hall AE, Schulze ED. Stomatal response to environment and a possible interrelation between stomatal effects on transpiration and CO2 assimilation. Plant, Cell and Environment. 1980;3:467–474. [Google Scholar]
- Hamilton EW, Heckathorn SA, Joshi P, Wang D, Barua D. Interactive effects of elevated CO2 and growth temperature on the tolerance of photosynthesis to acute heat stress in C3 and C4 species. Journal of Integrative Plant Biology. 2008;50:1375–1387. doi: 10.1111/j.1744-7909.2008.00747.x. [DOI] [PubMed] [Google Scholar]
- Hikosaka K. Modelling optimal temperature acclimation of the photosynthetic apparatus in C3 plants with respect to nitrogen use. Annals of Botany. 1997;80:721–730. [Google Scholar]
- Keenan T, Sabate S, Gracia C. Soil water stress and coupled photosynthesis-conductance models: bridging the gap between conflicting reports on the relative roles of stomatal, mesophyll conductance and biochemical limitations to photosynthesis. Agricultural and Forest Meteorology. 2010;150:443–453. [Google Scholar]
- Kim SH, Lieth JH. A coupled model of photosynthesis, stomatal conductance and transpiration for a rose leaf (Rosa hybrida L.) Annals of Botany. 2003;91:771–781. doi: 10.1093/aob/mcg080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriedemann PE. Photosynthesis in vine leaves as a function of light intensity, temperature, and leaf age. Vitis. 1968;7:213–220. [Google Scholar]
- Kull O, Kruijt B. Leaf photosynthetic light response: a mechanistic model for scaling photosynthesis to leaves and canopies. Functional Ecology. 1998;12:767–777. [Google Scholar]
- Le Roux X, Grand S, Dreyer E, Daudet FA. Parameterization and testing of a biochemically based photosynthesis model for walnut (Juglans regia) trees and seedlings. Tree Physiology. 1999;19:481–492. doi: 10.1093/treephys/19.8.481. [DOI] [PubMed] [Google Scholar]
- Leuning R. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant, Cell and Environment. 1995;18:339–355. [Google Scholar]
- Lieth JH, Pasian CC. A model for net photosynthesis of rose leaves as a function of photosynthetically active radiation, leaf temperature, and leaf age. Journal of the American Society for Horticultural Science. 1990;115:486–491. [Google Scholar]
- Lu ZM, Radin JW, Turcotte EL, Percy R, Zeiger E. High yields in advanced lines of pima cotton are associated with higher stomatal conductance, reduced leaf-area and lower leaf temperature. Physiologia Plantarum. 1994;92:266–272. [Google Scholar]
- Maroco JP, Rodrigues ML, Lopes C, Chaves MM. Limitations to leaf photosynthesis in field-grown grapevine under drought—metabolic and modelling approaches. Functional Plant Biology. 2002;29:451–459. doi: 10.1071/PP01040. [DOI] [PubMed] [Google Scholar]
- Medek DE, Evans JR, Schortemeyer M, Ball MC. Effects of growth temperature on photosynthetic gas exchange characteristics and hydraulic anatomy in leaves of two cold-climate Poa species. Functional Plant Biology. 2010;38:54–62. doi: 10.1071/FP10023. [DOI] [PubMed] [Google Scholar]
- Meinzer FC, Grantz DA. Stomatal control of transpiration from a developing sugarcane canopy. Plant, Cell and Environment. 1989;12:635–642. [Google Scholar]
- Meinzer FC, Goldstein G, Holbrook NM, Jackson P, Cavelier J. Stomatal and environmental control of transpiration in a lowland tropical forest tree. Plant, Cell and Environment. 1993;16:429–436. [Google Scholar]
- Meinzer FC, Goldstein G, Jackson P, Holbrook NM, Gutierrez MV, Cavelier J. Environmental and physiological regulation of transpiration in tropical forest gap species: the influence of boundary layer and hydraulic properties. Oecologia. 1995;101:514–522. doi: 10.1007/BF00329432. [DOI] [PubMed] [Google Scholar]
- Noe SM, Giersch C. A simple dynamic model of photosynthesis in oak leaves: coupling leaf conductance and photosynthetic carbon fixation by a variable intracellular CO2 pool. Functional Plant Biology. 2004;31:1195–1204. doi: 10.1071/FP03251. [DOI] [PubMed] [Google Scholar]
- Op de Beeck M, Gielen B, Jonckheere I, Samson R, Janssens IA, Ceulemans R. Needle age-related and seasonal photosynthetic capacity variation is negligible for modelling yearly gas exchange of a sparse temperate Scots pine forest. Biogeosciences. 2010a;7:199–215. [Google Scholar]
- Op de Beeck M, Löw M, Deckmyn G, Ceulemans R. A comparison of photosynthesis-dependent stomatal models using twig cuvette field data for adult beech (Fagus sylvatica L.) Agricultural and Forest Meteorology. 2010b;150:531–540. [Google Scholar]
- Pachepsky LB, Acock B. An adequate model of photosynthesis—II. Dependence of parameters on environmental factors. Agricultural Systems. 1996;50:227–238. [Google Scholar]
- Peak D, Mott KA. A new, vapour-phase mechanism for stomatal responses to humidity and temperature. Plant, Cell and Environment. 2011;34:162–178. doi: 10.1111/j.1365-3040.2010.02234.x. [DOI] [PubMed] [Google Scholar]
- Raulier F, Bernier PY, Ung CH. Canopy photosynthesis of sugar maple (Acer saccharum): comparing big-leaf and multilayer extrapolations of leaf-level measurements. Tree Physiology. 1999;19:407–420. doi: 10.1093/treephys/19.7.407. [DOI] [PubMed] [Google Scholar]
- Reynolds JF, Chen J, Harley PC, Hilbert DW, Dougherty RL, Tenhunen JD. Modeling the effects of elevated CO2 on plants: extrapolating leaf response to a canopy. Agricultural and Forest Meteorology. 1992;61:69–94. [Google Scholar]
- Rogiers SY, Greer DH, Hutton RJ, Landsberg JJ. Does night-time transpiration contribute to anisohydric behaviour in a Vitis vinifera cultivar? Journal of Experimental Botany. 2009;60:3751–3763. doi: 10.1093/jxb/erp217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salmon Y, Barnard RL, Buchmann N. Ontogeny and leaf gas exchange mediate the carbon isotopic signature of herbaceous plants. Plant, Cell and Environment. 2011;34:465–479. doi: 10.1111/j.1365-3040.2010.02256.x. [DOI] [PubMed] [Google Scholar]
- Sands PJ. Modelling canopy production. II. From single-leaf photosynthetic parameters to daily canopy photosynthesis. Australian Journal of Plant Physiology. 1995;22:603–614. [Google Scholar]
- Schultz HR. Differences in hydraulic architecture account for near-isohydric and anisohydric behaviour of two field-grown Vitis vinifera L. cultivars during drought. Plant, Cell and Environment. 2003;26:1393–1405. [Google Scholar]
- Sepúlveda G, Kliewer WM. Effect of high temperature on grapevines (Vitis vinifera L.). II. Distribution of soluble sugars. American Journal of Enology and Viticulture. 1986;37:20–25. [Google Scholar]
- Soar CJ, Collins MJ, Sadras VO. Irrigated Shiraz vines (Vitis vinifera) upregulate gas exchange and maintain berry growth in response to short spells of high maximum temperature in the field. Functional Plant Biology. 2009;36:801–814. doi: 10.1071/FP09101. [DOI] [PubMed] [Google Scholar]
- Suriyagoda LDB, Lambers H, Ryan MH, Renton M. Effects of leaf development and phosphorus supply on the photosynthetic characteristics of perennial legume species with pasture potential: modelling photosynthesis with leaf development. Functional Plant Biology. 2010;37:713–725. [Google Scholar]
- Thornley JHM. Dynamic model of leaf photosynthesis with acclimation to light and nitrogen. Annals of Botany. 1998;81:421–430. [Google Scholar]
- von Caemmerer S. Biochemical models of leaf photosynthesis. Collingwood, Victoria: CSIRO Publishing; 2000. [Google Scholar]
- von Stamm S. Linked stomata and photosynthesis model for Corylus avellana (hazel) Ecological Modelling. 1994;75–76:345–357. [Google Scholar]
- Williams LE. Effects of applied water amounts at various fractions of evapotranspiration (ETc) on leaf gas exchange of Thompson Seedless grapevines. Australian Journal of Grape and Wine Research. 2012;18:100–108. [Google Scholar]
- Wunsche JN, Palmer JW, Greer DH. Effects of crop load on fruiting and gas-exchange characteristics of ‘Braeburn’/M.26 apple trees at full canopy. Journal of the American Society for Horticultural Science. 2000;125:93–99. [Google Scholar]
- Yamori W, Noguchi K, Hanba YT, Terashima I. Effects of internal conductance on the temperature dependence of the photosynthetic rate in spinach leaves from contrasting growth temperatures. Plant and Cell Physiology. 2006;47:1069–1080. doi: 10.1093/pcp/pcj077. [DOI] [PubMed] [Google Scholar]
- Yu DJ, Kim SJ, Lee HJ. Stomatal and non-stomatal limitations to photosynthesis in field-grown grapevine cultivars. Biologia Plantarum. 2009;53:133–137. [Google Scholar]
- Yu GR, Wang QF, Zhuang J. Modeling the water use efficiency of soybean and maize plants under environmental stresses: application of a synthetic model of photosynthesis–transpiration based on stomatal behavior. Journal of Plant Physiology. 2004;161:303–318. doi: 10.1078/0176-1617-00972. [DOI] [PubMed] [Google Scholar]
- Zhu GF, Li X, Su YH, Lu L, Huang CL. Seasonal fluctuations and temperature dependence in photosynthetic parameters and stomatal conductance at the leaf scale of Populus euphratica Oliv. Tree Physiology. 2011;31:178–195. doi: 10.1093/treephys/tpr005. [DOI] [PubMed] [Google Scholar]
- Zsófi Z, Gál L, Szilágyi Z, Szü Cs E, Marschall M, Nagy Z, Bálo B. Use of stomatal conductance and pre-dawn water potential to classify terroir for the grape variety Kékfrankos. Australian Journal of Grape and Wine Research. 2009;15:36–47. [Google Scholar]