Three tests and three corrections: Comment on Koen and Yonelinas (2010)

Abstract

The slope of the z-transformed receiver-operating characteristic (zROC) in recognition memory experiments is usually less than 1, which has long been interpreted to mean that the variance of the target distribution is greater than the variance of the lure distribution. The greater variance of the target distribution could arise because the different items on a list receive different increments in memory strength during study (the “encoding variability” hypothesis). In a test of that interpretation, J. Koen and A. Yonelinas (2010, K&Y) attempted to further increase encoding variability to see if it would further decrease the slope of the zROC. To do so, they presented items on a list for two different durations and then mixed the weak and strong targets together. After performing three tests on the mixed-strength data, K&Y concluded that encoding variability does not explain why the slope of the zROC is typically less than one. However, we show that their tests have no bearing on the encoding variability account. Instead, they bear on the mixture-UVSD model that corresponds to their experimental design. On the surface, the results reported by K&Y appear to be inconsistent with the predictions of the mixture-UVSD model (though they were taken to be inconsistent with the predictions of the encoding variability hypothesis). However, all three of the tests they performed contained errors. When those errors are corrected, the same three tests show that their data support, rather than contradict, the mixture-UVSD model (but they still have no bearing on the encoding variability hypothesis).

The unequal-variance signal-detection (UVSD) model holds that the memory strength distributions of targets and lures on a recognition test are Gaussian in form, with the mean and standard deviation of the target distribution typically exceeding the mean and standard deviation of the lure distribution (Egan, 1958). The statistical properties of the target distribution relative to the lure distribution can be estimated by fitting the UVSD model to confidence-based receiver-operating characteristic (ROC) data or (equivalently, and more simply) by fitting a straight line to the z-transformed ROC (zROC: Green & Swets, 1966; Macmillan & Creelman, 2005). If the UVSD model is correct, then the slope of the zROC provides an estimate of σ_lure / σ_target. Typically, the zROC slope is less than one (e.g., Egan, 1958; Glanzer, Kim, Hilford, & Adams, 1999; Ratcliff, Sheu, & Gronlund, 1992), which suggests that the standard deviation of the target distribution is greater than that of the lure distribution.

Why would the variance of the target and lure distributions differ in this way? Wixted (2007) offered one possible explanation: “An equal-variance model would result if each item on the list had the exact same amount of strength added during study. However, if the amount of strength that is added differs across items, which surely must be the case, then both strength and variability would be added, and an unequal-variance model would apply” (p. 154). Koen and Yonelinas (2010: K&Y, hereafter) dubbed this the “encoding variability account” and set out to test it by having participants learn words in two conditions. In the pure condition, 160 study words were presented for 2.5 s each. In the mixed condition, half the items (80 words) were presented for 1 s each (weak memory), and the other half for 4 s each (strong memory). Different study durations were used in the mixed condition in an effort to increase encoding variability compared to the pure condition. Following both lists, participants made a confidence rating (using a 6-point scale) and a Remember-Know-New judgment for each test item. Using the obtained data, K&Y applied three different tests to evaluate the encoding variability account.

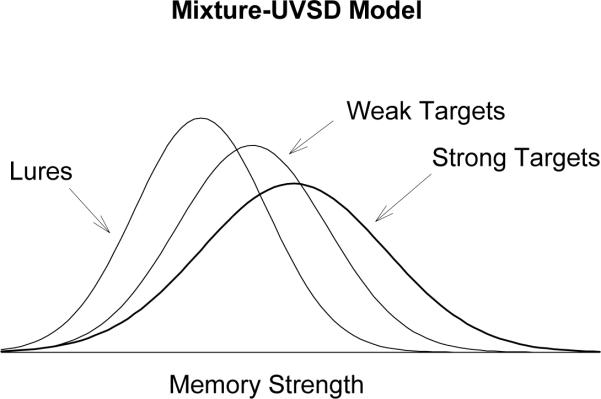
In the key test, K&Y assumed that mixing two distributions with different means yields a mixed target distribution with greater variance than the pure target distribution. If so, and if encoding variability explains why the zROC slope is usually less than 1, then, in their view, the slope of the zROC in the mixed condition should be less than that of the pure condition. Instead, the two slopes did not differ significantly, a result that K&Y considered to be inconsistent with the encoding variability hypothesis. However, this test and the other two tests reported by K&Y were compromised by both conceptual and analytical mistakes. Once the conceptual mistakes are corrected, it becomes clear that their experiment did not test the encoding variability hypothesis but instead tested a different idea. Specifically, their experiment tested whether the mixture-UVSD model shown in Figure 1 – which is the version of the standard UVSD model that applies to their experimental design – adequately accounts for the data from their mixed condition. K&Y argued that the mixture-UVSD model did not accurately predict the slope of the zROC in the mixed condition (which they took as evidence against the encoding variability hypothesis even though it would have made more sense to take it as evidence against the mixture-UVSD model). However, this test and the other two tests they reported contained a number of analytical mistakes. Once those analytical mistakes are corrected, it becomes clear that the mixture-UVSD does accurately predict the slope of the zROC in the mixed condition – a result that reflects well on the mixture-UVSD model but is still not relevant to the encoding variability hypothesis. Before describing the analytical mistakes that compromised their 3 tests, we begin with a description of the conceptual mistake that led K&Y to believe that they were testing the encoding variability hypothesis when they were in fact testing the mixture-UVSD model.

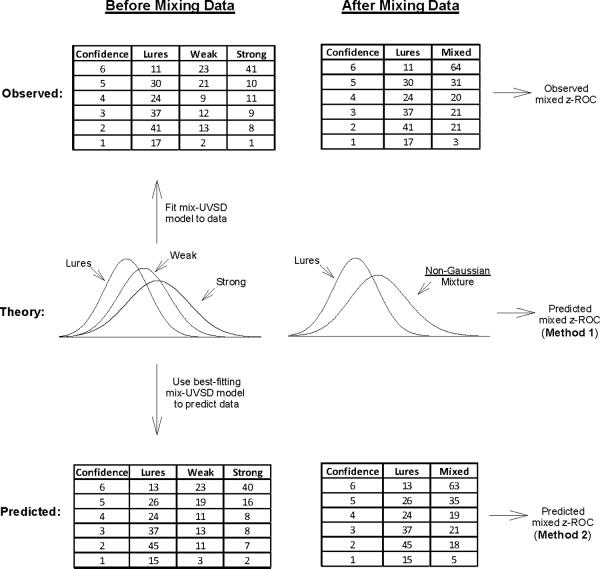
Figure 4.

Upper panel: Observed data from the mixed condition from one participant (subject #106 from Koen & Yonelinas, 2010) before mixing (left) and after mixing (right) confidence ratings made to the weak and strong targets. Middle panel: The mixture-UVSD model corresponding to the unmixed (left) and mixed (right) data. Lower panel: Predicted data from the mixed condition from the same participant before mixing (left) and after mixing (right) confidence ratings made to the weak and strong targets.

Adding Gaussian Random Variables Versus Mixing Gaussian Distributions

The main conceptual mistake in K&Y's effort to test the encoding variability hypothesis is that they equated adding random variables with mixing distributions. These are quite different operations, with different implications – facts that become clear when the mathematics of the encoding variability hypothesis are laid out.

Adding Gaussian Random Variables

The encoding variability hypothesis is based on the notion of adding random variables. It holds that the memory strength of a target item (T) can be conceptualized as having been created by adding memory strength (A) to the baseline memory strength (L) of a lure. Thus, T = L + A. In the simplest version of this account, both L and A are assumed to be independent, normally distributed random variables (N):

$$L~N({\mu }_{\mathit{lure}},{{\sigma }^2}_{\mathit{lure}})$$

$$A~N({\mu }_{\mathit{added}},{{\sigma }^2}_{\mathit{added}})$$

where μ_lure and σ²_lure represent the mean and variance of the lure distribution, and μ_added and σ²_added represent the mean and variance of the distribution of strength values added at study. Adding the Gaussian random variables L and A creates a new Gaussian random variable representing the strength of a target (T). When independent random variables are summed, the mean of the resulting distribution is equal to the sum of the means of the component distributions¹. Similarly, the variance of the resulting distribution is equal to the sum of the variances of the component distributions. That is:

$$T=L+A~N({\mu }_{\mathit{lure}}+{\mu }_{\mathit{added}},{{\sigma }^2}_{\mathit{lure}}+{{\sigma }^2}_{\mathit{added}}).$$

Thus, both the mean of the target distribution (μ_lure + μ_added) and the variance of the target distribution (σ²_lure + σ²_added) exceed the corresponding values for the lure distribution.

The critical feature of this encoding variability account is that the variance of the target distribution is greater than that of the lure distribution because the target distribution was created by adding one Gaussian random variable to another Gaussian random variable. A target distribution created in this way would remain Gaussian in form. Thus, the target and lure distributions in this model correspond to the longstanding Gaussian-based UVSD model. Because both distributions are Gaussian in form, empirical zROC data that are consistent with this model can be used to estimate the relative variance of the target and lure distributions. Specifically, under these conditions, the slope of the zROC provides a valid theoretical estimate of σ_lure / σ_target. This theoretical connection between the slope of the zROC and the underlying standard deviation ratio – a connection that holds for Gaussian distributions – will be a key consideration in our critique of K&Y's effort.

To test the encoding variability hypothesis, one might attempt to add variable amounts of memory strength to half of the study items on a list (e.g., by using a wide range of normally distributed study times) and to add less variable amounts of memory strength to the other half (e.g., by using a constant study duration). If the experimental manipulation were successful in influencing the distribution of confidence ratings supplied by the participants, then the encoding variability hypothesis would predict a lower zROC slope for the items that received the normally distributed study times than for the items that received constant study times. A test like this could encounter some practical difficulties (e.g., participants could surreptitiously rehearse the more briefly presented items in an effort to strengthen them), but at least it would be conceptually in line with the encoding variability hypothesis.

Mixing Gaussian Distributions

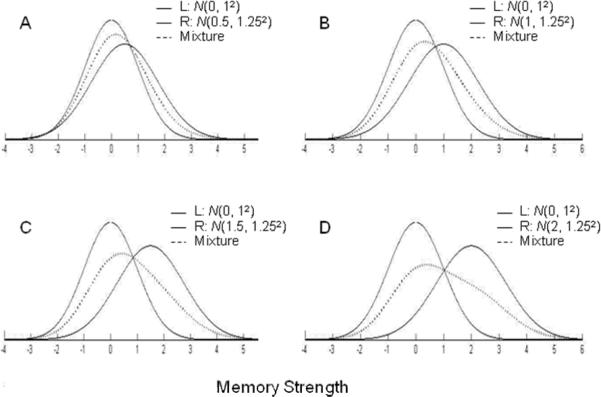
For reasons that are not clear, K&Y assumed that mixing weak and strong Gaussian distributions should have an effect analogous to that of adding Gaussian random variables. However, mixing two Gaussian distributions is quite unlike adding Gaussian random variables. Most importantly, mixing two Gaussian distributions with different means results in a non-Gaussian mixture distribution (though one that often remains Gaussian in appearance, as illustrated in Figure 2). Because a mixed target distribution is non-Gaussian, the slope of the mixed zROC does not provide a valid theoretical estimate of σ_lure / σ_target. Thus, comparing a theoretically valid estimate of σ_lure / σ_target in the pure condition to a theoretically invalid estimate of σ_lure / σ_target in the mixed condition is problematic, but it was the very essence of the approach used by K&Y. As they put it: “Thus, if encoding variability increases old item variance, the z-slope should be lower in the mixed list than in the pure list” (p. 1538).

Figure 2.

Non-Gaussian mixture distributions produced by mixing two Gaussian distributions, where the means of the left (L) and right (R) distributions differ by 0.5 (A), 1.0 (B), 1.5 (C) and 2.0 (D) standard deviations (the standard deviation of the left distribution is 1.0; and the standard deviation of the right distribution is 1.25 in each case). For each panel, the Gaussian distributions are shown as solid lines, and the resulting mixture distribution is shown as a dotted line. Note that the mixture distributions are all non-Gaussian even though the mixture distribution in Panel A appears to be Gaussian in form.

Whether or not the slope of the zROC is sensitive to the variance of a non-Gaussian mixture distribution is a purely empirical question, one that does not bear at all on the validity of the encoding variability hypothesis. Nothing in the encoding variability hypothesis (or in any other theory, for that matter) predicts that the Gaussian-based slope of the zROC will faithfully reflect the relative variance non-Gaussian mixture distributions. Thus, by focusing on the slope of the mixed zROC as their main dependent measure, K&Y addressed a purely empirical question that does not bear on any theory.

Further complicating matters is the fact that – contrary to intuition – mixing the weak and strong distributions in K&Y's experiment did not increase the variance of the mixed distribution to any appreciable degree. We show this later by simply fitting the mixture-UVSD model to the unmixed data and then using the estimated parameters of the weak and strong target distributions to computationally determine what the variance would be if those distributions were combined to create a single mixed distribution. When this is done, it becomes clear that the variance of the mixed distribution would be nearly identical to the variance of the weak and strong distributions considered separately, and this was true even for the 50% of participants for whom the strength manipulation had the greatest effect (whose data were separately analyzed by K&Y). This means that K&Y's main experimental objective – namely, to create a high-variance mixed distribution – was not achieved. Thus, even the purely empirical and theoretically irrelevant question of how the Gaussian-based mixed zROC slope behaves when the variance of the non-Gaussian mixed distribution increases cannot be answered by their experiment. Then again, even if they had achieved their objective, our criticism of their approach would not change because, even in that case, their experiment would still have addressed a question that differs from the one they intended to address (as we explain next).

What Question did K&Y's Experiment Address?

The encoding variability hypothesis does not hold that the slope of the zROC is less than 1 because distributions are mixed, so mixing distributions to investigate how the slope is affected provides no test of that hypothesis. Instead of addressing the encoding variability hypothesis, the theoretical issue addressed by K&Y's experiment concerns whether or not the mixture-UVSD model illustrated in Figure 1 can accommodate their findings. Indeed, the key feature of their experimental design (namely, mixing weak items and strong items on a single list) corresponds directly to that model. One can accept the validity of the mixture-UVSD model and can even accept the idea that, in principle, weak and strong target distributions can be combined to create a high-variance mixture distribution while still rejecting the essence of the encoding variability hypothesis (i.e., while still rejecting the idea that Gaussian random variables are added at study). Thus, the two accounts are not the same, and K&Y's experiment was properly designed to test only the mixture-UVSD model.

Although it is not the question that K&Y set out to answer, it is certainly legitimate to ask whether or not the mixture-UVSD model can accommodate their data. The most direct way to do that would be to simply fit the model to the unmixed data from the weak and strong conditions of K&Y's experiment. If it can accurately characterize the unmixed data, then it will automatically characterize the mixed data as well (including the mixed zROC slope). Indeed, it could be no other way. Thus, after fitting the mixture-UVSD model to the unmixed data and determining whether or not it fits the data well relative to competing models, taking the additional step of testing its ability to also account for the mixed data (e.g., testing whether it can predict the mixed zROC slope) is superfluous. Even so, we will consider the model's ability to account for the mixed data because that is the issue that K&Y emphasized, and in so doing, they made several analytical mistakes that we explain and correct. In addition, we will consider (and correct) other analyses that K&Y put forth to argue that the dual-process signal-detection (DPSD) model provides a more viable account of the data than an explanation grounded in signal-detection theory. Later, we simply fit the mixture-UVSD model to the unmixed data and assess how well it fits compared to the DPSD model. That simple test highlights what their experiment was really all about.

To investigate these issues as thoroughly as possible, we analyzed relevant data from four different experiments: (i) K&Y's experiment (i.e., we reanalyzed K&Y's data); (ii) Experiment 1, which is a replication study where we adopted exactly the same procedure as that of K&Y's experiment, with 22 participants; (iii) Experiment 2, which differed in that all three strength conditions appeared on a single list, with the pure condition consisting of study words presented for 1 s each and the mixed condition consisting of study words presented for 300 ms (weak) or 2 s (strong) – the complete procedure is reported in the Appendix; and (iv) Jang, Wixted, and Huber's (2011) experiment in which each study word was presented for 1 s, and weak (180 words) and strong (180 words) targets were manipulated by number of presentations (once versus three times, respectively). There was only the mixed condition in this experiment (i.e., it did not include a pure condition), and there was no Remember-Know (R-K) judgment task in (iii) and (iv) – only a 6-point confidence rating was given during the test phase. For each test that we correct from K&Y, we consider the data from their experiment as well as the relevant data from the additional experiments we conducted.

Three Tests and Three Corrections

Test 1 Correction

The first test involved a comparison between the observed mixed zROC slope and the observed pure zROC slope based on the intuition that mixing Gaussian distributions increased the variance of the mixed distribution beyond that of the component weak and strong target distributions, in which case it would be reasonable to assume that its variance was increased beyond that of the pure target distribution as well. However, there is no need to rely on intuition because it is possible to compute the variance of the mixed distribution based on the estimated parameters of the weak and strong distributions.

Assuming they are Gaussian in form, the means and standard deviations of the individual weak and strong target distributions (relative to the standard deviation of the lure distribution) can be estimated by fitting lines to the weak and strong zROCs. In the weak condition, K&Y reported that the average zROC slope for the 16 participants who showed the largest effect of the strength manipulation was 0.72 (σ_weak = 1 / 0.72, or 1.39) and the average intercept was 0.77 (μ_weak = 0.77 / 0.72, or 1.07). These estimates of σ_weak and μ_weak are scaled in terms of the standard deviation of the lure distribution (i.e., σ_lure = 1) and are based on standard signal-detection formulas (and they assume that the average slope and intercept values are representative of the individuals). In the strong condition, the average slope was 0.71 (σ_strong = 1 / 0.71, or 1.41) and the average intercept was 1.09 (μ_strong = 1.09 / 0.71, or 1.54).

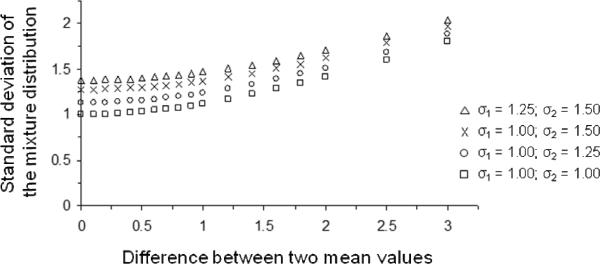
What is the standard deviation of the distribution that results from mixing a weak target distribution having a mean of 1.07 and a standard deviation of 1.39 with a strong target distribution having a mean of 1.54 and a standard deviation of 1.41? The answer can be obtained by randomly generating a large number of values from the weak and strong Gaussian distributions using a MATLAB routine and then simply computing the variance of those values after mixing them together. Using this method, we found that the resulting mixed distribution would have a mean of 1.31 and a standard deviation of 1.42. That is, despite a fairly large difference in the means of the weak and strong distributions (μ_strong − μ_weak = 1.54 − 1.07 = 0.47), the standard deviation the mixed distribution (1.42) was, counterintuitively, nearly identical to that of the weak and strong component distributions (1.39 and 1.41, respectively). Figure 3 provides a further illustration of the counterintuitive effect of mixing distributions with different means. Obviously, mixing distributions can result in a mixed distribution with greater variance, but, as shown in Figure 3, the difference between the means needs to be much greater than intuition would suggest (and much greater than the difference between the weak and strong means in K&Y's experiment).

Figure 3.

Standard deviation of the mixture distribution as a function of mean difference between two Gaussian distributions. Four situations are illustrated: an equal-variance case (each standard deviation of the weak and strong memory distributions is 1.0) and three unequal-variance cases (the difference in standard deviation is 0.25 or 0.50, which is often seen in empirical data). As shown in the figure, the effect of mixing targets on the standard deviation of the mixture distribution is negligible until the difference between the two means is large (at least 1.20).

This analysis shows that K&Y's strategy of mixing distributions did not create a high-variance mixed distribution (contrary to what they believed was true), and the fact that the mixed zROC slope was not reduced compared to the pure zROC slope needs to be considered in that light. If the mixed zROC slope provides an accurate estimate of σ_lure / σ_target for even non-Gaussian mixture distributions, then the results reported by K&Y are just as they should be. But does the Gaussian-based mixed zROC slope fortuitously provide an accurate estimate of σ_lure / σ_target for non-Gaussian mixture distributions even though there is no theoretical reason why it should? In this particular case, it would seem so. After all, the variance of the mixed distribution was not increased compared to the pure condition, and (correspondingly) the mixed zROC slope was not reduced compared to the pure zROC slope. However, it is easy to find examples where the underlying variance of the non-Gaussian mixed distribution is quite far removed from a Gaussian-based estimate obtained from the slope of the corresponding mixed zROC, so the correspondence that happened to be observed in this case is not likely to generalize. To take one such example, assume that the means of the weak and strong distributions were the same as before (1.07 and 1.54, respectively) but their standard deviations differed (1.0 and 1.5, respectively). In this case, the standard deviation of the mixed distribution based on simulated data drawn from those weak and strong Gaussian distributions turns out to be 1.30. However, as we show next, the slope of the mixed zROC for this situation does not reflect that value.

Using the simulated mixed target data drawn from the weak target distribution (μ_weak = 1.07, σ_weak = 1.0) and strong target distribution (μ_weak = 1.54, σ_weak = 1.5), coupled with additional simulated data drawn from a hypothetical lure distribution (μ_lure = 0, σ_lure = 1), one can create simulated mixed zROC data and then fit those simulated data with a straight line. Because the model producing the zROC data in this case involves a non-Gaussian mixture distribution (i.e., the lure distribution is Gaussian but the mixed target distribution is not), the data will not trace out a strictly linear path. Thus, obtaining a slope estimate is somewhat problematic because the estimate changes slightly depending on the range of hit and false alarm rate data that are included in the analysis. Indeed, this turns out to be the main source of the analytical error associated with K&Y's Test 2, which we discuss in more detail in the next section. Although the slope estimate changes with the range of zROC data considered (thus, there is no true slope estimate), it does not change much, and the key point for present purposes is that the mixed slope estimate in this example is never close to what it should be. Instead, for this case, the mixed zROC slope is generally close to 1.0, which is quite far from what would be expected given the mixed target standard deviation of 1.30 (i.e., it is quite far from 1 / 1.30, or 0.77).

This exercise shows that the Gaussian-based mixed zROC slope does not provide an accurate estimate of the underlying standard deviation of non-Gaussian mixed distributions (of course, there is no reason why it should), and it illustrates why, if the question has to do with the underlying variance of a mixed distribution, an analysis of the mixed zROC slope does not yield theoretically relevant results. Neither the mixture-UVSD model nor the encoding variability hypothesis predicts that the slope of the mixed zROC should faithfully track the variance of a non-Gaussian mixed distribution. Thus, even if K&Y had succeeded increasing the variance of the mixed distribution compared to pure condition, their findings about the effect of that manipulation on the mixed zROC slope would have had no relevance to the encoding variability hypothesis or the mixture-UVSD account.

Test 2 Correction

In Test 2, K&Y directly compared the observed mixed zROC slope to the value that they believed was theoretically predicted by the mixture-UVSD model (instead of comparing it to the slope from the pure condition, as was done in Test 1). Although the theory that was used to generate the predicted values was the mixture-UVSD model, K&Y nevertheless construed Test 2 as a test of the encoding variability hypothesis. It is important to emphasize again that, contrary to what they claimed throughout their paper, their experiment tested the mixture-UVSD model, not the encoding variability hypothesis.

In any case, the question of how to use the mixture-UVSD model to predict the mixed zROC slope is nontrivial because (as indicated above) the model is being used to predict a zROC slope for nonlinear zROC data (and a nonlinear function does not have a linear slope). The data are predicted to be nonlinear because the mixed target distribution is non-Gaussian (as illustrated in Figure 2). K&Y were not sensitive to this issue, so they ended up using a flawed method. The method used by K&Y to compute the predicted mixed slope is illustrated in Figure 4 and is labeled “method 1”, whereas the appropriate method is labeled “method 2”. Methods 1 and 2 begin the same way: the mixture-UVSD model is first fit to the data from the unmixed data for each participant. Here, it is important to fit the full model to the unmixed weak and strong data using maximum likelihood estimation (MLE) instead of more simply estimating the distributional parameters by fitting straight lines to the weak and strong zROC data. The MLE method involves simultaneously estimating 9 parameters for each participant: 5 confidence criteria, and a mean and standard deviation for both the weak target distribution and the strong target distribution (with the mean and standard deviation of the lure distribution set to 0 and 1, respectively). As mentioned above, the analysis should have stopped right there (with goodness-of-fit assessed against competing models), but K&Y proceeded to test the model's ability to also describe the mixed data using method 1 (because, in their view, this offered a test of the encoding variability hypothesis).

In method 1, the Gaussian densities for the weak and strong targets are averaged to create a non-Gaussian mixture distribution, and the resulting 2-distribution model is used to generate predicted zROC data by sweeping a criterion from left to right from −5 to 5 in steps of 0.1, where the values refer to standard deviations relative to the lure distribution (which has a mean of 0 and standard deviation of 1). This is the method used by K&Y², and it is essentially the same method we used in our discussion of Test 1 to show that the slope of the mixed zROC does not correspond to the underlying standard deviation of the mixed distribution. As indicated earlier, the problem with this method is that, because the predicted zROC data are nonlinear, the slope of the best fitting line will change depending on the range of hit and false alarm rates used in the zROC analysis.

Figure 5 illustrates this point. The figure shows four zROC plots based on method 1 for the data shown in the upper panel of Figure 4. The upper panel of Figure 5 shows zROC data that were generated by sweeping a criterion across the 2-distribution version of the mixture-UVSD model from −5 to 5 in steps of 0.1 (as K&Y did). The zROC data appear to be linear (just as a non-Gaussian mixture distribution often appears to be Gaussian: e.g., Panel A of Figure 2), but they are not. The slope of the best-fitting line is 0.77. The next panel shows the zROC data generated by sweeping a criterion over a smaller range (from −4 to 4) in steps of 0.1. Now, the slope of the best-fitting line is 0.78. The slope increases to 0.79 as the range decreases to −3 to 3, and it increases still further (to 0.80) when a range of −2 to 2 is used. These changes in slope are not due to error variance because there is no error in these model-generated points. Instead, the slope changes with the range because the predicted zROC data are nonlinear (which means that no single predicted estimate can be obtained using this approach). When fitting the observed zROCs to individual subject data, the range was typically on the order of −1 to 2 (much less than the −5 to 5 range used to generate the predicted slope), and it differed for different participants. This explains why K&Y found that the predicted mixed zROC slope (0.70) differed slightly, but significantly, from the obtained mixed zROC slope (0.74).

Figure 5.

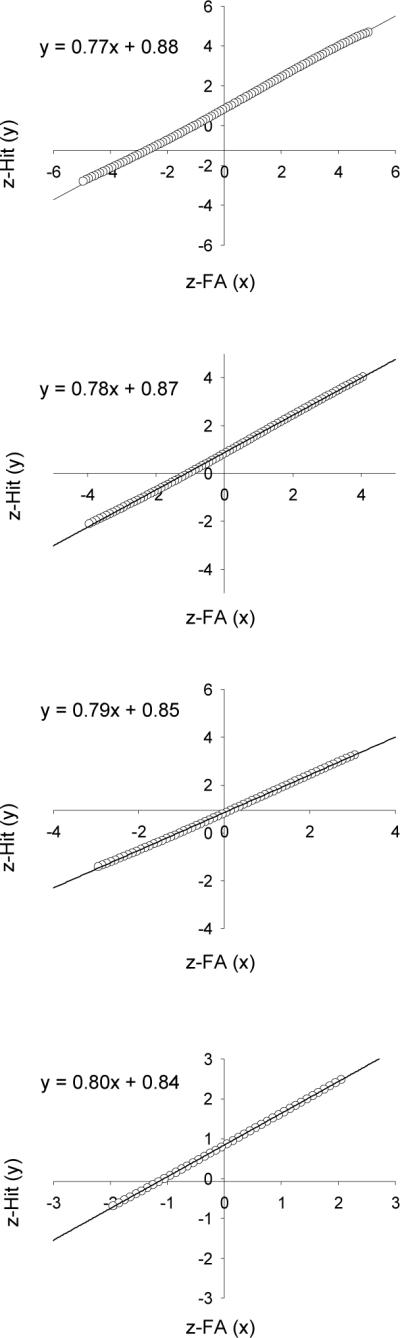
zROC data generated by sweeping a criterion across the 2-distribution non-Gaussian model shown in the middle right panel of Figure 2. The criterion was incremented in steps of 0.1. The only difference across the four zROC plots is the range over which the criterion was swept (from −5 to 5 in the top panel to −2 to 2 in the bottom panel). The straight lines represent least-squares fits, and the equation for each best-fitting line is shown on each plot.

The appropriate way to compute the predicted zROC slope is to simply generate from the best-fitting model predicted confidence ratings for the three item categories (lures, weak targets and strong targets), as shown in the lower left panel of Figure 4 for one participant. These predicted values can be used to compute a goodness-of-fit statistic for each participant (as is usually done) and can also be used to determine the predicted zROC slope for the mixed condition by following the same steps that were used for the observed data. More specifically, just as is done with the observed weak and strong confidence ratings to create mixed target data (upper panel of Figure 4), the predicted weak and strong confidence ratings are simply added together (lower panel of Figure 4). Using these predicted data, the predicted mixed zROC is then plotted and fit with a straight line via least squares regression. The slope of this line is the zROC slope that is predicted by the mixture-UVSD model. Even though both the observed mixed zROC and the predicted mixed zROC are theoretically nonlinear (because they are based on a model that involve a mixed non-Gaussian target distribution and a Gaussian lure distribution), the slopes of the straight lines fit to the data can be meaningfully compared because the observed and predicted data for each participant were treated in exactly the same way (i.e., the range of data and the number of data points are the same in both cases, so the effect of any nonlinearity in the data will be equated for each participant).

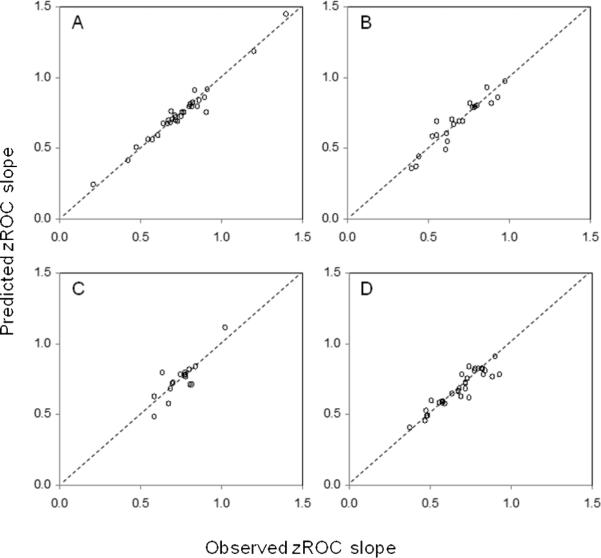
Table 1 shows the Observed versus Predicted mixed zROC slope values computed on an individual participant basis for each of the four experiments. Clearly, the observed mixed zROC slope is always close to the predicted zROC slope, and the slight differences that exist are never close to being significant. Thus, the results are consistent with the predictions of the mixture-UVSD model in all four experiments. Figure 6 shows the scatter plots of observed versus predicted zROC slopes. All four experiments (including K&Y's) show a close correspondence between the observed and predicted zROC slopes. As described earlier, this result merely indicates, in an indirect way, that the mixture-UVSD model provides a good fit of the unmixed data (in which case it will also accurately characterize the mixed data). The fact that it provides a good fit does not have any bearing on the encoding variability hypothesis, but it does lend some credence to the mixture-UVSD model.

Table 1.

Observed and the UVSD model's predicted mixed zROC slopes

		zROC slope		t
Data	ss	Observed	Predicted	Observed vs. Predicted
K&Y	32	0.75a	0.74	0.99
		(0.21)	(0.21)	p = .33
Exp 1	22	0.68	0.68	0.38
		(0.16)	(0.17)	p = .70
Exp 2	17	0.75	0.73	1.31
		(0.10)	(0.14)	p = .21
Jang et al. (2011)	35	0.68	0.68	0.36
		(0.14)	(0.13)	p = .72

Note. Mean values of the zROC slopes across individuals are on the upper row for each data set; Standard deviations are in parentheses; K&Y = Koen and Yonelinas (2010); Exp = experiment; ss = number of subjects.

^aK&Y reported the mean of 0.74 (p. 1539), but our reanalysis of their data yielded the mean of 0.75.

Figure 6.

Scatter plots of the observed zROC slope and the predicted zROC slope of the UVSD model: (A) Koen & Yonelinas (2010); (B) Experiment 1; (C) Experiment 2; and (D) Jang et al. (2011).

Test 3 Correction

In Test 3, K&Y used R-K judgment data to predict the confidence-based zROC slope in the mixed condition. They argued that the DPSD model could make use of the R-K data to more accurately predict the mixed zROC slope (based on confidence ratings) than the UVSD model could. However, the predicted zROC slope was calculated in very different ways for the two models, and the differing methods introduced a built-in advantage for the DPSD account. In this section, we show that simulated data generated by the UVSD model, when subjected to the same test performed by K&Y, are better explained by the DPSD model than by the model that actually generated the data (the UVSD model). This outcome shows that the test was uninformative because it was preordained to favor the DPSD model.

Predicting zROC slopes

The parameters of the DPSD model consist of a recollection parameter, a familiarity parameter, and 5 confidence criteria parameters. To calculate a predicted zROC slope, the 7 parameters of the DPSD model were first estimated in a way that made use of the R-K data. However, the R-K judgments were used to estimate only two of the parameters (the recollection parameter and the familiarity parameter). The recollection parameter estimate was a probability value obtained by subtracting the Remember false alarm rate (R_FA) from the Remember hit rate (R_Hit), and the familiarity parameter estimate was a d' score obtained from the Know hit rate (K_Hit) and Know false alarm rate (K_FA) after correcting them using the following formulas: K_Hit / (1 − R_Hit) and K_FA / (1 − R_FA), respectively. The 5 confidence criteria were not estimated from the R-K data and were instead estimated using the observed false alarm rates associated with each confidence rating. With the DPSD parameters fully specified in this way, the model was used to predict 5 hit and false alarm rate pairs from which the predicted zROC slope was obtained. This test was performed for both the pure and the mixed conditions, but we focus only on the latter (because the results were the same in both cases).

The method used for the UVSD model was altogether different. To calculate the predicted zROC slope from the R-K data using the UVSD model: “remember and know judgments were plotted in z-space as different confidence levels, and the slope and intercept of the best fitting line was measured” (p. 1540). Note that, in this method, only 2 hit and false alarm rate pairs were used to compute the predicted zROC slope. One pair consisted of the Remember hit and false alarm rates, and the other pair consisted of the Remember + Know hit and false alarm rates. K&Y found that the correlation between the predicted and observed zROC slopes was much higher for the DPSD model than for the UVSD model (.56 and .17, respectively). On that basis, they concluded that the DPSD model is superior to the UVSD model and that the “old item variance effect arises because both recollection and familiarity contribute to old item recognition” (p. 1540). As shown in Table 2, we confirmed their findings based on a reanalysis of their data, and we also replicated those findings in our Experiment 1 (see rows labeled “Empirical data”). Thus, both experiments show that R-K judgments can be used by the DPSD model to more accurately predict the slope of the mixed zROC than the UVSD model.

Table 2.

Correlation coefficient between the R-K predicted zROC slope and the zROC slope observed from the confidence rating data

		UVSD			DPSD
Data		ssa	r	P	ss	r	P
K&Y	Empirical data (p. 1540)	30	.17	.36	31	.56	< .05
	UVSD simulated data (N = 100)	30	.15		31	.47
Exp 1	Empirical data	21	.18	.43	22	.49	< .05
	UVSD simulated data (N = 100)	21	.30		22	.57

Note. Correlation coefficients were calculated with the individual zROC slopes for each data set (upper row) and averaged across 100 simulated experiments (lower row); R-K = Remember-Know judgments; UVSD = unequal-variance signal-detection model; DPSD = dual-process signal-detection model; K&Y = Koen and Yonelinas (2010); Exp = experiment; ss = number of subjects; N = number of simulated data per subject.

^aK&Y reported that "One participant was excluded from this analysis because her or his estimated z-slope was greater than five standard deviations from the group mean” (p. 1540). The same was true for the data analysis of Exp 1.

Testing simulated UVSD data

Despite appearances to the contrary, this result does not weigh in favor of the DPSD model. To show this, we generated simulated data from the UVSD model using the parametric bootstrap sampling technique (so that the true model was not in doubt) and then performed on the simulated data the same test that K&Y performed on the observed data. To generate the simulated data, the mixture-UVSD model was fit to the observed confidence ratings of each individual data set, and then, using the estimated parameters, a simulated data set for each individual was generated from the mixture-UVSD model. This was similar to generating precise predicted values (as in Figure 4), except that now target and lures were randomly selected from the underlying Gaussian distributions in numbers equivalent to the number of targets and lures used in the experiments. Thus, the predicted values were not exact but contained error variance (as real data do). Predicted R-K data were generated in much the same way. Specifically, we first fit the UVSD model to the observed R-K data to estimate model parameters for each participant. A saturated UVSD model can be estimated from such data, yielding 4 parameters: a discriminability parameter, a slope parameter, an old/new criterion parameter, and an R-K criterion parameter. Using the estimated parameters, a simulated set of RK data was generated for each individual. The simulated confidence data and simulated R-K data (both generated from the UVSD model) were then analyzed in the same way that the real data were analyzed by K&Y (i.e., using different methods for the two models), and the entire procedure was repeated 100 times for each individual data set (i.e., 100 simulated experiments).

Because the simulated data were generated by the UVSD model, one would naturally expect to find that the correlation between the R-K predicted zROC slope and the observed zROC slope (from the confidence rating) would be greater for the UVSD model than the DPSD model. However, the opposite was found. As shown in Table 2 (see rows labeled “UVSD simulated data”), the average correlation across 100 simulated experiments was much greater for the DPSD model even if the simulated data were generated by the mixture-UVSD model. The same results were found with the simulated data based on our Experiment 1. Thus, the DPSD model outperformed the mixture-UVSD model even when the mixture-UVSD model generated the data. This outcome demonstrates that Test 3 is not a useful way to differentiate between the models because it is strongly biased to favor the DPSD model (see also, Jang, Wixted, & Huber, 2009).

How could it happen that the wrong model outperformed the correct model in this simulated analysis? One possibility is that the number of points used in the linear regressions that were used to generate the predicted zROC slopes was different for the two models. To predict the zROC slope for the DPSD model, K&Y used 5 data points. By contrast, to predict the zROC slope for the UVSD model, only 2 data points were used. A slope estimate based on only 2 points is likely to be much noisier than one based on 5 points, and that alone would be expected to reduce the correlation between the observed and predicted slopes. Whatever the explanation, it is clear that K&Y's Test 3 yields the same outcome (in favor of the DPSD model) even when the data are known to have been generated by the UVSD model. That being the case, the test is not informative.

Which Model Provides a Better Account of Mixed-Strength Data?

Because the results reported by K&Y are clearly consistent with the mixture-UVSD model, those results cannot be taken as evidence against that model or against the encoding variability account of why the slope of the zROC is typically less than 1. In fact, the mixture-UVSD model and the validity of the encoding variability hypothesis are distinct issues, and the experiment conducted by K&Y bears only on the former (namely, the validity of the mixture-UVSD model). The issues are distinct because one can accept the validity of the mixture-UVSD model without accepting the encoding variability account of why the two target distributions have greater variance than the lure distribution. In addition, the results of their third test cannot be taken as evidence favoring the DPSD model over the mixture-UVSD model because the test was unintentionally biased to favor the DPSD model (so it chooses the DPSD model as the winner even when it is applied to simulated data generated by the UVSD model). A more informative way to compare the two models is the traditional way based on the chi-square goodness-of-fit statistic (after fitting the models to the individual data via maximum likelihood estimation). We performed this analysis on the data from all four experiments considered here. Both models were simultaneously fit to the data from the weak and strong conditions for each individual (which is possible because strength was manipulated within list: e.g., Jang et al., 2011), and Table 3 summarizes the results. As seen in the table, the UVSD model provided a better fit to a majority of the data (shown in boldface type: 63 out of 106 individual data, 59%, across all four experiments)³ although in K&Y's experiment, 15 versus 17 individuals (out of 32) were better fit by the UVSD and DPSD models, respectively. The summed chi square of K&Y's experiment was slightly lower for the DPSD model (UVSD – DPSD = 8.75). Thus, the two models were effectively tied in their experiment. However, the UVSD model provided a much lower chi square for the rest of the three experiments (−35.92, −27.06, and −66.03, respectively). Overall, these results exhibit an advantage for the UVSD model.

Table 3.

Sum of the chi-squares across individual data and percentage of individuals who are better explained by the UVSD model

		Σ χ 2		%
Data	ss	UVSD	DPSD	UVSD	DPSD
K&Y	32	251.73	242.98	47	53
Exp 1	22	202.56	238.48	64	36
Exp 2	17	105.46	132.52	59	41
Jang et al. (2011)	35	343.46	409.49	69	31

Note. UVSD = unequal-variance signal-detection model; DPSD = dual-process signal-detection model; K&Y = Koen and Yonelinas (2010); Exp = experiment; ss = number of subjects.

Conclusion

The slope of the zROC in studies of recognition memory is usually less than one. K&Y reported results from three tests that they believed weighed against an encoding variability account of the UVSD model's interpretation of that common finding (the interpretation being that the variance of the target distribution exceeds that of the lure distribution). In addition, they argued that their results favor a dual-process interpretation of the zROC slope based on the DPSD model. However, we have shown that none of their tests bear on the encoding variability hypothesis (even in principle) and that all of their tests, which actually bear on the mixture-UVSD model, contained errors. When those errors are corrected, the mixture-UVSD model is compatible with all of their findings, and it generally fits mixed-strength data better than the DPSD model. Thus, it is a mistake to conclude, as K&Y did in the title of their paper, that “memory variability is due to the contribution of recollection and familiarity, not to encoding variability.“ Instead, their results reinforce the idea that when the zROC slope is less than one, it indicates that the memory variability of the targets is greater than that of the lures (an interpretation that is specific to the UVSD model in the case of pure targets and to the mixture-UVSD model in the case of mixed-strength targets). Whether or not encoding variability adequately explains the greater memory variability of the targets compared to the lures remains to be tested.

Figure 1.

Illustration of the mixture-UVSD model that applies to the mixed condition from Koen and Yonelinas (2010). In this model, all three distributions are Gaussian in form.

Appendix

Method of Experiment 2

Experiment 2 was similar to Koen and Yonelinas (2010) with a few exceptions, which are described below.

Participants

Eighteen undergraduate students participated for psychology course credit. For data analysis, one was excluded because it appeared that this participant did not fully understand the instructions.

Materials

The three-to-seven letter words were pooled from the MRC Psycholinguistic Database (Coltheart, 1981), and they were high in concreteness, familiarity, and imaginability (i.e., ratings between 500 and 700), which yielded 682 total words. For each participant, 300 words were randomly selected from the pool, with 200 words randomly assigned as targets and 100 words randomly assigned as lures. Additional 16 words were randomly chosen for the practice trials, which were not included for data analysis.

Procedure

The experiment consists of study and test phases. During the study phase, a fixation mark first appeared for 250 ms. Following the mark, each study word was presented in random order. One hundred of the 200 words (randomly selected) were presented for 1 s (pure), one at a time. Half the remaining 100 words were presented for 300 ms (50 weak targets), and the other half for 2 s (50 strong targets). Participants were asked to think about as many related words, concepts, and associations as they could while a word was on the screen.

During the test phase, target and lure words appeared on the screen, one at a time, along with a 6-point confidence rating scale. A response of 1 through 3 indicated definitely new, probably new, and maybe new; and a response of 4 through 6 indicated maybe old, probably old, and definitely old. Using mouse, participants clicked on the rating scale to indicate the level of confidence that each word was old or new.