Dynamic Heterogeneity and Life Histories

Abstract

Biodemography is increasingly focused on the large and persistent differences between individuals within populations in fitness components (age at death, reproductive success) and fitness related components (health, biomarkers) in humans and other species. To study such variation we propose the use of dynamic models of observable phenotypes of individuals. Phenotypic change in turn determines variation among individuals in their fitness components over the life course. We refer to this dynamic accumulation of fitness differences as dynamic heterogeneity and illustrate it for an animal population in which longitudinal data are studied using multi-state capture-mark-recapture models. For our empirical example we use reproduction as the phenotypic character to define stages though our approach can be applied to any characteristic. We indicate how our stage-structured model describes the nature of the variation among individual characteristics that is generated by dynamic heterogeneity. We conclude by discussing our ongoing and planned work on animals and humans. We also discuss the connections between our work and recent work on human mortality, disability and health, and life course theory.

INTRODUCTION

An early focus of evolutionary ecology and demography was the “typical” age-pattern of mortality and reproductive status of individuals within species.¹ In recent years, increasing attention has been paid to the large and persistent differences between individuals within populations in age at death and reproductive success, as observed in humans and other species.^{2, 3, 4} Demographers come at these questions by decomposing variation into contributions from demographic, socioeconomic and biological characteristics of individuals and groups. Such decompositions now exploit results from mechanistic biology that suggest how causal relationships between genotypes, phenotypes, and environment may translate into observed variation in death and reproduction.^{5, 6} Evolutionary biologists have tended to focus on comparing variation among individuals within and between populations and species, and on explaining the results of such comparisons in terms of the forces of evolution,^{7, 8} as they play out in particular biological and environmental settings. These studies concern one or more levels of biological organization. Within a species, we are interested in describing variation among individuals and populations, the forces responsible for maintaining this variation, and in predicting the response of individuals to environmental change. Across species, we are interested in differences in both average patterns and variation in life histories, as well as species-level responses to environmental change. This paper focuses on variation among individuals, and argues that a key task of biodemography is to understand how variation among individuals is created and maintained across generations. Such an understanding is essential if we are to influence and reshape either phenotypic change at the individual level or population dynamics, in contexts as disparate as human health and ecological responses to global climate.

An influential argument says that variation in fitness-related traits such as age at death may be due to variation in fixed individual traits that affect relative fitness over life.^{9, 10} Such fixed traits are typically assumed to be fixed at birth and to affect fitness throughout life, may often be unobserved (or unobservable), and are elements of what may be called “frailty.” This argument is influential in part because of an explicit or implicit assumption that such fixed differences in phenotypic traits are determined by heritable genetic differences and are being maintained by evolutionary processes. We refer to this kind of variation as “fixed heterogeneity.” The assumption that frailty is the main determinant of individual fitness has been widely used to model and interpret data on human mortality¹¹ and also data on animal life histories.⁷ We propose an alternative view of the determinants of individual fitness. This view is rooted in the fact that the observed phenotypes of individuals (including, e.g., size, energy stores, immune competence, metabolic state, health, biomarkers) change over their lives, and that changes within individuals in their phenotypic traits over any age interval may differ among individuals. Hence any one individual follows a trajectory in a “space” of phenotypic values, and distinct individuals can follow distinct trajectories. An individual's fitness components (survival, reproduction) at any time are often largely determined by the individual's present (and past) phenotypic states, and so individuals can follow different trajectories of relative fitness over the life course. These trajectories are defined by observed values of phenotypic traits at different time points in a life course, and we describe the dynamics of such phenotypic trajectories over time by a stochastic (usually Markov) process. The distribution of alternative trajectories then determines observed variation among individuals in both phenotypic traits and fitness.³ We refer to this kind of variation as “dynamic heterogeneity.” This kind of dynamic heterogeneity in observable phenotypes has been relatively little used to analyze and explain variation in fitness components, although models of dynamic heterogeneity are often estimated for animal populations^{3, 12} and some longitudinal models of human mortality are similar in spirit.^{13, 14, 15}

In the next section we explain precisely what we mean by dynamic heterogeneity and provide an illustration from an animal population in which longitudinal data are studied using multi-stage capture-mark-recapture models.^{3, 12} Following that we explain the novel features of dynamic heterogeneity in the context of a simple mathematical model. We indicate how this model describes the average pattern of life histories as well as the nature of the variation among individual characteristics that is generated by dynamic heterogeneity. We then discuss our work on other animal species and the directions for subsequent analysis. We conclude by discussing the many connections between our work and recent work on human mortality, disability and health, and life course theory¹³ and our planned work on humans.

THE NATURE OF HETEROGENEITY

Dynamic heterogeneity

We focus on one or more observable phenotypic traits of individuals. These may include, e.g., continuous traits such as size,¹⁶ discrete states such as reproductive maturity or menopause^{17, 18} and states such as the level of reproduction in a year that may be treated as discrete or continuous.^19,3 More formally, every individual has a set of observable phenotypic traits P and individuals born at time t have a distribution f(P,0,t) of these traits. As an individual ages, its phenotypic traits may change for many reasons, such as maturation, growth, reproduction, or senescence. As a result of such processes, at age a the trait distribution of a cohort born at time t changes from the distribution at birth to a new distribution f(P,a, t+a). We can quantify the dynamics of phenotypic change by estimating transition probabilities p(P₂,t+1|P₁,t)from the rates at which individuals change their phenotypic state. We can also estimate the relationship between an individual's mortality and reproduction in year t and its phenotypic state P_t in that year. It is possible that these fitness components may depend on the individual's phenotypic trajectory and not just its current phenotype²⁰ but to keep things simple we assume for now that only the current state matters (i.e., the dynamics follow a Markov process²¹).

We describe a single individual by its phenotypic trajectory, i.e., a sequence of phenotypic states P₀, P₁, P₂,... at successive times 0, 1, 2, and so on. A cohort is described by a bundle of such trajectories, one for each individual; a population is described by many bundles of trajectories, one for each cohort. Dynamic heterogeneity means that individuals who are in the same phenotypic state in one year may follow distinct phenotypic trajectories in the future, e.g., when two individuals with phenotype P_t in year t end up with different phenotypes P_t+1, P̂_t+1 in year t+1. As a result a cohort's phenotypic distribution tends to become increasingly dispersed as the cohort ages. This dispersion is balanced by intracohort selection that results from differences in mortality among different phenotypic states of individuals. Over the life course, an individual's cumulative survival probability depends on its phenotypic trajectory. In addition to survival, an individual's reproduction in any year is also a function of its current phenotypic state, and thus reproduction will vary among individuals of the same age. Lifetime reproduction is a function of the entire phenotypic trajectory and can vary even among individuals who die at the same age.

Dynamic variation of this kind is generated by a stochastic process that causes individuals to follow divergent phenotypic trajectories. To illustrate we consider data on the mute swan, Cygnus olor, collected since 1976 on a well-known population in Abbotsbury, U.K. These are among the best longitudinal data on a natural population^{22, 23} and we have reported on these data elsewhere;³ the latter paper provides additional detail. We classify individuals using a single discrete phenotypic trait, reproductive state. In each year each female is categorized as being in one of five reproductive stages: immature (stage 1), having a “low” clutch size of 1-4 (stage 2), having a “medium” clutch size of 5-6 (stage 3), having a “high” clutch size of 7-12 (stage 4), or being non-reproductive in that year after having reproduced at least once previously (stage 5). Capture-mark-recapture analysis¹² is used to estimate a Markov transition matrix describing the probability of moving between stages in successive years as well as age and stage specific survival rates. In the Mute swan example and other examples the results and their interpretation in terms of dynamic heterogeneity are fairly robust to using different numbers of discrete classes, or different ranges to delineate classes³. However the choice of a focal phenotype (e.g. size instead of reproductive state) can lead to quite different transition dynamics. The use of discrete phenotypic classes versus continuous phenotypic values, or of just one phenotypic trait versus two or more, is driven by data quality and quantity and biological insight. When data allow, it is probably better to use continuous phenotypic values¹⁶ rather than a large number of classes.

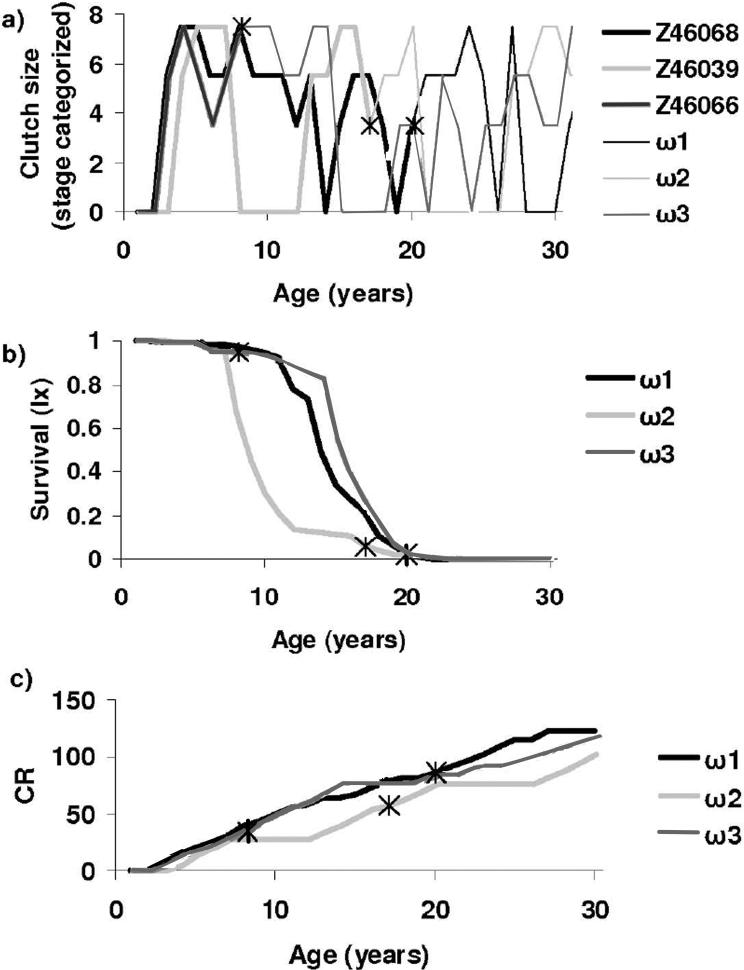
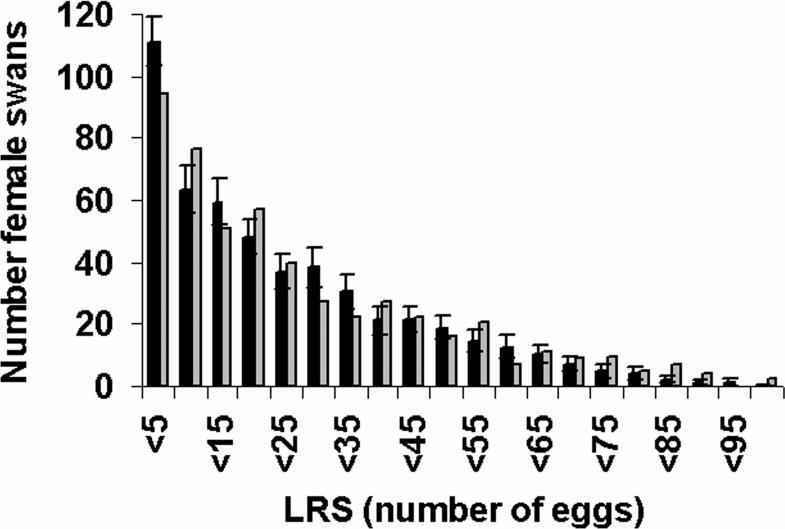
Figure 1 (a) displays stage trajectories for three swans: the stars indicate actual ages of last observation and the trajectories past the stars are simulations using the estimated stage transition rates. Survival rates depend on stage and age and thus for each trajectory in Figure 1 (a) we can compute a survivorship, as shown in Figure 1 (b). Finally Figure 1 (c) shows the cumulative reproduction at each age. Clearly individual birds achieve rather different lifetimes and cumulative reproduction. Using the estimated model, we can also simulate a sample of birds that matches the data (in numbers and censoring) and find that we can predict nicely the variation in lifetime reproductive success in the sample; see Figure 2. Figure 2 also drives home the point that there is very large variability among individuals in lifetime reproduction, a quantity that is often used as a proxy for fitness. But in fact, these birds are all members of a population that has one overall growth rate. We reviewed a number of studies on different species³ and found that large variation in fitness components is typical, not unusual. In studies that have been done over many generations, there is evidence that this large variation persists over time, suggesting that this level of variation is evolutionarily stable.

Figure 1.

(a) Reproductive stage trajectories for female Mute swans. Reproductive stage in each year has one of five values (see text). Observed sequences are shown for three birds and death or disappearance is indicated by a star. Past the star we have generated one possible trajectory by simulation using our estimated transition probabilities for the population. (b) Survivorship for the three trajectories shown in panel (a). A key point is that survival depends on stage and so every distinct sequence of stages (i.e., life course) determines a potentially distinct survivorship. (c) Cumulative reproduction (CR), the number of eggs laid to a given age, for the three trajectories shown in panel (a). Reproduction here varies by stage and so every distinct sequence of stages (i.e., life course) determines a potentially distinct trajectory of cumulative reproduction.

Figure 2.

Distribution of Lifetime Reproductive Success (LRS) for female Mute swans. The observed distribution (including potential latent factors) is shown by grey bars and the average distribution for 50 simulated synthetic populations is shown by black bars (± standard error). Strong fixed effects should lead to large deviances in distribution between the synthetic populations and the observed population. LRS is right censored for some of the observed individuals which has been taken into account for the simulations.

Thus dynamic heterogeneity is generated as individuals move along the life course. Even though every individual follows the same stochastic process, the vagaries of chance produce large differences among individuals as they age. In our fitted model, differences among individuals in marginal fitness at any age, or in measures of lifetime fitness, generated by dynamic heterogeneity reflect chance, not fixed differences in “frailty” or “quality.” In the real world, differences in fixed frailty could also contribute to variation among individual phenotypes or performance, but the detection of fixed differences has been difficult, as we now explain.

Fixed heterogeneity

When we observe variation in fitness components among individuals, it is tempting to argue that this variation is determined by inherent characteristics of these individuals. Suppose that the fitness components revealed in each individual's life depend on some unobserved individual trait(s), call them Z, that are set at birth and do not change in later life, and that an individual's mortality and fertility vary with its trait value. In demographic work such fixed traits are often called frailty and are assumed to affect mortality. Some ecological models assume two correlated components of frailty that affect mortality and reproduction, respectively. Every cohort of individuals is born with a distribution, say ϕ(Z) of trait values. Individual fitness components such as the age at death T and lifetime reproduction M will both vary with the trait value. A model of fixed heterogeneity attempts to infer the unknown ϕ(Z) from the observed distribution of, say, ages at death and lifetime reproduction, and then to explain the variance between individual fitness components in terms of the underlying variation in values of Z. The dispersion of the distribution ϕ(Z) measures the amount of fixed heterogeneity in the population. Variation among individuals in age at death and lifetime reproduction is proportional to the underlying variation in Z.

While the assumption of unobservable traits may be a useful first step, it is clearly essential to find the actual sources of fixed heterogeneity and determine whether they produce the variation we observe. But progress has been difficult since the usual suspects for the possible underlying traits (e.g., genetic variation or fetal condition) are often hard to measure and the quantification of their effects outside controlled lab environments is challenging.^{24, 25}

A deeper question is, what maintains variation in fixed traits? If a trait affects survival or reproduction then individuals with different trait values must differ in overall fitness and natural selection should act to eliminate variation in the trait.²⁶ For survival rates, previous work has suggested several possible reasons why fixed variation may persist including the continual injection of mutational variance²⁷, low heritability due to a low additive genetic contribution to the trait²⁸, and fluctuating selection caused by environmental variability²⁹. But there is little empirical evidence to quantify the contribution of such processes to the persistence of variation, in part because our understanding of the genotypephenotype mapping is limited³⁰.

DESCRIBING VARIATION AMONG INDIVIDUAL LIFE HISTORIES

We now examine in a little more detail a model of dynamic heterogeneity that is relatively simple but still applicable to many animal populations. We assume that any individual can be in one of 3 states, immature (state 1), breeding with low reproduction (state 2), and breeding with high reproduction (state 3). The model requires a matrix of transition probabilities between states, conditional on survival,

$$\Psi =\left(\begin{array}{ccc}\hfill {\psi }_{11}\hfill & \hfill {\psi }_{12}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\psi }_{22}\hfill & \hfill {\psi }_{23}\hfill \\ \hfill 0\hfill & \hfill {\psi }_{32}\hfill & \hfill {\psi }_{33}\hfill \end{array}\right).$$

Here an individual transitions to state 2 when it matures and then transitions between states 2 and 3 so long as it survives. In addition, we have survival probabilities s_i for each state i. Let the fertilities for states 2, 3 be f₂, f₃ and define a fertility matrix

$$\mathbf{F}=\left(\begin{array}{ccc}\hfill 0\hfill & \hfill f_2\hfill & \hfill f_3\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),$$

and finally a population projection matrix

$$\mathbf{A}=\mathbf{F}+\mathbf{S},$$

where

$$\mathbf{S}=\left(\begin{array}{ccc}\hfill s_1{\psi }_{11}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill s_1{\psi }_{12}\hfill & \hfill s_2{\psi }_{22}\hfill & \hfill s_3{\psi }_{32}\hfill \\ \hfill 0\hfill & \hfill s_2{\psi }_{23}\hfill & \hfill s_3{\psi }_{33}\hfill \end{array}\right).$$

It is worth noting that this matrix involves the elements of the transpose of the transition probability matrix (by sometimes confusing convention). We have no age dependence in these equations but we could easily include age dependence in the transition probabilities and survival rates. This formulation is well known in population biology as a stage-structured model.³¹ Purely as a description of mortality the model above is a version of a multi-stage life table.³²

Such a stage structured model with stages described in terms of observable phenotypes is a general and powerful way to describe population dynamics. What is new about our work is that we use this model not to describe population numbers, but rather to describe dynamic heterogeneity, i.e., variation in phenotypic traits and fitness components among individuals within a population.

Variation in the age at death T measured by its mean, variance and higher moments can be computed explicitly in terms of the matrix S, whose powers describe the probabilities of being alive in one of the three stages at any age. For example, the probability that an individual survives to age at least a and is in stage i at that age is the (1, i) element of S^a-1. The mean age at death, ET, and variance of age at death, E(T²) – (ET)², for only one type of offspring being born in stage 1 can be computed³¹ using

$$ET={\mathbf{e}}_1^T\mathbf{I}\stackrel{⌢}{\mathbf{N}}{\mathbf{e}}_1$$

and

$$E{T}^2={\mathbf{e}}_1^T\mathbf{I}\left(2\stackrel{⌢}{\mathbf{N}}\text{-}\mathbf{I}\right)\mathbf{I}\stackrel{⌢}{\mathbf{N}}{\mathbf{e}}_1$$

Here e₁ is a column vector of zeros except for element i = 1, I is the identity matrix, $\stackrel{⌢}{\mathbf{N}}$ is the transpose of the fundamental matrix N = (I-S)^–1, and a superscript T indicates a transpose.

Next consider an individual's lifetime reproduction, M. The average lifetime reproduction is known³¹ to be given by

$$EM={\mathbf{e}}_1^T\mathbf{F}\stackrel{⌢}{\mathbf{N}}{\mathbf{e}}_1,$$

and we have derived a new formula for the variance (details are given elsewhere and are available on request),

$$E{M}^2={\mathbf{e}}_1^T\mathbf{F}\left(2\widehat{\mathbf{N}}\text{-}\mathbf{I}\right)\widehat{\mathbf{F}}\widehat{\mathbf{N}}{\mathbf{e}}_1$$

Here F̂ is a matrix with only diagonal elements equal to the f_i. We can also compute these moments exactly when transitions are age and stage structured, using new formulas that we report elsewhere (details are available on request).

An interesting feature of phenotypically structured models is that they generally predict late age mortality plateaus. This is a consequence of the structure of Markovian models and we find plateaus in models for plant and animal populations.³³ The plateaus generated by dynamic heterogeneity are different from those found in models with fixed frailty, a matter we return to in the last section of this paper.

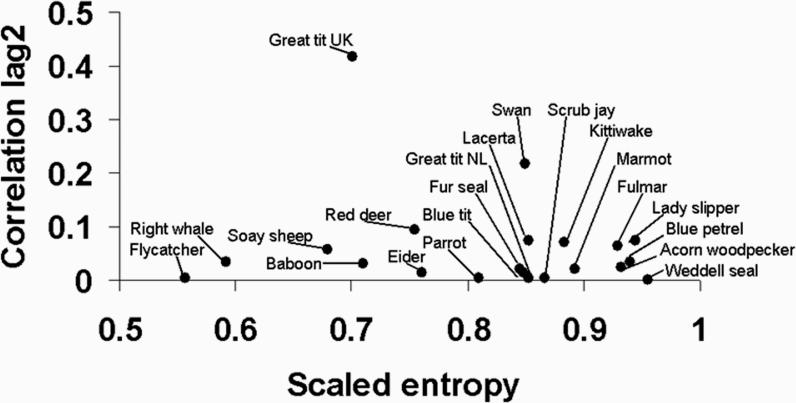
An overall measure of dynamic heterogeneity is given by the entropy, H, of the matrix Ψ which generates all possible phenotypic trajectories. Entropy is defined³⁴ by considering first all sequences ω of states of some length n; let the probability of sequence ω be p(ω) and define $h\left(n\right)=-{\sum }_{\omega }p\left(\omega \right)\text{log}p\left(\omega \right)$; then entropy is the limit as n → ∞ of (h(n)/n). This entropy describes the rate of diversification of trajectories conditional on survival and is estimated as $H=-{\sum }_{i=1}^K{\sum }_{j=1}^K{\pi }_i{\psi }_{ij}\text{log}{\psi }_{ij}$. ³ The π_i are the elements of the vector describing the stable stage distribution and K is the number of stages.³ Alternatively we can include survival weighting and compute the entropy of a matrix based on S that describes trajectories before death.³⁵ We are also interested in the persistence of an individual's current phenotypic state, i.e., if an individual is in state k at time t is it also likely to be in the same state at a later time? A useful measure of persistence is the correlation between an individual's states two years apart (i.e., correlation at a time lag of 2 years between states at t, t+2). Figure 3 displays the entropy and correlation at lag 2 for a large number of species, estimated using reproductive success as a stage variable. In general, phenotypic state has low persistence, meaning that individuals change reproductive state frequently over the life course. Entropy varies considerably across species³ but the level of entropy is high, meaning that individuals in all species follow diverse life course trajectories.

Figure 3.

Dynamic heterogeneity across species. The vertical axis indicates the absolute correlation between stages two years apart, and the horizontal axis the entropy for the generating matrix of transition probabilities, scaled to a maximum value of 1.

It is important to note that a pair of the matrices S, F constitutes a single life history phenotype. These matrices generate many alternative life course trajectories. Although individuals following distinct trajectories may have distinct marginal fitness at different stages of the life cycle, the overall phenotype's fitness is determined by all trajectories. The overall fitness r = logλ can also be expressed using reproductive trajectories, as the solution of the characteristic equation,

$$1=E\left\{\sum _{a=1}^{a=T}{F}_a\left(\omega \right)e^{-ra}\right\}$$

where E indicates an expectation (i.e., average) over the probability distribution of reproductive trajectories ω, and T is age at death. This overall fitness is the population growth rate. Evolutionary change comes about when the elements of these two matrices change, e.g., if a mutation produces a phenotype in which the probability to remain immature ψ₁₁ increases so that individuals on average take a longer time to mature. Thus dynamic heterogeneity is intrinsic to the life history phenotype and does not require arguments for its maintenance.

ANALYZING VARIATION AND ITS CAUSES

Although we have emphasized the difference between fixed and dynamic heterogeneity, we certainly expect to find both kinds of heterogeneity in nature. In our picture, we expect to find fixed and heritable variation among individuals in phenotypic transition probabilities and mortality. In looking for such variation, our current work focuses on several questions. In natural populations, how much fixed and dynamic heterogeneity can we detect among individuals using multistage models in which individuals also differ in fixed traits? What do statistical models tell us about the interaction between fixed and dynamic heterogeneity, and do they support the hypothesis that trade-offs act via fixed latent factors? Is dynamic heterogeneity associated with or predicted by individual covariates, environmental factors, and temporal variability? Is there evidence for the heritability of traits that determine fixed and dynamic heterogeneity?

A different analytical strategy that we are using for phenotypic models is to work with the change over time and age of the distribution f(P, a, t) of phenotypic traits. A powerful way to study this distribution is to use a generalization of the Price equation that we recently derived and applied to longitudinal data on natural populations of mammals.³⁶ This generalized Price equation enables us to study the evolution of phenotypic means and variances, and to exactly decompose changes in these moments into contributions from selection, phenotypic plasticity, and parent-offspring transmission. There is a natural connection between this approach and one based on estimating stage-structured models, and we aim to explore this in forthcoming work.

Researchers working on human mortality and health have long used longitudinal models that are similar in spirit to our stage structured approach. Recent studies have used an explicit analysis of trajectories of observed or self-reported health state,¹⁴ and entry into and exit from disability;³⁷ these studies also use a Markov process to predict health status as a phenotypic trait, but have not yet examined the nature of dynamic heterogeneity. There is also a close connection between our view of variation as generated along the life course and work on life course health development.¹³ The latter work marches with ours in focusing attention on the transition probabilities between stages of health and functioning as being critical targets for study and possible intervention.

Much of our work uses data from longitudinal studies of natural populations of animals and plants. We have also begun work on human populations, including a study by Michael Gurven of health, biomarkers, and demography among the Tsimane.³⁸ Our approach aims to study a broad set of phenotypic traits, analyze transition rates between them, and then map phenotypic trajectories onto health states. In our perspective, some phenotypic states will map onto high risks of mortality or morbidity, and we can estimate age and state dependent probabilities that an individual will transition into and out of such states. The population-level age-pattern of mortality reflects the distribution of individual phenotypes between low-risk and high-risk states. Old-age mortality plateaus are generated because individuals continue to make transitions among risk states at all ages, and as a cohort ages it displays a stable distribution of individuals across different risk states. These plateaus are not the result of the differential survival of hardy individuals. The power of our approach lies in quantifying the forces that determine phenotypic transitions and phenotypic trajectories. Transition rates can be related to mechanistic arguments about physiology, environment and genes. They provide the right setting in which to examine the consequences of interventions that aim to improve health over the life course. Finally, the use of phenotypic trajectories will make it possible to examine how much variation among individuals may be due to fixed effects such as genotypes rather than simply to dynamic heterogeneity.