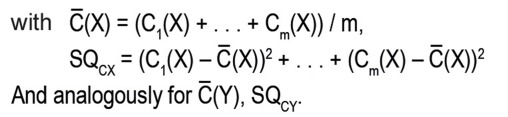On the Proper Use of the Crossover Design in Clinical Trials

Abstract

Background

Many clinical trials have a crossover design. Certain considerations that are relevant to the crossover design, but play no role in standard parallel-group trials, must receive adequate attention in trial planning and data analysis for the results to be of scientific value.

Methods

The authors present the basic statistical methods required for the analysis of crossover trials, referring to standard statistical texts.

Results

In the simplest and most common scenario, a crossover trial involves two treatments which are consecutively administered in each patient recruited in the study. The main purpose served by the design is to provide a basis for separating treatment effects from period effects. This is achieved via computing the treatment effects separately in two sequence groups formed via randomization. The differences between treatment effects can be assessed by means of a standard t-test for independent samples using the intra-individual differences between the outcomes in both periods as the raw data. The existence of carryover effects must be ruled out for this method to be valid. This assumption is usually checked using a pre-test, which is also described in this article. Finally, we briefly discuss the use of nonparametric tests instead of t-tests and more complicated designs with more than two test periods and/or treatments.

Conclusion

Crossover trials in which the results are not analyzed separately by sequence group are of limited, if any, scientific value. It is also essential to guard against carryover effects. Whenever ignoring such effects proves unjustified, the treatment effect must be analyzed solely via an analysis of the data obtained during the first trial period. Even the use of this restricted dataset yields results whose validity is not beyond question.

The crossover design has a long history in the planning of scientific trials ([1], sect. 1.4) and forms the basis of a large number of clinical studies year after year. Trials in almost all clinical disciplines use the crossover design, but it accounts for a particularly high proportion of studies in the “CNS specialties”—neurology and psychiatry—and of trials on pain treatment. One example of the latter is the frequently cited study of the analgesic effect of synthetic cannabinoids (2). This was a classic crossover trial involving a total of 21 patients with chronic neuropathic pain. In two consecutive treatment periods, both one week long, each patient received four or eight externally indistinguishable capsules daily. These capsules contained either placebo or dimethyl-heptyl-THC-11-carbonic acid (CT-3). The primary endpoint was the change in pain intensity at the end of each treatment period, measured using a visual analog scale (VAS).

The essential feature distinguishing a crossover trial from a conventional parallel-group trial is that each proband or patient serves as his/her own control. The crossover design thus avoids problems of comparability of study and control groups with regard to confounding variables (e.g., age and sex). Moreover, the crossover design is advantageous regarding the power of the statistical test carried out to confirm the existence of a treatment effect: Crossover trials require lower sample sizes than parallel-group trials to meet the same critieria in terms of type I and type II error risks.

To exploit these advantages to the full, a few specific pitfalls must be avoided in the planning and analysis of crossover trials. The two trial periods in which the patient receives the different treatments whose effects are being compared must be separated by a washout phase that is sufficiently long to rule out any carryover effect. In other words, the effect of the first treatment must have disappeared completely before the beginning of the second period. Researchers analyzing the data of crossover trials often proceed as though they were performing a simple pre/post comparison. Unfortunately this error can be observed time and time again, even in renowned journals (3– 8). Crossover trials in which the paired t-test (or any other procedure for paired samples) was used for analysis are methodologically flawed and do not contribute to evidence-based evaluation of the treatments concerned.

Correct procedure for statistical analysis

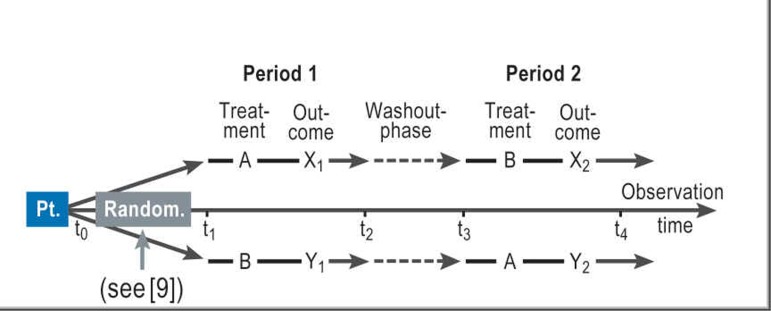
The formal structure of a crossover trial for comparison of two treatments A and B is shown in Figure 1 (where A is placebo and B is CT-3). The two phases that each patient has to complete in the course of the trial are usually referred to as the two study periods ([10], p. 79). The efficacy of A and B is assessed on the basis of the within-subject difference between the two treatments with regard to the outcome variable. The crucial difference between a crossover trial and a simple study yielding paired observations is as follows: In planning a crossover trial, it must be taken into account that patients who receive treatment A in period 1 and treatment B in period 2 (or vice versa) may show systematic differences in outcome even when A and B have identical effects (e.g., when the same drug is given each time), because of time effects. As a consequence, researchers planning and analyzing a crossover trial have to take special precautions to avoid any confounding (11, 12) of treatment effects and period effects. A simple example of a period effect is familiarization with the study situation.

Figure.

Design of a crossover trial: Pt., patient; Random., randomization

Main steps of confirmatory data analysis (Boxes 1 and 2)

Box 1. Steps in confirmatory statistical analysis of a crossover trial ([1], sect. 2.3; [10], sect. 4.1).

Symbols:

• X_1i, X_2i = result for patient i of sequence group A–B in period 1 or 2 respectively

• Y_1j, Y_2j = result for patient j of sequence group B–A in period 1 or 2 respectively

• C_i(X) = X_1i + X_2i, C_j(Y) = Y_1j + Y_2j [within-subject sums of the results from both periods]

• D_i(X) = X_1i – X_2i , D_j(Y) = Y_1j – Y_2j [within-subject differences of the results from period 1 and period 2]

• m, n = number of patients in sequence group A–B and sequence group B–A respectively

• N = m + n [total number of patients]

Note: for the example in Box 3 we have:

m = 7, n = 6;

X₁₁ = 310, X₂₁ = 270, C₁(X) = 310+270 = 580, D₁(X) = 310–270 = 40;

Y₁₁ = 370, Y₂₁ = 385, C₁(Y) = 370+385 = 755, D₁(Y) = 370–385 = –15;

And so on for the remaining patients.

1. Pre-test to check the assumption of negligible carryover effects

Has to be performed like an “ordinary” unpaired t-test (see [13]) with C₁(X), …, C_m(X) and C₁(Y), …, C_n(Y) as the two samples.

The test statistic thus has to be calculated according to the following equation:

The (two-sided) p value (see [14]) is then determined as always in the unpaired t-test, namely as the probability that the absolute value of a (centrally) t-distributed parameter with N-2 degrees of freedom exceeds the calculated absolute value of the test statistic T.

2. Test for differences between treatment effects

Formally, this test is carried out according to exactly the same scheme as the pre-test.

The crucial difference is that the customary formula for the unpaired t-test are now applied to the within-subject differences D₁(X),. .. , D_m(X) and D₁(Y),. .. , D_n`Y).

Box 2. Example of the confirmatory statistical analysis of a crossover trial (15, 16).

Trial:

Comparison of the bronchodilatory effect of inhaled formoterol (A) and salbutamol (B) on the peak expiratory flow (PEF) of children with asthma.

Data:

Table. Sequence group A–B.

Patient (i)	X1i	X2i	Ci(X)	Di(X)
1	310	270	580	40
2	310	260	570	50
3	370	300	670	70
4	410	390	800	20
5	250	210	460	40
6	380	350	730	30
7	330	365	695	–35

Table. Sequence group B–A.

Patient (j)	Y1j	Y2j	Cj(Y)	Dj(Y)
1	370	385	755	–15
2	310	400	710	–90
3	380	410	790	–30
4	290	320	610	–30
5	260	340	600	–80
6	90	220	310	–130

1. Pre-test to check assumption of negligible carryover effects:

2. Test for differences between treatment effects:

3. Significance decisions: Significant improvement in PEF with formoterol (A) compared with salbutamol (B); no evidence of relevant carryover effects.

Patients are assigned randomly to the two sequence groups A–B and B–A, comparison of which forms the basis for confirmatory analysis.

• The crucial variable for analysis is the within-subject difference in outcome between the two study periods. In order to assess the difference between treatment effects, a statistically valid test for independent samples has to be carried out with the values obtained for this variable.

• The assumption that the washout phase was long enough to rule out a carryover effect should be checked in a preliminary test. To this end, the sum of the values measured in the two periods is calculated for each subject and compared across the two sequence groups by means of another test for independent samples. If this test yields a statistically significant result, the usual test for differences between the effects of the two treatments should not be applied.

Calculation of power and sample sizes, efficiency

As in any clinical study (17), the planning of a crossover trial should include a well-grounded calculation of sample sizes, based on precise specification of the power of the test used to establish the primary hypothesis. In the case of the crossover design, this is the test for differences between the treatment effects. Planning of the trial will generally be done under the assumption that the washout phase is long enough to rule out carryover effects.

In principle, the procedure needed for calculation of power and sample sizes for a crossover trial is the same as that which is familiar from the t-test for unpaired samples (18). The sole difference lies in the specification of the assumptions under which a predefined power (e.g., 80%) should be attained (Box 3a).

Box 3a. Parameters that must be specified to determine the effect size in sample-size planning of a crossover trial.

1. Expected difference τ between A and B with regard to the outcome measure, disregarding period effects

2. Measurement variance σ_e² expected to occur if the measurement procedure would be repeated a large number of times in the same patient under identical conditions (same study period and same treatment)

3. Effect size to be inserted in the equations for power and sample size in the unpaired t-test is

One important question is whether the crossover design is superior or inferior in efficiency as compared with a standard two-arm study yielding data from one single study period. Efficiency here refers to the sample sizes required by the two designs to achieve the same power under otherwise identical conditions.

Under the usual statistical model assumptions for the parametric analysis of crossover trials (19), this question can be answered by means of the approximate equation shown in Box 3b. The formula implies that the crossover design is always the more efficient. Since the variance due to measurement error is generally smaller than that which can be ascribed to between-subject variability, the difference is very often substantial. In a situation where the between-subject variance is twice as large as that due to measurement error, for instance, six times as many patients are required to achieve the same power in a parallel-group study as in a crossover trial. From the cost-efficiency viewpoint, however, it must be taken into account that the crossover design involves twice as many measurements per patient. Moreover, the time required for a crossover trial is increased because every patient has to complete two study periods separated by a washout phase.

Box 3b. Conversion factor for the efficiency of the crossover design relative to the parallel-group design.

Figure.

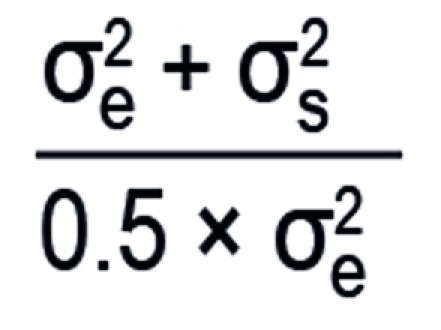
where σ;_s² is the between-subject variance and σ;_e² the within-subject variance.

Modifications and generalizations

The described confirmatory procedures based on unpaired t-statistics assume (approximate) normality of the distributions to be analyzed. Not infrequently, however, only a weaker model assumption seems realistic, according to which the variables under analysis have distributions of some unspecified form being common to both sequence groups. The medians of these distributions are assumed to decompose into a sum of terms representing the respective effects of treatment and period, as well as possible carryover effects. A strategy for confirmatory analysis whose validity is granted under these weaker conditions consists in replacing two-sample t-tests with Wilcoxon rank sum tests (20) throughout. Thus, the Wilcoxon test is used as a pre-test to ascertain the negligibility of the carryover effects, with the subject-wise sums C₁(X), …, C_m(X), C₁(Y), …, C_n(Y) as data (as described, for example, in [13]), and similarly to test for differences between the treatment effects.

A modification of a much more fundamental kind concerning the comparative evaluation of the treatment effects comes into play whenever a crossover trial is carried out in order to establish the bioequivalence of two different formulations of the same drug product. In this scenario the “statistical logic” of the test is radically altered: The alternative hypothesis that the researchers are seeking to confirm now specifies that there is essentially no difference between the treatments (drug formulations) A and B. A systematic account of basic principles and important special procedures for testing for equivalence is given in Wellek (21). Furthermore, methods for the evaluation of equivalence studies will be the subject of a future article in this Series on Evaluation of Scientific Publications.

Another important modification, albeit relatively rarely employed in medical studies, is extension of the trial to more than two measurement periods. The number of periods need not then be identical with the number of treatments being compared. For bioequivalence studies, for example, a replicated crossover design with a total of four periods is recommended, with treatments A and B each given twice (22). As a rule the analysis of multiperiod crossover studies is relatively complicated and requires special software for linear regression models with mixed effects (1).

Discussion

The popularity of the crossover design for both clinical and experimental studies remains undiminished, and not infrequently the word “crossover” appears already in the title of the publication. In a much too high proportion of cases, however, the critical reader will realize that the statistical analysis of the results falls far short of the standards laid out here. The most common error is failure to accommodate stratification by sequence group in that the investigators proceed as it would be appropriate in analyzing a study with fixed order of treatments, performing a paired t-test or a Wilcoxon signed-rank test. Proceeding in this way one takes the risk of putting the validity of the results of a crossover trial into question: In an extreme case, a significant result will solely mean that a pronounced period effect could be established, while the efficacy of the treatments in themselves was practically identical.

Another pitfall to be avoided in crossover trials presents itself right at the beginning: In the planning phase, it is crucial to make the washout phase long enough to definitively rule out a carryover effect from one treatment period to the next. The pre-test performed as an initial step of the confirmatory analysis of the study data, essentially serves the purpose to reveal such a shortcoming in planning. Even the primary literature on applied statistics provides no conclusive answer to the question of how one should proceed when the pre-test yields a significant result. For a long time the established biometric practice in presence of a significant carryover effect in a two-period crossover trial was to analyze the data from the first study period just as if it had been obtained from a conventional parallel-group study. This procedure is still routinely followed, although it was shown more than 20 years ago that the unpaired t-test, used as part of such a two-stage procedure, no longer exhibits its basic properties and may, under certain circumstances, become strongly anticonservative in the sense of markedly exceeding the target significance level (23).