Brief Review of Regression-Based and Machine Learning Methods in Genetic Epidemiology: The Genetic Analysis Workshop 17 Experience

Abstract

Genetics Analysis Workshop 17 provided common and rare genetic variants from exome sequencing data and simulated binary and quantitative traits in 200 replicates. We provide a brief review of the machine learning and regression-based methods used in the analyses of these data. Several regression and machine learning methods were used to address different problems inherent in the analyses of these data, which are high-dimension, low-sample-size data typical of many genetic association studies. Unsupervised methods, such as cluster analysis, were used for data segmentation and subset selection. Supervised learning methods, which include regression-based methods (e.g., generalized linear models, logic regression, and regularized regression) and tree-based methods (e.g., decision trees and random forests), were used for variable selection (selecting genetic and clinical features most associated or predictive of outcome) and prediction (developing models using common and rare genetic variants to accurately predict outcome), with the outcome being case-control status or quantitative trait value. We include a discussion of cross-validation for model selection and assessment and a description of available software resources for these methods.

Introduction

Machine learning methods have been used to study the genotype-phenotype relationship in genetic epidemiology [Szymczak et al., 2009]. New DNA sequencing technologies are making it feasible (in terms of both time and cost) to sequence all the exons or the complete genome of large numbers of people. This holds the promise of allowing identification of all genetic variants that contribute to disease. However, there are problems in analyzing these data that need to be surmounted. Each individual harbors millions of genetic variants, and many of these variants are individually quite rare in the population. The problem of searching this large set of potential predictors of disease to find the causal ones is not trivial in terms of data manipulation and adjustment for multiple testing. At least for the near future, the number of people sequenced in a study will be much smaller than the number of potential predictors (genetic variants) in the sequence data. In this scenario, traditional multivariable methods cannot solve this so-called high-dimension, low-sample-size problem. Some machine learning methods have been suggested to be useful for this type of problem. In Genetic Analysis Workshop 17 (GAW17), investigators applied a diverse group of regression-based and machine learning methods to study both rare and common genetic variants from exome sequences [Wilson et al., 2011].

GAW17 provided common and rare genetic variants from exome sequencing data and simulated phenotypic traits, both binary and quantitative, in 200 replicates. The exome sequencing data were derived from the 1000 Genomes Project (for more information about the 1000 Genomes Project, see http://www.1000genomes.org), and the simulated traits were modeled to have genetic and environmental determinants of both large and small effect size (see Almasy et al. [2011] for details on the GAW17 data set). In this paper we provide a brief review of the regression and machine learning methods that were used in GAW17 to tackle the problems inherent in analyses of sequence data. These methods include hierarchical and k-means cluster analysis, generalized linear models (logistic and Poisson regression), regularized regression methods (least absolute shrinkage and selection operator [LASSO]), logic regression, random forests, and support vector machines. General introductions to these methods are found in Hastie et al. [2009] and Clarke et al. [2009].

Different machine learning methods were used to address various analytical objectives represented in the analyses for GAW17. For unsupervised learning methods, the main objective is to segment or discover homogeneous subgroups within the genetic landscape presented by the data. Variable selection and prediction are the two primary objectives for supervised learning methods. Variable selection involves discovering the subset of genetic and clinical features that are most associated with or predictive of the outcome, be it case-control status or a quantitative trait. Prediction involves using common and rare genetic variants to develop models that can accurately predict the outcome within the training data and perform well on independent test data. The range of methods seen in GAW17 encompasses different philosophies of how variable selection and prediction are achieved, which we summarize here. We have generally considered regression methods to be a subset of supervised machine learning methods, because the standard regression models can be used in the machine learning framework to learn from the data and provide outcome predictions based on the inputs. We appreciate the fact that the commonly used interpretation of regression models is often quite different from the machine learning perspective, with particular conditional associations being emphasized and interpreted under the assumption of model truth. We do not delve into these differences but simply present a description of the methods.

Categories of Machine Learning Methods

We proceed by subdividing the methods used into three broad classes: unsupervised methods, regression-based supervised methods, and tree-based supervised methods. Unsupervised learning methods are methods used to understand the structure of a data set and the inherent patterns present. There is no dependent variable; all variables are treated equally with respect to one another. Examples of unsupervised methods include cluster analysis and principal components analysis. This is contrasted with supervised learning methods, which try to learn the relationship between a set of input or independent variables with an output or dependent variable. These methods are supervised because we are specifying certain kinds of relationships between variables. Examples of supervised learning methods include regression (in its myriad forms), decision trees, random forests, and support vector machines, among others.

Cross-Validation as a Method for Assessing Performance

Cross-validation is a general method for assessing performance of both unsupervised and supervised learning methods and for tuning parameters or models for optimal performance. A standard version of cross-validation is k-fold cross-validation, which works this way: The data are partitioned into k random subsets, and then the algorithm of interest (learning machine, regression model) is generated or trained on k − 1 of the subsets and applied or tested on the remaining subset. This is done repeatedly over all the k possible arrangements of the subsets into these two groups. At each iteration the measure of model performance (e.g., prediction error for supervised learning and distance matrix for unsupervised clustering) of the algorithm in the test set is computed, leading to k estimates. The final estimate of model performance is the average of these k performance estimates. The underlying idea is that the algorithm is being trained and tested on statistically independent subsets.

Three comments apply here: (1) k is often chosen to be at least 5 and usually not more than 10, because fewer than 5 tends to increase the variance of the estimate, making it unstable, whereas more than 10 usually does not improve the estimation in terms of bias or variance; (2) the segmentation into groups must be done so that, so far as possible, the groups are truly representative of the population, with, say, no subgroup containing all the high-cholesterol subjects; and (3) forming an averaged model or estimate after the repeated training and testing is not quite the same as generating a single model or estimate on all the data, because each subject in the data set has been used more than once, either as a test or training object. Despite the concern raised in Clarke et al. [2009], cross-validation generally leads to good estimates of a model or algorithm’s performance. This is naturally distinct from a claim that the model is itself optimal: If the signal is not in the data, it will not be recovered by any model [Kohavi, 1995].

The performance measure from k-fold cross-validation for a particular algorithm can be used to help tune the algorithm. For example, in linear regression, the set of independent variables that gives the lowest cross-validation error can be chosen for use in a final model. In decision trees, cross-validation error helps to determine the number of branches to keep (or prune) from a tree. In cluster analysis it can help to determine the number of groups in a particular data set.

Unsupervised Methods

Unsupervised learning methods generally are methods used to find patterns in the covariate or input landscape, irrespective of the outcome(s) of interest. In genetic epidemiology, one popular use of such methods is to use genetic variants and principal components analysis to define homogeneous subsets of individuals reflecting different ethnicities within a study sample. Two popular methods in the class of unsupervised learning methods are hierarchical clustering and k-means clustering. Cluster analysis provides a description of the data in terms of some similarity criteria. It is often not well reproduced in external data, because of variability between data sets, and should not be used for inferring associations or lack thereof. Both hierarchical clustering and k-means clustering allow an observation to be a member of one and only one group or cluster. Alternatives to this are model-based clustering and fuzzy clustering, which provide relative measures for each observation to be members of different groups. A fundamental concept in cluster analysis is that of distance—how close or similar two observations are. There are many choices of measures for this, but the most common are the Euclidean distance $\left[{\sum }_{i=1}^n{(x_i-y_i)}^2\right]$, the Manhattan distance $\left({\sum }_{i=1}^n\mid x_i-y_i\mid \right)$, the Chebychev distance (max_i|x_i − y_i|), and, more recently, the correlation distance (1 − correlation between two observations), where two observations are (x₁, …, x_n) and (y₁, …, y_n). For binary or categorical data, we can also define a distance between (x₁, …, x_n) and (y₁, …, y_n) as (number of x_i ≠ y_i)/n, the proportion of values for which there is disagreement. A good general reference for cluster analysis is Kaufman and Rousseeuw [1990].

Hierarchical Clustering

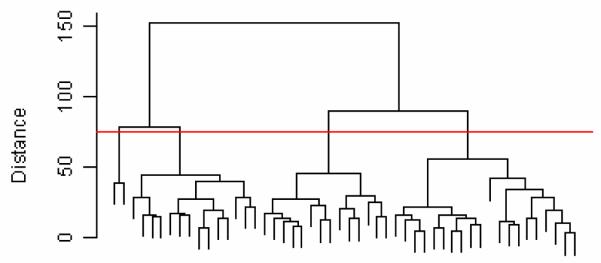
Hierarchical clustering is an algorithm by which data points are progressively incorporated into groups (agglomerative or bottom-up clustering) or the data set is progressively split into groups (divisive or top-down clustering) based on some similarity or distance criterion. The objective is to create groups of data in which the data within groups are more similar to each other than the data between groups. Typically agglomerative clustering is used, where at each step the two groups of the data closest to each other are combined to form a new group. There are several principles, called linkages, used to decide when groups are close. In single linkage, the distance between two groups is the distance between the two closest observations, one from each group. In complete linkage, the distance between two groups is the distance between the two farthest members of the two groups. In average linkage the distance between the groups is the average distance between all pairs of observations, one from each group. The choice of the distance measure between observations and the choice of linkage determine the general shapes of the groups that are created. Hierarchical clustering is typically represented by a dendrogram (see Fig. 1), where the height of each split is based on the distance between the two groups created by the split. The number of groups is not set beforehand; one can find the number of groups in the data based on how far apart groups have to be to be called distinct. In Fig. 1, if this distance is decided to be 75 (the red line), there are 4 groups that are at least 75 units apart from each other.

Fig. 1.

Hierarchical clustering dendrogram.

K-Means Clustering

K-means clustering [Hartigan and Wong, 1979] is a method of clustering data in which the number of groups is fixed by the user a priori—the k in k-means. Cluster centers are determined from the data, and individual observations are included in a particular cluster based on the cluster center that is closest to it. Once again, the choice of distance measure determines the shapes of the clusters. Often Euclidean distance is used, which results in spherical clusters. Several methods for choosing k have been suggested in the literature. The simplest way is to plot the percentage of the total variance explained by k clusters against k and to decide when adding a cluster does not change this metric much (the so-called elbow rule). Cross-validation can also be used to determine k [Nisbet et al., 2009].

Regression-Based Supervised Methods

Regression-based supervised methods attempt to explicitly model the relationship between inputs or independent variables and the outputs, typically in the form of parametric equations in which the parameters are estimated from the data. These methods often provide explicit estimates of measures of association between individual inputs and the outcome, adjusted for other inputs, with standard error estimates provided from the modeling paradigm used.

The most common class of regression methods in the literature comes from the class of generalized linear models [McCullagh and Nelder, 1989], which includes linear regression, logistic regression, and Poisson regression. These methods are commonly used in genetic epidemiology to detect association of genetic variants with a trait or disease of interest. Consider a group of k predictors X₁, …, X_k, which will be used to predict an outcome y. The basic structure of this class of models is that y is predicted by an appropriately transformed linear function of the inputs X₁, …, X_k. This is generally written as

$$g\left[E\right(y\left)\right]={\beta }_0+{\beta }_1{X}_1+\cdots +{\beta }_k{X}_k,$$ (1)

where g is the link function and β₀, β₁, and β_k are regression coefficients to be estimated. Some particular examples for the link function are g[E(y)] = E(y) (linear regression), g[E(y)] = log{E(y)/[1 − E(y)]} (logistic regression), and g[E(y)] = log[E(y)] (Poisson regression).

An extension of Poisson regression is the zero-inflated Poisson regression [Lambert, 1992; Hall and Shen, 2010]. Poisson modeling is typically used for count data, and the zero-inflated Poisson model is used for data in which the number of zero counts (no events) seen in the data is higher than would be expected by a Poisson model fitting the rest of the data. The outcome is modeled to come from one of two processes: one process producing only zero counts and the other producing data from a Poisson model. The determination of which process a particular observation comes from is modeled as a biased coin tossing experiment, with the probability of the data coming from the Poisson model being p. Symbolically, the ith outcome y_i can be expressed as

$$y_i=\{\begin{array}{cc}0\hfill & \text{with probability}1-p,\hfill \\ Z_i\hfill & \text{with probability}p,\hfill \end{array}\phantom{\}}$$ (2)

where Z_i is an observation from a Poisson model.

Another extension of the generalized linear modeling framework, when all the inputs are binary, is logic regression [Ruczinski et al., 2003]. The predictors used in the model are Boolean combinations of the binary predictors. For example, a possible predictor in logic regression is L₁ = {(X₃ AND X₄) OR X₅}, that is, either both X₃ and X₄ are 1 or X₅ is 1. The model is framed using the generalized linear model framework

$$g\left[E\right(y\left)\right]={\beta }_0+{\beta }_1{L}_1+\cdots +{\beta }_m{X}_m,$$ (3)

where each L_i is a Boolean combination of the binary input variables X₁, …, X_k. This method is easily applied to genotype data and presence/absence of rare genetic variants. It can also be used for survival data under the Cox proportional hazards framework. Note that m can be quite a bit bigger than k, the number of predictors, because of the way the L_i are constructed. This can make fitting a logic regression model computationally prohibitive. It can also make finding the best-fitting model difficult. Ruczinski et al. [2004] provide some suggestions for how to deal with this issue.

Regularized Regression Methods

A common problem in statistical modeling is variable selection, that is, which input variables should be retained in a model. Often variable selection is done by backward selection. This type of variable subset selection is a discrete process and often exhibits high variance. An alternative strategy is to use regularized regression methods (also called penalized regression or shrinkage regression methods), which fit generalized linear models for which the sizes of the coefficients are constrained. Two common regularized regression methods are ridge regression [Hoerl and Kennard, 1970] and the LASSO [Tibshirani, 1996; Wu et al., 2009]. A nice introduction to regularized regression methods is provided by Hastie et al. [2009].

Ridge regression fits a linear model, where the coefficients are constrained to

$$\sum _{j=1}^k{\beta }_j^2<t.$$ (4)

The coefficient estimates are obtained by minimizing

$$\sum _i{\left(y_i-{\beta }_0-\sum _{j=1}^k{x}_{ij}{\beta }_j\right)}^2+\lambda \sum _{j=1}^k{\beta }_j^2,$$ (5)

where λ is a tuning parameter that determines the degree of shrinkage (larger λ implies more shrinkage). The LASSO is a shrinkage method in which the coefficient estimates are obtained by minimizing

$$\sum _i{\left(y_i-{\beta }_0-\sum _{j=1}^k{x}_{ij}{\beta }_j\right)}^2+\lambda \sum _{j=1}^k\mid {\beta }_j\mid .$$ (6)

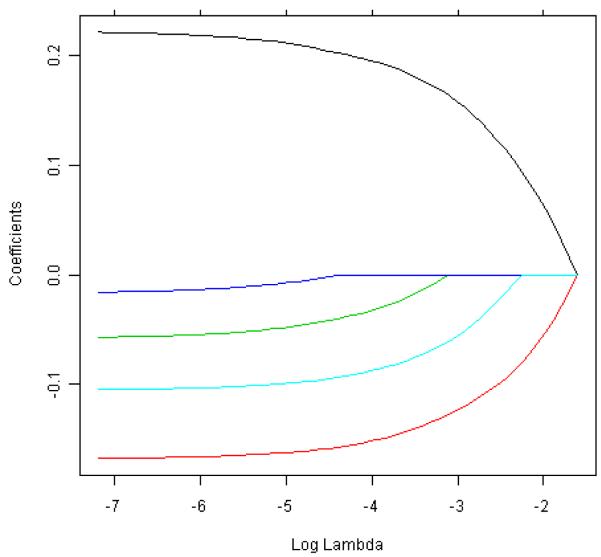
Note that the primary difference between ridge regression and the LASSO is that ridge regression constrains the L2 norm (sum of squares) of the coefficients, whereas the LASSO constrains the L1 norm (sum of absolute values) of the coefficients. Ordinary least-squares (OLS) multiple regression is a special case for both methods when λ equals 0. Both methods have the effect of forcing some of the coefficients toward 0, albeit at different rates. Both methods have been widely used for variable selection in genetic and genomic studies where there are many correlated independent variables. The number of variables that are forced to 0 depends on the value of λ (larger λ implies more coefficients forced to 0), and thresholding on λ allows the selection of variables that have retained nonzero coefficients at that λ threshold. Fig. 2 (taken from the example given in the glmnet package, version 1.5.1, in the statistical software R, version 2.11.1, but with five independent variables) shows how the estimated coefficient values change with λ for a LASSO model. A similar figure can be generated for ridge regression.

Fig. 2.

Coefficient values versus change in log λ for a LASSO model.

Several extensions of the LASSO method in the literature tweak the manner in which the coefficients are constrained. One extension is the group LASSO, which looks at groups of variables jointly [Meier et al., 2008]. The group LASSO and some of its variants have been widely used in genetic association and genome-wide association studies. This method allows groups or clusters of inputs to be in or out of the model together. Contrasting with the regular LASSO (expression (6)), the group LASSO minimizes

$$\sum _i{\left(y_i-{\beta }_0-\sum _{j=1}^k{x}_{ij}{\beta }_j\right)}^2+\lambda \sum _{g=1}^G{\Vert {\beta }_g\Vert }_2,$$ (7)

where ∥β_g∥₂ is the Euclidean norm (not squared) for the coefficients of the inputs in the gth group. The LASSO method and its derivatives are not always consistent for variable selection, but some consistency results exist for the LASSO [Meinshausen and Yu, 2009] and the group LASSO [Liu and Zhang, 2009].

Tree-Based Methods

Decision Trees

Decision trees are widely used in machine learning methods, and several methods for estimating tree models are described in the literature. The most common method is the classification and regression tree (CART) [Breiman et al., 1984], although other methods, such as C4.5 [Quinlan, 1993], are also used. Decision trees are broadly classified into classification trees (where the outcomes are binary or categorical) and regression trees (where the outcomes are continuous). Decision tree methods are attractive in genetic epidemiology because they allow nonparametric analyses of large numbers of predictors in small sets of data and because they can detect predictors with small marginal effects on the trait when there are strong interaction effects.

The basic strategy for growing decision trees is to split the input or covariate space into hypercubes (e.g., rectangles for two-dimensional input), within which the outcome is relatively homogeneous. This is done in a hierarchical manner using a sequence of binary splitting rules for the inputs. The algorithm efficiently looks at all possible binary splits over all the inputs and chooses the split that makes the corresponding values of the output variable as distinct as possible; that is, the distance between the two groups of outputs defined by the split is maximized. Trees can be grown to purity (i.e., until all the bottom or terminal nodes are completely homogeneous with respect to the outcome or dependent variable), although this is a poor practice in general and can lead to unstable or highly variable estimates. Once a tree is learned using training data, the predicted outcome for each observation is determined by sending the input values down the tree and taking the most frequent class (for classification trees) or the mean of the outcomes (for regression trees) of the test data in the terminal node into which the observation falls. Decision trees need to be optimized with respect to the number of variables used and the depth or size of the tree grown. The criterion used for optimizing decision trees is usually the prediction error, be it the misclassification rate (classification trees) or the mean-square error (regression trees). Optimization is typically done by cross-validation.

Decision trees have several advantages. They are typically easy to interpret, although some trees can be quite complex. They can accommodate binary, categorical, and continuous predictors in the same model, and they are relatively fast, even on large data sets with many predictors. However, decision trees tend to have a high variability; that is, changing the data slightly can change the tree quite significantly by changing the splitting rules that make up the tree. They also tend to overfit the training data and thus do not always have good external test set performance. This variability can be reduced by bagging [Breiman, 1996; Friedman and Hall, 2000; Evgeniou et al., 2004; Grandvalet 2004; Elisseeff et al., 2005], which averages several trees grown on resampled versions of the training data.

Random Forests

Random forests [Breiman, 2001] extend the idea of decision trees. Bootstrap samples [Efron, 1979; Efron and Tibshirani, 1993] of the training data (samples drawn with replacement from the training data with the same sample size as the original data) are drawn, and trees using a random subset (of a given size) of the predictors at each node are fitted to each bootstrap sample. Note that for each tree, the best split of the data at each node is based on a possibly different random subset of the predictors (of specified cardinality, specified by mtry). There are two fundamental tuning parameters in the random forest algorithm: the number of trees (same as the number of bootstrap samples) to be grown, typically denoted as ntree, and the number of predictors (mtry) to use at each node in growing each tree. A balance of these tuning parameters is desirable for both accuracy and computational cost. However, random forest models perform well over a fairly wide range of mtry values, and the defaults suggested by Breiman [2001] work pretty well. A point to note in random forests is that the trees are grown without any pruning or variable selection.

An important concept in the random forest framework is the concept of an out-of-bag (OOB) sample. Taking a bootstrap sample of a data set results in roughly 63% of the unique observations of the original data set being included in the bootstrap sample. Breiman [2001] referred to the set of observations not included in the bootstrap sample as the OOB sample. The OOB sample is thus an independent data set from the bootstrap sample on which a decision tree is trained and serves as a test set for assessing the performance of the tree. Each tree within a random forest uses a different bootstrap sample and thus a different OOB sample.

A random forest thus is composed of an ensemble of decision trees fitted to different bootstrap samples of the training data. The predicted outcome for each observation is estimated by the most frequent predicted outcome from each component tree (for classification) or the average of the predicted outcomes from each component tree (for regression). The performance of a random forest is assessed by the average prediction error of each component tree on the corresponding OOB sample. This is similar in flavor to cross-validation, but each component tree is evaluated on a different subset of the data (as determined by the corresponding bootstrap sample) rather than on the same set of data subsets that cross-validation would use. Random forests tend to provide low-bias, low-variance predictions, because of the low-bias nature of the component trees and the averaging across independent bootstrap samples, respectively.

Random forests also provide a means for variable selection by computing a variable importance score for each input variable. This is done by first finding the prediction accuracy of the OOB samples and then replacing the data for an input variable with a random permutation of its data (thus killing any predictive power the variable might have) and recomputing the prediction accuracy using the permuted data. The change in the prediction accuracy is a measure of the predictiveness of that input variable. Input variables can then be ranked in terms of their variable importance scores, and variables can be selected on the basis of some threshold of the variable importance score. Other measures of variable importance have also been proposed in the literature.

Random forests are scalable for large data sets, and fast parallelized implementations of the algorithm are available, including Random Jungle [Schwarz et al., 2010]. Random forests can take a mixture of input types and do provide a fairly robust predictive model of outcome. Random forests have proved useful in a wide variety of fields, including microarray analyses [Diaz-Uriarte, 2007] for variable selection using the variable importance scores.

Discussion

We have outlined several machine learning and statistical methods that are used (and have been used in GAW17) to describe genetic data and model the association of genes (mRNA expression levels, single-nucleotide polymorphism [SNP] genotypes) with binary or quantitative traits. Several challenges are posed by the genetic data sets generated using current technologies, not the least of which is that the number of genetic variants interrogated dwarfs the number of subjects in a study by orders of magnitude (the so-called high-dimension, low-sample-size problem). The parametric regression methods typically break down in this situation, and the regularized regression methods and tree-based methods have been found to be much more successful in modeling such data. They have also been successful in identifying genes predictive of a trait in a multivariate model, which is a more comprehensive and robust means of understanding associations between genes and traits than the univariate testing paradigms accompanied by multiple comparison corrections that dominate the literature.

These regression-based and machine learning methods, along with novel variations on them, were applied to whole-exome sequence data and simulated traits at GAW17 to examine their performance on such data [Wilson et al., 2011]. Although multiple genetic and environmental effects were simulated in the GAW17 quantitative and binary trait models, the complexity of these simulated traits may not be fully comparable to complex traits in real data (e.g., epistasis). Some advanced features of machine learning methods were not systematically invoked in the analysis of the simulated data, for example, a more refined tuning of the mtry parameter in random forests. Therefore the performance of machine learning methods compared to simple regression methods is somewhat limited in the GAW17 data. In the GAW17 data set, with its replicated but fixed sample size, investigators were presented with an opportunity to apply machine learning methods such as random forests and logic regression to the feature selection recurrency problem: finding a list of predictors that appear frequently at the top in a machine learning ordering of the features. However, the topic of recurrence in feature selection is still a matter of unresolved but intense research in the machine learning community. In genetic analysis of complex traits using real data, the amount, effects, and relationship of effective genetic variants are unknown and must be assumed to be quite complex. Therefore, as discussed by Sun [2010], truly nonparametric machine learning methods such as random forests can be efficient alternatives to address high dimensionality, genetic heterogeneity, and epistasis and to effectively combine a large number of weak predictors in the study of genetics of complex traits.

Software

Machine learning methods have a strong overlap with statistical methods, and, as such, most statistical software platforms, such as SAS (http://www.sas.com), SPSS (http://www.spss.com), Stata (http://www.stata.com), and R (http://www.r-project.org), contain methods for unsupervised learning and regression-based modeling to varying degrees. The tree-based methods and regularized regression methods are not so widely available, although packages in R and PROCS and macros in SAS (especially in Enterprise Miner) and in the open-source Weka [Hall et al., 2009] (http://www.cs.waikato.ac.nz/ml/weka/) and Rapid-Miner (http://www.rapid-i.com) platforms are widely used. Specialized software written by developers of particular methods are also available, for example, CART and RandomForest developed by Salford Systems and Random Jungle developed at University of Lübeck [Schwarz et al., 2010] (http://www.imbs-luebeck.de/imbs/de/node/227). There are also faster implementations of hierarchical clustering algorithms (pam, clara) available within R and elsewhere. There has been an increasing emphasis on computationally efficient implementations of machine learning algorithms that take advantage of modern multicore and cluster computing frameworks and distributed data infrastructures such as Hadoop. In other words, machine learning methods can increasingly be used on large data sets in a computationally efficient fashion, making them feasible tools for large genetic epidemiology studies and genome-wide studies.

There are several online resources for using popular statistical software for the methods described here. These include:

• The UCLA Academic Technology Services site (http://www.ats.ucla.edu/stat/dae), which provides sample code for regression analysis in SAS, R, SPSS, Stata, and others.

• The Comprehensive R Archive Network (CRAN), which provides task views (http://cran.r-project.org/web/views) that describe R packages that can be applied to particular analytic tasks. The following might be of interest to our audience:

  • ○ Cluster analysis (http://cran.r-project.org/web/views/Cluster.html).
  • ○ Machine Learning (http://cran.r-project.org/web/views/MachineLearning.html).
  • ○ Statistical Genetics (http://cran.r-project.org/web/views/Genetics.html).
  • ○ High Performance and Parallel Computing (http://cran.r-project.org/web/views/HighPerformanceComputing.html).

• Orange (http://orange.biolab.si), which is a Python environment for data mining and includes many of the methods described here as well as special widgets for functional genomics.

• Weka (http://www.cs.waikato.ac.nz/ml/weka/), which is a collection of data-mining algorithms in Java that can be directly applied to data or though custom Java programs.