Effects of sampling standardization on estimates of Phanerozoic marine diversification

Abstract

Global diversity curves reflect more than just the number of taxa that have existed through time: they also mirror variation in the nature of the fossil record and the way the record is reported. These sampling effects are best quantified by assembling and analyzing large numbers of locality-specific biotic inventories. Here, we introduce a new database of this kind for the Phanerozoic fossil record of marine invertebrates. We apply four substantially distinct analytical methods that estimate taxonomic diversity by quantifying and correcting for variation through time in the number and nature of inventories. Variation introduced by the use of two dramatically different counting protocols also is explored. We present sampling-standardized diversity estimates for two long intervals that sum to 300 Myr (Middle Ordovician-Carboniferous; Late Jurassic-Paleogene). Our new curves differ considerably from traditional, synoptic curves. For example, some of them imply unexpectedly low late Cretaceous and early Tertiary diversity levels. However, such factors as the current emphasis in the database on North America and Europe still obscure our view of the global history of marine biodiversity. These limitations will be addressed as the database and methods are refined.

Has biodiversity in the oceans increased dramatically throughout the history of animal life, or has the number of marine taxa varied without an overall direction since the explosive radiation of animals early in the Paleozoic? This key question is bound up with many others concerning radiation and extinction (1–9), all of which focus on counts of taxa through time. There are many unresolved problems with the counts that make up diversity curves, however. Even the basic question of how to count remains unresolved: should censuses include all taxa ranging anywhere into a time unit (the traditional approach), exclude those taxa found only in one unit (7, 8), or focus on cohorts of taxa crossing boundaries between time units (10–12)? Arguably, an even more important stumbling block is variation through time in sampling intensity: it seems clear that the amount of data varies significantly within some major parts of the fossil record (10, 11, 13–17).

Here, we explore ways to address the sampling problem as it pertains to Phanerozoic diversification. Our approach will be to standardize the amount of data we examine in each time unit (10, 11, 13), which hopefully will move us closer to a genuine biological pattern. We will present eight different sampling-standardized analyses of a large, rapidly growing paleofaunal database, employing four different subsampling methods and two highly complementary taxon-counting protocols. The preliminary data set focuses on North America and Europe through much of the Paleozoic and the Late Jurassic through Paleogene. Although the new database eventually will allow us to address many other issues, our sampling-standardized curves bracket the range of available methods for removing sampling filters from our picture of Phanerozoic diversification.

This comparison of two long intervals is of great interest regardless of the outcome. The traditional, synoptic data (Fig. 1) suggest that diversity continued to increase throughout our younger interval. Such a pattern would be consistent either with very slow logistic growth (3–5) or slow, but unconstrained, exponential growth (17). Alternatively, a reanalysis might indicate that diversity tracked a plateau during the Meso-Cenozoic, perhaps reflecting stochastic change around an equilibrium value resulting from logistic dynamics (3–5). Finding such a pattern would challenge hypotheses that seek to explain the Meso-Cenozoic radiation, including suggested increases in biogeographic provincialism (18, 19) and escalating biotic interactions (20).

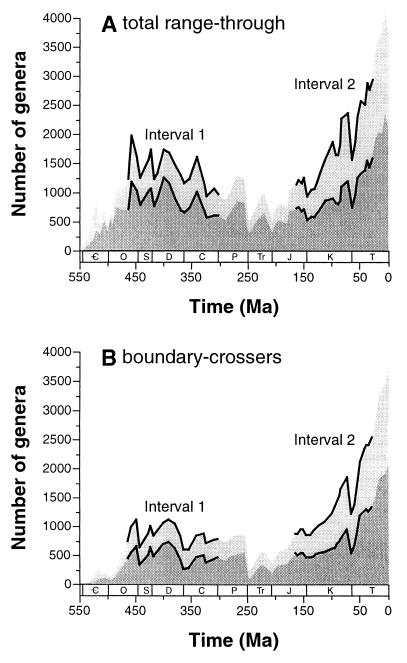
Figure 1.

Genus-level diversity curves for the two study intervals based on Sepkoski's widely cited, unpublished global synoptic compilation (7, 8). This data set attempts to capture all published information on first and last appearances through time. The current version includes 29,773 genera of marine animals and animal-like eukaryotes whose ranges can be resolved to one of 76 stage-long temporal intervals. Ranges are treated as continuous, and no information on sampling intensity is taken into consideration, with counts being either (A) totals of genera ranging into or across each bin or (B) totals of genera crossing the boundaries between each bin and the preceding bin. Upper curves (light shading) depict all marine taxa; lower curves (dark shading) depict core taxa analyzed in this paper (Anthozoa, Brachiopoda, Echinodermata, Mollusca, and Trilobita); legends and thick lines indicate this paper's two focal study intervals. = Cambrian; O = Ordovician; S = Silurian; D = Devonian; C = Carboniferous; P = Permian; Tr = Triassic; J = Jurassic; K = Cretaceous; T = Tertiary.

The Paleobiology Database

The Paleobiology Database is housed at the National Center for Ecological Analysis and Synthesis (NCEAS) in Santa Barbara, California (http://flatpebble.nceas.ucsb.edu/public/). Sources of data have included published systematic, paleoecological, and biostratigraphic investigations; unpublished faunal lists; and databases previously compiled by the authors for separate projects focused on particular stratigraphic intervals (10, 11, 21–31). In contrast to synoptic, range-based compilations (1–5, 7, 8, 17), the Paleobiology Database documents individual fossil collections, containing lists of genera, subgenera, and species, and, where available, abundance data. Any taxon may have multiple recorded occurrences in the database. Some collections pertain to entire outcrops or even basin-wide stratigraphic units, but most correspond to single localities and many to bed-scale inventories. The detailed primary data fields (Table 1) should facilitate a wide array of future paleoecological and macroevolutionary analyses. The database is intended eventually to cover the Phanerozoic terrestrial and marine fossil record for all geographic regions. Currently, the marine component of the database contains 8591 collections and 110,944 taxonomic occurrences and is dominated by North American and European localities (see below).

Table 1.

Major marine components of the Paleobiology Database

Category	Key information	Collections (%)
Primary spatial data	Country	8,588 (>99.9)
Secondary spatial data	County or latitude/longitude	7,077 (82.4)
Temporal data	Resolved to our 10-Myr bins	7,029 (81.8)
Lithostratigraphy	Formation	7,324 (85.3)
Lithology	Primary lithology (e.g., “packstone”)	7,913 (92.1)
Local stratigraphic control	Position in a measured section	2,707 (31.5)
Depositional environment	Principal facies (e.g., “prodelta”)	5,450 (63.4)
Preservation	Type of fossil (e.g., “original aragonite”)	5,663 (65.9)
Collection/preparation	Methods (e.g., “peel or thin section”)	5,097 (59.3)
Taxonomic list	Genus names	8,357 (97.3)
Abundance data	Counts of specimens or individuals	3,071 (35.7)

“Collections (%)” reports the number and proportion of the 8591 fossil collection records in the database including at least one item of “Key Information.” Categories in bold are used in the analyses reported here. Most categories include multiple distinct data fields. For example, the lithology category includes fields for adjectives describing the lithology, the degree of lithification, the primary and secondary lithology types, and a verbal description of the facies. 

Data

We focus on genus-level, Northern Hemisphere taxonomic richness across two broad, roughly equal periods of time (Fig. 1). Interval 1 is the Middle Ordovician (Llandeilo, 460 Ma) through Carboniferous (300 Ma). It spans two major extinctions (end-Ordovician; Late Devonian) and much of the hypothesized Paleozoic plateau in diversity (6, 7). Interval 2 is the mid-Jurassic (Callovian, 164 Ma) through Oligocene (24 Ma). In a widely cited synoptic compilation (Fig. 1), diversity at the beginning of interval 2 is markedly lower than during some parts of the Paleozoic—but toward the end of interval 2 there is a marked diversification, with Eocene richness far exceeding any earlier levels.

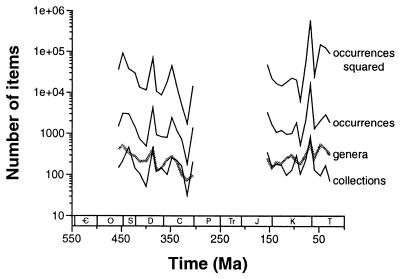
We attempted to maintain roughly uniform sampling intensity but found data easier to obtain for interval 2. Hence, the interval 1 data set contains 2491 collections and 19,824 genus occurrences, but the shorter interval 2 includes 3036 collections and 37,615 genus occurrences. Three direct measures of sampling based on these data each show the same basic pattern (Fig. 2): similar overall sampling in the two halves of the Phanerozoic, with a few short-term spikes at such times as the Maastrichtian (latest Cretaceous). Meso-Cenozoic coverage is substantially more intense for several sampling bins, not just the Maastrichtian. Nonetheless, the raw, unstandardized data set yields no large and consistent difference in genus-level richness between the two major intervals (Fig. 2).

Figure 2.

Current marine paleofaunal contents of the Paleobiology Database. The curves show only the amount of raw data available for analysis and have no necessary biological meaning. Log scale is used because the variables are highly skewed on a linear scale. Period names are given in the legend for Fig. 1. Top black line, sum of squared counts of occurrences in each collection in each 10-Myr-long bin. Middle black line, number of taxonomic occurrences summed across collections in each bin. Bottom black line: number of fossil collections per bin in the two major study intervals. Thick gray line, number of distinct genera sampled in each bin. High diversity peaks in the late Ordovician and Maastrichtian correspond to relatively well-sampled temporal intervals; smaller-scale variation in this diversity curve also tracks variation in sampling intensity.

Despite our relatively uniform sampling, geographic coverage is spotty outside of North America and Europe. Therefore, our initial analyses are mostly limited to these regions, although we included a small amount of data from North Africa and the Middle East because of their paleobiogeographical continuity with Europe. Additionally, we analyzed only a core set of well-reported higher taxa: the Anthozoa, Brachiopoda, Echinodermata, Mollusca, and Trilobita. These taxa together constitute 19,319 (64.9%) of the genera in Sepkoski's unpublished compendium, and 9815 (62.6%) of the genera found in more than one of the stage-long intervals in Fig. 1. Our sampling is not yet adequate for other groups like the Bryozoa, Conodonta, Graptolithina, interval 1 cephalopods, and interval 2 anthozoans and malacostracans. However, the core group of taxa does generally reflect overall trends (Fig. 1). An exception is that interval 2 core taxon diversity first rises above the Paleozoic maximum during the Eocene in the range-through data (Fig. 1A), but sometime during the Late Cretaceous in other treatments.

Using standard epochs and ages of international usage (32–37), we divided our Paleozoic and Mesozoic-early Cenozoic study intervals into 15 and 14 temporal bins, respectively. The bins are of approximately even duration (means 10.7 and 10.0 Myr, standard deviations 3.2 and 2.4 Myr). Of 7035 identified genera in the database, we used 4477 (63.6%) that (i) are identified in Sepkoski's compendium (7, 8) as belonging to the core taxonomic groups; (ii) occur in the geographically restricted area; and (iii) have first and last occurrences that could be resolved to one of the 10-Myr bins.

Methods

This study focuses on two key steps in preparing a diversity curve: drawing standardized amounts of data within each temporal bin, and translating these draws into counts of taxa. We employ four related standardization methods that interpolate diversity levels by repeatedly subsampling sets of fossil items, meaning either separated taxonomic occurrences or combined fossil collections (Table 2; Fig. 2). The items in each bin are placed in a sampling pool; they are drawn at random; genera are tallied as sampling proceeds up to the total; and the procedure is repeated many times to obtain an averaged subsampling curve relating item counts to observed diversity. A summary diversity curve can be defined by choosing a fixed sampling quota and then counting the number of genera ranging into or across each bin at this sampling level (10, 11, 13, 31). Thus, our working definition of diversity is simply taxonomic richness given a fixed amount of subsampling. Here, we do not address ecological extrapolation methods (38), because their assumptions may be violated by our highly heterogeneous data.

Table 2.

Subsampling methods used in this study

Method	Items drawn	Weighting	Assumption	References
Rarefaction	O	O	O proportional to N	13, 39
UW	L	L	O independent of N	40
OW	L	O	O proportional to N	10, 11
O2W	L	O2	O2 proportional to N	31

Each algorithm proceeds by drawing items until a quota is reached, with the quota being based on the weighting variable. “Assumption” is the assumed relationship between presence-absence data for collections used in the analysis and counts of individual fossil specimens within these collections. L, number of lists; N, number of specimens in a fossil collection; O, number of distinct genus occurrences. 

The first subsampling method involves rarefaction of individual taxonomic occurrences (13, 39), whereas the others involve randomly drawing entire taxonomic lists representing fossil collections. These three “by-list” methods differ in the way they set the quota of lists. The lists unweighted (UW) method bases the quota simply on the number of listsr (31, 40). By-lists occurrences weighted (OW) scales each list by the number of genus occurrences it includes (10, 11). Finally, by-lists occurrences-squared weighted (O2W) scales each list by the square of its occurrence count (31).

Although we are still investigating how the methods respond to qualitatively different underlying abundance distributions, we know they assume different things about the nature of sampling. Specifically, results depend on the relationship between (i) sizes or spatiotemporal scales of individual fossil collections and (ii) observed lengths of taxonomic lists (Table 2). Rarefaction and OW weight each taxonomic occurrence equally, as if each one always represented a similar number of individual specimens from a similar spatiotemporal region. This assumption is problematical for occurrences within long taxonomic lists, because long lists likely represent very large numbers of specimens and/or stratigraphically and geographically lumped assemblages. Meanwhile, UW weights all lists equally, which is problematical if the modal number of specimens per list varies systematically through time. In marked contrast, O2W weights lists by an implicit estimate of the number of specimens they include. Our preliminary data suggest that, in real fossil collections, richness tracks the number of specimens according to a power law with a slope of roughly 0.5—so the square of the number of genera is actually an estimate of the specimen count (31).

Many protocols for translating sampled fossil occurrence data into diversity curves are conceivable. All of them involve summing some combination of up to five underlying variables (41): a, the number of taxa found before and after a temporal bin and sampled within it; b, the number found before and after but not within a bin; c, the number first appearing in a bin and continuing into later bins; d, the number known before a bin and last appearing within it; and e, the number found only within a bin (= singletons). Traditional curves (e.g., Fig. 1) employ all five counts (quantities a + b + c + d + e), which follows from the inference that each genus existed through all of the intervals between its first and last appearance. Some additional measures, such as estimated mean standing diversity (42), are simple transforms of these total counts. However, clear alternatives do exist, such as excluding the singleton class (a + b + c + d; refs. 7, 8, and 43).

In our case, we will focus on two further equations that add up relatively distinct and complementary sets of variables, so we might reasonably expect them to bracket the range of possible outcomes. The first counts taxa actually sampled within bins (a + c + d + e; ref. 13), and the second counts taxa crossing boundaries between bins (a + b + d; refs. 10–12, 44, and 45); only quantities a and d appear in both expressions. The first method is intuitive because counted genera actually are seen in specific fossil collections falling within individual temporal bins, so there is no range interpolation; the second method is intuitive because it captures a cohort of taxa at each temporal boundary that must have actually coexisted. However, we might expect each method to respond differently to biases. Actually sampled counts should be inflated if many consecutive temporal bins are relatively long (known not to be true in our case) or if taxonomic turnover rates are persistently high (apparently true for the Paleozoic; refs. 46–48), because these effects inflate the available pool of species for sampling. By contrast, boundary-crosser counts should fall if bins are long or turnover rates are high, because taxa cannot cross boundaries unless they are drawn repeatedly, and drawing standardized amounts of data from expanded species pools decreases the chances of such repeated draws. Both types of counts should be inflated if taphonomic regimes and geographic, paleoenvironmental, and taxonomic coverage are consistently favorable, and these other factors remain to be explored in our data set.

Results

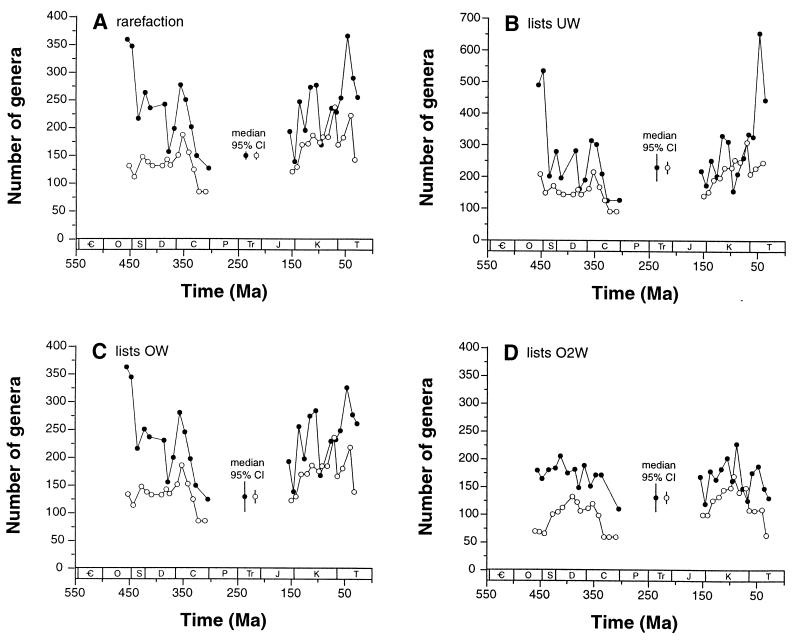
The subsampling methods yield generally concordant results, at least given a particular counting method (Fig. 3). For example, all methods decrease the artificial Maastrichtian diversity peak in our raw data (Fig. 2). Furthermore, the two methods that weight on the basis of occurrences (rarefaction and OW) unsurprisingly yield almost indistinguishable trajectories. However, important differences among the eight curves are evident.

Figure 3.

Diversity curves corrected for variation in sampling intensity by using four different subsampling algorithms (Table 2) and two methods of counting genera. Each data point represents the median value seen across 100 individual subsampling trials. Some data points are excluded when bins fail to meet the appropriate sampling quota. Filled circles show counts of genera actually sampled within a bin; open circles show counts of genera crossing the boundaries between consecutive bins. Legends labeled “95% CI” show the median 95% confidence interval across all intervals in a particular analysis; separate values for sampled-within-bin and boundary-crosser counts are illustrated. Only North American, European, North African, and Middle Eastern collections, and only occurrences of Anthozoa, Brachiopoda, Echinodermata, Mollusca, and Trilobita, are included in the analyses. Period names are given in the legend for Fig. 1. (A) Classical rarefaction of taxonomic occurrences. Individual taxonomic occurrences are randomly and independently drawn until each temporal bin includes 700 occurrences. (B) Subsampling by unweighted lists (UW). The algorithm draws 90 lists per bin. (C) Subsampling of lists weighted by taxonomic occurrences (OW). The number of taxonomic occurrences included in each list is summed, and lists are drawn until each bin includes lists totaling 700 occurrences. (D) Subsampling of lists weighted by taxonomic occurrences squared (O2W). This method counts the sum of the squared richness values for the lists that are drawn. Each bin includes 10,000 occurrences-squared.

First, interval 1's Late Ordovician points are remarkably high in most standardized curves employing sampled-within-bin counts. In these analyses, the Cretaceous-Paleogene rise is inconsistent (Fig. 3 A, C, and D), and only one of interval 2's data points (T2 = Early Eocene) generally rises to a comparable level (Fig. 3 A–C). The discrepancy between the Late Ordovician points and most of the interval 2 points far exceeds the 95% confidence intervals. The appropriate comparison is with the range-through treatment of the core taxa in Sepkoski's compendium (Fig. 1A), although the counting equations differ slightly (see Methods). The shapes of the four sampling-standardized curves do tend to bracket the synoptic data, but the high Ordovician data points and relatively flat Cretaceous-Paleogene points are a prominent exception.

Second, the boundary-crosser curves generally do suggest higher interval 2 diversity, with a substantial climb through the Cretaceous—as in the synoptic boundary-crosser data for the core taxa (Fig. 1). However, the tendency of high turnover rates to depress boundary-crosser counts may have exaggerated any perceived climb. Furthermore, even the most steeply rising sampling-standardized trajectory (UW analysis, Fig. 3B) shows diversity failing to recover completely during the Paleogene from the end-Maastrichtian diversity crash; one curve (O2W analysis, Fig. 3D) shows hardly any recovery. By contrast, the synoptic data always show a major, continuing diversity climb during the Paleogene. On balance, the results here do suggest a discrepancy with the traditional data, especially with respect to the Paleogene.

Third, the boundary-crosser curves show less variation in general, and smaller confidence intervals in particular, than the sampled-within bin curves. This difference perhaps reflects the insensitivity of boundary-crosser counts to short-term variation in the geographic, paleoenvironmental, taxonomic, or taphonomic pattern of sampling. On the other hand, it might reflect real differences in diversity trajectories between common, long-ranging taxa and rare, short-lived taxa, because the former should feature even more heavily in boundary-crosser counts.

Fourth, all three by-list methods generate broader confidence intervals than does classical rarefaction, regardless of the counting method. The reason is that rarefaction alone assumes complete independence among occurrences, which effectively inflates the number of independently drawn items by an order of magnitude (compare Fig. 2B and Fig. 2A). Because the fossil record presents itself in the form of fossil collections and not isolated occurrences, broader confidence intervals are arguably more realistic. The fact that collections tend to be spatially clustered, and certainly are so in our data set, makes it even more dangerous to treat occurrences as independent.

Fifth, variation within the sampled-within-bin curves relates to the nature of their assumptions: more variation in diversity is seen when less variation in the number of specimens collected per locality is assumed. Hence, UW (Fig. 3B) assumes no substantial sample size variation and implies great variation in estimated diversity. At the other extreme, O2W (Fig. 3D) assumes that specimen counts may vary by many orders of magnitude, and its estimated diversity curves are notably flat. Because real fossil collections do span a great range of sizes, it seems likely that the relatively directionless trends seen in all of the sampling-standardized curves are if anything still too variable. If true, this hypothesis would bear on the question of how tightly logistic dynamics regulate diversification patterns (3, 4, 10, 11): flatter curves imply tighter control.

Finally, the highly distinct O2W results merit particular attention. Using sampled-within-bin counts, the O2W curve alone fails to show a long-term decline going into the Silurian, although it does show a drop going into the very last Ordovician bin. This odd pattern is seen also in all of the boundary-crosser curves, perhaps suggesting that the O2W method has removed a sampling bias in this case. However, the result would not be consistent with strong prior evidence of an end- (not late-) Ordovician extinction event (1, 8, 46). Similarly, O2W removes any trace of a Maastrichtian diversity peak, which is still suggested by the boundary-crosser curves for the other methods; and it removes a questionable mid-Cretaceous (Aptian-Albian) peak in the sampled-within-bin curves. The two O2W curves (Fig. 3D) are in general the least similar to the classic curves (Fig. 1). Most important, O2W reconstructs Mesozoic-early Cenozoic diversity as being not only closer to Paleozoic levels than suggested by the traditional data, but even lower at times.

Discussion

At face value, our initial results support some published claims that the Meso-Cenozoic radiation is notably exaggerated in the synoptic data by sampling artifacts (14–16). Perhaps, then, marine life already had advanced quite a ways toward its all-time diversity peak during the early part of its initial Paleozoic radiation. This possibility also is suggested by at least one treatment of the synoptic data (curve for core taxa in Fig. 1A). Because of their relatively flat shapes, most of the sampling-standardized curves (Fig. 3) additionally imply that growth was closer to logistic (3–5, 8) than exponential (17) during both of our major intervals. These unexpected patterns may, however, relate to any of several additional biases.

First, sampled diversity within localized fossil assemblages was much higher late in interval 2 than at any point during interval 1 (49). Methods that weight lists (OW, O2W) or that sample occurrences instead of lists (rarefaction) therefore may overpenalize interval 2. A certain degree of concordance among the methods suggests that this factor is not overwhelming, as does the fact that the same basic pattern emerges from unweighted sampling of entire lists (UW).

Second, the number of geological formations represented in each of our temporal bins declines through time. Thus, interval 2 fossil localities may be more geographically and paleoenvironmentally concentrated. However, similar sampling-standardized results (not shown) are obtained by (i) lumping all of the collections in each formation to create a single formation-level list and then (ii) drawing an equal number of formations in each bin.

Third, our sampling focuses on well-studied geographic regions that were close to the equator during the Paleozoic and only later migrated into their present, temperate-zone positions (50). If a strong equator-to-pole diversity gradient existed during both of our study intervals, our sampling of higher-latitude faunas during interval 2 may mask an actual increase in global diversity. The same bias could be present in the traditional, synoptic data (50). However, evaluating this hypothesis will require compiling more data from low-latitude regions in interval 2.

Fourth, higher Paleozoic turnover rates (46–48) may exaggerate Paleozoic diversity in one set of analyses (sampled-within-bin counts; Fig. 3) and depress diversity in another set (boundary-crosser counts; Fig. 3). However, turnover rates estimated from Sepkoski's compendium (refs. 7 and 8, and equations 1 and 2 of ref. 44) imply that any exaggeration in the first set of analyses would be less than 10% for 10 Myr-long bins (equation A29 of ref. 51). Moreover, despite suffering from a bias in the opposite direction, the boundary-crosser results still suggest no more than a weak Meso-Cenozoic radiation.

Fifth and last, Sepkoski's compendium counts subgenera as distinct taxa, whereas our analysis counts only genera. Subgenera are used widely in the Meso-Cenozoic molluscan literature. We are working to record subgenus names so we can quantify this taxonomic effect on diversity patterns.

In summary, several substantial biases remain to be explored. However, these biases may not have strong, directional effects unique to our data set, and there is only one major methodological difference between our analysis and earlier ones: our attempt to standardize the amount of sampling in each temporal interval by using detailed, collection-level information. Because (i) we find substantial discrepancies between the old and new curves regardless of the exact method we use, (ii) the methods all attempt to control for variation in sampling intensity, and (iii) residual differences among the new curves can only reflect remaining sampling biases, we believe that sampling signals are important—despite recent claims to the contrary (52). Hence, traditional curves are likely to be more accurate than any of our estimates only if sampling variation is cancelled out fortuitously by additional, opposed biases that none of our methods address.

Conclusions

Our approach to data compilation and analysis represents a significant departure from previous assessments of Phanerozoic-scale diversity patterns. At a minimum, we have shown that a wide variety of diversity curves can be generated from the same data set just by varying sampling and analytical protocols. Thus, such steps as standardizing sampling levels and defining counts of taxa are crucial. It also is clear that grappling with these problems would be difficult, and arguably impossible, in the absence of a collection-level database like the one we are building.

We are confident that some combination of our analytical protocols eventually will give us a global Phanerozoic diversity curve that truly minimizes sampling biases. This objective will be met as the database grows in geographic and taxonomic coverage, and expands to include the entire Phanerozoic. Although we have not yet reached this point, at least some of our preliminary results do challenge a key conclusion of earlier diversity studies: that the late Mesozoic and Cenozoic witnessed a massive marine radiation exceeding anything that had gone before. Instead, we see evidence that taxonomic diversity may have neared Paleogene levels during the Paleozoic. Additional tests of this hypothesis will be performed as we refine our methods of computing diversity curves, and continue to document the biogeographic, paleoenvironmental, and preservational context of fossil collections.

Abbreviations

UW

lists unweighted

OW

by-lists occurrences weighted

O2W

by-lists occurrences-squared weighted