Spatiotemporal Estimation of Activation Times of Fractionated ECGs on Complex Heart Surfaces

Abstract

Identification of electrical activation or depolarization times on sparsely-sampled complex heart surfaces is of importance to clinicians and researchers in cardiac electrophysiology. We introduce a spatiotemporal approach for activation time estimation which combines prior results using spatial and temporal methods with our own progress on gradient estimation on triangulated surfaces. Results of the method applied to simulated and canine heart data suggest that improvements are possible using this novel combined approach.

I. Introduction

Activation times of points on the heart surface are an important characteristic of electrophysiological behavior because they represent the time at which an activation wave passes each point. By means of a single isochronal map activation times can capture the time course of an entire beat and thus provide valuable means of characterizing both normal and arrhythmic beats, hence their wide clinical use [1]. For example, isochronal maps can be used to identify the mechanisms of arrhythmias and guide ablation procedures [2]. Even in the general clinical setting, activation times are often taken as the most relevant characterization of the heart's electrical activity [3]. However, finding and characterizing activation times from sparse spatial samples on complex surfaces of cardiac chambers remains an incompletely solved problem.

In many settings in which activation times need to be determined, especially in the context of isochrone mapping, data are collected from an array of electrodes on the surface of the heart, either simultaneously or sequentially acquired. The most common approach is to analyze each lead independently to identify the time at which the temporal behavior of depolarization occurs [2], [4]–[7]. Computationally, algorithms for this purpose approximate the temporal derivative of each individual lead, by either interpolating or functionally approximating the recorded samples, and then identify the time of activation to be the time instant corresponding to the most negative temporal derivative [1], [8], [9]. Although these temporal-only methods are generally satisfactory, when presented with fractionated electrograms, it is not always obvious which occurrence of sharp changes in the signal constitute activation. Such fractionation arises very commonly in cases of arrhythmias but is also present in normal sinus beats [1], [2], [10]–[13].

Spatial derivative methods have been advocated for addressing these concerns [1], [14]. Due to the potential difference between neighboring points on opposite sides of an activation wavefront, these methods attempt to characterize this pattern in terms of its first- and second-order spatial derivatives. At the moment of activation, the magnitude of the potential distribution gradient at a point is expected to be at its highest. On the other hand, its second-order spatial derivative (specifically, its Laplacian) is expected to change signs at the time of activation [1], [15]. It has been shown that gradient-based methods, using densely-sampled electrodes on a relatively flat surface perform well under normal conditions and in the presence of fractionated electrograms [1]. Here we combine gradients estimated directly on curved surfaces with the temporal derivative to determine activation times on the heart surface.

Since activation is a wave propagation phenomenon, rapid temporal changes and sharp local spatial gradients should both be present and co-located when activation occurs [16]. Given this intimate relationship between the timing and location of activation, we propose a method of estimating activation times that looks for points that have sharp changes in electric potential values in both time and space simultaneously.

In the remainder of this paper, we outline a spatiotemporal method of determining activation times using estimated spatial and temporal derivatives. We report on numerical experiments in which we apply the spatiotemporal and temporal-only methods to two sets of fractionated electrograms on the heart: one was simulated from known activation times using ECGSIM [17], and another recorded from a canine heart. Finally, we compare and discuss these results below.

II. Methods

We assume that the heart surface is represented by a triangulation with a set of nodes ${\left\{x_i\right\}}_{i=1}^K$ at which we take sample measurements of an electric potential distribution f.

Let the value f_i,t ≡ f_t(x_i) denote an electric potential on the heart surface located at point x_i at the sample time indexed by t. Furthermore, let Df_i,t denote the approximated spatial gradient and ∂f_i,t/∂t denote the approximated temporal derivative (as described in [18] and [1], respectively). As a spatiotemporal method of detecting activation, we estimate the activation time τ_i at the point x_i as the index t which minimizes the function

$$R(i,t)={\Vert D{f}_{i,t}\Vert }_2\cdot \frac{\partial f_{i,t}}{\partial t}$$ (1)

over the available temporal samples. We assume that a point's potential values in a resting state are more positive than its potential values in a fully depolarized state, yielding negative values of ∂f_i,t/∂t at the time of depolarization. If the polarities were reversed, and the opposite were true, activation times would be calculated by maximization of that function instead.

III. Experiments

We applied our method to both simulated human data and recorded canine data that both contained fractioned electrograms. The simulated data was obtained by appropriate interactive manipulation of transmembrane potential waveforms in ECGSim. Thus here the true activation times are known. The canine data was acquired at the Cardiovascular Research and Training Institute (CVRTI) at the University of Utah and thus the ground truth activation times are unknown. Both sets of data were sampled at 1000 samples per second.

A. Simulated Heartbeats

Specifically, using ECGsim, activation times in a model heart and dataset supplied with the program were chosen such that the electrograms at several nodes exhibited fractionated behavior [17]. The temporal derivatives in the temporal-only method were approximated by quadratic fitting over a chosen window size, while the spatiotemporal method used simple first differencing. Window sizes of 3, 9, and 21 ms were tested. All of the estimated activation times were restricted to be sample times. Performance of each method was quantified in terms of correlation with ground truth and error norm (2-norm of the difference from ground truth) as reported in Table I.

TABLE I.

Performance Comparison of Spatiotemporal and Temporal-Only Methods for ECGSIM Simulated Data

Temporal Window	Correlation	Error Norm (ms)
w=21	0.954182	225.728514
w=9	0.997259	65.471213
w=3	0.999742	42.244625
Spatiotemporal	0.999772	23.640168

B. Experimentally Recorded Heartbeats

A typical cardiac cycle was chosen from the canine recordings, as illustrated by the sequence of isopotential maps in Figure 1. The spatiotemporal method was applied and the temporal-only method (with window sizes of 3, 9, and 21 samples) was computed for comparison. For the temporal derivative in the spatiotemporal method, we used an approximation based on a quadratic fit with a window of 3 samples.

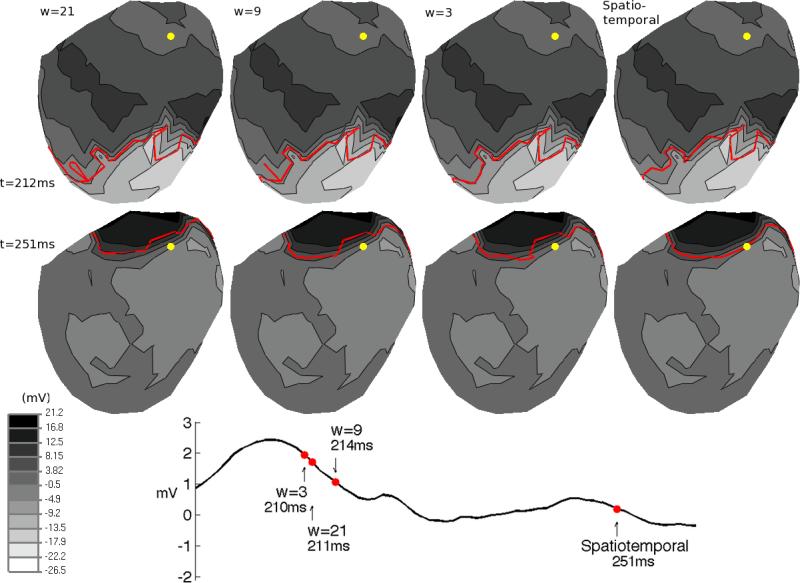
Fig. 1.

Isopotential maps of electric potentials from CVRTI canine data. Wavefront curves (red) are overlaid on each isopotential map, with each column showing the curve of a different method of estimation: temporal-only (for window sizes w=3, 9, 21) and spatiotemporal. The two rows of isopotential maps show the electric potentials of the same heartbeat at different times (212ms and 251ms). The electrogram shows the electric potentials recorded over time at the yellow node on the isopotential maps, with red dots showing the estimated activation times for the yellow node using each method.

IV. Results & Discussion

In this paper we introduced a new method of estimating activation times from electric potentials on a triangulated cardiac surface geometry. Previous methods estimated the activation time to be the time of minimum temporal derivative or maximum spatial gradient [1], [8], [9]. Maximum spatial gradient methods were shown to work well, but required samples on a regularly sampled grid to estimate the gradient [1]. In a recent paper, we introduced a way to estimate the gradient of scalar functions defined on the nodes of triangulated surface geometries [18]. In this work, we used that approach to formulate a spatiotemporal method that selects simultaneous occurrence of large gradient magnitude and minimum negative temporal derivative. The spatiotemporal method we developed was applied to simulated and experimentally recorded data that contained fractionated electrograms, a type of signal whose activation times were shown to be detected more accurately by spatial methods [1].

For the first experiment, we simulated a beat on a heart geometry by supplying activation times as input to ECGsim and exporting electric potentials [17]. Table I shows that the overall performance of the spatiotemporal method was an improvement over the temporal-only methods. Specifically, the error norms of the activation times were substantially lower using the spatiotemporal approach, between 44 and 89% depending on window size. Correlation was less sensitive to these improvements. This implies that the spatial weighting in the spatiotemporal method adds something significant to the temporal-only method.

Our second experiment applied the temporal-only and spatiotemporal methods to data recorded from the canine epicardium whose ground truth activation times were unavailable but which can be analyzed based on potential distributions. Figure 1 shows the isopotential maps at two times (212ms and 251ms) of this beat, from which it is clear that the potential wavefront travels smoothly from the apex to the base of the epicardium. However, although the spatial behavior of the electric potentials looks normal, the irregular temporal behavior of the potentials at the yellow node in Figure 1 can be seen in the electrogram. At the time of activation, the electrogram is typically expected to make a rapid transition from relatively positive potentials to negative potentials. However, at the time that this transition occurs in this electrogram, the wavefront has yet to reach the location of the recording electrode (yellow dot). One might hypothesize that the reason for this anomalous temporal behavior could be that the data recorded by the electrode at the yellow node is simply the result of a bad lead or poor connection. A noisy recording might account for such abnormal activation times, at least if the effect were localized to a single site. However this seems unlikely since, as illustrated in the two time samples shown in Figure 1, at all time samples in the QRS complex of this beat, the recorded potentials at this node were spatially consistent with its neighbors.

Given this spatially regular but temporally irregular behavior, it is unsurprising that each method estimated a different activation time for the yellow node in Figure 1. The electrogram in Figure 1 shows the activation times estimated by each method. Each column of isopotential maps shows the results of a different method (with window sizes of w = 3, 9, and 21 samples for the temporal-only method). The red wavefront curves overlaid on each isopotential map show the points that were activating at the same time. Therefore, each wavefront curve passes through the yellow node at the time of its activation. The wavefront propagating away from the apex towards the base seen at 212ms has arrived at the yellow node at 251ms. Therefore the temporal-only activation time estimates are spatially inconsistent with the expected behavior of wavefront propagation.

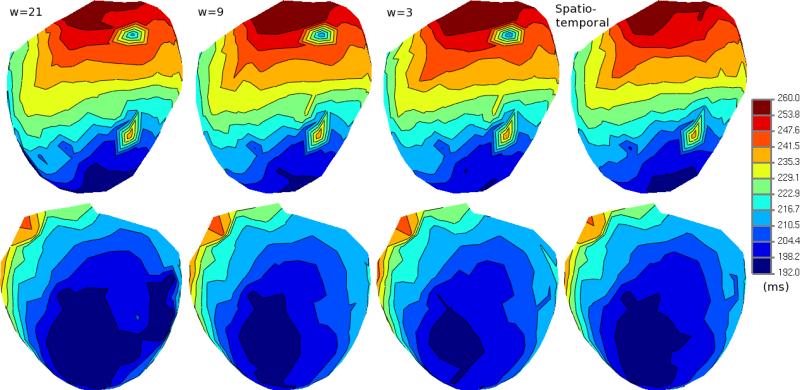
In Figure 2, we show activation times as isochrones mapped to the epicardial heart geometry of the canine. The first three columns show the activation times as estimated by the temporal-only methods while the last column shows the spatiotemporal method. The spatial inconsistency of the temporal-only estimates can be seen quite clearly on these maps. The location of the yellow node is shown by the colormap to be activated much sooner than its neighboring points on the epicardium. The isochrone map corresponding to the spatiotemporal method does not have the same inconsistent pattern. In this case, the spatiotemporal estimates suggest that the wavefront passed over this spatial region in a predictable manner.

Fig. 2.

Isochrone maps of activation times estimated from CVRTI canine data. Top and bottom rows show opposite sides of the epicardial geometry. The first three columns show the results of the temporal-only method shown for three window sizes (w=3, 9, and 21). The last column shows the results of the spatiotemporal method.

Overall, in both quantitative and qualitative terms, we have demonstrated that the spatiotemporal method has promise as an improvement on the temporal-only approach. We are currently carrying out a more extensive comparison between temporal-only estimation methods with the spatiotemporal method introduced in this paper.