Abstract
Second-order nonlinear optical imaging of chiral crystals (SONICC) is an emerging technique for crystal imaging and characterization. We provide a brief overview of the origin of second harmonic generation signals in SONICC and discuss recent studies using SONICC for biological applications. Given that they provide near-complete suppression of any background, SONICC images can be used to determine the presence or absence of protein crystals through both manual inspection and automated analysis. Because SONICC creates high-resolution images, nucleation and growth kinetics can also be observed. SONICC can detect metastable, homochiral crystalline forms of amino acids crystallizing from racemic solutions, which confirms Ostwald’s rule of stages for crystal growth. SONICC’s selectivity, based on order, and sensitivity, based on background suppression, make it a promising technique for numerous fields concerned with chiral crystal formation.
Keywords: second harmonic generation, protein crystallization, drug formulation
1. MOTIVATION
Crystal formation dictates the physical and chemical properties of solid-state materials. Chemical reactivity, stability, and dissolution kinetics are significantly influenced by the nature of the molecular packing and the orientation within the lattice. Fundamental studies of crystallization are often complicated by the so-called needle-in-a-haystack problem: Crystal nucleation is a rare and transient event. Information about the molecular interactions that lead to nucleation is often inferred from observations recorded long after the initial events take place.
The greater conformational flexibility and chemical complexity of typical organic molecules, compared with their inorganic counterparts, make these molecules particularly challenging to study and control, yet they arguably represent the most biologically important solid-state materials. Tools that can reduce the size scale for crystal characterization can approach such small-scale, short-lived structures, which may allow the description of crystal formation. Nonlinear optical (NLO) imaging may serve as a powerful complement to the existing suite of measurement tools for fundamental investigations of the initial stages of crystal formation.
Second-order NLO processes are dictated by unique symmetry conditions, compared with conventional, linear optical effects. In isotropic disordered media, second harmonic generation (SHG), or the frequency doubling of light, is symmetry forbidden. Essentially, coherent interference between individual SHG-active moieties within the focal volume in an isotropic medium results in cancellation and no net coherent output. However, certain classes of ordered systems allow for coherent addition, rather than cancellation. The best-established technique that exploits these unique symmetry properties is the application of SHG and sum frequency generation (SFG) in studies of surfaces and interfaces, in which only the comparatively few molecules at the interface that exhibit polar order contribute to the coherent detected signals (1–3).
Interfaces are not the only systems with appropriate symmetry for SHG and SFG. Through interactions closely related to the intrinsic sensitivity of second-order nonlinear optics to chirality, nearly all chiral crystals fall into symmetry classes that are symmetry allowed for bulk SHG (4–6). The terms chiral crystals and enantiomorphic crystals are synonymous; we define them as crystals composed of unit cells with nonsuperimposable mirror images. Because these effects are bulk allowed, and because SHG and SFG generally scale with the square of the number of molecules within the focal volume, these methods have the potential to serve as remarkably sensitive and selective tools for detection and characterization of small ordered assemblies. We briefly review the scope of this emerging field and assess the key strengths and limitations of specific targeted applications.
2. FUNDAMENTALS OF SECOND-ORDER NONLINEAR OPTICAL IMAGING OF CHIRAL CRYSTALS
2.1. Anharmonic Oscillator Model
The process of SHG can be qualitatively illustrated with a relatively simple anharmonic oscillator model (Figure 1) (7). Consider the linear interactions between a molecule and an incident oscillating field within the same framework: A polarization is induced by light within the medium through the harmonic “sloshing” of the electron cloud associated with the molecule. For moderate driving fields, the magnitude of the induced polarization scales linearly with the magnitude of the driving field and appears at precisely the same frequency. At the level of single atoms or molecules, the induced polarization acts as a source that radiates light through scattering. In bulk materials, the radiation emitted from each individual oscillator interferes coherently with that of its neighbors, resulting in reflection and refraction. Consequently, the linear polarizability of the medium is intimately connected to the refractive index.
Figure 1.
(a) Time-domain distortion of the induced polarization from anharmonicity in the molecular polarizability. (b) The corresponding frequency contributions combine to recover the distortion.
As the intensity of the driving field is increased, the electron cloud is sloshed at increasingly higher amplitudes away from the lower part of the energy well, such that the anharmonic terms begin to become significant. In the time domain, this anharmonicity causes a slight distortion away from sinusoidal oscillation; the polarization is slightly larger on the upstroke of the cycle (e.g., positive maximum) and slightly smaller and shallower on the downstroke (e.g., negative maximum). Which frequencies are required to reproduce this time-domain distortion? Inspection of Figure 1 suggests that such a distortion is recovered by the addition of a response at the doubled frequency. The sign of the SHG polarization can be either positive or negative, depending on the orientation of the molecule. Differences between the linear polarizability and the nonlinear polarizability can be illustrated by considering the coherent sum of the polarizations from two oppositely oriented molecules. For the linear polarizability, the two contributions add. However, in this case, the second harmonic polarizations are oppositely signed, which results in perfect cancellation and no net coherent SHG polarization. This idealized example provides a conceptual basis for understanding the origins of the disappearance of SHG in isotropic media and its corresponding sensitivity to local order.
2.2. Effect of Symmetry and Orientation on Nonlinear Polarizability
In practice, nonlinear polarizability is described in three-dimensional space by a 3 × 3 × 3 tensor, each βijk element of which describes the efficiency of generating i-polarized SHG when driven by fields polarized along the j and k molecular axes. Although SHG still disappears in three-dimensional isotropic systems, such self-cancellation need not necessarily arise in certain classes of ordered assemblies. Of the 32 available classes of crystals, only 11 are accessible for chiral crystals. By chance, nearly all of the remaining available enantiomorphic classes are symmetry allowed for SHG (with the exception of the relatively rare high-symmetry case of 432 = O, or the cubic gyroidal case). However, symmetry arguments alone dictate only whether something is or is not identically zero; they generally do not convey the underlying mechanisms of action that dictate the efficiency of a process.
Zyss & Oudar (8) and, later, Wampler et al. (9) made the first attempts to provide a predictive framework for relating the efficiency of NLO processes to molecular packing within chiral lattices. In these studies, the authors estimated the anticipated relative SHG efficiencies of different packing arrangements within crystals by coherent summation of the NLO properties of each individual molecule within the lattice. Through this approach, the greatest NLO activity is invariably generated by the relatively rare P1 lattice, in which every molecule within the lattice is oriented identically. The consideration of additional symmetry operations associated with the lattice generally causes some degree of internal cancellation of the NLO properties. For example, the P21 space group contains a screw axis along the crystallographic z′ axis. Because the translation element is much smaller than the wavelength of light, only the 180° rotation component in the screw axis operation is significant in terms of the interferences between molecules within the lattice. Rotating a molecule 180° corresponds to inverting the signs of both the x and y axes within each element in the molecular tensor. Addition of one tensor to itself, rotated 180°, doubles some tensor elements and removes others, depending on whether the sign of the tensor inverts upon rotation. Sign inversion occurs for all tensor elements that contain an odd combination of x and y indices (Figure 2). In the case of P21, the net tensor of the crystal is approximated by the sum of the top two hyperellipsoids. The rotation operation requires that the crystal be unchanged upon inverting the sign of the x and y coordinates, which removes the following tensor elements: χxxx, χxxy, χxyx, χyxx, χxyy, χyxy, χyyx, χyyy, χxzz, χyzz, χzxz, χzyz, χzzx, and χzzy. Here, the number of nonzero tensor elements is reduced from 27 to 13 through the introduction of a single 180° rotation or screw axis. In the case of the P212121 space group, only three unique tensor elements remain for SHG: χxyz = χxzy, χyzx = χyxz, and χzxy = χzyx (Figure 2) (10).
Figure 2.
Visual hyperellipsoid representation of the molecular tensor (selected arbitrarily) and illustration of the symmetry operations within a crystal lattice. The symmetry operations of a crystal in the P212121 space group yield the net hyperellipsoid representation shown at the bottom.
This analysis suggests some general guidelines for qualitatively predicting the SHG activity of chiral crystals. Generally, lower symmetry corresponds to higher SHG efficiency; the highest efficiencies are expected for systems that exhibit polar order, the next highest for systems that exhibit no polar order and no more than threefold or twofold rotational symmetry about any axis, and the lowest for nonpolar systems that exhibit high (fourfold or sixfold) rotational symmetry.
Macroscopic symmetry arguments are only the first piece of the puzzle, however. The NLO properties of a crystal also depend on the NLO properties of the individual molecules and their packing arrangement within the lattice. To a first approximation in the limit of a thin crystal (i.e., neglecting all linear effects and phase-matching conditions), the NLO properties of the crystal are estimated by the coherent summation of the individual molecular responses. This idea is simply an extension of the symmetry arguments described above, but it explicitly includes the tensors of the molecular building blocks of the crystal.
One can illustrate this process for two limiting cases of rod-like and Λ-like molecular building blocks (i.e., assuming molecular tensors dominated by βzzz and βxzx = βxxz, respectively) by using the common P212121 space group to illustrate the effects. The symmetry operations for a P212121 crystal require that the hyperpolarizability be unchanged by 180° rotation about each of the three orthogonal crystallographic axes, which results in a hyperellipsoid composed of two intertwined tetrahedra of opposite sign and orientation. The P212121 lattice contains no permanent electric dipole or polar order, which probably accounts in part for its energetic stability and ubiquity. The efficiency of a crystal for SHG qualitatively scales with the projection of the molecular tensor onto this hyperellipsoid structure. For rod-like molecules, the projection is optimized when the axis of the rod is oriented along the [111] plane (and related planes), but it approaches zero when the rod axis approaches a crystallographic axis or a plane containing crystallographic axes. Conversely, the Λ-like building blocks exhibit optimal overlap with the lattice hyperpolarizability for antiparallel molecular packing arrangements. These effects can also contribute to a significant variability in the SHG activities of chiral crystals—beyond those anticipated from symmetry arguments alone.
Finally, the orientation of the crystal relative to the image frame influences both the magnitude and the polarization dependency of the detected signal. In a defect-free single crystal, each node in the hyperellipsoid corresponds to an orientation of the crystal that produces a minimum in the intensity of the coparallel-polarized SHG. Analogous nodes also exist for cross-polarized SHG that often coincide with the coparallel-polarized nodes. For example, in the P212121 lattice hyperellipsoid shown in Figure 2, the coparallel-polarized SHG should approach zero when the beam is polarized along any of the crystallographic axes. A classic example of this effect can be found in studies of the P43212 crystals of lysozyme (11). Lysozyme crystallization tends to be surface nucleated; the fourfold rotation axis is oriented normal to the solid-liquid interface. In the most common measurement configurations, the normal of the solid-liquid interface often coincides with the direction of propagation of the beam. This orientation perfectly coincides with an anticipated node in the SHG. Furthermore, because of the relatively high fourfold screw axis in the crystal, the node holds for both coparallel- and orthogonally polarized light, regardless of the in-plane angle of the crystal, such that no detectable SHG is predicted for this system.
In addition to the phenomena described above, numerous other effects can influence the intensity and polarization dependency of the detected SONICC (second-order nonlinear optical imaging of chiral crystals) signal. These effects include phase-matching considerations, coherence length issues (12), the influence of the Gouy phase shift (4, 13), and other effects associated with performing measurements of extended materials with focused beams. For these reasons, these simplistic approaches are rigorously reliable only for materials whose thicknesses are significantly shorter than the wavelength of light. For longer path lengths through single crystals, complicating interactions from the film thickness and linear optical properties of the material can significantly influence the overall efficiency of SHG. Nevertheless, this framework still provides a starting point for describing the major features expected in SONICC measurements of microcrystalline samples.
2.3. Instrumentation
Instrumentation for SONICC measurements is essentially identical to that used for conventional multiphoton excited fluorescence microscopy. Typically, an ultrafast laser source is focused to a single focal volume within the field of view, and beam-scanning optics are used to scan the beam within the object plane (Figure 3). Data are acquired with single-channel detectors (photomultiplier tubes or avalanche photodiodes). Often, measurements are acquired at low magnification over relatively large fields of view to maximize the probability of detecting diffuse microcrystals.
Figure 3.
General instrument schematic for SONICC (second-order nonlinear optical imaging of chiral crystals) measurements. Abbreviations: DM, dichroic mirror; PMT, photomultiplier tube.
2.4. NLOPredict
An analysis and visualization program, NLOPredict (14), has been developed to help sift through the large number of coordinate transformations and tensor-element bookkeeping involved in relating the macroscopic observables back to crystal packing and molecular structure. NLOPredict enables estimation of the second-order NLO properties of crystals from the known or calculated NLO properties of the molecular building blocks (Figure 4). In protein crystals, the NLO properties of the individual proteins can also be predicted on the basis of coherent summation of the amide units (15, 16). The program is designed to be easily bridged to computational and plotting packages through the use of simple text files for data input and output. NLOPredict allows bridging all the way from molecular tensors to polarization-dependent intensities detected in the laboratory frame, including (a) contributions from polarizing optical elements (e.g., wave plates and polarizers), (b) local-field correction factors to connect the far-field polarization to the local fields experienced and generated within the NLO source, and (c) crystal symmetry. In addition, several unique visualization approaches incorporated into the package allow concise visual representation of the molecular and ensemble tensors that drive the measured NLO responses of ordered assemblies. The software package is open source and is freely available to download and run as a plug-in to the UCSF Chimera program. Links to the program can be found at http://nlopredict.sourceforge.net.
Figure 4.
Screen shots of NLOPredict, a program designed to help interpret polarization-dependent nonlinear optical (NLO) measurements of biopolymer and small-molecule assemblies (shown for Protein Data Bank entry 2RH1).
3. APPLICATIONS FOR SELECTIVE PROTEIN-CRYSTAL IMAGING
Protein-crystal identification is routinely carried out as an essential step in protein structure determination. Many high-throughput instruments (manufactured by, e.g., Formulatrix and Rigaku Americas Corporation) are available to expedite this process, given that potentially thousands of crystallization trials are screened before suitable crystals are formed. In these systems, optical microscopy (OM) techniques are employed for crystal identification because they can probe small volumes with high resolution in relatively short amounts of time. Volume, resolution, and time are the key parameters because of the number of trials that must be screened. For example, a common 96-well plate requires ~0.1 mg of purified protein (96 1-µl drops at 10 mg ml−1) and 10 min of analysis time (~6 s to translate the plate, locate the droplet, and identify the presence of crystals, if any).
Currently, the optical techniques used for protein-crystal identification include bright-field microscopy, birefringence microscopy, trace fluorescence labeling, and intrinsic UV fluorescence imaging. Normal bright-field microscopy can be used to identify crystals both manually and automatically through the use of image-analysis software. However, optical scattering is common in many crystallization trials (e.g., from protein film of precipitation) and can greatly reduce the contrast available for manual inspection or image analysis. Furthermore, bright-field images are difficult to reliably score by automated algorithms, particularly for small (<5-µm) crystals. Therefore, in most high-throughput instruments, bright-field microscopy is limited to the detection of relatively large (≥10-µm) crystals and for centering the crystallization droplets for analysis by alternative optical methods (e.g., fluorescence and birefringence).
Birefringence microscopy improves the contrast for crystal detection by imaging only light transmitted through crossed polarizers placed on either side of the sample (17, 18). Any material in the sample that can rotate or significantly affect the polarization of light (e.g., birefringent crystals), if appropriately oriented, appears bright, while the solution or aggregated protein remains dark. The success of this technique depends strongly on the thickness of the birefringent material. Small (≤10-µm) crystals generally do not rotate a sufficient amount of light to be detectable above the background from material imperfections and scattering. Birefringence increases selectivity over that of bright-field microscopy, but it can cause false positives from scattering centers or from precipitant crystals.
Numerous fluorescence-based methods have been developed to improve detection limits and selectivity for protein-crystal detection. Crystals can be identified through fluorescence additives; by the addition of dye to the solution of a crystallization trial; by trace fluorescent labeling of the protein; or by intrinsic UV fluorescence of aromatic amino acid residues, mainly tryptophan (19–22). Intrinsic UV fluorescence has become popular because it does not require any label. However, this technique is generally limited to proteins that contain tryptophan, and it exposes the protein crystal to damaging radiation (23). All these methods operate by generating high-fluorescence intensities in regions of high protein concentration, which provides selectivity for the protein over other precipitants but does not indicate crystallinity. The most significant problem with fluorescence-based detection methods is the nonzero background from proteins present in the solution, which can significantly limit the contrast, particularly for small crystals. Fluorescence techniques are also susceptible to optical scatter, which lowers their effectiveness in highly scattering media, such as heavy-protein aggregation or turbid lipidic phases.
3.1. Characteristics of Second-Order Nonlinear Optical Imaging of Chiral Crystals for Protein-Crystal Detection
SONICC is well suited to protein-crystal imaging and automatic identification because SHG signals are generated only by certain ordered assemblies and only in highly intense optical fields. These properties provide selectivity in two ways. First, the signal is generated only in the focal point of the femtosecond pulsed laser. In contrast to fluorescence techniques, the signal is generated only in the focal plane, which eliminates the possibility of any signal being generated out of plane and makes the measurement far less sensitive to optical scatter. Turbid media attenuate the light reaching the focus (which can be corrected by simply increasing the incident power) and scatter the signal generated (which again attenuates the signal but does not degrade resolution because all the scattered signal has been generated in the focus). Second, the selectivity based on order means that only crystalline materials generate significant signal. The solution, aggregated protein crystals, and many nonprotein crystals do not generate signal. With the rare exception of the cubic gyroidal crystal class (215 out of more than 67,000 entries in the Protein Data Bank) and racemic protein crystals (24), all protein crystals are bulk allowed for SHG. Unfortunately, protein crystals are not necessarily the only objects that can generate signal. Certain precipitants, both chiral and achiral, can form SHG active crystals as well. Such precipitants are generally recognized through high SHG activity, relative to proteins, and through the absence of significant UV-excited fluorescence. The average SHG efficiency per unit cell for a protein is approximately the same as that of a small molecule. However, the density of unit cells is ~102–103 times higher by volume, and the SHG signal scales with the square of the number of monomers in the focal volume (i.e., the signal is ~104–106 times higher).
The capabilities of SONICC for protein-crystal imaging have been assessed by imaging crystallization trials in lipidic mesophases (25). Lipidic mesophases promote crystal formation of integral membrane proteins by providing a matrix similar to that appearing within the membranes of cells. However, the high viscosity intrinsic to lipidic mesophases often causes occlusions, scattering centers, and heterogeneities that complicate conventional imaging methods for crystal detection. SONICC images have been acquired and compared with those obtained through traditional methods. Qualitative comparisons between the images shown in Figure 5 highlight the distinct practical advantages of SONICC detection in crystallization trials. Line traces comparing the intrinsic UV fluorescence with the SONICC image in the trial in Figure 5b are shown in Figure 6. The key advantage of SONICC is the signal-to-background enhancement that arises primarily from the nearly complete suppression of the background. In addition to increasing contrast, SONICC can reliably identify much smaller protein crystals than conventional techniques can. SHG signal can frequently be observed from structures that are approximately the same size as or even smaller than the lateral resolution of the microscope (~1 µm).
Figure 5.
Comparison of SONICC (second-order nonlinear optical imaging of chiral crystals) and conventional optical methods for protein-crystal detection, from six representative outcomes of crystallization trials (a–f). Bright-field microscopy and birefringence (cross-polarized) images were obtained through the use of white-light illumination with UV and Cy3 fluorescence excited by ~280-nm and ~543-nm light, respectively. All SONICC images were acquired with 800-nm incident light with detection at 400 nm. The images in panels c and f appear identical according to all four conventional methods. SONICC analysis reveals that the image in panel c contains a shower of microcrystals (~2 µm or less in diameter), whereas that in panel f is completely clear. The presence of small crystals can be determined in trials that are highly turbid (b,e). The dotted lines indicate the origin of the line traces in Figure 6. Abbreviation: N/A, not applicable.
Figure 6.
Line traces, corresponding to the dashed lines in Figure 5b, comparing UV fluorescence and SONICC (second-order nonlinear optical imaging of chiral crystals) for detection of unlabelled protein crystals prepared in meso. Whereas the intrinsic UV enables detection of one crystal with a moderate signal-to-background ratio, SONICC clearly indicates the presence of at least five crystals spanning the line trace. Even in the clear positive case shown in Figure 5a, the signal-to-background ratios for UV fluorescence, Cy3 fluorescence, and SONICC are 1.5:1, 5:1, and 12,000:1, respectively.
3.2. Second-Order Nonlinear Optical Imaging of Chiral Crystals Image Analysis for Automated Scoring
The low background of SONICC imaging enables the straightforward application of simple image-analysis algorithms for automated crystallization scoring. Many automated scoring methods for high-throughput crystallization screening applications that use traditional imaging methods as inputs (26–32) have been developed. Results from a simple image-analysis method that uses SONICC images as inputs are shown in Figure 7. A total of 41 images were measured by combinations of these methods and were scored on the basis of (a) manual expert inspection of the set of conventional images, (b) automated scoring by SONICC through the use of a simple threshold-based particle-counting algorithm, and (c) manual inspection of the SONICC images. The automated scoring approach produced positive hits for well-formed large crystals, small crystals, and microcrystal showers for 80% of the trials analyzed and yielded no false negatives, according to a visual inspection of the SONICC and conventional images. By comparison, only 49% of the trials were scored highly by expert visual inspection, according to a 10-point scale (33). This finding suggests that expert manual inspection of the in meso trials, on the basis of the available commercial imaging approaches, resulted in a false-negative rate of ~40%. For example, the crystallization trial shown in Figure 5b earned a score of zero upon expert inspection with conventional imaging methods, yet it clearly contains diffraction-quality crystals that were easily identified by SONICC. Whereas UV fluorescence provided only a marginal positive for a single crystal (signal-to-background ratio of 0.5:1), SONICC identified at least five crystals with a signal-to-background ratio of well over 50:1. Given the limited number (41) of trials used, statements regarding the general applicability of this particular algorithm can be made only cautiously. However, the absence of a detectable background from noncrystalline materials intrinsically generated images that were easily amenable to a host of more generally applicable image-analysis algorithms.
Figure 7.
Comparison between manual scoring and automated scoring for different sets of images. The graph is divided into four regions on the basis of the minimum score that was considered a positive in each case. Color coding and shapes indicate manual categorization based on inspection of the SONICC (second-order nonlinear optical imaging of chiral crystals) images.
4. APPLICATIONS FOR ACTIVE PHARMACEUTICAL INGREDIENT–CRYSTALLIZATION CHARACTERIZATION
Solid-state forms of active pharmaceutical ingredients (APIs) are significant in pharmaceutical applications. Different forms (e.g., crystalline hydrates, salts, and amorphous preparations) determine key physical and chemical properties of APIs, which in turn affect the potency and stability of final products. In a chilling example, a change in crystal polymorphism in ritonavir (34, 35), an inhibitor of human immunodeficiency virus protease, resulted in substantial losses in bioavailability, which required reformulation and delays in delivery of the medication. Because APIs increasingly encounter poor water solubility, numerous strategies have been used to combat this issue and to increase bioavailability. One of the more promising approaches is to formulate an API in an amorphous form, which is most commonly a metastable state that usually demonstrates enhanced solubility (36–40). Challenges in developing amorphous APIs remain due to the relative instability of most amorphous solids relative to their crystalline analogs. Crystal formation within an amorphous API can negatively influence the potency of the drug, which in turn dramatically reduces the product’s shelf life. Therefore, intense research effort has been devoted to stabilizing the amorphous APIs and inhibiting crystallization [e.g., by forming a solid dispersion of API in a polymer matrix (41, 42)]. Arguably, a major challenge that increases the time and expense involved in developing amorphous APIs is the need to observe crystal formation at the earliest possible stages.
Conventional techniques based on spectroscopic, thermal, and X-ray diffraction methods have been widely utilized to detect API crystals (43–47). Such techniques readily allow quantification of the relative amount of crystalline materials within a sample; their detection limits correspond to approximately 1–10% crystallinity, which makes them inadequate for probing trace crystallinity. Additionally, these techniques are based on ensemble-average measurements; therefore, there is a lack of microscopic information (e.g., crystal nucleation kinetics). OM enables determination of the nucleation rate and the growth rate of crystals within pristine, optically transparent materials (48). The major limitation of OM in characterizing crystallization is the requirement of optically transparent samples, which are needed because scattering in complex matrices and powders complicates definitive crystal detection. Therefore, with current technology, studies of crystallization kinetics have been limited largely to regimes with >1% crystallinity or to transparent films whose behaviors are substantially different from those expected from powdered preparations (49, 50). Clearly, we need methods that can (a) probe the lower-crystallinity regimes that are most relevant to the key steps in nucleation and growth and (b) provide a bridge between measurements of thin films and powders.
SONICC has the potential to play such a role because it simultaneously allows for quantitative real-time monitoring of crystal nucleation, growth, and the macroscopic crystallization rate from a single set of measurements (Figure 8) (51). As in OM, threshold-based particle counting and size analysis can be directly applied to SONICC images, which enable studies of crystal nucleation and growth rates. In addition to microscopy-related events, quantification of ensemble-average crystallinity can be performed with SONICC simply by integrating SHG intensity over the probed volumes, relative to SHG intensity of 100%-crystallinity references. For example, the reference for probing crystallization kinetics through the use of SONICC is the integrated SHG over the probed volume when the crystallization is complete.
Figure 8.
(a) Real-time crystallization of griseofulvin monitored by SONICC (second-order nonlinear optical imaging of chiral crystals). Individual crystals (circled in red) can be analyzed using standard threshold-based particle analysis. (b) Isothermal crystallization kinetics of griseofulvin probed by SONICC. The overall crystallization rate, nucleation rate, and growth rate of individual crystals can be simultaneously analyzed.
4.1. Detection Limits for Crystal Size and Percentage Crystallinity
Routine methods for detecting crystals in APIs have a detection limit of 1% to 10% relative crystallinity, which is insufficient for probing trace amounts of crystal. The detection limit of SONICC can be estimated by taking advantage of the coherent nature of SHG. By use of arguments based on the relative intensity in the forward versus backward directions (i.e., copropagating or counter-propagating, respectively, with the incident beam) (12), from differences in the coherence lengths, a point of calibration can be defined to relate the observed intensity back to the crystal size (51). Application of this approach to single-pixel crystals (Figure 8a) yields detection limits for a single microcrystal of approximately 90 nm in all dimensions. If we consider the depth of field and field of view of the image, this value corresponds to a minimum crystallinity of 3.4 × 10−9%, or 1 part in 30 billion by volume. Furthermore, this approximately eight-orders-of-magnitude improvement represents a conservative estimate, given that these images were acquired for a single z slice under relatively low (10×, numerical aperture = 0.3) magnification. The SHG signal nominally scales with the fourth power of the beam waist; the use of higher magnification and sample translation to recover a large probed volume is likely to result in significant improvements in this detection limit.
4.2. Kinetics of Crystallization
Despite the progress in research on amorphous APIs, there have been relatively few studies on thermodynamics and kinetics of API crystallization (48, 52–54). The molecular mechanisms that govern crystal formation within amorphous materials and the thermodynamics and crystallization kinetics of such materials depend on various external driving forces (e.g., temperature, humidity, and chemical environment). The crystallization kinetics of amorphous solids has been extensively explored for ceramics and inorganic glasses; such studies were later extended to organic molecules in glassy states. Provided that the crystal nucleation and growth can be described by Arrhenius processes, the kinetics of isothermal crystallization in glass may be reliably modeled by the Johnson-Mehl-Avrami (JMA) equation (55, 56), α = 1 − e{−[k(t−t0)]n}, where k is an apparent rate of crystallization, t0 is the induction time, and n is the order of reaction associated with the mechanism of nucleation. According to the JMA equation, the crystal fraction α is independent of the means used to perform the measurements. Through the use of thermal analysis (57, 58) and X-ray diffraction (49), crystallization from the amorphous phase of several organic molecules has been described by the JMA equation.
As in previous studies, SONICC was applied to monitor the isothermal crystallization kinetics of amorphous griseofulvin, an antifungal therapeutic. Investigators quantified the relative crystallinity by SONICC by integrating the SHG intensity over the area probed, which was referenced to the intensity approached asymptotically with time. Crystallization of amorphous griseofulvin determined via SONICC was well described by the JMA equation; the activation energy of crystallization was 140 × 20 kJ mol−1 (51). A thermal analysis study by Zhou et al. (57) reported an activation energy of 167 kJ mol−1 for the isothermal crystallization of griseofulvin. The comparable activation energy determined independently by SONICC and thermal analysis suggests that both measurements reliably probed similar ensemble-averaged phenomena. Along with macroscopic information, SONICC simultaneously generated complementary microscopic information about the nucleation rate and growth rates of individual crystallites. Use of a standard threshold-based particle-counting algorithm (Figure 8b) allowed the authors to obtain the crystal nucleation rates.
5. INSIGHTS INTO OSTWALD RULE OF STAGES
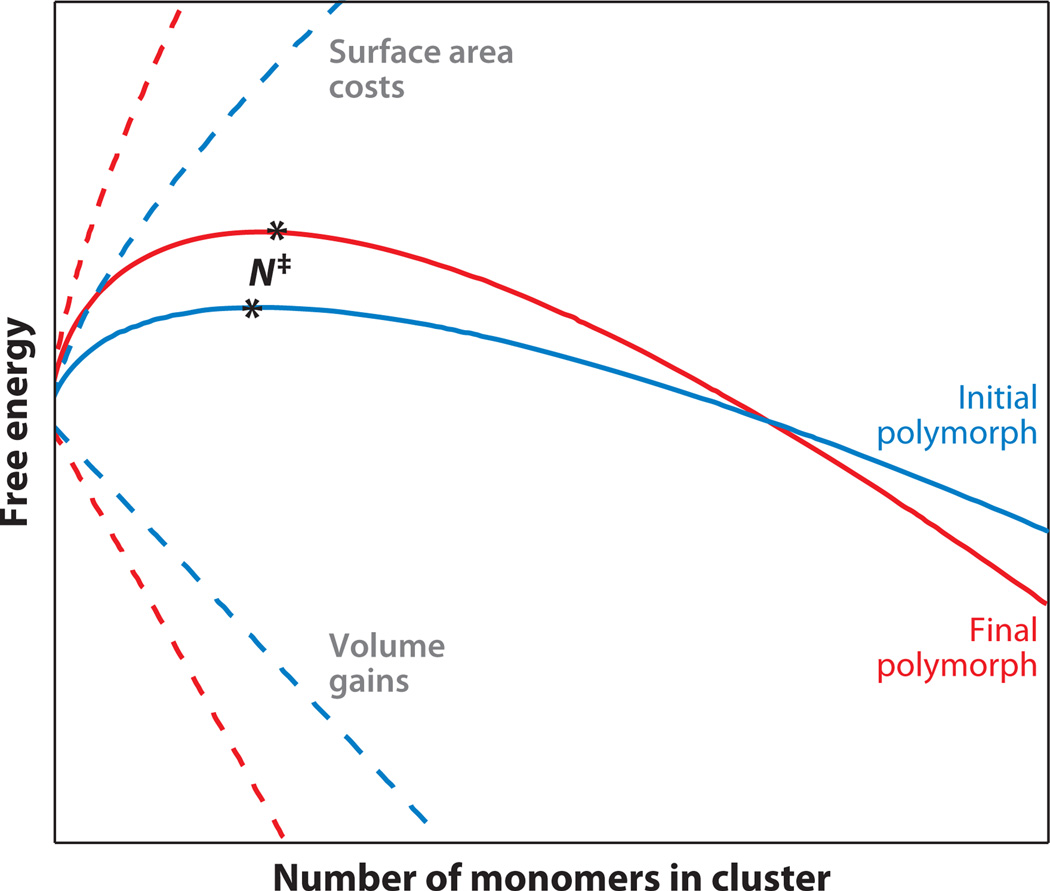
In 1897, Ostwald (59) suggested that the crystal polymorphs initially formed during crystallogenesis would generally be significantly different from those observed in the final macroscopic crystal. On the basis of thermodynamic arguments, the crystal polymorphs with free energies that were most closely matched to the solution would initially be the most readily formed and would transition adiabatically through stages of different polymorphs of decreasing free energy until, ultimately, arriving at the most stable bulk form. One such mechanism from classical nucleation theory that is consistent with this trend is illustrated in Figure 9, which shows that the barrier for crystal nucleation is reduced for a polymorphic form with low interfacial free energy and that, at larger sizes, it transitions to a polymorph with greater bulk stability. This hypothesis is distinctly different from the well-known Ostwald ripening phenomenon, which describes the time evolution of particle sizes (60, 61). According to this rule of stages, both the mechanism and the kinetics for crystal nucleation may be dramatically influenced by the presence of Ostwald transitioning.
Figure 9.
Hypothetical free-energy curves highlighting the possibility of polymorph curve crossing during crystallization. Solid lines represent the net free energy as a function of the cluster size, generated from the sum of the surface area and volume terms (dashed lines). The critical cluster size for nucleation, N‡, is indicated by asterisks.
Evidence supporting Ostwald’s rule of stages comes from model systems of atomic layers and colloidal crystals (62, 63), but the greater conformational flexibility and diversity of molecular interactions in organic molecules and proteins have complicated efforts to observe such transient structures during crystallogenesis of more complex molecular structures. Yet these structurally richer organic molecules are the most biologically important. The many challenges associated with observing such polymorph transitioning stem largely from the inherent difficulty of detecting and characterizing structures that are rare, small, and short-lived. Recent SONICC measurements of amino acids offered unique insights into Ostwald’s rule of stages in organic crystals (64).
Crystals grown from racemic solutions can form racemic cocrystals (i.e., crystals containing both enantiomers within the unit cell) or homochiral conglomerates (i.e., mixtures of homochiral crystals, each containing a single enantiomer). Typically, the racemic cocrystals are the more thermodynamically stable structures for the amino acids when crystallized from aqueous solutions under ambient conditions, and they are often centrosymmetric and SHG inactive. In accordance with this trend, single-enantiomer serine crystals adopt an SHG-active P212121 space group, whereas the racemic cocrystals of P21/n symmetry are SHG inactive. Consequently, the presence of detectable SHG can serve as a sensitive indicator of the presence of homochiral serine microcrystals. Because interconversion from a homochiral conglomerate to a racemic cocrystal requires physical changes in the composition of the lattice, interconversion may be slow enough to allow detection.
Select still shots from SONICC videos of crystallization from racemic serine solutions are shown in Figure 10. Upon initiation of crystal formation, transient and localized domains of SHG were observed; in some cases, these domains survived for only a few seconds. Although these transient domains were short-lived and sparsely populated, the ability to detect them through the use of SONICC provides compelling direct evidence that polymorphic changes occur upon serine crystallization, in agreement with Ostwald’s 1897 predictions. These results represent the first study of molecular systems whose considerable inter- and intramolecular conformational freedom demonstrates short-lived polymorphic transient domains, consistent with Ostwald’s rule of stages. In the future, this capability may help address key mechanistic questions about crystal nucleation and growth.
Figure 10.
(a) SONICC (second-order nonlinear optical imaging of chiral crystals) images of transient second harmonic generation–active crystallites (red circles) during solvent evaporation of an aqueous serine solution. (b) Similar measurements performed with a homochiral solution. Time zero was defined by the presence of detectable SONICC signals, which corresponded to the onset of crystal formation. Panel b has been rescaled by a factor of two to promote comparison. Images adapted from Reference 64.
6. FUTURE PROSPECTS AND CURRENT CHALLENGES
Although significant progress in SONICC has been made over a relatively short time frame, numerous unanswered questions remain. In protein studies, key practical issues include assessment of possible sample damage to delicate crystals from local heating, multiphoton absorption, or other mechanisms. In small-molecule studies, many of the key target applications require analysis of powdered or otherwise highly scattering media. Although in principle SONICC should have the same insensitivity to optical scattering as multiphoton excited fluorescence, the strengths and limitations of SONICC measurements of powdered samples should be rigorously explored. For all crystalline samples, the sensitivity of the SHG intensity to both polarization and crystal orientation may be a complicating factor for interpreting image contrast. However, this sensitivity is also a largely unexploited tool for characterizing crystal polymorphism and orientation. The recent development of high-precision polarization-dependent measurement approaches that are compatible with SHG microscopy techniques (65–67), in combination with theoretical and computational tools to aid in polarization analysis (14), has the potential to bridge macroscopic observables with microscopic structure and orientation. These capabilities may aid the identification of domain boundaries within crystals, including those from twinning. Finally, all the current SONICC approaches have been performed far from electronic or vibrational resonance. Both the sensitivity and the selectivity may be positively influenced by resonance-enhanced measurements either through electronic resonance with the doubled or incident frequency or through vibrational resonance enhancement (e.g., sum frequency vibrational microscopy). It will be interesting to learn how collective efforts in these areas (among others that have yet to be identified) will shape further developments in the nascent field of nonlinear optics.
ACKNOWLEDGMENTS
The authors gratefully acknowledge financial support from the National Science Foundation (NSF-MRI-0922987, NSF-CHE-0722558, andNSF-CHE-0923637) and the National Institutes of Health (1R01RR026273 and 1P50GM088499).
Glossary
- Nonlinear optical (NLO)
describes the behavior of light in media that exhibit an NLO polarization response to electric fields
- Second harmonic generation (SHG)
the specific case of SFG in which the two incident optical fields are of identical frequency
- SONICC
second-order nonlinear optical imaging of chiral crystals
- OM
optical microscopy
- API
active pharmaceutical ingredient
Footnotes
DISCLOSURE STATEMENT
D.J.K. and G.J.S. are authors on a pending patent licensed by Formulatrix for the application of SONICC for protein-crystal detection. The authors are not aware of any other affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- 1.Stehlin T, Feller M, Guyot-Sionnest P, Shen YR. Optical second-harmonic generation as a surface probe for noncentrosymmetric media. Opt. Lett. 1988;13:389. doi: 10.1364/ol.13.000389. [DOI] [PubMed] [Google Scholar]
- 2.Shen YR. Surface properties probed by second-harmonic and sum-frequency generation. Nature. 1989;337:519–525. [Google Scholar]
- 3.Eisenthal KB. Equilibrium and dynamic processes at interfaces by second harmonic and sum frequency generation. Annu. Rev. Phys. Chem. 1992;43:627–661. [Google Scholar]
- 4.Boyd RW. Nonlinear Optics. 2nd ed. Amsterdam: Academic; 2003. [Google Scholar]
- 5.Shen YR. The Principles of Nonlinear Optics. New York: Wiley; 1984. [Google Scholar]
- 6.Wampler RD, Kissick DJ, Dehen CJ, Gualtieri EJ, Grey JL, et al. Selective detection of protein crystals by second harmonic microscopy. J. Am. Chem. Soc. 2008;130:14076–14077. doi: 10.1021/ja805983b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wampler RD, Moad AJ, Moad CW, Heiland R, Simpson GJ. Visual methods for interpreting optical nonlinearity at the molecular level. Acc. Chem. Res. 2007;40:953–960. doi: 10.1021/ar600055t. [DOI] [PubMed] [Google Scholar]
- 8.Zyss J, Oudar JL. Relations between microscopic and macroscopic lowest-order optical nonlinearities of molecular crystals with one- or two-dimensional units. Phys. Rev. A. 1982;26:2028–2048. doi: 10.1103/physreva.36.5463. [DOI] [PubMed] [Google Scholar]
- 9.Wampler RD, Begue NJ, Simpson GJ. Molecular design strategies for optimizing the nonlinear optical properties of chiral crystals. Cryst. Growth Des. 2008;8:2589–2594. [Google Scholar]
- 10.Butcher PN, Cotter D. The Elements of Nonlinear Optics. New York: Cambridge Univ. Press; 1990. [Google Scholar]
- 11.Wampler RD, Kissick DJ, Dehen CJ, Gualtieri EJ, Grey JL, et al. Selective detection of protein crystals by second harmonic microscopy. J. Am. Chem. Soc. 2008;130:14076–14077. doi: 10.1021/ja805983b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.LaComb R, Nadiarnykh O, Townsend SS, Campagnola PJ. Phase matching considerations in second-harmonic generation from tissues: effects on emission directionality, conversion efficiency, and observed morphology. Opt. Commun. 2008;281:1823–1832. doi: 10.1016/j.optcom.2007.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gouy LG. Sur une proprieté nouvelle des ondes lumineuses. C.R. Acad. Sci. Paris. 1890;110:1251–1253. [Google Scholar]
- 14.Moad AJ, Moad CW, Perry JM, Wampler RD, Goeken GS, et al. NLOPredict: visualization and data analysis software for nonlinear optics. J. Comput. Chem. 2007;28:1996–2002. doi: 10.1002/jcc.20706. [DOI] [PubMed] [Google Scholar]
- 15.Perry JM, Moad AJ, Begue NJ, Wampler RD, Simpson GJ. Electronic and vibrational second-order nonlinear optical properties of protein secondary structural motifs. J. Phys. Chem. B. 2005;109:20009–20026. doi: 10.1021/jp0506888. [DOI] [PubMed] [Google Scholar]
- 16.Simpson GJ, Perry JM, Moad AJ, Wampler RD. Uncoupled oscillator model for interpreting second harmonic generation measurements of oriented chiral systems. Chem. Phys. Lett. 2004;399:26–32. [Google Scholar]
- 17.Echalier A, Glazer RL, Fülöp V, Geday MA. Assessing crystallization droplets using birefringence. Acta Crystallogr. D. 2004;60:696–702. doi: 10.1107/S0907444904003154. [DOI] [PubMed] [Google Scholar]
- 18.Nollert P. Microscope detection options for colorless protein crystals in lipidic cubic phases. J. Appl. Crystallogr. 2003;36:1295–1296. doi: 10.1107/S0021889803013724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Groves MR, Müller IB, Kreplin X, Müller-Dieckmann J. A method for the general identification of protein crystals in crystallization experiments using a noncovalent fluorescent dye. Acta Crystallogr. D. 2007;63:526–535. doi: 10.1107/S0907444906056137. [DOI] [PubMed] [Google Scholar]
- 20.Forsythe E, Achari A, Pusey ML. Trace fluorescent labeling for high-throughput crystallography. Acta Crystallogr. D. 2006;62:339–346. doi: 10.1107/S0907444906000813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fry EH, Qin W, Fleck EN, Judge RA, Chiu ML. Improved protein crystal in detergent and lipidic meso-phases. Open Struct. Biol. J. 2009;3:11–15. [Google Scholar]
- 22.Judge RA, Swift K, Gonzalez C. An ultraviolet fluorescence–based method for identifying and distinguishing protein crystals. Acta Crystallogr. D. 2005;61:60–66. doi: 10.1107/S0907444904026538. [DOI] [PubMed] [Google Scholar]
- 23.Nanao MH, Ravelli RBG. Phasing macromolecular structures with UV-induced structural changes. Structure. 2006;14:791–800. doi: 10.1016/j.str.2006.02.007. [DOI] [PubMed] [Google Scholar]
- 24.Mandal K, Pentelute BL, Tereshko V, Thammavongsa V, Schneewind O, et al. Racemic crystallography of synthetic protein enantiomers used to determine the X-ray structure of plectasin by direct methods. Protein Sci. 2009;18:1146–1154. doi: 10.1002/pro.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kissick DJ, Gualtieri EJ, Simpson GJ, Cherezov V. Nonlinear optical imaging of integralmembrane protein crystals in lipidic mesophases. Anal. Chem. 2010;82:491–497. doi: 10.1021/ac902139w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cumbaa CA, Lauricella A, Fehrman N, Veatch C, Collins R, et al. Automatic classification of sub-microlitre protein-crystallization trials in 1,536-well plates. Acta Crystallogr. D. 2003;59:1619–1627. doi: 10.1107/s0907444903015130. [DOI] [PubMed] [Google Scholar]
- 27.Spraggon G, Lesley SA, Kreusch A, Priestle JP. Computational analysis of crystallization trials. Acta Crystallogr. D. 2002;58:1915–1923. doi: 10.1107/s0907444902016840. [DOI] [PubMed] [Google Scholar]
- 28.Wilson J. Towards the automated evaluation of crystallization trials. Acta Crystallogr. D. 2002;58:1907–1914. doi: 10.1107/s0907444902016633. [DOI] [PubMed] [Google Scholar]
- 29.Bern M, Goldberg D, Stevens RC, Kuhn P. Automatic classification of protein crystallization images using a curve-tracking algorithm. J. Appl. Crystallogr. 2004;37:279–287. [Google Scholar]
- 30.Zhu XQ, Sun SH, Bern M. Proc. 26th Annu. Int. Conf. IEEE Eng. Med. Biol. Soc; 2004. pp. 1628–1631. [DOI] [PubMed] [Google Scholar]
- 31.Walker CG, Foadi J, Wilson J. Classification of protein crystallisation images using Fourier descriptors. J. Appl. Crystallogr. 2007;40:418–426. [Google Scholar]
- 32.Liu R, Freund Y, Spraggon G. Image-based crystal detection: a machine-learning approach. Acta Crystallogr. D. 2008;64:1187–1195. doi: 10.1107/S090744490802982X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Caffrey M, Cherezov V. Crystallizing membrane proteins using lipidic mesophases. Nat. Protoc. 2009;4:706–731. doi: 10.1038/nprot.2009.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chemburkar SR, Bauer J, Deming K, Spiwek H, Patel K, et al. Dealing with the impact of ritonavir polymorphs on the late stages of bulk drug process development. Org. Process Res. Dev. 2000;4:413–417. [Google Scholar]
- 35.Dunitz JD, Bernstein J. Disappearing polymorphs. Acc. Chem. Res. 1995;28:193–200. [Google Scholar]
- 36.Hancock BC, Zografi G. Characteristics and significance of the amorphous state in pharmaceutical systems. J. Pharm. Sci. 1997;86:1–12. doi: 10.1021/js9601896. [DOI] [PubMed] [Google Scholar]
- 37.Hancock BC, Zografi G. The relationship between the glass transition temperature and the water content of amorphous pharmaceutical solids. Pharm. Res. 1994;11:471–477. doi: 10.1023/a:1018941810744. [DOI] [PubMed] [Google Scholar]
- 38.Hancock BC, Parks M. What is the true solubility advantage for amorphous pharmaceuticals. Pharm. Res. 2000;17:397–404. doi: 10.1023/a:1007516718048. [DOI] [PubMed] [Google Scholar]
- 39.Leuner C, Dressman J. Improving drug solubility for oral delivery using solid dispersions. Eur. J. Pharm. Biopharm. 2000;50:47–60. doi: 10.1016/s0939-6411(00)00076-x. [DOI] [PubMed] [Google Scholar]
- 40.Craig DQM, Royall PG, Kett VL, Hopton ML. The relevance of the amorphous state to pharmaceutical dosage forms: glassy drugs and freeze dried systems. Int. J. Pharm. 1999;179:179–207. doi: 10.1016/s0378-5173(98)00338-x. [DOI] [PubMed] [Google Scholar]
- 41.Chiou WL, Riegelma S. Pharmaceutical applications of solid dispersion systems. J. Pharm. Sci. 1971;60:1281–1302. doi: 10.1002/jps.2600600902. [DOI] [PubMed] [Google Scholar]
- 42.Serajuddin ATM. Solid dispersion of poorly water-soluble drugs: early promises, subsequent problems, and recent breakthroughs. J. Pharm. Sci. 1999;88:1058–1066. doi: 10.1021/js980403l. [DOI] [PubMed] [Google Scholar]
- 43.Bugay DE. Characterization of the solid-state: spectroscopic techniques. Adv. Drug Deliv. Rev. 2001;48:43–65. doi: 10.1016/s0169-409x(01)00101-6. [DOI] [PubMed] [Google Scholar]
- 44.Newman AW, Byrn SR. Solid-state analysis of the active pharmaceutical ingredient in drug products. Drug Discov. Today. 2003;8:898–905. doi: 10.1016/s1359-6446(03)02832-0. [DOI] [PubMed] [Google Scholar]
- 45.Shah B, Kakumanu VK, Bansal AK. Analytical techniques for quantification of amorphous/crystalline phases in pharmaceuticals solids. J. Pharm. Sci. 2006;95:1641–1665. doi: 10.1002/jps.20644. [DOI] [PubMed] [Google Scholar]
- 46.Buckton G, Darcy P. Assessment of disorder in crystalline powders—a review of analytical techniques and their application. Int. J. Pharm. 1999;179:141–158. doi: 10.1016/s0378-5173(98)00335-4. [DOI] [PubMed] [Google Scholar]
- 47.Taylor LS, Zografi G. The quantitative analysis of crystallinity using FT-Raman spectroscopy. Pharm. Res. 1998;15:755–761. doi: 10.1023/a:1011979221685. [DOI] [PubMed] [Google Scholar]
- 48.Andronis V, Zografi G. Crystal nucleation and growth of indomethacin polymorphs from the amorphous state. J. Noncryst. Solids. 2000;271:236–248. [Google Scholar]
- 49.Yoshioka M, Hancock BC, Zografi G. Crystallization of indomethacin from the amorphous state below and above its glass transition temperature. J. Pharm. Sci. 1994;83:1700–1705. doi: 10.1002/jps.2600831211. [DOI] [PubMed] [Google Scholar]
- 50.Konno H, Taylor LS. Ability of different polymers to inhibit the crystallization of amorphous felodipine in the presence of moisture. Pharm. Res. 2008;25:969–978. doi: 10.1007/s11095-007-9331-3. [DOI] [PubMed] [Google Scholar]
- 51.Wanapun D, Kestur US, Kissick DJ, Simpson GJ, Taylor LS. Selective detection and quantitation of organic molecule crystallization by second harmonic generation microscopy. Anal. Chem. 2010;82:5425–5432. doi: 10.1021/ac100564f. [DOI] [PubMed] [Google Scholar]
- 52.Andronis V, Yoshioka M, Zografi G. Effects of sorbed water on the crystallization of indomethacin from the amorphous state. J. Pharm. Sci. 1997;86:346–351. doi: 10.1021/js9602711. [DOI] [PubMed] [Google Scholar]
- 53.Schmitt EA, Law D, Zhang GGZ. Nucleation and crystallization kinetics of hydrated amorphous lactose above the glass transition temperature. J. Pharm. Sci. 1999;88:291–296. doi: 10.1021/js980387s. [DOI] [PubMed] [Google Scholar]
- 54.Alie J, Menegotto J, Cardon P, Duplaa H, Caron A, et al. Dielectric study of the molecular mobility and the isothermal crystallization kinetics of an amorphous pharmaceutical drug substance. J. Pharm. Sci. 2004;93:218–233. doi: 10.1002/jps.10520. [DOI] [PubMed] [Google Scholar]
- 55.Avrami M. Kinetics of phase change. I. General theory. J. Chem. Phys. 1939;7:1103–1112. [Google Scholar]
- 56.Avrami M. Kinetics of phase change. III. Granulation, phase change, and microstructure. J. Chem. Phys. 1941;9:177–184. [Google Scholar]
- 57.Zhou D, Zhang GGZ, Law D, Grant DJW, Schmitt EA. Thermodynamics, molecular mobility and crystallization kinetics of amorphous griseofulvin. Mol. Pharm. 2008;5:927–936. doi: 10.1021/mp800169g. [DOI] [PubMed] [Google Scholar]
- 58.Zhou DL, Grant DJW, Zhang GGZ, Law D, Schmitt EA. A colorimetric investigation of thermodynamic and molecular mobility contributions to the physical stability of two pharmaceutical glasses. J. Pharm. Sci. 2007;96:71–83. doi: 10.1002/jps.20633. [DOI] [PubMed] [Google Scholar]
- 59.Ostwald W. Studien über die Bildung und Umwandlung fester Körper. Z. Phys. Chem. 1897;22:289–330. [Google Scholar]
- 60.Marqusee JA, Ross J. Theory of Ostwald ripening: competitive growth and its dependence on volume fraction. J. Chem. Phys. 1984;80:536–543. [Google Scholar]
- 61.Ng JD, Lorber B, Witz J, Theobald-Dietrich A, Kern D, Giegé R. The crystallization of biological macromolecules from precipitates: evidence for Ostwald ripening. J. Cryst. Growth. 1996;168:50–62. [Google Scholar]
- 62.Stoica C, Tinnemans P, Meekes H, Vlieg E, van Hoof PJCM, Kaspersen FM. Epitaxial 2D nucleation of metastable polymorphs: a 2D version of Ostwald’s rule of stages. Cryst. Growth Des. 2005;5:975–981. [Google Scholar]
- 63.Kim K, Plass KE, Matzger AJ. Kinetic and thermodynamic forms of a two-dimensional crystal. Langmuir. 2003;19:7149–7152. [Google Scholar]
- 64.Hall VJ, Simpson GJ. Direct observation of transient Ostwald crystallization ordering from racemic serine solutions. J. Am. Chem. Soc. 2010;132:13598–13599. doi: 10.1021/ja106728c. [DOI] [PubMed] [Google Scholar]
- 65.Begue NJ, Simpson GJ. Chemically selective analysis of molecular monolayers by nonlinear optical stokes ellipsometry. Anal. Chem. 2010;82:559–566. doi: 10.1021/ac901832u. [DOI] [PubMed] [Google Scholar]
- 66.Begue NJ, Moad AJ, Simpson GJ. Nonlinear optical stokes ellipsometry. 1. Theoretical framework. J. Phys. Chem. C. 2009;113:10158–10165. [Google Scholar]
- 67.Begue NJ, Everly RM, Hall VJ, Haupert L, Simpson GJ. Nonlinear optical stokes ellipsometry. II. Experimental demonstration. J. Phys. Chem. C. 2009;113:10166–10175. [Google Scholar]