Viscoelastic properties of cell walls of single living plant cells determined by dynamic nanoindentation

Abstract

Plant development results from controlled cell divisions, structural modifications, and reorganizations of the cell wall. Thereby, regulation of cell wall behaviour takes place at multiple length scales involving compositional and architectural aspects in addition to various developmental and/or environmental factors. The physical properties of the primary wall are largely determined by the nature of the complex polymer network, which exhibits time-dependent behaviour representative of viscoelastic materials. Here, a dynamic nanoindentation technique is used to measure the time-dependent response and the viscoelastic behaviour of the cell wall in single living cells at a micron or sub-micron scale. With this approach, significant changes in storage (stiffness) and loss (loss of energy) moduli are captured among the tested cells. The results reveal hitherto unknown differences in the viscoelastic parameters of the walls of same-age similarly positioned cells of the Arabidopsis ecotypes (Col 0 and Ws 2). The technique is also shown to be sensitive enough to detect changes in cell wall properties in cells deficient in the activity of the chromatin modifier ATX1. Extensive computational modelling of the experimental measurements (i.e. modelling the cell as a viscoelastic pressure vessel) is used to analyse the influence of the wall thickness, as well as the turgor pressure, at the positions of our measurements. By combining the nanoDMA technique with finite element simulations quantifiable measurements of the viscoelastic properties of plant cell walls are achieved. Such techniques are expected to find broader applications in quantifying the influence of genetic, biological, and environmental factors on the nanoscale mechanical properties of the cell wall.

Introduction

Plant cell walls are tough and flexible polymeric layers with a thickness that may reach a few hundred nanometres. The structure of the plant cell wall acts as an effective mechanism that prevents over-expansion under hydrostatic pressure (Cosgrove, 1997). In addition to structural support and protection, the mechanical properties of cell walls are key factors involved in the control of cell growth and in determining the size and the shape of the plant cell (Green, 1980; Thompson, 2005; Guimil and Dunand, 2006). Through its stiffness, which counteracts the turgor pressure of the vacuole, the wall controls the size, the shape, and the morphology of plant cells; through its extensibility, the wall distends under turgor pressure allowing the cell to grow. Increased hydrostatic pressure generates additional tensile loads within the wall and causes cell wall expansion—an irreversible process in young growing cells (Nobel, 2005). Thus, the magnitude of the mechanical stress in the cell wall is related to the turgor pressure, the cell wall composition and organization, and the interface conditions between the cells.

The main components of plant cell walls (cellulose, pectin, and hemicellulose) behave as an effective anisotropic composite material (Roland et al., 1989), whose function is additionally complicated by biological factors that can affect both the composition and the interactions between the components. As polymers, cell wall components exhibit time-dependent behaviour representative of viscoelastic media. The mechanical strains and stresses in the cell wall are time-dependent even if their biological constituents are fixed. For example, the orientation of the cellulose fibrils is a key factor governing the mechanical response of the cell wall with respect to the direction of cell expansion under tension, the plastic deformation, and the elasticity of cell walls (Baskin, 2005). Currently, the available data on the viscoelastic behaviour of cell walls come from studies of lumber (dead tree tissues), whole plant organs representing mixed cell types (Cleland, 1984; Kutschera, 1996), or from peeled layers of epidermal cells (Ryden et al., 2003). Also, Burgert (2006) provides an overview of different micromechanical test protocols that allow plant cell wall structure to be linked with functionality with respect to different plants and tissues. Recent Raman spectral data for wood at the micron level (acquired with linear polarized laser light) provided information about polymer composition as well as the alignment of cellulose microfibrils with respect to the fibre axis in cross-sections of spruce normal, opposite, and compression wood (Gierlinger et al., 2010). Finally, tools such as the pressure probe (Hüsken et al., 1978; Murphy and Ortega, 1995) and the pressure chamber (Urban et al., 1993) have been widely employed to determine indirectly the cell volumetric elastic modulus which is a measure of cell wall elasticity. Indeed, the cortical-cell turgor pressure as well as the cell volume or tissue water mass must be obtained in order to estimate the elastic modulus of the wall. Those techniques are powerful but are limited to applications on large cells (>20 μm) which makes them inapplicable on small cells such as Arabidopsis cells. Earlier, the mechanical properties of spruce wood cell walls were studied by nanoindentation (Gindl et al., 2004).

Instead of using walls detached from the underlying tissues, the interest here is in techniques that can be used to quantify directly the in vivo behaviour of a living cell wall under specific loading conditions. For that purpose, the dynamic nanoindentation technique has been used to achieve quantifiable measurements of the time-dependent response of the cell wall in single living cells at a micron or sub-micron scale. Since turgor pressure and wall thickness at the positions of indentation may influence the outcome of the measurements, extensive computational modelling has been performed to quantify the uncertainty of the experimental results. Similar work on suspension-cultured tomato cells (Wang et al., 2004) and Aspergillus nidulans (Zhao et al., 2005) has shown the value of combining modelling and experiments for estimating the Young’s modulus of plant cell walls. Here, the focus is on viscoelastic properties.

Viscoelasticity is the type of behaviour attributed to materials that exhibit both elastic and viscous qualities under deformation. Viscous materials resist shear flow and strain with time when a constant stress is applied. By contrast, elastic materials strain instantaneously when loaded and return to their original state immediately after the load is removed. Viscoelastic materials deform according to a combination of these properties and, as such, exhibit time-dependent strain. Elasticity is often associated with the stretching of atomic bonds, which is a fully recoverable process, while viscosity may result from the diffusion of molecules inside amorphous materials (Meyers and Chawla, 1999). Viscoelasticity is often studied using dynamic mechanical analysis (DMA). Here, nanoDMA is performed by applying a small oscillatory displacement and measuring the resulting force (Pethica and Oliver, 1987; see further below). Instruments such as broadband viscoelastic spectroscopy (BVS) and resonant ultrasound spectroscopy (RUS) are commonly used to quantify the mechanical responses of polymers. However, dynamic nanoindentation analysis has advantages over BVS and RUS, particularly in cases in which the length scales of interest are very small. Nanoindentation techniques have made it possible to measure the mechanical properties of media at submicrometre length scales using submilliNewton loads. Data from such measurements, plus an additional theoretical model, allow the calculation of material properties such as the storage and loss moduli (Odegard et al., 2005; Syed Asif et al., 1999).

The storage modulus, E′ (also called the dynamic stiffness) is a measure of the energy stored by the sample during a cycle of loading. Any resulting phase lag between the force applied and the displacement is related to a loss of energy known as the loss modulus or damping, E′. Overall, in viscoelastic solids the storage and the loss moduli represent the stored energy in the elastic portion and the energy dissipated as heat in the viscous portion.

Here, the viscoelastic properties of the cell wall are determined for Arabidopsis thaliana plants from two related and widely used laboratory ecotypes, Columbia (Col 0) and Wassilewskija (Ws 2). In addition, the qualitative effects on cell wall viscoelasticity caused by the ATX1-loss-of function in the atx1 mutant (the mutant allele is in the Ws background) are investigated by this technique as a demonstration of the sensitivity of the measurement. The Trithorax-like protein ATX1 is a histone methyltransferase tri-methylating the lysine 4 residue of histone H3, a mark associated with actively transcribed genes (Avramova, 2009; Eissenberg and Shilatifard, 2009). ATX1 influences the development of organ primordia, organ shape, and identity. Its disruption causes pleiotropic phenotypes including stem, root, and leaf growth defects illustrating the multiple plant developmental, morphogenic, and adaptation processes regulated by the chromatin modifier (Alvarez-Venegas et al., 2003). Among the ATX1-regulated genes are members of the cell wall-remodelling XTH family (Cosgrove, 2005; Saladié et al., 2006; Van Sandt et al., 2007), of pectin-modifying activities involved in altering the physical properties of the gel embedding the fibres (Jarvis, 1984; Michelli, 2001), of expansins inducing slippage and loosening of the cell wall by disrupting non-covalent bonds between the cellulose microfibrils and matrix polymers (Sampedro and Cosgrove, 2005; Cannon et al., 2008), of more than 30 glycosyl hydrolase/transferase genes, as well as the IRX3 and IRX5 cellulose synthase subunits (Alvarez-Venegas et al., 2006; Ndamukong et al., 2009). The large number of wall-related activities regulated by ATX1 implies that ATX1-deficient cells could display numerous aberrations in the properties of their walls. It is demonstrated here that our method successfully captures the altered wall properties of the mutant cells compared with the parameters measured for the wild-type cell walls, but it is not possible to draw conclusions about the specific role of ATX1 on the properties of the cell wall. These results validate the applicability of the nanoidentation technique for detecting aberrations in the viscoelastic properties of cell walls from mutants in different genetic backgrounds. Below, brief descriptions are presented of the theoretical basis of the nanoDMA technique and of the finite element method (FEM) used in this study.

NanoDMA technique

The nanoDMA technique (Syed Asif et al., 1999; Odegard et al., 2005) has been developed as a dynamic indentation test augmenting the currently available indentation capabilities (Pethica and Oliver, 1987). The method utilizes sinusoidal loading concurrent with quasi-static loading as the basis for a wide array of tests. As with any indentation system, nanoindentation consists of the well-controlled application of a hard tip, typically diamond, into the sample. The load (or displacement) is controlled, while the displacement (or load) is monitored. With such a measurement, force-displacement behaviour is extracted which is then cast into a stress–strain relationship using appropriate models of the tip-sample contact mechanics. These types of measurements may also be made as a function of time such that the viscoelastic behaviour of a sample may be quantified (a schematic illustration of such an experiment is shown in Supplementary Fig. S1A at JXB online). During testing, a small dynamic oscillation (here the frequency range is 10–250 Hz) is superposed over a constant load on the indenter head. The applied force drives the indenter into the sample (the cell wall), while the displacement of the indenter column is continuously recorded. The displacement response is measured at the same frequency as the applied oscillating force, at a point on the viscoelastic sample, giving a local measurement of properties.

The interaction of the tip and the sample is often represented using a simple mechanical model as illustrated in Supplementary Fig. S1B at JXB online. Specifically, m is the mass of the tip and shaft, K_i and $K_{\text{s}}^{\prime }$, are the stiffnesses of the instrument and sample, respectively, and C_i and C_s, represent the damping elements of the instrument and sample, respectively. The tip is assumed to be driven sinusoidally with a force amplitude F₀ at a circular frequency ω. Using a force balance of this model system, we can write an equation governing the motion of the indenter tip as

(1)

where x(t) defines the position of the tip as a function of time and the overdots denote temporal derivatives. For the steady-state solution, the displacement oscillates at the same frequency and displays the following form:

(2)

where X is the displacement amplitude and ϕ is the phase lag between the force applied and the tip displacement. Substituting equation (2) into equation (1) and simplifying yields:

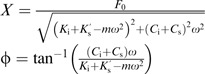(3)

These two equations relate the measured values of displacement amplitude, X, and phase lag, ϕ, to the sample properties which can be written as

(4)

where $K_{\text{s}}^{\prime }$ and $K_{\text{s}}^{\prime }$ are the storage and loss stiffnesses, respectively. Note that the loss stiffness is defined as the product of the excitation frequency ω and the damping of the sample C_s. Both $K_{\text{s}}^{\prime }$ and $K_{\text{s}}^{\prime \prime }$ are directly related to measured parameters of amplitude and phase without the use of any assumptions. Thus, these properties alone are of interest with respect to biological differences between plant cells.

The ultimate goal here is to determine the viscoelastic properties of the cell wall since the organization of the constituents will control these properties. In order to relate the measured quantities $K_{\text{s}}^{\prime }$ and $K_{\text{s}}^{\prime }$ to the cell wall properties, a model of the tip-sample contact mechanics is needed. Robust models have been developed for cases when the sample is homogeneous and large in all directions relative to the contact area (Oliver and Pharr, 1992). In this case,

(5)

and

(6)

relate the measured storage stiffness and loss stiffness to the storage modulus (E′) and loss modulus (E′′) of the sample. In equations (5) and (6), A defines the area of contact between the indenter tip and the sample. Note that indentation data are associated with the ‘reduced’ moduli which are related to the sample moduli through a factor of 1–v² with v the Poisson’s ratio (Oliver and Pharr, 1992). For biological samples, the common assumption that v≈0.49 is used. The moduli of the sample are thus determined as a function of frequency over the range of measurements. This relation is not so straightforward when living plant cells are involved. The storage stiffness and loss stiffness will be functions of the cell wall properties as well as the wall thickness and turgor pressure of the cell, such that the values of $K_{\text{s}}^{\prime }$ and $K_{\text{s}}^{\prime \prime }$ may depend on the depth of indentation used for the measurements. In particular, the force-displacement behaviour for the measurements here does not match that for the half-space problem normally used to interpret nanoDMA measurements (Fischer-Cripps, 2004). In order to clarify this complication, a computational model of the indentation is used. The experimental values for $K_{\text{s}}^{\prime }$ and $K_{\text{s}}^{\prime \prime }$ indicate that the nanoDMA technique is capable of quantifying these properties in living plant cells and that it is sensitive enough to identify differences between plants from different genetic backgrounds. The computational model is used to relate these measurements to the cell wall moduli, as shown later.

Finite Element Method (FEM)

Among several available computational methods, the finite element method (FEM) is used for simulating physical phenomena such as the nanoindentation measurements described here. The FEM uses a discretization procedure to divide the geometry of the model problem into small components (elements) that are assumed to behave according to a prescribed material deformation law. FEM has been used by many researchers in applications related to plants (Bolduc et al., 2006). A brief description of the FEM is presented here to facilitate our discussion of the data obtained experimentally in this study.

The simulations are performed using the commercial finite element software ABAQUS. The computational model of the system of interest here requires several aspects to be defined including: geometry, constraints, deformation law, material model, material symmetry, and force application. It is not possible in all cases to quantify all of these aspects with great certainty. Fortunately, computational models allow the influence of all inputs to be examined separately with respect to their impact on the results. Thus, reasonable assumptions are made in several cases. For example, it is assumed that the deformation of one cell during nanoindentation is not affected by adjacent cells. These effects are thought to be of higher order. The problem is also assumed axisymmetric for a cell of radius R with wall thickness t subjected to an internal turgor pressure p as shown schematically (see Supplementary Fig. S2 at JXB online). Although Arabidopsis cells have complex patterns with several lobes, the goal here is to use a simple model that describes the main aspects of the load-deformation behaviour. For computational efficiency, a spherical indenter is used and modelled as a rigid surface (its deformation is negligible relative to the cell wall deformation) with a radius of 2.5 μm, although a pyramidal indenter is used in the experiments. Such a choice for the tip used in the simulations allows an axisymmetric model to be used. Full 3D simulations are much more difficult and are the subject of future work. This choice is physically reasonable as extraction of elastic modulus from nanoindentation measurements is, in general, independent of the tip geometry (as long as the tip area is calibrated). In particular, our simulations using a conical indenter (with a profile that matches the pyramidal indenter used in the experiments) were studied and shown to affect the results by less than 6% regardless of other model parameters (see Supplementary Fig. S3 at JXB online). The cell geometry is also approximated as circular, so that axisymmetry can be exploited in the model. Although the epidermal cells in Arabidopsis are jig-saw puzzle-shaped, each lobe can be approximated as a circle with radius of 7±3 μm, corresponding to values from confocal images (see Materials and methods). Preliminary finite element simulations (see Supplementary Fig. S3 at JXB online) showed that variations in the radius of the plant cell wall (ranging from 5–20 μm) changed the modulus values by only 2–4% for the depth used in the experiments. The thickness of the cell wall and the turgor pressure have a much greater influence on modulus extracted from the measurements, such that the radius used in all simulations was fixed at 7 μm. The model is discretized using a 2D axisymmetric mesh consisting of four-node axisymmetric elements with reduced integration. A variable-sized mesh is used such that a very fine mesh is present in the regions near the indenter where stress gradients are large while a coarser mesh is used elsewhere where gradients are much smaller. The upper surface (see Supplementary Fig. S2 at JXB online) is assumed to be stress free outside of the region of the indenter, while the lower surface is subject to a uniform pressure p (turgor pressure). The cell wall is modelled as a neo-Hookean hyperelastic material with viscoelastic behaviour. Such choices have been used successfully to describe the behaviour of polymers (Treolar, 1975). The cell wall is assumed to be isotropic in the model, although it is recognized that the anisotropy known to be present must be considered in future work. The viscoelasticity is assumed to follow a generalized Maxwell mechanical model with two Maxwell elements (spring and dashpot) in parallel with an elastic spring to capture low and high frequency response. A low frequency (long time) relaxation is added to reflect the fact that slow relaxation may occur during the load profile. Other plant tissues have been observed to exhibit two distinct relaxation times that overlap the experiments here (Hansen et al., 2011): a quickly relaxing one which is shorter than 2 s and a slowly relaxing one which is larger than 10 s. The relaxation modulus for such a mechanical model is given by

(7)

where E_∞, E₁ and E₂ are the elastic moduli of the springs representing the modulus and τ₁=η₁/E₁ and τ₂=η₂/E₂ are the relaxation times associated with two dashpots where η₁ and η₂ are the viscosity (the value of the dashpot constant). The relaxation modulus represents two different elastic regions. For early times (t<<τ₁ and τ₂), E(t) approaches the instantaneous modulus E₀=E_∞+E₁+E₂ while for late times (t>>τ₁ and τ₂), E(t) reduces to the long-term modulus E_∞ The viscoelastic model described by equation (7) is readily available in ABAQUS with five required input parameters of instantaneous modulus E₀, the two relaxation times and the two moduli. The moduli are often cast in terms of dimensionless moduli $\stackrel{-}{g}$ which are given by

(8)

The experimental results from the nanoDMA measurements cover a limited range of frequencies (10–250 Hz) such that only the shorter time scale can be assessed. To include the effect of slow relaxation, the low frequency relaxation time is assumed as 10 s as reported by (Hansen, et al., 2011). For simplicity, it is assumed that ${\stackrel{-}{g}}_1={\stackrel{-}{g}}_2$ with the value determined from the nanoDMA measurements. In the preliminary simulations, it was found that the results are most sensitive to the cell wall thickness and turgor pressure (for example, the variation with respect to assumptions associated with the longer time behaviour changed the outcome by less than 1%). Thus, the thickness and pressure are the primary sources of uncertainty when wall properties are determined by matching the FEM simulation results with the experimental results.

Materials and methods

Plant material and growth conditions

Wild-type Columbia (Col-0) and Wassilewskija (Ws-2) ecotypes were used. The atx1 mutant line containing a Ti insertion in the ATX1 gene in the Ws background (the atx1-1 allele) is as described in Alvarez-Venegas et al. (2003). Amplified DNA sequences from the promoter region of the ATX1 gene were cloned in the pCambia1303 vector (Canberra, Australia) after substituting the original 35S promoter with the desired experimental sequence. Constructs were verified by sequencing and transgenic GUS-expressing lines were generated by the dip-infiltration method. Details are described in Saleh et al. (2008). All plants were grown in parallel and were handled under exactly the same conditions. Plants were grown in the greenhouse for 3 weeks under a regimen of 12/12 h light/dark at 24 °C and a relative humidity between 50–60%.

Sample preparation

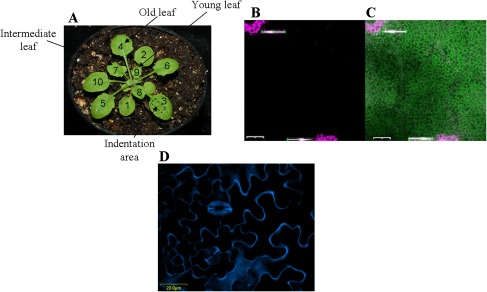
Rosette leaves were numbered and analysed according to their appearance reflecting their age, as shown in Fig. 1A. Selected leaves were detached from the stem with a thin blade and an area of estimated 7.09 mm² on the abaxial (lower) side of the leaf (as shown in Fig. 1A) was used for the measurements. The density of trichomes on the abaxial epidermis is lower (Cardoso, 2008) and our estimates indicated approximately three times higher trichome density on the adaxial than on the abaxial sides for the areas used in the experiments. Furthermore, to ensure a better contact between the sample holder and the leaf tissue, the trichomes of the upper epidermal side were gently removed with a razor blade under a low magnification stereoscope, as described by Ntefidou and Manetas (1996). The upper side of the leaf was adhered to a metallic plate using a double-sided carbon tab. The plate was then mounted to the sample holder of the nanoindentation instrument. To avoid possible changes in the molecular orientations within the wall due to drying, a drop of water was placed on the surface of the leaf during measurements.

Fig. 1.

Rosette leaves used in the nanoindentation measurements and cell viability after indentation. (A) Three-week-old Arabidopsis Col plant. Rosette leaves are numbered according to the stage (age) of development. Leaves 4 (old), 7 (intermediate), and 9 (young) were used. Nanoindentation measurements were made on the abaxial side in the indicated area. (B) Confocal micrograph of leaf cells stained with the viability assay kit show needle-damaged cells fluorescing magenta (arrows). Nanoindentation measurements were made between the large holes. (C) Merged image of the FDA-PI detection. Nanoindented cells are viable, fluorescing in green (the scale bars are 200 μm). (D) Confocal micrograph of cells of a young leaf stained with fluorescent brightener 28 shows cells boundary (the scale bar shown is 20 μm).

Viscoelasticity studies of plant cell walls

The nanoindentation tests were performed at room temperature using a Hysitron Bio-Ubi^® nano dynamic mechanical analysis (nano DMA) system with a 120° angle Berkovich indenter tip (a three-sided pyramidal tip; note that it does not have a perfect point in the atomistic sense). The dynamics of the tip were first calibrated within the drop of water on the surface of the leaf. After calibration, the tip was engaged with the sample and loaded to a quasistatic load of 40 μN at a rate of 15 μN s⁻¹. Superposed on this load was a dynamic load of 0.4 μN covering a frequency range of 10–250 Hz. When the sweep was complete, the sample was unloaded at a rate of –15 μN s⁻¹. Note that the amplitude and phase during the frequency sweep were used to determine the storage and loss moduli (equations 3–4). As plant cell walls are composed of a hydrated polymer network in which water may account for up to 70% of the volume of a primary wall (Rose, 2003), the extension state of the cell wall material is dependent on the water content (Wilson et al., 2000). To avoid possible changes in the molecular orientations within the wall due to drying, all measurements were made using a drop of water placed on the leaf surface.

Cell viability assays

The viability of cells was determined by using the plant cell viability assay kit (Sigma Aldrich PA0100) containing a dual-colour fluorescent staining system: fluorescein diacetate (FDA) and propidium iodide (PI) to highlight viable and non-viable cells, respectively. Cell staining with the viability assay kit was observed with a confocal microscope (Olympus FluoView 500 mounted on an Olympus BX60 compound microscope). The wavelength for excitation of FDA is 488 nm and detected between 505–525 nm; the 488 nm laser was from a mixed gas laser (Krypton, Argon, and Helium). The wavelength for PI excitation was 543 nm and detected between 560–600 nm (Fig. 1B, C).

Estimation of cell size

Rosette leaves were stained by using the fluorescent brightener 28 (F3543 Sigma Aldrich) that binds to the cellulose of cell walls. Leaves were observed with a confocal microscope (Olympus FluoView 500 mounted on an Olympus BX60 compound microscope) (Fig. 1D).The dye fluoresces (peak emission wavelength 450 nm) when excited with UV or near-UV light (optimum excitation wavelength 347 nm). The size of the cell was determined by drawing circles within the lobes of the cells.

Estimation of the cell wall thickness

Sections of three leaves per age and genetic variance were prepared following the protocol of Paparozzi (1981) and observed at a resolution of 30k using a Hitachi H7500 TEM with a W95/NT-based computerized operating system for ultrastructural analysis on sections of sample. Pictures at the left-end, middle, and right-end of the cell wall of different epidermal cells were captured for the different sections of each leaf. Overall, a total of more than 150 images have been analysed for the results reported here. The wall thickness was determined by drawing a tangent to the outer side of the cell wall and then by measuring the amount of cell wall material perpendicular to the tangent. The thickness of the cell wall was estimated at 10 different locations on each picture. The values presented in Table 1 represent the average of at least 100 measurements. Example TEM images are shown in Supplementary Fig. S4 at JXB online.

Table 1.

Summary of the results (mean ±confidence interval: 95% confidence level) for the thickness of the cell wall of leaves according to age and genetic variance.

		Cell wall thickness (nm)
Col	Young leaves	771±101
	Intermediate leaves	664±84.9
	Old leaves	1290±125
WS	Young leaves	667±93.9
	Intermediate leaves	604±80.1
	Old leaves	604±102
ATX1	Young leaves	442±26.7
	Intermediate leaves	452±33.6
	Old leaves	694±196

Estimation of turgor pressure

The turgor pressure of cells was estimated using a psychrometer (HR-33T) since the size of the cells of Arabidopsis prohibits the use of a pressure probe. The probe is a widely used method to quantify accurately and directly turgor in single cells with a diameter greater than 20 μm (Hüsken et al., 1978). An earlier study (Nonami et al., 1987) demonstrated the successful use of a psychrometer to measure accurate values of turgor pressure in tissue not accessible by a pressure probe. The thermocouple chamber was successively loaded with five intermediary leaves from the two ecotypes as well as five leaves per age for the mutant. The water potential, ψ_w, was measured by the dew point method. Immediately after this measurement, the tissue was frozen in liquid nitrogen and thawed in order to estimate the osmotic pressure, ψ_s, within the same tissue using the same technique. The turgor pressure was obtained indirectly by subtracting ψ_s from ψ_w. The turgor pressure values are presented in Table 2.

Table 2.

Summary of the results (mean ±confidence interval: 95% confidence level) for the turgor pressure of the cells according to age and genetic variance

		Turgor pressure (MPa)
Col	Intermediate leaves	0.18±0.09 (immediately after excision of the leaf)
		0.06±0.05 (2 h after excision)
WS	Intermediate leaves	0.23±0.17
ATX1	Young leaves	0.18±0.05
	Intermediate leaves	0.13±0.04
	Old leaves	0.13±0.03

Image analysis

Image analysis was performed on confocal images of leaves stained with the fluorescent brightener 28 in order to determine the probability that the nanoindenter tip makes contact with anticlinal walls or guard cells (undesired regions). The undesired area was assessed by measuring the ratio of the area of the cell wall and guard cells to the whole area using ImageJ analysis software and the modified protocol of Straatman (2008). First the image scale was set using the known micron/pixel values (Analyse→Set Scale). Next the brightness and contrast was adjusted using the ‘Image→Adjust brightness, contrast’. Then, the image was inverted using ‘Edit→Invert’ followed by ‘Process→Make binary’ to change the image to a binary format. The guard cells and anticlinal walls were filled in black colour using a paint brush tool. Finally, the undesired area (black to white ratio) percentage was quantified using the ‘Analyse→Measure’ tool.

Statistical analysis

A two-tailed paired Student’s t test was applied to the results to quantify the significance of the changes in the stiffnesses with respect to the frequency as well as the significance of the stiffnesses changes with respect to the age of the leaf sample and genetic variation for specific frequencies. Specifically, changes with respect to frequency were quantified by pairing the frequencies for each stage of development and for each species. Also, in order to detect the changes with respect to age, the age results were paired (young–intermediate, intermediate–old, young–old) for each frequency and each genetic variation. Finally, in order to obtain the influence for the change of stiffness with respect to the genetic variation, the species were paired for each specific frequency and stage of development.

Each data point is given within a confidence level of 95%. The confidence level chosen gives the cell wall stiffness when the indenter was placed near the centre of pavement cells. Thus it excludes the values from the indentations made near guard cells or anticlinal walls for instance (the probability to indent those areas is 15–20%). NanoDMA curves that were more than three standard deviations from the mean were excluded and attributed to poor indenter placement.

Results

Nanoindentation measurements

The viscoelastic parameters of cell walls of single cells were measured in leaves at three different developmental stages in two ecotypes, Col and Ws plants, as well as in the atx1 mutant background. Examined cells were from leaves defined as young (leaf 9), intermediate (leaf 7), and old (leaf 4), as indicated in Fig. 1A, reflecting the order of their appearance after the cotyledons. Possible changes in the cell wall viscoelasticity were measured in cells within the same area on the abaxial (lower) side of leaves at the indicated developmental stage (see Materials and methods). The dynamic nanoindentation tests (nanoDMA) were performed over the frequency range from 10–250 Hz. The frequency range was chosen so that the viscoelastic properties of the cell wall can be investigated over a short time-scale for comparison with other plant tissue experiments made using quasi-static methods. It is important to note that the quasi-static and dynamic loads were determined for an appropriate indentation depth. This depth must be large enough to minimize surface effects (for consistent results; Oliver and Pharr, 1992), but small enough so that effects from turgor pressure are also minimal. For this purpose, the wall thickness for all examined samples was determined using cross-sectional images of the cell walls from a (TEM) transmission electron microscope (see Materials and methods). The thickness for all samples varied from 200 nm to 1500 nm (with an average of 800 nm). The thickness results for the different genotypes and the different ages are given in Table 1. The thickness of the Arabidopsis leaf cuticles was estimated to be about 25–30 nm (Nawrath, 2006). Based on experimental and published data, the indentation depth was restricted to approximately 110 nm. To ensure reproducibility of the measurements, 10 indents were performed per leaf and five leaves per age and per genotype were characterized. Overall, more than 750 single indentations comprise the analysis set for the results presented with an indentation depth of 109.74±7.45 nm. For clarity, the comparison of single-point storage and loss stiffness values was made only for 113 Hz. However, the conclusions extracted from the analysis at 113 Hz can be applied over the whole range of frequency.

Cell viability after indentation

To assess the impact of the dynamic nanoindentation (nanoDMA) tests on cell viability, a set of initial measurements was performed using a plant cell viability staining assay (see Materials and methods; Fig. 1B, C). Two large holes were made with a needle to induce clear damage on the specimen to serve as positive indicators of cell damage. A series of dynamic nanoindentation tests were performed between those two holes using positioning through the optical microscope. Staining with the dual colour fluorescent system highlights viable and non-viable cells: the cells damaged by the needle are clearly non-viable (fluoresce bright magenta), while the cells in between on which the nanoDMA tests were performed fluoresce green, indicating that no damage was induced from these nanoindentation measurements.

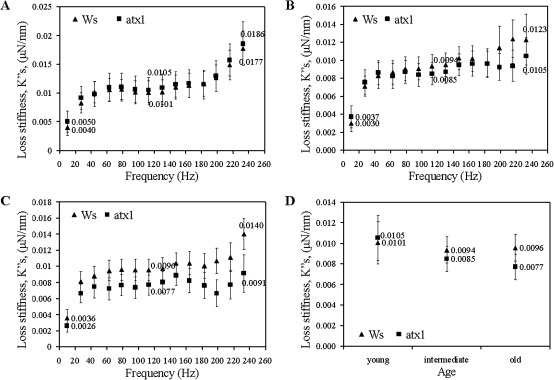
Storage stiffness profiles in the Columbia (Col) and Wassilewskija (Ws) ecotypes

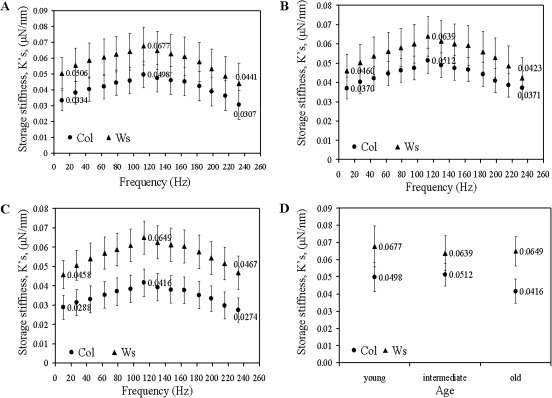
The storage stiffness $K_{\text{s}}^{\prime }$ was determined as a function of frequency for young, intermediate and old leaves in the Col and Ws varieties, respectively (Fig. 2A–C). The values of the storage stiffness for Ws are significantly higher (p <0.05) than the Col stiffness in the cells at all three tested developmental stages (Table 3). These results indicate higher stiffness of the walls of Ws than of Col cells. The difference is even more pronounced for the aged leaves, as the greatest difference in $K_{\text{s}}^{\prime }$ values is observed in the cell walls of the oldest leaves (Fig. 2C, D; Table 3).

Fig. 2.

Changes in the storage stiffnesses, $K_{\text{s}}^{\prime }$, of cell walls of the Col and Ws leaves: (A) young; (B) intermediate; and (C) old leaves. (D) Age-dependent differences in the storage stiffnesses at 113 Hz.

Table 3.

Summary of the results (mean ±confidence interval: 95% confidence level) for age and genetic variance at 113 Hz for both the storage and loss stiffnesses

		Storage stiffness, $K_{\text{s}}^{\prime }$ (μN nm−1)	Loss of stiffness, $K_{\text{s}}^{\prime \prime }$ (μN nm−1)
Col	Young leaves	0.0498±0.0085	0.0072±0.0011
	Intermediate leaves	0.0512±0.0064	0.0059±0.0007
	Old leaves	0.0416±0.0071	0.0058±0.0007
WS	Young leaves	0.0677±0.0119	0.0101±0020
	Intermediate leaves	0.0639±0.0102	0.0094±0.0013
	Old leaves	0.0649±0.0086	0.0096±0.0013
ATX1	Young leaves	0.0764±0.0157	0.0105±0.0022
	Intermediate leaves	0.0678±0.0089	0.0085±0.0012
	Old leaves	0.0525±0.0078	0.0077±0.0012

Another interesting observation is the similar pattern of age-related alterations in wall stiffness displayed by the ecotypes: the $K_{\text{s}}^{\prime }$ values vary slightly for young (no. 9), intermediate (no. 7), and old (no. 4) leaves both in the Ws and the Col samples (Fig. 2A–D).

In summary, nanoscale analysis uncovered significant changes in storage stiffness for the two ecotypes over the range of the examined frequencies. Both ecotypes display changes in viscoelasticity during development but the profiles of these changes are different. The walls of Ws leaf cells showed higher stiffness than Col suggesting structural variations in the organization of their cell walls. These may include differences in the material constituents and/or in the interaction of cell wall constituents with one another. Both ecotypes show a rather constant frequency-dependent behaviour of the cell walls with regard to the storage stiffness at all three leaf-developmental stages tested. At this point, our data do not allow us to conclude whether these differences reflect the volumetric concentrations of the material constituents in the cell wall, their structural interactions, or organization of the constituents.

Loss stiffness profiles in the Col and Ws ecotypes

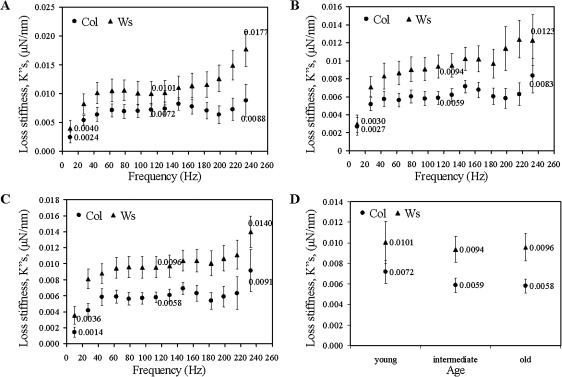
The cell walls of the Ws ecotype show higher loss stiffness, $K_{\text{s}}^{\prime \prime }$ (representing the loss of energy) than Col for the leaf samples at the three developmental stages (Fig. 3A–C). For Col, as well as for Ws, young, intermediate and old leaves loss stiffnesses are not significantly different (p >0.05 for nearly all frequencies). Again, the highest difference between the Col and Ws is with respect to the oldest leaf samples (Fig. 3D; Table 3).

Fig. 3.

Changes in the loss stiffnesses, $K_{\text{s}}^{\prime \prime }$, of cell walls of the Col and Ws leaves: (A) young; (B) intermediate; and (C) old leaves. (D) Age-dependent differences in the loss stiffnesses at 113 Hz.

Like the storage stiffnesses, both ecotypes display a rather constant frequency-dependent behaviour of the cell walls with regard to the loss stiffness at the three leaf-developmental stages tested. The origin of this dependence pattern is unknown at present.

Sensitivity of nanoDMA for detecting cell wall changes

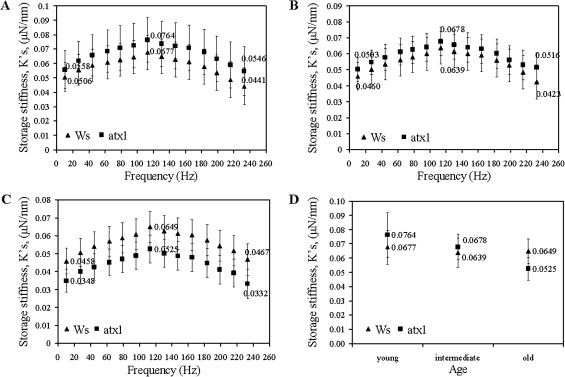
Next, the applicability of nanoindentation for detecting potential differences in the viscoelastic properties of the walls in cells deficient in activity of a known regulator of wall-modifying genes is tested simply as a demonstration of the sensitivity of the nanoDMA technique—no conclusive biological inferences can be made at this time. In atx1 mutants (the mutant allele is in the Ws background; Alvarez-Venegas et al., 2003) ∼80 genes encoding wall-modifying activities showed aberrant expression due to the loss of ATX1 function (Alvarez-Venegas et al., 2003; Ndamukong, et al., 2009). Interestingly, in young leaves, no significant differences in storage stiffness (p >0.05) were detected between the walls of the wild type Ws and the atx1 cells over the entire range of frequencies (Fig. 4A). By contrast, significant differences between the mutant and wild-type cell walls are displayed later in development. In wild-type cells, wall stiffness remained relatively constant in the young, intermediate, and older leaves. However, the properties of atx1 cell walls shows an erratic pattern deviant from ATX1 cells: storage stiffness values are higher in intermediate leaves but lower in the older leaves than the storage stiffness measured in the in the Ws ecotype (Fig. 4B–D; Table 3).

Fig. 4.

Changes in the storage stiffnesses, $K_{\text{s}}^{\prime }$, of cell walls of the wild type Ws and atx1 mutant leaves: (A) young; (B) intermediate; and (C) old leaves. (D) Age-dependent differences in the storage stiffnesses at 113 Hz.

Significant differences in loss stiffness parameters are observed with respect to the stage of development of the leaves for the atx1 cell walls as well (Fig. 5A–D). Subsequent to higher damping in the younger leaves, the cell walls of the oldest atx1 leaves show a significant drop in $K_{\text{s}}^{\prime \prime }$ values deviating from the behaviour of wild-type cell walls at this developmental stage (Fig. 5C, D; Table 3). Thereby, the perturbed properties reflected by both the $K_{\text{s}}^{\prime }$ and $K_{\text{s}}^{\prime \prime }$ values in atx1 cell walls illustrate the important contribution of ATX1 in maintaining the stability of these characteristics during leaf maturation in the wild-type Ws. It is relevant to note that the expression profile of ATX1 also changes in an age-dependent pattern: newly emerging leaves show low ATX1-expression levels, while senescing tissues show an increasing ATX1 promoter activity (Fig. 6; also see Saleh et al., 2008). It is also relevant to mention that a similar dependence of the expression pattern on the stage of the leaf emergence has been reported for another gene regulated by ATX1, ACS7 (Wang et al., 2005) suggesting that a variable expression of a gene in developing rosette leaves might be a more general feature in Arabidopsis. Capturing this trend, as reflected by the viscoelastic properties of the cell wall is particularly exciting (Fig. 5A–D) because it illustrates the sensitivity of this technique. It is capable of registering abnormalities caused by misregulation of a multitude of genes implicated in wall remodelling functions.

Fig. 5.

Changes in the loss stiffnesses, $K_{\text{s}}^{\prime \prime }$, of cell walls of the wild type Ws and atx1 mutant leaves: (A) young; (B) intermediate; and (C) old leaves. (D) Age-dependent differences in the loss stiffnesses at 113 Hz.

Fig. 6.

Expression of the GUS gene under the ATX1 promoter in transgenic plants stably expressing the P-ATX1::GUS construct during Arabidopsis development. (A) Young seedlings showing strong staining of cotyledons but not in the younger first true leaves Strong staining of the shoot apical meristem and vasculature suggest high expression of the ATX1 gene throughout development. (B) In maturing plants, older rosette leaves show activation of the ATX1 promoter but not in newly emerging leaves (leaves 9 and 10 are indicated by the arrowhead and arrow, respectively). (C) Closer look at the newly emerged leaves 9 and 10 indicated as in (B). Note the strong staining of the tip of the shoot meristems.

Quantification of the cell wall properties

The storage and loss stiffness, $K_{\text{s}}^{\prime }$ and $K_{\text{s}}^{\prime \prime }$ reported above come directly from the dynamic nanoindentation measurements without the need for additional assumptions. These quantities may be functions of the cell wall storage and loss moduli, E′ and E′′, cell wall thickness, and turgor pressure, a dependence that is related to the depth of the measurements. In this section, the computational model (FEM) is used to interpret the measurements. The preliminary finite element simulations (see Supplementary Fig. S5 at JXB online) showed that, for a depth of 110 nm, the exact computational contact radius is at most 9% different from the contact radius calculated using the projected-area method (see Fig. 8). Therefore, the modulus values were determined from the experimental storage/loss stiffness and the contact area from the projected-area method using equations (5) and (6). In the model, the uncertainties of the moduli values were quantified with respect to variations in cell wall thickness and turgor pressure.

Fig. 8.

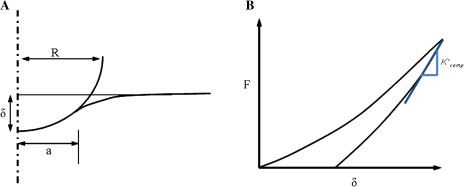
Indentation definitions. (A) Definition of contact radius, a, from the Hertzian contact theory: δ is the deflection, R is the radius of the indenter. (B) Determination of contact stiffness $K_{\text{comp}}^{\prime }$ from initial slope of a line tangent to the unloading curve, where F is the applied load. The tangent is projected back to the zero load intersection from which the contact area at the moment of unloading is estimated (Fischer-Cripps, 2004). (This figure is available in colour at JXB online.)

The analysis was performed in various steps as shown in Fig. 7. In the first step, the turgor pressure p was applied at the bottom face of the disc such that the cell wall deforms in the shape of a hemisphere. Since the cell wall is viscoelastic, the pressure was applied for enough time in the simulation for the wall to relax fully in order to create a model condition representing that of a plant cell in vivo (although it should be recognized that the zero pressure state of a real plant cell wall is not likely to be flat, as assumed here). After this step, the indenter contacted the cell wall and began the load and unload procedure to the prescribed depth. The slope of the tangent to the load-displacement curve (Fig. 8) at the beginning of the unloading segment, the maximum indentation load, defined the computational storage stiffness $K_{\text{comp}}^{\prime }$. The tangent was projected back to zero load from with the ‘projected-area’ contact radius (a) was calculated (Fischer-Cripps, 2004). The computational storage stiffness and contact area can then be used to determine the modulus using the procedure described above.

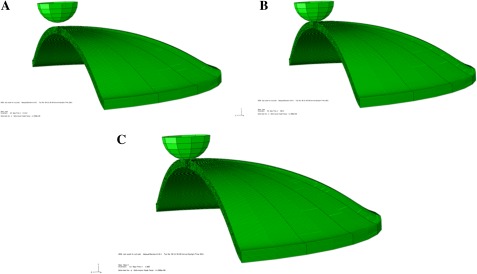
Fig. 7.

Steps used in performing the finite element simulation. (A) Turgor pressure is initially applied; (B) cell wall relaxes fully; (C) indenter in contact with the cell wall at 110 nm indentation depth. All images shown are made by revolving the axisymmetric model about the symmetry axis. Thus, the 3D images shown should not be misinterpreted—the model used is axisymmetric.

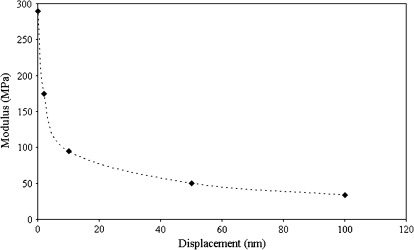
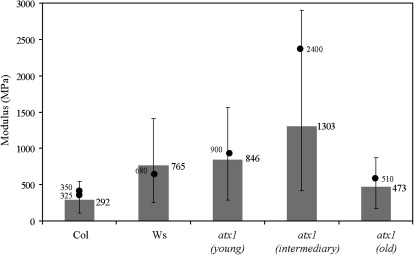
Since the purpose of the simulations was to quantify the influence of the indentation depth on the modulus estimation, the simulations were repeated at the measurement depth (110 nm) for different values of the cell wall modulus until the simulation modulus matched the experimental value. An example result is shown in Fig. 9 (Col). For this example, the experimental modulus estimation was ∼34 MPa for a measurement made at 110 nm (the modulus at this depth is referred to here as the ‘apparent measured modulus’ because it includes effects from wall bending and turgor pressure). This process results in an estimated cell wall instantaneous modulus of E′=292 MPa (Col) for a cell wall thickness of 500 nm and pressure of 0.2 MPa. Three important aspects of the simulations can be observed from Fig. 9. First, it is clear that the use of very shallow depths allows the cell wall modulus to be recovered without the need for any approximations. Unfortunately, the nanoindentation technique is not reliable at such shallow depths for plant cells due to surface effects. Second, it is clear that the wall modulus can be severely underestimated if the thickness and turgor pressure are not included in the analysis. It is also clear from Fig. 9 that the depth dependence is a critical factor for accurate extraction of wall modulus and that this depth dependence is related to thickness and turgor pressure (i.e. a thinner wall and lower turgor pressure result in a larger indentation depth).

Fig. 9.

Change of the apparent measured storage modulus from nanoindentation with respect to displacement depth as determined from the FEM simulations. The cell wall instantaneous modulus in the model is varied to match the value at ∼110 nm (values that are matched are shown in Table 4). Depths that approach zero allow recovery of the modulus input into the model. Deeper values reflect a combination of factors including the cell wall modulus, thickness and turgor pressure.

Moduli profiles of Col, Ws, and atx1

The instantaneous modulus of the cell wall was estimated using the experimental measurements in conjunction with the computational simulations. The procedure described above was used for all experimental measurements. The measured storage and loss stiffness were used directly with the projected-area approximation for contact radius to determine the storage and loss moduli E′ and E′′, from equations (5) and (6), for the given measurement depth. These intermediate results are shown in Table 4. Then the computational model was used in the iterative manner described above, by adjusting the wall modulus, until the simulation results match the experimental at the measurement depth of 110 nm. The iterative simulation procedure is repeated for the range of thickness values from 400–1000 nm consistent with the literature (Rezvani and Wilman, 1998) and are in the range of Table 1 determined from TEM. In addition, the analysis with respect to turgor pressure covers the range of 0.1–0.5 MPa which again is consistent with values from the literature (Green et al., 1971; Martin et al., 2004; Geitmann, 2006) and from pressure measurements (Table 2). Due to the uncertainty in turgor pressure and thickness, the simulations were performed for the two extremes in the range of values (t=400 nm, p=0.1 MPa; and t=1000 nm, p=0.5 MPa). The wall modulus is changed until the simulation matched the experimental measurements at 110 nm depth. The wall modulus for Col for these two particular cases were 540 MPa and 110 MPa, respectively. An additional simulation was performed at t=500 nm and p=0.2 MPa which gave a modulus of 293 MPa—a value that is close to an average of the two extremes considered. The cell wall modulus estimates for all leaf samples are shown in Fig. 10 for which the average modulus is for t=500 nm, p=0.2 MPa and the error bar corresponds to the two extreme cases (t=400 nm, p=0.1 MPa; t=1000 nm, p=0.5 MPa). These results exhibit similar trends as observed for the raw experimental data (results for Ws and Col are shown without age distinction since the differences shown in Table 4 are not significant). The Ws modulus is higher than Col. In addition, the result for young atx1 leaves is the same as the background (Ws), but a clear change with age is observed.

Table 4.

Summary of the results (mean ±confidence interval: 95% confidence level) for age and genetic variance at 113 Hz for both the storage and loss moduli The storage (E′) and loss (E′′) moduli are calculated from equations (5) and (6) for measurements at ∼110 nm (‘apparent measured moduli’ for which the pressure and thickness effects have not yet been corrected).

		Storage modulus, E′(MPa),	Loss modulus, E′′(MPa)
Col	Young leaves	38.9±7.6	5.7±1.0
	Intermediate leaves	35.8±6.0	5.8±1.3
	Old leaves	27.6±6.2	4.0±0.9
WS	Young leaves	66.0±14.3	9.0±1.7
	Intermediate leaves	64.8±15.0	9.6±2.0
	Old leaves	69±12.4	10.5±2.0
ATX1	Young leaves	69.8±20.2	10.2±3.0
	Intermediate leaves	94.4±28.4	11.7±3.7
	Old leaves	50.5±14.8	7.4±2.3

Fig. 10.

Estimated modulus of the cell wall from the procedure defined in the text. The modulus of the cell wall used in the finite element model (shown in this plot) is varied until the apparent measured modulus at the ∼110 nm depth matches the results given in Table 4. No age distinction is made for Col or Ws since those differences are not significant. The error bar shows the extreme range of values for turgor pressure and thickness (t=400 nm, p=0.1 MPa; t=1000 nm, p=0.5 MPa) with the average at t=500 nm, p=0.2 MPa. The modulus of the cell wall is also estimated (shown by dots) for all the leaves using thickness values obtained from TEM images (Table 1) and turgor pressure measurements obtained from thermocouple psychrometer (Table 2).

Consistency of the model predictions

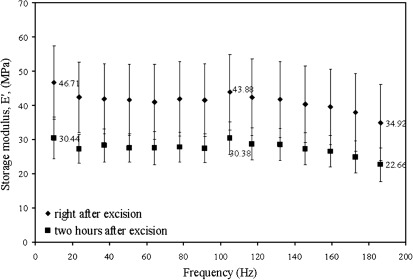
To verify that the derived cell wall modulus by the procedure described here corresponds to a true predictive value and is independent of thickness and turgor pressure, additional experiments were performed. NanoDMA was performed on intermediate leaves of the Columbia ecotype (since no age-dependent storage modulus was observed) for two different values of turgor pressure (Fig. 11). The leaves were tested in air when freshly excised and then 2 h after excision. Within those two hours, dehydration of the leaves occurred which led to a change of turgor pressure. At 117 Hz the value of the apparent measured storage modulus (at 110 nm depth) was 43.88±11.01 MPa when tested right after excision and 30.38±4.71 MPa when tested 2 hours after excision. Using a thermocouple psychrometer, the turgor pressure of the leaves was estimated to be 0.18±0.09 MPa right after excision and 0.06±0.05 MPa 2 h after excision (Table 2). Using the thickness of Col from Table 1 as 750 nm and the turgor pressure as 0.18 MPa and 0.06 MPa, respectively, the cell wall modulus was estimated for freshly excised Col sample in air and 2 h after excision by fitting the experimental values of modulus at the 110 nm depth. The modulus values obtained were 350 MPa and 325 MPa (shown by two dots in Fig. 10 for Col) which are in the range of values from the other measurements suggesting that cell wall properties are affected only slightly by the change in turgor pressure. The small change may indicate a reaction to the osmotic stress, but no conclusions can be drawn from the limited data set. Similarly, the estimation of the wall modulus was performed for all the leaves using thickness values obtained from TEM images shown in Table 1 and turgor pressure measurements obtained from thermocouple psychrometer shown in Table 2 and fitting the modulus obtained at 110 nm depth as shown in Table 4. The wall modulus obtained (shown by dots for Ws and atx1) in Fig. 10 are again in the range of the other values showing the self-consistency of the approach. The turgor pressure plays a much larger role in our measurements in contrast to data reported by Milani et al. (2011), possibly due to the much larger contact area here relative to the wall thickness.

Fig. 11.

Changes in the storage moduli, E′, of cell walls of the Col immediately after excision and 2 h after excision of intermediate leaves.

Discussion

Using the nanoDMA technique, changes in viscoelastic properties of the cell walls of two Arabidopsis ecotypes and of a mutant in the Ws background have been measured. The results demonstrate that this technique can clearly capture differences in cell wall properties. In addition, by combining nanoDMA and FEM, a quantitative approximation of the plant cell wall modulus has been established. Earlier work on the giant alga Nitella and Chara corallina cell wall (Probine and Preston, 1962; Toole et al., 2001) produced values of 400–1000 MPa for longitudinal tensile modulus. Available information on Arabidopsis wild-type hypocotyl cell wall indicates a tensile modulus ranging from 21.3–27.5 MPa (Ryden et al., 2003). Although these values are in a much lower range than those obtained for the ecotypes here (Fig. 10), it must be recognized that their results represent the tissue-scale response. In addition, the values shown here are much lower than the Young’s modulus established for cotton fibres (∼10 GPa) (Huber and Mussig, 2007), which are nearly pure cellulose. The lower modulus values obtained under uniaxial loading or under nanoindentation reflect the complex three-dimensional arrays of microfibrils, as well as the presence of additional architectural and gel components, in the walls of Arabidopsis cells.

All changes in cell wall properties are statistically significant and are observed over the entire range of frequencies tested for the storage moduli. Some variations in individual measurements may be attributed to the nature of the samples, representing living cells as opposed to detached or dead tissues, and/or to local irregularities in wall thickness along the lower epidermis.

The data obtained by the nanoDMA technique revealed unsuspected differences in cell wall properties of the Col and Ws varieties displayed at each of the three developmental stages examined. These results are particularly intriguing as they suggest still unknown structural and/or compositional variations in their cell walls, either in the organization of the material constituents (orientation of the polymeric network according to the frequency) or in the interaction of cell wall constituents with one another. Because the cell wall is a composite, the mechanical behaviour of such a polymeric network is significantly affected by the orientation of the cellulose microfibrils—a response that may have a strong frequency dependence. It would be of great interest to analyse, for instance by micro X-rays, the possible change in orientation of the fibrils in the wall during loading and to relate those observations to the force-displacement behaviour from nanoindentation using a more comprehensive anisotropic material model.

The technique was also shown to be sensitive to differences in properties of one particular Ws mutant. The significant differences in moduli in the walls of atx1 mutant cells revealed the importance of ATX1 in maintaining the biomechanical properties of the wall, consistent with its regulation of wall-modifying genes. Over 400 proteins are implicated in cell wall biogenesis and wall remodelling including organization, loosening, and rearrangement of the polysaccharide networks [Arabidopsis Genome Initiative (AGI), 2000]. Among them, a subfraction of ∼80 genes encoding cell wall-associated proteins are regulated by ATX1 (Alvarez-Venegas et al., 2003) in a development- and/or tissue-specific manner (Saleh et al., 2008; Ndamukong et al., 2009). Of particular importance are the results showing that the same wall-remodelling factor may also have opposite effects upon cell wall behaviour making walls stiffer or looser (Chanliaud et al., 2004; Saladié et al., 2006). They indicate that the genetic interactions among the genes encoding various components of the wall and their regulation by ATX1 activity are complex and that the effects on the wall phenotype and behaviour are not straightforward. However, regardless of what biological factors underlie the ATX1 leaf stage-specific expression pattern (Fig. 6), loss of a functional ATX1 causes aberrations in the viscoelastic profiles of the wall that correlate with the ATX1 expression patterns (Figs 4A–D, 5A–D). The demonstration that these aberrations can be captured by the nanoindentation technique is another exciting result of this study.

Conclusions

The nanoidentation technique, in conjunction with the finite element method (FEM), provides a sensitive combination for quantifiable measurements of the time-dependent response of a material representing a combination of viscoelastic properties, in a living single cell at a nanometer scale. Differences in cell wall stiffness and damping were detected in cells of the wild-type Col and Ws varieties and the perturbations in the cell wall viscoelastic properties resulting from the loss of ATX1-function were measured, demonstrating the power of the technique. Although the indentation depths here were kept small (∼110 nm), it is clear from the simulations that effects from the wall thickness and turgor pressure are important factors that must be considered when the modulus estimation is made. Other factors, such as the orientation of the fibrous cellulose infrastructure in the cell walls, are involved as well and will require further studies.

Supplementary data

Supplementary data can be found at JXB online.

Supplementary Fig. S1. Schematic of the nanoindentation system and a mechanical model for the dynamic behaviour of the nanoindenter-sample system.

Supplementary Fig. S2. Finite element axisymmetric model for a plant cell wall subjected to turgor pressure and indentation load.

Supplementary Fig. S3. Apparent measured modulus at 110 nm depth as a function of the radius of the cell used for the finite element model for various values of thickness (t) and pressure (P), and wall modulus (E) for both a conical (blue circles) and spherical indenter (all other symbols).

Supplementary Fig. S4. Transmission electron microscope (TEM) images. (A) Two adjacent walls of an old Columbia leaf (×15k; the scale bar is 1 μm); (B) wall of an old WS leaf (×30k; the scale bar is 0.5 μm).

Supplementary Fig. S5. Contact radius for a spherical indenter at a depth of 110 nm as a function of turgor pressure (p) and cell wall thickness (t).